Материалы по физике

Опыт Дэвиссона - Джермера

Любая гипотеза, как бы она ни была привлекательна и правдопо- добна, остается гипотезой до тех пор, пока она не подтвердится опы- том. Только прямые опыты, в которых отчетливо проявлялись бы вол- новые свойства частиц, могли бы подтвердить правильность идеи де Бройля.

В 1922 г. по заказу американской фирмы "Белл-телефон" Клинтон Джозеф Дэвиссон (1881–1958) и его сотрудник Кансмен изучали от- ражение электронов от поверхности металла и при этом обнаружили какие-то аномалии. В 1925 г. Дэвиссон, находясь в Европе, показал

свои графики Максу Борну, Джеймсу Франку (аспиранту Борна) в Геттингене и Дугласу Хартри в Оксфорде.

Все они признали, что аномалии на графиках свидетельствуют о проявлении волновых свойств электронов, т.е. волн де Бройля, хотя и не убедили в этом Дэвиссона. Вскоре после возвращения в Америку в экспериментальной установке Дэвиссона во время работы случилась авария: треснула вакуумная трубка, и нагретый в это время поликри- сталлический Ni под действием кислорода воздуха окислился. После восстановления установки и прокаливания образца в вакууме иссле- дования совместно с Лестером Альбертом Джермером (1896–1971) были продолжены. Вскоре выяснилось, что спектр отраженных элек- тронов имеет отчетливо выраженные интерференционные максиму- мы. В результате к концу 1927 г. они убедились в реальности сущест- вования волн материи. Но еще в 1925 г. студент М. Борна Вальтер Эльзассер, получив задание разобраться с этим явлением, предполо- жил, что аномалии на графиках Дэвиссона объясняются электронны- ми волнами де Бройля. Он послал в журнал краткую заметку, в кото- рой объяснил результаты опытов Дэвиссона и Кансмана дифракцией волн материи. Однако на эту заметку тогда никто не обратил внима- ние.

Схема экспериментальной установки Дэвиссона представлена на рис. 1.2.1.

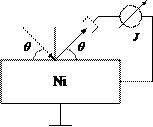Рис. 1.2.1. Схема установки Девиссона

Если теперь при заданном значении угла скольжения θ и полярно- го угла менять энергию первичных электронов, то график должен иметь вид, изображенный на рис.2.2.2.

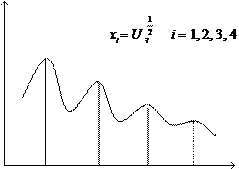I

Рис. 1.2.2. Интерференция картины электронов

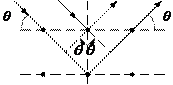
1      2

Рис. 1.2.3. Модель интерференции волн в кристалле

Известно, что монокристалл Ni можно представить в виде сис- темы кристаллографических плоскостей. Если принять, что отражение волн материи происходит от кристаллографических плоскостей, то в результате интерференции волн максимум отраженной волны будет возникать в случае разности хода лучей, кратной длине волны (рис. 1.2.3). Из рис. 1.2.3 следует, что разность хода у интерферирующих лучей 1 и 2

  2d sin  .

Отсюда

2d sin   m,      m  1, 2, 3, ... ,       (1.2.1)

где d – межплоскостное расстояние, θ – угол скольжения. Если счи- тать, что гипотеза де Бройля правильна, то длина волны

и после подстановки в (1.2.1) получаем:

12,3 10^10

12,3 10^10

2d sin   m

⎛ U 2 ⎞ 2

;

1

⎛ U3 ⎞ 2

 mc1 ,

1

⎛ U 4 ⎞ 2

c1 

2d sin  ;

⎜      ⎟

⎝ U1 ⎠

 2 ;

⎜      ⎟

⎝ U1 ⎠

 3 ;

⎜      ⎟

⎝ U1 ⎠

 4 .

Таким образом, возникновение максимумов на экспериментальных графиках следует рассматривать как результат интерференции волн неизвестной пока природы, которые связаны с движущимся электро- ном в пространстве. Значит, движение электронов в пределах кри- сталлической решетки можно рассматривать как волновой процесс.

Наличие экспериментально наблюдаемых максимумов и миниму- мов и их правдоподобное объяснение является доказательством пра- вильности гипотезы де Бройля о наличии в природе волн материи. Как оказалось впоследствии, волновыми свойствами обладают не только электроны, но и любые микрочастицы.

Скачано с www.znanio.ru