Материалы по физике

             Физический смысл волновой функции

 

Физический смысл волновой функции раскроем на примере опти- ческого явления, последовательно рассматривая его с волновой и кор- пускулярной точек зрения.

Допустим, что экран освещается пучком параллельных лучей мо- нохроматического света. Площадь поверхности экрана равна S. Пусть на поверхность экрана за 1 с попадает N квантов.

Из уравнений Максвелла для электромагнитных волн следует, что энергия электромагнитных волн в равной степени определяется вели- чиной электрической и магнитной составляющей волны. Но при энер- гетическом взаимодействии потока электромагнитной волны с веще-

ством существенную роль играет лишь ее электрическая составляю- щая. Поэтому уравнение плоской электромагнитной волны будет иметь вид

E = E0e

- i (e t - p x)

h                  .

0

Известно, что энергетический поток излучения Ф для поверхности S пропорционален E₀² , где E₀ – амплитуда колебаний напряженности электрического поля в электромагнитной волне, падающей на поверх- ность S. Но так как, по определению, поток электромагнитной волны есть мощность электромагнитной энергии (энергии облучения по- верхности за 1с), то тот же поток равен числу квантов N, попадающих на поверхность S за 1с. Каждый квант несет энергию h , поэтому полная энергия, переносимая N квантами за 1с, будет N h . Следова- тельно,

Ф = a

1E ² = N × hn.

(1.4.1)

0i

Выделим теперь в пределах поверхности экрана S его элемент площади ∆s_i. На выделенный элемент площади ∆s_i будет падать энер- гетический поток ∆Ф_i, он пропорционален E_0i² и n_i, где E_0i – амплитуда колебаний напряженности электрического поля той части электромаг- нитной волны, которая падает на выделенный элемент площади экра- на, n_i – число квантов, которые падают на тот же выделенный элемент площади за 1с. Тогда имеем

 

Разделим (2) на (1):

DФi = a i E ²

= n i hn.

(1.4.2)

DФ    a E ²   n  hn      n

=   1    0i  =    i          = i .

(1.4.3)

Ф      N hn     N hn     N

Отношение n_i/N есть отношение числа благоприятных случаев, со- стоящих в попадании n_i квантов за 1с на выделенный элемент площа- ди ∆s_i, к общему числу наблюдаемых случаев, состоящих в том, что на всю поверхность экрана S за 1с попадает N квантов. Как известно из курса  высшей  математики,   это   отношение   (строго   говоря,   при ni ® 0 ) представляет собой вероятность осуществления данного со-

N

бытия. Так как n_i << N, то это отношение обозначим

dw = ni  << 1.

N

Тогда с учетом (1.4.3) имеем

dw = a E ² ,

2     0i

a   =    a1  .

2 N hn

Отсюда видно, что квадрат напряженности электрического поля в электромагнитной волне пропорционален вероятности попадания n _i квантов за 1 с на выделенный участок поверхности ∆s_i, т.е. мы при- шли к новой физической интерпретации амплитуды напряженности электрического поля электромагнитной волны.

Теперь воспользуемся понятием волновой функции. Вспомним, как мы ввели это понятие. Это понятие нами было введено на основе ана- логии, существующей между оптическими и электрическими явле- ниями, на основе существующей аналогии движения между потоком фотонов в пучке параллельных лучей и потоком свободных электро- нов. Для фотонов можем записать:

Ei = E0ie

-  i (e t - p x )

h                  ,

y = y0e

-  i (e t - p x )

h                  .

Из  сравнения  этих  двух  функций  мы  можем  заключить,  что ψ₀

0

0i

аналогично E_0i , ψ ² аналогично E  ². Так как волновую функцию  мож-

но применить не только к электронам, но и к фотонам, то примени- тельно к фотону E_0i² также аналогична ψ₀². Исходя из сказанного, мо- жем записать E_0i = a₃ψ₀ .

Тогда для фотонов имеем:

dw = a E ² = ay ² .

Но, кроме того, dω = a₄ds.

2    0i                 0

Заметим, амплитуда волновой функции ранее никак не была опре- делена, поэтому можно перейти от знака пропорциональности к знаку равенства, записав dω = ψ₀² ds.

2

Волновая функция – комплексная величина, следовательно,

 

 

0

Отсюда

y = yy* = y0e

-  i (e t - px)

h

× y0e

-  i (e t - p x )

h

= y².

y ² = dw.

ds

Итак, квадрат модуля волновой функции пропорционален вероят- ности попадания одного фотона на единицу площади участка облу- чаемой поверхности.

Очевидно, точно такой же физический смысл должна иметь волно- вая функция не только при описании потока фотонов, но и при описа- нии потока электронов и других микрочастиц. Подобное статистиче-

ское толкование волновой функции было предложено М. Борном (1882–1970) в 1926 г. И лишь в 1954 г. за статистическую интерпрета- цию волновой функции ему была присуждена Нобелевская премия.

Если теперь провести подобные рассуждения для пространствен- ного случая, т.е. поставить вопрос о том, какое число фотонов или других микрочастиц может находиться в микрообъеме dV в течение какого-то промежутка времени, то вероятность местонахождения микрочастицы в указанном микрообъеме dV будет определяться вы- ражением

dw = y ²dV ,

(1.1.4)

где dV = dxdydz, этот объем охватывает изменение координат от x до

x+dx, от y до y+dy, от z до z+dz.

Следовательно, в общем случае,

y ² = dw .

dV

(1.1.5)

Таким образом, |ψ|² есть плотность вероятности распределения микрочастиц в пространстве, это есть вероятность местонахождения микрочастицы в единице объема геометрического пространства. |ψ|² есть плотность вероятности.

Тогда вероятность найти микрочастицу в объеме V, как следует из

(1.4.5), равна

V

w = ò y 2 dV .                              (1.1.6)

0

И если известна ψ-функция, соответствующая данному состоянию частицы, то вероятности различных процессов определяются одно- значно, что дает возможность судить о поведении множества частиц с вероятностной точки зрения, т.е. описать их поведение методами тео- рии вероятности.

Если считать, что местонахождение микрочастицы в пространстве

- событие достоверное, т. е.  частица все время находится в объеме V,

то вероятность такого события всегда равна единице. Поэтому

V

ò y ² dV = 1.

0

(1.1.7)

Условие (1.1.7) называется условием нормировки, поскольку это условие накладывает определенные ограничения на величину ампли- туды волновой функции ψ₀ . Условие нормировки по существу есть иная форма записи закона сохранения полного числа микрочастиц в пространстве. Так как ψ=ψ(x, y, z, t), то условие нормировки должно

выполняться для любого момента времени, в противном случае оно не имеет физического смысла.

Знание волновой функции позволяет описать процессы природы вероятностным способом, а также позволяет определить средние зна- чения физических величин, например, среднее значение координаты, среднее значение скорости и др.:

При определении средних значений других физических величин часто используют операторную форму записи:

V

e  = òy^*eˆ ydV ,

0

V

òy²dV = 1.

0

V

p

r = òy

0

ˆ

r

* ˆ

pydV ,

r

где e – оператор полной энергии, p – оператор импульса.

Среднее значение энергии при переходе из состояния m в состоя- ние n тогда записывается следующим образом (рис. 2):

V

ò m         n

                         

e  =  y^* eˆy dV =  m eˆ n .

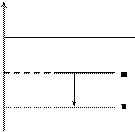0

 

 

 

0

 

em

en

 

Рис. 2. Квантовый переход между двумя скачками

Допустим, микрочастица некоторое время находится в объеме

V=hs. Тогда

V

ò y ² dV < 1.

0

Это обстоятельство следует учитывать, например, при определе- нии вероятности взаимодействия электронов с веществом в процессе облучения вещества потоком электронов. Допустим, облучаемое ве- щество представляет собой металлическую пленку.

 

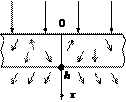
Рис. 1.4.2. Модель облучения пленки электроном

Объем облучаемой пленки   изображен на   рис. 1.4.2. А так как часть потока электронов проходит через пленку, то

V1

ò y ² dV < 1.

0

Следовательно, условие нормировки для волновой функции в этом конкретном случае должно иметь вид:

0

ò y1

-¥

h

2

2 dx + ò y

0

¥

2 dx + ò

h

y ²dx = 1.

3

Тогда знаменатель в выражении для среднего значения физической величины не будет равен единице. Например, теперь среднее значение энергии в пределах металлической пленки следует вычислять по фор- муле

⎛ h *

⎞    ⎛ h

2 ⎞ .

e  = ⎜òy eˆy ⎟

⎜ò y

dx ⎟

⎜

⎝ 0

Обобщим сказанное.

⎟     ⎜               ⎟

⎠    ⎝ 0                  ⎠

1.  Волновая функция сама по себе не выражает физического смыс- ла, физический смысл имеет лишь ее квадрат модуля – он равен плот- ности вероятности местонахождения микрочастицы в единице объема геометрического пространства в пределах выделенного микрообъема dV .

2.   В квантовой механике параметры состояния микрочастицы, на-

пример,  e, p , определяются вероятностным способом, точное  значе-

ние полной энергии и импульса, а также других параметров опреде- лить невозможно, точно можно определить лишь их средние значения

 

Скачано с www.znanio.ru