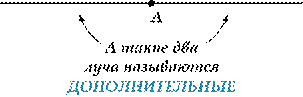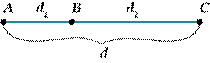Материалы для подготовки к итоговому государственному экзамену по геометрии для учеников 10 класса учебно-консультационных пунктов
|
Иркутская область Ангарский городской округ Государственное бюджетное профессиональное образовательное учреждение Иркутской области «Ангарский педагогический колледж» Отделение учебно-консультационных пунктов
Материалы для подготовки к экзамену по геометрии для учеников учебно- консультационных пунктов геометрия среднее общее образование
базовый очно-заочная Москвитина Лариса Васильевна авторская программа: Атанасян В.Ф. издательство «Просвещение», 2011г 2017 |
административный
(территориальный округ) образовательная организация
учебный предмет
уровень образования
уровень форма обучения учитель:
примерная (авторская) программа, на основе которой разработана рабочая программа год издания
СОДЕРЖАНИЕ
страница
1 ОСНОВНЫЕ ПОНЯТИЯ 3
1.1 ОСНОВЫ ПЛАНИМЕТРИИ 4
1.1.1 ОСНОВНЫЕ ОБЪЕКТЫ И АКСИОМЫ ПЛАНИМЕТРИИ 4
1.2 ТРЕУГОЛЬНИК. КОРОТКО О ГЛАВНОМ 8
1.3 ЧЕТЫРЕХУГОЛЬНИК. КОРОТКО О ГЛАВНОМ 11
1.4 АКСИОМЫ СТЕРЕОМЕТРИИ 13
2 ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 15 2.1 ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ 15
2.2 ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ 15
2.3 ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ 16
2.4 УГЛЫ С СОНАПРАВЛЕННЫМИ СТОРОНАМИ 17
2.5 ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ 17
2.6 ТЕОРИЯ O ТЕТРАЭДРАХ 18 2.7 ТЕОРИЯ O ПАРАЛЛЕЛЕПИПЕДАХ 19
2.8 ПОСТРОЕНИЕ СЕЧЕНИЯ ТЕТРАЭДРА И ПАРАЛЛЕЛЕПИПЕДА 20 3 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 24 3.1 ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ И ПЛОСКОСТИ 24
3.2 ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ. УГОЛ МЕЖДУ ПРЯМОЙ И 25
ПЛОСКОСТЬЮ
3.4 ДВУГРАННЫЙ УГОЛ. МНОГОГРАННЫЕ УГЛЫ. 27
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
3.5 ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД 28
1 ОСНОВНЫЕ ПОНЯТИЯ
Планиметрия изучает фигуры и их свойства на плоскости. Образно говоря, планиметрия изучает всѐ, что можно нарисовать или начертить на листе бумаги.
Основные объекты планиметрии - это точки, линии и замкнутые фигуры (например - квадрат, треугольник, круг, трапеция, ромб). Множество всех точек, рассматриваемых в планиметрии образует плоскость. Множество точек в планиметрии называется фигурой. Замкнутая фигура в планиметрии - это множество точек, ограниченных линией.
Стереометрия изучает фигуры и их свойства в пространстве (слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять). Образно говоря, стереометрия изучает всѐ, что можно склеить из бумаги, сколотить из досок, построить из кирпичей и т.п.
Точки обозначаются прописными латинскими буквами A,B,C,D,E,K,… Прямые обозначаются строчными латинскими буквами a,b,c,d,e,k,… Плоскости обозначаются греческими буквами α, β, γ и т. д.
В основе каждого курса геометрии лежат аксиомы - утверждения, которые принимаются без доказательств. С помощью этих утверждений определяются остальные объекты и их свойства.
1.1 Основы планиметрии
1.1.1 Основные объекты и аксиомы планиметрии Точка и прямая - это и есть самые главные понятия планиметрии.

Теперь первые правила обращения с точками и прямыми. Эти правила математики называют «аксиомы»- утверждения, которые принимаются за основу , из которых потом все основное будет выводиться (помнишь, что у нас большая кулинарная миссия по «приготовлению» геометрии?). Так вот, первая серия аксиом называется I. Аксиомы принадлежности.
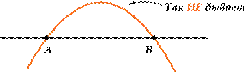
Аксиома 1.1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Обрати внимание, эта аксиома рассматривает два случая:
|
1 |
|
|
2 |
|
Аксиома 1.2. Через любые две точки можно провести прямую, и только одну.
|
Вот так: было две точки: |
И тут же нашлась прямая: |
А другой – нет! |
|
|
|
|
Если тебе все это кажется слишком очевидным, то вспомни, что ты – на другой планете и до сих пор совершенно не знал, что делать с объектами «точка» и «прямая».
Луч, отрезок, угол.
Вот теперь мы научились наносить точки на прямые и проводить прямые через точки, поэтому уже можем приготовить первые простейшие "блюда" - луч, отрезок, угол.
ЛУЧ
![]()
Любая точка, лежащая на прямой, делит эту прямую на две полупрямые. Каждая из этих полупрямых называется еще лучом.
Вот он, луч:
|
|
|
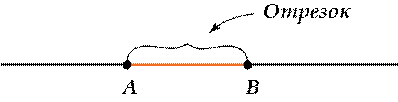
ОТРЕЗОК
Любые две точки на прямой ограничивают отрезок прямой.
УГОЛ
Углом называется часть плоскости, заключенная между двумя лучами этой плоскости, имеющими общее начало.
|
|
Лучи, образующие угол, называются сторонами угла, а их общее начало – вершиной угла. |
|
|
Угол, образованный дополнительными лучами, называется развернутым. |
Теперь наведем порядок. Следующая серия аксиом так и называется:
II. Аксиомы порядка.
Аксиома 2.1. Из трех точек на прямой одна и только одна лежит между двумя другими.
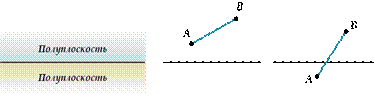
Аксиома 2.2. Прямая, лежащая в плоскости, разбивает эту плоскость на две полуплоскости. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Теперь - следующий уровень. Нам нужны инструкции по измерению отрезков и углов. Эти аксиомы называются
III. Аксиомы мер для отрезков и углов.
Аксиома 3.1. Каждый отрезок имеет определенную длину, больше нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
|
|
d=d1+d2 |
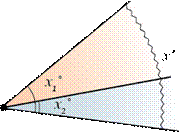
![]() Аксиома 3.2. Каждый
угол имеет определенную градусную меру, большую нуля. Развернутый угол равен
180. Градусная мера угла равна сумме градусных мер углов, на которые он
разбивается любым лучом, проходящим между его сторонами.
Аксиома 3.2. Каждый
угол имеет определенную градусную меру, большую нуля. Развернутый угол равен
180. Градусная мера угла равна сумме градусных мер углов, на которые он
разбивается любым лучом, проходящим между его сторонами.
|
|
x=x1+x2 |
IV. Аксиомы существования треугольника, равного данному.
Аксиома 4.1. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
Более понятными являются два следствия из этой аксиомы:
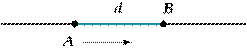
Следствие 1. От данной точки данной прямой в данную сторону можно отложить отрезок данной длины, причем единственным образом.
Следствие 2. От данного луча в данную полуплоскость можно отложить угол данной величины, причем единственным образом.
Ну, и последняя легендарная аксиома параллельных!
Но сперва, определение: Прямые называются параллельными, если они не имеют общих точек.
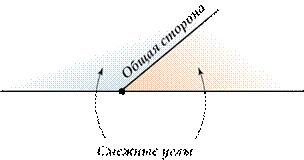
Смежные и вертикальные углы.
|
|
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. |
Лучи, образующие угол, называются сторонами угла, а их общее начало – вершиной.
Теорема. Сумма смежных углов равна 180°
|
|
180°=x1°+x2° |
Это совсем простая теорема, правда?
Ведь общая сторона смежных углов просто-напросто разбивает развернутый угол на два угла и поэтому (ВНИМАНИЕ: работает Аксиома 3.2!) сумма смежных углов равна величине развернутого, то есть 180°.
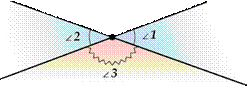
Вертикальные углы проще нарисовать, чем описывать – смотри картинку.

Теорема. Вертикальные углы равны.
Эта тоже легкая теорема. Убедись:
|
|
∠1+∠3=180° ∠1=∠2 |
Прямой, острый и тупой углы.
Если угол равен смежному с ним, то он называется ПРЯМЫМ УГЛОМ
|
|
|
|
|
Его величина равна 90° (ну конечно, 90°+90°=180°) |
Углы, меньшие 90°, называются острыми углами. |
Углы от 90 до 180° называются тупыми углами. |
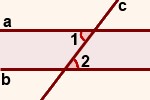
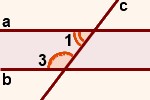
V. Аксиома параллельных прямых.
Параллельные прямые - это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали: a∥b.
Секущая - прямая, пересекающая две параллельные прямые: c.
Аксиома 5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
|
|
1 |
∠4 и ∠6; ∠3 и ∠5 - внутренние накрест лежащие углы; |
|
|
2 |
∠5 и ∠4; ∠6 и ∠3 - внутренние односторонние углы; |
|
|
3 |
∠1 и ∠8; ∠2 и ∠7 - внешние односторонние углы; |
|
|
4 |
∠1 и ∠5; ∠4 и ∠8; ∠2 и ∠6; ∠3 и ∠7 - соответственные углы. |
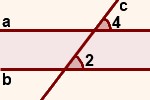
Свойства параллельных прямых:
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
1 внутренние накрест лежащие углы равны: ∠3=∠5; ∠4=∠6;
2 соответственные углы равны: ∠1=∠5; ∠4=∠8; ∠2=∠6; ∠3=∠7;
3 сумма любых двух внутренних односторонних углов равна 180°: ∠3+∠6=180°; ∠4+∠5=180°;
4 сумма любых двух внешних односторонних углов равна 180: ∠1+∠8=180°; ∠2+∠7=180°.
Признаки параллельных прямых:
|
Если внутренние накрест лежащие углы равны, то прямые параллельны
|
|
|
Если соответственные углы равны, то прямые параллельны.
|
|
|
Если сумма внутренних односторонних углов равна 180, то то прямые параллельны.
|
|
|
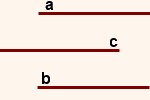
Если две прямые параллельны третьей прямой, то они параллельны между собой.
|
|
|
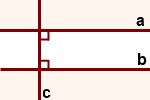
Если две прямые перпендикулярны третьей прямой, то они параллельны между собой
|
|
1.2 ТРЕУГОЛЬНИК. КОРОТКО О ГЛАВНОМ
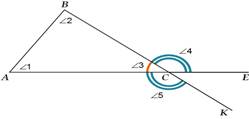
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Основные понятия.
|
|
∠1, ∠2, ∠3 - внутренние углы△ABC. Внешний угол треугольника - угол, смежный внутреннему углу треугольника, т.е. ∠4 и ∠5 - внешние углы △ABC при вершине C. |
Основные свойства треугольника:
1. Сумма
внутренних углов любого треугольника равна 180°: ![]() 1+
1+![]() 2+
2+![]() 3=180°
3=180°
2. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним, т.е.
![]() 4=
4=![]() 1+
1+![]() 2 ;
2 ;![]() 5=
5=![]() 1+
1+![]() 2
2
3. Сумма длин любых двух сторон треугольника больше длины его третьей стороны,
т.е. AB+BC>AC; AB+AC>BC; AC+BC>AB
4. В
треугольнике против большего угла лежит большая сторона, против большей стороны
лежит больший угол, т.е. если ![]() 2>
2>![]() 1, то AC>BC и
наоборот; Если AC>BC\, то
1, то AC>BC и
наоборот; Если AC>BC\, то ![]() 2>
2>![]() 1.
1.
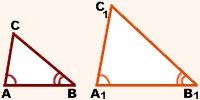
Признаки равенства треугольников.
|
1. Первый признак – по двум сторонам и углу между ними. |
|
|
2. Второй признак – по двум углам и прилежащей стороне. |
|
|
3. Третий признак – по трѐм сторонам |
|
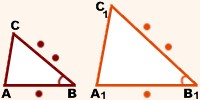
Признаки подобия треугольников
|
Первый признак – Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. |
|
|
|
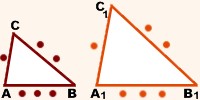
2. Второй признак Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. |
|
|
|
3. Третий признак Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. |
|
|
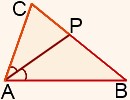
Элементы треугольника
|
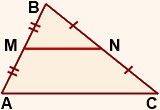
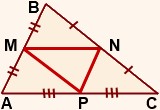
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. |
|
|
Свойства средней линии треугольника: Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
|
|
|
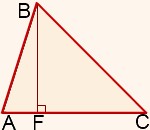
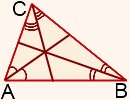
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону |
|
|
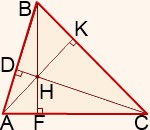
Свойство высот треугольника. Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника. |
|
|
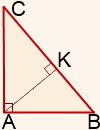
В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты, проведенные из вершин острых углов к катетам). Высота, проведенная к гипотенузе, лежит внутри треугольника (позднее рассмотрим ее свойства). |
|
|
В тупоугольном треугольника внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла. Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника. |
|
|
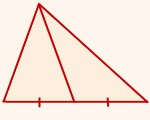
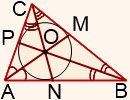
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Как построить медиану треугольника? Чтобы построить медиану треугольника, надо: 1) С помощью линейки найти и отметить середину стороны треугольника. 2) Соединить полученную точку с вершиной, лежащей напротив этой стороны. |
|
|
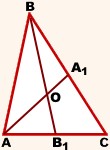
Свойство медиан треугольника: Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.
|
|
|
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне. |
|
|
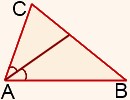
Свойство биссектрисы треугольника Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам
|
|
|
Все три биссектрисы треугольника пересекаются в одной точке |
|
|
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности |
|
|
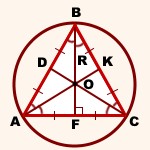
Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам. |
|
|
Радиус описанной около правильного треугольника окружности
|
|
1.4 ЧЕТЫРЕХУГОЛЬНИКИ.КОРОТКО О ГЛАВНОМ
|
Прямоугольник — это параллелограмм, у которого все углы прямые. |
|
|
Так как прямоугольник — это частный случай параллелограмма, то для прямоугольника выполняются все свойства параллелограмма. Свойства прямоугольника 1. Противолежащие стороны прямоугольника равны. 2. Диагонали прямоугольника в точке пересечения делятся пополам. 3. Все углы прямоугольника прямые. 4. Диагонали прямоугольника равны. |
|
|
Квадрат — это прямоугольник, у которого все стороны равны. |
|
|
Свойства квадрата: 1) Все углы квадрата — прямые. 2) Все стороны квадрата равны. 3) Диагонали квадрата равны. 4) Диагонали квадрата в точке пересечения делятся пополам. 5) Диагонали квадрата взаимно перпендикулярны. 6) Диагонали квадрата являются биссектрисами его углов |
|
|
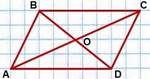
Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны, то есть лежат на параллельных прямых. |
|
|
Центром симметрии параллелограмма является точка пересечения его диагоналей. |
|
|
Свойства параллелограмма 1) Противоположные стороны параллелограмма параллельны и равны. 2) Противоположные углы параллелограмма равны. 3) Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º. 4) Диагонали параллелограмма в точке пересечения делятся пополам. 5) Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. 6) Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма. 7) Угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма. |
|
|
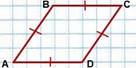
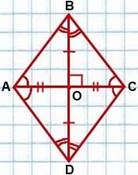
Ромб — это параллелограмм, у которого все стороны равны. |
|
|
Свойства ромба: 1) Стороны ромба равны (по определению ромба). 2) Противолежащие углы ромба равны (по свойству параллелограмма). 3) Сумма углов, прилежащих к одной стороне ромба, равна 180º (по свойству параллелограмма). 4) Диагонали ромба пересекаются и точкой пересечения делятся пополам (по свойству параллелограмма). 5) Диагонали ромба взаимно перпендикулярны. 6) Диагонали ромба являются биссектрисами его углов. 7) Сумма квадратов диагоналей ромба равна сумме квадратов его сторон (по свойству параллелограмма). 8) Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба (по свойству параллелограмма). 9) Угол между высотами ромба, проведенными из вершины острого угла, равен тупому углу ромба. |
|
|
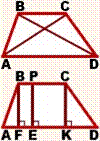
Трапеция — это четырехугольник, у которого две стороны параллельны, и две — не параллельны. Параллельные стороны трапеции называются основаниями, не параллельные — боковыми сторонами. Отрезки, соединяющие вершины трапеции, не принадлежащие одной стороне — это диагонали трапеции. Высотой трапеции называется расстояние между ее основаниями. |
|
|
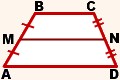
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции. Свойства средней линии трапеции 1) Средняя линия трапеции параллельна основаниям. 2) Средняя линия трапеции равна полусумме оснований. |
|
|
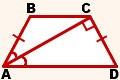
Если диагональ равнобедренной трапеции перпендикулярна боковой стороне и делит острый угол трапеции пополам, то 1) диагональ разбивает трапецию на два треугольника: один — равнобедренный, другой — прямоугольный; 2) углы трапеции равны 60º и 120º; 3) большее основание трапеции в два раза больше меньшего основания и еѐ боковых сторон; 4) высота трапеции равна половине еѐ диагонали. |
|
|
1. Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. 2. Биссектрисы углов при боковых сторонах трапеции пересекаются в точке, лежащей на средней линии трапеции. |
|
1.5 АКСИОМЫ СТЕРЕОМЕТРИИ
Простейшие фигуры в пространстве: точка, прямая, плоскость.
Простейшая поверхность - плоскость. В окружающем мире поверхность множества предметов подобна геометрической плоскости, например, пол в комнате, стол, поверхность воды в озере или бассейне. Большинство упомянутых предметов прямоугольной формы, при разглядывании их с большого расстояния, они напоминают параллелограммы. Поэтому достаточно часто плоскость на рисунке изображается в виде параллелограмма, но еѐ можно изобразить и по-другому - любой замкнутой линией. В стереометрии, так же как и в планиметрии, определяется равенство двух геометрических тел или фигур.
Две фигуры (или тела) называются равными, если их можно совместить наложением.
Главная величина геометрических тел - это их объѐм.
Объѐм геометрического тела - это величина, которая описывает занимающую этим телом часть пространства.
Из определения следует, что объѐм не зависит ни от местонахождения тела в пространстве, ни от того, как это тело делится на части.
Величину объѐма вычисляют, основываясь на аксиомах:
1) Равные тела имеют равные объѐмы.
2) 2) Объѐм тела равен сумме объѐмов его отдельных частей.
Чтобы объѐм можно было измерить, т.е., чтобы объѐм можно было бы выразить в виде числа, необходимо выбрать единицу измерения объѐма.
Единица объѐма - это объѐм такого куба, ребро которого равно одной единице длины. Если ребро куба равно 1 см, то его объѐм обозначается кубическими сантиметрами - см3, если ребро куба равно 1 м, то объѐм обозначается кубическими метрами - м3. Тела с равными объѐмами называются равновеликими.
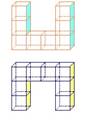
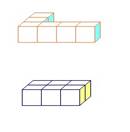
|
Равные тела |
Равновеликие тела |
|
|
|
|
равные тела с объѐмом 8см3 |
равновеликие тела с объѐмом 6см3 |
Все равные тела равновелики, но не все равновеликие тела равны.
Множество всех точек, рассматриваемых в стереометрии, называется пространством. Любое множество точек называется фигурой. Замкнутая фигура в стереометрии - это множество точек, ограниченных поверхностью.
Так как каждая прямая и каждая плоскость содержат какие-либо точки, то прямая и плоскость тоже являются фигурами стереометрии
Плоскость бесконечна и делит пространство на две части.
|
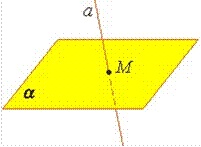
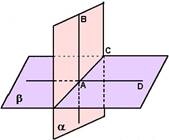
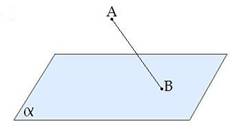
Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны. |
|
|
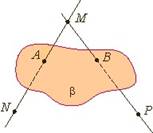
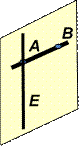
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко
это записывают так: А |
|
Аксиомы стереометрии и их следствия
|
Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. |
|
|
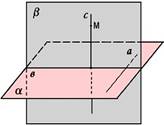
Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). |
|
|
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. |
|
|
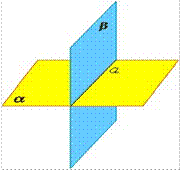
Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. |
|
Некоторые следствия из аксиом
|
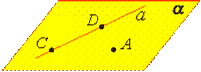
Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна. |
|
|
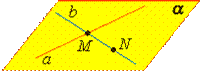
Теорема 2. Через две пересекающиеся прямые a и проходит плоскость, и при том только одна. |
|

Определение. Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются.
|
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. |
|
|
Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. |
|
|
Теорема о трех прямых в пространстве. Если
две прямые параллельны третьей прямой, то они параллельны (если a |
|
Параллельность прямых a и b обозначается так: a![]() b или b
b или b![]() a.
a.
2.2 Параллельность прямой и плоскости
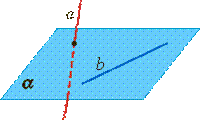
Согласно аксиомам, если две точки прямой находятся в некоторой плоскости, то прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:
1) прямая лежит (находится) в плоскости.
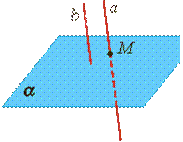
2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются)
3) прямая и плоскость не имеют общих точек
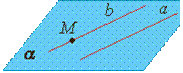
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
|
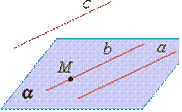
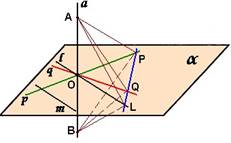
Теорема - признак параллельности прямой и плоскости Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. |
|
|
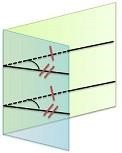
Утверждение 1 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Утверждение 2 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. |
|
2.3 Взаимное расположение прямых в пространстве
Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем представить ситуацию, когда две прямые не пересекаются, но они и не параллельны.
|
|
|
|
|
Одна дорога проходит по эстакаде, а другая под эстакадой |
Кабели моста
|
Горизонтальные линии крыши и вертикальные линии стен |
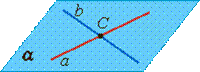
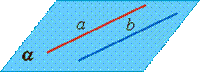
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Три случая взаимного расположения прямых в пространстве:
|
|
|
|
|
Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку. |
Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются) |
Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются) |
|
Теорема
|
|
|
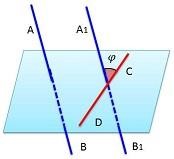
2.4 Углы с сонаправленными сторонами
Два луча ОА и О1А1, лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной плоскости с границей ОО1. Два луча ОА и О1А1, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.
Если стороны двух углов соответственно сонаправлены, то такие углы равны.
|
|
Углы между прямыми
|
1. Если прямые параллельны, то угол между ними 0°. 2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол 90°). 3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимися прямым. |
|
Обрати внимание!
Провести соответственные параллельные прямые данным скрещивающимися прямым можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую параллельную другой из скрещивающихся прямых.
2.5 Параллельность плоскостей
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются или не пересекаются.
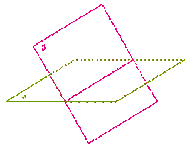
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются
α![]() β Пример:
β Пример:
Любая конструкция с полом, потолком и стенами даѐт нам представление о параллельных плоскостях - пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.
|
|
|
|

|
|
|
||||
|
|
|
 2.6
Теория o тетраэдрах
2.6
Теория o тетраэдрах
Тетраэдр (четырехгранник) - многогранник, гранями которого являются четыре треугольника. (от греческого tetra - четыре и hedra - грань). У тетраэдра 4 грани, 4 вершины и 6 ребер.
Один из треугольников называется основанием тетраэдра, а три остальные - боковыми гранями тетраэдра.
В зависимости от видов треугольников и их расположения, выделяют разные виды тетраэдров.
В школьном курсе чаще говорят о следующих видах тетраэдра:
- равногранный тетраэдр, у которого все грани - равные между собой треугольники; - правильная треугольная пирамида – основание равносторонний треугольник, все боковые грани одинаковые равнобедренные треугольники.
- правильный тетраэдр, у которого все четыре грани - равносторонние треугольники.
|
|
|
|
Правильный тетраэдр |
Равногранный тетраэдр |
Свойство правильного тетраэдра:
 Из
определения правильного многогранника следует, что все ребра тетраэдра имеют
равную длину, а грани - равную площадь.
Из
определения правильного многогранника следует, что все ребра тетраэдра имеют
равную длину, а грани - равную площадь.
2.7 Теория o параллелепипедах
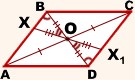
Параллелепипедом называется многогранник, у которого 6 граней параллелограммы.
У параллелепипеда, как отмечено, 6 граней, 8 вершин и 12 ребер.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.
Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (АС1; BD1; CA1; DB1;).
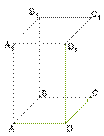
|
|
|
|
|
Правильный прямой параллелепипед |
Диагонали параллелепипеда |
Наклонный параллелепипед |
В зависимости от видов параллелограммов и их расположения, выделяют разные виды параллелепипедов. Параллелепипеды могут быть прямые и наклонные.
У прямых параллелепипедов боковые грани прямоугольники, у наклонных - параллелограммы.
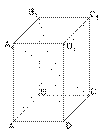
Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.
Длины непараллельных рѐбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
У прямоугольного параллелепипеда три линейных размера DA, DC, DD1.
|
Свойства параллелепипеда: |
|
|
|
1. Противоположные грани параллелепипеда равны и параллельны. 2. Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. 3. Боковые грани прямого параллелепипеда — прямоугольники. |
2.8 Построение сечения тетраэдра и параллелепипеда.
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.
Секущая плоскость пересекает грани многогранников по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Так как у тетраэдра 4 грани, то сечением тетраэдра может быть треугольник или четырехугольник.
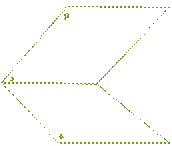
|
|
|
|
Сечение - треугольник |
Сечение - четырѐхугольник |
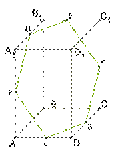
 У параллелепипеда 6
граней, поэтому сечением этого многогранника может быть треугольник,
четырехугольник, пятиугольник или шестиугольник.
У параллелепипеда 6
граней, поэтому сечением этого многогранника может быть треугольник,
четырехугольник, пятиугольник или шестиугольник.
|
Вид сечения |
|
|
|
|
|
Название сечения |
треугольник |
четырехугольник |
пятиугольник |
шестиугольник |
|
Условие образовани я |
Точки на ребрах, соединѐнных одной вершиной |
Точки на гранях, соединѐнных одной вершиной |
Точки не затрагивают одну грань параллелепипеда |
Точки лежат на всех гранях параллелепипеда |
При построении сечения надо вспомнить следующие знания из предыдущих тем:
1. Если две точки прямой принадлежит плоскости, то прямая находится в этой плоскости.
2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.
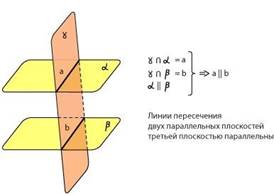
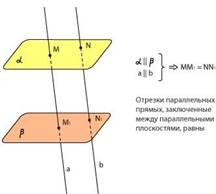
3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны. Примеры:
Задача 1
Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре его грани и будут четырьмя равными треугольниками. Задача решена.
Задача 2
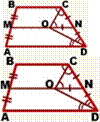
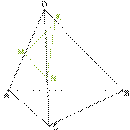
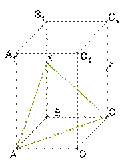
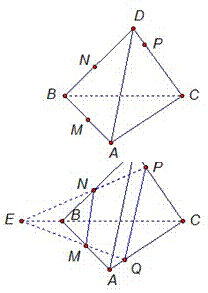
Дан тетраэдр АВСD. Точка M принадлежит ребру АВ, точка N принадлежит ребру ВD и точка Р принадлежит ребру. Постройте сечение тетраэдра плоскостью MNP.
Решение:
Рассмотрим грань DВС. В этой грани точки N и P принадлежат грани DВС, а значит, и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит, NP это линия пересечения двух плоскостей: плоскости грани DВС и секущей плоскости.
Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е.
Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.
Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.
Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях – АВС и MNP.
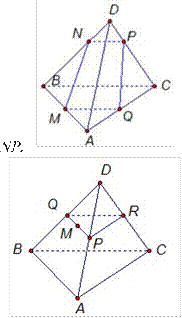 Соединим точки М и
Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку
пересечения прямых ЕМ и АС обозначим Q. Итак, в этом
случае NPQМ - искомое сечение.
Соединим точки М и
Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку
пересечения прямых ЕМ и АС обозначим Q. Итак, в этом
случае NPQМ - искомое сечение.
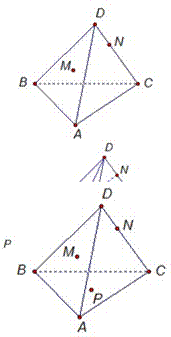 Рассмотрим
теперь случай, когда NP параллельна BC. Если прямая NP параллельна
какой-нибудь прямой, например, прямой ВС из плоскости АВС, то
прямая NP параллельна всей плоскости АВС. Искомая плоскость сечения
проходит через прямую параллельную плоскости АВС, и пересекает
плоскость по прямой МQ. Значит, линия пересечения МQ параллельна
прямой NP. Получаем, NPQМ - искомое сечение.
Рассмотрим
теперь случай, когда NP параллельна BC. Если прямая NP параллельна
какой-нибудь прямой, например, прямой ВС из плоскости АВС, то
прямая NP параллельна всей плоскости АВС. Искомая плоскость сечения
проходит через прямую параллельную плоскости АВС, и пересекает
плоскость по прямой МQ. Значит, линия пересечения МQ параллельна
прямой NP. Получаем, NPQМ - искомое сечение.
Задача 3
Точка М лежит на боковой грани АDВ тетраэдра АВСD. Постройте сечение тетраэдра плоскостью, которое проходит через точку М параллельно основанию АВС.
Решение:
Секущая плоскость φ параллельна плоскости АВС по условию, значит, эта плоскость φ параллельна прямым АВ, АС, ВС.
В плоскости АВD через точку М проведем прямую PQ параллельно АВ. Прямая PQ лежит в плоскости АВD. Аналогично в плоскости АСD через точку Р проведем прямую РR параллельно АС. Получили точку R. Две пересекающиеся прямые PQ и РR плоскости РQR соответственно параллельны двум пересекающимся прямым АВ и АС плоскости АВС, значит, плоскости АВС и РQR параллельны. РQR – искомое сечение. Задача решена.
Задача 4
Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани АВD. N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС.
Решение:
Для решения построим вспомогательную плоскость DМN. Пусть прямая DМ пересекает прямую АВ в точке К. Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.
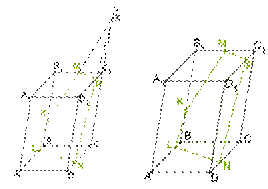
Задача 5
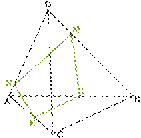
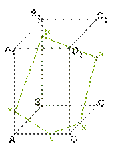
Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.
Решение:
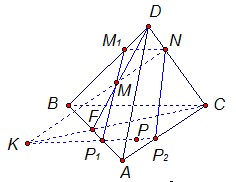 Рассмотрим первый
случай, когда прямая MN не параллельна плоскости АВС. В прошлой
задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это
точка К, она получена с помощью вспомогательной плоскости DМN,
т.е. мы проводим DМ и получаем точку F. Проводим СF и на
пересечении MN получаем точку К.
Рассмотрим первый
случай, когда прямая MN не параллельна плоскости АВС. В прошлой
задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это
точка К, она получена с помощью вспомогательной плоскости DМN,
т.е. мы проводим DМ и получаем точку F. Проводим СF и на
пересечении MN получаем точку К.
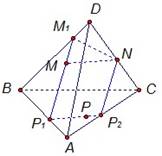 Проведем прямую КР.
Прямая КР лежит и в плоскости сечения, и в плоскости АВС.
Получаем точки Р1 и Р2. Соединяем Р1
и М и на продолжении получаем точку М1.
Соединяем точку Р2 и N. В результате получаем искомое
сечение Р1Р2NМ1. Задача в первом случае
решена.
Проведем прямую КР.
Прямая КР лежит и в плоскости сечения, и в плоскости АВС.
Получаем точки Р1 и Р2. Соединяем Р1
и М и на продолжении получаем точку М1.
Соединяем точку Р2 и N. В результате получаем искомое
сечение Р1Р2NМ1. Задача в первом случае
решена.
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС. Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямая Р1Р2 параллельна данной прямой MN.
Теперь проведем прямую Р1М и получим точку М1. Р1Р2NМ1 – искомое сечение.
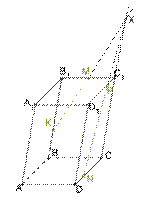
Задача 6
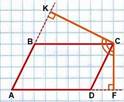
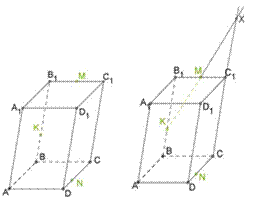
Построить сечение параллелепипеда плоскостью, которая проходит через точки K, M и N.
|
1. Проводим MK так как обе точки находятся в одной плоскости 2. MK∩CC1=X непараллельные прямые в одной плоскости пересекаются 3. Проводим XN так как обе точки находятся в одной плоскости 4. XN∩D1C1=P |
|
|
5. Проводим MP так как обе точки находятся в одной плоскости 6.
7. Соединяем N и L и получаем сечение MPNLK. |
|
3.ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
3.1 Перпендикулярные прямые и плоскости
Определение. Две прямые называются перпендикулярными, если угол между ними равен
90°.
В пространстве перпендикулярными называют не только пересекающиеся прямые, но и скрещивающиеся прямые, так как мы говорим об угле, который могут образовать эти прямые, если их поместить в одной плоскости.
|
Через любую точку пространства проходит прямая |
|
|
перпендикулярно данной плоскости, притом только одна. |
|
 Так же как и в
плоскости, в пространстве перпендикулярные прямые a и b обозначают a
Так же как и в
плоскости, в пространстве перпендикулярные прямые a и b обозначают a![]() b.
b.
|
Теорема – связь между параллельностью прямых и их перпендикулярностью к плоскости. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. |
|
|
|
|
|
|
|
Теорема – признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости |
|
|
|
Теорема о прямой, перпендикулярной к плоскости. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна |
|
|
1.Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. 2. Две прямые, перпендикулярные одной и той же плоскости, параллельны. |
|
||
|
|
3.2 Перпендикуляр и наклонные. Угол между прямой и плоскостью |
|
|
|
|
|||
|
Определение. Наклонной, проведенной из данной точки к данной плоскости, называется |
|||
Свойства перпендикулярных прямой и плоскости. 
 любой отрезок,
соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к
плоскости.
любой отрезок,
соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к
плоскости.
Конец отрезка, лежащий в плоскости, называется основанием наклонной. AB - наклонная.
B - основание наклонной.
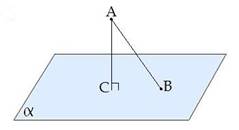 Определение.
Перпендикуляром, проведенным из данной точки к данной плоскости, называется
отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой,
перпендикулярной плоскости.
Определение.
Перпендикуляром, проведенным из данной точки к данной плоскости, называется
отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой,
перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. AC - перпендикуляр.
C - основание перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости.
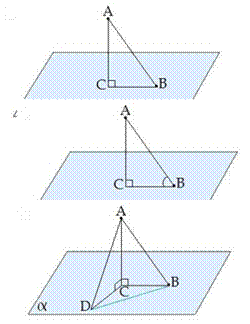 Отрезок,
соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же
точки, называется проекцией наклонной.
Отрезок,
соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же
точки, называется проекцией наклонной.
CB - проекция наклонной AB на плоскость α.
Треугольник ABC прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и еѐ проекцией на плоскость.
![]() CBA - угол между
наклонной AB и плоскостью α. Если AD>AB, то DC>BC
CBA - угол между
наклонной AB и плоскостью α. Если AD>AB, то DC>BC
Если из данной точки к данной плоскости провести
несколько наклонных, то большей наклонной соответствует большая проекция.
![]() DAB - угол между
наклонными
DAB - угол между
наклонными
![]() DCB - угол между проекциями
DCB - угол между проекциями
Отрезок DB - расстояние между основаниями наклонных.

|
Теорема. |
|
||
|
|
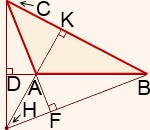
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, то она перпендикулярна и самой наклонной. |
|
|
|
Теорема обратная. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. |
|||
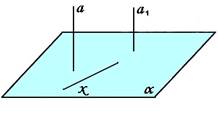
Угол между прямой и плоскостью
Понятие угла между прямой и плоскостью можно ввести для любого взаимного расположения прямой и плоскости:
1. Если прямая l перпендикулярна плоскости π, то угол между l и π считается равным 90°.
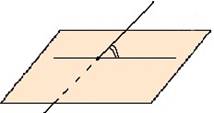
2. Если прямая l параллельна плоскости π или лежит в этой плоскости, то угол между l и π считается равным нулю.
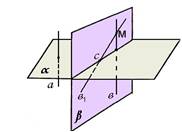
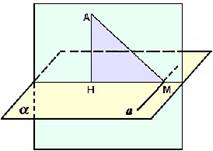
3. Если прямая l является наклонной к плоскости π, то угол между l и π — это угол ϕ между прямой l и еѐ проекцией p на плоскость π (рис. 1). l π p ϕ
Определение. Если прямая является наклонной, то угол между прямой и плоскостью есть угол между этой прямой и еѐ проекцией на данную плоскость.
2.3 Двугранный угол. Многогранные углы. Перпендикулярность плоскостей
Определение. Двугранный угол - это часть пространства, заключѐнная между двумя полуплоскостями, имеющими одну общую границу.
|
|
|
|
Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла (аналогично как при пересечении двух прямых получаются четыре угла). Рассмотрим один из них.
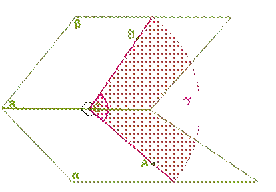 Полуплоскости α
и β, образующие двугранный угол, называются его гранями.
Полуплоскости α
и β, образующие двугранный угол, называются его гранями.
Общая прямая a этих граней называется ребром двугранного угла.
Выберем на ребре a двугранного угла произвольную точку C и проведѐм две пересекающиеся прямые AC⊥a и BC⊥a, а через эти прямые плоскость γ перпендикулярно ребру a.
Линии пересечения AC и BC полуплоскостей α и β с плоскостью γ образуют некоторый угол ∡ACB.
Определение. Линейный угол -- угол, стороны которого являются лучами, перпендикулярными к ребру двугранного угла, а вершина лежит на его ребре.
Величина линейного угла не зависит от выбора точки C на ребре a. Обрати внимание!
Величина двугранного угла 0°<∡ACB<180°. Если плоскости параллельны, то угол между ними равен 0° по определению.
Если при пересечении плоскостей один из двугранных углов 90°, то три остальные углы тоже 90°. Эти плоскости называют перпендикулярными.
Следующие теоремы, которые здесь приведѐм без доказательств, могут пригодится при решении задач.
1. Если одна из двух плоскостей проходит через прямую перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
2. Плоскость, перпендикулярная прямой, по которой пересекаются две плоскости, перпендикулярна каждой из этих плоскостей.
3.
 Если
две плоскости перпендикулярны и в одной из них проведена прямая перпендикулярно
линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.
Если
две плоскости перпендикулярны и в одной из них проведена прямая перпендикулярно
линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.
Многогранные углы.
Представим несколько лучей в пространстве с общим началом. Их можно представить тоже как часть линий пересечения плоскостей - трѐх, четырѐх или больше и назвать рѐбрами многогранного угла.
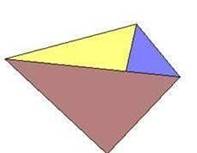
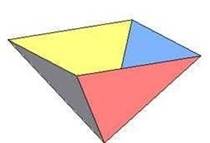
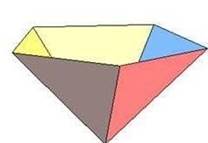
|
|
|
|
|
Трѐхгранный угол |
Четырѐхгранный угол |
Пятигранный угол |
Каждые два луча образуют угол, который называют плоским углом многогранного угла.
Обрати внимание!
Каждый плоский угол трѐхгранного угла меньше суммы двух других плоских углов.
Сумма плоских углов многогранного угла меньше 360°.
Признак перпендикулярности двух плоскостей
Определение. Если при пересечении плоскостей один из углов прямой (т.е. фи равен 90°), то и остальные три угла прямые. Такие плоскости называют перпендикулярными.
|
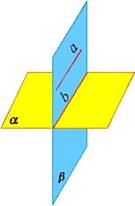
Теорема. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. |
|
|
Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей |
3.5 Прямоугольный параллелепипед
Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы.
Параллелепипеды, как и призмы, могут быть прямыми и наклонными.
Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом.
У прямоугольного параллелепипеда все грани — прямоугольники. Длины трѐх ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями.
Куб — прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
Свойства параллелепипеда:
1. В прямоугольном параллелепипеде все шесть грани – прямоугольники.
2. У параллелепипеда противоположные грани параллельны и равны.
3. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины и высоты).
5. Диагонали прямоугольного параллелепипеда равны.
© ООО «Знанио»
С вами с 2009 года.
![]()