

П. 1. Радианная мера угла. ...................................................................................... 3
П. 2. Поворот точки вокруг начала координат ..................................................... 4
П. 3. Определение синуса, косинуса, тангенса и котангенса угла ..................... 6 П. 4. Знаки синуса, косинуса, тангенса и котангенса угла. ............................. 10
П. 5. Зависимость между синусом, косинусом, тангенсом и котангенсом
одного угла. ............................................................................................................ 12
П. 6. Тригонометрические тождества ................................................................ 14
П. 7. Синус, косинус, тангенс и котангенс углов 𝜶 и − 𝜶. ................................ 15 П. 8. Формулы сложения. ................................................................................... 17
П. 9. Формулы двойного угла. ........................................................................... 19 П. 10. Формулы приведения. .............................................................................. 23
П. 11. Формулы суммы и разности одноименных тригонометрических
функций. ................................................................................................................. 25
П. 1. Радианная мера угла.

Примеры решения задач.
|
Типовое задание |
Используемая формула |
Пример |
|
Задача 1: Выразите в радианах величины углов, градусная мера которых равна α. |
𝜋 1° = рад
𝜋 𝛼° = ∙ 𝛼 рад 180° |
|
|
|
|
|
|
градусах величины углов, радианная мера которых равна α. |
1 = °
|
|
|
𝛼 > 0 точка 𝑃(1; 0)движется по единичной окружности против часовой стрелки |
𝛼 < 0 точка 𝑃(1; 0)движется по единичной окружности по часовой стрелке |
|
|
|
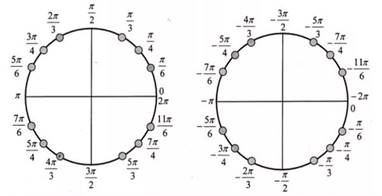
Примеры решения задач.
|
Типовое задание |
Используемая формула |
Пример |
|
Задача 1: Изобразите угол, полученный поворотом точки nградусов |
|
|
|
координаты точки, полученной поворотом точки угол |
|
|
|
Задача 3:Записать все углы, на которые нужно повернуть точку чтобы получить точку |
|
|
|
В геометрии |
В тригонометрии |
|
Определение синуса угла |
|
|
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
|
Синусом угла называется ордината точки 𝑃(1; 0), движущейся по единичной окружности.
|
|
Определение косинуса угла |
|
|
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
|
Косинусом угла называется абсцисса точки 𝑃(1; 0), движущейся по единичной окружности.
cos 𝛼 ∈ [−1; 1] |
|
Определение тангенса угла |
|
|
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
|
Линия тангенсов — это касательная к тригонометрической окружности, проведённая в точке A(1; 0)
Возьмём для начала острый угол α. Соответствующая точка α расположена в I четверти. Проведём прямую, проходящую через точку α и начало координат O; эта прямая пересекает линию тангенсов в точке T. Из тригонометрического определения тангенса вытекает, что AT = tg α. Тангенс угла α равен ординате точки
|
|
Определение котангенса угла |
|
|
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
|
Линия котангенсов — это касательная к тригонометрической окружности, проведённая в точке B(0; 1).
Соответствующая точка α расположена в I четверти. Проведём прямую через точку α и начало координат O; эта прямая пересекает линию котангенсов в точке T. Тогда оказывается, что BT = ctg α. Котангенс угла α равен абсциссе точке T.Котангенс не определен для углов 𝜶 = 𝝅𝒏,𝒏 ∈ 𝒁. |
![]()
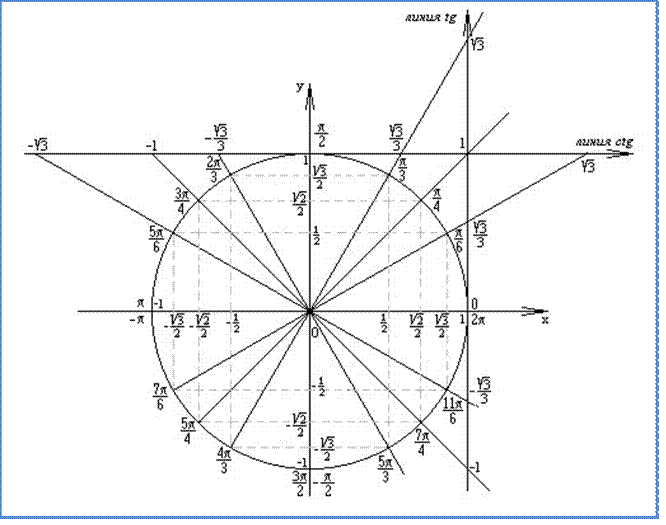
Рисунок 1 ТРИГОНОМЕТРИЧЕСКИЙ КРУГ
Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: Найти значения sin 𝛼, cos 𝛼, t𝑔 𝛼 и 𝑐𝑡𝑔𝛼, если: |
||
|
𝛼 = −𝜋 а) sin 𝛼 = sin(−𝜋) = 0
б) cos(−𝜋) = −1 в) 𝑡𝑔(−𝜋) = 0
г) 𝑐𝑡𝑔(−𝜋)не |
На единичной окружности поворачиваем точку 𝑃(1; 0)на угол – 𝜋 (точка 𝑀(−1; 0)). Ордината точки М равна 0. Значит sin(−𝜋) = 0. Абсцисса точки М равна -1. На линии тангенсов находим ординату точки пересечения с лучом МО. Она совпадает с ординатой точки Р, следовательно 𝑡𝑔(−𝜋) = 0 |
|
|
существует. |
Луч МО параллелен линии котангенсов. Следовательно, точек пересечения нет. |
|
|
|
||
|
sin 𝑥 = 0 𝑥
𝑥 = 2𝜋𝑛, 𝑛 ∈ 𝑍.
|
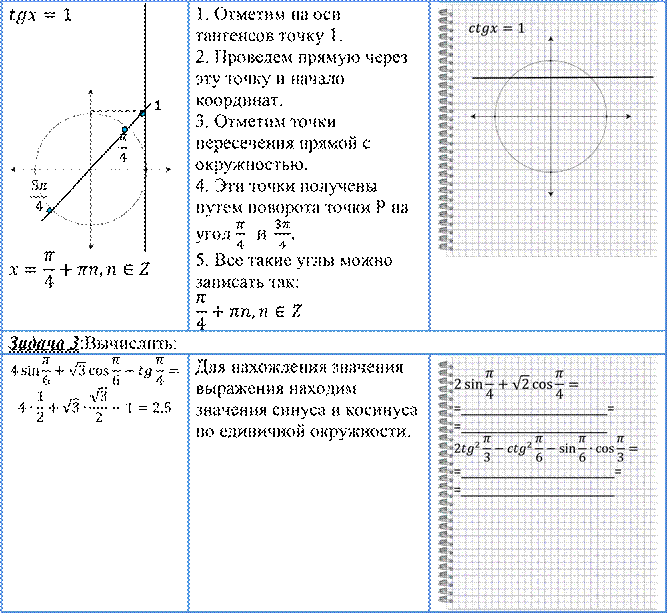
Это значит найти все углы, синус которых равен 0. 1. Построить единичную окружность. 2. На оси синусов отметить точку 0. 3. Через нее проведем прямую, параллельную оси Ox. 4. Отметим точки пересечения этой прямой с окружностью. 5. Эти точки получены поворотом точки 𝑃(1; 0)на углы 𝜋 и 0 радиан. 6. Все такие углы можно записать так: 𝑥 = 𝜋𝑛, 𝑛 ∈ 𝑍.
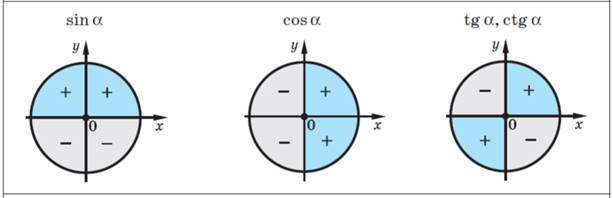
1. На оси косинусов отметим число 1. 2. Проведем прямую, параллельную оси Оу. 3. Отметим точки пересечения этой прямой с окружностью. 4. Эти точки получены поворотом точки Р на угол 0 и 2𝜋 радиан.
|
|
Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
: Выяснить знаки синуса, косинуса, тангенса и котангенса угла: |
||
|
Ответ:
2) 𝛼 = 745° = 2 ∙ 360° + 25° Ответ: sin 745° > 0 cos 745° > 0 𝑡𝑔745° > 0 𝑐𝑡𝑔745° > 0
|
Углу
Повороту точки Р на угол 745 градусов соответствует точка, расположенная в первой четверти. В первой четверти синус, косинус, тангенс и котангенс положительны.
Так как повороте на угол четверти. Поэтому синус и косинус отрицательны, а тангенс и котангенс положительны. |
|
Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: Зная значение |
одной из тригонометрически |
х функций и интервал, в |
|
котором находится α, на функций:1) |
|
ых тригонометрических
|
|
|
||
|
Задача 2: а) б) в) |
|
|
|
|
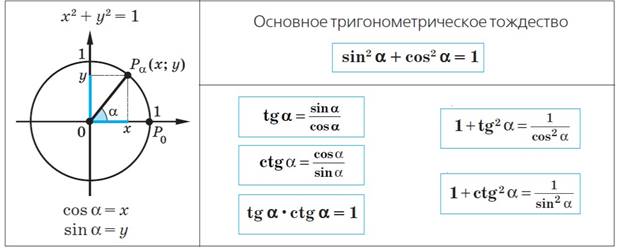
Для преобразования тригонометрических выражений используются и алгебраические формулы, например, формулы сокращенного умножения. Так, выражение sin4 𝛼 − cos4 𝛼 можно рассматривать как разность квадратов. Тогда его можно разложить на множители (на произведение суммы и разности sin2 𝛼 и cos2 𝛼) , а затем применить основное тригонометрическое тождество.
|
|
Напомним, что тождеством называется равенство, верное при всех допустимых значениях букв, входящих в него.

Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: |
|
|
|
2=2
Таким образом, данное равенство является тождеством. |
Докажем, что левая часть равенства равна правой. Для этого в знаменателе используем формулу
а в числителе возведем выражение в скобках в квадрат и используем формулу sin2 α + соs2 α = 1. Поэтому данное равенство является тождеством только при условии tg α ≠ 0 и соs α ≠ 0. |
|
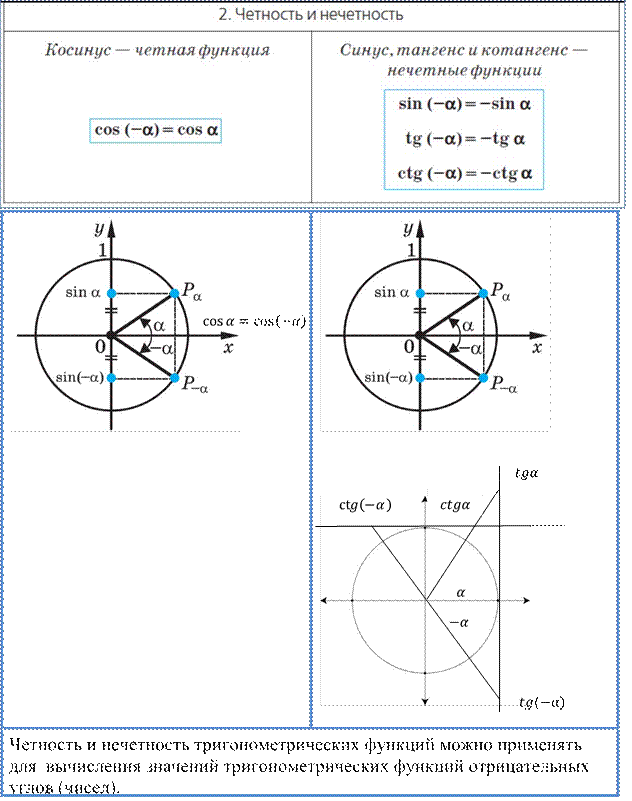
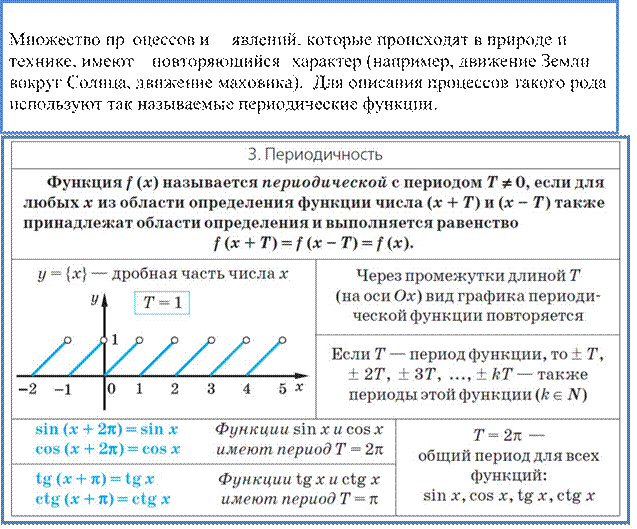
Чтобы исследовать тригонометрические функции на четность и нечетность, заметим, что на единичной окружности точки Pα и P–α расположены симметрично относительно оси Ox. Следовательно, эти точки имеют одинаковые абсциссы и противоположные ординаты.
Таким образом, четные и нечетные функции представлены в таблице:
Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: |
|
|
|
|
|
|
|
Задача 2: |
|
|
|
|
Для преобразования числителя и знаменателя дроби применим формулы косинуса суммы и косинуса разности и приведем подобные члены.
|
|
|
Задача 3: |
|
|
|
|
|
|
|
|
|
|
|
Задача 4: |
|
|
|
|
Для обоснования этих тождеств докажем, что их правые части равны левым, применяя формулы синуса суммы и синуса разности. |
|

Вывести данные формулы можно, если в формулах сложения

Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: |
|
|
|
|
|
|
|
|
|
|
|
Задача 2: |
|
|
|
|
Докажем, что
левая часть тождества равна правой. Заметим, что в числителе дроби находится
выражение, которое можно непосредственно преобразовать по формуле (3). Но применение этой формулы уменьшит аргумент вдвое. Желательно и в знаменателе дроби перейти к тому же аргументу. Для этого рассмотрим его как синус двойного угла:
|
|
|
Задача 3: |
|
|
|
|
Преобразовывая тригонометрические выражения, следует помнить не только тригонометрические, но и алгебраические формулы. В частности, если в знаменателе дроби применить формулу косинуса двойного угла, то получится выражение, которое является разностью квадратов |
|
|
|
Его можно разложить на множители как произведение суммы и разности косинуса и синуса одного и того же угла: Учитывая вид выражения, полученного в знаменателе, в числителе представим синус двойного угла как удвоенное произведение синуса на косинус:
Тогда для получения квадрата суммы этих выражений нам необходима еще сумма которую по основному тригонометрическому тождеству дает единица.
|
|
|
Задача 4:
|
|
|
|
|
|
|
|
приводят к тригонометрическим функциям от аргумента α |
|
|
Алгоритм |
Примеры |
|
1.
2. Знак полученного выражения определяется знаком исходного выражения, если условно считать угол α острым.
|
1. Упростите по формулам приведения tg(3π – α).
Комментарий Название заданной функции не меняется, поскольку число 3π изображается на горизонтальном диаметре (слева) единичной окружности. Если угол α острый, то угол 3π – α находится во II четверти, где тангенс отрицателен, поэтому в правой части формулы ставится знак «–».
Комментарий
|
Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1:
|
|
|
|
|
|
|
|
Задача 2: |
|
|
|
|
Докажем, что левая часть тождества равна правой. Сначала используем формулы приведения, а потом упростим полученные выражения, применяя другие тригонометрические формулы
. При упрощении выражений можно использовать как непосредственно формулы приведения, так и периодичность функций. Например,
|
|
|
|
|
|

Примеры решения задач.
|
Типовые задания |
Комментарий |
Пример |
|
Задача 1: |
|
|
|
|
В первом задании можно непосредственно применить формулу
а потом использовать табличные значения
|
|
|
|
Во втором задании выражение cos2 α – cos2 β можно рассмотреть как разность квадратов и разложить его на множители, а затем к каждому из полученных выражений применить формулы преобразования разности или суммы косинусов в произведение. Для дальнейшего упрощения полученного выражения используем формулу синуса двойного аргумента. |
|
|
Задача 2:
|
|
|
|
|
Мы умеем преобразовывать в произведение сумму синусов или косинусов. Для перехода к таким выражениям достаточно вспомнить, что
|
|
|
Задача 3: |
|
|
|
|
Для упрощения заданной дроби можно попытаться сократить ее: для этого представим числитель и знаменатель в виде произведений, которые содержат одинаковые выражения. В числителе используем формулы преобразования разности синусов и косинусов в произведение (а также нечетность синуса: sin (–3α) = –sin 3α), а в знаменателе воспользуемся формулой
|
|
Для заметок.

АНОНС
Тригонометрия.
Часть II. Тригонометрические уравнения.
В следующей части мы научимся решать тригонометрические уравнения.
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.