Данная рабочая тетрадь предназначена для учителей и учащихся 8-ых классов, учащиеся ее могут использовать как для актуализации знаний, а также для самостоятельной отработки решения заданий. Учителями рабочая тетрадь может быть использована как дополнительный инструмент для работы на уроках или же для индивидуальной работы со слабыми учениками

Оглавление

Предисловие ....................................................................................................................... 2

Глава 1. Рациональные дроби .......................................................................................... 4

1.1. Рациональные дроби и их свойства .......................................................................... 4

1.2. Арифметические действия над рациональными дробями ....................................... 7

Глава 2. Квадратные корни ........................................................................................... 12

2.1. Арифметический квадратный корень ..................................................................... 12

2.2. Свойства арифметического квадратного корня ..................................................... 13

Глава 3. Уравнения и системы уравнений .................................................................. 18

3.1. Квадратное уравнение и его корни ......................................................................... 18

3.2. Квадратный трехчлен .............................................................................................. 25

3.3. Дробные рациональные уравнения ......................................................................... 32

3.4. Уравнения с двумя переменными и их системы .................................................... 42

Глава 4. Неравенства ...................................................................................................... 54

4.1. Числовые неравенства и их свойства ...................................................................... 54

4.2. Неравенства с одной переменной и их системы .................................................... 57

Глава 5. Функции............................................................................................................. 62

5.1. Функция и ее свойства ............................................................................................ 62

5.2. Свойства некоторых видов функций ...................................................................... 63

Глава 6. Степень с целым показателем ........................................................................ 71

6.1. Степень с целым показателем и ее свойства .......................................................... 71

6.2. Стандартный вид числа ........................................................................................... 75

Итоговая проверка знаний ............................................................................................. 77

Справочные материалы ................................................................................................. 79

Библиографический список ........................................................................................... 95

Предисловие Дорогие восьмиклассники! Предлагаемая вам рабочая тетрадь по алгебре предназначена для закрепления и углубления знаний, приобретенных вами в процессе изучения математики. Алгебра – это удивительный раздел математики, который поможет вам лучше понять мир вокруг себя, научиться решать сложные задачи и развивать логическое мышление.

В этой тетради вы найдете необходимую теорию и разнообразные задания, которые помогут вам отточить навыки работы с алгебраическими выражениями, уравнениями, системами уравнений, а также познакомитесь с основами функций научитесь строить графики. Помните, что успех изучении алгебры зависит от регулярной практики и упорства.

Желаю вам увлекательного путешествия в мир алгебры и надеюсь, что эта тетрадь станет надежным помощником в вашем обучении. Пусть каждое изученное правило и каждое решенное уравнение приносит вам радость от открытий и уверенность в своих силах. Успехов!

- примеры

Определение:

- формулы, теоремы, алгоритмы, правила

- место для написания решения, ответов

Глава 1. Рациональные дроби

1.1. Рациональные дроби и их свойства

Определение:

Рациональная дробь является частным случаем рационального выражения.

Основное свойство дроби, сформулированное ранее для обыкновенных дробей, имеет место быть и для рациональных дробей.

Если числитель и знаменатель рациональной дроби умножить или разделить на один и тот же ненулевой многочлен, то получится рациональная дробь, тождественно равная исходной.

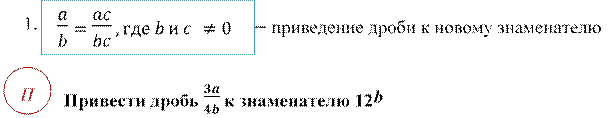
𝟐𝒕 ^𝟐− 𝟒

Привести дробь к знаменателю 𝒌

Так как 𝑘²− 4 = (𝑘 − 2)(𝑘 + 2), то

2. Для сокращения дроби нужно разложить ее числитель и знаменатель на множители, а затем разделить их на общие множители (еслитакие есть).

соркажение дроби на общий множитель.

Определение:

Область определения выражения (область допустимых значений

переменных) – множество значений переменных, при которых выражение имеет смысл.

Область определения целого выражения состоит из любых значений входящих в него переменных.

Область определения дробного выражения состоит их значений входящих в него переменных, при которых:

1. знаменатели дробей выражения не обращаются в 0;

2. выражения, состоящие под знаком корня чётной степени, принимают неотрецательные значения.

Область пределения выражения для 𝑎𝑡²+ 5; 𝑡 и 𝑎 – любые действительные числа 𝑎, 𝑡 ∈ 𝑅;

Укажите допустимые значения переменных выражения:

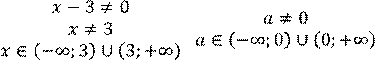
Задание 1. Укажите допустимые значения переменной в выражении:

2𝑥 + 7 5 + 𝑥

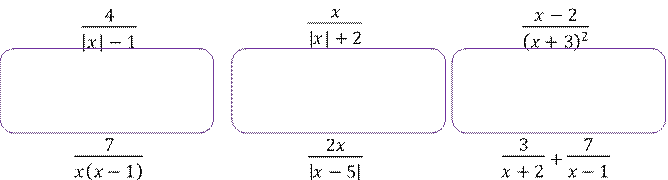
Задание 2. Сократите дробь:

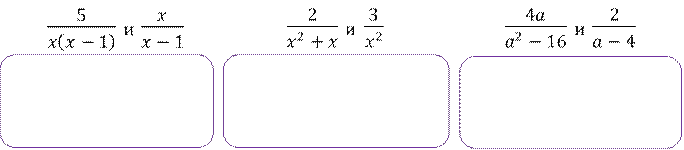
Задание 3. Приведите дроби к наименьшему общему знаменателю:

1.2. Арифметические действия над рациональными дробями

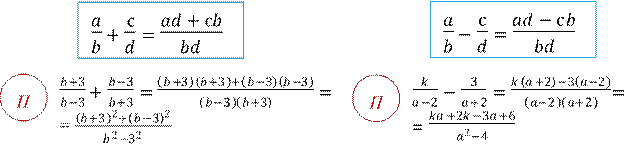
Арифметические действия над рациональными дробями производятся по правилам действий над обыкновенными дробями.

o Сложение и вычитание рациональных дробей

1. С одинаковым знаменателем.

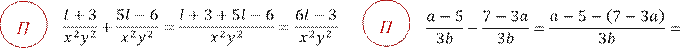
2. С разными знаменателями.

Сводится к сложению (вычитанию) дробей с одинаковыми знаменателями, с помощью приведения к общему знаменателю

o Возведение в степень

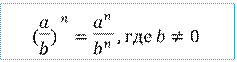
Задание 1. Выполните действие:

Задание 2. Упростите выражение:

Задание 3. Решите уравнение:

Итоговая работа по теме «Рациональные дроби»

Выполните действия:

Решите уравнение:

Глава 2. Квадратные корни

2.1. Арифметический квадратный корень

Определение:

Определение: Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен а.

Арифметический квадратный корень из числа а обозначают .

Знак √𝟏 называют знаком арифметического квадратного корня или знаком радикала. Выражение, стоящее под знаком корня, называют подкоренным выражением.

√9 = 3, так как 3 число не отрицательное и 3²= 9.

	, если выполняются два условия: 𝑏 ≥ 0; 𝑏²= 𝑎
При 𝑎 < 0 выражение не имеет смысла.

Выражение не имеет смысла, так как не существует такого числа, квадрат которого равен отрицательному числу.

Решим уравнение: . Из определения арифметического 5𝑥 + 6 = 6²

квадратного корня следует, что .

𝑥 = 6

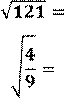
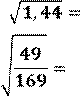
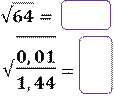
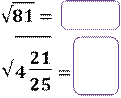
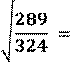Задание 1. Найдите значение корня:

Задание 2. Найдите значение выражения:

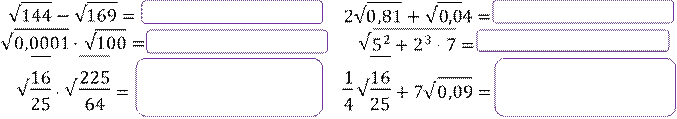
2.2. Свойства арифметического квадратного корня

Если . – корень из произведения двух неотрицательных множителей равен произведению корней из этих множителей.

Если – корень из дроби, числитель которого

неотрицательный, а знаменатель положителен, равен корню из числителя, деленому на корень из знаменателя.

при любом значении 𝑥 верно равенство:

Так как Вынесение множителя из-под знака корня:

1. Разложить подкоренное выражение на множители так, чтобы из большинства множителей извлекался квадратный корень.

2. Извлечь корень из каждого множителя.

3. Множители, из которых не извлекается квадратный корень оставить под знаком корня без изменений.

Внесение множителя под знак корня:

1. Возведите множитель перед корнем в квадрат и запишите его под знак √𝟏𝟖 = √𝟗 ⋅ 𝟐 = √𝟗 ⋅ √𝟐 = 𝟑 ⋅ √𝟐 = 𝟑√𝟐 корня.

2. Выполните умножение корней.

3. Выполните умножение под знаком корня.

𝟒√𝟑 = √𝟒^𝟐⋅ √𝟑 = √𝟏𝟔 ⋅ 𝟑 = √𝟒𝟖

Задание 1. Найдите значение выражения:

Задание 2. Найдите значение корня:

Задание 3. Внесите множитель под знак корня:

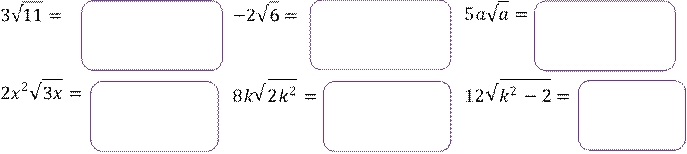
Задание 4. Вынесите множитель из-под знака корня:

Задание 5. Решите уравнение

Задание 6. Освободитесь от иррациональности в знаменателе дроби:

Задание 7. Упростите выражение:

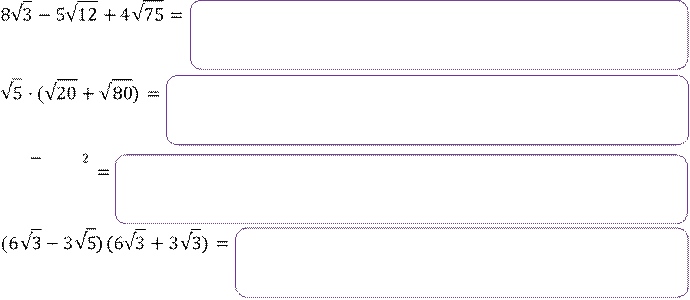(2√7 + 3)

Итоговая работа по теме «Квадратные корни»

1. Вычислите

3√2 2√3 3

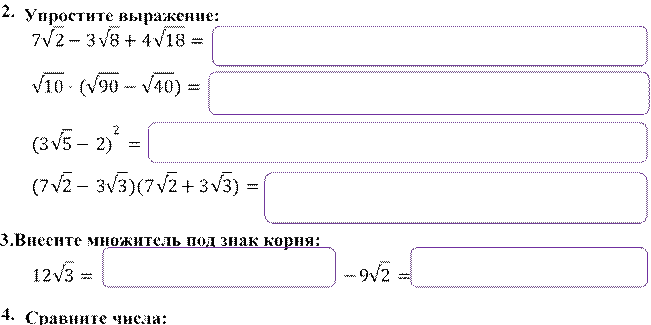
5. Освободитесь от знака корня в знаменателе дроби:

6. Найдите значение выражения:

Глава 3. Уравнения и системы уравнений

𝑎𝑥2 + 𝑏𝑥 = 0, 𝑎 ≠ 0, 𝑏 ≠ 0, с = 0

Решаем вынесением 𝑥 за скобки. Уравнение всегда имеет два корня, один из которых равен 0.

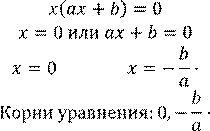
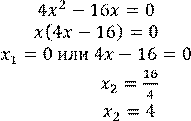
Ответ: 0; 4.

𝑎𝑥²+ с = 0, 𝑎 ≠ 0, с ≠ 0, 𝑏 = 0

Переносим коэффициент 𝑐 в правую часть уравнения, делим на 𝑎. Корни находим в зависимости от знака выражения

Если то уравнение имеет два корня .

Если , то уравнение корней не имеет.

𝑥²𝑥−²⁼4 =⁴0 𝑥₂²+=4−=40

𝑥

𝑥₁= −2 или 𝑥₂= 2 нет корней Ответ: − 2; 2.

𝑎𝑥²= 0, 𝑎 ≠ 0, 𝑏 = с = 0

3. 𝑥 = 0 − корень

5 ²97

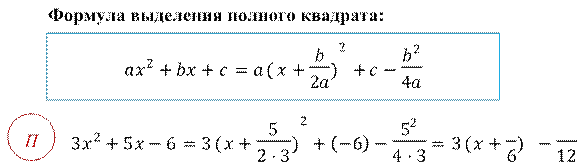
Формула корней квадратного уравнения:

Корни квадратного уравнения ax²+ bx + c = 0, можно найти по формуле

𝐷 = 𝑏²− 4𝑎𝑐

, где - дискриминант квадратного уравнения

Количество корней квадратного уравнения зависит от знака дискриминанта.

1. Если 𝐷 > 0, то уравнение имеет 2 корня

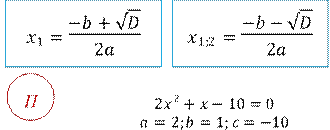
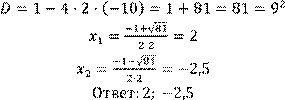
2. Если 𝐷 < 0, то уравнение имеет единственный корень (два равных корня)

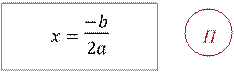𝑥²− 6𝑥 + 9 = 0

𝑎 = 1; 𝑏 = −6; 𝑐 = 9

𝐷 = 62 − 4 ⋅ 9 −=6 36 − 36 = 0

3. Если 𝐷 = 0, то уравнение корней не имеет

4𝑥²− 𝑥 + 5 = 0

𝐷 = 1 − 4 ⋅ 4 ⋅ 5 = 1 − 80 = −79 < 0 − корней нет

Теорема Виета.

Если 𝑥₁ и 𝑥₂ – корни квадратного уравнения 𝑥²+ 𝑝𝑥 + 𝑞 = 0, то

- Теорема Виета

𝑥²− 7𝑥 + 10 = 0

от сюда 𝑥₁= 2, 𝑥₂= 5

Ответ: 2;5.

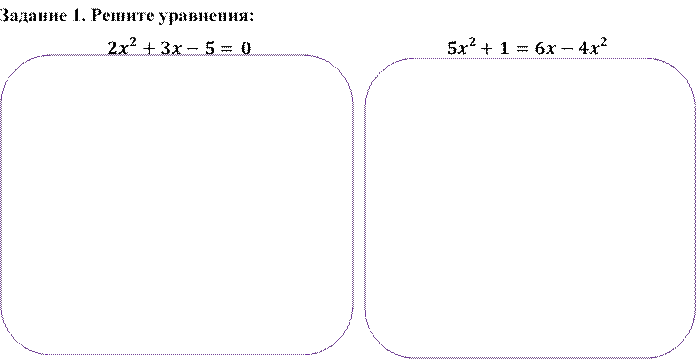
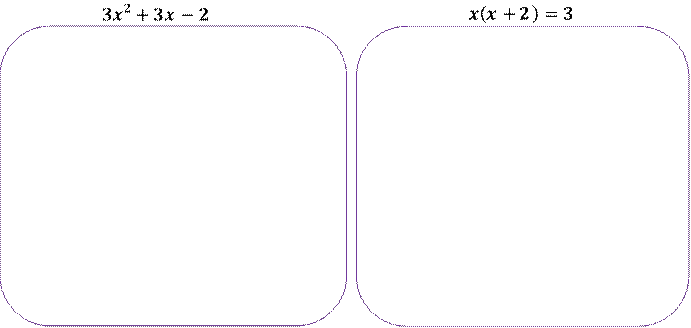
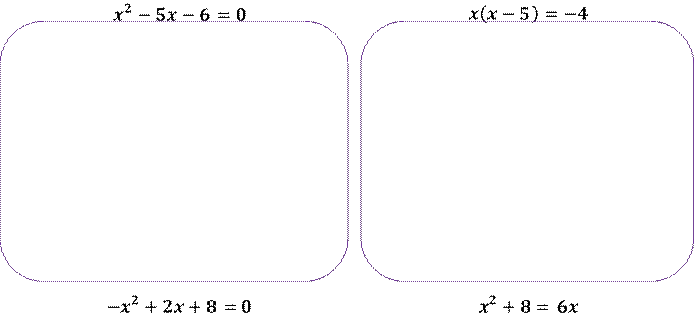
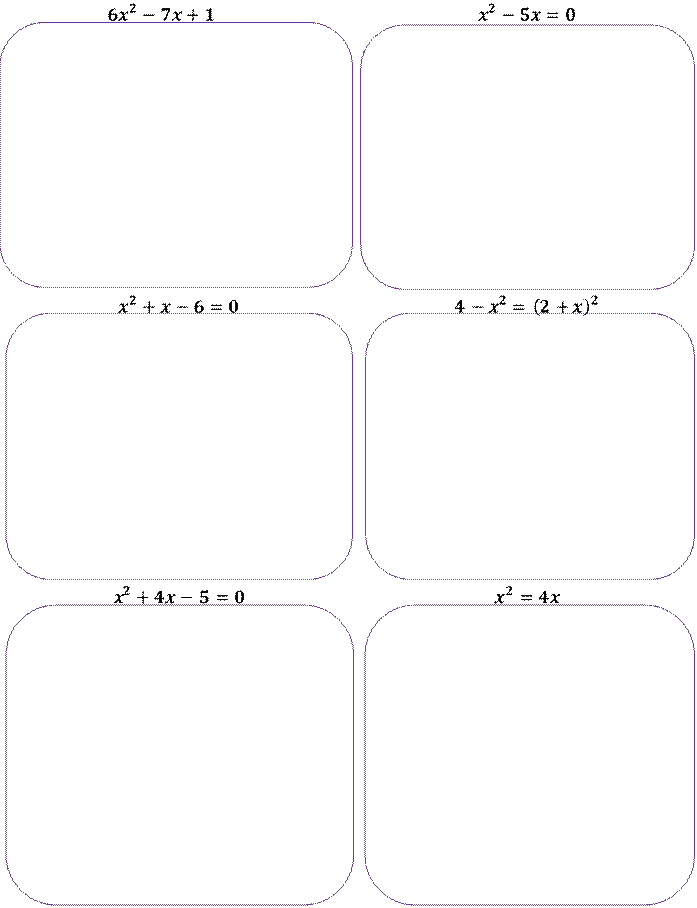
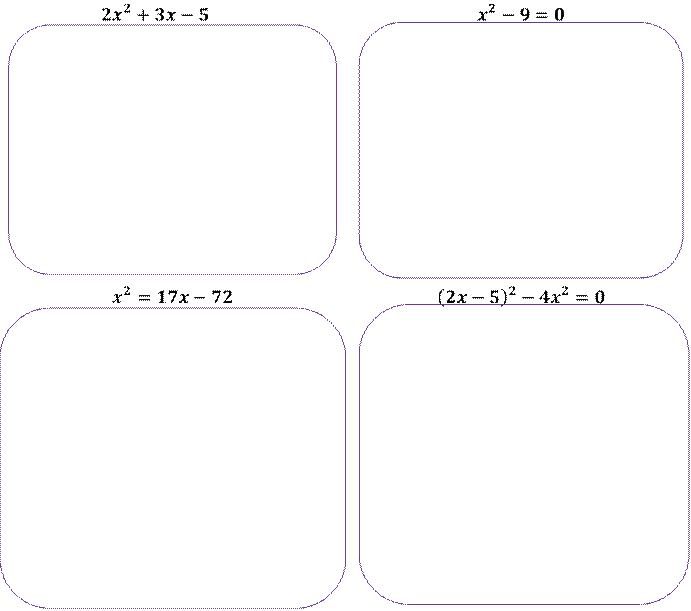
Задание 2. Составьте квадратное уравнение по его коэффициентам и найдите его корни:

𝒂 = 𝟏; 𝒃 = 𝟎; 𝒄 = 𝟎

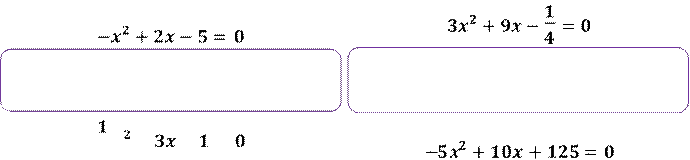
Задание 3. Преобразуйте квадратное уравнение в приведенное:

3.2. Квадратный трехчлен

Определение: Квадратным трёхчленом называется многочлен вида 𝑎𝑥2 + 𝑏𝑥 + 𝑐, где 𝑥 – переменная, 𝑎, 𝑏 и 𝑐 − некоторые числа, причем 𝑎 ≠ 0.

Коэффициент 𝑎 называют старшим коэффициентом, а 𝑐 – свободным членом квадратного трехчлена.

Корни квадратного трехчлена 𝑎𝑥²+ 𝑏𝑥 + 𝑐 – это корни уравнения 𝑎𝑥²+ 𝑏𝑥 + 𝑐 = 0. Формула разложения квадратного трехчлена на множители:

Если 𝑥₁ и 𝑥₂ – корни квадратного трехчлена 𝑎𝑥²+ 𝑏𝑥 + 𝑐, то справедливо равенство 𝑎𝑥²+ 𝑏𝑥 + 𝑐 = 𝑎(𝑥 − 𝑥₁)(𝑥 − 𝑥₂). Если квадратный трехчлен имеет один корень, то представим его в виде полного квадрата

𝑎𝑥²+ 𝑏𝑥 + 𝑐 = 𝑎(𝑥 − 𝑥₁)²

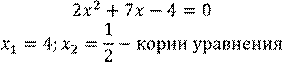
Значит

2𝑥²+ 7𝑥 − 4 = (𝑥 + 4)(2𝑥 − 1)

Если квадратный трехчлен 𝑎𝑥²+ 𝑏𝑥 + 𝑐 не имеет корней, то соответствующий многочлен (со старшим коэффициентом 1) называется неприводимым многочленом 2-й степени. Его разложить на множители нельзя!

7𝑥²+ 𝑥 + 12 – не имеет корней, так как 𝐷 < 0, следовательно на множители разложить нельзя.

Уравнения, приводимые к квадратным:

1. Биквадратные уравнения.

𝑎𝑥⁴+ 𝑏𝑥²+ 𝑐 = 0

, где 𝑎, 𝑏, 𝑐 – числа.

Бинарное уравнение решают методом замены

𝑥²= 𝑡, 𝑡 ≥ 0

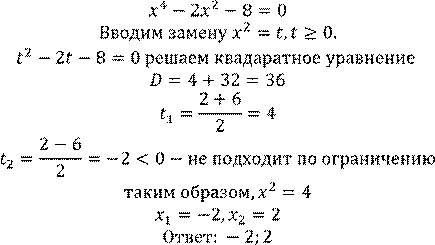
2. Уравнения, приводимые к квадратному пути введения новой переменной.

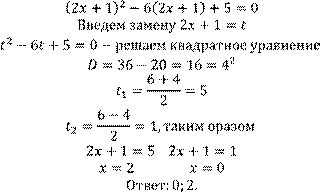
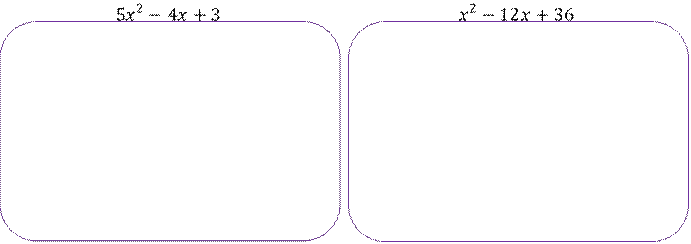
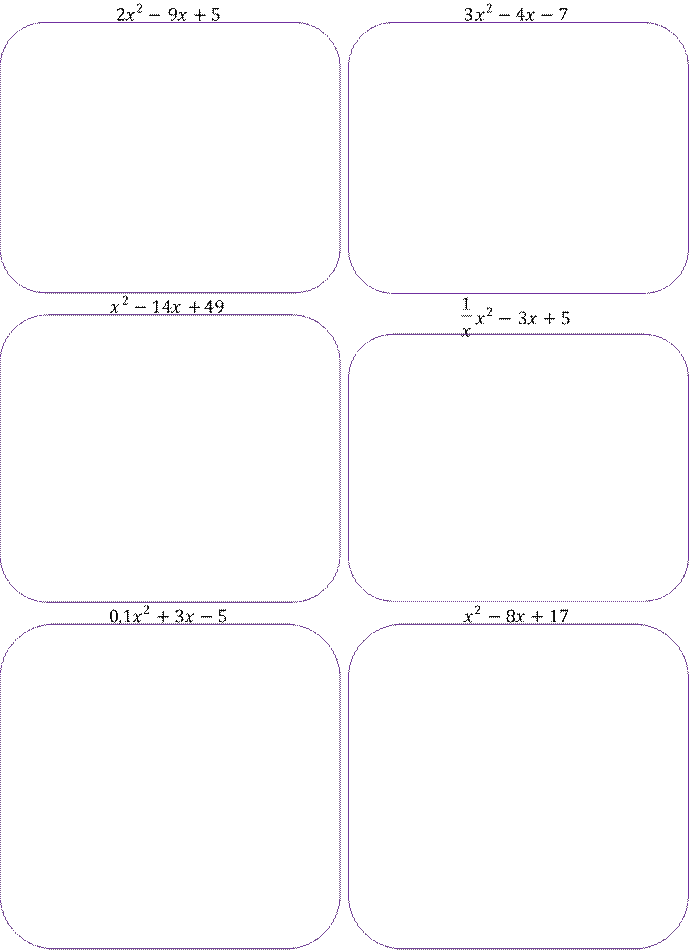
Задание 1. Найдите корни квадратного трехчлена

Задание 2. Какой многочлен необходимо поставить вместо многоточия, чтобы было равенство:

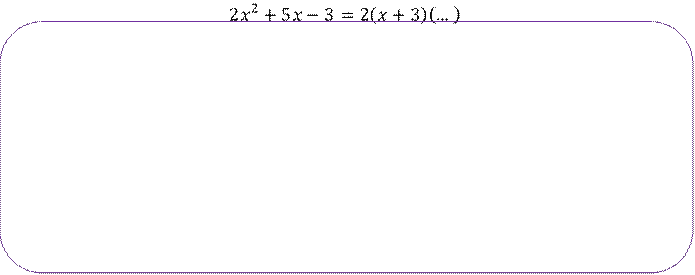
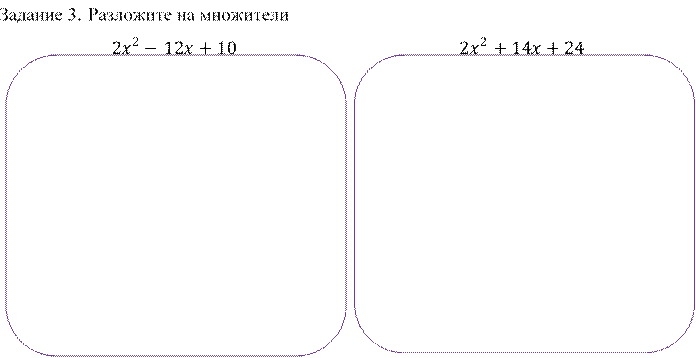
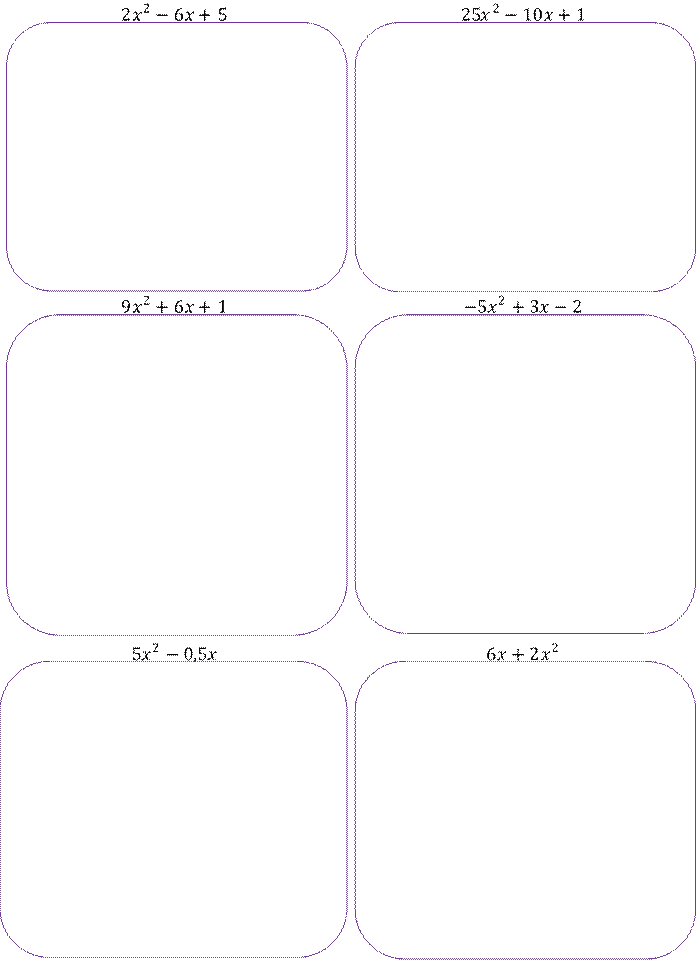
Задание 4. Решите уравнение:

Рациональные уравнения

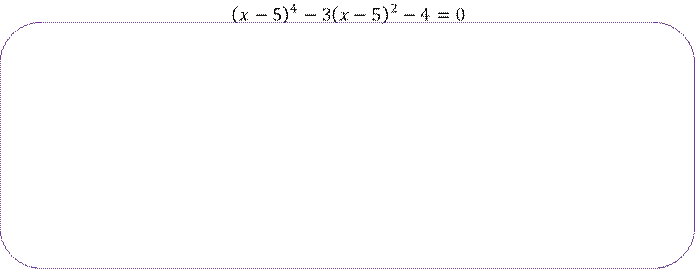
^{Определение:}Рациональные уравнения включают в себя целые уравнения и дробно рациональные уравнения.

Целым рациональным уравнением называется уравнение вида 𝑃(𝑥) = 0, где 𝑃(𝑥) – целая рациональная функция.

𝑃(𝑥)

Дробно рациональным уравнением называется уравнение вида , где 𝑃(𝑥) и 𝑄(𝑥) – многочлены.

Дробно-рациональные уравнения

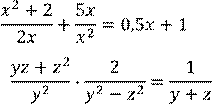
При решении рациональных уравнений используются метод разложения на множители и метод замены переменной.

Решить уравнение: (𝑥²− 6𝑥)²− 2(𝑥 − 3)²= 81

(𝑥²− 6𝑥)^𝑧− 2(𝑥²− 6𝑥 + 9) = 81

Вводим замену 𝑡 = 𝑥²− 6𝑥 – переходим к квадратному уравнению

𝑡²− 2(𝑡 + 9) − 81 = 0

𝑡²− 2𝑡 − 99 = 0, которое имеет корни 𝑡₁= −9 или 𝑡₂= 11 Возвращаемся к переменной 𝑥:

𝑥²− 6𝑥 = −9 или 𝑥²− 6𝑥 = 11

(𝑥 − 3)²= 0 или 𝑥²− 6𝑥 − 11 = 0

𝑥₁= 3 или 𝑥_2,3= 3 ± √5

Ответ: 3; 3 ± √5.

Уравнение вида , где решаем

заменой и переходим к квадратному

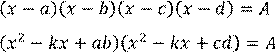
Пусть тогда

Решим уравнение:

Поскольку в данном уравнении , то делим правую и левую часть уравнения на . Получаем:

Замена: ,

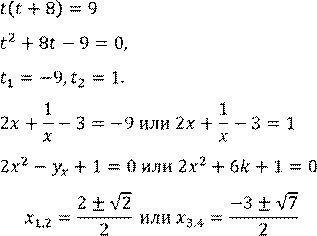
Ответ:

Алгоритм решения дробно рациональных уравнений

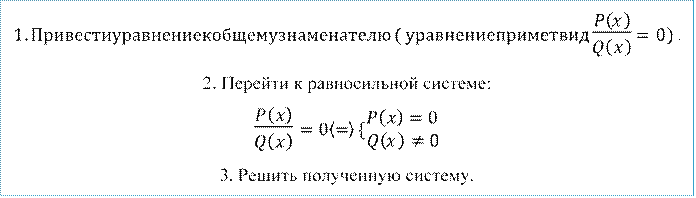
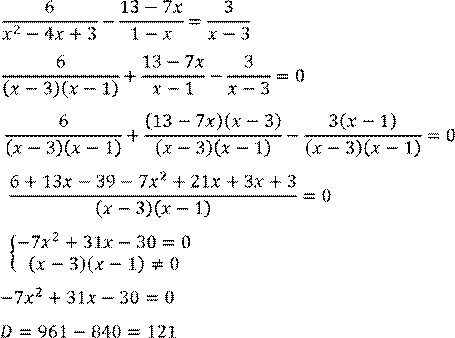
– не подходит по ограничению во втором неравенстве

системы.

Ответ:

Задание 1. Решите уравнение:

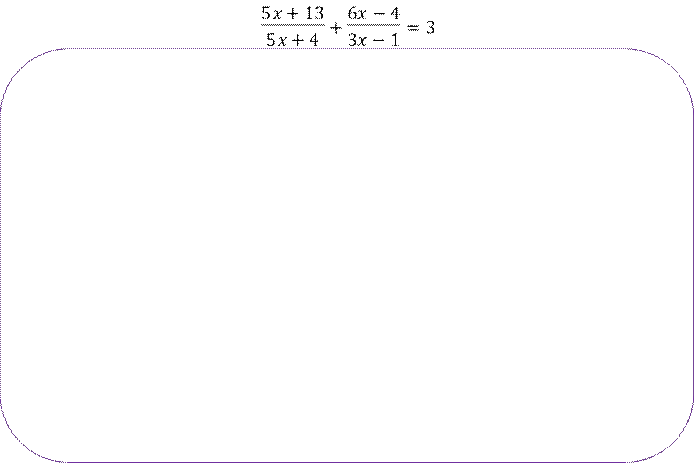
Задание 2. Найдите сумму всех значений 𝑥, при которых значение дроби равно 1.

Задание 3. Найдите произведение всех значений 𝑥, при которых значение дроби равно 2.

Задание 4. Первый лыжник проходит расстояние 20 км на 20 мин быстрее второго, так как его скорость на 2 км/ч больше. Найдите скорость первого и скорость второго лыжника.

Задание 5. Велосипедисту надо проехать 15 км. Он выехал на 15 мин позже намеченного срока и, чтобы приехать вовремя, увеличил скорость на 2 км/ч. С какой скоростью ехал велосипедист?

3.3. Уравнения с двумя переменными и их системы

Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верные равенство.

Два уравнения, имеющие одно и то же множество решений, называю равносильными уравнениями.

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное

равенство.

Графический способ решения систем уравнений

Решить графически систему уравнений – значит найти координаты общих точек графиков уравнений.

Решим с помощью графиков систему уравнений

Построим в одной системе координат графики уравнений, входящих в систему. Для этого выразим из каждого уравнения переменную 𝑦 через переменную 𝑥. Получим систему:

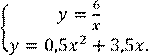Графиком первого уравнения является гипербола, а графиком

второго парабола (рис.1)

На рис.1 мы видим, что гипербола и парабола пересекаются в трех точках. Это означает, что

рассматриваемая система имеет три решения.

C помощью рисунка найдем приближенные значения

координат точек A, B, C.

Получим: A (-6,8; -1), B (-1,5; -4); С (1,2; 5).

Следовательно, решениями системы являются следующие

пары чисел: 𝑥₁≈ −6,8, 𝑦₁≈ −1;

𝑥₂≈ −1,5, 𝑦₂≈ −4;

𝑥₃≈ 1,2; 𝑦₃≈ 5. Найденные решения данной системы являются приближенными.

Рис.1

Алгебраический способ решения систем уравнений

Основным способом решения систем уравнения с двумя переменными является алгебраический способ.

^1.выражаем из уравнения первой степени одну переменную через другую;

^2.подставляем полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;

^3.решаем получившиеся уравнение с одной переменной;

^4.находим соответствующие значения второй переменной.

Решим систему уравнений:

𝑥²− 3𝑥𝑦 − 2𝑦²= 2,

{

𝑥 + 2𝑦 = 1.

1. выразим из второго уравнения переменную 𝑥 через 𝑦:

𝑥 = 1 − 2𝑦

2. подставим в первое уравнение вместо 𝑥 выражение 1 − 2𝑦, получим уравнение с переменной 𝑦:

(1 − 2𝑦)²− 3(1 − 2𝑦)𝑦 − 2𝑦²= 2 после упрощения получим равносильное уравнение 8𝑦²− 7𝑦 − 1 = 0

Решив его, найдем, что .

3. Соответствующие значение 𝑥 можно найти, воспользовавшись формулой

𝑥 = 1 − 2𝑦

Подставим в формулу 𝑥 = 1 − 2𝑦 значения , получим

Подставим в формулу 𝑥 = 1 − 2𝑦 значения 𝑦₂= 1, получим 𝑥₂= −1 4. Итак, система имеет два решения:

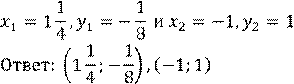Задание 1. Решите графически систему уравнений:

Задание 2. Решите систему уравнений методом подстановки

𝑥²+ 𝑦 = 83

Задание 3. Решите систему уравнений методом алгебраического сложения/вычитания:

𝑥²− 𝑦²= 7

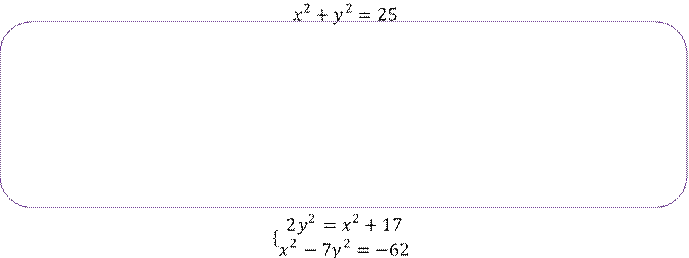
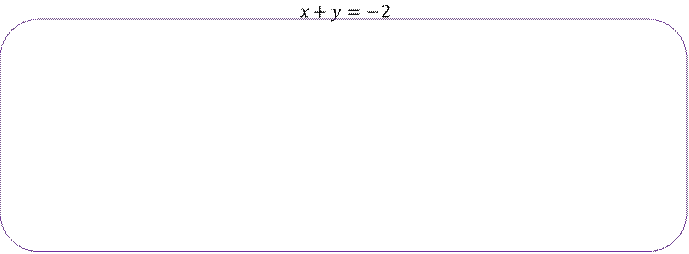
Задание 4. Решите систему уравнений:

3𝑥 − 𝑦²= 11

Глава 4. Неравенства

4.1. Числовые неравенства и их свойства Определение:

Выражение, в котором знаком неравенства объединены два числа или два числовых выражения, называются числовым неравенством.

3 < 10

2 + 6 ≥ 2 − 1

Числовые неравенства - {

0 + 3 ≤ 3

15 > 6

Определение:

Если неравенство содержит знак «>» или «<», то неравенство

называется строгим, если знаки «≥» или «≤», то нестрогим неравенством.

При сравнении чисел:

𝑎 < 𝑏 ⇔ 𝑎 − 𝑏 < 0 ⇔ 𝑎 меньше 𝑏

𝑎 > 𝑏 ⇔ 𝑎 − 𝑏 > 0 ⇔ 𝑎 больше 𝑏

𝑎 = 𝑏 ⇔ 𝑎 − 𝑏 = 0 ⇔ 𝑎 равно 𝑏

Двойные числовые неравенства

𝑎 < 𝑏 < с ⇔ 𝑏 больше 𝑎 и меньше с

𝑎 ≤ 𝑏 < с ⇔ 𝑏 больше или равно 𝑎 и меньше с

𝑎 < 𝑏 ≤ с ⇔ 𝑏 больше 𝑎 и меньше или равно 𝑐

𝑎 ≤ 𝑏 ≤ с ⇔ 𝑏 больше или равно 𝑎 и меньше или равно 𝑐

Свойства числовых неравенств:

Если 𝑎 > 𝑏, то 𝑏 < 𝑎 (𝑎 ≥ 𝑏, то 𝑏 ≤ 𝑎)

Если 𝑎 < 𝑏, то 𝑏 > 𝑎 (𝑎 ≤ 𝑏, то 𝑏 ≥ 𝑎)

Если 𝑎 < 𝑏, и 𝑏 < 𝑐, то 𝑎 < с

Если 𝑎 ≤ 𝑏, и 𝑏 ≤𝑐, то 𝑎 ≤ с

Если 𝑎 ≤ 𝑏, и 𝑏 < 𝑐, то 𝑎 < с

Если 𝑎 > 𝑏, и 𝑏 > 𝑐, то 𝑎 > с

Если 𝑎 ≥ 𝑏, и 𝑏 ≥ 𝑐, то 𝑎 ≥ с

Если 𝑎 ≥ 𝑏, и 𝑏 > 𝑐, то 𝑎 > с

Если 𝑎 < 𝑏, и с − любое число, то 𝑎 ± 𝑏 < 𝑏 ± 𝑐

Если 𝑎 > 𝑏, и с − любое число, то 𝑎 ± 𝑏 > 𝑏 ± 𝑐

Если 𝑎 ≤ 𝑏, и с − любое число, то 𝑎 ± 𝑏 ≤ 𝑏 ± 𝑐

Если 𝑎 ≥ 𝑏, и с − любое число, то 𝑎 ± 𝑏 ≥ 𝑏 ± 𝑐

Действия над неравенствами:

1. Сложение неравенств

𝑎 < 𝑏 и 𝑐 < 𝑑, то 𝑎 + 𝑐 < 𝑏 + 𝑑

Если

𝑎 > 𝑏 и 𝑐 > 𝑑, то 𝑎 + 𝑐 > 𝑏 + 𝑑

5 < 7 и 9 < 20, то 5 + 9 < 7 + 20 - верно

13 > 2 и −6 > −10, то 13 − 6 > 2 − 10 − верно

2. Умножение неравенств

𝑎 < 𝑏 и 𝑐 < 𝑑, то 𝑎𝑐 < 𝑏𝑑

𝑎 > 𝑏 и 𝑐 > 𝑑, то 𝑎𝑐 > 𝑏𝑑

12 >5

2>1, то 12 ⋅ 2 > 5 ⋅ 1 – верно

3. Возведение в натуральную степень

𝑎 < 𝑏, то 𝑎𝑛 < 𝑏𝑛

𝑎 > 𝑏, то 𝑎^𝑛> 𝑏^𝑛

3 < 12, то 3²< 12²

7 > 5, то 7³> 5³

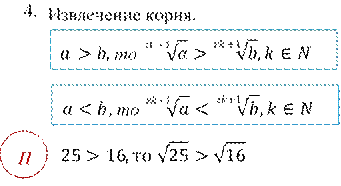
Числовые промежутки:

𝑥 ∈ (𝑎; 𝑏) или 𝑎 < 𝑥 < 𝑏

𝑥 ∈ [𝑎; 𝑏) или 𝑎 ≤ 𝑥 < 𝑏

𝑥 ∈ (𝑎; 𝑏] или 𝑎 < 𝑥 ≤ 𝑏

𝑥 ∈ 𝑎; +∞ или 𝑥 ≥ 𝑎

𝑥 ∈ (𝑎; +∞) или 𝑥 > 𝑎

𝑥 ∈ (−∞; 𝑎) или 𝑥 < 𝑎

𝑥 ∈ (−∞; 𝑎] или 𝑥 ≤ 𝑎

𝑥 ∈ [𝑎; 𝑏] или 𝑎 ≤ 𝑥 ≤ 𝑏

[ )

𝑥 ∈ (−∞; +∞) или 𝑅; −∞ < 𝑥 < +∞

4.2. Неравенства с одной переменной и их системы

Определение: называют два выражения с

Неравенством с одной переменной

переменной, соединенные знаками «<», «>», «≤», «≥». Определение: с одной переменной – это значение переменной,

Решение неравенства которое обращает его в верное числовое неравенство.

Определение: Решить неравенство – значит найти все его решения или доказать, что их нет.

Определение: Неравенства называются равносильными, если они имеют одни и те же решения, или одновременно решений не имеют.

Свойства неравенств:

Равносильные неравенства получаются если:

1. Перенести слагаемые из одной части неравенства в другую с противоположным знаком.

2. Умножить или разделить обе части неравенства на одно и то же положительное число.

3. Умножить или разделить обе части неравенства на одно и то же отрицательное число и изменить при этом знак неравенства на противоположный.

2𝑥 ≤ 10

𝑥 ≤ 5

Ответ: 𝑥𝜖 (−∞; 5]

7 − 2(𝑥 − 3) ≤ −𝑥 + 3

7 − 2𝑥 + 6 ≤ −𝑥 + 3

5𝑥 − 2 ≤ 3𝑥 + 8

5𝑥 − 3𝑥 ≤ 8 + 2

−2𝑥 + 𝑥 ≤ 3 − 7 − 6

−𝑥 ≤ −10

𝑥 ≥ 10

Ответ: 𝑥𝜖[10; +∞)

2𝑥 − 7 ≤ 3 + 2𝑥

2𝑥 − 2𝑥 ≤ 3 + 7

0𝑥 ≤ 10

𝑥 − любое число

Ответ: 𝑥 ∈ (−∞; +∞)

3(𝑥 + 7) − 2 ≥ 3𝑥 + 40

3𝑥 + 21 − 2 ≥ 3𝑥 + 40

3𝑥 − 3𝑥 ≤ 40 − 21 + 2

0𝑥 ≥ 21 − нет решений Ответ: 𝑥 ∈ ∅

Задание 1. Определите положительное или отрицательное число 𝑎, если

56𝑎 < 0	−3,5𝑎 > 0	−2,8𝑎 < 0	85𝑎 > 0

Задание 2. сравните числа 𝑎 и 𝑏 , если:
𝑎 − 𝑏 > 0	𝑎 − 𝑏 < −3	𝑎 − 𝑏 > 5	𝑎 − 𝑏 = 0

Задание 3. Даны выражения 7𝑐(𝑐 + 3) и 3𝑐(𝑐 − 5). Сравните их значения при 𝑐 = −4(>, < или = )

Задание 4. Известно, что 𝑎 < 𝑏. Сравните:


√121𝑎 √121𝑏

Задание 4. Докажите, что, если 4𝑎 − 5𝑏 > 2𝑎 − 3𝑏, то 𝑎 > 𝑏 Задание 5. Назовите числовой отрезок промежуток:

Задание 6. Изобразите на координатной прямой промежуток и назовите его:

(−1; 5)

(−∞; 4]

(−5; +∞)

[−1,5; 2]

[−3; 1,5)

(−2,7; 2]

(−3; 5) ∪ (5; 9]

Задание 7. Покажите штриховкой на координатной прямой объединение промежутков:

[−2; 7] и [0; 6]

(−5; 7) и (−1; 6

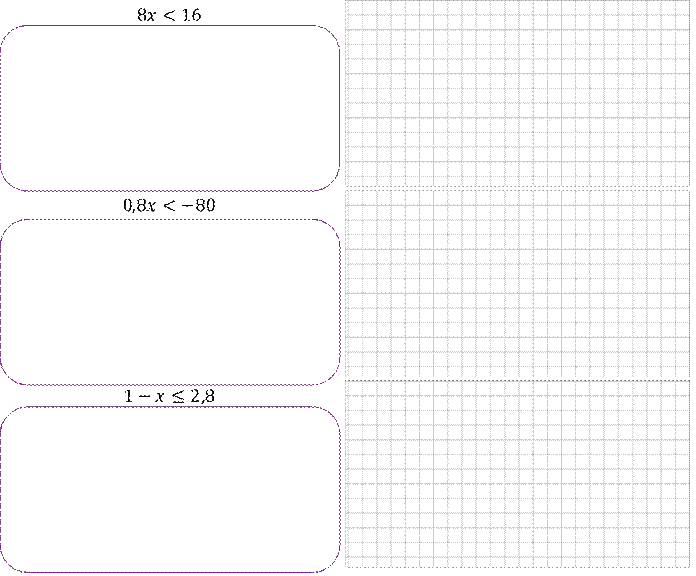
Задание 8. Решите линейные неравенства, изобразите его решение на числовой прямой и запишите ответ в виде числового промежутка.

Глава 5. Функции

5.1. Функция и ее свойства

Определение: функцией называют такую зависимость переменной 𝑦 от переменной

𝑥, при которой каждому значению переменной 𝑥 соответствует

единственное значение переменной 𝑦.

Переменную 𝑥 называют независимой переменной или аргументом.

Переменную 𝑦 называют зависимой переменной. Говорят также, что переменная 𝑦 является функцией от переменной 𝑥. Значения зависимой переменной называют значениями функции.

Все значения независимой переменной образуют область определения функции𝐷(𝑓).

Все значения, которые принимает зависимая переменная, образуют множество значений функции𝐸(𝑓). Определение:

Графиком функции называется множество всех точек координатной

плоскости, абсциссы которых равны значениям аргумента, а

ординаты – соответствующим значениям функции.

Графиком функции 𝑦 = 𝑘𝑥 + 𝑏 является прямая.

График функции называется гиперболой.

График функции 𝑦 = 𝑥² называется параболой.

Свойства функций Определение:

Нулями функции называется значение аргумента, при которых

функция обращается в нуль.

Определение: Промежутки, на которых функция сохраняет знак, называют промежутками знакопостоянства.

^{Определение:} Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

𝑓(𝑥₂) > 𝑓(𝑥₁)

^{Определение:} Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

𝑓(𝑥₂) < 𝑓(𝑥₁)

Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то – убывающей функцией. Промежутки возрастания и убывания функции называется промежутками монотонности функции.

5.2. Свойства некоторых видов функций

Свойства линейной функции:

Рассмотрим свойства функции, заданной формулой 𝑦 = 𝑘𝑥 + 𝑏, где 𝑘 ≠ 0 (рис.2)

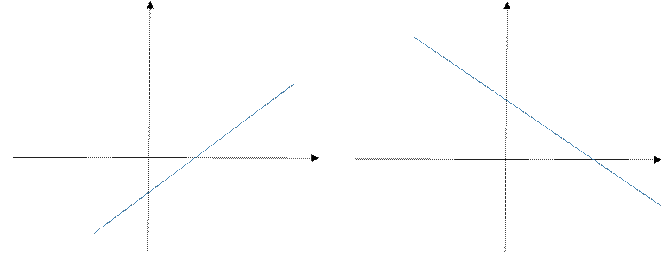
Рис.2

1. Функция определена при любых значениях переменной 𝑥, т.е. 𝐷(𝑦) = 𝑅

2. Значением функции может быть любое число, т.е. 𝐸(𝑦) = 𝑅.

3. Функция обращается в нуль при

4. При 𝑘 > 0 функция принимает отрицательные значения на промежутке

и положительные значения на промежутке .

Свойства функций

Рис.3

1. Функция определена для любых значений аргумента, кроме нуля, т.е.

2. Значение функции может быть любое число, кроме нуля, т.е.

3. Функция нулей не имеет.

4. Функция при принимает отрицательные значения на промежутке и положительные на промежутке .

5. При функция является убывающей на каждом из промежутков

. При функция является возрастающей на каждом

из промежутков.

Свойства функции (рис.4)

Рис.4

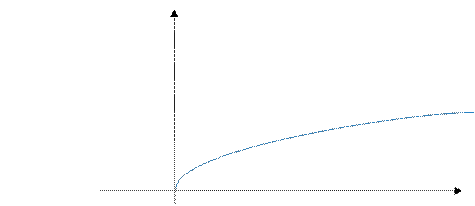
1. Функция определена при любых неотрицательных значениях аргумента, т.е. 𝐷(𝑦) = [0; +∞)

2. Функция принимает только неотрицательные значения, причем любое неотрицательное число может являться её значением, т.е. 𝐸(𝑓) = [0; +∞) 3. Функция обращается в нуль при 𝑥 = 0

4. Функция является возрастающей.

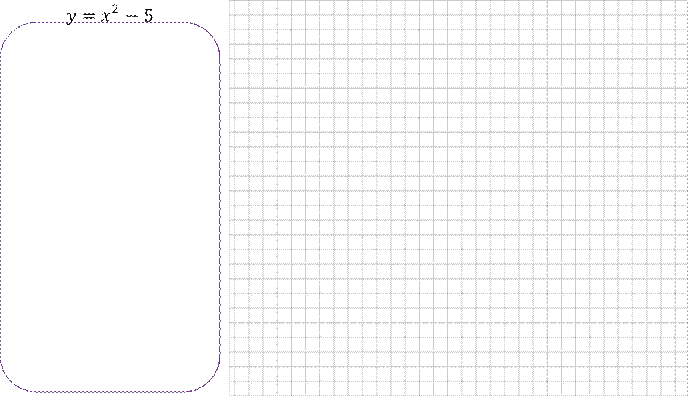
Задание 1. Используя шаблон параболы 𝑦 = 𝑥², постройте график функций:

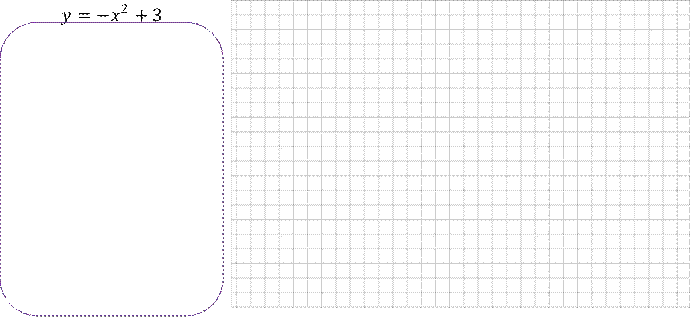
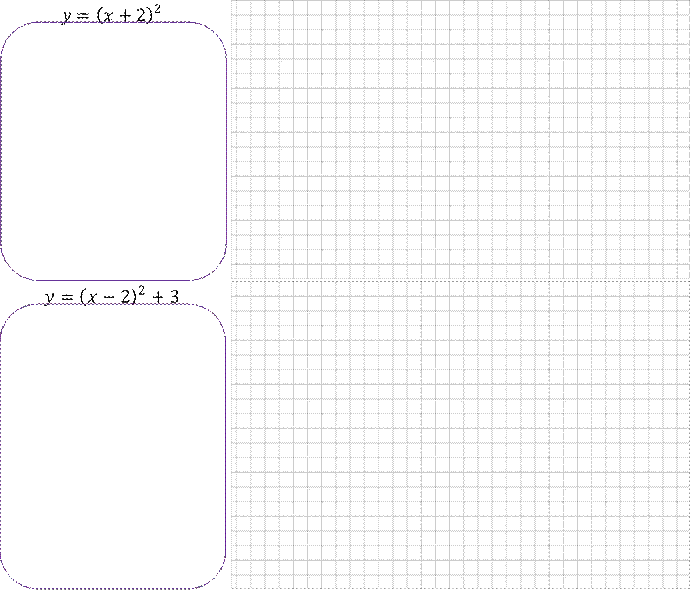
Задание 2. Постройте график функций

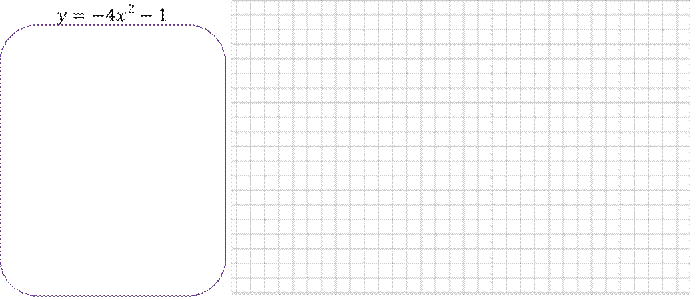
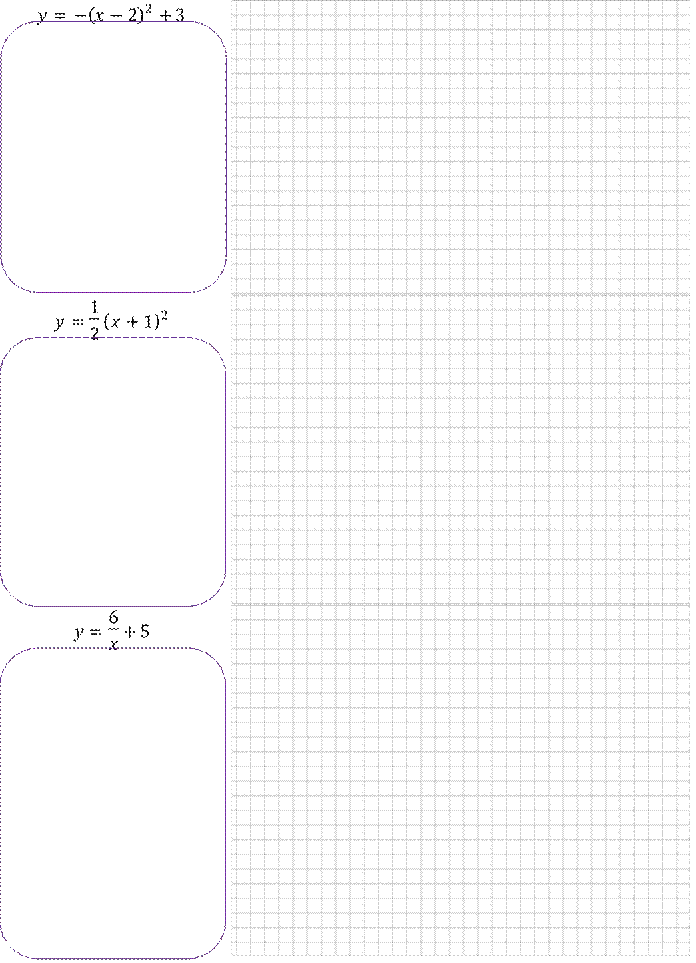
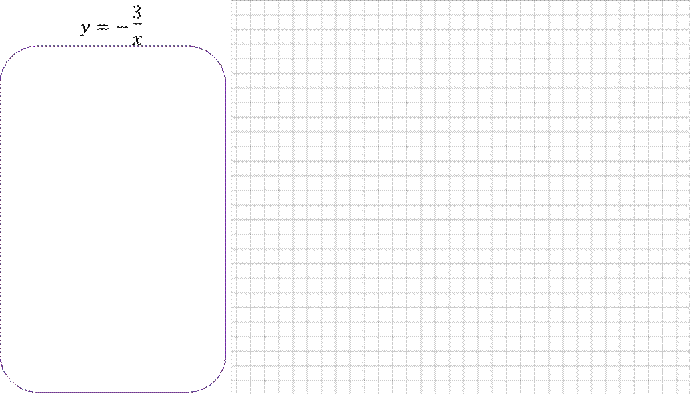
Задание 3. Для функции 𝑦 = 0,5𝑥² найдите:

а. значение 𝑦 при 𝑥 = −2; 0; 3 б. значения 𝑥, если 𝑦 = 8

в. 𝑦_наиб и 𝑦_наим на отрезке [−4; 0]

Задание 4. Принадлежит ли графику функции 𝑦 = 0,5𝑥² точка 𝐴(−10; 50)?

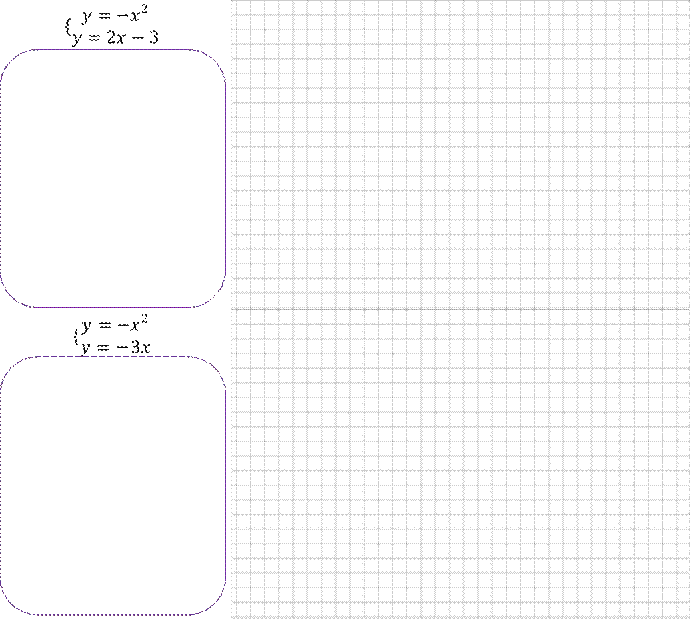
Задание 5. Решите графически систему уравнений:

Задание 6. Дана функция 𝑦(𝑥) = 6𝑥 + 2. Найдите 𝑦(𝑎 + 1) − 𝑦(𝑎).

Задание 7. Дана функция 𝑦(𝑥) = 3𝑥 − 6. Найдите 𝑦(𝑎 + 1) − 𝑦(𝑎).

Задание 8. Дана функция 𝑦(𝑥) = 7𝑥 + 4. Найдите 𝑦(𝑎 + 1) − 𝑦(𝑎).

Задание 9. Дана функция 𝑦(𝑥) = −7𝑥 − 1. Найдите 𝑦(𝑎 + 1) − 𝑦(𝑎).

Глава 6. Степень с целым показателем

6.1. Степень с целым показателем и ее свойства

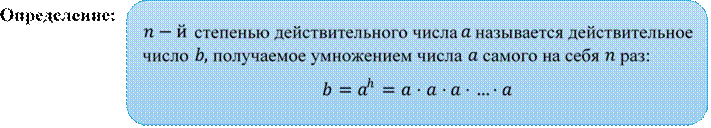
𝑎 – основание степени;

𝑛 – показатель степени.

Основные свойства степеней с целым показателем:

𝑎^𝑚⋅ 𝑎^𝑛= 𝑎^𝑚+ 𝑛

𝑎𝑚: 𝑎𝑛 = 𝑎𝑚−𝑛

(𝑎𝑛)𝑚 = 𝑎𝑛⋅𝑚

(𝑎 ⋅ 𝑏)^𝑛= 𝑎^𝑛⋅ 𝑏^𝑛

32: 3(−5) = 32−(−3) = 37 = 2187

(3 ⋅ 5)²= 15²= 225

(−2 ⋅ 𝑘 ⋅ 𝑙²)⁴= (−2)⁴⋅ 𝑘⁴⋅ (𝑙²)⁴= 16 ⋅ 𝑘⁴⋅ 𝑙⁸

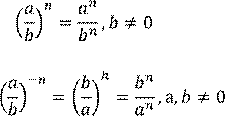
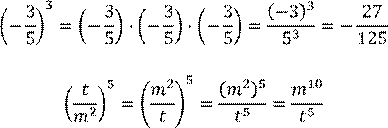
Задание 1. Преобразуйте выражение:

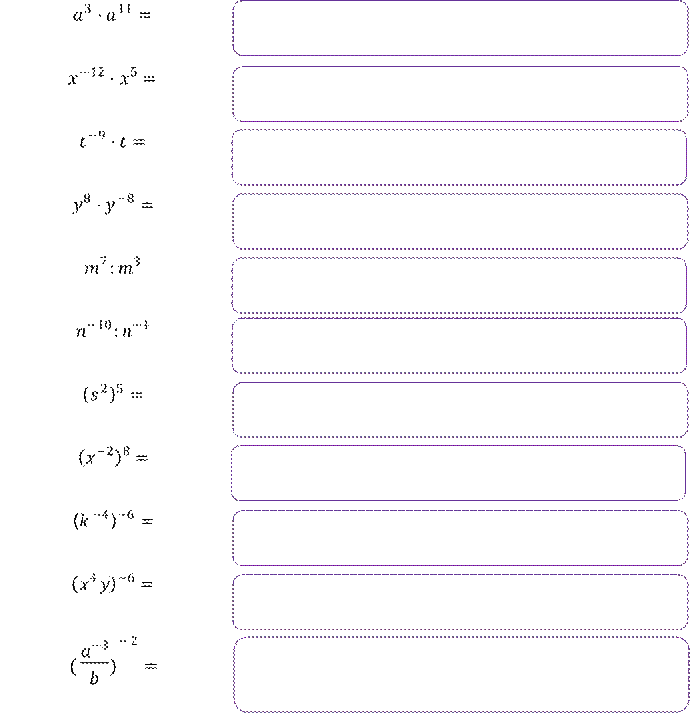
Задание 2. Вычислите:

Задание 3. Упростите:

Задание 4. Вычислите:

Задание 5. Вычислите:

Задание 6. Найдите значения выражения:

6.2 Стандартный вид чисел

Определение: Стандартным видом числа 𝑎 называют его запись в виде 𝑎 ⋅ 10𝑛, где

1 ≤ 𝑎 < 10 и 𝑛 – целое число. Число 𝑛 называется порядком числа 𝑎.

Представим в стандартном виде число 𝛼 = 4350000.

В числе 𝛼 представим запятую так, чтобы в целой части оказалась одна отличная от нуля цифра. В результате получится 4,35. Отделив запятой 6 цифр

справа, мы уменьшили число 𝛼 в 10⁶ раз. Поэтому 𝛼больше числа 4,35 в 10⁶ раз.

Отсюда:

𝛼 = 4, 35 ⋅ 10⁶

Запишите в стандартном виде число: 52000000 = 5.2 ⋅ 10⁷

Задание 1. Запилите в стандартном виде число:

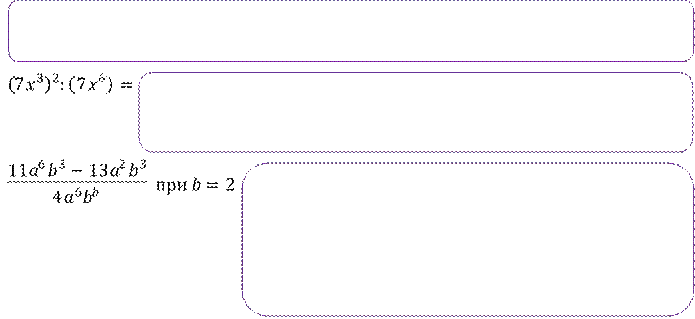
Задание 2. Выполните действия:

Итоговая проверочная работа по алгебре

за курс 8 класса Часть 1.

1. При 𝑝 = 0,2 значение дроби равно:

2. Сократите дробь

3. Найдите значение выражения: (1,84 + 0,96) ⋅ 3,5

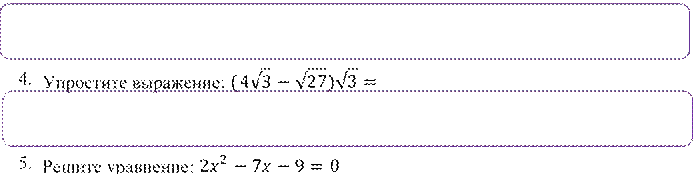
6. Решите неравенство: 64 − 6𝑥 ≥ 1 − 𝑥

7. Прямая 𝑦 = 𝑘𝑥 − 4 проходит через точку (3; −19). Найдите 𝑘.

Часть 2

8. Решите систему неравенств:

10. Два велосипедиста одновременно отправились в 96-километровые заезд. Первый ехал со скоростью, на 4 км/ч больше, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

Справочные материалы

Страницы для заметок

Библиографический список

1. Видеоурок: образовательный портал [Электронный ресурс]. – Режим доступа :

https://videouroki.net/ (дата обращения: 20.03.2024)

2. ИНФОУРОК: [Электронный ресурс]. – Режим доступа :

https://infourok.ru/itogovaya-kontrolnaya-rabota-po-algebre-umk-makarychev-8-klass-

5233182.html (дата обращения 10.04.24).

3. Макарычев Ю.М. Математика. Алгебра : 8-й класс : учебник / Ю.М. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – Москва : Просвешение, 2023. – 319с.

4. Математика и точка: сайт учителя Наиля Кашапова [Электронный ресурс]. –

Режим доступа : https://nailkashapov.ru/ (дата обращения: 03.04.2024

5. Математическое образование // Общедоступная электронная библиотека [Электронный ресурс]. – Режим доступа : https://www.mathedu.ru (дата обращения: 25.03.24).

6. Мордкович А.Г. Математика. 5 – 7 класс / А.Г. Мордкович. – М. : ООО «Издательство Оникс», 2006. – 112 с.

7. Мошкарева С.М. Справочное пособие «Алгебра весь школьный курс в таблицах» / С.М. Мошкачева. – Минск : Принтбук, 2021. – 299 с.

8. Сдам ГИА: решу

9. ЕГЭ // Образовательный портал для подготовки к ВПР. [Электронный ресурс].

– Режим доступа : https://math8-vpr.sdamgia.ru/ (дата обращения: 10.0.2024).

Рабочая тетрадь по алгебре для 8 класса

Оглавление Предисловие .

В этой тетради вы найдете необходимую теорию и разнообразные задания, которые помогут вам отточить навыки работы с алгебраическими выражениями, уравнениями, системами уравнений, а также познакомитесь…

Определение : - формулы, теоремы, алгоритмы, правила - место для написания решения, ответов