
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ СВЕРДЛОВСКОЙ ОБЛАСТИ
|
|
|
|
ГАПОУ СО «Нижнетагильский торгово-экономический колледж»
|
|
РАБОЧАЯ ТЕТРАДЬ
по дисциплине «Дискретная математика с элементами математической логики»
для студентов специальности 09.02.07 «Информационные системы и программирование»
Зятикова ТЮ
Нижний Тагил 2023 |
|
Пояснительная записка»
Рабочая тетрадь содержит задания для самостоятельной работы студентов, изучающих дисциплину «Дискретная математика с элементами математической логики».
Самостоятельная работа студентов при выполнении заданий в рабочей тетради преследует следующие цели:
– закрепление пройденного теоретического материала;
– отработка алгоритмов решения задач;
– применение теоретических знаний и освоенных алгоритмов к решению задач повышенной сложности.
Рабочая тетрадь содержит вопросы и задания по всем темам, предусмотренным рабочей программой по учебной дисциплине «Дискретная математика с элементами математической логики» и соответствуют требованиям ФГОС к обязательному минимуму содержания и уровню подготовки по специальности 09.02.07 «Информационные системы и программирование»
Задания представлены в следующих формах:
– заполнить пропуски;
– записать символически;
– заполнить таблицу;
– установить соответствие;
– выполнить тождественные преобразования;
– заштриховать область на рисунке;
– изобразить графически.
В рабочей тетради имеются задачи разного уровня сложности, предназначенные для решения как дома, так и на практическом занятии.
СОДЕРЖАНИЕ
Тема 1. Основы теории множеств
Тема 2. Алгебра высказываний
Тема 3. Основы языка и алгебры предикатов
Тема 4. Основы теории алгоритмов
ЛИТЕРАТУРА
1. Заполните пропуски:
1) Под множеством будем понимать ______________________________ _______________________________________________________________
2) Объекты, из которых состоит множество, называют ______________ _______________________________________________________________
3) Множества, состоящие из одних и тех же элементов, называются ___ ________________________________________________________________
4) Множество A называется подмножеством множества B, если _______ _________________________________________________________________
5) Пересечением множеств A и B называется _______________________ _______________________________________________________________
6) Объединением множеств A и B называется ______________________ _______________________________________________________________
7) Разностью множеств A и B называется ______________________ _______________________________________________________________
8) Универсальным множеством называется ________________________ __________________________________________________________________
9) Дополнением множества A называется _________________________ __________________________________________________________________
2. Запишите обозначения:
1) объект x содержится во множестве A ___________________________
2) объект x не является элементом множества A ____________________
3) Множества A и B равны ______________________________________
4) Множество A является подмножеством множества B ______________
5) Множества Aи B пересекаются ________________________________
6) Пересечение множеств Aи B __________________________________
7) Объединение множеств Aи B _________________________________
8) Разность множеств Aи B _____________________________________
9) Универсальное множество ____________________________________
10) Дополнение множества A ____________________________________
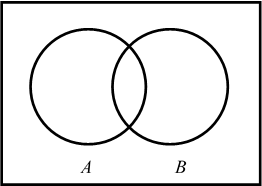
3. На диаграммах обозначьте следующие множества:
1) ![]()
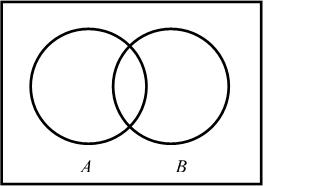
2) ![]()
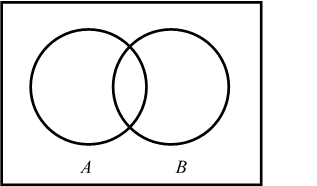
3) ![]()
4. С помощью диаграмм Эйлера-Венна решите задачи:
1) В классе обучаются 35 учеников. Из них 16 занимаются в секции по лёгкой атлетике; 17 – в футбольной секции; 11 – и в секции по лёгкой атлетике, и в футбольной. Сколько учеников не занимаются ни футболом, ни лёгкой атлетикой?
2) Из 100 учащихся, изучающих английский и немецкий языки, 85 изучают английский, 45 — немецкий. Сколько человек изучает оба языка?
3) В классе 30 человек, посещающих факультативные занятия по физике и математике. Известно, что углублённо изучают оба предмета 10 человек, а математику — 25. Сколько человек посещают факультативные занятия только по физике?
4) В классе каждый ученик занимается спортом в какой-либо из двух секций. 20 человек занимаются волейболом, 16 — плаванием, 7 — ходят в обе секции. Сколько человек в классе?
5) Из 100 студентов английский язык изучают 28, немецкий — 30, французский — 42, английский и немецкий — 8, английский и французский — 10, немецкий и французский — 5. Все три языка изучают три студента. Сколько студентов изучают только один язык? Сколько студентов не изучает ни одного языка?
6) На заседании присутствуют 29 академиков, 12 из них имеют бороду, а 18 — усы. У трёх академиков нет ни бороды, ни усов. Сколько академиков имеют и бороду, и усы?
1. Заполните пропуски:
1) Высказыванием называется ___________________________________ __________________________________________________________________ __________________________________________________________________ __________________________________________________________________
2) Отрицанием высказывания A называется ________________________ __________________________________________________________________ __________________________________________________________________ __________________________________________________________________
3) Конъюнкцией высказываний A и B называется ___________________ __________________________________________________________________ __________________________________________________________________ ________________________________________________________________
4) Дизъюнкцией высказываний A и B называется ___________________ __________________________________________________________________ __________________________________________________________________ ________________________________________________________________
5) Импликацией высказываний A и B называется ___________________ __________________________________________________________________ __________________________________________________________________ ________________________________________________________________
6) Эквиваленцией высказываний A и B называется __________________ __________________________________________________________________ __________________________________________________________________ ________________________________________________________________
2. Среди предложений подчеркните высказывания и укажите их значения истинности:
1) Москва — столица России.
2) Берлин — столица Франции.
3) Пейте дети молоко — будете здоровы!
4) Все студенты второго курса, успешно сдавшие летнюю сессию, будут переведены на третий курс;
5) Курица — не птица.
6) ![]() .
.
7) Для
всех действительных чисел a
и b имеет
место равенство: ![]()
8) Ты сделал домашнее задание по математической логике?
9) Сегодня хорошая погода.
10) Картины Пабло Пикассо слишком абстрактны.
3. Установите соответствие между названиями логических операций над высказываниями и их обозначениями:
|
|
Эквиваленция |
|
|
Импликация |
|
|
Конъюнкция |
|
|
Дизъюнкция |
|
|
Штрих Шеффера |
|
|
Сумма по модулю два |
|
|
Отрицание |
|
|
Стрелка Пирса |
4. Пусть высказывания a: «Сегодня идёт дождь»; b: «Завтра будет ясная погода». Запишите высказывания:
![]() ____________________________________________________________
____________________________________________________________
_____________________________________________________________
![]() __________________________________________________________
__________________________________________________________
_____________________________________________________________
![]() _________________________________________________________
_________________________________________________________
_____________________________________________________________
![]() ________________________________________________________
________________________________________________________
_____________________________________________________________
![]() ________________________________________________________
________________________________________________________
_____________________________________________________________
5. По значению истинности составного высказывания установить значение истинности высказывания a.
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
|
|
|
5) |
|
|
|
6) |
|
|
|
7) |
|
|
|
8) |
|
|
6. Среди перечисленных цепочек символов выберите формулы алгебры высказываний:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() .
.
7. Составив таблицы истинности, проверьте равносильность формул:
1) ![]() и
и ![]() .
.
|
a |
b |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
Вывод: формулы A и B _________________________________________.
2) ![]() и
и ![]()
|
a |
b |
с |
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
Вывод: формулы С и D ________________________________________.
8. Докажите следующие равносильности алгебры высказываний:
1) ![]()
|
a |
b |
с |
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
2) ![]()
|
a |
b |
с |
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
3) ![]()
|
a |
b |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
4) ![]()
|
a |
b |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
5) ![]()
|
a |
b |
|
|
|
0 |
0 |
|
|
|
0 |
1 |
|
|
|
1 |
0 |
|
|
|
1 |
1 |
|
|
6) ![]()
|
a |
b |
|
|
|
0 |
0 |
|
|
|
0 |
1 |
|
|
|
1 |
0 |
|
|
|
1 |
1 |
|
|
7) ![]()
|
a |
b |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
8) ![]()
|
a |
b |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
9) ![]()
|
a |
|
|
|
0 |
|
|
|
1 |
|
|
10) ![]()
|
a |
|
|
|
0 |
|
|
|
1 |
|
|
11) ![]()
|
a |
|
|
|
0 |
|
|
|
1 |
|
|
12) ![]()
|
a |
b |
|
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
1 |
1 |
|
|
|
|
13) ![]()
|
a |
b |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
14) ![]()
|
a |
b |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
15) ![]()
|
a |
b |
|
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
1 |
1 |
|
|
|
|
16) ![]()
|
a |
b |
|
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
1 |
1 |
|
|
|
|
9. Для каждой из нижеприведённых формул определить, является ли она ДНФ, КНФ, СДНФ, СКНФ:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
10. Данную формулу привести к ДНФ, КНФ, СДНФ, СКНФ.
1) ![]() ____________________________________________
____________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) ![]() ___________________________________________
___________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
11. По таблице истинности составить СДНФ, СКНФ (вариант выбирается в соответствии с номером по списку в журнале).
|
a |
b |
c |
d |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
a |
b |
c |
d |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
___________________________________________________________________________________________________________________________________________________________________________________________________
12. Упростить СДНФ, полученную в предыдущей задаче:
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
13. Является ли система функций полной:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ?
?
14. По истинностным значениям функции постройте СДНФ, СКНФ.
1) ![]() ;
;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
15. Ввести соответствующие обозначения и записать утверждения формулой алгебры высказываний:
1) Если студент решает все задачи из рабочей тетради и не имеет пропусков учебных занятий, то он получит отметку «отлично» по математической логике.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) Студент получает академическую стипендию тогда и только тогда, когда он учится на бюджетной основе и сдал сессию на «хорошо» и «отлично».
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
3) Завтра будет либо дождь, либо снег.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
4) Натуральное число делится на 5 тогда и только тогда, когда оно оканчивается на 0 или на 5.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
16. Решите задачу:
Четыре друга – A, B, C, D – решили провести свой отпуск в четырёх различных городах – Москве, Петербурге, Киеве и Ташкенте. В какой город должен поехать каждый из них, если имеются следующие ограничения:
– Если A не едет в Москву, то C не едет в Петербург.
– Если B не едет ни в Москву, ни в Ташкент, то A едет в Москву.
– Если C не едет в Ташкент, то B едет в Киев.
– Если D не едет в Москву, то B едет в Москву.
– Если D не едет в Петербург, то B едет в Москву?
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
17. Для релейно-контактной схемы составить функцию, описывающую её работу:
1)
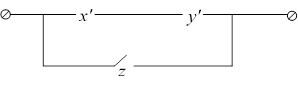
___________________________________________________________
2)
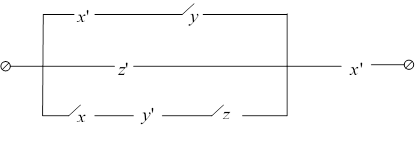
_____________________________________________________________
18. Для заданной функции составить релейно-контактную схему, её реализующую:
1) ![]() ;
;
2) ![]() _____________________________________
_____________________________________
_____________________________________________________________
_____________________________________________________________;
3) ![]() ___________________________________________
___________________________________________
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________.
19. Каждый из трёх членов комитета, голосуя «за», нажимает на кнопку. Построить по возможности более простую схему, через которую проходил бы ток и включал электрическую лампочку тогда и только тогда, когда не менее двух членов комитета голосуют «за».
|
x |
y |
z |
|
|
0 |
0 |
0 |
|
|
0 |
0 |
1 |
|
|
0 |
1 |
0 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
0 |
|
|
1 |
1 |
1 |
|
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1. Продолжите предложение:
1) Предикатом называется ______________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) Областью определения предиката называется ____________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
3) Областью истинности предиката называется _____________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
4) Отрицанием
предиката ![]() , определённого на множестве
, определённого на множестве ![]() называется
___________________________________________________
называется
___________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
5) Конъюнкцией
предикатов ![]() и
и ![]() ,
определённых на одном и том же множестве D,
называется _________________________________
,
определённых на одном и том же множестве D,
называется _________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
6) Дизъюнкцией
предикатов ![]() и
и ![]() ,
определённых на одном и том же множестве D,
называется _________________________________
,
определённых на одном и том же множестве D,
называется _________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
7) Импликацией
предикатов ![]() и
и ![]() ,
определённых на одном и том же множестве D,
называется _________________________________
,
определённых на одном и том же множестве D,
называется _________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
8) Эквиваленцией
предикатов ![]() и
и ![]() ,
определённых на одном и том же множестве D,
называется _________________________________
,
определённых на одном и том же множестве D,
называется _________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
9) Два предиката называются равносильными, если _________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
10) Предикат
![]() логически следует из предиката
логически следует из предиката ![]() , если _______
, если _______
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2. Среди предложений подчеркнуть те, которые являются предикатами:
1) Река x впадает в озеро Байкал.
2) ![]() .
.
3) ![]() .
.
4) ![]() .
.
5) ![]() .
.
6) Студент x учится в группе y.
7) ![]() .
.
8) Река Волга впадает в Каспийское море.
9) ![]() .
.
10) Город ![]() очень красив летом.
очень красив летом.
3. Изобразите область истинности предиката:
1) ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

2) ![]()
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

3) ![]()
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

4) ![]() , если
, если ![]() ,
, ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

5) ![]() , если
, если ![]() ,
, ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

6) ![]() , если
, если ![]() ,
, ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

7) ![]() , если
, если ![]() ,
, ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________

8) ![]() .
.

9) ![]() .
.

10) Даны предикаты ![]() и
и ![]() .
Изобразить области истинности следующих предикатов
.
Изобразить области истинности следующих предикатов
а) ![]()

б) ![]()
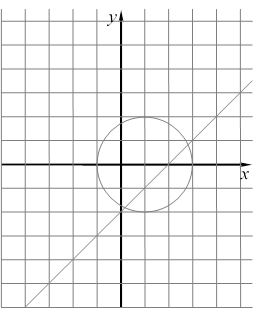
в) ![]()
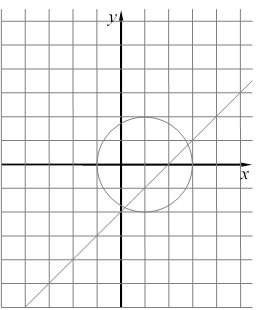
г) ![]()
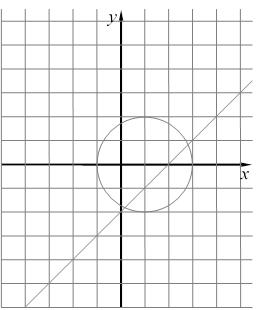
д) ![]()
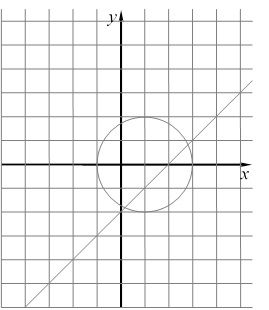
4. Определить, равносильны ли предикаты.
1) ![]() и
и ![]() на
множестве N.
на
множестве N.
2) ![]() и
и ![]() на
множестве Z.
на
множестве Z.
3) ![]() и
и ![]() на
множестве N.
на
множестве N.
4) ![]() и
и ![]() на
множестве N.
на
множестве N.
5. Из следующих предикатов с помощью кванторов постройте всевозможные высказывания и определите, какие из них истинны, а какие ложны:
1) ![]() ;
;
_____________________________________________________________
_____________________________________________________________
2) ![]() ;
;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
3) ![]() .
.
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
6. Запишите в виде формулы следующие высказывания, введя кванторы, одноместные предикаты и указав область значений предметной переменной:
1) «Ни один студент не опоздал на занятия»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) «Всякое комплексное число есть действительное или мнимое»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
3) «Существуют чётные тригонометрические функции, но любая тригонометрическая функция – периодическая»
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
4) «Некоторые прямоугольники являются правильными, а некоторые неправильными фигурами»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
5) «По крайней мере одно чётное число делится на 8»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
6) «Всякая
функция непрерывная на отрезке ![]() , сохраняет знак
или принимает нулевое значение»;
, сохраняет знак
или принимает нулевое значение»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
7) «Некоторые змеи ядовиты»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
8) «Все рациональные числа действительные»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
9) «Некоторые рациональные числа не являются действительными»;
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
1. Перечислите основные свойства алгоритмов и поясните их:
1) ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
3) ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
4) ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
5) ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2. Приведите пример алгоритма заданного:
1) словесно:
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2) формулой:
_____________________________________________________________
3) Таблично:
4) блок-схемой.
3. Согласно ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» определите название и назначение каждого блока:
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() ________________________________________________
________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() ________________________________________________
________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _______________________________________________
_______________________________________________
_____________________________________________________________
![]() _______________________________________________________
_______________________________________________________
_____________________________________________________________
![]() ________________________________________________________
________________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
 _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() ________________________________________________
________________________________________________
_____________________________________________________________
![]() ________________________________________________
________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _______________________________________________________
_______________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() _________________________________________________
_________________________________________________
_____________________________________________________________
![]() ________________________________________________________
________________________________________________________
_____________________________________________________________
![]() ______________________________________________________
______________________________________________________
_____________________________________________________________
Основная
1. Игошин В. И. Задачи и упражнения по математической логике и теории алгоритмов / В. И. Игошин. – М.: Издательский центр «Академия», 2005. – 304 с.
2. Игошин В. И. Математическая логика и теория алгоритмов. – М.: Издательский центр «Академия», 2004. – 448 с.
3. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: ФИЗМАТЛИТ, 2004. – 240 с.
4. Спирина М. С. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М. С. Спирина, П. А. Спирин. – М.: Издательский центр «Академия», 2010. – 368 с.
Дополнительная
1. Лихтарников Л. М., Сукачева Т. Г. Математическая логика. – СПб, 1999. – 288 с.
2. Мощенский В.А. Лекции по математической логике. – Минск, 1973. – 160 с.
Интернет-ресурсы
http://it.kgsu.ru/TI_4/oglav.html
http://it.kgsu.ru/TI_5/falg_004.html
http://it.kgsu.ru/TI_5/falg_005.html
http://tablica-istinnosti.ru/logika.html
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.