Система задач по теме Прогрессия для подготовки к ОГЭ

Управление образования и молодежной политики администрации Городецкого муниципального района Нижегородской области

муниципальное бюджетное общеобразовательное учреждение

«Строчковская средняя школа»

Система задач

по теме

«Прогрессии»

для подготовки к заданию №14 ОГЭ

Подготовила:

Тихонова М. Н.

учитель математики

2025 год

Введение.

    Суть этого задания теперь состоит в том, что надо сначала определить, о какой последовательности идёт речь в задании, и только потом начинать применять формулы. Для этого надо искать в тексте условия задачи ключевые слова "каждый, следующий, предыдущий ...", "на ... больше (меньше)", "в ... раз больше (меньше)" и, опираясь на их смысл, вспоминать определения последовательностей и прогрессий.

    В настоящее время проблема применения математических знаний для исследования явлений и процессов, описываемых в других областях науки и практики, является крайне актуальной. Методы математики глубоко проникают в различные области знаний. Владение конкретными математическими знаниями помогает в практической деятельности, формирует представление о математике как о части человеческой культуры.

    В школьном куре алгебры 9 класса изучается тема «Арифметическая и геометрическая прогрессии». Важность этой небольшой темы заключается в широких возможностях ее применения для решения различных задач, реально встречающихся в бытовой и профессиональной деятельности человека. Подборка задач в данном дидактическом материале такова, что ученики повторяют теорию по теме «Прогрессии» и решение задач на применение формул, знакомятся с задачами из разных сфер жизни, где встречаются прогрессии,  успевают оценить применение формул прогрессий и выработать навыки решения практико – ориентированных задач на применение прогрессий.

Теория по прогрессиям.

Вопросы для обсуждения.

1.     Какую последовательность называют арифметической прогрессией? Приведите примеры арифметических прогрессий.

2.     Как найти разность арифметической прогрессии?

3.     Сформулируйте свойство арифметической прогрессии.

4.     Как написать формулу n-го члена арифметической прогрессии?

5.     По каким формулам вычисляют сумму первых n членов арифметической прогрессии?

6.     Сформулируйте определение геометрической прогрессии. Приведите примеры геометрических прогрессий.

7.     Как найти знаменатель геометрической прогрессии?

8.     Сформулируйте свойство геометрической прогрессии.

9.     Как написать формулу n-го члена геометрической прогрессии?

10. По каким формулам вычисляют сумму первых n членов геометрической прогрессии?

Во время обсуждения заполняем таблицы.

Устные упражнения.

1.     Какая из последовательностей является арифметической прогрессией?

1)   ; ;;;

2)  ; 2,25; -0,125;-2,5;

3)  ; 3(3+5); 4(4+5);

4)   (2²+1); (3²+1); (4²+1).

2.     Является ли геометрической прогрессией последовательность:

1) 1; ; ; ; …;

2)  5; -25; 125; -625;…;

3)  1; 1; 1; 1;…;

4)  3; 1; 3; 1; …;

5)  1; 0,2; 0,4; 0,8;…;

3.     Заполните пустые ячейки в таблицах.

4.     Выполнить задания:

1)    Решите уравнение, в котором слагаемые, записанные в левой части, образуют арифметическую прогрессию:     30+27+24+…+х = 162.

2)    Найдите четыре первых члена геометрической прогрессии, если разность между третьим и первым членами этой прогрессии равна 12, а разность между пятым и третьим членами равна 48.

3)    Третий член геометрической прогрессии равен 4. Найдите произведение первых пяти ее членов.

4)    Первый и третий члены возрастающей арифметической прогрессии – корни квадратного уравнения   х² – 2х – 8 = 0. Найдите сумму первых двадцати шести членов этой прогрессии.

5.     Тренировочные задания (домой):

1) Решите уравнение, в котором слагаемые, записанные в левой части, образуют арифметическую прогрессию:     2+6+10+…+х = 450.

2) Сумма трех членов арифметической прогрессии равна 54. Если второй член прогрессии уменьшить на 9, а третий – на 6, то получим геометрическую прогрессию. Какой была арифметическая прогрессия?

Задачи на арифметическую прогрессию.

1.     В амфитеатре 13 рядов. В первом ряду 22 места, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в одиннадцатом ряду амфитеатра?

Решение: В условии задачи встречаются слова, что в каждом следующем больше на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой

(a_n) – a₁=22, d = 3,n=13, а₁₁ -?

а₁₁ = а₁ + 10d = 22 + 10•3 = 52.

Ответ: в одиннадцатом ряду 52 места.

2.     При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 6° C. Найдите температуру вещества (в градусах Цельсия) через 4 минуты после начала проведения опыта, если его начальная температура составляла − 7° C .

Решение: В условии задачи встречаются слова, что  каждую минуту уменьшалась на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой

(a_n) – a₁=-7, d = -6,n=4, а₄ -?

а₄ = а₁ + 3d = -7 + 4•(-6) = -31.

Ответ: -31 градус.

3.     В амфитеатре 14 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в восьмом ряду 36 мест. Сколько мест в последнем ряду амфитеатра?

Решение: В условии задачи встречаются слова, что в каждом следующем больше на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой

 (a_n) – a₅=27, а₈= 36,n=14, а₁₄ -?

решаем систему: a₁  = 13, d= 3

a₁₄ = a₁+13d= 13 + 13•3= 52

Ответ: в последнем  ряду 52 места.

4.     В амфитеатре 10 рядов. В первом ряду 19 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение: В условии задачи встречаются слова, что в каждом следующем больше на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой

(a_n) – a₁=19, d = 3,n=10, S₁₀ -?

а₁₀ = а₁ + 9d = 19 + 9•3 = 46;S₁₀= (a₁+a₁₀)5=(19+46)•5=325

Ответ: 325 мест в амфитеатре.

5.     Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 9 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?

Решение: В условии задачи встречаются слова, что  каждую следующую секунду больше на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой

(a_n) – a₁=9, d = 10,n=5,a₅-?

а₅ = а₁ + 4d = 9 + 4•10 = 49.

Ответ: 49 метров пролетит камень.

6.     В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной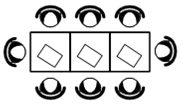

линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 16 квадратных столиков вдоль одной линии?

7.     На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 190.

8.     Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.

Решение: В условии задачи встречаются слова, что  ежедневно увеличивает норму  на одно и то же число. И это значит, что мы имеем арифметическую прогрессию в которой

(a_n) – a₁ +a_n=60,S_n=240, n-?

S_n= n   _,         240= •n, n = 8

Ответ: 8 дней бригада красила забор

9.     Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.

Решение: В условии задачи встречаются слова, что  ежедневно увеличивает норму  на одно и то же число. И это значит, что мы имеем арифметическую прогрессию в которой

(a_n) – a₁=3, n= 10,S_n=500, a_n-?

S_n= n   _,         500= •10, a₁₀ = 97

Ответ: в последний день проложили 97 метров тоннеля.

10. Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.

Решение: В условии задачи встречаются слова, что  ежедневно решает больше  на одно и то же число. И это значит, что мы имеем арифметическую прогрессию в которой

(a_n) – a₁=5, n= 14,S_n=434, a_n-?

S_n= n   _,         434= •40, a₁₄ = 57

Ответ: в последний день Вася решил 57 задач..

11. Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 14 дней.

Решение: В условии задачи встречаются слова, что  ежедневно увеличивает норму  на одно и то же число. И это значит, что мы имеем арифметическую прогрессию в которой

(a_n) – a₁=2,n=14,S₁₄=210, a₉-?

S₁₄₌ n   _,         210= •14, d = 2

а₉ = а₁ + 8d = 2 + 8•2 = 18.

Ответ: 18 тонн щебня перевезено за девятый день.

12. Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв в день 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Решение: Из содержания данной задачи видно, что по схеме лекарство увеличивалось с каждым днем на одно и то же количество капель – на 3 капли, следовательно, это арифметическая прогрессия

(a_n) – a₁=3,d=3,сколько пузырьков лекарства-?

a_n=a₁ +(n-1)d , 30= 3 +(n-1)(3), n=10, S₁₀=165

a_n=a₁ +(n-1)d , 3= 27 +(n-1)(-3), n=9, S₉=135

Лекарство= 165 капель+ 3•30 капель+135 капель=390 капель,

нужно 2 пузырька.

Ответ: 2 пузырька лекарства.

Задачи на геометрическую прогрессию.

1.     У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 15 см?

Решение: Из содержания данной задачи видно, что после каждого отскока уменьшалось в одно и то же количество раз , следовательно, это геометрическая прогрессия

b_n  › b₁•q^n-1, ()^n-1 ‹ , n=4

Ответ: после 4 отскока.

2.     У Яны есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 240 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 5 см?

3.     В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 7 минут. В начальный момент масса изотопа составляла 160 мг. Найдите массу изотопа через 28 минут. Ответ дайте в миллиграммах.

4.     В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 18 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 60 минут после начала эксперимента. Ответ дайте в миллиграммах.

5.     В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б. В начальный момент масса изотопа А составляла 480 мг. Найдите массу образовавшегося изотопа Б через 35 минут. Ответ дайте в миллиграммах.

6.     Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?

Решение: Поскольку каждый год прибыль увеличивалась на 300%, она увеличивалась в 4 раза по сравнению с предыдущим годом. И это значит, что мы имеем геометрическую прогрессию в которой

Ищем четвертый член геометрической прогрессии: за 2003 год Бубликов заработал  5000•4³= 320000руб.

Ответ: 320000 рублей за 2003 год.

7.     Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?

Решение: Каждый год прибыль компании «Альфа» составляла 200% от капитала предыдущего года, значит, капитал каждый год составлял 300% от капитала предыдущего года. В конце 2006 года на счёте компании «Альфа» была сумма

 5000•3^2006-2001=   5000•3⁵= 1215000долларов.

Каждый год прибыль компании «Бета» составила 400% от капитала предыдущего года, значит, капитал каждый год составлял 500% от капитала предыдущего года. В конце 2006 года на счёте компании «Бета» была сумма

10000•5^2006-2003=   10000•5³= 1250000долларов.

    Таким образом, капитал компании «Бета» был на 35 000 долларов                                      больше.

            Ответ: 35000 долларов больше.

8.     Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т. д. Сколько бактерий окажется в организме через 4 часа, если по истечении четвертого часа в организм из окружающей среды попала еще одна бактерия?

Решение: В четырех часах двенадцать 20-минутных интервалов, следовательно, произойдет 12 циклов деления бактерий. Количество бактерий составляет геометрическую прогрессию с первым членом 1 и знаменателем 2, поэтому через 12 циклов деления количество бактерий составит

b₁₃ = b₁•q¹² = 1•2¹² = 4096, после того, как в организм попадет еще одна бактерия, их количество составит 4096 + 1 = 4097.

Ответ: 4097 бактерий.

Тренировочные задачи на арифметическую и геометрическую прогрессии.

1.     При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется 0,4 г осадка. Найдите массу осадка (в граммах) в растворе спустя девять минут после начала реакции.

2.     При проведении химического опыта реагент равномерно охлаждали на 7,3 °С в минуту. Найдите температуру реагента (в градусах Цельсия) спустя 6 минут после начала проведения опыта, если начальная температура составляла –8,4 °С.

3.     Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 5 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 10 минут?

4.     Для получения витамина D могут быть рекомендованы солнечные ванны. Загорать лучше утром до 10 часов или вечером после 17 часов. Михаилу назначили курс солнечных ванн. Михаил начинает курс с 10 минут в первый день и увеличивает время этой процедуры в каждый следующий день на 12 минут. В какой по счету день продолжительность процедуры достигнет 1 часа 10 минут?

5.     В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7–й день акция стоила 813 рублей, а в 12–й день – 908 рублей.

6.     Ира зовет гостей на день рождения в ресторан. В ресторане в наличии имеются лишь квадратные столики, за которыми умещается не более 4 человек. Если соединить два квадратных стола, то получится стол, за которым умещается до 6 человек. На рисунке изображен случай, когда соединили 3 квадратных столика. В этом случае получился стол вместимостью до 8 человек. Найдите наибольшую вместимость стола, который получится при соединении 11 квадратных столиков в ряд.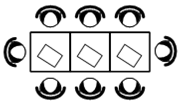   

7.     К концу 2007 года в городе проживало 64 100 человек. Каждый год число жителей города возрастало на одну и ту же величину. В конце 2016 года в городе проживало 72 470 человек. Какова была численность населения этого города к концу 2013 года?

8.     В 11:00 часы сломались и за каждый следующий час отставали на одно и то же количество минут по сравнению с предыдущим часом. В 21:00 того же дня часы отставали на сорок минут. На сколько минут отставали часы спустя 24 часа после того, как они сломались?

9.     Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в сумме 8,5 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 51 метру.

10. В амфитеатре 20 рядов. В первом ряду 58 мест, а в каждом следующем ряду на 2 места меньше, чем в предыдущем. Сколько всего мест в амфитеатре?

11. Грузовик перевозит партию щебня массой 216 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 7 тонн щебня. Определите, сколько тонн щебня было перевезено на восьмой день, если вся работа была выполнена за 12 дней.

12. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах – одно штрафное очко, за каждый последующий – на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 13,5 штрафных очков?

13. Врач прописал больному капли по следующей схеме: в первый день 10 капель, а в каждый следующий день – на 5 капель больше, чем в предыдущий, до тех пор, пока дневная доза не достигнет 40 капель. Такую дневную дозу (40 капель) больной ежедневно принимает пять дней, а затем уменьшает приём на 5 капель в день до последнего дня, когда больной принимает последние десять капель. Сколько пузырьков лекарства нужно купить на весь курс, если в каждом пузырьке 10 мл лекарства, то есть 200 капель?

14. Каждое простейшее одноклеточное животное инфузория–туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после пятикратного деления их стало 800?

15. Митя играет в компьютерную игру. Он начинает с 0 очков, а для перехода на следующий уровень ему нужно набрать не менее 15 000 очков. После первой минуты игры добавляется 2 очка, после второй – 4 очка, после третьей – 8 очков и так далее. Таким образом, после каждой следующей минуты игры количество добавляемых очков удваивается. Через сколько минут Митя перейдет на следующий уровень?

Заключение.

В предложенной системе рассмотрены задачи о практическом применении последовательностей, а именно арифметической и геометрической прогрессии; основные определения и формулы; рассмотрены примеры применения арифметической и геометрической прогрессии в различных отраслях, решены задачи из различных источников на применение арифметической и геометрической прогрессии с практическим содержанием.

Список ИКТ-ресурсов для учителя и литературы

1. http://www.prosv.ru – Сайт издательства «Просвещение» (рубрика «Математика»)

2. http:/www.drofa.ru – Сайт издательства Дрофа (рубрика «Математика»)

3. Сайт Федерального института педагогических измерений (ФИПИ): http://www.fipi.ru/. Здесь публикуется много материалов о ОГЭ и тестовых технологиях в образовании в целом, в том числе есть демо-версии ОГЭ с 2004 г. (новые демо-версии сначала появляются именно здесь). 4. Информационная поддержка ОГЭ и ЕГЭ: http://www.ctege.info/. Мощный ресурс, свежие новости, есть библиотека книг по подготовке к ГИА

 5. Сайт информационной поддержки ЕГЭ и ОГЭ в компьютерной форме: http://www.ege.ru/

6. Сообщество взаимопомощи учителей: http://pedsovet.su/. Много тренажеров по подготовке, созданных учителями, по адресу: http://pedsovet.su/load/62

7. Большая коллекция материалов по ОГЭ и подготовке к ним: http://www.alleng.ru/

 8. Сборник заданий ОГЭ на "Яндексе Репетитор" - https://yandex.ru/tutor/?exam_id=2

 9. Каталоги прототипов экзаменационных заданий с решениями, система тестов-тренажеров для подготовки к экзаменам. Учитель может сгенерировать тесты самостоятельно и оценивать результаты учеников - https://inf-oge.sdamgia.ru

10. В. С. Крамор Задачи на составление уравнений и методы их решения

11.Математика ОГЭ под редакцией И. В. Ященко

Скачано с www.znanio.ru