административный

(территориальный округ) образовательная организация

учебный предмет уровень образования

 класс

количество часов  уровень форма обучения

Количество зачетов

учитель: примерная (авторская) программа, на основе которой разработана рабочая программа учебный год

СОДЕРЖАНИЕ

                                                                                                                                                                                            страница

  ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ДИДАКТИЧЕСКОГОМАТЕРИАЛА                      3

  ЗАЧЕТЫ В СООТВЕТСТВИИ С ТРЕБОВАНИЯМИ МОДУЛЕЙПРОГРАММЫ                    4

ЗАЧЕТ 1  ОСНОВЫ ПЛАНИМЕТРИИ. АКСИОМЫ СТЕРЕОМЕТРИИ                                           7

ЗАЧЕТ 2  ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ                                                                  8

ЗАЧЕТ 3  ПЕРПЕНДИРУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ                                                  15

ЗАЧЕТ 4  РЕШЕНИЕ ПРАКТИЧЕСКИХ ЗАДАЧ                                                                                           21

  ЛИТЕРАТУРА                                                                                                                                                                      22

  ПРИЛОЖЕНИЕ                                                                                                                                                                   23

ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ДИДАКТИЧЕСКОГО МАТЕРИАЛА

Данные дидактические материалы предназначены для подготовки или проведения зачетов по темам 10 класса предмета геометрия.

В данный сборник для зачетов 1-3 собраны задания разных уровней. Уровень сложности определен * и соответственно оценивается:

— ** - очень сложный уровень – выполнение оценивается в 3 балла; — *- сложный уровень – выполнение оценивается в 2 балла; — без * - простой - выполнение оценивается в 2 балл.

Задачи для зачета 4 оцениваются по 5 баллов за каждую правильно решенную.

В приложении приведена таблица перевода набранных баллов в оценку для каждого зачета.

ЗАЧЕТЫ В СООТВЕТСТВИИ С ТРЕБОВАНИЯМИ МОДУЛЕЙ ПРОГРАММЫ 

Зачет 1 по МОДУЛЮ «ВВОДНО-КОРРЕКТИВНЫЙ»

Успешное освоение данного модуля оценивается по двум результатам:

Результат 2 (аксиомы стереометрии). Решать задачи с использованием соответствующих аксиом стереометрии.

Критерии оценивания результата 2:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем планиметрии;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 11 вопросов зачета и решение одной задачи. Все критерии оценки результата охвачены от а до г.

Зачет 2 по МОДУЛЮ «ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ»

Успешное освоение данного модуля оценивается по четырем результатам:

Результат 1. Решать задачи с применением теорем параллельности прямых и плоскостей.

Критерии оценивания результата 1:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем параллельности прямых и плоскостей;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 17 вопросов зачета (первые 17) и решение одной задачи. Все критерии оценки результата охвачены от а до г.

Результат 2. Решать задачи с применением теорем параллельности плоскостей.

Критерии оценивания результата 2:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем параллельности плоскостей;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 11 вопросов зачета (с 18 по 28) и решение одной задачи. Все критерии оценки результата охвачены от а до г.

Результат 3. Решать задачи на вычисление параметров тетраэдра/ параллелепипеда с использованием соответствующих теорем.

Критерии оценивания результата 3:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления;

Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем планиметрии;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 6 вопросов зачета (с 30 по 35) и решение одной задачи на вычисление. Все критерии оценки результата охвачены от а до г.

Результат 4. Выполнить задачу на построение сечения тетраэдра/ параллелепипеда с использованием соответствующих теорем.

Критерии оценивания результата 4:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Ход построения сечения выполнен правильно с обоснованием правил и теорем планиметрии;

В) Построение сечения выполнено правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 1 вопросов зачета (36) и выполнение одной задачи на построение сечения. Все критерии оценки результата охвачены от а до в.

Зачет 3 по МОДУЛЮ «ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ»

Успешное освоение данного модуля оценивается по двум результатам:

Результат 1. Решать задачи с применением теорем перпендикулярности прямых и плоскостей.

Критерии оценивания результата 1:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем перпендикулярности прямых и плоскостей;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 17 вопросов зачета (первые 17) и решение одной задачи. Все критерии оценки результата охвачены от а до г.

Результат 2. Решать задачи с применением теорем перпендикулярности плоскостей.

Критерии оценивания результата 2:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем перпендикулярности плоскостей;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменные ответы на 11 вопросов зачета (с 18 по 28) и решение одной задачи. Все критерии оценки результата охвачены от а до г.

Зачет 4 по МОДУЛЮ «РЕШЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ»

Успешное освоение данного модуля оценивается по двум результатам:

Результат 1. Решать практическую задачу с применением теорем параллельности и перпендикулярности прямых и плоскостей.

Критерии оценивания результата 1:

А) «Дано» записано правильно в соответствии с условием задачи и правилами оформления; Б) Рисунок к задаче выполнен правильно в соответствии с условием задачи и правилами оформления;

В) Ход решения простроен правильно с обоснованием правил и теорем параллельности и перпендикулярности прямых и плоскостей;

Г) Вычисления и ответ записаны правильно.

Описание уровней: уровни этого результата полностью охвачены в критериях оценки результата.

Требования к доказательствам: письменно решить шесть практических задач. Все критерии оценки результата охвачены от а до г.

ЗАЧЕТ 1. ОСНОВЫ ПЛАНИМЕТРИИ. АКСИОМЫ СТЕРЕОМЕТРИИ

Закончи предложение, вписав пропущенное слово:

1.             Истина, которая принимается без доказательства _____________.

2.             Тела, объемы которых равны, называют _______________.

3.             Через две пересекающиеся прямые можно провести _____________________.

4.             *Что устойчивее: табуретка на трѐх ножках или стул на четырѐх ножках?

(В ответе напиши просто: «табуретка» или «стул») _______________. Выберите правильный ответ:

5.             Точки A, B, M, N не лежат в одной плоскости. Пересекаются ли плоскости, проходящие через точки A, B, M и через точки B, N, A по прямой NB?

                А) Нет            Б) Да

6.             Могут ли только 3 вершины A, B, C параллелограмма ABCD находиться в одной плоскости?

                А) Нет            Б) Да

7.             Верно ли, что через 3 точки, которые находятся на одной прямой, проходит плоскость и только одна?

                А) Нет            Б) Да

8.             Четыре точки A, D, B, C не находятся в одной плоскости. Верно ли, что любые три точки из данных четырѐх находятся на одной прямой?

                А) Нет            Б) Да

9.             Сколько прямых, которые не пересекают прямую a, можно провести в пространстве через точку K, если известно, что Ka? А) Три;  Б) Бесконечное множество; В) Одну;  Г) Две;  Д) ни одну.

10. 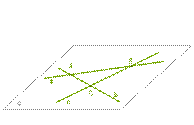        Даны 2 различные прямые a и b, которые пересекаются в точке A.

a)   Возможно ли что все прямые, пересекающие данные две прямые и не проходящие через точку A, не находятся в одной плоскости?

                         А) Нет                 Б) Да

b)   Могут ли две различные плоскости иметь только одну общую точку?

                         А) Нет                 Б) Да

c)   Две плоскости α и β пересекаются по прямой m. Прямая a находится в плоскости α, а прямая b находится в плоскости β. Прямые b и a пересекаются в точке A. Точка A принадлежит прямой m?

                         А) Нет                 Б) Да

11.         **Во всех задачах должны быть определено количество плоскостей однозначно.

a)   Определи, какое максимальное возможное количество разных плоскостей можно провести через 8 данных параллельных прямых в пространстве (никакие три прямые не лежат в одной плоскости)?

Ответ:_______________

b)   Определи, какое максимальное возможное количество разных плоскостей можно провести через 3 данных лучей в пространстве с общей начальной точкой (никакие два луча не лежат на одной прямой, никакие три лучи не лежат в одной плоскости)?

Ответ:_______________

c)   Определи, какое максимальное возможное количество разных плоскостей можно провести через 6 данных точек в пространстве (никакие три точки не лежат на одной прямой, никакие четыре точки не лежат в одной плоскости)?

                                Ответ:_______________                                                 

ЗАЧЕТ 2. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Выберите или впишите правильный ответ:

1.        Основание AB трапеции ABCD лежит в плоскости α. Основание CD не лежит в этой плоскости. Дополни данные предложения, которые характеризуют взаимное расположение данных прямых и плоскости α. 

a)      Tак как прямая DB имеет общую точку с данной плоскостью, то эта прямая по отношению плоскости α:

А) параллельная плоскости;

Б) пересекается с плоскостью;

В) находится в плоскости.

b)      Прямая CD параллельна прямой AB в данной плоскости, значит она ____________.

2.        Дан треугольник ABC. На сторонах AB и AC соответственно отложены точки D и E так, что DE=7 см и AD/BD=9/4. Через точки B и C проведена плоскость α, которая параллельна отрезку DE.

3.        *Точка C принадлежит отрезку AB. Через точку A проведена плоскость, через точки B и C проведены параллельные прямые, которые пересекают данную плоскость соответственно в точках B₁ и C₁.

Вычисли длину отрезка CC₁, если AC:BC=2:5 и BB₁=2  

(Если необходимо, дробь сократи)

Ответ: CC

4.        Точки M, N, P и Q являются соответственно серединами отрезков AD,CD, BC и AB.

Вычислите периметр четырѐхугольника MNPQ, если AC= 11 см и BD= 17 см.

Ответ: периметр четырехугольника MNPQ равен ______см.

5.        Точка O не находится в плоскости треугольника ABC. Точки

D, E, F являются соответственно серединами отрезков AO, BO, CO. Вычисли площадь треугольника DEF, если площадь треугольника ABC равна 292 см².

Ответ: площадь треугольника DEF равна______см²

6.        Будут ли параллельны плоскости, проведѐнные через две скрещивающиеся прямые d и c?

                А) Нет                        Б) Да

7.        Используя данный куб

1.      Определи взаимное расположение плоскостей AA₁B и

DD1C1  

А) пересекаются;

Б) параллельны.

2.      Назови плоскость параллельную DCB

                        А) A₁B₁C₁;           Б) DD₁C₁;       В) A₁D₁D;      Г) ABC;          Д) BB₁C₁.

8.        Определи взаимное расположение данной прямой и плоскости.

a)      Прямая AA₁ и плоскость (BCD):

А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

b)      Прямая BC и плоскость (ABC):

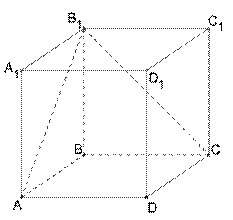А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

c)      Прямая CC₁и плоскость (ABD):

А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

d)      Прямая CB₁ и плоскость (BB1C1):

А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

e)      Прямая AB₁ и плоскость (BCD):

А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

9.        *Определи взаимное расположение данной прямой и плоскости.

a) 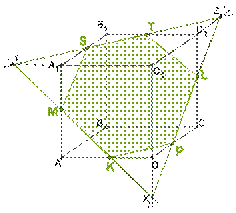     Прямая DD₁ и плоскость (ADD₁):  А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

b)      Прямая LP и плоскость (CDD₁): 

А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

c)      Прямая XY и плоскость (ABC): А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

d)      Прямая DC и плоскость (AA₁B):

А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость;

В) Прямая принадлежит плоскости.

e)      Прямая MS и плоскость (ABB₁): А) Прямая параллельная плоскости;

Б) Прямая пересекает плоскость; В) Прямая принадлежит плоскости.

10.    Боковые стороны CD и AB трапеции ADCB параллельны плоскости α. Каковыми являются плоскости α и плоскость трапеции ADCB?

А) пересекаются;

Б) параллельны.

11.    Даны три параллельные плоскости α, β и γ. В каждой из них соответственно проведены прямые a, b и c.

Угол между прямыми a и b равен 60°, угол между прямыми b и c равен 57°. Определи угол между прямыми a и c.

Ответ: _______

12. 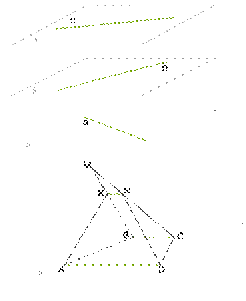   *Трапеция ABCD, основание BC которой равно 48cм, лежит в плоскости α. Точка M не находится в плоскости трапеции. Точка K делит отрезок MB так, что MK:KB=3:5. Плоскость ADK пересекает отрезок MC в некоторой точке N.

a)      Определи длину отрезка KN (ответ округли до одной десятой).

Ответ: KN=_______

b)      Назови пучок параллельных прямых (достаточно ввести одну прямую в каждое окошко):

Ответ: ____∥________∥_______

c)      Назови подобные треугольники: Ответ: ΔKMN~Δ_______

13.    **Точка M         не        лежит в          плоскости прямоугольника ABCD. Докажи, что прямая DC параллельна       плоскости      (AMB).           (Дополни доказательство   нужными       словами      или выражениями из списка).

a)      Прямые          DC      и          AB      (перпендикулярны/ пересекаются/            параллельны)             как противоположные стороны прямоугольника.

b)      Прямая AB лежит в плоскости (AMB), так как две еѐ точки A и B (принадлежат этой плоскости/ не принадлежат этой плоскости/ принадлежат в разных полупространствах от этой плоскости).

c)      Если прямая (параллельна/ пересекается с/ совпадает с) прямой, которая находится в некоторой плоскости, то она (перпендикулярна/ находиться в/ параллельна) этой плоскости.

d)      Значит прямая DC (перпендикулярна/ находиться в/ параллельна) плоскости (AMB).

14.    Дан куб ABCDA₁B₁C₁D₁. Определи взаимное расположение данных прямых (Впишите нужное слово: параллельные, пересекающиеся, скрещивающиеся)

Ответ: BB₁ и A₁D₁_________________________

15.    В плоскости лежит треугольник ABC, a точка D не находится в этой плоскости.

Точки М, N и K соответственно серединные точки отрезков         DA,     DB      и          DC.      Определи       взаимное расположение прямых MK и MN

А) пересекаются;

Б) скрещиваются;

В) параллельны.

16.    *Прямая EF не лежит в плоскости квадрата ABCD, но параллельна стороне квадрата BC. Какой угол образуют прямые EF и AC

Ответ (в градусах):_________

17.    Прямые BM и CD параллельные, прямые BN и CD скрещивающиеся. Найти угол между прямыми BN и CD, если ∡NBM=90° Ответ (в градусах):_________

18.    *Пирамида SABCD пересечена плоскостью KLNM, параллельной основанию

a)      Каково взаимное расположение прямых:

а) BS и CS?

А) пересекаются;

Б) скрещиваются; В) параллельны.

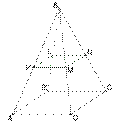б) AD и BC?

А) пересекаются;

Б) скрещиваются; В) параллельны.

в) CS и KL?

А) пересекаются;

Б) скрещиваются;

В) параллельны.

b. Каково взаимное расположение плоскостей:

а) ASD и DSC?

А) пересекаются; Б) параллельны.

б) ABD и ASD?

А) пересекаются;

Б) параллельны.

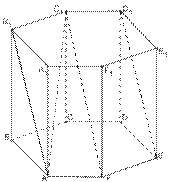
19.    Определи взаимное расположение прямых в правильной шестиугольной призме.

a)       AA₁ и DD₁:

А) пересекаются;

Б) скрещиваются; В) параллельны.

b)       FC₁ и DD₁:

А) пересекаются;

Б) скрещиваются; В) параллельны.

c)       BC и FC₁:

А) пересекаются;

Б) скрещиваются; В) параллельны.

20.    *Дан кубABCDA₁B₁C₁D₁. 

a)       Вычисли угол между прямыми DA₁ и DC₁

Ответ (в градусах): _________

b)       Определи величину угла между прямыми AB₁ и BD₁ Ответ (в градусах): _________

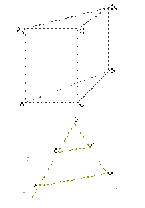
21.    **Дана правильная треугольная призма ABCA₁B₁C₁, все рѐбра которой равны. 1) Определи взаимное расположение прямых CA₁ и BB₁

А) пересекаются;

Б) скрещиваются;

В) параллельны.

2) Рассчитай, какой угол образуют эти прямые. Ответ (в градусах): _________

22.    Дан угол AOD и две параллельные плоскости α и β.

Плоскость           α          пересекает     стороны          угла    OA      и          OD соответственно в точках A и D, плоскость β эти стороны пересекает соответственно в точках B и C.

Дано: OB= 8; AB= 3; BC= 6; CD= 2; (Дроби должны быть сокращены)

Найти: AD; OD

23.    Как могут быть расположены две плоскости α и β, если

a)       Одна из двух параллельных прямых находится в одной плоскости, а вторая прямая в другой плоскости

А) параллельны;

Б) пересекаются;

В) параллельны или пересекаются.

b)       У каждой прямой, которая находится в одной плоскости, можно найти параллельную прямую в другой плоскости

А) параллельны;

Б) пересекаются;

В) параллельны или пересекаются.

24.    Как могут быть расположены две прямые, если они

a)       Находятся каждая в одной из параллельных плоскостей

А) параллельны или скрещивающиеся;

Б) параллельны или пересекаются;

В) пересекаются или скрещивающиеся.

b)       Находятся в одной плоскости

А) параллельны;

Б) пересекаются;

В) параллельны или пересекаются.

25.    *Через точку O, которая находится между параллельными плоскостями α и β, проведены прямые a и b, пересекающие плоскости так, что точки A и B находятся в плоскости α, а точки C и D - в плоскости β  AB=17см, DO=30см и

AC=3⋅AO. Вычисли: BD;CD

Ответ: BD =________ см; CD=_________ см.

26. 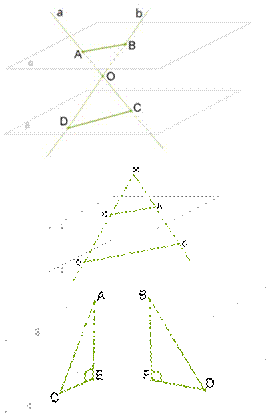   *Стороны ∡M пересекают параллельные плоскости β и α в точках C, D и A, B. Вычисли длину отрезка AB, если MA=13см, MC=20см и CD=57см. Ответ: AB =________ см

27.    **Даны параллельные плоскости α и β. Точки A и B находятся в плоскости β, а точки C и D в плоскости α. Длина отрезка AC=14, длина отрезка BD=10.           Сумма            проекций       этих      отрезков         в плоскости α равна 12. Высчитай длину проекций обоих отрезков.

1.   Чтобы определить проекции отрезков AC и BD, из точек A и B надо провести _______________ AE и BF к плоскости α.

2.   AE и BF ____________________.

3.   AE       и          BF       ________________   как      отрезки          параллельных            прямых             между параллельными плоскостями.

4.   Длины проекций CE и FD высчитаем из треугольников ACE и BDF:

Ответ: CE =________ см; FD =________ см

28.    Дан тетраэдр DABC. 

1.      Определи, которые из рѐбер скрещивающиеся с данным ребром.

а) с ребром AB:

                А) BC;            Б) DB;            В) AC;            Г) DA;            Е) DC.

2.      Определи сумму всех рѐбер, если это правильный тетраэдр и длина его ребра 4см. Ответ: ________ см

29.    На рѐбрах BB₁ и AA₁ параллелепипеда ABCDA₁B₁C₁D₁ даны соответственно точки K и L.

1. Которые из рѐбер в основаниях параллелепипеда пересекаются с прямой KL.

a.             в верхнем основании:

                А) D₁A₁;         Б) A₁B₁;          В) C₁D₁;         Г) B₁C₁.

b.             в нижнем основании:

                А) BC;            Б) DA;            В) AB;            Г) CD.

30. 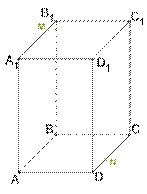   *Дан параллелепипед ABCDA₁B₁C₁D₁. На рѐбрах A₁B₁ и DC соответственно находятся точки M и N. 

Объясни шаги изображения сечения данного параллелепипеда плоскостью, проходящей через эти точки. 

1.      Если плоскости имеют хотя бы одну общую точку, то они ____________________.

2.      В данной ситуации плоскость сечения будет пересекать ____________________ грани параллелепипеда.(запиши число граней)

3.      Если две параллельные плоскости пересекает третья плоскость, то линии пересечения ________________.

4.      В противоположных гранях через данные точки проводим ____________ линии сечения.

5.      Искомое сечение параллелепипеда ________________ (назови вид фигуры сечения)

31.    Отметь, какие свойства имеет параллелепипед, рисунок и описание которого перед тобой:

1.   Куб - параллелепипед, все грани которого квадраты Свойства:

все грани одинаковые четырехугольники         все боковые рѐбра одинаковые    четырехугольники в основаниях одинаковые все диагонали параллелепипеда пересекаются в одной

точке

все диагонали параллелепипеда одинаковые    все боковые грани одинаковые четырехугольники       стороны четырехугольника в основании одинаковые

             все рѐбра одинаковые

2.   Наклонный параллелепипед с параллелограммом в основании Свойства:

все диагонали параллелепипеда одинаковые    все диагонали параллелепипеда пересекаются в одной

точке

все ребра одинаковые       все боковые ребра одинаковые     четырехугольники в основаниях одинаковые   все боковые грани одинаковые четырехугольники       стороны четырехугольника в основании одинаковые    все грани одинаковые четырехугольники

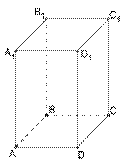
3.   Прямой параллелепипед с ромбом в основании Свойства:

             стороны четырехугольника в основании одинаковые

все боковые ребра одинаковые   все ребра одинаковые       все диагонали параллелепипеда одинаковые         все грани одинаковые четырехугольники     все боковые грани одинаковые четырехугольники     четырехугольники в основаниях одинаковые       все диагонали параллелепипеда пересекаются в одной

точке

32.    Сумма всех ребер параллелепипеда NMKLN1M1K1L1

240cm. Определи длину рѐбер NM, MK и MM1 если NMMK=23, а MKMM1=35.

Ответ: NM =______ см; MK =______ см; MМ₁ =______см.

33.    *Дан тетраэдр DABC, у которого три ребра с общей вершиной D перпендикулярны. Назовѐм грани между этими

рѐбрами боковыми гранями. Определи общую площадь боковых граней, если DA=8; DB=8; DC=8 Ответ: ______см.

34.    **На рѐбрах DB и DC тетраэдра DABC соответственно расположены точки M и N (не серединные точки рѐбер).

1.   В которой плоскости из названных находится прямая MN?

            А) DAC;            Б) DBC;          В) DAB.

2.   С которой из прямых в основании тетраэдра пересекается прямая MN?

             А) BC;              Б) AB;            В) AC.

35.    Внимательно подумай, что называется сечением многогранника, и         определи,       на      которых         рисунках        изображены   сечения параллелепипеда, а на которых нет.

ЗАЧЕТ 3. ПЕРПЕНДИРУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

1.        Дан куб. Определи, какая из названных в ответе прямых перпендикулярна названной плоскости?

а) плоскость (ABC) перпендикулярна

         А) B₁C₁;              Б) BD₁;           В) AC;            Г) AA₁; 

          Д) AC₁;               Е) BD;            Ж) AB.

б) плоскость (ACC₁) перпендикулярна

          А) AC₁;               Б) AA₁;           В) B₁C₁;          Г) AC; 

          Д) BD;                 Е) AB;            Ж) BD₁.

2.        В какой ситуации проведенная прямая, которая не лежит в плоскости названной фигуры, перпендикулярна к плоскости этой фигуры? прямая проведена перпендикулярно диагоналям прямоугольника прямая проведена перпендикулярно сторонам ромба с общей вершиной прямая проведена перпендикулярно основаниям трапеции прямая проведена перпендикулярно двум диаметрам окружности прямая проведена перпендикулярно двум сторонам параллелограмма

3.        Прямая PQ параллельна плоскости α. От точек P и Q к плоскости проведены прямые PP1α и QQ1α. Известно,     что      PQ=PP₁=16,2см.        Определи       вид четырехугольника PP₁Q₁Q и рассчитай его периметр. Ответ: 

PP₁Q₁Q— ________________________

PPP1Q1Q=__________ см

4. 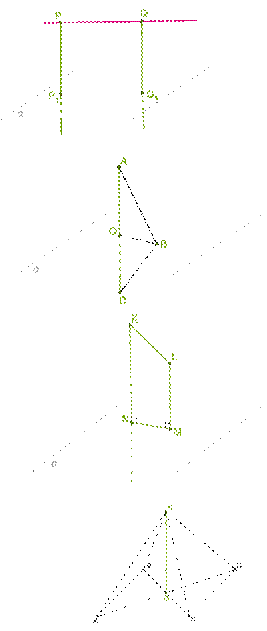       Проведенная к плоскости перпендикулярная прямая пересекает плоскость в точке O.

На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка. Определи вид и периметр треугольника ABD, если AD= 11см, а OB=

4см (ответ округли до одной десятой). Ответ: 

ΔABD —_________________

P _ΔABD  ==__________ см

5.        *Две прямые образуют прямой угол с плоскостью α.

Длина отрезка KN= 33,5cm , длина отрезка LM= 21,5см. 

Рассчитай длину KL, если NM=9см. Ответ: 

KL==__________ см

6.        *К плоскости квадрата ABCD со стороной 4см через точку пересечения диагоналей O проведена прямая, перпендикулярная плоскости квадрата.

На прямой отложен отрезок OK длиной 3 см.

Рассчитай расстояние от точки K к вершинам квадрата (результат округли до одной десятой).

Ответ: 

KA ==_______ см; KВ ==_______ см; KС ==_______ см;  KD ==_______ см. 

7.        *Дано, что в тетраэдре DABC ребро DA перпендикулярно ребру BC. На ребрах AC и AB отмечены серединные точки K и L.

Докажи, что DA перпендикулярно KL, для этого нужно вписать пропущенные слова:

1.      Так как K и L — серединные точки AC и AB, то KL — ___________________________ треугольника ABC.

2.      Средняя линия _______- третьей стороне треугольника, то есть BC.

3.      Если DA перпендикулярна одной из _________ прямых, то она_________________ и другой прямой.

8.        *В тетраэдре DABC точка M серединная точка ребра AC. Дано, что у тетраэдра BA=BC; DA=DC

Докажи, что прямая, на которой расположено ребро AC, перпендикулярна плоскости (BDM). Для этого :

1.      Определи вид треугольников.

ΔABC —_________________

ΔDAC —_________________

2.      Какой угол образует медиана с основанием этих треугольников?

—_________________

4. Согласно признаку, если прямая _______________ к _____________________ и _________________ прямым в некой плоскости, то она ____________________ к этой плоскости.

9. 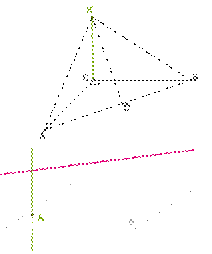       *Через     вершину         прямого         угла    C         к          плоскости прямоугольного      треугольника             ABC    проведѐн перпендикуляр KC.

Точка D — серединная точка гипотенузы AB.

Длина катетов треугольника AC = 48мм и BC = 64 мм. Расстояние KC = 9мм. Рассчитай расстояние KD.

Ответ: KD ==_______ мм. 

10.    *Прямая d перпендикулярна плоскости α и прямой v, которая не лежит в плоскости α.

Докажи, что прямая v параллельна плоскости α. Для этого вставь пропущенные слова:

1.      Согласно данной информации, если прямая не лежит в плоскости, она может или быть _______________ плоскости, или ________________ плоскость.

2.      Допустим, что прямая v не ___________________, а _____________________ плоскость α.

3.      Если прямая d по данной информации перпендикулярна плоскости α, то она ___________________ каждой прямой в этой плоскости, в том числе и прямой, которая проведена через точки, в которых плоскость пересекает прямые d и v.

4.      Мы имеем ситуацию, когда через одну точку к прямой d проведены две __________________ прямые.

5.      Это противоречие, из чего следует, что прямая v ________________ плоскости α, что и требовалось доказать.

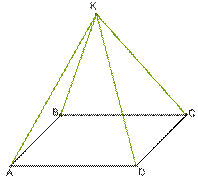
11.    **От вершины K к плоскости квадрата ABCD проведена прямая KB так, что углы ∡KBA=90° и ∡KBC=90°.

Рассчитай расстояние от K к вершинам квадрата, если сторона квадрата равна 11 см, а KB =12 см.

Ответы введи округлѐнными до одной десятой:

Ответ: KA ==______ см; KC ==_____ см; KD ==_____ см.

12.    К плоскости α проведена наклонная, длина которой равна 26 см, проекция наклонной равна 10 см. На каком расстоянии от плоскости находится точка, из которой проведена наклонная?

Ответ: Точка находится на расстоянии __________ см от плоскости.

13.    Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 60°. P∈a, точка R - проекция точки P на плоскость β. PC=14см. Найди RC. Ответ: RC ==______ см.

14.    К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 8 см, наклонная с плоскостью образует угол 45°. Вычисли, на каком расстоянии от плоскости находится точка B.

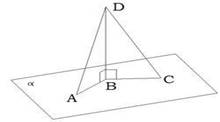Ответ: Расстояние от точки B до плоскости равно________________см

15.    *Наклонная AD с плоскостью α образует угол 30°, а наклонная DC с плоскостью α образует угол 45°.

Длина перпендикуляра DB равна 28см.

Вычисли длины обеих наклонных.

Ответ:

1.AD=

          А) 14;                  Б) 28√2;          В) 56;              Г) 28√3.

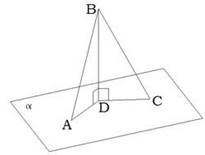2.DC=

          А) 14;                  Б) 28√2;          В) 56;              Г) 28√3.

16.    Дано, что BD перпендикулярен плоскости α. ∢BAD=30°,∢BCD=45°. Меньшая из проекций наклонных на плоскость α равна:

           А) AB;  Б) AD;              В) DC;            Г) BC.

17.    *Длина отрезка VB равна 20м. Он пересекает плоскость в точке O. Расстояние от концов отрезка до плоскости соответственно равны 8м и 2м. 

a.    Найди острый угол, который образует отрезок VB с плоскостью. Отрезок с плоскостью образует угол __________________

b.   Отрезок VB точкой O делится на отрезки _______ м и _______ м. (первой пиши длину меньшего отрезка)

18. 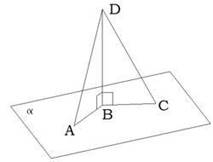   *Проекции наклонных AD и DC на плоскости α равны соответственно 8 см и 8 см, а угол между ними равен 120°.

a.    Вычисли расстояние между концами проекций наклонных.

Расстояние равно _____________см.

b.   Название отрезка DB  _________________.

19.    *Равнобедренный треугольник ABE находится в плоскости α. Боковые стороны треугольника ABE равны по 20см, а сторона основания AE=32см. К этой плоскости проведены перпендикуляр CB, который равен 9см, и наклонные CA и CE.  a. Вычислите расстояние от точки C до стороны треугольника AE. Расстояние равно _____________см.

b. Впиши просушенные слова:

Если    прямая,           проведенная в          плоскости      через   основание      наклонной, перпендикулярна __________________ наклонной, то она _______________ и самой _____________________.

20.    *Прямоугольный треугольник MBE (M=90°) находится в плоскости α. BE=13см, а ME=5см. К этой плоскости проведѐн перпендикуляр CB длиной 5 см. a. Вычисли расстояние от точки C до стороны треугольника ME.

Расстояние равно _____________см.

b.        Сколько перпендикуляров можно провести из точки к прямой (если точка не принадлежит этой прямой)?

                   А) один;       Б) два;            В) бесконечное множество;            Г) ни одного.

c.         Какие теоремы используются в решении задачи?

                       Теорема пирамиды

                       Теорема высоты

                       Теорема о трех перпендикулярах

                       Теорема Пифагора

                       Теорема косинусов

21.    **Точка K отмечена в расстоянии 39cm от плоскости прямоугольника ABCD и в равных расстояниях от вершин прямоугольника.

a.    Рассчитай, на каком расстоянии от вершин прямоугольника отмечена точка K, если стороны прямоугольника 128cm и 96cm.

Ответ: KA=KB=KC=KD= _________см.

b.   Обоснуй, в какой точке находится проекция точки

K в плоскости прямоугольника

Проекция точки K в плоскости прямоугольника находится там, где ____________________ прямоугольника.

22.    Двугранный угол равен 60 градусов. Внутри его дана точка A, которая находится на расстоянии 30см от обеих граней угла. Чему равно расстояние от точки A до ребра двугранного угла?

Расстояние равно _______________ см

23.    *Дан четырѐхугольник ABCD и перпендикуляр KB проведѐнный к плоскости четырѐхугольника через вершину B. На четырех рисунках изображены углы. На котором из них правильно изображѐн линейный угол двугранного угла между плоскостями AKD и ABC, если

                А) 1;                Б) 2;               В)3;                 Г) 4;       Д) 1 и 3;         Е) во всех рисунках.

24. 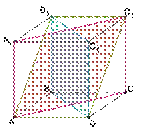   *Дан куб с некоторыми плоскостями сечений. Определи величины двугранных углов между плоскостями

1.(ABB1) и (CDD1) А) 0°;        Б) 45°;            В) 90°;            Г) невозможно определить.

2.  (ADD1) и (CDD1) А) 0°;      Б) 45°;            В) 90°;            Г) невозможно определить.

3.  (ACC1) и (ADD1)

          А) 0°;       Б) 45°;            В) 90°;            Г) невозможно определить.

25. 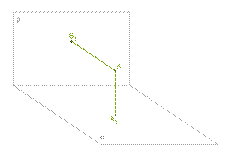   В двугранном    угле,   грани которого перпендикулярны, дана точка A. Расстояния от точки до      граней            AA1=5cm       и          AB1=12cm.    Рассчитай расстояние AB до общей прямой граней этого угла.

Ответ: AB ==______ см.

26.    Двугранный угол равен 30°. На одной грани двугранного угла дана точка B, расстояние от которой до ребра равно 6см. Чему равно расстояние от точки B до второй грани двугранного угла? Ответ: расстояние равно______ см.

27. 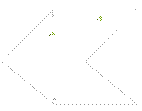   В одной из граней двугранного угла даны точки A и B, расстояния которых до ребра этого угла соответственно 10cm и 20cm. Расстояние от точки A до второй грани угла 6cm. Какое расстояние от точки B до второй грани угла?  Ответ: расстояние от точки B до второй грани угла равно______ см.

28. 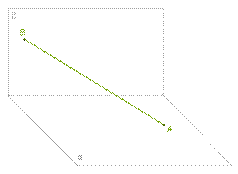   *В прямом двухгранном углу дан отрезок AB так, что один конец отрезка находится в одной грани угла, а второй конец в другой грани угла. Расстояния от точек A и B до ребра угла AA₁=14cm, BB₁=18cm. Длина отрезка A₁B₁=3cm.

1.      Нарисуй соответствующий рисунок.

2.      Определи вид треугольников ΔAA1B1, ΔBB1A1, ΔAB1B, ΔBA1A.

Ответ: ΔAA₁B₁ - _______________;  ΔBB₁A₁- _______________; ΔAB₁B  - _______________;  ΔBA₁A - _______________;  

3.      Рассчитай длину отрезка AB.

Ответ: AB ==______ см.

29. 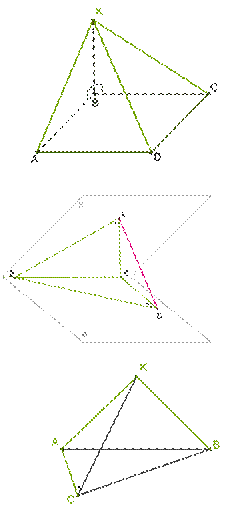   *К плоскости, в которой лежит квадрат ABCD через вершину B проведѐн отрезок KB так, что KB⊥AB и

KB⊥BC. Сторона квадрата 9cm, а длина отрезка KB=40cm.

Рассчитай синус линейных углов α и β между плоскостью квадрата и плоскостями KAD и KCD.

Ответ введи как несокращѐнную дробь:

30.    **На каждой из граней двугранного угла, линейный угол которого 60°, находятся равнобедренные прямоугольные треугольники ABC и DBC с общей гипотенузой BC, лежащей на ребре угла. BC=5cm. Рассчитай расстояние между вершинами A и D.

Ответ: AD ==______ см.

31.    **Плоскости равнобедренного треугольника AKB и прямоугольного треугольника ACB образуют прямой двугранный угол. Какое будет расстояние CK, если KA=KB=CA=42cm, CB=56cm, AB=70cm. Ответ: KC ==______ см.

ЗАЧЕТ 4 РЕШЕНИЕ ПРАКТИЧЕСКИХ ЗАДАЧ

Задача № 1. Три латунных куба с ребрами 3 см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба?

Задача № 2. Металлический куб имеет внешнее ребро 10,2 см и массу 514,15 г. Толщина стенок равна 0,1 см. Найдите плотность металла, из которого сделан куб.

Задача № 3. Кирпич размером 25х12х6,5 имеет массу 3,51 кг. Найдите его плотность.

Задача № 4. Требуется установить резервуар для воды емкостью 10м³на площадке размером 2,5 мх1,75 м, служащей для него дном. Найдите высоту резервуара.

Задача № 5. Чугунная труба имеет квадратное сечение, еѐ внешняя ширина 25 см, толщина стенок 3 см. какова масса погонного метра трубы (плотность чугуна 73 г/см³)

Задача № 6. Деревянная плита в форме правильного восьмиугольника со стороной 3,2 см и толщиной 0,7 см имеет массу 17,3 г. Найдите плотность дерева.

ЛИТЕРАТУРА

Основная литература:

1. Атанасян Л.С., БутьузовВ.Ф..э Кадомцев С.Б. ПозднякЭ.Г., Юдина И.И. Геометрия в 10-11 классах[Текст]: учебник для общеобразовательных учреждений. – 20-е изд. – М.: Просвещение, 2010г. Дополнительная литература:

1.        Закон Российской Федерации «Об образовании» [Текст]. - М.: Просвещение, 2013.-126с. 

2.        Базисный учебный план общеобразовательных учреждений РФ[Текст], 2010.

3.        Обязательный минимум содержания основного общего образования. [Текст]// Вестник образования. -2011. -№ 9.

4.        Стандарт среднего общего образования по математике //Математика в школе.[Текст] – 2004. – №4, – с.4. 

5.        Бурмистрова Т.А. Программы образовательных учреждений. Геометрия.10-11 классы [Текст]: сборник программ образовательных учреждений/ сос. Бурмистрова Т.А. − М.: «Просвещение»,2011. – 51с.

6.        Н.Ф.Гаврилова       Рабочие          программы     по        геометрии:     7-11     классы

[Текст]:программы/ Сост. Н.Ф.Гаврилова. - М.: ВАКО, 2011.

7.        Зив Б. Г. Геометрия [Текст]:дидактические материалы: 10 кл. / Б. Г. Зив, В. М. Мейлер. — М.: Просвещение, 2014—89с.

8.        Зив Б. Г. Геометрия [Текст]:дидактические материалы: 11 кл. / Б. Г. Зив. — M.: Просвещение, 2014—102с.

Средства обучения для учителя и учащихся (ЭОР):

1.        Стереометрия ч.1(10класс) ЗАО «Новый диск», 2013. – электрон.опт. диск (CDROM);

2.        Уроки геометрии КиМ (10 класс)ЗАО «Новый диск», 2015. – электрон.опт. диск (CD-ROM);

3.        Открытая Математика 2,5 (Стереометрия) ЗАО «Новый диск», 2012. – электрон.опт. диск (CD-ROM).

ПРИЛОЖЕНИЕ

ТАБЛИЦА ПЕРЕВОДА НАБРАННЫХ БАЛЛОВ В ОЦЕНКУ