
Лекция 1. Матрицы и определители.
· Определители, их свойства и вычисление.
· Основные понятия для матриц.
· Действия с матрицами.
Литература:
Высшая школа,1997(с.70-94)
1.1 Определители, их свойства и вычисление.
Определение. Определителем
![]() -го порядка называется число
-го порядка называется число 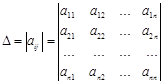 , где
, где ![]() -
элемент определителя, расположенный на пересечении строки с номером
-
элемент определителя, расположенный на пересечении строки с номером ![]() и столбца с номером
и столбца с номером ![]() ,
, ![]() .
.
Определители второго и третьего порядков вычисляют соответственно по формулам:
![]() ;
- определитель 2-го порядка
;
- определитель 2-го порядка
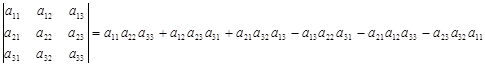 .
– определитель 3-го порядка
.
– определитель 3-го порядка
Пример. Вычислить определитель второго порядка
![]()
Пример. Вычислить
определитель третьего порядка: 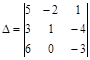 .
.
Решение. по правилу треугольников ![]()
![]()
1.2 Основные понятия для матриц.
Определение. Матрицей
размерности ![]() называют прямоугольную таблицу
чисел, состоящую из
называют прямоугольную таблицу
чисел, состоящую из ![]() строк и
строк и ![]() столбцов. Обозначают,
столбцов. Обозначают, 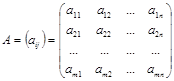 .
. ![]() .
При
.
При ![]() получим квадратную матрицу
получим квадратную матрицу ![]() -го порядка.
-го порядка.
Матрицы бывают: однородные,
квадратичные, двухмерные, трехмерные и до ![]() -мерного,
а также обратная матрица, единичная матрица, матрица-строка, матрица-столбец.
-мерного,
а также обратная матрица, единичная матрица, матрица-строка, матрица-столбец.
1.3 Действия с матрицами.
Определение. Суммой
[разностью] матриц ![]() и
и ![]() одинаковой размерности называют
матрицу
одинаковой размерности называют
матрицу ![]()
![]() .
.
Определение. Произведением
числа ![]() на матрицу
на матрицу ![]() называют
матрицу
называют
матрицу ![]() .
.
Определение. Произведением
матрицы ![]() размерности
размерности ![]() на матрицу
на матрицу ![]() размерности
размерности
![]() называют матрицу
называют матрицу ![]() размерности
размерности ![]() где
где ![]() ,
,
![]() .
.
![]() ,
но
,
но ![]() .
.
Пример. Даны матрицы А = 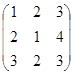 ; B
=
; B
= 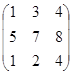 , найти 2А + В.
, найти 2А + В.
Решение. 2А = 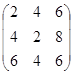 ,
2А + В =
,
2А + В = 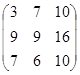 .
.
Пример. Даны матрицы А = 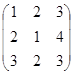 ; B
=
; B
= 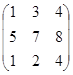 , найти А*В.
, найти А*В.
Решение.
А*В=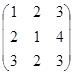 *
*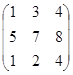 =
=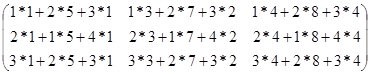 =
=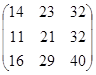
Определение. Обратной к
матрице ![]() называют матрицу
называют матрицу ![]() , обладающую свойством:
, обладающую свойством: ![]() .
.
Теорема. Если матрица 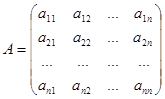 неособая, то она имеет обратную
матрицу
неособая, то она имеет обратную
матрицу 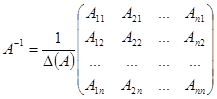 .
.
Пример. Найти ![]() ,
если
,
если ![]()
Решение: 1) Находим ![]()
2) Находим ![]()
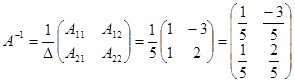
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.