Поделиться
Mechanical properties of the solid bodies Jigsaw.docx
Jigsaw
Group 1
Part I. Multiple Choice
1 Which of the following correctly defines the terms stress, strain and Young modulus?
2 In stress-strain experiments on metal wires, the stress axis is often marked in units of 108 Pa and the strain axis is marked as a percentage.
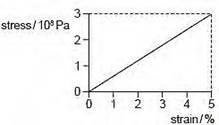This
is shown for a particular wire in the diagram.
What is the value of the Young modulus for the material of the wire?
A 6.0×107Pa B 7.5 × 108Pa C 1.5×109Pa D 6.0×109 Pa
3 Nylon breaks when the stress within it reaches 1x109 Pa. Which range includes the heaviest load that can be lifted by a nylon thread of diameter 1 mm?
A 2N to 20 N B 20N to 200N
C 200N to 2000N D 2000N to 20 000N
Part II. Structured Questions
1 (a) Define the terms
(i) tensile stress
……………………………………………………………………………………
………………………………………………………,…………………….. [1]
(ii) tensile strain
……………………………………………………………………………………
………………………………………………………,…………………….. [1]
(iii) The Young modulus
……………………………………………………………………………………
………………………………………………………,…………………….. [1]
(b) A metal wire has an unstretched length L and area of cross-section A. When the wire supports a load F, the wire extends by an amount ∆L. The wire obeys Hooke’s law.
Write down expressions, in terms of L, A, F and ∆L, for
(i) the applied stress,
………………………………………………………,…………………….. [1]
(ii) the tensile strain in the wire
………………………………………………………,…………………….. [1]
(iii) the Young modulus of the material of the wire.
………………………………………………………,…………………….. [1]
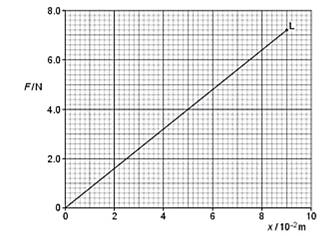2
(a) The variation with extension x of the
force F for a spring A is shown in Fig. 2.1
The point L on the graph is the elastic limit of the spring.
(i) Describe the meaning of elastic limit.
……………………………………………………………………………………
………………………………………………………,…………………….. [1]
(ii) Calculate the spring constant, kA for spring A.
kA = ……………………………………… Nm-1 [1]
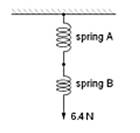(b)
The second spring B of spring constant 2kA,
is now joined to spring A, as shown in Fig. 2.2.
Fig. 2.2
A force of 6.4 N extends the combination of springs.
For the combination of springs, calculate
(i) the total extension
extension = ………………………….. m [1]
(ii) the spring constant
spring constant = ………………………………… Nm-1 [1]
Group 2
Part I. Multiple Choice
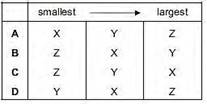
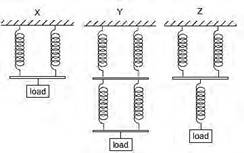1 A
number of similar springs, each having the same spring constant, are joined in
three arrangements X, Y and Z. The same load is applied to each.
What is the order of increasing extension for these arrangements?
2 A wire is stretched by 8 mm when a load of 60 N is applied.
What will be the extension of a wire of the same material having four times the cross-sectional area and twice the original length, when the same load is applied?
A 2 mm B 4 mm C 8 mm D 16 mm
3 Nylon breaks when the stress within it reaches 1x109 Pa. Which range includes the heaviest load that can be lifted by a nylon thread of diameter 1 mm?
A 2N to 20 N B 20N to 200N
C 200N to 2000N D 2000N to 20 000N
Part II. Structured Questions
1 (a) Define, for a wire,
(i) stress.
……………………………………………………………………………….......
…………………………………………………………………………… [1]
(ii) strain
……………………………………………………………………………….......
…………………………………………………………………………… [1]
(b) A wire of length 1.70 m hangs vertically from a fixed point, as shown in Fig.
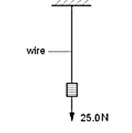1.1.
Fig. 1.1
The wire has cross-sectional area 5.74 x 10-8 m2 and is made of a material that has a Young Modulus of 1.60 x 1011 Pa. A load of 25.0 N is hung from the wire.
(i) Calculate the extension of the wire.
extension = …………………………….m [3]
(ii) The same load is hung from a second wire of the same material. This wire is twice the length but the same volume as the first wire. State and explain how the extension of the second wire compares with that of the first wire.
………………………………………………………………………………..
………………………………………………………………………………...
…………………………………………………………………………… [3]
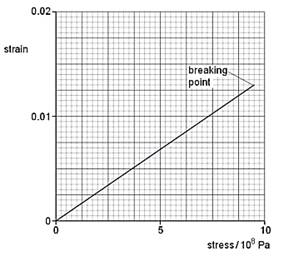2 A
sample of material in the form of a cylindrical rod has a length L and uniform
area of cross-section A. The rod undergoes an increasing tensile stress until
it breaks. Fig. 2.1 shows the variation with stress of the strain in the rod.
(a) State whether the material of the rod is ductile, brittle or polymeric.
………………………………………………………,…………………….. [1]
(b) Determine the Young modulus of the material of the rod.
Young modulus = ……………………………… Pa [2]
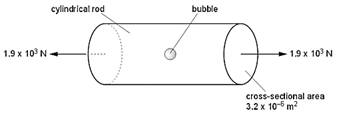(c)
A second cylindrical rod of the same
material has a spherical bubble in it, as illustrated in Fig. 2.2.
Fig. 2.2
The rod has an area of cross-section of 3.2 x 10-6 m2 and is stretched by forces of magnitude 1.9x103 N.
By reference to Fig. 2.1, calculate the maximum area of cross-section of the bubble such that the rod does not break.
Area = …………………………………….. m2 [3]
Group 3
Part I. Multiple Choice
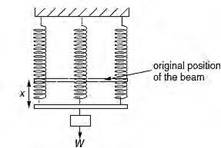1 A
beam, the weight of which may be neglected, is supported by three identical
springs. When a weight W is hung from the middle of the beam, the
extension of each spring is x.
The middle spring and the weight are removed.
What is the extension when a weight of 2W is hung from the middle of the beam?
A 3x/2 B 4x/3 C 2x D 3x
2 Two steel wires P and Q have lengths l and 2l respectively, and cross-sectional areas A and A/2 respectively. Both wires obey Hooke’s law.
What is the ratio when both wires are stretched to the same extension?
3 Nylon breaks when the stress within it reaches 1x109 Pa. Which range includes the heaviest load that can be lifted by a nylon thread of diameter 1 mm?
A 2N to 20 N B 20N to 200N
C 200N to 2000N D 2000N to 20 000N
Part II. Structured Questions
1 (a) Define the Young modulus.
.……………………………………………………………………………….......
… …………………………………………………………………………… [1]
(b) A load F is suspended from a fixed point by a steel wire. The variation with extension x of F for the wire is shown in Fig 1.1.
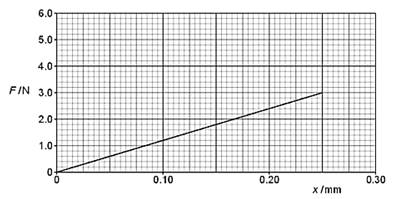
Fig.1.1
(i) State two quantities, other than the gradient of the graph in Fig. 1.1, that are required in order to determine the Young modulus of steel.
1..………………………………………………………………………………......
2 … …………………………………………………………………………….…
[1]
(ii) Describe how the quantities you listed in (i) may be measured.
………………………………………………………………………………..
………………………………………………………………………………...
…………………………………………………………………………… [3]
(c) A copper wire has the same original dimensions as the steel wire. The Young modulus for steel is 2.2 x 1011 Nm-2 and for copper is 1.1 x 1011 Nm-2.
On Fig. 1.1, sketch the variation with x of F for the copper wire for extensions up to 0.25 mm. The copper wire is not extended beyond its limit of proportionality. [2]
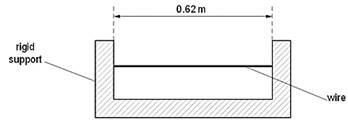2 A
steel wire of uniform cross-sectional area 7.9 x 10-7 m2
is heated to a temperature of 650 K. It is then clamped between two rigid
supports, as shown in Fig. 2.1.
Fig. 2.1
The wire is straight but not under tension and the length between the supports is 0.62 m. The wire is then allowed to cool at 300 K.
When the wire is allowed to contract freely, a 1.00m length of the wire decreases in length by 0.012 mm for every 1K decrease in temperature.
(i) Show that the change in length of the wire, if it were allowed to contract as it cools from 650K to 300 K, would be 2.6 mm.
(ii) The Youndg Modulus of steel is 2.0 x 1011 Pa. Calculate the tension in the wire at 300K, assuming that the wire obeys Hooke’s law.
tension = …………………… [2]
(iii) The ultimate tensile stress of steel is 250 MPa. Use this information and your answer in (ii) to suggest whether the wire will, in practice, break as it cools.
…………………………………………………………………………………..
………………………………………………………………………………...
…………………………………………………………………………… [3]
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
