Механические свойства твердых тел.

Тепловое расширение твердых тел и жидкостей. Плавление и кристаллизация.

Механические свойства твердых тел

Твёрдые тела – тела, которые со временем не меняют своей формы и объёма.

Твёрдые тела делятся на…

1.                   Кристаллы (кристаллические тела)

2.                   Аморфные тела

3.                   Композиты (композитные тела) (рис. 1)

Рис. 1. Примеры кристаллических (соль) и аморфных (воск) твёрдых тел соответственно

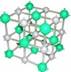
Рис. 2. Пример кристаллической решётки (каменная соль)

Кристаллы – твёрдые тела, у которых наблюдается упорядоченное расположение атомов или молекул  (рис.2).

Кристаллы, в свою очередь, также делятся на два класса:

1.                   Монокристаллы, то есть вся структура тела представлена единым кристаллом (алмаз, рубин, сапфир…)

2.                   Поликристаллы, то есть структура тела представляет собой объёдинение большого количества малых кристаллов (гранит, большинство металлов…)

Следует также знать, что кристаллическая структура не является свойством, характерным для одних химических элементов или соединений, а для других нехарактерным. Дело в том, что многие твёрдые тела обладают так называемым свойством полиморфизма.

Полиморфизм – свойство твёрдых тел существовать в состоянии с различной кристаллической решёткой. Например, уже приводимые на одном из прошлых уроков в качестве примера алмаз и графит оба состоят из углерода, однако с различным расположением его атомов.

Кристаллы могут быть распределены на две группы также и по следующим свойствам: изотропия и анизотропия.

Анизотропия – зависимость физических свойств кристалла от направления. То есть кристаллическая структура не симметрична, и существует несколько осей, вдоль которых у кристалла проявляются различные свойства (механические, электрические, оптические). Анизотропия свойственна монокристаллам.

Изотропия – независимость физических свойств кристалла от направления. Свойственна поликристаллам, потому как несимметрические монокристаллы ориентируются хаотически, сводя на нет несимметричность.

Ещё одним принципом, по которому можно классифицировать кристаллы, является природа связей, которые удерживают узлы кристаллической решётки вместе:

1.                  Молекулярные связи характерны для кристаллов с очень низкой механической твёрдостью (кристаллы на основе водорода и гелия)

2.                  Ковалентные связи характерны, напротив, для кристаллов с высокой прочностью (алмаз)

3.                  Ионные связи (соли)

4.                  Металлические связи (металлы)

Особенный интерес представляют собой тела, называющиеся жидкими кристаллами.

Жидкие кристаллы – тела, одновременно обладающие свойствами кристаллов (упорядоченное строение молекул и атомов) и жидкостей (текучесть). Важнейшее свойство жидких кристаллов – оптическая анизотропия, то есть неодинаковое прохождение света по разным направлениям. Все жидкие кристаллы разделены на три типа (рис. 5):

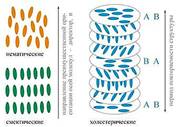
1.                  Нематики – кристаллы имеют нитевидную структуру

2.                  Смектики – представляют собой некие мыльные растворы

3.                  Холестерики – содержат в своём составе холестерин

Рис. 5. Схема ориентации молекул различных типов жидких кристаллов

Аморфные тела – тела, не имеющие строгой кристаллической решётки, бесформенные тела (смола, стекло, графит…). Аморфные тела ещё называют переохлаждёнными вязкими жидкостями в связи с тем, что у них нет строгой температуры плавления, потому как нет явного перехода от твёрдого состояния до жидкого: с увеличением температуры аморфные тела стают только более текучими, а свойство текучести сохраняется у них даже при низких температурах.

Композитные тела – искусственно созданные твёрдые тела, состоящие из жёсткой матрицы и нитевидного кристаллического наполнителя. Благодаря разнообразным комбинированиям этих двух составляющих, можно получать желаемую прочность, гибкость, упругость и т. д. материала.

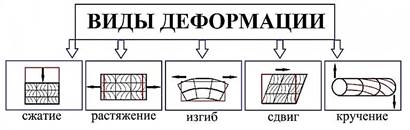
Деформацией называют изменение размеров и формы тела под действием приложенных усилий. Деформация может вызываться приложенными внешними силами или различными физико-механическими процессами, возникающими в материалах вследствие температурного градиента или изменения объёма кристаллов при фазовых превращениях.

1.                   Растяжение – увеличение расстояния между молекулярными рядами

2.                   Сжатие – уменьшение расстояния между молекулярными рядами

3.                   Сдвиг – смещение молекулярных рядов друг относительно друга без изменения расстояния между ними

4.                   Кручение – поворот молекулярных рядов друг относительно друга

5.                   Изгиб – комбинация деформаций сжатия и растяжения

Диаграмма растяжений

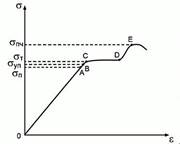Для иллюстрации деформационных качеств твёрдого тела очень хорошо подходит диаграмма растяжений, то есть график зависимости механического напряжения от относительной деформации (см. рис. 4).

Участок ОА называется участком упругости, то есть при растяжениях, попадающих в этот участок, после снятия напряжения с образца тело принимает свою первоначальную форму и объём. Значение механического напряжения в точке А называется механическим напряжением пропорциональности. Участок СD, напротив, называется областью текучести, и при деформации большей, чем значение в точке C, деформация становится эластичной, то есть тело не возвращается в начальное состояние после снятия напряжения.

Рис. 4. Диаграмма растяжений

Именно по величине этой зоны определяется устойчивость образца к разрыву. Значение механического напряжения в точке E называется пределом прочности и соответствует той границе, при переходе которой образец разрушается. В технике часто используется понятие «коэффициент безопасности».

Коэффициент безопасности – отношение механического напряжения пропорциональности к максимальному механическому напряжению, которое испытывает деталь, строение.

Закон Гука

Совершенно очевидно, что для того, чтобы произвести деформацию тела, необходимо приложить силу.  Но, по третьему закону Ньютона, со стороны тела будет действовать сила противодействия, или, как её назвали, сила упругости. Существует закон, позволяющий определить величину этой силы в зависимости от величины деформации. Этот закон носит имя Роберта Гука – английского учёного (рис. 3).

Но прежде, чем вывести его, сформулируем некоторые параметры материала и деформации.

Абсолютная деформация (сдвига) - :            .   Здесь:  - конечная длина тела;  - начальная длина тела.       .   

Относительная деформация – :                     

Механическое напряжение – :  .   Здесь:  - сила упругости, действующая внутри тела;  - площадь сечения тела, перпендикулярного к направлению вектора силы.        

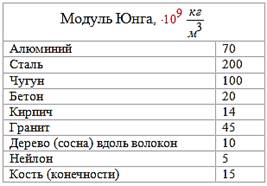
Закон Роберта Гука в общем виде выглядит следующим образом:     .   Здесь:  - модуль Юнга или модуль упругости, табличная величина, характеризующая упругие качества вещества.

Увидим теперь, как можно связать вышеприведённую формулировку закона Гука со знакомой нам ещё из курса динамики:    .  Подставим в формулу закона Гука в общем виде все определения для нововведенных величин:  ,       ;  Выразим из этого выражения силу:    ; Следовательно:        

Очень важным является тот факт, что, во-первых, закон Гука, сформулированный на этом уроке, является более общим, нежели известный нам ранее, а во-вторых, закон Гука выполним только при небольших деформациях.

При непрерывном увеличении внешней нагрузки непрерывно растут напряжение σ и деформация ε. При некотором напряжении σ_s, характерном для каждого материала, наблюдается или разрушение образца, или нарушение прямой пропорциональности между σ и ε и возникновение остаточной (пластической) деформации ε_ост, не исчезающей после снятия внешней нагрузки. В первом случае материал является хрупким, во втором — пластичным. Напряжение σ_s, при котором начинается заметное течение тела, называется пределом текучести; области OA и AB – соответственно областями упругой и пластической деформации (в области ОА выполняется закон Гука).

Тепловое расширение твёрдых тел и жидкостей

1. Кроме теплопроводности, одним из тепловых свойств твёрдого тела является его расширение при нагревании. Вспомните опыт с металлическим шаром, который проходил через кольцо при комнатной температуре (см. рис. 3) и застревал в нём, когда шар нагревали. Это говорит о том, что объём шара при нагревании увеличивался.

Изменение размеров тела при его нагревании называют тепловым расширением. У твёрдого тела различают линейное расширение — изменение длины, ширины, высоты тела (его линейных размеров) и объёмное расширение — изменение объёма при нагревании.

Различные твёрдые вещества по-разному расширяются при нагревании: одни больше, другие меньше. Тепловое расширение характеризуется величиной, называемой температурным коэффициентом расширения.

2. Длина l тела при нагревании от 0 °С до температуры t °С вычисляется по формуле: , где l₀ — длина тела при температуре 0 °С, β — температурный коэффициент линейного расширения. Этот коэффициент показывает, во сколько раз от своего первоначального значения изменяется линейный размер тела при его нагревании на 1 °С.

Единицей температурного коэффициента линейного расширения является градус в минус первой степени (1град¹ или 1 К^-1) : .  Температурные коэффициенты линейного расширения для большинства веществ измерены и приведены в специальных таблицах.

3. Объём V тела при нагревании от 0 °С до температуры t °С вычисляется по формуле: , где V₀ — объём тела при температуре О °С, α — температурный коэффициент объёмного расширения, его единицей является 1 град^-1 или 1 К^-1. Например, температурный коэффициент объёмного расширения алюминия при 20 °С равен 13,7 • 10^-6 град^-1, олова — 21,4 • 10^-6 град^-1, бетона — примерно 12 • 10-6 град-1, эбонита — 70 • 10^-6 град^-1.

4. Поликристаллы одинаково расширяются по всем направлениям. Для них температурный коэффициент объёмного расширения приблизительно в 3 раза больше температурного коэффициента линейного расширения (α ≈ 3β). Монокристаллы по-разному расширяются в разных направлениях. Если вырезать шар из какого-либо монокристалла и нагреть, то он превратится в эллипсоид (примет вытянутую форму). У некоторых веществ температурные коэффициенты линейного расширения для разных направлении различаются довольно существенно. Так, у гипса он для трёх направлений равен соответственно 1,6 • 10^-6 град^-1, 42 • 10^-6 град^-1, 29 • 10^-6 град^-1. Существуют монокристаллы, у которых по некоторым направлениям температурный коэффициент линейного расширения имеет отрицательные значения. Это значит, что при нагревании в этих направлениях кристаллы сжимаются, а в других расширяются.

5. Тепловое расширение твёрдых тел учитывается в технике. Железнодорожные рельсы так же, как и все тела, меняют свою длину при охлаждении и нагревании. Если бы рельсы были плотно пригнаны друг к другу, то при изменении температуры в них возникали бы огромные напряжения, которые могли бы привести к разрушению путей. Поэтому, укладывая рельсы между участками длиной 100—150 м, оставляют зазор. Зимой этот зазор увеличивается, а летом уменьшается. 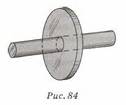Тепловое расширение используют, если нужно одну деталь плотно насадить на другую, например колесо на вал (рис. 84). Диаметр отверстия в колесе делают чуть меньше диаметра вала. При нагревании колесо расширяется, и его свободно насаживают на вал. Остывая, колесо сжимается и плотно охватывает вал. Если тело нагревается неравномерно, то разные его участки расширяются по-разному. В теле возникают напряжения, оно деформируется и может разрушиться. По этой причине лопается стеклянный стакан, когда в него наливают кипяток.

В настоящее время существуют специальные стёкла, которые очень незначительно расширяются при повышении температуры. Таким является кварцевое стекло, которое на 96—99% состоит из кварца. Кварцевое стекло делают из горного хрусталя — особо чистого кварца. А обычное стекло изготавливают из смеси кварцевого песка, соды и мела. Если изготовить палочки длиной 10 см из кварцевого и из обыкновенного стекла и нагреть их на 100 °С, то палочка из обычного стекла удлинится на 0,01 см, а палочка из кварцевого стекла — всего на 0,0005 см. Поэтому в посуде из кварцевого стекла можно кипятить воду. Свойство тел, изготовленных из разных веществ, по-разному изменять свою длину при нагревании также широко используется.

Возьмём две пластины, изготовленные, например, из меди и железа, соединим их (рис. 85, а) и будем нагревать. Медная пластина расширяется сильнее, чем железная, поэтому они прогнутся (рис. 85, б). Такие пластины называют биметаллическими. Их используют в термометрах, в регуляторах температуры. Например, в регуляторе температуры биметаллическая пластина, нагреваясь до предельно допустимой температуры, изгибается и размыкает цепь. В результате этого дальнейшее нагревание не происходит.

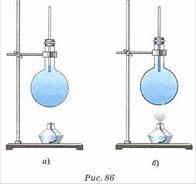
6. Жидкости, так же как и твёрдые тела, расширяются при нагревании. Поскольку они не имеют определённой формы, то нельзя говорить о линейном расширении жидкостей. Их объёмное расширение можно наблюдать на следующем опыте. Возьмём колбу, наполним её водой. Закроем колбу пробкой со вставленной в неё трубкой (рис. 86). При нагревании вода начнёт подниматься по трубке в колбе. Тепловое расширение жидкостей объясняется увеличением средних расстояний между положениями равновесия её молекул. Различные жидкости при нагревании расширяются по-разному: керосин, например, расширяется сильнее, чем вода.

7. Пусть при температуре 0 °С жидкость имела объём V₀, а при температуре t °С — объём V. Тогда объём жидкости при нагревании вычисляется по формуле: 

где α — температурный коэффициент объёмного расширения жидкости. Его единица 1 град^-1 или 1 К^-1.

Значения температурного коэффициента объёмного расширения для разных жидкостей различны и лежат в пределах от 10^-3 до 10^-4 град^-1. Он примерно в 10³ раз больше, чем температурный коэффициент объёмного расширения твёрдых тел. Например, температурный коэффициент объёмного расширения ртути 0,18 • 10^-3 град^-1, эфира — 1,7 • 10^-3 град^-1, воды (при 20 °С) — 2,1 • 10^-4 град^-1. Сравнив значения температурного коэффициента объёмного расширения ртути и эфира, можно заметить, что для ртути он примерно в 10 раз меньше. Это означает, что при изменении температуры на 1 °С относительное изменение объёма ртути в 10 раз меньше, чем объёма эфира. Сравнение значений температурного коэффициента объёмного расширения жидкостей и твёрдых тел показывает, что для эфира он примерно в 100 раз больше, чем для алюминия.

8. Тепловое расширение жидкостей, так же как и твёрдых тел, учитывают и в технике, и в быту. Если жидкость, доверху заполняющая закрытый сосуд, нагревается, то из-за высокого давления сосуд может разорваться. Поэтому баки, в которых нагревают жидкости, делают из материала с большим температурным коэффициентом расширения. Цистерны, в которых перевозят жидкости, не заполняют доверху.

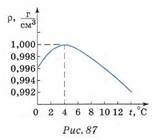
9. Все жидкости достаточно равномерно расширяются с повышением температуры. Исключение составляет вода. Вода расширяется только при нагревании до температуры выше 4 °С. При нагревании от 0 до 4 °С она сжимается, её объём уменьшается, а плотность увеличивается. Наибольшую плотность вода имеет при 4 °С.

На рисунке 87 приведён график зависимости плотности воды от температуры.

Пусть вода имеет низкую температуру. Под действием солнечных лучей верхние слои воды нагреваются, предположим, до температуры 2 °С. Плотность воды в этом слое больше, чем в слое, лежащем ниже и имеющем температуру О °С. Нагретая вода опускается вниз. Её место занимает вода, имеющая более низкую температуру. Таким образом, происходит непрерывная смена слоёв воды и равномерное прогревание всей её толщи. Это будет происходить, пока температура воды не станет равной 4 °С. При дальнейшем нагревании верхние слои становятся менее плотными и остаются вверху. Поэтому большие толщи воды прогреваются быстро лишь до 4 °С, дальнейшее прогревание нижних слоёв идёт медленно из-за плохой теплопроводности и отсутствия конвекции. Охлаждение воды до 4 °С идёт быстро, а дальнейшее охлаждение замедляется по той же причине. Это приводит к тому, что глубокие водоёмы, начиная с некоторой глубины, имеют температуру +2 - +3 °С. Даже зимой вода в водоёмах не промерзает до дна. Верхние более холодные слои воды опускаются вниз, а тёплые занимают их место. Такое перемещение происходит до тех пор, пока температура воды не станет равной 4 °С. При дальнейшем охлаждении верхние слои не будут опускаться вниз и постепенно замёрзнут.

Плавление и кристаллизация

Плавление вещества это переход вещества из твердого состояния в жидкое.

Этот фазовый переход всегда сопровождается поглощением энергии, т. е. к веществу необходимо подводить теплоту. При этом внутренняя энергия вещества увеличивается. Плавление происходит только при определенной температуре, называемой температурой плавления. Каждое вещество имеет свою температуру плавления. Например, у льда 0⁰С.

Пока происходит плавление, температура вещества не изменяется.

Что надо сделать, что расплавить вещество массой? Сначала нужно его нагреть до температуры плавления, сообщив количество теплоты, где   удельная теплоемкость вещества. Затем необходимо подвести количество теплоты, где   удельная теплота плавления вещества. Само плавление будет происходить при постоянной температуре, равной температуре плавления.

Кристаллизация (затвердевание) вещества  переход вещества из жидкого состояния в твердое.

Это процесс, обратный плавлению. Кристаллизация всегда сопровождается выделением энергии, т. е. от вещества необходимо отводить теплоту. При этом внутренняя энергия вещества уменьшается. Она происходит только при определенной температуре, совпадающей с температурой плавления.

Пока происходит кристаллизация, температура вещества не изменяется.

Что надо сделать, что вещество массой  кристаллизовалось? Сначала нужно его охладить до температуры плавления, отведя количество теплоты, где   удельная теплоемкость вещества. Затем необходимо отвести количество теплоты, где   удельная теплота плавления вещества. Кристаллизация будет происходить при постоянной температуре, равной температуре плавления.

Скачано с www.znanio.ru