
Оглавление
Введение ………………………………………………………………………………… 3
Лекция 1. Понятие о комплексных числах. Алгебраическая,
тригонометрическая, показательная формы записи комплексных
чисел. Геометрическая интерпретация комплексных чисел.
Действия над комплексными числами. ……………………………………………… 3
Лекция 2. Матрицы. Определитель матрицы. Свойства определителей
и их вычисление. Решение простейших матричных уравнений. Теорема Крамера.
Применение формул Крамера к решению систем линейных уравнений ……….. 8
Лекция 3. Функции одной независимой переменной. Пределы.
Непрерывность функций. Производная, геометрический смысл.
Исследование функций. ………………………………………………………………. 11
Лекция 4. Неопределенный интеграл. Методы интегрирования.
Определенный интеграл. Вычисление определенного интеграла.
Геометрический смысл определенного интеграла. ……………………………….. 21
Лекция 5. Задачи, приводящие к дифференциальным уравнениям.
Дифференциальные уравнения с разделяющимися переменными. Общие и
частные решения. Однородные дифференциальные уравнения первого
порядка. Линейные однородные уравнения второго порядка с
постоянными коэффициентами. ……………………………………………………… 30
Лекция 6. Методы интегрирования. Метод прямоугольников. Метод трапеций.
Метод Симпсона. Абсолютная погрешность при численном
интегрировании ………………………………………………………………………. 35
Лекция 7. Понятие о численном решении дифференциальных уравнений.
Формулы приближенного дифференцирования, основанные на
интерполяционных формулах Ньютона. Погрешности в определении
производной. Построение интегральной кривой. Метод Эйлера……………….. 40
Лекция 8-9. Числовые ряды. Сходимость и расходимость числовых рядов.
Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и
условная сходимость рядов. Интегральный признак Коши. Признак
Лейбница. Степенные ряды. Ряды Фурье …………………………………………… 60
Лекция 10. Понятие события и вероятности события. Достовернее и
невозможные события. Классическое определение вероятности. Теорема
сложения вероятностей. Применение теории вероятности при
решении профессиональных задач. ………………………………………………… 68
Лекция 11. Случайная величина. Дискретная и непрерывная случайные
величины. Закон распределения случайной величины…………………………… 74
Лекция 12. Математическое ожидание дискретной случайной величины.
Дисперсия случайной величины. Среднее квадратное отклонение
случайной величины………………………………………………………………….. 80
Литературные и интернет – источники …………………………………………….. 84
ВВЕДЕНИЕ
Конспект лекций составлен в соответствии с программой базового курса по математике для студентов 2 курса средних профессиональных учебных заведений, обучающихся по специальностям 150415 «Сварочное производство», 150402 «Металлургия цветных металлов», 270843 «Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий» Он содержит как теоретическую часть, так и большое количество примеров и задач.
Основное назначение данного пособия состоит в том, чтобы помочь студенту преодолеть трудности при решении практических работ по математике.
При самостоятельном решении задач многие студенты нуждаются в постоянных консультациях относительно приемов и методов их решения. Такие консультации студент может получить при изучении этого пособия.
Такая форма изложение позволяет студенту сначала познакомиться с приемами решения типовых задач и оформлением записи их решений, а затем приступить к выработке навыков при решении практических работ.
Лекция 1. Понятие о комплексных числах. Алгебраическая, тригонометрическая, показательная формы записи комплексных чисел. Геометрическая интерпретация комплексных чисел. Действия над комплексными числами.
Понятие мнимой единицы Допустим, что существует такое число, квадрат которого равен – 1. Обозначим это число буквой i; тогда можно записать:
i2 = – 1.
Число i будем называть мнимой. Из этого
равенства находим ![]()
Введение мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.
Например,
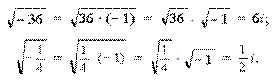
Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.
Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.
Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.
Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей, т.е., если
a + bi = c +di, то a = c, b = d.
Геометрическая интерпретация комплексного числа Комплексное число z= a + bi можно изобразить точкой Z плоскости с координатами (a; b) (рис.1).

Рис.1
Для этого выберем на плоскости декартову прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которую называют действительной (или вещественной) осью; чисто мнимые числа – точками оси ординат, которую будем называть мнимой осью.
Каждой точке плоскости с координатами (a; b) соответствует один и только один вектор с началом O(0; 0) и концом Z(a; b). Поэтому комплексное число z = a + bi можно изобразить в виде вектора с началом в точке O(0; 0) и концом в точке Z(a; b).
Пример 1. Изобразить на плоскости числа z1 = 5; z2 = – 3i; z3 = 3 + 2i; z4 = 5 – 2i; z5 = – 3 + 2i; z6 = – 1 – 5i.
Решение. Заданные числа изображены на рис. 2.
|
|
Рис. 2 |
Действие над комплексными числами a+bj и c+dj в алгебраической форме
1) Правило сложения и вычитания комплексных чисел.
(a + bi) + (c + di) = (a + c) + (b + d)i.
Например:
![]() +
+ ![]() =
=
![]()
Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:
(a + bi) – (c + di) = (a – c) + (b – d)i.
Например:
![]() -
- ![]() =
= ![]()
2) Правило умножения комплексных чисел.
(a + bi)(c + di) = (aс + bd) + (ad + bc)i.
Из определений 4 и 5 следует, что операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i2 = – 1.
Действительно: (a + bi)(c + di) = ac + adi + bdi2 = (ac – bd) + (ad + bc)i.
Например, ![]() *
* ![]() =
=
![]()
В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Действительно:
(a + bi)(a – bi) = a2 – abi + abi – b2i2 = a2 + b2.
Произведение двух чисто мнимых чисел – действительное число.
Например: 5i•3i = 15i2 = – 15.
3) Деление комплексного числа a + bi на комплексное число c + di определяется как операция обратная умножению и выполняется по формуле:
![]() .
.
Формула теряет смысл, если c + di = 0, так как тогда c2 + d2 = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.
Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.
Например,
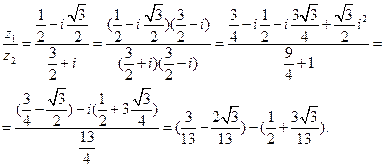
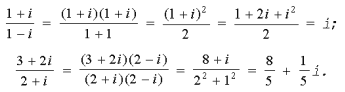
Тригонометрическая форма комплексного числа
|
Пусть комплексное число z = a + bi изображено в виде вектора с началом в точке O(0; 0) и концом Z(a; b)
рис. 3 Определение 3. Модулем комплексного числа z = a + bi называется длина вектора , которую можно найти по формуле
Обозначив модуль комплексного числа буквой r. |
Рис. 3 |
Определение 4. Аргументом комплексного
числа называется угол φ, который образует вектор с положительным
направлением оси абсцисс. Величину угла φ можно найти с помощью
формул: 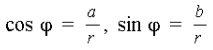
z = r (cos φ + i sin φ) называется тригонометрической формой комплексного числа.
Сформулируем правило перехода от алгебраической формы комплексного числа к тригонометрической.
1. Находят
модуль комплексного числа r, для чего используют формулу ![]()
2. Для нахождения φ сначала определяют геометрически, в какой четверти находится точка z.
3.
Составляют уравнения ![]() и
и ![]() и по решению одного из них находят угол φ.
и по решению одного из них находят угол φ.
4. Записывают комплексное число z в тригонометрической форме.
Показательная форма комплексного числа
Если комплексному числу z = (cos φ + i sin φ), модуль которого равен 1, поставить в соответствие показательное выражение eiφ, то получим соотношение
cos φ + i sin φ = eiφ называется формулой Эйлера.
Любое комплексное число z можно записать в виде z = r eiφ
Эта форма записи комплексного числа называется показательной формой.
Действия над комплексными числами в тригонометрической форме:
1. ![]()
2. z1/z2 = ![]() =
= ![]()
3. zn = (r(cos j + i sin j ))n = rn(cos nj + i sin nj )
4. ![]() =
= ![]() =
= ![]() , где k = 0, 1, 2 , …, n-1
, где k = 0, 1, 2 , …, n-1
Последняя формула называется формулой Муавра.
Пример 2: z1 = ![]() (cos (-
(cos (- ![]() ) + i sin (-
) + i sin (- ![]() ) ) и z2 = 2 (cos
) ) и z2 = 2 (cos ![]() + i sin
+ i sin ![]() )
)
![]()
= ![]()
![]()
= ![]()
(z2)3 = 23
(cos 3*![]() + i sin 3*
+ i sin 3*![]() ) = 8 (cos
) = 8 (cos ![]() + i sin
+ i sin ![]() )
)
![]() =
= ![]()
![]() =
= ![]()
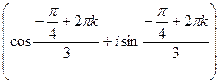
полагая k = 0, 1, 2, найдем
при к = 0
![]() =
= ![]()
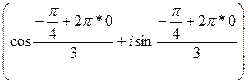 =
= ![]()
![]()
при к = 1
![]() =
= ![]()
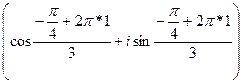 =
= ![]()
![]()
при к = 2
![]() =
= ![]()
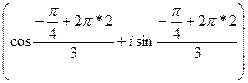 =
= ![]()
![]()
Действия над комплексными числами в показательной форме:
z1z2 = ![]()
z1/z2 = ![]()
zn =rn en i j
Пример 3: z1
= ![]()
![]() и z2 = 2
и z2 = 2![]()
z1z2 = ![]()
z1/z2 = ![]()
(z2 )3 = 23![]() = 8
= 8![]()
x2 = – 1.
Покажем, что расширив поле действительных чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное уравнение разрешимо, т.е. имеет решение. Так, уравнение x2 = – 1 имеет два решения: x1 = i, x2 = – i.
ПРИМЕР: Решите уравнение x2 – 4x + 5 = 0.
Решение. D = 16 – 4•1•5 = – 4 < 0, уравнение имеет
мнимые корни: 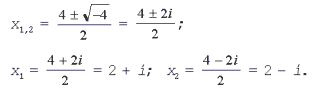
Лекция 2. Матрицы. Определитель матрицы. Свойства определителей и их вычисление. Решение простейших матричных уравнений. Теорема Крамера. Применение формул Крамера к решению систем линейных уравнений
Теорема. Система n уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.
Пусть дана система n линейных уравнений с n переменными:
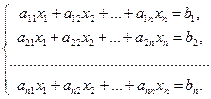
Из коэффициентов при неизвестных составим матрицу А, а из свободных членов — матрицу-столбец В, т. е.
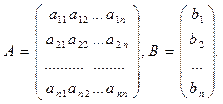
Определитель матрицы А обозначим ∆ и назовем определителем системы. Таким образом,
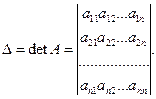
Пусть ∆ ≠ 0. Если в
определителе системы заменить поочередно столбцы коэффициентов при ![]() на столбец свободных членов, то
получим n определителей (для n
неизвестных)
на столбец свободных членов, то
получим n определителей (для n
неизвестных)
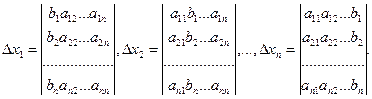
Тогда формулы Крамера для решения системы n линейных уравнений с n неизвестными запишутся так:
![]()
или короче
![]() где
где ![]()
Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:
1. ![]() и
каждый определитель
и
каждый определитель ![]() . Это имеет место только
тогда, когда коэффициенты при неизвестных
. Это имеет место только
тогда, когда коэффициенты при неизвестных ![]() пропорциональны,
т. е. каждое уравнение системы получается из первого уравнения умножением обеих
его частей на число k. Очевидно, что при этом система имеет бесчисленное
множество решений.
пропорциональны,
т. е. каждое уравнение системы получается из первого уравнения умножением обеих
его частей на число k. Очевидно, что при этом система имеет бесчисленное
множество решений.
2. ![]() и
хотя бы один из определителей
и
хотя бы один из определителей ![]() . Это имеет
место только тогда, когда коэффициенты при всех неизвестных, кроме
. Это имеет
место только тогда, когда коэффициенты при всех неизвестных, кроме ![]() , пропорциональны. При этом
получается система из противоречивых уравнений, которая не имеет решений.
, пропорциональны. При этом
получается система из противоречивых уравнений, которая не имеет решений.
Пример 1. Решить систему уравнений
![]()
Решение.
Вычислим определитель системы ∆ и определители ![]() и
и
![]() :
:
![]()
Найдем значения х и у по формулам Крамера:
![]()
Итак, решение системы есть (3; —1).
Пример 2. Решить систему уравнений
![]()
Решение.
Вычислим определитель системы ∆ и определители ![]() и
и
![]() :
:
![]()
Так
как ![]() , а
, а ![]() то
система не имеет решений (уравнения противоречивы).
то
система не имеет решений (уравнения противоречивы).
Пример 3. Решить систему уравнений
![]()
Решение.
Вычислим определитель системы ∆ и определители ![]() и
и
![]() :
:
![]()
Данная система имеет бесчисленное множество решений (коэффициенты при неизвестных пропорциональны).
Пример 4. Решить систему уравнений

Решение. Вычислим определитель системы и определители при неизвестных:
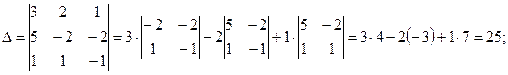

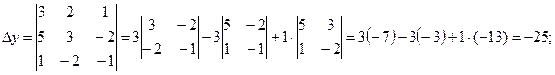
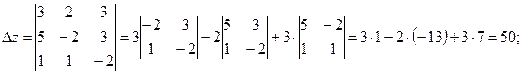
Найдем значения x,y,z по формулам Крамера:
![]()
![]()
![]()
Ответ: (1; -1; 2).
Лекция 3. Функции одной независимой переменной. Пределы. Непрерывность функций. Производная, геометрический смысл. Исследование функций.
3.1 Предел функции.
Пусть функция y=f(x) определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0.
О (на « языке последовательностей», или по
Гейне): Число
А называется пределом функции y=f(x) в точке x0, если для любой
последовательности допустимых значений аргумента xn, nÎN (xn¹x0), сходящейся к x0 ( т.е. ![]() ),
последовательность соответствующих значений f(xn),nÎN, сходиться к
числу А.
),
последовательность соответствующих значений f(xn),nÎN, сходиться к
числу А.
Техника вычисления пределов.
При вычисление предела элементарной функции f(x) приходиться сталкиваться с двумя различными типами примеров.
1. Функция f(x) определена в
предельной точке х = а. Тогда ![]()
2. Функция f(x) в предельной точке х = а не определена или же вычисляется предел функции при х ® ¥ . Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях ( наиболее простых) вопрос сводиться непосредственно к применению теорем о свойствах бесконечно больших и бесконечно малых функций и связи между ними.
Более сложными случаями нахождения предела
являются такие, когда функция f(x) в точке х = а или при х ® ¥ представляет собой неопределенность (
типа ![]()
Приведем основные теоремы, на которых основано вычисление пределов.
1)
Если
существуют ![]() и
и ![]() ,
то
,
то
·
![]() =
= ![]() +
+
![]()
·
![]() =
= ![]() -
-
![]()
·
![]() =
= ![]() *
*
![]()
·
![]() =
= ![]() /
/
![]() при
при ![]() ¹ 0
¹ 0
2)
![]() = С*
= С*![]() ,
где С – некоторое число
,
где С – некоторое число
3)
Связь
между бесконечно малой и бесконечно большой величинами (С– некоторое число): ![]()
Рассмотрим некоторые ПРИМЕРЫ:
Пример
1.
Найти предел функции 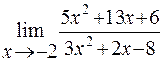
Решение:
Имеем неопределенность вида![]() . Для ее
раскрытия разложим числитель и знаменатель на множители и сократим на общий
множитель
. Для ее
раскрытия разложим числитель и знаменатель на множители и сократим на общий
множитель ![]() , который при
, который при ![]() не равен
нулю. В результате неопределенность будет раскрыта.
не равен
нулю. В результате неопределенность будет раскрыта.
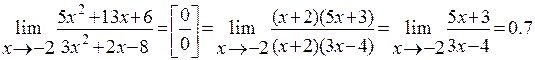
Пример
2.
Найти предел функции 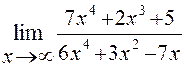
Решение:
Имеем неопределенность вида ![]() . Для ее
раскрытия можно либо разделить числитель и знаменатель на наибольшую степень
переменной x и учитывая, что
величина обратная бесконечно большой величине есть бесконечно малая величина,
раскроем исходную неопределенность, либо вынести переменную в наибольшей
степени в числители и знаменатели дроби и сократить на наибольшую степень.
. Для ее
раскрытия можно либо разделить числитель и знаменатель на наибольшую степень
переменной x и учитывая, что
величина обратная бесконечно большой величине есть бесконечно малая величина,
раскроем исходную неопределенность, либо вынести переменную в наибольшей
степени в числители и знаменатели дроби и сократить на наибольшую степень.
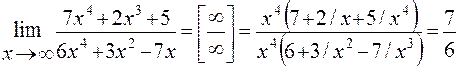
Пример
3.
Найти предел функции 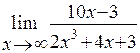
Решение: Имеем
неопределенность вида ![]() . Раскрываем ее
аналогично тому как это сделано в примере 2.
. Раскрываем ее
аналогично тому как это сделано в примере 2.
Пример
4.
Найти предел функции 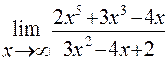
Решение:
Имеем неопределенность вида ![]() . Раскрываем ее
аналогично тому как это сделано в примере 2.
. Раскрываем ее
аналогично тому как это сделано в примере 2.

Пример
5.
Найти предел функции 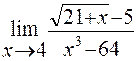
Решение:
Имеем неопределенность вида ![]() . Для ее
раскрытия умножим числитель и знаменатель на выражение сопряженное числителю,
разложим выражение стоящее в знаменателе на множители по формуле разности кубов
и сократим числитель и знаменатель на общий множитель
. Для ее
раскрытия умножим числитель и знаменатель на выражение сопряженное числителю,
разложим выражение стоящее в знаменателе на множители по формуле разности кубов
и сократим числитель и знаменатель на общий множитель ![]() , который
при
, который
при ![]() не равен нулю. В результате
неопределенность будет раскрыта.
не равен нулю. В результате
неопределенность будет раскрыта.
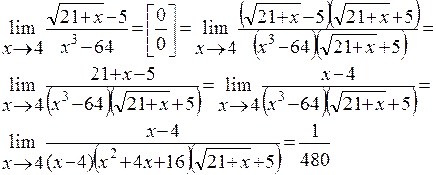
Вычисление пределов с использованием замечательных пределов.
Применение замечательных пределов
![]() и
и 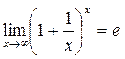
Пользуясь этими формулами, можно вычислить ряд пределов.
Пример
6.
Вычислить ![]() .
.
![]() , заменяя 3x = y и
учитывая, что y → 0 при x → 0, получаем:
, заменяя 3x = y и
учитывая, что y → 0 при x → 0, получаем:
![]() .
.
Пример
7
. Вычислить 

Здесь мы воспользовались известным из курса средней школы пределом:
![]() .
.
Пример
8
. Вычислить 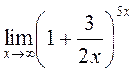
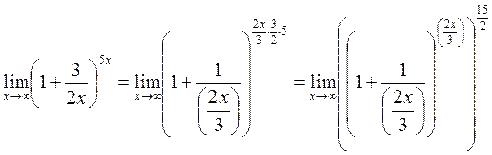
Заменяя
![]() и учитывая,
что y → ∞ при x → ∞, можем написать:
и учитывая,
что y → ∞ при x → ∞, можем написать:
 .
.
3.2 Непрерывность функции
О: Функция y = f(x) называется
непрерывной в точке х = а, если существует предел функции в этой точке, который
равен значению функции в этой точке, т.е. ![]() .
.
Примером непрерывной функции может служить любая элементарная функция, которая непрерывна в каждой точке своей области определения.
Точка х = а называется точкой разрыва функции y=f(x), если эта функция определена в некоторой окрестности точки х = а, но в самой точке х = а не удовлетворяет условию непрерывности.
Точки разрыва функции делятся на два типа.
К точкам разрыва I рода относятся такие
точки, в которых существуют конечные односторонние пределы:![]() (левый предел) и
(левый предел) и ![]() (правый предел). К точкам
разрыва II рода относятся те точки, в которых хотя
бы один из односторонних пределов не существует или бесконечен.
(правый предел). К точкам
разрыва II рода относятся те точки, в которых хотя
бы один из односторонних пределов не существует или бесконечен.
Задание 4. Исследовать данную функцию на непрерывность и построить ее график
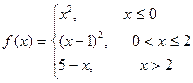
Решение:
Функция ![]() является
неэлементарной, так как на разных интервалах представлена различными
аналитическими выражениями. Эта функция определена на интервалах (-∞;0),
(0;2) и (2; +∞), где она задана непрерывными элементарными функциями.
Внутри каждого интервала указанные элементарные функции не имеют точек разрыва,
следовательно, разрыв возможен только в точках перехода от одного
аналитического выражения к другому, т.е. в точках х1 = 0 и х2
= 2.
является
неэлементарной, так как на разных интервалах представлена различными
аналитическими выражениями. Эта функция определена на интервалах (-∞;0),
(0;2) и (2; +∞), где она задана непрерывными элементарными функциями.
Внутри каждого интервала указанные элементарные функции не имеют точек разрыва,
следовательно, разрыв возможен только в точках перехода от одного
аналитического выражения к другому, т.е. в точках х1 = 0 и х2
= 2.
Для точки х1 = 0 имеем:
![]()
Так
как ![]() , то функция
, то функция ![]() в точке х1 = 0
имеет разрыв первого рода.
в точке х1 = 0
имеет разрыв первого рода.
Для точки х2 = 2 находим:
![]()
Так
как ![]() , то функция
, то функция ![]() в точке х2 =
2 имеет разрыв первого рода.
в точке х2 =
2 имеет разрыв первого рода.
График данной функции изображен на рис. 1.
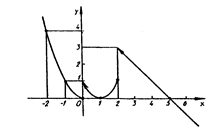
Рис. 1.
3.3 Производная, геометрический смысл.
Основные правила дифференцирования
а) c’ = 0; б) (и ± υ)’ = и’ ± υ’; в) (иυ)’ =
и’υ + иυ’; г ) ![]()
д) дифференцирование сложной функции, если ![]() ,
, ![]() то
то ![]() - сложной функция. Тогда,
- сложной функция. Тогда, ![]() или
или ![]()
Здесь c = const, а и и υ - дифференцируемые функции.
Таблица производных основных элементарных функций
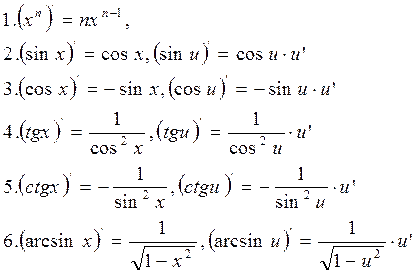
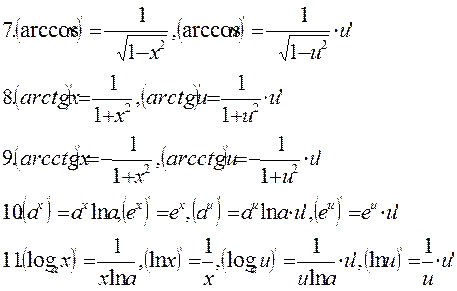
Пример: Найти производные следующих функций :
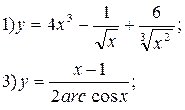
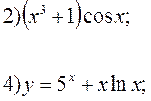
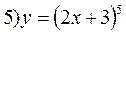
Решение. 1) Запишем данную функцию следующим образом:
![]() .
.
Тогда
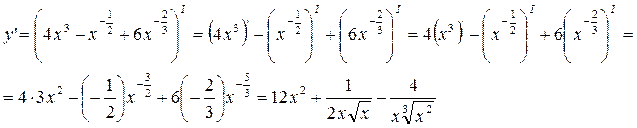
2) Имеем
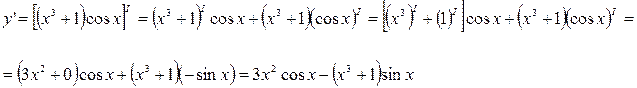
3) Имеем
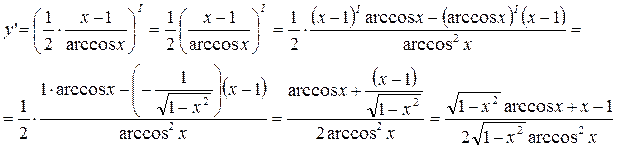
4) Имеем
![]()
5) Имеем
![]() ;
;
Геометрическое приложение производной.
Производная функции y = y (x) при данном значении аргумента x = x0 равна угловому коэффициенту касательной, проведённой к графику этой функции в точке с абсциссой x0. (См. рис.):
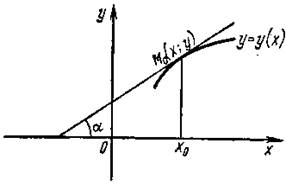 y'(x0)=tgα.
(1)
y'(x0)=tgα.
(1)
Уравнение прямой к графику функции
y = y (x) в точке М0 (x0 ; y0) имеет вид
y - y0 = y’(x0) (x - x0) . (2)
Если y (x) имеет при x = x0 бесконечную производную, то уравнение касательной таково:
x = x0. (3)
Уравнение нормали, т.е. прямой, проходящей через точку касания М0 (x0 ; y0) перпендикулярно касательной, записывается в виде
![]() (4)
(4)
Пример: Составить уравнение касательной и нормали к параболе y = 2x2 - 6x + 3 в точке М0 (1 ; -1).
Решение. Найдём производную функции y = 2x2 - 6x + 3 при x = 1. Имеем y’ = 4x - 6, откуда y’ (1) = -2.
Воспользовавшись уравнением (2), получим искомое уравнение касательной :
y - (-1) = -2 (x - 1), или 2x + y - 1 = 0.
Уравнение нормали получим, используя уравнение (4) :
![]() , или x - 2y - 3 = 0.
, или x - 2y - 3 = 0.
3.4 Исследование функции.
Исследование функции методами дифференциального исчисления.
v Интервалы монотонности.
Функция называется возрастающей ( убывающей) в некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее ( меньшее) значение функции. Как возрастающие, так и убывающие функции называются монотонными.
Правило нахождения интервалов монотонности:
- найти нули и точки разрыва f ’(x);
- определить методом проб знак f ’(x) в интервалах, на которые полученные в п.1 точки делят область определения функции f (x);
- интервалы в которых f ’(x) > 0, являются интервалами возрастания функции, а интервалы в которых f ’(x) < 0, - интервалами убывания функции. При этом если на двух соседних интервалах, граничная точка которых является нулем производной f ’(x), знак f ’(x) одинаков, то они составляют единичный интервал монотонности.
v Экстремум функции.
Точка х = х0 называется точкой максимума ( минимума) функции y = f(x), если существует такая окрестность точки х0, что для всех х ( х ¹ х0) этой окрестности выполняется неравенство:
f(x) < f(x0), [f(x) > f(x0)].
Точками максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума ( минимума) - максимумом ( минимумом) или экстремумом функции.
Правило отыскания экстремумов функции:
- найти нули и точки разрыва f ’(x);
- определить методом проб знак f ’(x) в интервалах, на которые полученные в п.1 точки делят область определения функции f (x);
- из этих точек выделить те, в которых функция f(x) определена и по разные стороны от каждой из которых производная f ’(x) имеет разные знаки – это и есть экстремальные точки; при этом экстремальная точка х = х0 является точкой максимума если в этой точке происходит смена знака с « + » на « - », и точкой минимума – с « - » на « + ».
v Общая схема исследования функции и построение ее графика.
1. Найти область определения функции.
2. Исследовать функцию на четность или нечетность; проверить так же не является ли она периодической.
3. Найти точки пересечения функции с осями координат.
4. Найти интервалы знакопостоянства.
5. Найти интервалы монотонности, ее экстремумы.
6. Построить график функции, используя полученные результаты.
ПРИМЕР:
Пример 1. Исследовать функцию и построить график.
![]()
1) Область определения (это множество тех значений, которое может принимать аргумент, т.е. х).
х – любое.
Исследовать функцию у = х2 – 5х + 6 и построить ее график.
1. О.о.: х Î (- ¥; + ¥)
2. f( - x) = ( - x)2 – 5( - x) + 6 = х2 + 5х + 6 Þ функция нечетная; непереодичная.
3. Точки пересечения с осями координат:
- с осью Оу: х = 0, 02 – 5*0+6 = 0 Þ у = 6
- с осью Ох: у = 0 , х2 – 5х + 6 = 0
Д = ( - 5)2 – 4*1*6 = 25 – 24 = 1
х1 = 3, х2 = 2
4. Найдем интервалы знакопостоянства:
У’ = 2x – 5
2x – 5 = 0
x = 2,5
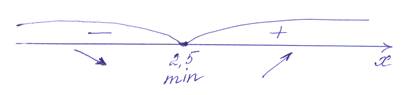
5. Интервалы монотонности:
f( x ) возрастает при х Î ( 2,5; + ¥)
f( x ) убывает при х Î (- ¥; 2,5)
6. Экстремумы:
Хmin = 2,5 Ymin = 2,52 – 5 * 2,5 + 6 = - 0,25
7. График:
7)График.
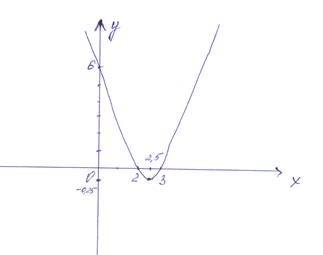
3.5. Функции нескольких переменных. Частные производные
Пусть задана функция z=f(x,y). Так как x и y - независимы переменные, то одна из них может изменяться, а другая сохранять свое значение.
О: Если существует предел
 ,
,
то он называется частной производной функции z=f(x,y) в точке М(х,у) по переменной х и обозначается одним их символов:
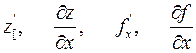 .
.
Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(x,y) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х и у считается постоянной величиной ).
Формула полного дифференциала функции 
ПРИМЕР: Найти полный дифференциал функции двух переменных
![]()
Решение.
Полный дифференциал функции двух переменных находим по формуле:
![]()
где z/x ; z/y – частные производные данной функции z.
Частные производные берем по обычным формулам дифференцирования для функции одной переменной, причем z/x находим, считая “y” постоянной величиной; аналогично при отыскании z/y считаем “x” постоянным:
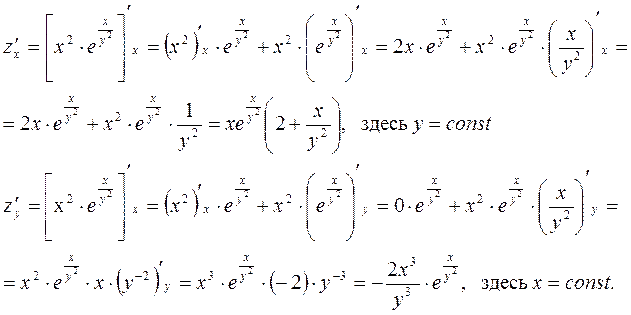
Отсюда полный дифференциал функции :
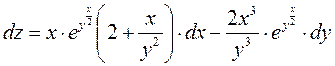
Лекция 4. Неопределенный интеграл. Методы интегрирования. Определенный интеграл. Вычисление определенного интеграла. Геометрический смысл определенного интеграла.
4.1 Неопределенный интеграл.
Определение 1. Функция F(x) называется
первообразной для функции f(x) в промежутке ![]() , если в
любой точке этого промежутка ее производная равна f(x):
, если в
любой точке этого промежутка ее производная равна f(x):
![]() ,
, ![]() . (1)
. (1)
Определение 2. Совокупность всех первообразных функций F(x) + с для функции f(x) на некотором промежутке называется неопределённым интегралом и обозначается
![]()
![]() (2)
(2)
где f(x)dx называется
подынтегральным выражением, х - переменной интегрирования, а С -произвольной постоянной интегрирования. Процесс
нахождения первообразной функции называется интегрированием. Например
![]() , т.к.
, т.к.
![]()
4.2 Метод непосредственного интегрирования.
Под непосредственным интегрированием понимают способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводятся к одному или нескольким табличным интегралам.
Формулы интегрирования:
1. ![]() 2.
2.
![]()
где
![]()
3. ![]() 4.
4.
![]()
5. ![]() 6.
6.
![]()
7. ![]() 8.
8.
![]()
9. ![]() 10.
10.
![]()
11. ![]() 12.
12.
![]()
13. ![]() 14.
14.
![]()
15. ![]()
Свойства неопределённого интеграла
1) ![]() 2)
2) ![]() 3)
3) ![]()
![]()
4) ![]()
Примеры
1) ![]()
Проверка:
![]()
![]()
Проверка:
![]()
4.3 Интегрирование способом подстановки (замена переменной)
Сущность
интегрирования методом подстановки заключается в преобразовании интеграла ![]() в
интеграл
в
интеграл ![]() , который легко вычисляется по
какой-либо из основных формул интегрирования. Для нахождения
, который легко вычисляется по
какой-либо из основных формул интегрирования. Для нахождения ![]() заменяем
переменную х новой переменной и с помощью подстановки.
заменяем
переменную х новой переменной и с помощью подстановки. ![]() .Дифференцируя это равенство,
получаем
.Дифференцируя это равенство,
получаем ![]() . Подставляя в подынтегральное
выражение вместо х и dx их значения, выраженные через
. Подставляя в подынтегральное
выражение вместо х и dx их значения, выраженные через ![]()
![]() , имеем
, имеем
![]() (3)
(3)
После
того, как интеграл относительно новой переменной и будет найден, с
помощью подстановки ![]() он приводится к
переменной х.
он приводится к
переменной х.
Примеры:
l) ![]() 2)
2) ![]()
Решение:
1) положим 1 + х = z. Продифференцируем это неравенство: ![]() или
dx = dz.
или
dx = dz.
Заменим в интеграле: ![]()
2) Сделав
замену: ![]() , получим
, получим ![]() . Тогда
. Тогда
![]()
4. 4 Интегрирование “по частям”
Интеграл из пункта в) вашей контрольной работы берется методом интегрирования “по частям”. Этим методом интегрируются некоторые произведения, например произведения степенной функции на логарифмическую или на показательную, или на тригонометрическую, или на обратные тригонометрические функции и др.
Интегрирование “по частям” производится по формуле
![]()
Чтобы воспользоваться этой формулой, следует один множитель в подынтегральном выражении обозначить за “u”, а оставшийся множитель вместе с dx принять за “dv”.
Для того, чтобы интеграл в правой части был проще данного интеграла, надо правильно выбрать “u” и “dv”.
В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за “u”. Если подынтегральная функция содержит произведение степенной функции на показательную или тригонометрическую, то за “u” принимается степенная функция.
Пример.
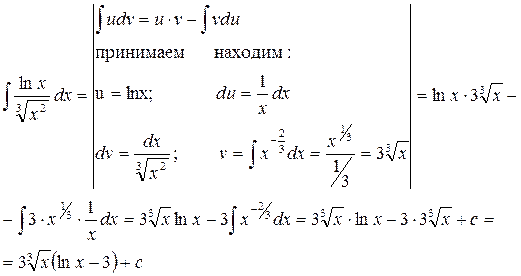
![]()
Пример.
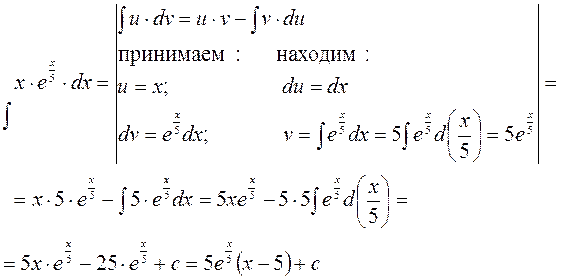
4. 5 Интеграл от рациональной дроби.
В пункте г) вашей контрольной работы предлагается взять интеграл от рациональной дроби.
Пример.
![]()
Под знаком интеграла стоит рациональная дробь.
1. Так как подинтегральная рациональная дробь неправильная (степень многочлена в числителе выше степени многочлена в знаменателе),то выделим целую часть, разделив числитель на знаменатель “углом” (аналогично тому, как в задачах 41-50):

Итак, подынтегральную функцию можно записать в виде:
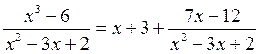
Тогда данный интеграл (обозначим его J), можно представить как сумму интегралов:
![]()
2. Чтобы взять полученный новый интеграл от правильной рациональной дроби (обозначим его J1, разложим знаменатель подынтегральной функции на множители.
Для этого найдем корни квадратного трехчлена, стоящего в знаменателе: x2-3x+12=0.
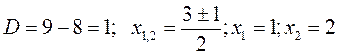
Тогда
![]()
3. Представим полученную правильную дробь в виде суммы элементарных дробей:
4.
![]() (*)
(*)
Здесь А и В - числа, которые нужно найти. Сделаем приведение к общему знаменателю в правой части:
![]()
Так как дроби тождественно равны и равны их знаменатели, то должны быть равны и их числители:
7x-12=A(x-2)+B(x-1);
7x-12=Ax-2A+Bx-B;
7x-12=(A+B)x+(-2A-B).
Это тождество выполняется тогда и только тогда, когда слева и справа равны коэффициенты при одинаковых степенях х:
![]()
Получена система двух уравнений с двумя неизвестными А и В, решив которую, найдем А=5; В=2.
Подставим найденные числа в равенство (*):
![]()
4. Вернемся к интегралу J1:
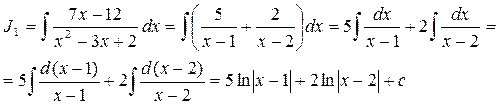
5. Окончательно искомый интеграл равен:
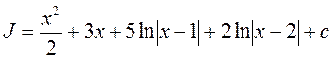
4.6 Определенный интеграл.
Определение.
Приращение F (b) - F (а) любой из первообразных функций F (х) + С
функции f (х) при изменении аргумента от х = а до х = b называется
определённым интегралом от а до b
функции f(x) и обозначается: 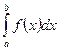 (1)
(1)
Числа а и b называются пределами интегрирования, а - нижним, b - верхним. Отрезок [а;b] называется отрезком интегрирования. Функция f(x) называется подынтегральной функцией, а переменная х - переменной интегрирования.
Таким образом, по определению  (2)
(2)
Данное равенство называется формулой Ньютона - Лейбница.
Геометрический смысл определенного интеграла: если интегрируемая на отрезке [а;b] функция
f (х) неотрицательна, то определённый интеграл 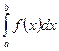 численно равен площади S криволинейной трапеции, ограниченной графиком функции f (x), осью абсцисс и прямыми х = аих = b:
численно равен площади S криволинейной трапеции, ограниченной графиком функции f (x), осью абсцисс и прямыми х = аих = b:
|
|
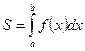
Пример
1: Вычислить 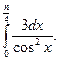
Решение:
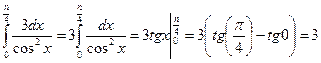
Пример
2: Вычислить 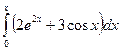
Решение:

Методы вычисления определенного интеграла.
Непосредственное интегрирование предполагает использование основных свойств определенного интеграла и формулы Ньютона - Лейбница.
Пример
3. Вычислить 
Решение:
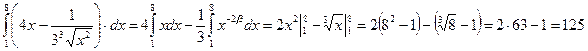
Метод
подстановки сводит определенный интеграл 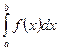 с
помощью подстановки
с
помощью подстановки ![]() к определенному
интегралу относительно новой переменной и. При этом старые пределы интегрирования а и b заменяются
соответственно новыми пределами интегрирования а1
и b1, которые находятся из исходной подстановки:
к определенному
интегралу относительно новой переменной и. При этом старые пределы интегрирования а и b заменяются
соответственно новыми пределами интегрирования а1
и b1, которые находятся из исходной подстановки: ![]() ,
, ![]()
Пример 4. Решение:
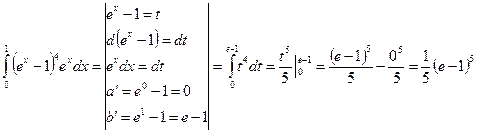
4.5 Геометрический смысл определенного интеграла
Геометрический смысл определённого интеграла:
площадь фигуры, ограниченной кривой у = f (х), где f (х)![]() 0, осью ОХ и двумя
прямыми х = а и х = b (рис. 1), выражается
0, осью ОХ и двумя
прямыми х = а и х = b (рис. 1), выражается
|
|
определённым интегралом: S =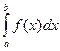
Рис1
Пример 1: определить площадь S фигуры, заключённой между ветвью кривой у = х2, осью ОХ и прямыми х = 0, х = 3 (рис.2).
Решение: S=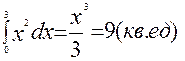
|
|
Пример 2: Найти площадь S фигуры, заключённой между осью ОХ и кривой у=х2-4х (рис.3)
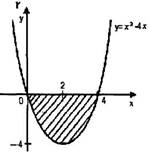
рис. 3
Решение: рассмотрим точки пересечения кривой у = х2 - 4х с осью ОХ
![]()
![]() х2-4х
= 0
х2-4х
= 0 ![]() х(х-4) = 0
х(х-4) = 0 ![]()
![]() или
х2 = 4.
или
х2 = 4.
Найдём производную функции ![]() =
2х - 4 и точки экстремума:
=
2х - 4 и точки экстремума:
![]() = 0
= 0 ![]() 2х-4
= 0:
2х-4
= 0:![]() х = 2:
у" =2>0
х = 2:
у" =2>0 ![]() х = 2 - точка
min y(2) = - 4
х = 2 - точка
min y(2) = - 4
Искомая площадь ограничена сверху OX, снизу y = х2 – 4x, слева х = 0, справа
х = 4. Так как у < 0, то
S= ![]() (x2 -4х)dх =
(x2 -4х)dх =  =
= ![]() =
=
![]() =
= ![]() =
=
![]() (кв. ед.)
(кв. ед.)
Пример 3: Найти площадь фигуры, заключённой между ![]() и осью OX
(рис.4 )
и осью OX
(рис.4 )

рис. 4
Найдем
точки пересечения графика функции ![]() с осью абсцисс
с осью абсцисс ![]()
![]()
![]()
![]() .
.
Точки
экстремума: ![]() ;
; ![]()
![]()
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() меняет
знак при переходе через х=0
меняет
знак при переходе через х=0 ![]() т.
(0;0) - точка перегиба. Значит,
искомая площадь состоит из двух частей:
т.
(0;0) - точка перегиба. Значит,
искомая площадь состоит из двух частей:
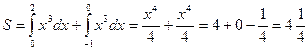 (кв.ед.)
(кв.ед.)
Лекция 5. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения. Однородные дифференциальные уравнения первого порядка. Линейные однородные уравнения второго порядка с постоянными коэффициентами.
5.1 Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения.
Дифференциальным уравнением первого порядка называется равнение вида:
F(x,y,y') = 0. (1)
т.е. содержит независимую переменную х, искомую функцию у(х) и её производную у'(х).
Разрешая уравнение (1), если это возможно, относительно производной у' получим
y'=f(x,y). (2)
Иногда уравнения (1), (2) записывают в дифференциалах:
P(x,y)dx + Q(x,y)dy = O. (3)
Дифференциальное
уравнение имеет, вообще говоря, бесконечное множество решений. Всякое отдельно
взятое решение дифференциального уравнения называется его частным
решением.
Для многих дифференциальных уравнений
первого порядка общее решение можно задать
формулой вида:
у - у(х, С), (4)
где С - произвольная постоянная такая, что при любом С функция (4) является частным решением дифференциального уравнения. С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой семейство кривых, называемых интегральными кривыми, а каждое частное решение представляет собой отдельную интегральную кривую. Иногда не удаётся получить решения дифференциального уравнения в явной форме, т.е в виде у = у(х, С), а получают их в неявной форме, т.е. решение задаётся формулой вида:
Ф (у, х,С)=0 (5)
Выражение типа Ф (х, у, С) = 0 в этом случае называют интегралом (частным, общим) дифференциального уравнения.
Задача Коши.
В случае дифференциального уравнения первого порядка
задача Коши формулируется следующим образом: найти решение у =
у(х) уравнения у' =f(x, у), удовлетворяющее начальному условию у![]() = у, где
= у, где ![]() -
заданные числа. Задача Коши кратко записывается так:
-
заданные числа. Задача Коши кратко записывается так:
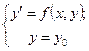 при
х=х0. (6)
при
х=х0. (6)
Геометрически решение, удовлетворяющее начальному условию у (х 0)=у 0, представляет интегральную кривую, проходящую через данную точку (хо;уо).
Дифференциальные
уравнения 1-го порядка с разделяющимися переменными.
Дифференциальное уравнение (2) называется уравнением с
разделяющимися переменными, если имеет
следующий вид:
![]() (7)
(7)
В
предположении, что f2 (y) ![]() 0,
уравнение с разделяющимися переменными (7) можно переписать в виде (разделить
переменные):
0,
уравнение с разделяющимися переменными (7) можно переписать в виде (разделить
переменные):
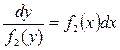 (8)
(8)
Уравнение вида (8) называется уравнением с разделёнными переменными.
Теорема
1. Если существуют интегралы ![]() и
и ![]() , то общий интеграл уравнения с
разделёнными переменными (8) задаётся уравнением
, то общий интеграл уравнения с
разделёнными переменными (8) задаётся уравнением
F2 (у) = F1(x) + C, (9)
где F2 (у) и Fx (х) - некоторые первообразные соответственно функций.
При решении дифференциальных уравнений с разделяющимися переменными можно руководствоваться следующим алгоритмом:
1) разделить переменные (с учётом условий, когда это можно делать);
2) проинтегрировать почленно полученное уравнение с разделёнными переменными;
3) найти его общий интеграл;
4) выяснить, имеет ли уравнение (5) решения, не получающиеся из общего интеграла;
5) найти частный интеграл (или решение), удовлетворяющий начальным условиям (в случае задачи Коши).
Пример1. Найти
частное решение уравнения: ![]() 2уу' = 1 - Зх2;
у0 = 3 при х0 = 0
2уу' = 1 - Зх2;
у0 = 3 при х0 = 0
Решение: это уравнение с разделяющимися переменными. Представим его в дифференциалах.
Учитывая, что ![]() получим 2у— = 1-3х
получим 2у— = 1-3х![]() .
.
Разделим переменные:
2ydy = (1 - Зх2 )dx. Интегрируя обе части последнего равенства, найдём
![]() 2ydy =
2ydy = ![]() (1 -
Зх2 )dx, т.е.
у2=х-х3+С. Подставив начальные значения х0 =1,
уо=3,
(1 -
Зх2 )dx, т.е.
у2=х-х3+С. Подставив начальные значения х0 =1,
уо=3,
найдём С: 9=1-1+С, т.е. С=9. Следовательно, искомый частный интеграл будет у2=х-х3+9, или х3+у2-х-9 = 0
5.2 Однородные дифференциальные уравнения первого порядка.
Уравнение вида ![]() (1) называется однородным уравнением.
(1) называется однородным уравнением.
Однородное
уравнение приводится к уравнению с разделяющимися переменными подстановкой y=ux, где u – новая искомая
функция. Дифференцируя равенство y=ux, получим ![]() (2) .
(2) .
Подставив
выражения у и ![]() в уравнение (1), имеем
в уравнение (1), имеем
![]()
откуда
![]() (3)
(3)
Это уравнение с разделяющимися переменными. Найдя общее решение уравнения (3), получаем общее решение данного уравнения (1), заменив u на у/х.
Пример: Найти I) общее решение
уравнения ![]()
II) частное решение данного уравнения, удовлетворяющий заданным начальным условиям: у(2)=0
Решение:
I) Разрешим уравнение
относительно производной ![]() :
: 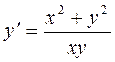 .
.
Поделив числитель и знаменатель правой части уравнения на х2, получим
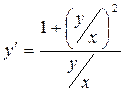 (*)
(*)
Замены:
u=y/x и ![]() в уравнение (*).
в уравнение (*).
Уравнение (*) преобразуется в уравнение с разделяющимися переменными:
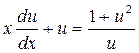 Û
Û  Û
Û ![]() откуда
откуда

Интегрируя
это уравнение, получим ![]() Û
Û 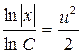 т.е. х=С
т.е. х=С![]()
Заменяя
в последнем равенстве u на y/x, окончательно
получаем общее решение данного уравнения х=С![]()
II) Используя начальные
условия у(2)=0, подставляем в общее решение данного уравнения х=С![]() , заданные значения переменных х=2,
у=0 – тем самым определяем значение произвольной постоянной С: 2=С
, заданные значения переменных х=2,
у=0 – тем самым определяем значение произвольной постоянной С: 2=С![]() Û С= 2.
Û С= 2.
Итак, искомое частное решение х=2![]()
5.3 Линейные дифференциальные уравнения
Уравнение вида ![]() (1)
называется линейным уравнением.
(1)
называется линейным уравнением.
Линейное уравнение сводится к двум уравнениям с разделяющимися переменными заменой искомой функции у произведением двух вспомогательных функций u и v, т.е y = uv .
Тогда ![]() ,
и уравнение (1) принимает вид
,
и уравнение (1) принимает вид ![]() . (2)
. (2)
Пользуясь тем, что одно из вспомогательных
переменных, например v, выбрано произвольно, подберем его так,
чтобы выражение в квадратных скобках обратилось в нуль, т.е. в качестве v возьмем одно из
частных решений v=v(x) уравнения с разделяющимися
переменными ![]() .
.
Подставив
выражение v=v(x) в уравнение (2),
получим уравнение относительно функции u: ![]() .
.
Это также уравнение с разделяющимися переменными. Найдя общее решение этого уравнения u=u(x,C), получим общее решение уравнения (1):
y = u(x,C)v(x).
Пример:
Найти
общее решение уравнения ![]() .
.
Решение: Делаем замены ![]() и
и ![]() .
.
Получаем
![]() (*)
(*)
Решаем
уравнение ![]() Û
Û ![]() Û
Û ![]() Û v = x-1 Û v =
Û v = x-1 Û v = ![]()
Подставляем v в уравнение (*), получаем уравнение:
![]() Û
Û ![]() Û
Û ![]()
Итак, искомое общее решение 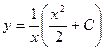
5.4 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Дифференциальные уравнения второго порядка в общем случае записывается в виде:
F(x,y,y',y") = 0. (1)
или, если это возможно, в разрешённом относительно у" виде
y"
= f(x,y,y![]() ). (2)
). (2)
Определение
1. Говорят, что формула у = f(х,С1,С2) представляет общее решение дифференциального уравнения второго порядка
(1) или (2), если для любых значений С![]() и
С'2 постоянных С
и
С'2 постоянных С![]() , и С
, и С![]() функция f(х,С,',С'2) является решением данного
уравнения, и любое его частное решение
может быть получено из формулы у=f(х,Сх,С2)
при некоторых значениях С
функция f(х,С,',С'2) является решением данного
уравнения, и любое его частное решение
может быть получено из формулы у=f(х,Сх,С2)
при некоторых значениях С![]() и
С'2.
и
С'2.
Для дифференциальных уравнений второго порядка задача Коши формулируется следующим образом: найти решение у= у(х) уравнения у" = f(x,y,y'), удовлетворяющее начальным условиям у(х0) = у0, у'(х0) = у'о или, в другой записи,
 (3)
(3)
где х0,у0,у'о - заданные числа. Геометрически общее решение уравнения (1) или (2) представляет собой семейство интегральных кривых, а решение, удовлетворяющее начальным условиям у(х0) = у0, у'(х0) = у'о, представляет интегральную кривую, проходящую через данную точку (дг0; >>0) в данном направлении - угловой коэффициент касательной к интегральной кривой (графику решения у = у(х)), проведённой в точке (х0; у0) равен данному числу у'о. Простейшее уравнение второго порядка имеет вид
y![]() = f(x) (4)
= f(x) (4)
Уравнения этого вида решаются двукратным интегрированием:
полагаем у' = р(х), тогда у" = р' и уравнение (4) принимает вид p' = f(x), или dp=f(x) dx.
Отсюда р = ![]() f(x)dx = F(x) + С,,
где F(x) - одна
из первообразных для функции f(x).
f(x)dx = F(x) + С,,
где F(x) - одна
из первообразных для функции f(x).
Так как р =у', то у' = F(x) + C или dy = (F(x) + Сх )dx. Отсюда, интегрируя ещё раз, находим, как нетрудно проверить, общее решение уравнения (4) (в области, где существуют рассматриваемые интегралы):
у = ![]() F{x)dx + С,х +
С2
F{x)dx + С,х +
С2
Пример 1. Найти общее решение уравнения у" = cos2x.
Решение: положим у' = р(х); тогда у" = р', и, следовательно, р' = cos 2x или dp = cos 2xdx.
Интегрируя это уравнение, находим: р = — sin 2x + С,, или у' = -sin2х + С,
т..е. dy = -sin2xdx + Cdx.
Интегрируя второй раз, находим
общее решение: ![]() dy =
dy = ![]() — sin 2xdx + С,
— sin 2xdx + С, ![]() dx, т.е. y = —cos 2x + С, x + С2.
dx, т.е. y = —cos 2x + С, x + С2.
Уравнение вида ![]() (5)
(5)
где ![]() -
действительные числа
-
действительные числа ![]() , называется линейным
однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Чтобы решить уравнение (1), нужно решить характеристическое уравнение:
, называется линейным
однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Чтобы решить уравнение (1), нужно решить характеристическое уравнение:
![]() (6)
(6)
При решении характеристического уравнения (6) возможны три случая, в зависимости от которых строится общее решение данного дифференциального уравнения (5)
|
Корни уравнения (2) |
Частные решения уравнения (1) |
Общее решение уравнения (1) |
|
Действительные и различные:
|
|
|
|
Равные:
|
|
|
|
Комплексно
сопряженные |
|
|
Пример 2. Найти общее решение уравнений:
а)
![]()
б)
![]()
в)
![]()
Решение:
а)
Составим характеристическое уравнение: ![]()
Его
корни ![]() и
и ![]() Значит,
общее решение уравнения имеет вид
Значит,
общее решение уравнения имеет вид ![]()
б)
Составим характеристическое уравнение: ![]()
Его
корни ![]() Тогда общее решение имеет вид
Тогда общее решение имеет вид ![]()
в)
Составим характеристическое уравнение: ![]()
Решая
его, получим D = -4 и комплексно
сопряженные корни ![]() и
и ![]() Тогда его общим решением будет
Тогда его общим решением будет ![]()
Лекция 6. Методы интегрирования. Метод прямоугольников. Метод трапеций. Метод Симпсона. Абсолютная погрешность при численном интегрировании
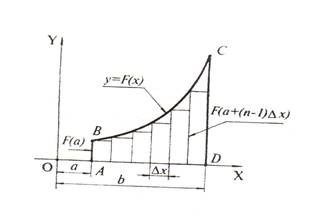
1. Метод прямоугольников.
Предположим,
что перед нами ![]() Перепробовав все
известные способы, нам не удалось его вычислить.
Перепробовав все
известные способы, нам не удалось его вычислить.
Теперь попробуем построить в системе XOY фигуру, которой данный интеграл соответствует, хотя бы ориентировочно.
Вычислить
![]() - это значит найти площадь фигуры ABCD.
- это значит найти площадь фигуры ABCD.
Разобьем ее как показано на чертеже. Очевидно, что площадь АВСД=Q1+Q2, где Q1- площадь всех прямоугольников, а Q2- площадь всех криволинейных треугольников.
Если
число делений высоты фигуры AD велико, то Q2 значительно
меньше Q1(Q2<<Q1), и тогда можно
принять, что S ABCD=Q1, но ![]() , где Si - площадь одного
прямоугольника.
, где Si - площадь одного
прямоугольника.
По чертежу находим:
![]() и т.д.
и т.д.
Таким образом получаем:
![]()
Итак,
данный интеграл ![]() свелся к нахождению
площади Q1
свелся к нахождению
площади Q1
ВЫВОД:
![]()
![]()
Очевидно, что чем больше число делений n, следовательно число слагаемых в скобке, тем точнее результат получим при вычислении того или иного определенного интеграла.
2. Способ трапеций
Пусть
мы имеем интеграл ![]() который так же
известными способами вычислять не удалось.
который так же
известными способами вычислять не удалось.
Построим в системе координат XOY фигуру, которой данный интеграл соответствует, хотя бы ориентировочно.
Вычислить
![]() - это значит найти площадь фигуры
ABCD. Разобьем ее как
показано на чертеже. Очевидно, что SАВСД =Q1+Q2, где Q1- площадь всех
трапеций, а Q2- площадь всех
криволинейных треугольников.
- это значит найти площадь фигуры
ABCD. Разобьем ее как
показано на чертеже. Очевидно, что SАВСД =Q1+Q2, где Q1- площадь всех
трапеций, а Q2- площадь всех
криволинейных треугольников.
Если
делений основания AD фигуры велико, то тогда можно принять, что SАВСД ≈ Q1, но ![]() , где Si- площадь i-той трапеции.
, где Si- площадь i-той трапеции.
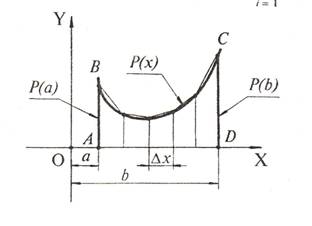
Из чертежа находим:
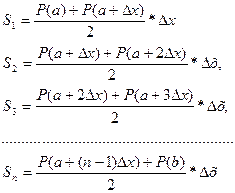 Здесь
Здесь ![]()
Таким образом, получаем:

Окончательно имеем
![]() =
=![]()
Существует еще более точный способ вычисления определенных интегралов- способ парабол ( метод Симпсона- по имени немецкого математика, предложившего его), но в данной практической он не рассматривается.
Пример
1 Вычислить
![]() по методу прямоугольника и
трапеции, сравнить результаты. Число делений n принять равным 5.
по методу прямоугольника и
трапеции, сравнить результаты. Число делений n принять равным 5.
Решение
1) по методу прямоугольников имеем
![]() =
=![]()
здесь
![]() , тогда
, тогда
![]()
![]()
![]()
![]()
![]()
![]()
Получаем
![]() по методу прямоугольников примерно
равен 0,83
по методу прямоугольников примерно
равен 0,83
2) По методу трапеций
Получаем
![]() =
=![]()
Здесь
![]()
y1 = f(0) = 1
![]()
![]()
![]()
![]()
![]()
Окончательно
![]() по способу трапеций примерно равен
0,791.
по способу трапеций примерно равен
0,791.
Очевидно что метод трапеций более точный способ, так как значение данного интеграла до 3-го знака после запятой будет
![]()
Пример 2. Вычислить приближённое значение определённого интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления производить с округлением третьего десятичного знака.
Решение. Формула Симпсона или формула парабол имеет вид:
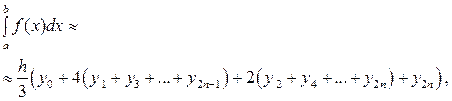 (1)
(1)
где 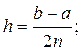
![]()
![]()
![]() .
.
Рассмотрим 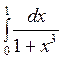 при
при
![]() тогда
тогда ![]() .
.
Составим таблицу значений подынтегральной функции, необходимых для вычисления данного интеграла.
|
|
|
|
|
уk (k - нечетное) |
уk (k - четное) |
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
∑ |
|
|
|
|
|
В последней строке таблицы находятся суммы чисел соответствующих столбцов.
Так как
![]()
![]()
![]()
по формуле (1) находим
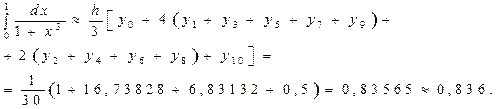
3. Точностные оценки
Оценка погрешности усечения рассматриваемых формул численного интегрирования по выражениям для остаточных членов часто оказывается малоэффективной из-за трудностей оценки производных высокого порядка подынтегральных функций. На практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов. Задают значения допустимой погрешности и начальное число n0 шагов. Вычисляют величину интеграла по выбранной квадратурной формуле при числе интервалов n0 и 2n0 (соответственно In и I2n). По правилу Рунге оценивается погрешность приближенного значения интеграла
![]() - для формулы
трапеций;
- для формулы
трапеций;
![]() - для формулы
Симпсона.
- для формулы
Симпсона.
Если D³e, то количество интервалов разбиения увеличивают вдвое, т.е. значения интеграла вычисляются для последовательных значений n=n0,2n0,4n0,...Вычисления заканчиваются при выполнении условия D<e.
Оценка погрешности усечения при интегрировании функций, заданных таблично:
![]() - для формулы
трапеций
- для формулы
трапеций
![]() - для формулы
Симпсона.
- для формулы
Симпсона.
D2y, D4y, - средние арифметические значения конечных разностей соответствующего порядка. Данные оценки применяются для функций, которые достаточно хорошо интерполируются многочленом соответствующей степени.
Ошибки
округления носят случайный характер, но с увеличением числа интервалов
разбиения возрастают в среднем пропорционально ![]() .
Вследствие этого при увеличении n общая погрешность уменьшается за счет
уменьшения ошибки усечения лишь до некоторого значения n. Затем
погрешности округления преобладают, и общая погрешность увеличивается.
.
Вследствие этого при увеличении n общая погрешность уменьшается за счет
уменьшения ошибки усечения лишь до некоторого значения n. Затем
погрешности округления преобладают, и общая погрешность увеличивается.
Лекция 7. Понятие о численном решении дифференциальных уравнений. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. Погрешности в определении производной. Построение интегральной кривой. Метод Эйлера
1. Постановка задачи
При решении практических задач часто нужно
найти производные указанных порядков от функции ![]() ,
заданной таблично, либо, в силу сложности аналитического выражения функции f(x) непосредственное
ее дифференцирование затруднено. В этих случаях обычно прибегают к приближенному
дифференцированию.
,
заданной таблично, либо, в силу сложности аналитического выражения функции f(x) непосредственное
ее дифференцирование затруднено. В этих случаях обычно прибегают к приближенному
дифференцированию.
Для вывода формул приближенного
дифференцирования исходную функцию f(x) заменяют на
интересующем отрезке [a, b] интерполирующей
функцией P(x), а затем
полагают, что ![]() , при
, при ![]() .
.
Аналогично поступают при нахождении производных высших порядков.
Если для интерполирующей функции P(x) известна
погрешность ![]() , то погрешность производной
, то погрешность производной ![]() выражается формулой
выражается формулой ![]() , т.е.:
, т.е.:
● Погрешность производной интерполирующей функции равна производной от погрешности этой функции.
![]() То же самое справедливо и для производных
высших порядков.
То же самое справедливо и для производных
высших порядков.
Следует отметить, что приближенное
дифференцирование представляют собой операцию менее точную, чем
интерполирование: близость друг к другу двух кривых ![]() и
и
![]() на отрезке [a, b] еще не
гарантирует близости на этом отрезке их производных
на отрезке [a, b] еще не
гарантирует близости на этом отрезке их производных ![]() и
и
![]() , т.е. малого расхождения угловых
коэффициентов касательных к рассматриваемым кривым при одинаковых значениях
аргумента.
, т.е. малого расхождения угловых
коэффициентов касательных к рассматриваемым кривым при одинаковых значениях
аргумента.
Как видно из рисунка, касательные,
проведенные к графикам функций ![]() и
и ![]() в точке xi, имеют разный
угол наклона (тангенс угла наклона касательной равен производной функции в
данной точке).
в точке xi, имеют разный
угол наклона (тангенс угла наклона касательной равен производной функции в
данной точке).
2. Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона
Пусть функция y(x), задана таблично в равноотстоящих узлах xi на отрезке [a,b]:
|
x |
x0 |
x1 |
x2 |
… |
xn |
|
f(x) |
y0 |
y1 |
y2 |
… |
yn |
Для нахождения на [a,b] производных ![]() ,
, ![]() и
т.д., функцию y приближенно заменим интерполяционным полиномом
Ньютона, построенным для системы узлов
и
т.д., функцию y приближенно заменим интерполяционным полиномом
Ньютона, построенным для системы узлов ![]() :
:
![]()
где
![]() и
и ![]() .
.
Производя перемножение биномов, получим:
![]()
Будем дифференцировать данный многочлен
как сложную функцию: ![]() . Получим:
. Получим:
|
|
|
(1) |
Так как ![]() ,
формула вычисления второй производной будет выглядеть следующим образом:
,
формула вычисления второй производной будет выглядеть следующим образом:
|
|
|
(2) |
Таким же способом можно вычислить производные любого порядка.
Чтобы уменьшить погрешность вычисления, при нахождении производных в фиксированной точке х в качестве х0 следует выбирать ближайшее табличное значение аргумента (уменьшить таблицу).
Иногда требуется находить производные функции в основных табличных точках xi. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x=x0, следовательно, t=0.
Получим:
|
|
|
(3) |
|
|
|
(4) |
Погрешность приближенного вычисления первой производной в нулевой точке будет равна
![]()
Пример 1. Приняв шаг h = 0,05, построить на отрезке [3,5; 3,6] интерполяционный полином Ньютона для функции у = ех, заданной таблицей
|
х |
3,50 |
3,55 |
3,60 |
3,65 |
3,70 |
|
у |
33,115 |
34,813 |
36,598 |
38,475 |
40,447 |
Составляем таблицу разностей (Таблица 3).
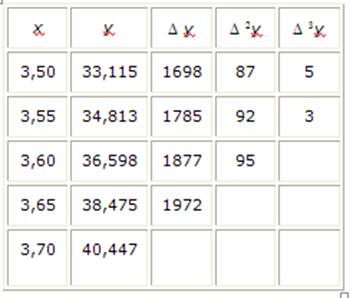
Заметим, что в столбцах разностей, следуя обычной практике, мы не указываем десятичные разряды (которые ясны из столбца значений функции). Так как разности третьего порядка практически постоянны, то в формуле (15) полагаем n = 3. Приняв x0 = 3,50, y0= 33,115, будем иметь:
P3 (x) = 33,115 + 1,698 t +
0,087![]() + 0,005
+ 0,005![]()
или
P3 (x) = 33,115 + 1,698 t +
0,0435![]() + 0,00083
+ 0,00083![]() ,
,
где
![]() .
.
На практике часто необходимо для функции, заданной таблично, подобрать аналитическую формулу, представляющую с некоторой точностью данные табличные значения функции. Такая формула называется эмпирической, причем задача построения ее неоднозначна.
При построении эмпирической формулы следует учитывать общие свойства функции. Если из таблицы разностей будет обнаружено, чтоn-е разности функции для равностоящих значений аргумента постоянны, то в качестве эмпирической формулы можно взять соответствующую первую интерполяционную формулу.
Пример 2. Построить эмпирическую формулу для функции у, заданной таблично
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
|
у |
5,2 |
8,0 |
10,4 |
12,4 |
14,0 |
15,2 |
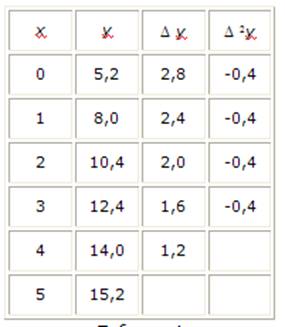
Таблица 4
Составляя таблицу разностей (Таблица 4), убеждаемся, что вторая разность постоянна.
Используя интерполяционную формулу Ньютона в форме (14) и учитывая, что h = 1, будем иметь:
у = 5,2 + 2,8 х - ![]()
или
у = 5,2 + 3 х - 0,2 х2.
Вторая интерполяционная формула Ньютона
Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае:
t= ![]() ,
,
o. е. t 0 и интерполяционную формулу Ньютона можно получить в виде:
|
|
(16) |
Формулу (16) называют второй интерполяционной формулой Ньютона для интерполирования назад.
Пример 3. Дана таблица значений y = lg x семизначных логарифмов
|
х |
у |
|
1000 |
3,0000000 |
|
1010 |
3,0043214 |
|
1020 |
3,0086002 |
|
1030 |
3,0128372 |
|
1040 |
3,0170333 |
|
1050 |
3,0211893 |
Найти lg 1044.
Составляем таблицу разностей (Таблица 1).
Таблица 1.
Таблица разностей функции у = lg x
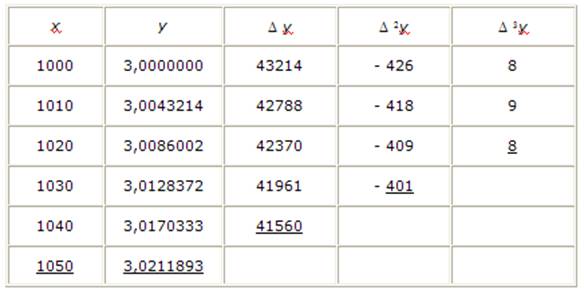
Примем xn = 1050,
тогда
![]()
Используя подчеркнутые разности, в силу формулы (16) будем иметь:
lg 1044 = 3,0211893 + (-0,6) 0,0041560 + ![]() 0,0000401
+
0,0000401
+ ![]() 0,0000008
= 3,0187005.
0,0000008
= 3,0187005.
Как первая, так и вторая интерполяционные формулы Ньютона могут быть использованы для экстраполирования функции, т. е. для нахождения значений функции y для значений аргументов х, лежащих вне пределов таблицы. Если х < х0 и х близко к х0, то выгодно применять первую интерполяционную формулу Ньютона, причем тогда
![]() <
0.
<
0.
Если х < хn и х близко к хn, то удобнее пользоваться второй интерполяционной формулой Ньютона, причем
![]() > 0.
> 0.
Таким образом, первая интерполяционная формула Ньютона обычно используется для интерполирования вперед и экстраполирования назад, а вторая интерполяционная формула Ньютона, наоборот - для интерполирования назад и экстраполирования вперед.
Операция экстраполирования менее точна, чем операция интерполяции в узком смысле слова.
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
![]() , где x – независимая переменная,
, где x – независимая переменная, ![]() -
i-ая производная от искомой функции. n - порядок уравнения. Общее решение ОДУ
n–го порядка содержит n произвольных постоянных
-
i-ая производная от искомой функции. n - порядок уравнения. Общее решение ОДУ
n–го порядка содержит n произвольных постоянных![]() , т.е. общее решение имеет вид
, т.е. общее решение имеет вид ![]() .
.
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:

Примеры краевых задач:
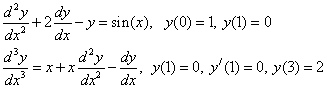
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.
Постановка задачи. Найти решение ОДУ первого порядка
![]() на отрезке
на отрезке ![]() при
условии
при
условии ![]()
При
нахождении приближенного решения будем считать, что вычисления проводятся с
расчетным шагом ![]() , расчетными
узлами служат точки
, расчетными
узлами служат точки ![]() промежутка [x0, xn].
промежутка [x0, xn].
Целью является построение таблицы
|
xi |
x0 |
x1 |
… |
xn |
|
yi |
y0 |
y1 |
… |
yn |
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя
уравнение на отрезке ![]() , получим
, получим
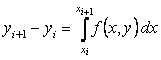
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
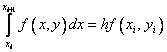 ,
,
то получим явную формулу Эйлера:
![]() ,
, ![]() .
.
Порядок расчетов:
Зная ![]() , находим
, находим ![]() , затем
, затем ![]() т.д.
т.д.
Геометрическая интерпретация метода Эйлера:
Пользуясь
тем, что в точке x0 известно решение y(x0) = y0 и значение его производной ![]() , можно записать уравнение
касательной к графику искомой функции
, можно записать уравнение
касательной к графику искомой функции ![]() в точке
в точке ![]() :
:![]() . При достаточно малом шаге h ордината
. При достаточно малом шаге h ордината ![]() этой
касательной, полученная подстановкой в правую часть значения
этой
касательной, полученная подстановкой в правую часть значения ![]() , должна мало отличаться от ординаты y(x1) решения y(x) задачи Коши.
Следовательно, точка
, должна мало отличаться от ординаты y(x1) решения y(x) задачи Коши.
Следовательно, точка ![]() пересечения касательной с прямой x = x1 может быть приближенно принята за
новую начальную точку. Через эту точку снова проведем прямую
пересечения касательной с прямой x = x1 может быть приближенно принята за
новую начальную точку. Через эту точку снова проведем прямую ![]() , которая приближенно отражает
поведение касательной к
, которая приближенно отражает
поведение касательной к ![]() в точке
в точке ![]() . Подставляя сюда
. Подставляя сюда ![]() (т.е.
пересечение с прямой x = x2),
получим приближенное значение y(x)
в точке x2:
(т.е.
пересечение с прямой x = x2),
получим приближенное значение y(x)
в точке x2: ![]() и
т.д. В итоге для i–й точки
получим формулу Эйлера.
и
т.д. В итоге для i–й точки
получим формулу Эйлера.
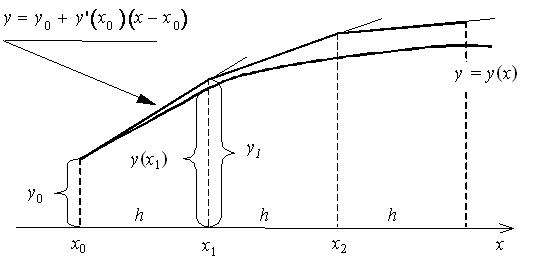
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если
использовать формулу правых прямоугольников: 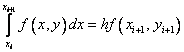 , то придем к
методу
, то придем к
методу
![]() ,
, ![]() .
.
Этот метод
называют неявным методом
Эйлера, поскольку для вычисления неизвестного значения ![]() по
известному значению
по
известному значению ![]() требуется решать уравнение, в общем случае
нелинейное.
требуется решать уравнение, в общем случае
нелинейное.
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у'=f(x,y).
1. Метод Эйлера.
Рассмотрим два варианта вывода расчетных формул
· вариант 1 (аналитический) у=f (x,y)
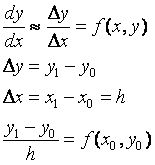
|
y1=y0+h*f(x0,y0) x1=x0+h |
Расчетные формулы для 1-го шага |
|
yi+1=yi+h*f(xi,yi) xi+1=xi*h |
Расчетные формулы для i-го шага |
· вариант 2 (графический)
|
|
y1=y0+f(x0,y0)*h; x1=x0+h yi+1=yi+h*f(xi,yi) |
|
k1=h*f(xi,yi) yi+1=yi+ki xi+1=xi+h |
Аналогично варианту 1 |
Пример. Решить задачу Коши:
![]() .
.
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
Точное
решение: ![]()
Расчетные формулы по явному методу Эйлера для данного примера:
![]()
Расчетные формулы модифицированного метода Эйлера:
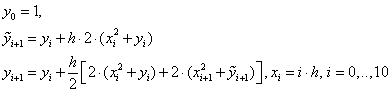
Расчетные формулы метода Рунге – Кутта:
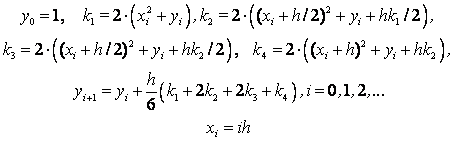
|
x |
y1 |
y2 |
y3 |
точное |
|
0 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
0.1 |
1.2000 |
1.2210 |
1.2221 |
1.2221 |
|
0.2 |
1.4420 |
1.4923 |
1.4977 |
1.4977 |
|
0.3 |
1.7384 |
1.8284 |
1.8432 |
1.8432 |
|
0.4 |
2.1041 |
2.2466 |
2.2783 |
2.2783 |
|
0.5 |
2.5569 |
2.7680 |
2.8274 |
2.8274 |
|
0.6 |
3.1183 |
3.4176 |
3.5201 |
3.5202 |
|
0.7 |
3.8139 |
4.2257 |
4.3927 |
4.3928 |
|
0.8 |
4.6747 |
5.2288 |
5.4894 |
5.4895 |
|
0.9 |
5.7377 |
6.4704 |
6.8643 |
6.8645 |
|
1 |
7.0472 |
8.0032 |
8.5834 |
8.5836 |
y1 – метод Эйлера, y2 – модифицированный метод Эйлера, y3 – метод Рунге Кутта.
Видно, что самым точным является метод Рунге – Кутта.
Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений первого порядка.
Покажем это для случая системы двух уравнений первого порядка:

Явный метод Эйлера:
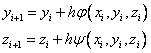
Модифицированный метод Эйлера:

Схема Рунге – Кутта четвертого порядка точности:

К решению систем уравнений ОДУ сводятся также задачи Коши для уравнений высших порядков. Например, рассмотрим задачу Коши для уравнения второго порядка
![]()
Введем
вторую неизвестную функцию ![]() . Тогда задача
Коши заменяется следующей:
. Тогда задача
Коши заменяется следующей:

Т.е. в
терминах предыдущей задачи: ![]() .
.
Пример. Найти решение задачи Коши:
![]() на отрезке [0,1].
на отрезке [0,1].
Точное
решение: ![]()
Действительно:

Решим задачу явным методом Эйлера, модифицированным методом Эйлера и Рунге – Кутта с шагом h=0.2.
Введем
функцию ![]() .
.
Тогда получим следующую задачу Коши для системы двух ОДУ первого порядка:
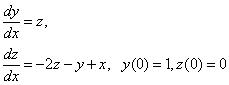
Явный метод Эйлера:
![]()
Модифицированный метод Эйлера:

Метод Рунге – Кутта:

Схема Эйлера:
|
X |
y |
z |
y теор |
z теор |
y-y теор |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0.2 |
1 |
-0.2 |
0.983685 |
-0.14622 |
0.016315 |
|
0.4 |
0.96 |
-0.28 |
0.947216 |
-0.20658 |
0.012784 |
|
0.6 |
0.904 |
-0.28 |
0.905009 |
-0.20739 |
0.001009 |
|
0.8 |
0.848 |
-0.2288 |
0.866913 |
-0.16826 |
0.018913 |
|
1 |
0.80224 |
-0.14688 |
0.839397 |
-0.10364 |
0.037157 |
Модифицированный метод Эйлера:
|
X |
ycv |
zcv |
y |
z |
y теор |
z теор |
y-y теор |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0.2 |
1 |
-0.2 |
1 |
-0.18 |
0.983685 |
-0.14622 |
0.016315 |
|
0.4 |
0.96 |
-0.28 |
0.962 |
-0.244 |
0.947216 |
-0.20658 |
0.014784 |
|
0.6 |
0.904 |
-0.28 |
0.9096 |
-0.2314 |
0.905009 |
-0.20739 |
0.004591 |
|
0.8 |
0.848 |
-0.2288 |
0.85846 |
-0.17048 |
0.866913 |
-0.16826 |
0.008453 |
|
1 |
0.80224 |
-0.14688 |
0.818532 |
-0.08127 |
0.839397 |
-0.10364 |
0.020865 |
Схема Рунге - Кутта:
|
x |
Y |
z |
k1 |
l1 |
k2 |
l2 |
k3 |
l3 |
k4 |
l4 |
|
0 |
1 |
0 |
0 |
-1 |
-0.1 |
-0.7 |
-0.07 |
-0.75 |
-0.15 |
-0.486 |
|
0.2 |
0.983667 |
-0.1462 |
-0.1462 |
-0.49127 |
-0.19533 |
-0.27839 |
-0.17404 |
-0.31606 |
-0.20941 |
-0.13004 |
|
0.4 |
0.947189 |
-0.20654 |
-0.20654 |
-0.13411 |
-0.21995 |
0.013367 |
-0.2052 |
-0.01479 |
-0.2095 |
0.112847 |
|
0.6 |
0.904977 |
-0.20734 |
-0.20734 |
0.10971 |
-0.19637 |
0.208502 |
-0.18649 |
0.187647 |
-0.16981 |
0.27195 |
|
0.8 |
0.866881 |
-0.16821 |
-0.16821 |
0.269542 |
-0.14126 |
0.332455 |
-0.13497 |
0.317177 |
-0.10478 |
0.369665 |
|
1 |
0.839366 |
-0.1036 |
-0.1036 |
0.367825 |
-0.06681 |
0.40462 |
-0.06313 |
0.393583 |
-0.02488 |
0.423019 |
Max(y-y теор)=4*10-5
Постановка задачи: найти решение линейного дифференциального уравнения
![]() , (1)
, (1)
удовлетворяющего
краевым условиям:![]() . (2)
. (2)
Теорема. Пусть ![]() . Тогда
существует единственное решение поставленной задачи.
. Тогда
существует единственное решение поставленной задачи.
К данной задаче сводится, например, задача об определении прогибов балки, которая на концах опирается шарнирно.
Основные этапы метода конечных разностей:
1) область
непрерывного изменения аргумента ([a,b]) заменяется дискретным множеством
точек, называемых узлами: ![]() .
.
2) Искомая
функция непрерывного аргумента x, приближенно заменяется функцией дискретного
аргумента на заданной сетке, т.е. ![]() . Функция
. Функция ![]() называется
сеточной.
называется
сеточной.
3) Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена называется разностной аппроксимацией.
Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки, которые находятся из решения алгебраических уравнений.
Аппроксимация производных.
Для аппроксимации (замены) первой производной можно воспользоваться формулами:
![]() - правая разностная производная,
- правая разностная производная,
![]() - левая разностная производная,
- левая разностная производная,
![]() - центральная разностная производная.
- центральная разностная производная.
т.е., возможно множество способов аппроксимации производной.
Все эти
определения следуют из понятия производной как предела: ![]() .
.
Опираясь на разностную аппроксимацию первой производной можно построить разностную аппроксимацию второй производной:
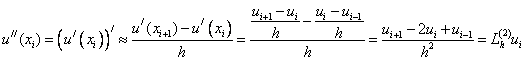 (3)
(3)
Аналогично можно получить аппроксимации производных более высокого порядка.
Определение. Погрешностью аппроксимации n- ой
производной называется разность: ![]() .
.
Для определения порядка аппроксимации используется разложение в ряд Тейлора.
Рассмотрим правую разностную аппроксимацию первой производной:
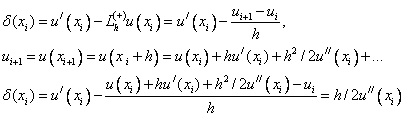
Т.е. правая разностная производная имеет первый по h порядок аппроксимации.
Аналогично и для левой разностной производной.
Центральная разностная производная имеет второй порядок аппроксимации.
Аппроксимация второй производной по формуле (3) также имеет второй порядок аппроксимации.
Для того чтобы аппроксимировать дифференциальное уравнение необходимо в нем заменить все производные их аппроксимациями. Рассмотрим задачу (1), (2) и заменим в(1) производные:
![]() .
.
В результате получим:
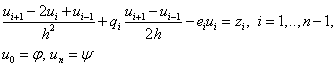 (4)
(4)
Порядок аппроксимации исходной задачи равен 2, т.к. вторая и первая производные заменены с порядком 2, а остальные – точно.
Итак, вместо
дифференциальных уравнений (1), (2) получена система линейных уравнений для
определения ![]() в узлах сетки.
в узлах сетки.
Схему можно представить в виде:

т.е., получили систему линейных уравнений с матрицей:

Данная матрица является трехдиагональной, т.е. все элементы, которые расположены не на главной диагонали и двух прилегающих к ней диагоналях равны нулю.
Решая полученную систему уравнений, мы получим решение исходной задачи.
Для решения таких СЛАУ имеется экономичный метод прогонки.
Рассмотрим метод прогонки для СЛАУ:
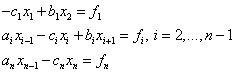 (1)
(1)
Решение данной системы ищем в виде:
![]() (2)
(2)
Подставляя в первое уравнение, получим:
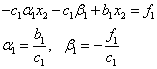
Здесь
учтено, что данное соотношение должно выполняться при любом ![]()
Так как
![]() , (3)
, (3)
то подставляя (3) во второе уравнение, получим:
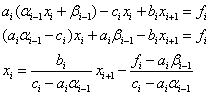
Сравнивая с (2) получим
![]() .
.
Таким
образом, можно найти все ![]() .
.
Тогда из последнего уравнения (1) находим:
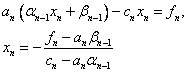
Затем последовательно находим:
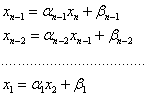
Таким образом, алгоритм метода прогонки можно представить в виде:
1) Находим ![]()
2) Для
i=1,n-1: ![]() (4)
(4)
3) Находим ![]()
4) Для i=n-1
до 1 находим: ![]()
![]()
Шаги 1),2) – прямой ход метода прогонки, 3),4) – обратный ход метода прогонки.
Теорема. Пусть коэффициенты ai, bi системы уравнений при i =2, 3, …, n–1 отличны от нуля и пусть
![]() при i =1, 2, 3, …, n. Тогда прогонка корректна и
устойчива.
при i =1, 2, 3, …, n. Тогда прогонка корректна и
устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге вычислений, не будет возрастать при переходе к следующим шагам. Данное условие есть ни что иное, как условие диагонального преобладания.
Для нашей краевой задачи имеем :

Тогда: ![]() ,
, ![]() ,
,
![]()
Для нашей задачи условие устойчивости имеет вид:
![]() .
.
Пусть
![]() . (6)
. (6)
Тогда 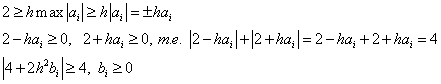
Пример. Найти решение задачи:
![]()
Выпишем разностную схему
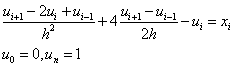
Условие
устойчивости примет вид ![]()
Возьмем ![]() .
.
Тогда ![]()
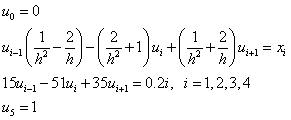
Или
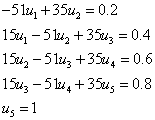
Формулы прогонки были получены для СЛАУ (1):
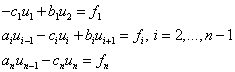
Здесь x замены на u.
Следовательно,
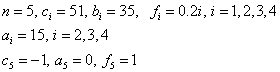
Решим СЛАУ методом прогонки. Вычисления оформим в виде таблицы:
|
I |
ai |
ci |
bi |
fi |
alfai |
betai |
ui |
|
1 |
|
51 |
35 |
0.2 |
0.6863 |
-0.0039 |
0.4701 |
|
2 |
15 |
51 |
35 |
0.4 |
0.8598 |
-0.0113 |
0.6906 |
|
3 |
15 |
51 |
35 |
0.6 |
0.9186 |
-0.0202 |
0.8164 |
|
4 |
15 |
51 |
35 |
0.8 |
0.9403 |
-0.0296 |
0.9107 |
|
5 |
0 |
-1 |
|
1 |
|
|
1.0000 |
Порядок вычислений по формулам (4):
![]()
![]()
![]()
![]()
Ответ в столбце ui.
Если забыли формулы, то их можно легко вывести. Главное запомнить основную формулу:
![]()
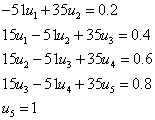
Прямой ход

Обратный ход
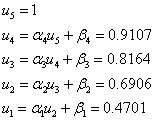
На практике часто граничные условия могут иметь более общий вид.
Рассмотрим следующую краевую задачу:
Найти решение ОДУ 2-го порядка
![]() ,
,
удовлетворяющую краевым условиям:
![]()
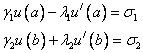
![]()
В этом случае при построении разностной схемы необходимо еще аппроксимировать и краевые условия.
Аппроксимация:
![]()
В результате получим разностную схему:
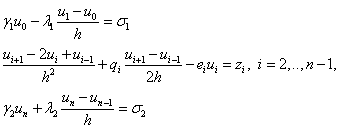
Или
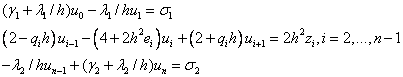
Мы получили СЛАУ типа (5) с трехдиагональной матрицей, решение которой также можно найти методом прогонки.
Лекция 8-9. Числовые ряды. Сходимость и расходимость числовых рядов. Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и условная сходимость рядов. Интегральный признак Коши. Признак Лейбница. Степенные ряды. Ряды Фурье.
Основные понятия.
Числовым рядом называется выражение вида а1+а2+а3+…+аn+…, где а1, а2, а3,…аn , , называемые членами ряда, образуют бесконечную последовательность.
Ряд называется сходящимся, если последовательность его частичных сумм
S1 = a1,
S2 = a1 + a2
S3 = a1 + a2 + an
…………………
S1 = а1+а2+а3+…+аn
при
n ®µ имеет конечный
предел: ![]() . Этот предел называется суммой
сходящегося ряда. Если конечный предел
. Этот предел называется суммой
сходящегося ряда. Если конечный предел ![]() не
существует , то ряд называется расходящимся.
не
существует , то ряд называется расходящимся.
· Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
Ряд может сходиться только при условии,
что его общий член an при неограниченном увеличении номера n стремиться к
нулю: ![]() - это необходимый признак
сходимости ряда.
- это необходимый признак
сходимости ряда.
Если же ![]() ,
то ряд расходиться – это достаточный признак расходимости ряда.
,
то ряд расходиться – это достаточный признак расходимости ряда.
Для знакоположительных числовых рядовимеют местоследующие достаточные признаки, по которым можно установить их сходимость или расходимость.
1. Признак сравнения. Если члены знакоположительного ряда
а1+а2+а3+…+аn+…, (1)
начиная с некоторого номера, не превосходят соответствующих членов ряда
b1+b2+b3+…+bn+…, (2)
то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
При исследовании рядов на сходимость и расходимость по этому признаку часто используются геометрическая прогрессия
a + aq + aq2 + aq3 + … + aqn +… (a > 0),
которая сходиться при ½q½ < 1 и расходиться при ½q½ ≥ 1, и гармонический ряд
![]() ,
,
Являющийся расходящимся рядом.
2. Признак Даламбера. Если для ряда (1) 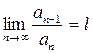 , то при l < 1 ряд
сходиться, при l > 1 – расходиться (при l = 1 вопрос о
сходимости остается нерешенным).
, то при l < 1 ряд
сходиться, при l > 1 – расходиться (при l = 1 вопрос о
сходимости остается нерешенным).
· Признак сходимости Лейбница.
Знакочередующимся рядом называется ряд вида
а1 - а2 + а3 - …+ (-1)n-1an + …, (1)
где а1, а2, а3,…аn - положительные числа.
Для знакочередующихся рядов имеет место следующий признак сходимости.
Признак Лейбница. Ряд (1) сходиться, если его слены монотонно убывают по абсолютной величине и общий член стремиться к нулю при n® µ/
· Абсолютная и условная сходимость знакопеременного ряда.
Ряд а1 +а2+а3+…+аn+… (1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Признак сходимости знакопеременного ряда. Если ряд
½а1 ½+½а2½+½а3½+…+½аn½+…, (2)
составленный из абсолютных величин членов ряда (1), сходится, то ряд (1) также сходиться.
Знакопеременный ряд (1) называется абсолютно сходящимся, если, сходиться ряд (2), составленный из абсолютных величин членов данного ряда (1).
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд , составленный из абсолютных величин его сленов, расходиться..
· Степенные ряды.
Степенным рядом называется ряд вида
а0 + а1х + а2х2 + … + anxn + …, (1)
где а0, а1, а2, а3,…аn ,… - постоянные числа, называемые коэффициентами ряда.
Областью сходимости степенного ряда называется совокупность всех значений х, при которых данный ряд сходится.
Нахождение области сходимости состоит из двух этапов.
1. Определяется интервал сходимости степенного ряда, т.е. интервал (-R,R) числовой оси, симметричный относительно точки х = 0 и обладающий тем свойством, что при всех ½х ½ < R – ряд сходиться и притом абсолютно, а при всех ½х ½ > R – ряд расходится. Для этого применяется признак Даламбера к ряду ½а0½ + ½а1½½х ½+ ½а2½½х2½ + … +½ an½½xn½ + …, члены которого есть абсолютные величины членов данного ряда (1).
2. Исследуется сходимость ряда (1) на концах интервала сходимости в точках х = -R и х = R.
Пример 1. Исследовать сходимость ряда
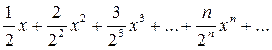
в точках х = 1, х = 3, х = - 2.
Решение.
При
х = 1 данный ряд превращается в числовой ![]()
По признаку Даламбера этот ряд сходиться, так как

При
х = 3 имеем ряд 
Применяя признак Даламбера, получим
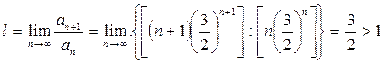 .
.
Следовательно, в точке х = 3 данный ряд расходится.
При х = -2 получаем следующий числовой ряд: -1 + 2 – 3 + 4 - ..+ (-1)n n + …, который расходится (так как не выполняется необходимый признак сходимости ряда).
Пример 2. Исследовать на
сходимость степенной ряд 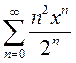 .
.
Решение.
Здесь  ,
,  ;
тогда радиус сходимости
;
тогда радиус сходимости
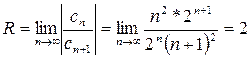 . Область сходимости -2 < x < 2. Исследуем
сходимость ряда в граничных точках. При х = ±
2 степенной ряд принимает вид
. Область сходимости -2 < x < 2. Исследуем
сходимость ряда в граничных точках. При х = ±
2 степенной ряд принимает вид
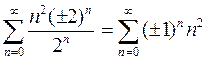 . Оба эти ряда расходятся, так как для них
не удовлетворяется необходимый признак сходимости.
. Оба эти ряда расходятся, так как для них
не удовлетворяется необходимый признак сходимости.
Ряды Тейлора и Маклорена
Если функция
разложима в некоторой окрестности точки ![]() в
степенной ряд по степеням
в
степенной ряд по степеням ![]() ,то этот ряд
имеет вид:
,то этот ряд
имеет вид:
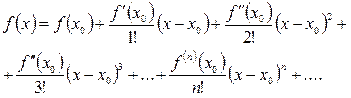 (1.1)
(1.1)
Ряд (1.1)
называется рядом Тейлора для функции![]() .
.
При ![]() ряд (1.1) принимает вид:
ряд (1.1) принимает вид:
![]() (1.2)
(1.2)
Ряд (1.2)
называется рядом Маклорена для функции ![]() .
.
Таким образом,
если функция разлагается в ряд по степеням![]() ,
то этот ряд является рядом Тейлора (или рядом Маклорена при
,
то этот ряд является рядом Тейлора (или рядом Маклорена при ![]() ). Очевидно, если функция
разлагается в ряд Тейлора в точке
). Очевидно, если функция
разлагается в ряд Тейлора в точке![]() , то она имеет
производные любого порядка в точке
, то она имеет
производные любого порядка в точке ![]() , т.е.
бесконечно дифференцируема в точке
, т.е.
бесконечно дифференцируема в точке ![]()
Пример 1. Записать два первых отличных от нуля члена ряда
Тейлора функции ![]() по степеням
по степеням![]() .
.
Решение. Найдём производные функции ![]() :
:
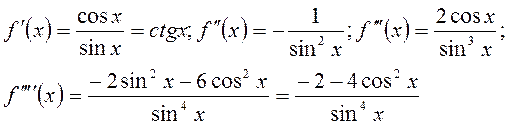
При ![]() получим
получим
 ;
;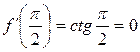 ;
; 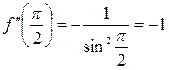 ;
;
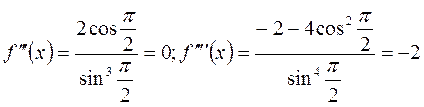 .
.
Запишем формально
ряд Тейлора для функции ![]() :
:
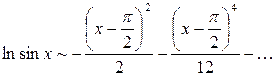 , или, после сокращения
, или, после сокращения 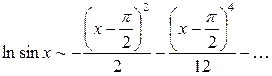 .
.
Разложение функций в ряд Маклорена
Имеют место следующие равенства:
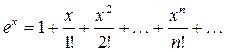 ,
,![]() , (2.1)
, (2.1)
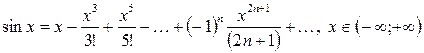 (2.2)
(2.2)
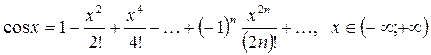 (2.3)
(2.3)
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
В частном случае, при ![]() получаем
функцию
получаем
функцию ![]() , которая является суммой
геометрической прогрессии с первым членом
, которая является суммой
геометрической прогрессии с первым членом ![]() и
со знаменателем
и
со знаменателем
![]() . Поэтому
. Поэтому
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
 (2.8)
(2.8)
Пример 2. Разложить функцию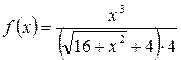 в
ряд Маклорена и найти интервал сходимости ряда.
в
ряд Маклорена и найти интервал сходимости ряда.
Решение. Преобразуем функцию ![]() к виду:
к виду:
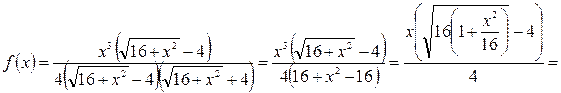
Разложим функцию 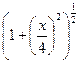 в
степенной ряд по формуле (2.5)
в
степенной ряд по формуле (2.5)

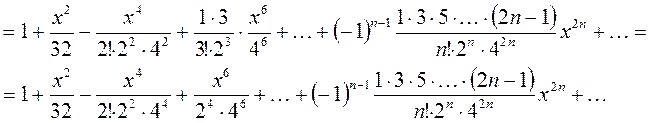
Это разложение верно при ![]() , т.е.
, т.е. ![]() при
. Тогда
при
. Тогда
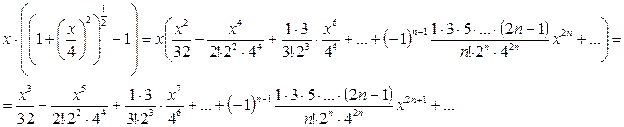
Этот ряд сходится
при ![]() .
.
Пример 3. Разложить функцию ![]() в
ряд Маклорена и найти интервал сходимости ряда.
в
ряд Маклорена и найти интервал сходимости ряда.
Решение: Внутри общего интервала сходимости ![]()
![]() имеет
место формула
имеет
место формула
![]() ,
,
где ![]() .
Тогда, используя разложения (2.1) и (2.3), получим для
.
Тогда, используя разложения (2.1) и (2.3), получим для ![]()

Итак:
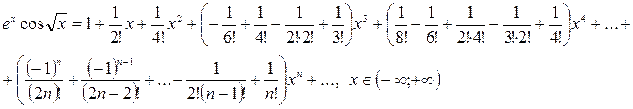
Вычисление определённых интегралов с помощью рядов
ПРИМЕР: Вычислить интеграл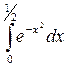 с точностью
с точностью ![]() .
.
Решение: Разложим в ряд Маклорена подынтегральную функцию:
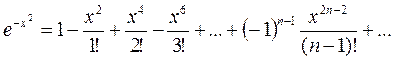 .
.
Это равенство имеет место при всех ![]() . Проинтегрировав его почленно в
пределах от 0 до 1, получим:
. Проинтегрировав его почленно в
пределах от 0 до 1, получим:
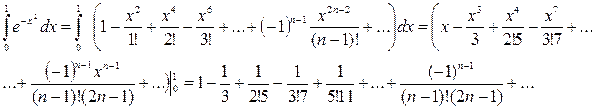 . (3.2)
. (3.2)
Так как вычисления нужно производить с тремя верными десятичными знаками, то погрешность не должна превышать 0,0005.
В правой части равенства стоит знакопеременный ряд. Если сумму знакопеременного ряда заменить суммой его первых n членов, то, как известно, возникающая при этом погрешность не превосходит модуля первого отброшенного члена. Поэтому в разложении (3.2) нужно оставить столько членов, чтобы первый отброшенный был меньше 0, 0005, причём следует учесть погрешности от округления бесконечных десятичных дробей, которые получатся в вычислениях.
Вычисляем члены нашего ряда, начиная со второго:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Следовательно, сохранив в сумме первые шесть членов, получим, что погрешность по абсолютной величине меньше первого отброшенного члена (седьмого члена) и она будет меньше, чем 0,00004, т.е. условие задачи выполнено.
Итак
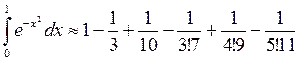 .
.
Теперь нужно вычислить приближённое значение 4 членов
этой суммы (т.к. дробь ![]() округлять не
нужно). Со сколькими верными знаками следует вычислять каждую из 4-х
бесконечных десятичных дробей
округлять не
нужно). Со сколькими верными знаками следует вычислять каждую из 4-х
бесконечных десятичных дробей ![]() ;
; ![]() ;
; ![]() ;
;
![]() ?
?
Если каждую из них вычислять с тремя десятичными знаками, то погрешность вычислений для каждой дроби будет 0,0005, а для суммы 4-х дробей она будет равна 4 0,0005=0,002, т.е. превзойдёт заданную в условии погрешность.
Если вычисление дробей вести с четырьмя десятичными знаками, то погрешность вычислений для каждой дроби - 0,00005, а для их суммы 4 0,00005=0,0002.
Сложим погрешность вычислений 0,0002 с погрешностью 0,00004 от отбрасывания членов 0,0002+0,00004=0,00024<0,0005.
Итак, промежуточные вычисления выполняем с 4-мя верными знаками:
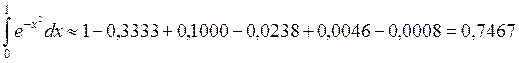
Округляя это число до трёх знаков, получим  .
.
Лекция 10. Понятие события и вероятности события. Достовернее и невозможные события. Классическое определение вероятности. Теорема сложения вероятностей.
10.1 Комбинаторика
При решении ряда теоретических и практических задач требуется из конечного множества элементов по заданным правилам составлять различные комбинации и производить подсчет числа всех возможных таких комбинаций. Такие задачи принято называть комбинаторными, а раздел математики, занимающийся их решением, называется комбинаторикой. Комбинаторика широко применяется в теории вероятностей, теории массового обслуживания, теории управляющих систем и вычислительных машин и других разделах науки и техники. Основными элементами комбинаторики являются размещения, перестановки, сочетания.
Размещения.
Определение
1. Пусть дано множество, состоящее из n элементов. Размещением из n
элементов по ![]() элементов называется упорядоченное
множество, содержащее m различных элементов данного множества.
элементов называется упорядоченное
множество, содержащее m различных элементов данного множества.
Из определения вытекает, что размещения из n элементов по m элементов – это все m – элементные подмножества, отличающиеся составом элементов или порядком их следования.
Число
всех возможных размещений из n элементов по m элементов
обозначают ![]() и вычисляют по формуле
и вычисляют по формуле ![]() или
или ![]() . (1)
. (1)
Здесь
![]() и
и ![]() .
Условимся считать 0! = 1, поэтому
.
Условимся считать 0! = 1, поэтому ![]()
Пример 1. В группе из 30 учащихся нужно выбрать комсорга, профорга, физорга. Сколькими способами это можно сделать, если каждый из 30 учащихся комсомолец, член профсоюза и спортсмен?
Решение:
искомое число способов равно числу размещений из 30 элементов по 3 элемента,
т.е. ![]() Положив по формуле (1)
Положив по формуле (1) ![]()
![]() получаем
получаем
![]()
Перестановки
Определение 2. Перестановкой из n элементов по n элементов.
Так
как каждая перестановка содержит все n элементов множества, то
различные перестановки отличаются друг от друга только порядком следования
элементов. Число всех возможных переустановок из n элементов
обозначают ![]() . Из определения перестановок
следует
. Из определения перестановок
следует
![]() т.е.
т.е. ![]() (2)
(2)
Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?
Решении: Искомое число способов равно числу переустановок из 6 элементов, т.е.
![]()
Сочетания
Определение
3. Пусть дано множество, состоящее из n элементов. Сочетанием из n
элементов m элементов по ![]() элементов
называется любое подмножество, которое содержит m различных
элементов данного множества.
элементов
называется любое подмножество, которое содержит m различных
элементов данного множества.
Следовательно, сочетания из n – элементного множества, причем различными подмножествами считаются только те, которые имеют неодинаковый состав элементов. Подмножества, отличающиеся друг от друга лишь порядком следования элементов, не считаются различными.
Число
всех множественных сочетаний из n элементов по m элементов
обозначают ![]() и вычисляются по формуле
и вычисляются по формуле ![]() . (3)
. (3)
![]() . (4)
. (4)
Пример 3. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?
Решение:
т.к. порядок выбранных четырех человек не имеет значения, то это можно сделать ![]()
Способами.
По формуле (4) находим ![]()
Вероятность события.
Пусть
![]() - случайное событие, связанное с
некоторым опытом. Повторим опыт
- случайное событие, связанное с
некоторым опытом. Повторим опыт ![]() раз в одних и
тех же условиях и пусть при этом событие
раз в одних и
тех же условиях и пусть при этом событие ![]() появилось
появилось
![]() раз.
раз.
Определение 1. Отношение![]() числа
числа ![]() опытов, в которых
событие
опытов, в которых
событие ![]() появилось, к общему числу
появилось, к общему числу ![]() проведённых опытов называется
частотой события
проведённых опытов называется
частотой события ![]() .
.
Оказывается, что при многократном повторении опыта частота события принимает значения, близкие к некоторому постоянному числу. Например, при многократном бросании игральной кости частота выпадения каждого из чисел очков от 1 до 6 колеблется около числа 1/6.
Свойство устойчивости частоты случайного события было подмечено и на явлениях демографического характера. Подсчитано, например, что частота рождения мальчика колеблется около числа 0,517.
Описанные в приведенных примерах явления, а также неоднократные наблюдения и других массовых явлений позволяют сделать вывод, что если опыт повторяется в одинаковых условиях достаточно большое количество раз, то частота некоторого события А приобретает статистическую устойчивость, колеблясь около некоторой постоянной величины р, к которой она все более приближается с увеличением числа повторений опыта.
Определение 2.
Постоянная величина р, к которой все более приближается частота событий А при
достаточно большом повторении опыта, называется вероятностью события А и
обозначается ![]()
Классическое определение вероятности.
![]() ,
,
где ![]() - попарно несовместные и
равновозможные элементарные события. Пусть некоторому событию А благоприятствуют т
из п элементарных событий пространства U.
- попарно несовместные и
равновозможные элементарные события. Пусть некоторому событию А благоприятствуют т
из п элементарных событий пространства U.
Определение 3. Вероятностью p(A) события А называется отношение числа т элементарных событий, благоприятствующих событию А, к общему числу п равновозможных элементарных событий:
![]() (1)
(1)
Из определения вероятности вытекают следующие её свойства:
1. ![]()
2. ![]() ,
так как
,
так как ![]()
3. ![]() так
как
так
как ![]()
Пример 1. В урне 3 белых и 9 черных шаров. Из урны наугад вынимают один шар. Какова вероятность того, что вынутый шар окажется черным (событие А)?
Решение: Имеем п = 12, т = 9, и поэтому
![]()
Пример 2. Подбрасывают две игральные кости. Найти вероятность того, что на них в сумме выпадает 6 очков (событие А).
Решение: При
подбрасывании двух игральных костей общее число равновозможных элементарных
исходов равно числу пар![]() где х и у
принимают значения 1, 2, 3, 4, 5, 6:
где х и у
принимают значения 1, 2, 3, 4, 5, 6:
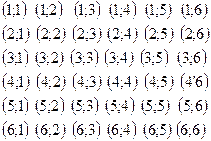
т.е. ![]() .
Событию А благоприятствуют пять пар:
.
Событию А благоприятствуют пять пар: ![]() ,
т.е.
,
т.е. ![]() .
.
Следовательно, искомая вероятность
![]()
10.2 Понятие события и вероятности события. Достовернее и невозможные события.
Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием. Примеры: сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, педагогический эксперимент.
Результат, исход испытания называется событием.
Примеры: успешная сдача экзамена, дорожно-транспортные происшествия со смертельным исходом, попадание в цель, появление того или иного числа очков на брошенной игральной кости, получение результата при проведении педагогического эксперимента.
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, человек читает и человек спит, число иррациональное и четное.
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.
Примеры: если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он не читает; если число иррациональное, то оно не является четным.
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом. Событие называется невозможным, если в данном испытании оно заведомо не может произойти.
Примеры: если в урне все шары белые, то достать белый шар является достоверным событием, а достать черный шар является невозможным событием; если человек прыгнул в воду, то выйти мокрым является достоверным событием, а выйти сухим является невозможным событием.
Событие называется случайным, если его наступление или ненаступление в некотором испытании (эксперименте) зависит от ряда случайных факторов. Примеры: успешная сдача экзамена; выигрыш в лотерее; рождения мальчика или девочки; всхожесть семян; попадание в цель и т. д.
10. 3 Классическое определение вероятности. Теорема сложения вероятностей.
Определение вероятности Совокупность образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них. Например, при сдаче зачета возможны следующие исходы: "зачтено", "не зачтено", "не явился"; при подбрасывании монеты - "орел", "решка"; при подбрасывании игральной кости - 1, 2, 3, 4, 5, 6.
События, образующие полную группу попарно несовместных и равновозможных событий, будем называть элементарными событиями.
Классическое определение вероятности
Вероятностью P(A)
события A называется отношение числа элементарных событий m, благоприятствующих
событию A, к числу всех элементарных событий n: ![]()
Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Вероятность случайного события больше 0 и меньше 1.
Статистическое определение вероятности
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Например, оно неприемлемо, если результаты испытания не равновозможны. В таких случаях используется статистическое определение вероятности. Пусть проводится n опытов, событие A наступило m раз, тогда
![]() ,
,
где m - абсолютная частота события A; P(A) - относительная частота
события A.
Вероятностью события А для испытания в данном опыте называется число P(A),
около которого группируются значения относительной частоты при больших n.
Свойства вероятности
Суммой событий A и B называется событие C = A + B, состоящее в наступлении, по крайней мере, одного из событий - A или B.
Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).
Примеры: пусть А - идет дождь, а В - идет снег, то (А + В) - либо дождь, либо снег, либо дождь со снегом, т. е. осадки; А - пошли на дискотеку; В - пошли в библиотеку, то А + В - пошли либо на дискотеку, либо в библиотеку, т. е. вышли из дома.
Следствие. Сумма вероятностей противоположных событий А и равна единице:
P(A) + P = 1.
Вероятность суммы полной группы событий равна 1.
Примеры: если А - число четное, то - число нечетное; если А - зима, то - не зима (либо осень, либо лето, либо весна); если А - сдал экзамен, то –
не сдал экзамен.
Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.
Примеры: пусть А - из урны вытянули белый шар, В - из урны вытянули белый шар, то АВ - из урны вытянули два белых шара; А - идет дождь, В - идет снег, то АВ – дождь со снегом; А - число четное, В - число кратное 3, то АВ - число кратное 6.
Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.
Чаще всего зависимые испытания происходят тогда, когда тянут из одной колоды, не возвращая карты в колоду, вытаскивают из одной урны и т.д.
Теорема. Вероятность произведения двух независимых событий A и B равна произведению их вероятностей:
P(AB) = P(A) P(B).
Пусть А и В - зависимые. Условной вероятностью PA (B) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:
P (AB) = P (A) PА (B).
Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения
P (A + B) = P (A) + P (B) - P (AB).
Теорема (формула полной вероятности). Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий B1, B2,…, Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
![]()
Теорема (формула Байеса). Если существуют n попарно несовместных событий B1, B2, …, Bn, образующих полную группу, и известны условные вероятности события А, то можно найти вероятности того, что событие А произошло при условии появления некоторого события Bk по формуле:
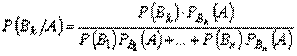
Лекция 11. Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.
Если результатом испытания является случайное событие, принимающее числовое значение, то говорят о случайной величине.
Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной. Примеры: число очков, выпавших при бросании игральной кости; число родившихся детей в семье; число шаров, которые можно достать из урны и т. д.
Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.
Примеры: прирост веса домашнего животного за месяц есть случайная величина, которая может принять значение из некоторого промежутка; прогнозируемая температура воздуха по области и т. д.
Закон распределения случайной величины
![]()
где x1, x2, …, xn - случайные величины, соответствующие полной группе событий, т. е. p1 + p2 + … + pn = 1.
При возрастании количества исходов полной группы событий закон распределения становится менее наглядным, и оценить наиболее вероятный исход становится достаточно трудно. Поэтому вводят характеристики случайных величин: математическое ожидание - ожидаемая величина в данном опыте, дисперсия - разброс значений.
Некоторые законы распределения
Биномиальное распределение
Пусть производится n испытаний, причем вероятность появления события А в каждом испытании равна р и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события А в одном испытании равна р, то вероятность его ненаступления равна q = 1 - р.
Найдем вероятность того, что при n испытаниях событие А наступит m раз (m < n). Пусть событие А наступило в первых n испытаниях m раз и не наступило во всех последующих испытаниях. Это сложное событие можно написать в виде произведения:
![]()
Общее число сложных событий, в которых событие А наступает т раз, равно числу сочетаний из n элементов по m элементов. Так как эти сложные события несовместимы, то вероятность их суммы равна сумме вероятностей. При этом вероятность каждого сложного события равна pm Ч qn-m. Вероятность появления события А m раз в n испытаниях равна:
![]()
![]() (формула Бернулли).
(формула Бернулли).
Закон биномиального распределения

Нормальное распределение
Закон распределения
вероятностей непрерывной случайной величины Х называется нормальным, если ее
дифференциальная функция f (x) определяется формулой: ![]()
где а совпадает с математическим ожиданием величины Х: а = М(Х), параметр a совпадает со средним квадратическим отклонением величины Х: σ = σ (Х).
График функции нормального
распределения, как видно из рисунка, имеет вид куполообразной кривой,
называемой Гауссовой, точка максимума имеет координаты (а; ![]() ). Значит, эта ордината убывает
с возрастанием значения s (кривая "сжимается" к оси Ох) и возрастает
с убыванием значения s (кривая "растягивается" в положительном
направлении оси Оу). Изменение значений параметра а (при неизменном значении s)
не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.
). Значит, эта ордината убывает
с возрастанием значения s (кривая "сжимается" к оси Ох) и возрастает
с убыванием значения s (кривая "растягивается" в положительном
направлении оси Оу). Изменение значений параметра а (при неизменном значении s)
не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.

Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным. Дифференциальная функция в случае такого распределения будет:
![]()
Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу (a; b)
Пример 1. Бросаются две правильные однородные монеты. Сколько из них выпадает гербом кверху?
При подбрасывании двух монет пространство элементарных событий имеет вид:
U = {ЦЦ,ЦГ,ГЦ,ГГ}, где Ц- «цифра», Г- «герб».
Первый символ показывает, как выпала первая монета, а второй - вторая монета. Например, ЦГ означает, что первая монета выпала цифрой кверху, а вторая - гербом. Так как монеты правильные и однородные, то можно считать, что все элементарные события пространства U равновероятны, и тогда вероятность каждого из них равна %. Обозначим через X число монет, выпавших гербом кверху, составим таблицу:
|
U |
ЦЦ |
ЦГ |
ГЦ |
ГГ |
|
X |
0 |
1 |
1 |
2 |
|
р |
|
|
|
|
Так как элементарным событиям ЦГ и ГЦ соответствует
одно и то же значение величины Х, равное ![]() , то можно полагать,
что это значение величина X принимает с 4х вероятностью. Таким образом, значение величины X - число монет, выпавших
гербом кверху и соответствующие им вероятности можно записать в виде таблицы.
, то можно полагать,
что это значение величина X принимает с 4х вероятностью. Таким образом, значение величины X - число монет, выпавших
гербом кверху и соответствующие им вероятности можно записать в виде таблицы.
|
X |
0 |
1 |
2 |
|
р |
|
|
|
Итак, каждое значение величины X есть число, определяемое исходом опыта и зависящее от случая.
Определение 1. Случайной называется величина, которая в результате опыта принимает с определенной вероятностью, то или иное значение, зависящее от исхода опыта. Случайные величины обозначают прописными буквами латинского алфавита: X, Y, Z и т.д., а их значения - соответствующими буквами : х, у, z и т.д.,
Определение 2. Случайная величина называется дискретной, если множество её значений конечно или счётно, т.е. множество её значений представляет собой конечную последовательность х],х2,х3,...,хп. Вероятность того, что случайная величина X примет значение х, обозначают Р{х) = Р(Х = х)
Определение 3. Соответствие между возможными значениями xvx2,...,xn случайной величины X и их вероятностями pvp2,—,Pn называется законом распределения случайной величины X.
Закон распределения случайной величины может быть представлен в виде таблицы:
|
X |
х |
х2 |
... |
х |
... |
Х |
|
р |
Р1 |
P2 |
... |
Pi |
... |
Рп |
События X = xv X = х2,...,Х = хп образуют полную систему попарно несовместных событий, поэтому сумма их вероятностей равна единице р1 + р2 +... + рп = 1.
Пример 2. Закон распределения вероятностей случайной дискретной величины Х- числа очков, выпадающих при бросании правильной игральной кости, имеет вид, заданный таблицей:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
р |
1 6 |
1 6 |
1 6 |
1 6 |
1 6 |
1 6 |
2. Биноминальное распределение случайной дискретной величины.
Пусть случайная величина Х- число появлений события А в п независимых испытаниях, в каждом из которых вероятность появления событий А равно р , а непоявления - q = 1-р. Очевидно, что Сможет принимать значения 0,1,2,..., п, вероятности которых определяются по формуле Бернулли:
Рп(т) = Р(Х = т) =
С![]() *рт -qn m, m = 0,1,2,...,
и. (1)
*рт -qn m, m = 0,1,2,...,
и. (1)
Определение. Закон распределения случайной величины X, имеющий вид:
|
X |
0 |
1 |
2 |
|
т |
|
п |
|
р |
C |
С |
C |
... |
С |
|
C |
называется биноминальным распределением.
Пример 3. Составить закон распределения числа попаданий в цель при четырёх выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Случайная величина Х- число попаданий в цель при четырёх выстрелах - может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли (2):
P(Х = 0) = С4° • 0,9° • О,14 = 0,0001;
Р(Х =
1) = С![]() • 0,9 • 0,13
= 0,0036;
• 0,9 • 0,13
= 0,0036;
Р(Х = 2) =
С![]() • 0,92 • О,12
= 0,0486;
• 0,92 • О,12
= 0,0486;
Р(Х = 3) =
С![]() • 0,93 • О,1
= 0,2916;
• 0,93 • О,1
= 0,2916;
P(Х = 4) = С44 • 0,94 • 0,1° = 0,6561;
Итак, искомый закон распределения имеет вид.
|
X |
0 |
1 |
2 |
3 |
4 |
|
р |
0,0001 |
0,0036 |
0,486 |
0,2916 |
0,6561 |
Пример 4. В ОТК измерялась длина в мм у 50 деталей, изготовленных на одном станке – автомате. В результате измерений получены следующие данные:
|
83 |
85 |
81 |
82 |
84 |
82 |
79 |
84 |
80 |
81 |
|
82 |
82 |
80 |
82 |
80 |
82 |
83 |
84 |
79 |
83 |
|
79 |
82 |
83 |
85 |
82 |
82 |
81 |
80 |
82 |
82 |
|
83 |
80 |
82 |
85 |
81 |
83 |
81 |
81 |
83 |
82 |
|
81 |
85 |
83 |
79 |
81 |
85 |
81 |
84 |
81 |
82 |
Требуется произвести первичную статистическую обработку данных:
1) Составить статистический ряд распределения частот и относительных частот длины деталей (случайная величина Х)
2) построить полигоны частот и относительных частот
3) найти эмпирическую функцию распределения и построить ее график
РЕШЕНИЕ:
1) Для составления статистических рядов исходные данные располагаются в порядке возрастания, затем подсчитываются частоты ni и относительные ni/n появление каждого из наблюдаемых значений (n=50).
|
Наблюдаемые значения |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
|
Подсчет частоты |
4 |
5 |
10 |
14 |
8 |
4 |
5 |
|
Относительные частоты |
0,08 |
0,1 |
0,2 |
0,28 |
0,16 |
0,08 |
0,1 |
2) Изобразим полигон частот и относительных частот
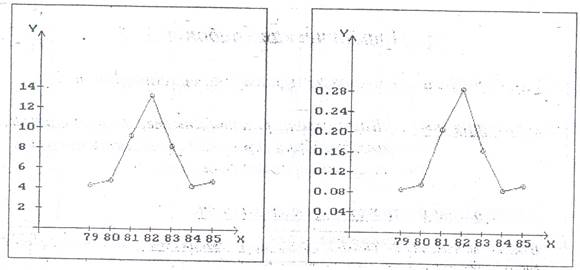
3) Эмпирическая функция распределения F*(x) определяется как отношение накопленных частот n*, т.е числа выборочных значений меньших х, объему выборки n.
|
При х ≤ 79, |
nx = 0, |
F*(x) = 0/50 = 0 |
|
При 79 < x ≤ 80, |
nx = 4, |
F*(x) = 4/50 = 0,08 |
|
При 80 < x ≤ 81, |
nx = 4+5=9, |
F*(x) = 9/50 = 0,18 |
Аналогично вычисляются значения F*(x) на других интервалах.
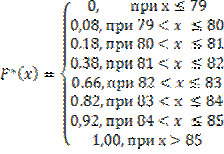
График функции F*(x):
Лекция 12. Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратное отклонение случайной величины
Характеристики случайной величины
1. Математическое ожидание
Кроме закона распределения, который даёт полное представление о случайной величине, часто используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. Среди числовых характеристик весьма важной является математическое ожидание, которое указывает, какое среднее значение случайной величины следует ожидать в результате испытаний или наблюдений.
Определение 1. Математическим ожиданием М(Х) дискретной случайной величины X называется сумма произведений всех её возможных значений х, на их вероятности pi:
М(Х) = ххрх +х2р2+... + х„р„ = ![]()
Пример
1. Найти математическое ожидание М(Х) случайной величины X, зная закон её
распределения.
|
X |
-1 |
0 |
1 |
2 |
3 |
|
р |
0,2 |
0,1 |
0,25 |
0,15 |
0,3 |
Решение: по формуле (1) находим
М(Х) = -1*0,2 + 0*0.1 + 1*0,25 + 2*0,15 + 3*0,3 =1,25. Приведём без доказательства свойства математического ожидания:
1. Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CM(X)
2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий (теорема математических ожиданий):
М(Х + Y) = М(Х) + M(Y).
3. Математическое ожидание постоянной величины С равно самой этой величине:
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий (теорема умножения математических ожиданий):
m(xy)=m(x)-m(y).
Пример 2. Куплено 100 лотерейных билетов, причем на каждый из 10 билетов выпал выигрыш в 50 руб., 5 билетов -100 руб. 2 билета -300руб. Найти средний выигрыш, выпавший на один
билет.
Решение: введём случайную величину Х- размер выигрыша. Тогда эта случайная величина принимает следующие значения х, = 0, х2 = 50, х3 = 100, х4 = 300, а вероятность того,
что р(Х
= 50) = ![]() = 0,1; р(Х = 100) =
= 0,1; р(Х = 100) = ![]() = 0,05; р(Х = 300) =
= 0,05; р(Х = 300) = ![]() = 0,02 и значит
= 0,02 и значит
р(Х = О) = 1 - 0,1 - 0,05 - 0,02 = 0,83. Значит случайная величина X имеет закон распределения:
|
х |
0 |
50 |
100 |
300 |
|
Pi |
0,83 |
О,1 |
0,05 |
0,02 |
Тогда средний выигрыш выпавший на один билет есть М (X), поэтому
М(х) = 0 • 0,83 + 50 • 0,1 +100 • 0,05 + 300 • 0,02 = 16(руб).
2.Дисперсия случайной величины.
Рассмотрим следующий пример.
Пример 3. Найти математическое ожидание случайных величиной Y, зная законы их распределения.
|
X |
-8 |
-4 |
L -1 |
1 |
3 |
7 |
|
р |
1/ 12 |
1 /6 |
1/4 |
1/ 6 |
1/12 |
1/ 4 |
|
|
||||||
|
Y |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
Р |
1/ 6 |
1 /6 |
1/12 |
1/3 |
0 |
1/4 |
По
формуле (1) имеем М(х) = ![]()
M(y) = ![]()
Мы получили любопытный результат: законы распределения величиной Г разные, а их математические ожидания одинаковы.
Из рисунка видно, что значения величины Y более сосредоточены около математического ожидания М(У), чем значения величины X, которые разбросаны относительно ее математического ожидания М(х).
Основной числовой характеристикой степени рассеяния значений случайной величины X относительно ее математического ожидания М(х) является дисперсия, которая обозначается через D(X).
Определение 2. Отклонением называется разность между случайной величиной X и ее математическим ожиданием Х-М(х).
Заметим, что отклонение X - М(х) и его квадрат (X - M(x))2 также являются случайными величинами. Причем если X случайная величина распределена по закону,
|
X |
|
|
|
|
|
р |
Р\ |
Pi |
... |
Рп |
то квадрат её" отклонения имеет следующий закон распределения
|
(x-M(x)f |
(х,-м(х)У |
(х2-м(х)У |
|
(xn-M(X)f |
|
р |
P1 |
Рг |
|
Рп |
Введём теперь определение дисперсии случайной величины X.
Определение 3. Дисперсией случайной дискретной величины X называется математическое ожидание квадрата ее отклонения:
D(X) = M(X - M(x)2) (2)
Приведем без доказательства некоторые свойства дисперсии.
Дисперсия постоянной величины С равна нулю: D(c) = О
Если Х- случайная величина, С - постоянная, то D(CX) = C2D(x) и D{X + С) = D(X)
Если
X u Y- независимые случайные величины, то D(X + Y) = D(x) + D(Y)
Для вычисления дисперсий более удобной
является формула
D(X)=M(X2)-M(X)Y (3)
Пример 4. Случайная дискретная величина распределена по закону
|
X |
-1 |
0 |
1 |
2 |
|
р |
0,2 |
од |
0,3 |
0,4 |
Найти: D(X).
Сначала находим М(х) = -1 • 0,2 + 0 • 0,1 +1 • 0,3 + 2 • 0,4 = 0,9, а затем
М(Х2)= 1-0,2 + 0-0,1 + 1-0,3 + 4- 0,4 = 2,1.
По формуле (3) имеем D(x) = м(х2)- М2 (X) = 2,1 - 0,81 = 1,29.
Пример 5. Сравнить дисперсии случайных величин Х и Y, заданных законами распределения
|
X |
-1 |
1 |
2 |
3 |
|
р |
0,48 |
0,01 |
0,09 |
0,42 |
|
Y |
-1 |
1 |
2 |
3 |
|
Р |
0,19 |
0,51 |
0,25 |
0,05 |
Находим
М(Х) = (-1) • 0,48 +1 • 0,01 + 2 • 0,09 + 3 • 0,42 = 0,97;
М(х2) = 1 * 0,48 +1 • 0,01 + 4 • 0,09 + 9 • 0,42 = 4,63;
D(X) = 4,63 -0,972 =3,69;
M(Y) = (-1)*0,19 +1 • 0,51 + 2 • 0,25 + 3 • 0,05 = 0,97
M(Y2)=1*0,19 +1*0,51+ 4*0,25+ 9*0,05 = 2,15;
D(Y) = 2,15 -0,972 =1,21.
Полученные результаты показывают, что несмотря на то, что значения и математические ожидания случайных величиной У одинаковы, их дисперсии различны, причем D(x)> D(y). Это означает, что случайная величина Y с большей вероятностью принимает значения, близкие к математическому ожиданию, чем случайная величина X.
Пример 6. Найти числовые характеристики (n = 50)
|
Наблюдаемые значения |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
|
частоты |
4 |
5 |
10 |
14 |
8 |
4 |
5 |
1) Выборочное среднее
![]()
2) Выборочная дисперсия:
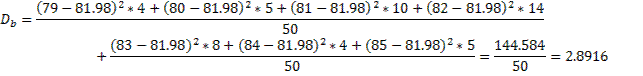
3) Выборочное среднее квадратическое отклонение:
![]()
Биноминальное распределение случайной дискретной величины.
Пусть случайная величина Х- число появлений события А в п независимых испытаниях, в каждом из которых вероятность появления событий А равно р , а непоявления - q = 1-р. Очевидно, что Сможет принимать значения 0,1,2,..., п, вероятности которых определяются по формуле Бернулли:
Рп(т) = Р(Х = т) = С![]() *рт
-qn m, m = 0,1,2,...,
и. (1)
*рт
-qn m, m = 0,1,2,...,
и. (1)
Определение. Закон распределения случайной величены X, имеющий вид:
|
X |
0 |
1 |
2 |
|
т |
|
п |
|
р |
C |
С |
C |
... |
С |
|
C |
называется биноминальным распределением.
Пример 3. Составить закон распределения числа попаданий в цель при четырёх выстрелах, если вероятность попадания при одном выстреле равна 0,9.
Случайная величина Х- число попаданий в цель при четырёх выстрелах - может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли (2):
P(Х = 0) = С4° • 0,9° • 0,14 = 0,0001;
Р(Х = 1) = С![]() * 0,9 •
0,13 = 0,0036;
* 0,9 •
0,13 = 0,0036;
Р(Х = 2) =
С![]() * 0,92 • 0,12
= 0,0486;
* 0,92 • 0,12
= 0,0486;
Р(Х = 3) =
С![]() * 0,93 • 0,1 =
0,2916;
* 0,93 • 0,1 =
0,2916;
P(Х = 4) = С44 • 0,94 • 0,1° = 0,6561;
Итак, искомый закон распределения имеет вид.
|
X |
0 |
1 |
2 |
3 |
4 |
|
р |
0,0001 |
0,0036 |
0,486 |
0,2916 |
0,6561 |
Литературные и интернет – источники:
2. Лисичкин В.Т., Соловейчик И.Л. Математика. – М., Высшая школа, 2011.
3. Богомолов Н. В. Практические занятия по математике. - М., Высшая школа, 2003.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.