Методическая разработка "Множества и операции над ними"

Элементы и множества. Операции над множествами и их свойства.

Множество - это совокупность объектов, рассматриваемая как одно целое, или - совокупность объектов, объединенных по какому-либо признаку.

Например, множество M-множество цифр от 0 до 9; М={0,1,2,3,4,5,6,7,8,9}.

Если в множестве А имеется элемент , то пишут  или и говорят, что элемент   входит в множество А

Если элемент  в множество А не входит, то пишут  или 

Множество, которое не содержит элементов называют пустым множеством и обозначают символом: Ø.

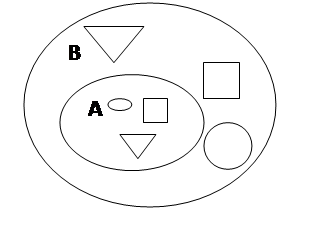
                                         Рис.1

Из рис.1 видно, что каждый элемент множества А принадлежит  также множеству В.

Если каждый элемент множества А является элементом множества В, то говорят, что множество А является подмножеством множества В. Это обозначается  

Если каждый элемент множества А является одновременно элементом множества В и каждый элемент множества В является одновременно элементом множества А , то множества А и В называют равными.

Обозначение: А=В.

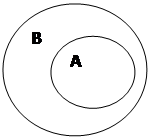
Пустое множество считается подмножеством любого множества.

Различают конечные и бесконечные множества.

Множество называется конечным, если в нем содержится конечное число элементов.

Множество, которое не является ни конечным, ни пустым, называется бесконечным.

Например, множество натуральных чисел, множество точек на окружности – бесконечные множества; множество цифр – конечное множество.

Круги, с помощью которых наглядно изображаются множества, называются кругами Эйлера-Венна, а способ изображения множеств с помощью кругов называется диаграммами Эйлера-Венна.

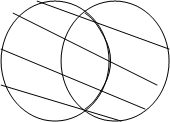
Объединением множеств А и В называется множество С, состоящее из всех элементов множеств А и В и только из них. Объединение множеств обозначают:  (рис. 2)

Т.е.

          А               В

              Рис.2

При этом, если множества А и В имеют общие элементы, то каждый из этих общих элементов в объединение входит только один раз.

Например: Даны два множества А и В.

А={a, b, c, d, e, f}  B={m, n, k, e, f, h} Найти объединение этих множеств.

 = {a, b, c, d, e, f , m, n, k, h}.

Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат каждому из данных множеств А и В (рис. 3а). Пересечение множеств обозначают: 

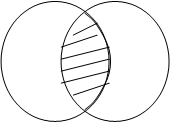Т.е.

          А              В  

Рис.3а                                                      Рис.3б

Если множества А и В не имеют общих элементов, то пересечением таких множеств является пустое множество: Ø (рис. 3б).

Разностью множеств А и В называется множество С, которое состоит из всех элементов множества А, не принадлежащих множеству В. Разность множеств обозначают: А\В=С. (рис.4а)

Т.е.

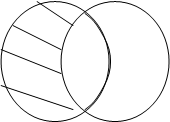              А               В

                                                                  А\В=Ø.

Рис.4а                                                Рис.4б

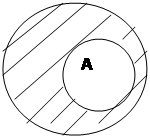                                В

- дополнение множества В до множества А.

Рис.4с