
Тема урока: «Решение неравенств с одной переменной»
Кто с ранних лет занимается математикой, тот
развивает внимание, тренирует свой мозг,
свою волю, воспитывает в себе настойчивость
и упорство в достижении цели.
А.Макрушевич
Цели урока:
Ø Образовательные: Обобщить и систематизировать решение неравенств второй степени с одной переменной графическим способом и методом интервалов, уметь работать с тестом, строить графики функций. Подготовка к ГИА. Совершенствовать навыки и умения.
Ø Воспитательные: Активизировать учебную деятельность путём вовлечения их в процесс подготовки урока, поиск нового, интересного материала необходимого для жизни. Формирование доброжелательного отношения друг к другу, формирование умения оценивать друг друга и самих себя.
Ø Развивающие: Формирование умения формулировать для себя цели урока, показать межпредметные связи, формирование умения применять знания о квадратичной функции и неравенствах. Развитие логического мышления, самостоятельности, создание проблемной ситуации.
Тип урока: урок-практикум.
Оборудование: мультемедийный проектор, презентация к уроку, карточки для проведения теста, таблица «Алгоритм решения квадратных неравенств», координатные досточки, «светофоры», папки для подготовки к ГИА, плакат «Фокус параболы».
Ход урока.
I. Ребята! Перед вами план урока. Давайте вместе попытаемся сформулировать цели нашей работы. Открыли папки, тетради и записали
(Число, классная работа, тема урока «Решение неравенств с одной переменной».
(Основная цель: подготовка к ГИА, уметь применять знания о квадратичной функции, уметь решать квадратные неравенства и показать многообразие применения квадратичной функции и неравенств в различных областях науки и техники).
Урок проходит под девизом «Покоряет вершины тот, кто к ним стремится». Мы стремимся к тому, чтобы сдать ГИА. А нас сопровождает «Талисман хорошего настроения», я надеюсь, что оно у вас такое.
Каждый ученик имеет оценочный лист, в котором проставляются баллы за его работу.
II. Вершина 1 - «Математическая разминка».
Девиз: «Спешите видеть, ответить, решать»
В это время у доски работают 6 учеников, самостоятельно выполняют задания с карточек). ( 1 балл).
|
Карточка 1.
Решить неравенство: х2-100≤ 0
|
Карточка 2.
Построить график квадратичной функции у=-2х2 +4х-3. Укажите наибольшее значение этой функции. |
|
Карточка 3. Решить неравенство методом интервалов: (х- 0,3) (х+2) (х- 4) > 0 |
Карточка 4. Разложить на множители квадратный трёхчлен : 3х2 -7х +2 |
|
В1. При каких
значениях х имеет смысл выражение
|
Докажите, что при любом а верно неравенство:5а2-2а+1>0 |
Сформулируйте алгоритм решения квадратных неравенств.
Устно: +тетрадь. «Ищите убедительные доводы».
1.По графику квадратичной функции определите знаки коэффициентов а, в, с и Д.
Ответы: 1. а > 0, в < 0, с > 0, Д > 0
2. а > 0, в < 0, с > 0, Д = 0
3. а < 0, в < 0, с < 0, Д< 0
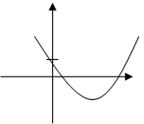
2.Найди корни квадратного трёхчлена
Х2 -7х+6=0 (1,6)
3.По тренажёру решить квадратное уравнение №60 х2-3х-10=0 (5,-2)
№ 107 х2+22х+40=0 (-20,-2)
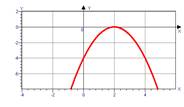
4. На рисунке изображён график функции у= х2 + 2х.
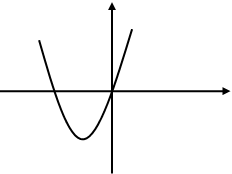
Используя график, решите неравенство х2 + 2х < 0
Ответ: [-2; 0 ]
5. Взяли шаблон параболы у=- ½ х2 сдвинули на 3 единиц влево и на 2единицы вверх. Покажите на координатной досточке эту параболу.
Графиком какой функции является парабола.
1) у=(-½ х +3)2 + 2 у=½ х2
2) у=- ½ (х-3)2-2
3) у=- ½ (х+3)2 -2
4) у=- ½ (х+3)+2
Учащиеся отвечают у доски ( по карточкам).
III. И, так, мы повторили материал по теме «Квадратичная функция» и «Решение неравенсв с одной переменной», задания взяты из сборника для подготовки к экзамену, и пришло время проверить свои знания, тем самым по настоящему поверить в себя, и если на ГИА будут задания по данной теме, то я обязательно решу.
IV. Перед тем, как выполнять задания теста, сделаем шаг в сторону. Интеллектуальная пауза
А находят ли применение неравенства в окружающем нас мире ?! А может этот прихоть математиков?! Наверно нет. Ведь всякое явление можно описать с помощью функции, а умение решать неравенства позволяет отвечать на многие вопросы.
Сколько теплых воспоминаний навеивают эти фотографии! Каскады падающей воды, фонтаны украшают многие города, развлекательные центры, дома. А при чем здесь квадратные неравенства? Чтобы ответить на этот вопрос нужно вспомнить, что для тел, брошенных вверх при отсутствии сопротивления воздуха, механика устанавливает следующее соотношение между высотой подъема тела над землей(h), начальной высотой тела над землей (h0), начальной скоростью (v0), ускорением свободного падения (g), углом наклона струи воды α:
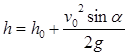 |
Фонтан смотрится лучше, если капли воды достигают высоты, большей, чем высота статуи. При высоте статуи Евы 3м и угле наклона 60º, получим неравенство:
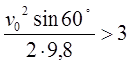 |

Квадратичная функция-математическая модель, описывающая зависимости между реальными величинами, графиком которой является парабола.
А теперь мы сейчас узнаем, что имеет каждая парабола, и это применяется в жизненных ситуациях, в различных областях науки и техники, а для этого нужно установить соответствие между функцией и её графиком и буквы соотнести правильным ответам.
1) ![]() у=х2-2
у=х2-2
2) 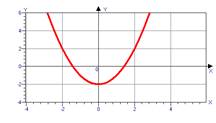 у=-х2-2
у=-х2-2
3) ![]() у=х2+2
у=х2+2
4) 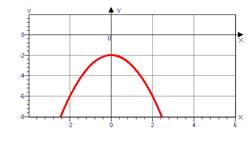 у=-(х-2)2
у=-(х-2)2
5) у=(х-2)2-2
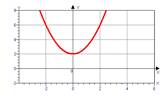
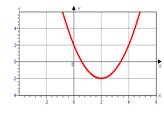
Слайд «Фокус параболы». (Сообщение о применении в науке и технике).
Ответ: ФОКУС – точка на оси параболы, луч света, помещенный при помощи зеркала в эту точку, отражается параллельно оси симметрии. Используется в приборостроении, отражатели (телескоп, автомобильные фары, прожектор, карманный фонарик). Из биографии Архимеда (сжег неприятельский флот).
Делай, как здесь (на доске рисунки, изображающие образ параболы)
V. Физкультминутка.
Вы с параболой дружны
Как она вы хороши,
Поднимите руки вверх, повернитесь вправо.
Упражнение друзья, сделали на славу.
Опустите руки вниз.
Поднимите снова ввысь.
А теперь вам поворот надо сделать влево.
Ой, Денис, ну что ж так робко!
Делать надо смело!
А, теперь, наклон вперёд.
Да, на пользу вам урок!
Порезвились от души,
Поразмяли тело,
А, теперь, за дело!
VI. Мини-экзамен.
Девиз: «Решу, и я на вершине».
Ребята! Давайте проверим наши знания о квадратичной функции, умение решать неравенства двумя способами и оценим себя, решив тест, форма и содержание которого похожа на ГИА.
Условием успешности выполнения заданий является осмысленность, осознанность, осознанность действий и просто здравый смысл. В противном случае, даже имея необходимые знания можно прийти к неверному ответу.
Сначала повторим правила работы с тестом.
1этап. Решаем все задания по порядку. Если одно из них не получается, то не останавливаемся на нём, а решаем дальше.
2 этап. Возвращаемся к тем заданиям, которые мы знаем как решать, но они не получились по техническим причинам.
3 этап. Думаем над новым типом задач.
Вариант 1.
Часть 1.
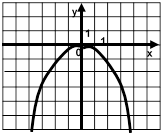
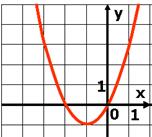 А1. График какой функции изображен на рисунке?
А1. График какой функции изображен на рисунке?
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
![]()
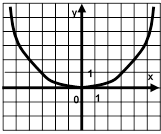
А2. На каком рисунке изображен график
функции ![]() ?
?
1) 2) 3) 4)
![]()
![]()
![]()
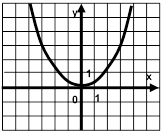
А3 Найдите наименьшее значение функции:
![]() .
.
1) -7 2) -16 3) 3 4) -18
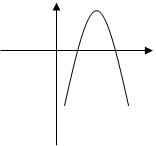
А4. На рис. изображён график функции у=ах2+вх+с. Определите знаки коэффициента а и дискриминанта Д.
1) а > 0, Д >0
2) а > 0, Д < 0
3) а< 0, Д >о
4) а< 0, Д< 0
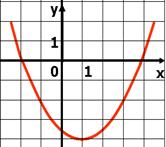
А5. По графику функции ![]() , изображенному на рисунке,
определите количество целых решений неравенства
, изображенному на рисунке,
определите количество целых решений неравенства ![]() .
.
 1) 7 2) 2 3)
1 4) 5
1) 7 2) 2 3)
1 4) 5
А6. Для каждого неравенства укажите множество его решений. В таблице под каждой запишите номер соответствующего ответа.
А) X2+1>0 1) (-∞; -1) U (1; +∞)
Б) X2-1>0 2) (-∞; +∞)
В) X2-1<0 3) ( -1; 1)
Ответ:
|
А Б В
|
Часть 2.
При выполнении заданий части 2 используйте отдельный лист(бланк). Сначала укажите номер задания, а затем запишите его решение.
1. Определите наибольшее целое отрицательное число, при котором функция у=х2-рх+16 принимает положительные значения при всех значениях .
Вариат 2.
Часть 1.
А1. График какой функции изображен на рисунке?
1) ![]() 2)
2)
![]()
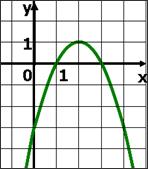 3)
3) ![]() 4)
4) ![]()
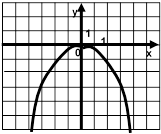
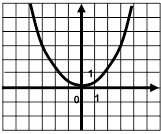
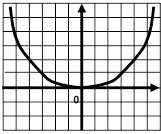
А2. На каком рисунке изображен
график функции ![]() ?
?
1) 2) 3)
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() А3.
Найдите наибольшее значение функции
А3.
Найдите наибольшее значение функции ![]() .
.
1) -16 2) 7 3) -4 4) 6
А4. На рисунке изображён график функции у= ах2+вх+с. Определить знаки коэффициента а и дискриминанта Д.
1) а > 0, Д > 0
2) а > 0, Д< 0
3) а < 0, Д > 0
4) а < 0, Д< 0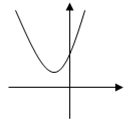
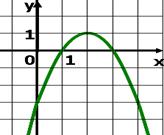
А5. По графику функции ![]() , изображенному на рисунке,
определите количество целых решений неравенства
, изображенному на рисунке,
определите количество целых решений неравенства ![]() .
.
1) 4 2) 2 3) 1 4) 3
А6. Для каждого неравенства укажите множество его решений. В таблице под каждой буквой запишите номер соответствующего ответа.
А) х2-9 >0 1) (-∞; +∞ )
Б) х2-9< 0 2) (-∞; -3)U(3;+ ∞)
В) х2+9 >0 3) (-3; 3 )
Ответ:
|
А Б В
|
Часть 2.
При выполнении заданий части 2 используйте отдельный лист (бланк). Сначала укажите номер задания, а затем запишите его решение.
1. Определите наибольшее целое отрицательное число, при котором функция у=х2-рх+4 принимает положительные значения при всех значениях.
2.
VII. Покоряем вершину «Ум без догадки гроша не стоит».
Вставьте число вместо «?» по аналогии с первой строкой
(8х – 3)2 = 5 64 64х-1= 0
(5 –х)2=3 ? х – 7 = 0 Ответ: 1 – старший коэф.
VIII. Задание на дом: Вариант экз. работы ( в папках)
Дополнительная задача
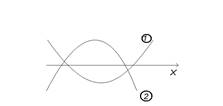
На чертеже изображены графики функций у=ах2+с и у=х2+bx+d, причем ось Оу стерта. Какая функция имеет график 1, а какая – 2? Определите знаки b, с,д.
IX. Рефлексия. (выставление баллов в оценочный лист).
Закончить урок я хочу словами одного дореволюционного учёного:
«Смысл жизни не в том, чтобы делать то, что нравится, а в том, чтобы с любовью делать то, что должен».
И, так, 1.На уроке я работал активно/ пассивно
2.Своей работой на уроке я доволен/ не доволен
3.Урок для меня показался коротким/ длинным
4. За урок я не устал/ устал
5. Моё настроение стало лучше/ стало хуже
6. Материал урока мне был понятен/ не понятен
полезен/ бесполезен
интересен/ скучен
7.Домашнее задание мне кажется лёгким/ трудным
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.