Методическая разработка открытого занятия по математике по теме "Логарифм числа" 1 курс СПО

МИНОБРНАУКИ РОССИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Вологодский государственный университет»

(ВоГУ)

Университетский колледж

Методическая разработка открытого занятия по теме

«Определение логарифма числа. Основное логарифмическое тождество».

Составитель: преподаватель УК Шутова Светлана Витальевна

 Вологда

2022

ВВЕДЕНИЕ

Методическая разработка открытого занятия предназначена для изучения темы «Определение логарифма числа. Основное логарифмическое тождество» обучающимися 1 курсов СПО.

 Открытое занятие по теме «Определение логарифма числа. Основное логарифмическое тождество» построено с применением методов проблемного обучения, способствует развитию логического мышления, вычислительной культуры обучающихся, необходимых  для будущей профессиональной деятельности, воспитанию  чувства ответственности для достижения конкретных результатов, понимая значимость математики.

Для  установления связи преемственности в изучении нового материала с изученным, необходимо включить новые знания в систему ранее усвоенных. Повторяется тема «Показательная функция», которая подготавливает обучающихся к восприятию нового материала.

Тема «Определение логарифма числа. Основное логарифмическое тождество» является основой  при изучении последующих тем, таких как «Логарифмическая функция», «Решение логарифмических уравнений и неравенств», «Производная логарифмической функции», «Интегральное и дифференциальное исчисление»,  следовательно, от успешности ее изучения зависит качество усвоения других тем.

Тема занятия: Логарифм числа. Основное логарифмическое тождество.

         Цели урока: Познакомить обучающихся с понятием логарифма и основным логарифмическим тождеством. Закрепить первичные навыки вычисления логарифмов.

         Задачи урока:

Образовательные

·        сформировать на занятии новые понятия по теме «Логарифм числа. Основное логарифмическое тождество»;

·        познакомить обучающихся с некоторыми свойствами логарифмов;

·        формирование умений применять изученные свойства логарифма для преобразования логарифмических выражений.

Развивающие

·        применять сформированные знания, умения и навыки в конкретных ситуациях;

·        развитие аналитического и логического мышления, внимания, памяти, математической речи;

·        развитие познавательного интереса к предмету  через содержание учебного материала.

·        - развитие навыков исследовательской деятельности (выдвижение гипотез, анализ, обобщение);

Воспитательные

·        воспитание чувства ответственности для достижения конкретных результатов, умения объективно оценивать результаты своей деятельности;

·        воспитание культуры общения, навыков самостоятельности и саморазвития, взаимоконтроля;

·        воспитание нравственных качеств личности: ответственность, аккуратность, дисциплинированность

Обучающийся должен знать: обозначение определение логарифма числа, основное логарифмическое тождество.

Обучающийся должен уметь: выполнять преобразования выражений, содержащих логарифмы; находить логарифм числа, число по значению логарифма, применять основное логарифмическое тождество.

         Тип учебного занятия: урок открытия новых знаний, обретения новых умений и навыков.

         Вид учебного занятия: комбинированный.

        Форма проведения урока: фронтальная, индивидуальная, работа в парах.

Основные методы обучения: фронтальный, проблемный, частично-поисковый, наглядно-иллюстративный, практический, самопроверка, взаимопроверка.

Элементы  педагогических технологий:

·        технология формирования критического мышления

·        технология проблемного обучения

·        технология поэтапного формирования умственных действий

·        технология развивающего обучения

·        технология сотрудничества

·        здоровьесберегающие технологии (чередование видов деятельности)

Продолжительность занятия: 60 минут

Метапредметные связи: физика, химия, астрономия

Межпредметные связи: Темы: «Степень с действительным показателем», «Показательная функция. Показательные уравнения и неравенства»

Место проведения: кабинет Математики

Оборудование: доска, раздаточный материал.

Методическая разработка предназначена для преподавателей естественнонаучных дисциплин.

Планируемые образовательные результаты:

 Предметные УУД

-             освоение систематических знаний, их преобразование, применение и самостоятельное выполнение, владение представлениями о логарифмах и их свойствах.

Личностные УУД

-            развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;

-            овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

-            готовность и способность к самостоятельной творческой и ответственной деятельности;

-            готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;

Метапредметные УУД:

-            умение продуктивно общаться и взаимодействовать в процессе совместной деятельности;

-            владение навыками познавательной, учебно-исследовательской и проектной деятельности; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

-            готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;

-            владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

Познавательные УУД:

-            уметь искать и обрабатывать информацию, записывать ее и воспринимать; использовать модели, знаки, символы и схемы; осуществлять логические операции: анализ, синтез, сравнение, подведение под понятие, аналогия, суждение, выбирать способы решения задач в зависимости от конкретных условий.

Коммуникативные УУД: 

-            формировать умение сотрудничать с учителем и сверстниками при решении учебной задачи, принимать на себя ответственность за результат своих действий; формировать умение слушать и вступать в диалог; формировать внимательность и аккуратность в вычислениях; воспитывать чувство взаимопомощи, культуру учебного труда, требовательное отношение к себе и к своей работе.

Регулятивные УУД:

-             умение применять и сохранять учебную задачу, планировать решение задания, вносить изменения в процесс, намечать способы устранения ошибок, осуществлять итоговый контроль.

Усвоение нового материала  организуется через создание проблемной ситуации. Для развития  познавательного интереса, формирования положительной мотивации обучающихся, преподавателем были разработаны упражнения. Выполнение предложенных заданий  способствуют созданию  ситуации успеха обучающихся, сотрудничества друг с другом, умение работать в команде.

Элементы самоконтроля и взаимоконтроля на каждом этапе способствуют качественному изучению темы занятия.

Технологическая карта открытого занятия «Определение логарифма. Основное логарифмическое тождество»

ХОД ЗАНЯТИЯ

1.     Организационный момент

Взаимные приветствия преподавателя и студентов; проверка внешнего состояния кабинета; проверка подготовленности студентов к  занятию,  их настроя на работу; организация внимания и внутренней готовности.

-Здравствуйте. Я рада видеть всех сегодня на нашем уроке, и вас ребята, и наших гостей. Я уверена, что как обычно вы будете работать в полную  меру сил, атмосфера на уроке будет доброжелательная, можно ошибаться, сомневаться, консультироваться, но давайте дадим себе установку со всеми ошибками разобраться и уйти с урока с усвоенным материалом.

Сегодня,  изучая  тему, мы проведем урок, в ходе которого вы сможете оценить свои знания.  Желаю всем удачи!

2.     Актуализация опорных знаний

Ребята, давайте вспомним, какую тему мы изучали на предыдущих занятиях?

- Решение показательных уравнений.  Устно:

4)   Найдите корень уравнения:  =   = 125   ;  = -27

5)   Найдите сумму корней уравнения:     = 1

6)    Укажите промежуток, которому принадлежит корень уравнения:

=

                  а) ( 0 ; 2 )          б) ( -2 ; 0 )       в)  ( -3 ; -1 )

3.     Постановка проблемной ситуации

Какой способ мы используем при решении показательных уравнений?

- Обе части уравнения необходимо представить в виде степени с одинаковым основанием.

Рассмотрим уравнения:     = 8        и         = 3

                                             =                  =

                                              х= 3                    х=?

Каким способом можно решить второе уравнение?

Уравнение имеет корень, притом единственный. Это можно показать с помощью графического метода решений уравнений.

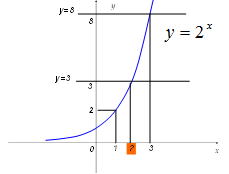
      Но результат будет приближенный. А как записать точный ответ?

У нас с вами пока не хватает знаний для этого. Такая же проблема стояла перед математиками на определенном этапе развития математики. Чтобы решить это уравнение, было введено новое понятие – логарифм числа.

     Какая тема нашего занятия?            

     Запишем тему урока: «Определение логарифма числа. Основное логарифмическое тождество»

Итак, сформулируем  цели урока:

·        Познакомиться с определением логарифма, его обозначением, некоторыми свойствами логарифма

·        Научиться вычислять значения логарифмических выражений

4.     Мотивация изучаемой темы

         Тема «Логарифмы» является важной темой в математике. Понятие логарифма  используются при решении практических задач в частности в физике, химии, астрономии и др. Логарифмы были придуманы для упрощения вычислений. Многие математики одновременно, не зависимо друг от друга,  занимались этой темой, но понятие логарифма было введено шотландским математиком в 16 веке, имя которого мы узнаем сегодня.

Темы рефератов по этой теме:

4.     «История возникновения логарифмов»

5.     «Применение логарифмов»

6.     «Логарифмы вокруг нас»

5.     Изучение нового материала. Основная часть

Что такое логарифм? Давайте попробуем сформулировать  определение логарифма самостоятельно. Вернемся к показательному уравнению:

= b, где а а , b > 0. Это уравнение имеет единственный корень, который называют логарифмом числа а по основанию b.

Обозначают:   

Таким образом, мы можем записать точный корень уравнения:

        = 3 

       х =

Что такое логарифм? Сформулируем определение.

Определение. Логарифмом положительного числа b по  основанию a , где а а называется  показатель степени, в которую надо возвести число а, чтобы получить число b.

Проверим по учебнику. Учебник стр. 91.

Запишем определение в тетрадь.

Каким числом может быть значение логарифма? Основание логарифма?

Рассмотрим примеры:

№1. Найдите значение логарифмов:

 = 4,  т.к.    = 16

 = -3,  т.к.    =

 =  ,  т.к.   = 2

Операцию нахождения логарифма называют логарифмированием. Из решенных примеров мы можем сделать вывод, что эта операция является обратной по отношению к возведению в степень с соответствующим основанием (взаимно-обратные операции). Запишем важное правило:

 = c   = b

Из определения логарифма легко вывести следующие формулы:

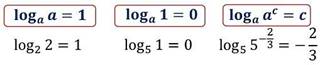
№2. Вычислить:

 =  = -

Давайте ещё раз посмотрим на определение логарифма.

Поскольку логарифм – это такой показатель степени, в которую нужно возвести основание а, чтобы получить число b

 = c

 = b, то можно записать:  = b

Это равенство называется основным логарифмическим тождеством.

Его используют при вычислении значений выражений.

№3 Вычислить:

4)      = 7

5)     = ==9

6)    =  =  = 49

6.     Первичное закрепление изученного материала 

И вот теперь вы должны проявить свои умения при решении заданий и узнать имя изобретателя логарифмов, которое закодировано.  Решив задания, вы узнаете это.

Джон Непер в начале 16 века первый ввел понятие логарифма.

7.     Практическая часть.

Давайте рассмотрим какие еще задания можно выполнять, используя определение логарифма.

1). Логарифмирование.

Вычислить:

 = х

По определению логарифма:

 = 128

 =

5х = 7

х=1,4           Ответ:   = 1,4

2)   -    =  -    3 =   -  = -

3). Потенцирование (действие нахождения числа по его логарифму).

Решить уравнения:

а)   = -2

     х =  =

б)  = 2

     2-х =

     2-х = 9

     х = -7

8.     Закрепление новых знаний.

Самостоятельная работа с взаимопроверкой.

                 Вариант № 1

№1 Вычислите:

8)   +  =

9)   -  =

10)             + 5 =

11)                 - =

12)                   =

13)                 =

14)                =

№2 Решите уравнение:

3)   = 4

4)   = 6

                     Вариант № 2

      №1.Вычислите:

8)    +  =

9)     -   =

10) + 12  =

11)  - =

12)   =

13) =

14)   =

№2 Решите уравнение:

3)   = 3

4)   = 3

Критерии оценивания:

Все верно! (9 заданий) -  «5»

7-8 задания  верно  – «4»

 5-6 задания верно  –«3»

 менее 5 заданий –«2»

9.     Домашнее задание:  № 271, 276

10. Подведение итогов занятия (анализ и оценка успешности достижения цели, результативность занятия)

Сегодня на уроке мы рассмотрели определение логарифма, основное логарифмическое тождество. Вспомним, какие цели перед собой мы сегодня поставили? Достигли ли Вы поставленные цели?

Рефлексия. Выставление оценок.

Выводы

Все поставленные задачи и цели занятия были достигнуты. Чередование разных видов деятельности, способствовало созданию положительной эмоциональной атмосфере проведенного занятия. Все студенты активно работали.

В ходе занятия использовались словесно-наглядные, показательно-иллюстративные, практические, контролирующие  методы обучения.

Используемые формы и методы проведенного занятия способствовали развитию общих компетенций обучающихся, культуры учебных взаимоотношений между обучающимися и преподавателем.

Приложение № 1

Приложение №2