Методическая разработка «Прямая и обратная пропорциональные зависимости.docx

Конспект урока

Математика

6 класс

Урок № 7

Прямая и обратная пропорциональность. Решение задач

Перечень рассматриваемых вопросов:

• Понятия прямой и обратной пропорциональной зависимости.
• Краткая запись условия задачи.
• Составление и решение пропорций по условию задачи.
• Решение задач на прямую и обратную пропорциональную зависимость.

Тезаурус

Равенство двух отношений называют пропорцией.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Прямая пропорциональность.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

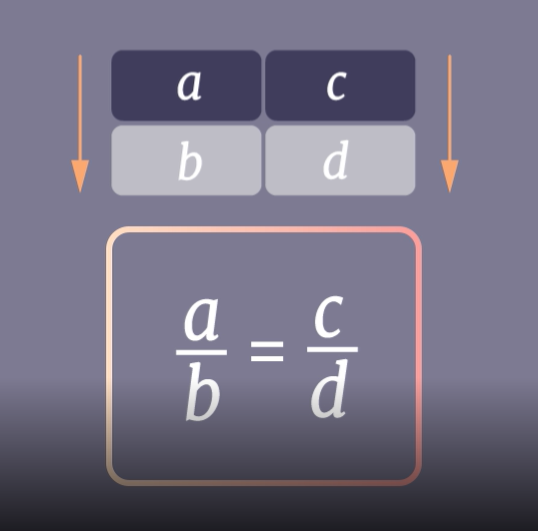
Обратная пропорциональность.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

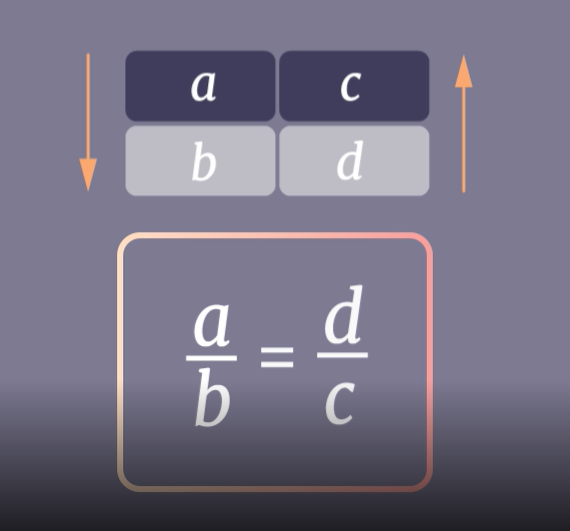
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.

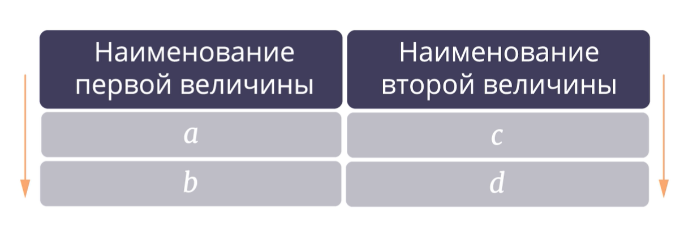
Столбцы таблицы соответствуют наименованиям зависимых величин.

Строки таблицы соответствуют значениям величин при первом и втором измерении.

Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.

Задача.

Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?

Решение.

При постоянном пути скорость и время движения обратно пропорциональны.

Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.

Сделаем краткую запись условия.

Задача.

Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?

Решение.

При постоянной скорости путь прямо пропорционален времени движения.

Пусть х м проедет велогонщик за 45 с.

Сделаем краткую запись условия.

Задача.

Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?

Решение:

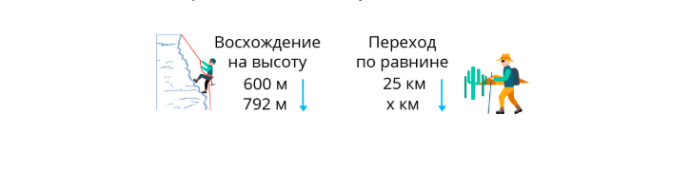
Решение.

Задача.

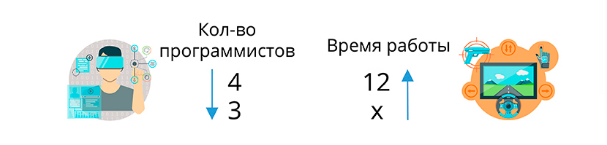
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?

Решение.

Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.

Разбор заданий тренировочного модуля

№ 1. Подстановка элементов в пропуски в тексте.

Подставьте нужные элементы в пропуски.

Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?

Решение:

При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.

Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.

Составим пропорцию:

_________

х=_______

х=_______(ч).

Правильный ответ.

Решение:

При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.

Пусть х часов – пешеход идёт со скоростью 6 км/ч.

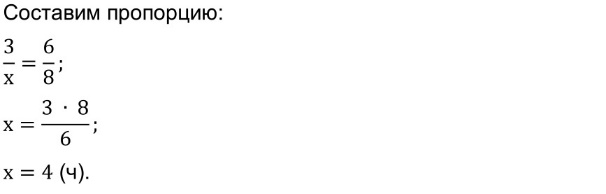
№ 2. Подстановка элементов в пропуски в таблице.

Заполните таблицу.

Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.

Варианты ответов:

135 км;

180 км;

225 км;

270 км.

Решение.

При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.

Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.

Ответ: