Методическая разработка "Третий признак равенства треугольников. Решение задач"

Министерство образования и науки

ФГБОУ ВПО «Нижегородский государственный педагогический университет им. Козьмы Минина»

Кафедра математики и математического образования

Урок 10

«3 признак равенства треугольников. Решение задач»

                                                                                      Выполнила:

                                                                                      студентка ФЕМиКН,

                                                                                                                                      Шемякина Анна Анатольевна

Нижний Новгород

2019

Конспект урока

Характеристика урока

Учебник: Геометрия: учебник для 7-9 классов средней школы/А. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2008. – 384с. – ГлаваII. Треугольники. §3. «Второй и третий признаки равенства треугольников».

Тема: Признаки равенства треугольников.

Тип урока: урок решения задач.

Учебная задача урока: рассмотреть основные виды задач, решаемых на основе 3 признака равенства треугольников, методы (приёмы) их решения

Диагностируемые цели урока:

В результате урока ученик

знает:

- какие виды задач и как решаются на основе 3 признака равенства треугольников, методы (приёмы) их решения

умеет: 

- применять 3 признак равенства треугольников для решения основных видов задач

понимает:

- различие одних видов задач от других, которые решаются на основе 3 признака равенства треугольников.

Учебные действия, формируемые на уроке:

•  Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика
• Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно, планирование - определение последовательности промежуточных целей с учётом конечного результата, оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения
• Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение
• Познавательные: анализ объектов  с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей

Методы обучения: репродуктивный, частично-поисковые, УДЕ.

Форма работы: фронтальная

Средства обучения: традиционные, презентация.

Структура урока:

Мотивационно-ориентировочная часть (10 минут)

Операционно-познавательная часть (30 минут)

Рефлексивно-оценочная часть (5 минут)

Ход урока

Мотивационно-ориентировочная часть

Актуализация

Работа идёт устно

Учитель: Какие способы сравнения существуют? (существует 3 способа сравнения: наложение, сравнение 6 элементов, по 3 признакам равенства треугольников)

Работа идёт фронтально со всем классом

Учитель: На рисунках изображены треугольники, какие из них равны и почему?

А)

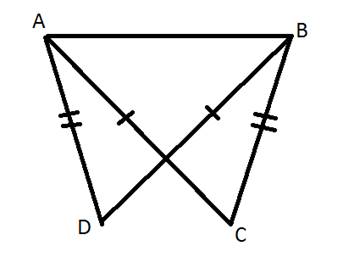(△ABC=△BAD, по третьему признаку треугольников, т.к. AB-общая, AD=BC, AC=BD)

Б)

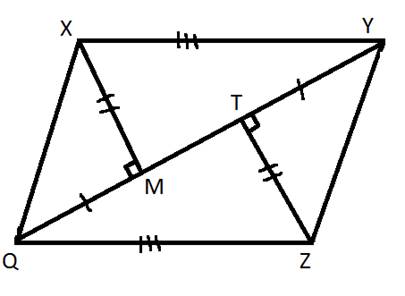  (△XMQ=△ZTY (1признак равенства треугольников, т.к. QM=TY, MX=TZ, ∠QMX=∠YTZ),

△XYM=△ZQT (3 признак равенства треугольников, т.к. XY=QZ, XM=TZ, QT=YM(т.к. QT=TM+QM, YM=TM+TY, QM=TY)),

 △QXY=△YZQ (2 признак равенства, т.к. QY-общая , ∠XQY=∠QYZ(накрестлежащие при секущей QY и XQ||YZ), ∠XYQ=∠YQZ (накрестлежащие при секущей QY  и XY||QZ)).

        Учитель: Сформулируйте 1 признак равенства треугольников. (Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны)

Учитель: Сформулируйте 2 признак равенства треугольников. (Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны)

Учитель: Сформулируйте 3 признак равенства треугольников. (Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны)

 Для экономии времени на уроке 3 признак равенства треугольников доказывается 1-2 учениками на листочках на передней или задней парте.

Мотивация

- На предыдущих уроках вы изучали 3 признак равенства треугольников.

Постановка учебной задачи

- Поэтому сегодня на уроке мы должны рассмотреть, как этот признак используются при решении различных задач.

Урок решения задач. 3 признак равенства треугольников

Операционно-познавательная часть

Задачи из учебника №№138, 141, 168, 142(1 случай)

№138

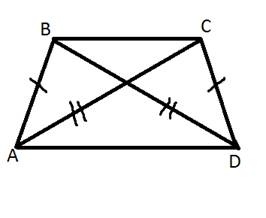
Дано: AB=CD, BD=AC.

Доказать: а) ∠CAD=∠ADB; б) ∠BAC=∠CDB.

Поиск доказательства:

а) -Что нужно доказать? (∠CAD=∠ADB)

-Как мы доказываем равенство углов? (через равенство треугольников)

-Какие треугольники содержат эти углы? (△ABD и △DCA)

-Что можно сказать про них? (они равны по 3 сторонам)

-Что еще можно сказать про эти треугольники? (соответственные элементы в них равны)

-Какие углы равны? (∠CAD=∠ADB)

-Почему они равны? (по определению равных треугольников)

-Против каких сторон лежат эти углы? (∠CAD против стороны CD, ∠ADB против стороны АВ)

-Какие еще углы равны? (∠ABC=∠DCA, ∠D=∠А)

б) -Что нужно доказать? (∠BAC=∠CDB)

-Как мы доказываем равенство углов? (через равенство треугольников)

-Какие треугольники содержат эти углы? (△ВАС и △ВDС)

-Что можно сказать про них? (они равны по 3 сторонам)

-Что еще можно сказать про эти треугольники? (соответственные элементы в них равны)

-Какие углы равны? (∠BAC=∠CDB)

-Почему они равны? (по определению равных треугольников)

-Против каких сторон лежат эти углы? (∠ВАС против стороны ВС, ∠СDB против стороны ВC)

-Какие еще углы равны? (∠ВСА=∠DВС, ∠С=∠В)

Доказательство: а) Рассмотрим △ABD и △DCA: AB=CD; BD=AC; AD-общая; △ABD = △DCA (3 признак) ⇒ ∠ADВ=∠CAD;

б) Рассмотрим △ВАС и △ВDC: AB=CD; BD=AC; ВС-общая; △ВАС = △ВDC (3 признак) ⇒ ∠BAC=∠CDB

Доказано.

- Итак, равенство треугольников может быть использовано для нахождения углов. В этом случае нужно действовать по следующей схеме:

- найти треугольники, в которых содержатся эти углы;

- доказать равенство треугольников;

- вывести равенство соответствующих углов.

- Мы рассмотрели равенство углов, перейдем к равенству треугольников через другие треугольники.

№141

Дано: △ABC и △; AD, - биссектрисы; AB=; BD=; AD=

Доказать: △ABC = △

Поиск доказательства:

-Что необходимо доказать? (△ABC = △)

-Будут ли они равны? Что известно у этих треугольников? (нет,  AB=)

-В каком признаке используется только одна сторона? (в втором признаке)

-Какие треугольники Вы можете еще назвать, и что мы можем о них сказать?  (△ABD = △)

-По какому признаку они равны? (они равны по 3 признаку)

-Какой вывод можно сделать? (∠В=∠, ∠ВAD=∠)

-Что мы еще не использовали из дано? (AD, - биссектрисы)

-Что это значит? (∠DAС=∠)

-Что теперь мы может сказать про △ABC = △? (AB=, ∠В = ∠, ∠A = =∠, эти треугольники равны)

Доказательство: 1) Рассмотрим △ABD и △: AB=; BD=; AD= ⇒ △ABD = △ (3 признак равенства) ⇒ ∠BAD=∠ (по определению равных треугольников); ∠В=∠; т.к. AD, - биссектрисы, то ∠BAС=∠.

2) Рассмотрим △ABC и △; AB=, ∠В=∠, ∠А=∠ ⇒ △ABC = △(по 1 признаку)

Доказано.

- Итак, равенство одних треугольников может быть использовано для равенства других треугольников. В этом случае нужно действовать по следующей схеме:

- доказать равенство одних треугольников, которые очевидны равны;

- вывести равенство соответствующих элементов;

-доказать равенство других треугольников.

Рассмотрим следующий вид задач, связанный с равенством треугольников. Нахождение градусной меры угла.

№168

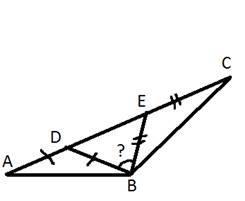
Дано: △АВС, ∠А=38°, ∠В=110°, ∠С=32°, BD=DA, BE=EC.

Найти: ∠DBE.

Поиск доказательства:

-Что мы можем сказать о треугольниках на рисунке? (△АВD, △BEC - равнобедренные)

-Что мы знаем о равнобедренных треугольниках? (углы при основании равны)

-И какие же углы будут равны? Какова будет их градусная мера? (∠A=∠ABD=38°, ∠C=∠EBC=32°)

-Какой угол еще известен? (∠В=110°)

-Из каких углов он состоит? (из суммы ∠ABD, ∠DBE, ∠CBE)

-Что необходимо нам найти? (∠DBE)

-Каким образом можно узнать градусную меру этого угла? (вычесть из ∠B углы ∠ABD и CBE)

-Какая градусная мера угла ∠DBE? (40°)

Решение: 1) △ ADB -  равнобедренный, то ∠А=∠АBD=38 ̊, △BEC – равнобедренный, то ∠С=∠EBC=32 ̊.

2) ∠B=∠ABD+∠DBE+∠CBE; 110 ̊=38 ̊+∠DBE+32 ̊, ∠DBE=110 ̊-70 ̊=40 ̊.

Ответ: 40 ̊.

- Итак, равенство треугольников может быть использовано для нахождения градусной меры углов. В этом случае нужно действовать по следующей схеме:

- определить в составе какого угла находится необходимый угол;

- узнать другие составляющие этого угла;

-с помощью простых вычислений узнать градусную меру необходимого угла.

- А также есть более сложные задачи, связанные с равенством треугольников. Комбинированные задачи.

№142

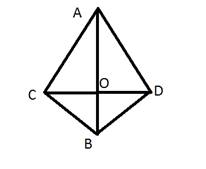
Дано: △ADC, △BCD- равнобедренные, DC-общее основание, AB пересекает CD в точке О.

Доказать: а) ∠ADB=∠ACB

                      б) DO=OC

Поиск доказательства:

а) -Что нужно доказать? (∠ADB=∠ACB)

-Как мы доказываем равенство углов? (через равенство треугольников)

-Какие треугольники содержат эти углы? (△АВС и △АDВ)

-Что можно сказать про них? (они равны по 3 сторонам)

-Что еще можно сказать про эти треугольники? (соответственные элементы в них равны)

-Какие углы равны? (∠ADB=∠ACB)

-Почему они равны? (по определению равных треугольников)

-Против каких сторон лежат эти углы? (∠ADB против стороны АО, ∠ ACB против стороны АО)

-Какие еще углы равны? (∠САВ=∠DАВ, ∠СВА=∠DBА)

б) -Что нужно доказать? (ОС=ОD)

-Как доказываем равенство отрезков? (через равенство треугольников)

-Какие треугольники содержат эти углы? (△СВО и △DВО)

-Что можно сказать про них? (они равны по 1 признаку)

-Что еще можно сказать про эти треугольники? (соответственные элементы в них равны)

-Какие стороны равны? (ОС=ОD)

-Против каких углов они лежат? (ОС против ∠СВО, ОD против ∠ОВD)

-Какие еще стороны равны? (СВ=ВD, ОВ - общая)

Доказательство: 1 способ:

а) Рассмотрим △ABC и △ABD. △ABC=△ABD по 3 признаку (AB-общая, AC=AD, BC=BD, т.к. △ADC и △BCD равнобедренные), следовательно, ∠ADB=∠ACB.

б) Т.к. ∠CAB= ∠BAD (△ABC=△ABD), AO-биссектриса равнобедренного △ACD, следовательно AO-медиана, из этого следует, что CO=OD.

Теорема доказана.

-Задача под буквой а, решается аналогично задаче 138. Для доказательства равенства отрезков, нужно действовать по следующей схеме:

- найти треугольники, в которых содержатся эти стороны;

- доказать равенство треугольников;

- вывести равенство соответствующих сторон.

2 случай обсуждается устно и идет в домашнее задание.

Рефлексивно-оценочная часть.

- Какова была цель урока? (рассмотреть, как 3 признак равенства треугольников используются при решении различных задач)

- Достигли мы её? (да)

- Как мы её достигли? (рассмотрели различные задачи на использование равенства треугольников: нахождение углов, равенство углов и комбинированные задачи)

Домашнее задание.

№139, 142(2случай)

№139

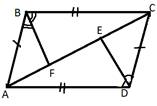
Дано: AB=CD, AD=BC, BF, DE-биссектрисы, ∠ABE=∠CBE; ∠ADF=∠CDF

Доказать: а) ∠ABF=∠ADE; б) △ABF=△CDE.

Доказательство:

a)    Рассмотрим △CDA и △ABC: AB=CD; BC=AD; сторона АС-общая ⇒ △CDA =△ABC ⇒ ∠B=∠D, тогда ∠ВАС=∠DCA, ∠ACD=∠CAD. BF, DE-биссектрисы  ⇒ ∠ABF=1/2∠ABC; ∠ADE=1/2∠ADC ⇒ ∠ABF=∠ADE.

b)   Рассмотрим △CDE и △ABF: AB=CD, ∠BAC=∠DCA, ∠ABF=∠EDC, т.к. ∠ABF=∠ADE=∠CDE ⇒ △CDE=△ABF(по второму признаку).

Доказано.

№142(2 случай)

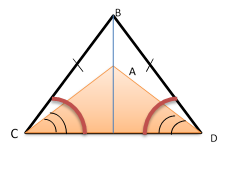Дано: △ADC, △BCD- равнобедренные, DC-общее основание, AB пересекает CD в точке О.

Доказать: а) ∠ADB=∠ACB

                      б) DO=OC

Доказательство:

а) Рассмотрим  и  : BC=AD (из условия)

                                                AC=AD (из условия)

                                               AB- общая

следовательно,    по 3 признаку  по опр. равенства треугольника

б) Рассмотрим  и  : CB=BD (из условия)

                                                 ( из а)

                                               OB- общая

следовательно,    по 1 признаку   по опр. равенства треугольника. Теорема доказана.