Методическая разработка занятия по дисциплине ПД.01 Математика на тему: Правила вычисления производных

Министерство образования и молодежной политики Чувашской Республики

Государственное автономное профессиональное

образовательное учреждение Чувашской Республики

«Чебоксарский техникум транспортных и строительных технологий»

Методическая разработка занятия по дисциплине

ПД.01Математика

На тему: «Правила вычисления производных»

Разработала:

преподаватель математики

Андреева Н.А.

Чебоксары 2021

Содержание

Пояснительная записка                                                                            3

Дидактическая структура урока                                                              4

Учебно-методическая карта урока                                                          5

Ход урока                                                                                                6

Пояснительная записка

Методическая разработка учебного занятия по дисциплине ПД.01 Математика на тему «Правила вычисления производных» с применением основных методов обучения: словесный, наглядный, проблемный, частично-поисковый, наглядно-иллюстративный.

Цель изучения данной темы: Формировать навыки вычисления производных, проверить знания и умения по вычислению производных элементарных функций, развивать логическое мышление и воображение, воспитывать активность, самостоятельность, интерес к предмету.

Описание материала: данная методическая разработка предназначена для изучения темы «Правила вычисления производных» студентами средних специальных заведений, материал будет полезен преподавателям математики в старших классах и средних специальных учебных заведений. Урок построен с применением методов проблемного и частично-поискового обучения.

Дидактическая структура урока

Цель урока: Формирование навыков вычисления производных.

Задачи урока:

1.     Образовательные: закрепить знание таблицы производных, формировать знание о правилах дифференцирования, выработать умение и навыки применять полученные знания при нахождении производной алгебраической суммы, произведения и частного;

2.     Развивающие: развивать память, мышление, самостоятельность;

3.     Воспитательные: воспитывать интерес к предмету, ответственность, настойчивость для достижения конечных результатов при нахождении производных.

Тип урока: урок усвоения новых знаний.

Методы обучения: словесный, наглядный, проблемный, частично-поисковый, наглядно-иллюстративный.

Формы обучения: фронтальная, индивидуальная.

Оборудование: учебник «Алгебра и начала математического анализа» под редакцией А.Н. Колмогоров, презентация, раздаточный материал, компьютер, проектор, экран.

Учебно-методическая карта урока

Ход урока

1.                 Организационный момент.

       Здравствуйте ребята. Садитесь. Сегодня мы с вами продолжим изучение темы «Производная» и проверим ваши знания и умения по этой теме. С каждого урока ученик должен унести хоть что-то новое: знания, умения, навыки. Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Успехов вам.

Визуальная проверка присутствующих и готовность студентов к занятию.

2.                 Актуализация опорных знаний.

На данный момент мы с вами знаем, что? (Ответ: определение производной, таблицу производных); умеем что? (Ответ: находить производные элементарных функций по таблице).

Как называется операция нахождения производной? (Ответ: дифференцированием).

При решении каких задач применяется производная? (Ответ: при решении задач на нахождении мгновенной скорости при неравномерном движении тела.)

Для закрепления таблицы производной решаем устно.

Вычислите производную функций:

Молодцы все задания выполнены верно!

3.                 Постановка цели.

Мы повторили вычисления производных элементарных функций. Как же решить задачи с более сложной функцией?

Обучающимся предлагается вычислить производные следующих функций:

Возникает проблемная ситуация (не хватает знаний для их решения). Для решения данной проблемы нам потребуется правила дифференцирования.

Значит мы сегодня должны познакомиться с правилами вычисления производных и научиться вычислять производные функций, используя их. В течения урока вы должны активно и внимательно работать. И в конце урока выполним самостоятельную работу, чтобы оценить ваши знания.

4.                 Изучения нового материала.

Запишите тему урока «Правила вычисления производных».

Рассмотрим основные правила дифференцирования без доказательств.

Правило 1. Производная суммы (разности) равна сумме(разности) производных

(u  v) ′= u′  v′

Пример: f ′(x)= (3′ = 3

Правило 2. Производная произведения равна

(u v) ′= u′v + uv′

Пример: Найдите производную функции f′(x)=((2x1)(3x+6))′=(2x1)′(3x+6)+(2x1)(3x+6)′=2(3x+6)+(2x1)3=6x+12+6x=12x+9

Следствие: Постоянный множитель можно вынести за знак производной

(kf(x))′ =k f ′(x)

Примеры:

1)f ′(x)=( 4sinx)′=

2)f ′(x)=(55

Правило 3. Производная частного (дроби) равна

Пример:

 f ′(x)= =

5.                 Закрепление изученного материала

Вернемся к тем примерам, которые рассматривали ранее. Теперь зная правила дифференцирования, как бы вы их решили?

1) 

2) 

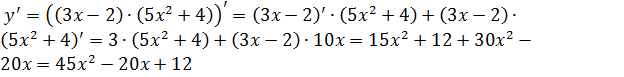
3) 

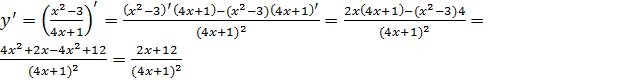
Обучающиеся выполняют упражнения из учебника с объяснением у доски:

№№ 208(а, б); 209(а, б); 210(а, б); 211(а, б)

6.                 Проверка усвоения нового материала

Самостоятельная работа по двум вариантом.

Вариант 1

Найдите производные функций:

а)

б)

в)

Вариант 2

Найдите производные функций:

а)

б)

в)

7.                 Домашнее задание

Выучить правила нахождения производных. Выполнить упражнения из учебника №№ 208(в, г); 209(в, г); 210(в, г); 211(в, г)

8.                 Подведение итогов. Рефлексия.

Преподаватель поощряет активных студентов оценками.

Посмотрите внимательно на те цели, которые мы с вами поставили для сегодняшнего урока:

Что на ваш взгляд нам удалось сделать?

Что получилось не очень хорошо?

Что вам особенно понравилось и запомнилось?

Сегодня на уроке я повторил…

Сегодня на уроке я узнал…

Сегодня на уроке я научился…