Методические рекомендации

Методические рекомендации

Цель методических рекомендаций оказать помощь студентам в подготовке и выпол-нении лабораторных работ. Лабораторные работы способствуют развитию умений экспериментального решения задач, умению сравнивать, обобщать, делать вывод по выполненной работе, а также со-ставлять отчет о проделанной работе.

Филиал бюджетного профессионального образовательного учреждения

Омской области «Сибирский профессиональный колледж» в р.п.Черлак

Методические рекомендации

проведения лабораторных работ

по учебной дисциплине

ФИЗИКА

Черлак 2019

СОГЛАСОВАНО

Заведующий учебной части

___________________

«___» _____________ 201___ г.

Рассмотрено и одобрено

на заседании методической комиссии

ЧФ БПОУ ОО «СПК» РПЧ

протокол № ______

от «___» _____________ 201___ г.

Председатель МК

____________

(подпись)

Методические рекомендации составлены в соответствии с рабочей программой учебной дисциплины «Физика»:

ОУД.11. Физика – специальности 35.02.07. Механизация сельского хозяйства;

ОУД.10. Физика – профессии 23.01.03. Автомеханик;

ПОО.01. Физика – профессии 43.01.09. Повар – кондитер;

УД.03. Естествознание (Раздел 1. Физика) профессии – 39.01.01. Социальный работник.

Цель методических рекомендаций оказать помощь студентам в подготовке и выполнении лабораторных работ.

Лабораторные работы способствуют развитию умений экспериментального решения задач, умению сравнивать, обобщать, делать вывод по выполненной работе, а также составлять отчет о проделанной работе.

Организация-разработчик: филиал бюджетного профессионального образовательного учреждения Омской области «Сибирский профессиональный колледж» в р.п.Черлак

Автор-составитель:

Карачинцев Виктор Викторович преподаватель филиала бюджетного профессионального образовательного учреждения Омской области «Сибирский профессиональный колледж» в р.п.Черлак

Рекомендована МК ЧФ БПОУ ОО «СПК» РПЧ для применения в учебном процессе.

СОДЕРЖАНИЕ

Введение…………………………………………………….…………….……......	4
1 Погрешности измерении…………………………………………………………..	5
2 Сведения о приближенных значениях……………………………………….	11
3 Методика выполнения лабораторных работ………………………………	11
3.1 Подготовка к лабораторной работе……………………………….……….	11
3.2 Сборка электрической цепи……………………………………..………..…	12
3.3 Выполнение измерений и вычислений ………………………………..….	12
3.4 Составление отчета………………………..……………………..……..…...	13
3.5 Инструкции по технике безопасности………………………………..……	14
4 Описание лабораторных работ………………………………………………..	15
Лабораторные работа №1 «Движение тела по окружности под действием силы тяжести упругости» ………………………………………………………………………...……	15
Лабораторные работа № 2 «Изучение закона сохранения механической энергии»……	16
Лабораторные работа № 3«Определение модуля упругости материала» ………………	17
Лабораторные работа № 4 «Определение ЭДС и внутреннего сопротивления источника тока» ………………………………………………………………………………….	18
Лабораторное занятие № 5 «Изучение явления электромагнитной индукции»........	20
Лабораторные работа № 6 «Измерение ускорения свободного падения с помощью математического маятник» ………………………………………………………………...	22
Лабораторные работа № 7 «Измерение показателя преломления стекла» ……………..	24
Лабораторное занятие № 8 «Измерение длины световой волны с помощью дифракционной решетки» ……………………………………………………………..…..............	26
Лабораторное занятие № 9 «Наблюдение сплошного и линейчатого спектров» ……...	29
Лабораторное занятие №10 «Изучение треков заряженных частиц по готовым фотографиям»………………………………………………………………..	30
Список использованных источников…………………………………………..........	32

ВВЕДЕНИЕ

Курс «Физика» служит основой для изучения ряда дисциплин, формирующих технологические компетенции.

Физика — наука экспериментальная, поэтому физический эксперимент является корневой структурой физического образования. Лабораторные работы проводятся с целью повторения, углубления, расширения и обобщения полученных знаний из разных тем курса физики; развития и совершенствования у учащихся экспериментальных умений; формирования у них самостоятельности при решении задач, связанных с экспериментом. Составной частью современного научного познания является эксперимент, отличающийся от наблюдения активным оперированием реальными объектами, позволяющий изолировать изучаемый объект или процесс от побочных явлений или предметов. "Задача физики - по Галилею, - придумать эксперимент, повторить его несколько раз, исключив или уменьшив влияние возмущающих факторов...". Получая в ходе проведения эксперимента числовой результат, обучающихся должен понимать, какие допущения и пренебрежения были сделаны при постановке опыта и проведении расчетов. С этой позиции он должен оценивать и сопоставлять с табличными данными полученный результат, формулировать вывод.

Описание лабораторных работ составлено по традиционному принципу с включением целей, теоретической и экспериментальной части работы с примерами записи полученных результатов в виде таблиц и графиков. Отдельно вынесены вопросы для самостоятельной проработки, приведен перечень рекомендуемой литературы. В теоретической части описания лабораторных работ сформулированы основные понятия и физические законы по теме работы, приведено обоснование и вывод рабочих формул. В экспериментальной части описания предлагается применение различных методик определения характеристик физических систем или универсальных физических постоянных, проверки физических законов.

Лабораторные работы выполняются бригадами по 2 человека.

В предлагаемом пособии дано описание 10 лабораторных работ, каждая из которых рассчитана на 2 часа занятия. Лабораторные работы проводятся в порядке изучения программного материала.

1 ПОГРЕШНОСТИ ИЗМЕРЕНИИ

Измерение- это нахождение числового значения физической величины опытным путем с помощью средств измерений (линейки, вольтметра, часы и т.д.).

Измерения могут быть прямыми и косвенными.

Прямое измерение- это нахождение числового значения физической величины непосредственно средствами измерений. Например, длину - линейкой, атмосферное давление- барометром.

Косвенное измерение- это нахождение числового значения физической величины по формуле, связывающей искомую величину с другими величинами, определяемыми прямыми измерениями. Например: сопротивление проводника определяют по формуле R=U/I, где U и I измеряются электроизмерительными приборами. Поэтому измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный. Неопределенность в измерении характеризуется погрешностью - отклонением измеренного значения физической величины от ее истинного значения.

Перечислим некоторые из причин, приводящих к появлению погрешностей.

1. Ограниченная точность изготовления средств измерения.

2. Влияние на измерение внешних условий (изменение температуры, колебание напряжения ...).

3. Действия экспериментатора (запаздывание с включением секундомера, различное положение глаза...).

4. Приближенный характер законов, используемых для нахождения измеряемых величин.

Перечисленные причины появления погрешностей неустранимы, хотя и могут быть сведены к минимуму. Для установления достоверности выводов, полученных в результате научных исследований, существуют методы оценки данных погрешностей.

2. Случайные и систематические погрешности

Погрешности, возникающие при измерениях, делятся на систематические и случайные.

Систематические погрешности- это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней.

Причины возникновения систематических погрешностей:

1) несоответствие средств измерения эталону;

2) неправильная установка измерительных приборов (наклон, неуравновешенность);

3) несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают;

4) несоответствие измеряемого объекта с предположением о его свойствах (наличие пустот и т.д).

Случайные погрешности- это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Абсолютные и относительные погрешности

Для количественной оценки качества измерений вводят понятия абсолютной и относительной погрешностей измерений.

Как уже говорилось, любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение

А_пр- DА < А_ист < А_пр+ DА

Величина DА называется абсолютной погрешностью измерения величины А. Абсолютная погрешность выражается в единицах измеряемой величины. Абсолютная погрешность равна модулю максимально возможного отклонения значения физической величины от измеренного значения. А_пр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений.

Но для оценки качества измерения необходимо определить относительную погрешность e:

e= DА/А_пр или e= (DА/А_пр)*100%. (1)

Если при измерении получена относительная погрешность более 10%, то говорят, что произведена лишь оценка измеряемой величины. В лабораториях физического практикума рекомендуется проводить измерения с относительной погрешностью до 10%. В научных лабораториях некоторые точные измерения (например определение длины световой волны), выполняются с точностью миллионных долей процента.

Погрешности средств измерений

Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки. Обычно довольствуются о допустимых инструментальных погрешностях, сообщаемых заводом изготовителем в паспорте к данному прибору. Эти допустимые погрешности регламентируются ГОСТами. Это относится и к эталонам. Обычно абсолютную инструментальную погрешность обозначают DА.

Случайные погрешности - это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Абсолютные и относительные погрешности

Как уже говорилось, любое измерение дает лишь приближенное значение физической величины, однако можно указать интервал, который содержит ее истинное значение:

А_пр- DА < А_ист < А_пр+ DА, (2)

Но для оценки качества измерения необходимо определить относительную погрешность e:

e= DА/А_пр или e= (DА/А_пр)*100%.

Если сведений о допустимой погрешности не имеется (например у линейки), то в качестве этой погрешности можно принять половину цены деления.

При взвешивании абсолютная инструментальная погрешность складывается из инструментальных погрешностей весов и гирь. В таблице приведены допустимые погрешности наиболее часто встречающихся в школьном эксперименте средств измерения.

Таблица 1 – Допустимые погрешности

Средства измерения	Предел измерения	Цена деления	Допустимая погрешность
линейка ученическая	до 50 см	1 мм	1 мм
линейка демонстрационная	100 см	1 см	0.5 см

Продолжение таблицы 1

лента измерительная	150 см	0.5 см	0.5 см
мензурка	до 250 мл	1 мл	1 мл
гири 10,20, 50 мг			1 мг
гири 100,200 мг			2 мг
гири 500 мг			3 мг
гири 1 г			4 мг
гири 2 г			6 мг
гири 5 г			8 мг
гири 10 г			12 мг
гири 20 г			20 мг
гири 50 г			30 мг
гири 100 г			40 мг
штангенциркуль	150 мм	0.1 мм	0.05 мм
микрометр	25 мм	0.01 мм	0.005 мм
динамометр	4 Н	0.1 Н	0.05 Н
весы учебные	200 г		0.1 г
Секундомер	0-30 мин	0.2 с	1с за 30 мин
барометр-анероид	720-780 мм рт.ст.	1 мм рт.ст	3 мм рт.ст
термометр лабораторный	0-100 градусов С	1 градус	1 градус
амперметр школьный	2 А	0.1 А	0.08 А
вольтметр школьный	6 В	0.2 В	0.16 В

Класс точности электроизмерительных приборов

Стрелочные электроизмерительные приборы по допустимым значениям погрешностям делятся на классы точности, которые обозначены на шкалах приборов числами 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности g _пр прибора показывает, сколько процентов составляет абсолютная погрешность от всей шкалы прибора:

g _пр= (D_иА/А_макс)*100% . (2)

Например абсолютная инструментальная погрешность прибора класса 2,5 составляет 2,5% от его шкалы.

Если известен класс точности прибора и его шкала, то можно определить абсолютную инструментальную погрешность измерения

DА = ( g _пр* А_макс)/100. (3)

Для повышения точности измерения стрелочным электроизмерительным прибором надо выбирать прибор с такой шкалой, чтобы в процессе измерения располагались во второй половине шкалы прибора.

Погрешность отсчета

Погрешность отсчета получается от недостаточно точного отсчитывания показаний средств измерений.

В большинстве случаев абсолютную погрешность отсчета принимают равной половине цены деления. Исключения составляют измерения стрелочными часами (стрелки передвигаются рывками).

Абсолютную погрешность отсчета принято обозначать DА

Полная абсолютная погрешность прямых измерений

При выполнении прямых измерений физической величины А нужно оценивать следующие погрешности: D иА, D оА и D сА (случайную). Конечно, иные источники ошибок, связанные с неправильной установкой приборов, несовмещение начального положения стрелки прибора с 0 и пр. должны быть исключены.

Полная абсолютная погрешность прямого измерения должна включать в себя все три вида погрешностей.

Если случайная погрешность мала по сравнению с наименьшим значением, которое может быть измерено данным средством измерения (по сравнению с ценой деления), то ее можно пренебречь и тогда для определения значения физической величины достаточно одного измерения. В противном случае теория вероятностей рекомендует находить результат измерения как среднее арифметическое значение результатов всей серии многократных измерений, погрешность результата вычислять методом математической статистики. Знание этих методов выходит за пределы школьной программы.

Запись окончательного результата прямого измерения

Окончательный результат измерения физической величины А следует записывать в такой форме

А=А_пр+ D А, e= (DА/А_пр)*100%. (4)

А_пр- значение физической величины, полученное экспериментально, если измерение проводилось многократно, то среднее арифметическое этих измерений. D А- полная абсолютная погрешность прямого измерения.

Абсолютную погрешность обычно выражают одной значащей цифрой.

Пример: L=(7,9 + 0,1) мм, e=13%. (9)

Погрешности косвенных измерений

При обработке результатов косвенных измерений физической величины, связанной функционально с физическими величинами А, В и С, которые измеряются прямым способом, сначала определяют относительную погрешность косвенного измерения e= DХ/Х_пр, пользуясь формулами, приведенными в таблице (без доказательств).

Абсолютную погрешность определяется по формуле DХ=Х_пр *e,

где e выражается десятичной дробью, а не в процентах.

Окончательный результат записывается так же, как и в случае прямых измерений.

Таблица 2 – Погрешность косвенных измерений

Вид функции

Формула

Х=А+В+С

Х=А-В

Х=А*В*С

Х=Аⁿ

Х=А/В

Х=

2 СВЕДЕНИЯ О ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЯХ

При работе с приближенными числами необходимо соблюдать следующие правила:

1. При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в числе с наименьшим количеством десятичных знаков.

Пример: 1,82 + 14, 368 3 + 5,8 = 1,82 + 14,37 + 5,8 = 22,0. (6)

2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их в приближенном числе с наименьшим количеством значащих цифр.

Примеры: 83 973 ∙ 0,4 = 84 ∙10³ ∙ 0,4 = 33,6 ∙ 10³ = 3 ∙10⁴. (7)

3. При возведении в квадрат и клуб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближенное число.

Примеры: 1,32² = 1,74; 3,6³ = 46. (8)

4. При извлечении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их в подкоренном приближенном числе.

Примеры: = 1,89 ∙ 10^-4; = 1,61. (9)

5. При вычислении промежуточных результатов следует брать на одну цифру больше, чем рекомендуют правила. В окончательном результате эта "запасная" цифра отбрасывается.

6.
Пример: (10)

3 МЕТОДИКА ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ

3.1 ПОДГОТОВКА К ЛАБОРАТОРНЫМ РАБОТАМ

Подготовка к проведению лабораторных работ начинается в начале теоретического изложения изучаемой темы на уроках физики и продолжается по ходу её изучения при освоении материала на занятиях в техникуме и работе над ним в ходе самостоятельной подготовки дома и в библиотеках. Для качественного выполнения лабораторных работ студентам необходимо:

1) повторить теоретический материал по конспекту и учебникам;

2) ознакомиться с описанием лабораторной работы;

3) в специальной рабочей тетради записать название и номер работы, перечень необходимого оборудования, подготовить схему или зарисовку установки, таблицы для записи результатов измерений и вычислений, подготовить миллиметровую бумагу и графический масштаб для построения графиков;

4) выяснить цель работы, четко представить себе поставленную задачу и способы её достижения, продумать ожидаемые результаты опытов;

5) ответить устно или письменно на контрольные вопросы по изучаемой теме или решить ряд задач;

6) изучить порядок выполнения лабораторной работы. Подготовить лабораторное оборудование к работе, если нужно собрать электрическую схему. После проверки правильности собранной схемы преподавателем можно начинать выполнение лабораторной работы.

3.2 СБОРКА ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

При сборке электрических цепей требуется придерживаться следующих правил:

1) Проводить сборку цепи при отключенном источнике напряжения;

2) Вначале собирается последовательная цепь, а затем к ней присоединяются параллельные участки;

3) Сборку цепи начинают с "+" источника, а заканчивают на источнике напряжения;

4) При сборке цепей постоянного тока необходимо соблюдать полярность включения электроизмерительных приборов. "+" приборов необходимо подключать к "+" источника, а "-" приборов к "–" источника.

5) При выполнении лабораторных работ необходимо соблюдать правила техники безопасности, быть аккуратным, бережно относиться к оборудованию и приборам.

3.3 ВЫПОЛНЕНИЕ ИЗМЕРЕНИЙ И ВЫЧИСЛЕНИЙ

1) Выполните лабораторную работу. При этом будьте внимательны при снятии показаний измерительных приборов. Старайтесь снять показания точнее, без излишне грубого округления. Результаты измерений занесите в таблицу.

2) Проведите вычисления искомых величин. При этом не нужно оставлять лишние цифры после запятой. Например, если U=12,3В и I=0,53А, то R=U/I=12,3B/0,53A=23,20754 Ом. Нет никакого смысла в результате вычисления сопротивления оставлять после запятой 5 знаков. Так как напряжение измерено с точностью до десятых долей вольта, то результат измерения сопротивления не будет превосходить эту точность. Точность измерения сопротивления будет ниже, чем точность измерения напряжения, поэтому в качестве ответа необходимо оставить R=23,2 Ом.

3) При вычислении относительной погрешности измерения, если δx < 10%, то результаты хорошие, δx < 20% - удовлетворительные и δx >20% - неудовлетворительные.

4) При вычислении абсолютной и относительной погрешностей необходимо знать правила округления:

4.1. В результате оставить одну значащую цифру, если число начинается с цифр 4,5,6,7,8,9

4.2. В результате оставить две значащие цифры, если число начинается с цифр 1,2,3 Например: δx =12,3%. Применяя правила округления, в качестве ответа запишем: δx =12%. Если δx=43,1%, то ответ будет δx =40%

5) При построении графиков необходимо выяснить функциональную зависимость. Аргумент (независимая переменная) откладывается по горизонтальной оси, а функция – по вертикальной. Необходимо правильно выбрать масштаб по осям координат. Масштаб не должен быть слишком большим или слишком малым. В противном случае график будет или очень маленьким, или очень большим. По осям координат откладываются не произвольные числа, а числа кратные (1,2,3,4,5)*10 , где К=0,1,2,…

6) Сделать выводы по лабораторной работе.

3.4 СОСТАВЛЕНИЕ ОТЧЕТА

Составление отчета - индивидуальная работа студента. Отчет является документом о проделанном эксперименте, поэтому в нем должны быть приведены все необходимые сведения для проверки результатов опытов и расчетов. Страницы отчета должны быть оформлены в соответствии с ГОСТ.

Также в отчет должны входить:

· цель работы;

· теория;

· оборудование;

· схема опыта, если она приводится;

· таблицы данных;

· применяемые формулы и расчеты по ним;

· графики зависимости при требовании в порядке выполнения работы;

· выводы по результатам измерений и вычислений;

· ответы на контрольные вопросы или решения задач.

Схемы, таблицы, графики и другие построения выполняются только черным карандашом (тушью), чертежными инструментами. При выполнении схем должны соблюдаться стандартные обозначения (ГОСТы) указываемых элементов. Исправления и помарки в отчете не допускаются.

При выполнении всех вышеуказанных требований выполненная работа зачитывается преподавателем автоматически, в противном случае зачет производится по результатам собеседования с преподавателем.

3.5 ИНСТРУКЦИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ

Общие требования безопасности

· Перед началом выполнения лабораторных работ по физике преподаватель проводит инструктаж по технике безопасности.

· Студенты допускаются к выполнению лабораторных работ по физике при личной записи об ознакомлении и росписи в "Журнале по технике безопасности".

· В случае появления дыма, специфического запаха горелой изоляции, студент должен выключить установку и немедленно сообщить о произошедшем преподавателю.

Основные правила техники безопасности

· Не держите на рабочем месте предметы, не требующиеся при выполнении задания.

· Перед тем как приступить к выполнению работы, тщательно изучите её описания, уясните ход её выполнения.

· Произведите сборку электрических цепей, переключения в них, монтаж и ремонт электрических устройств только при отключении источника питания. Запрещается подключать к электрической сети 220В приборы и оборудование без разрешения преподавателя.

· Следите, чтобы изоляция проводов была исправна, а на концах проводов были наконечники.

· При сборке электрической цепи, провода располагайте аккуратно, а наконечники плотно зажимайте клеммами.

· Выполняйте наблюдения и измерения, соблюдая осторожность, чтобы случайно не прикоснуться к оголённым проводам (токоведущим частям, находящимся под напряжением).

· По окончании работы отключите источник электропитания, после чего разберите электрическую цепь.

· Обнаружив неисправность в электрических устройствах, находящихся под напряжением, немедленно отключите источник электропитания и сообщите об этом преподавателю.

ЛАБОРАТОРНАЯ РАБОТА №1

Изучение движения тела по окружности

под действием силы тяжести и упругости

Цель: определить центростремительное ускорение шарика при его равномерном движении по окружности.

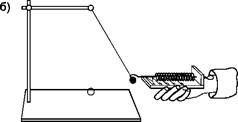
Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, лист бумаги, линейка, пробка.

Рисунок 1 - Шарик на нити

ХОД РАБОТЫ

1. Определите массу шарика на весах с точностью до 1 г.

2. Шарик, подвешенный на нити, закрепите в лапке штатива, используя кусок пробки.

3. Вычертите на листе бумаги окружность радиусом 20 см.

4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.

5. Взяв нить пальцами у точки подвеса, приведите маятник во вращательное движение над листом бумаги так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.

6. Измерьте время 20 полных оборотов маятника.

7. Рассчитайте период обращения маятника по формуле: T = t/N, (1.1)

8. Рассчитайте значение центростремительного ускорения. Определите высоту конического маятника. Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса.

9. Рассчитайте значение центростремительного ускорения а = gR / h (1.2)

10. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль равнодействующей силы.

11. Используя второй закон Ньютона , рассчитайте значение центростремительного ускорения. F= m а. (1.3)

13. Результаты измерений и вычислений занесите в таблицу:

Таблица 1.1 – Результаты измерений и вычислений

Номер

опыта

кг

а_п = 4n²R/ T²,

м/с²

а_п = gR / h,

м/с²

а_п = F /m,

м/с²

ВЫВОД: (сравните полученные три значения модуля центростремительного ускорения, объясните полученный результат)

ЛАБОРАТОРНАЯ РАБОТА №2

Изучение закона сохранения механической энергии

Цель: научиться измерять потенциальную энергию поднятого над землей тела и упругодеформированной пружины, сравнивать два значения потенциальной энергии системы.

Оборудование: штатив с муфтой и лапкой, динамометр лабораторный с фиксатором, лента измерительная, груз на нити длиной около 25 см.

Подготовительные вопросы:

1. Определение, обозначение, направление, единицы измерения силы тяжести в СИ

2. Определение, обозначение, направление, единицы измерения силы упругости в СИ

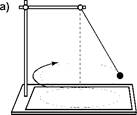
3. Сформулируйте закон сохранения механической энергииПривяжите груз к нити, другой конец нити привяжите к крючку динамометра и измерьте вес груза F₁= mg (можно использовать массу груза, если она известна).

4. Измерьте расстояние l от крючка динамометра до центра тяжести груза.

5. Поднимите груз до высоты крючка динамометра и отпустите его. Поднимая груз, расслабьте пружину и укрепите фиксатор около ограничительной скобы.

6. Снимите груз и по положению фиксатора измерьте линейкой максимальное удлинение пружины D l.

7. Растяните рукой пружину до соприкосновения фиксатора с ограничительной скобой и отсчитайте по шкале максимальное значение модуля силы упругости пружины. Среднее значение силы упругости равно F.

8. Найдите высоту падения груза: h = l + D l. (2.1)

Таблица 2.1 - Результаты измерений и вычислений

F₁= mg	l, м	D l, м	F. Н	h = l + D l	E_p = F₁(l + D l).	E_p= F ^.D l/2

9. Вычислите потенциальную энергию системы в первом положении груза, т.е. перед началом падения, приняв за нулевой уровень значение потенциальной энергии груза в конечном его положении: Ep ⁷ = mgh = F₁(l + А l).

10. В конечном положении груза его потенциальная энергия равна нулю. Потенциальная энергия системы в этом состоянии определяется лишь энергией упруго деформированной пружины:

Вычислите ее. Результаты измерений и вычислений внесите в таблицу:

ВЫВОД: (сравните значения потенциальной энергии в первом и во втором состояниях системы)

ЛАБОРАТОРНАЯ РАБОТА №3

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА

Один из способов измерения модуля упругости основан на использовании закона Гука Проще всего измерить модуль упругости резины, так как она испытывает значительные деформации при небольших нагрузках.

Приборы и материалы: разновес, линейка измерительная с миллиметровыми делениями или штангенциркуль, штатив, резиновый образец длиной около 40 см.

Ход работы

1. Измерить толщину b и ширину a сторон образца с прямоугольным сечением или диаметр образца d с круглым сечением.

2. Подвесить образец за один конец на штативе.

3. Нанести на среднем участке образца карандашом две тонкие метки на расстоянии 30 см друг от друга.

4. Измерить начальное расстояние между метками.

5. Прикрепить к нижнему концу резинового образца гирю. Записать массу m и измерить расстояние l между метками. Опыт повторить со второй и третьей гирями.

6. Результаты измерений занести в таблицу.

Таблица 3.1 -

№ п/п	Начальное расстояние между метками недеформированного образца l_o, м	Размеры сечения		Масса гирь m, кг	Расстояние между метками деформи-рованного образца l_,м	Абсолютное удлинение Ál части образца между метками Ál , м	Площадь сечения образца в недеформи-рованном состоянии *S_o=аЬ***, м²
№ п/п		a, м	b, м	Масса гирь m, кг	Расстояние между метками деформи-рованного образца l_,м	Абсолютное удлинение Ál части образца между метками Ál , м
1
2
3

7. Рассчитать площадь сечения S образца в деформированном состоянии, исходя из того, что объем резины увеличивается незначительно и при малых деформациях:

(3.1)

8. Вычислить модуль упругости резины сравнить, полученный результат табличными данными и сделать вывод

(3.2)

Оценка погрешностей измерения модуля упругости резины в данной работе не производится потому, что относительная деформация резины зависит от времени действия силы, вызывающей деформацию образца. Кроме того, весьма приблизителен способ измерения размеров сечения, которое различно в разных местах образца.

ЛАБОРАТОРНАЯ РАБОТА № 4

ОПРЕДЕЛЕНИЕ ЭДС И ВНУТРЕННЕГО СОПРОТИВЛЕНИЯ

ИСТОЧНИКА ТОКА.

Цель работы: научиться определять ЭДС и внутреннее сопротивление источника тока.

Оборудование

1.Источник постоянного напряжения

2. Реостат.

3. Амперметр.

4. Вольтметр.

5. Ключ.

6. Соединительные провода.

Теория

Для поддержания тока в проводнике необходимо, чтобы разность потенциалов (напряжение) на его концах была неизменной. Для этого используется источник тока. Разность потенциалов на его полюсах образуется вследствие разделения зарядов на положительные и отрицательные внутри источника тока. Работу по разделению зарядов выполняют сторонние силы(силы не электрического происхождения: сила Лоренца, силы химической природы). Величина, измеряемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда внутри источника тока, называется электродвижущей силой источника тока(ЭДС)

Е=А/q (4.1)

Единица измерения ЭДС вольт (В). 1В - это ЭДС такого источников в котором для перемещения(разделения)заряда 1Кл сторонние силы совершают работу 1Дж. Когда цепь замкнута, то разделенные в источнике тока заряды образуют электрическое поле которое перемещает заряды во внешней цепи. Внутри источника тока заряды движутся навстречу электрическому полю под действием сторонних сил. Таким образом, энергия, запасенная в источнике тока, расходуется на работу по перемещению заряда во внешней и внутренней цепях с сопротивлениями R и г.

Е=ІR+Іг =U_вн+Іг (4.2)

Из последнего выражения следует, что если сила тока в цепи равна нулю (цепь разомкнута), то Е= U _вн.., т.е. ЭДС источника равна напряжению на полюсах разомкнутого источника тока. Зная ЭДС источника тока, напряжение на внешнем участке при замкнутой цепи и ЭДС источника, можно найти внутреннее сопротивление источника тока

г= (Е-U _вн.)/І (4.3)

Порядок выполнения работы

1. Собрать электрическую цепь

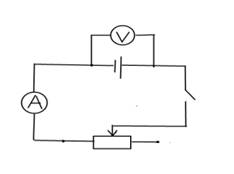
Рисунок 4.1.- Схема

2. Измерить напряжение на полюсах источника тока при разомкнутом ключе К. Это напряжение равно ЭДС источника тока Е.

3. Замкнуть ключ К и измерить напряжение С и силу тока I в цепи при трех различных сопротивлениях реостата.

4. Результаты занести в таблицу 4.1.

Таблица 4.1

№	Е (В)	U_вн. (В)	І (А)	г (Ом)
1
2
3

5. Найти среднее значение г_ср =(r ₁+ r ₂+ r ₃)/3. (4.4)

6.Найти абсолютные погрешности измерения каждого сопротивления г.

7.Найти относительную погрешность для каждого измерения.

8. Сделать вывод о проделанной работе.

Контрольные вопросы

Вариант 1

1. Что такое ЭДС источника тока?

2. ЭДС источника тока 1В.Что это означает?

3. Какие силы совершают работу по перемещению зарядов во внутренней цепи? Назовите эти силы.

4. Для перемещения заряда 5 Кл внутри источника тока совершается работа 10 Дж.
Чему равна ЭДС источника?.

5. Два источника тока соединяются последовательно. Для перемещения заряда 2Кл
внутри источников совершается работа 2 и 4 Дж. Найти ЭДС этой батареи.

Вариант 2

1. Что такое напряжение?

2. Напряжение на участке цепи 1В. Что это означает?

3. Какие силы перемещают заряды во внешней цепи?

4. Для перемещения заряда 1 Кл во внешней цепи совершается работа 20 Дж. Чему равно напряжение на этом участке?

Два резистора соединяются последовательно .Для перемещения заряда 5Кл по этим резисторам совершается работа 5 и 10 Дж. Найти напряжение на концах этих резисторов

ЛАБОРАТОРНАЯ РАБОТА № 5

ИЗУЧЕНИЕ ЯВЛЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Цель работы

Практически на примерах опытов Фарадея изучить явление электромагнитной индукции.

Теория

Явление электромагнитной индукции было открыто М. Фарадеем в 1831 году. Электромагнитная индукция - явление возникновения индукционного тока в замкнутой цепи при изменении магнитного потока сквозь этот контур.

Закон электромагнитной индукции : Э.Д.С индукции ε _инд в замкнутом контуре равна скорости изменения магнитного потока Ф через поверхность, ограниченную контуром.

ε _инд = - Δ Ф / Δ t или ε _инд = - Ф '(t) - Для контура; (5.1)

ε_инд ⁼ - Δ Ψ/ Δ t или ε_инд = - Ψ '(t) - для катушки, (5.2)

где Ψ = ωФ - потокосцепление ( Вб ) (ω - число витков катушки).

Знак минус в формулах показывает, что индукционный ток всегда имеет такое направление, чтобы своим магнитным полем препятствовать изменению внешнего магнитного поля. Этот вывод носит название правила Ленца. Э.Д.С индукции, возникающей при движении проводника в магнитном поле, пропорциональна индукции В магнитного поля, скорости движения ν проводника, его длине ℓ и синусу угла α , образованного векторами В и ν.

ε_инд=Вνℓsinα (5.3)

Для определения направления индукционного тока при движении проводника в магнитном поле пользуются правилом правой руки : правую руку располагают так, чтобы линии магнитной индукции входили в ладонь, а большой отогнутый палец показывал направление движения проводника. Тогда четыре вытянутых пальца укажут направление индукционного тока.

Порядок выполнения работы

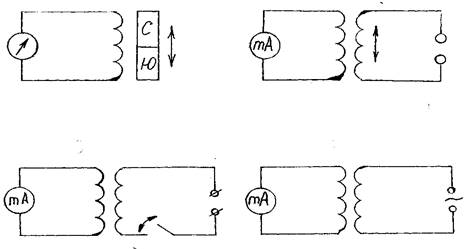
Опыт 1

1. Присоединить зажимы гальванометра к зажимам катушки.

2. Внести полосовой магнит внутрь катушки, наблюдая одновременно за стрелкой гальванометра.

3. Повторить наблюдение, выдвигая сердечник из катушки, а также меняя полюса магнита.

4. Зарисовать схему опыта 1 и проверить выполнение правила Ленца в каждом случае.

Опыт 2

1. Присоединить первую катушку к источнику постоянного тока 6,3 В, через выключатель.

2. Присоединить вторую катушку к миллиамперметру.

3. Ввести вторую катушку в первую, наблюдая за стрелкой миллиамперметра.

4. Повторить наблюдение, выдвигая катушку.

5. Зарисовать схему опыта 2 и проверить выполнение правила Ленца в каждом случае.

Опыт 3

1. Вставить вторую катушку в первую.

2. Замыкая и размыкая ключ, наблюдать отклонение стрелки миллиамперметра.

3.Зарисовать схему опыта 3 и проверить выполнение правила Ленца.
Опыт 4

1. Присоединить первую катушку к источнику переменного тока 6,3 В.

2. Присоединить вторую катушку к миллиамперметру для переменного тока.

3. Включить первую катушку и пронаблюдать отклонение стрелки миллиамперметра.

4. Зарисовать схему опыта 4.

Рисунок 5.1 - Схемы

Контрольные вопросы

Вариант 1

1. Одинаковую ли работу нужно совершить для того, чтобы вставить магнит в катушку, когда ее обмотка замкнута и когда разомкнута?

2. Всегда ли при изменении потока магнитной индукции в проводящем контуре в нем возникает э.д.с.

3.Замкнутое кольцо движется в однородном магнитном поле поступательно: вдоль линий магнитной индукции; перпендикулярно к ним. Возникнет ли в кольце индукционный ток?

4.Как надо перемещать в магнитном поле Земли замкнутый проволочный прямоугольник, чтобы в нем наводился ток?

5.Верно ли утверждение, что электромагнит не действует на медную пластинку?

Вариант 2

1. Два одинаковых магнита одновременно начинают падать с одной и той же высоты через закрепленные проводящие кольца. Первый - через замкнутое кольцо, второй - через разомкнутое. Какой магнит упадет раньше? Почему?

2. Проводящий контур движется поступательно в магнитном поле: однородном; неоднородном. Возникает ли э.д.с. индукции в этих случаях?

3. Всегда ли при изменении магнитной индукции в проводящем контуре, расположенном перпендикулярно к линиям магнитной индукции, в нем возникает э.д.с. индукции? индукционный ток?

4. Почему для обнаружения индукционного тока замкнутый проводник лучше брать в виде катушки, а не в виде прямолинейного провода?

5. Усовершенствованные телефонные (радио) наушники используют как телефон и как микрофон. Объясните действие радионаушника в качестве микрофона.

ЛАБОРАТОРНАЯ РАБОТА №6

ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Цель: вычислить ускорение свободного падения при помощи математического маятника.

Оборудование:

1. Часы с секундной стрелкой.

2. Измерительная лента.

3. Шарик с отверстием.

4. Нить.

5. Штатив с муфтой и кольцом.

Теория:

Как известно, гравитационное поле Земли в любой точке ее поверхности характеризуется ускорением свободного падения g. Ускорение свободного падения можно определить экспериментально с помощью математического маятника. Математическим маятником называют материальную точку массой m, подвешенную на невесомой, нерастяжимой нити и совершающей гармонические колебания в вертикальной плоскости. Период колебаний математического маятника выражается следующей формулой:

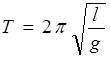, (6.1)

где –длина подвеса, g-ускорение свободного падения, T – период малых колебаний маятника. Из формулы (1) можно вычислить ускорение свободного падения:

. (6.2)

Из формулы (2) видно, что для определения ускорения свободного падения необходимо знать длину подвеса и период малых колебаний маятника. Длина может быть измерена непосредственно с помощью линейки (мерной ленты).

Порядок выполнения работы

1. Установите на краю стола штатив. У верхнего конца укрепите при помощи муфты кольцо и подвесьте к нему шарик на нити. Шарик должен висеть на расстоянии 3–5 см от пола.

2. Отклоните маятник от положения равновесия на 5–8 см и отпустите его.

3. Измерьте длину подвеса мерной лентой.

4. Измерьте время Δt 40 полных колебаний (N).

5. Повторите измерения Δt (не изменяя условий опыта) и найдите среднее значение Δt_ср

6. Вычислите среднее значение периода колебаний Т_ср по среднему значению Δt_ср.

7. Вычислите значение g_ср по формуле:

(6.3)

8. Полученные результаты занесите в таблицу 6.1:

Таблица 6.1

9. Сравните полученное среднее значение для g _срсо значением g =9.8м/с² и рассчитайте относительную погрешность измерения по формуле:

ε_g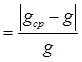 (6.4)

Контрольные вопросы

Вариант 1

1. Что называется математическим маятником?.

2. Что называется механическим колебанием?.

3. Чтобы помочь шоферу вытащить автомобиль, застрявший в грязи, несколько человек

раскачивают автомобиль, причем толчки, как правило, производятся по команде. Важно ли, через какие промежутки времени подавать команду?.

4. Математический маятник за 10 с совершил 20 полных колебаний. Найти период колебаний.

5. Во сколько раз изменится частота колебаний математического маятника при увеличении длины нити в 3 раза?.

Вариант 2

1. Какие колебания называют вынужденными?.

2. Что называют резонансом?.

3. Спортсмен раскачивается при прыжках на батуте со строго определенной частотой. От чего зависит эта частота?.

4. Частота колебаний крыльев комара 600 Гц, а период колебаний крыльев шмеля 5 мс. Какое из насекомых сделает при полете больше взмахов крыльями за 1 мин и на сколько?.

5. Как относятся длины математических маятников, если за одно и то же время один

совершает 10, а второй 30 колебаний? .

ЛАБОРАТОРНАЯ РАБОТА № 7

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА

Цель работы: научиться на практике рассчитывать показатель преломления стекла.

Оборудование

1. Стеклянная пластинка с двумя параллельными гранями.

2. Транспортир.

3. Линейка.

4. Два цветных карандаша.

5. Таблица синусов.

Теория

Изменение скорости и направления распространения света на границе раздела двух прозрачных сред различной оптической плотности называют преломлением света. При этом свет меняет свое направление. Преломление света подчиняется следующим законам'.

Отношение синуса угла падения α к синусу угла преломления β есть величина постоянная для двух данных сред и называется относительным показателем преломления второй среды относительно первой:

n = sin α / sin β. (7.1)

Луч падающий и луч преломленный, а также перпендикуляр, проведенный через точку падения луча к границе двух сред, лежат в одной плоскости.

Порядок выполнения работы

1. На листе тетради провести две параллельные линии разного цвета на расстоянии 0,5-1,5 см друг от друга.

2. Положить на эти линии плоскопараллельную пластинку так, чтобы линии входили в одну из параллельных граней.

3. Поворачивать пластинку так, чтобы начало одной цветной линии совпало с продолжением линии другого цвета.

4. Обвести параллельные грани пластинки, это и будет граница раздела двух сред в соответствии с рисунком 7.1.

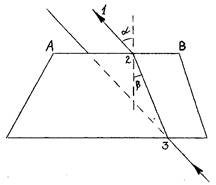
Рисунок 7.1 – Построение преломления света

5. Снять пластинку с листа бумаги, прочертить ход преломленного луча в пластинке.

6. Провести перпендикуляр к границе раздела двух сред «воздух-стекло» через точку падения светового луча (к одной из параллельных граней).

7. Отметить и измерить транспортиром угол падения светового луча.

8. Отметить и измерить транспортиром угол преломления светового луча.

9. По формуле (1) вычислить показатель преломления стекла.

10. Всего проделать 3 таких опыта, меняя расстояния между двумя разноцветными линиями.

11. Рассчитать абсолютную погрешность вычислений для каждого опыта

Δn= | n_табл-n| , где для стекла n_табл⁼ 1,5

12. Рассчитать относительную погрешность вычислений для каждого опыта.

δn= Δn ^.100% /n_табл(7.2)

13. Результаты измерений и вычислений записать в отчет по лабораторной работе.

Контрольные вопросы

Вариант 1

1. Чем отличается относительный показатель преломления от абсолютного показа
теля?

2. На чем основано явление рефракции в атмосфере⁷

3. Почему, сидя у костра, мы видим предметы по другую сторону костра колеблю
щимися?

4. Показатель преломления алмаза 2,4. Чему равна скорость света в алмазе?

5. Почему изменяется направление луча света при его переходе из одной прозрачной
среды в другую?

Вариант 2

1. В чем сущность явления преломления света и какова причина этого явления?

2. В каких случаях свет на границе раздела двух прозрачных сред не преломляется?

3. Покажите на чертеже ход луча и стекла в воду?

4. Что можно сказать о длине и частоте светового луча при переходе его из воздуха в алмаз?

5. Показатель преломления воды 1,33. Чему равна скорость света в воде

ЛАБОРАТОРНАЯ РАБОТА № 8

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ

ДИФРАКЦИОННОЙ РЕШЕТКИ

Цель работы: экспериментально определить длину световой волны.

Оборудование

1. Прибор для определения длины световой волны.

2. Дифракционная решетка.

3. Люминесцентная лампа.

Теория

Часть 1

Параллельный пучок света, проходя через дифракционную решетку, вследствие дифракции на решетке, распространяется по всевозможным направлениям и интерферирует. На экране, установленном на пути интерферирующего света, можно наблюдать интерференционную картину. Максимумы света наблюдаются в точках экрана, для которых выполняется условие-

∆=nλ, (8.1)

где ∆ - оптическая разность хода волн; λ - длина световой волны; n-номер максимума. Центральный максимум называют нулевым; для него ∆=0. Слева и справа от него располагаются максимумы высших порядков. Условие возникновения максимума (1) можно записать иначе:

nλ= dsin (8.2)

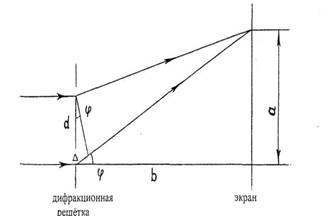
Рисунок 8.1 – Дифракционная решетка

На рисунке 8.1 - d-период дифракционной решётки; - угол, под которым виден световой максимум (угол дифракции). Так как углы дифракции, как правило, малы, то для них можно принять sin = tg , a tg = a/b (рис. 1). Поэтому

n λ = d a / b (8.3)

λ = d a / n b (8.4)

В данной работе эту формулу используют для вычисления длины световой волны.

Часть 2

Анализ формулы показывает, что положение световых максимумов зависит от длины волны монохроматического света: чем больше длина волны, тем дальше максимум от нулевого. Белый свет по составу - сложный.. Нулевой максимум для него белая полоса, а максимумы высших порядков представляют собой набор семи цветных полос, совокупность которых называют спектром соответственно 1,2... порядка показано на рисунке 8.2.

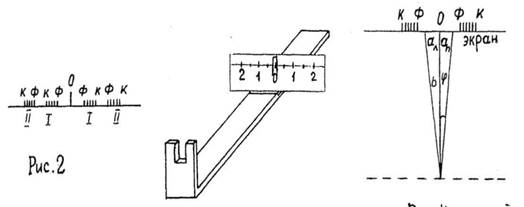
Рисунок 8.2 - Прибор для определения длины световой волны

Получить дифракционный спектр можно, используя прибор для определения длины световой волны показан на рисунке 8.2. Прибор состоит из бруска 1 со шкалой 2 (по ней определяется расстояние Ь). Вдоль бруска в боковых пазах его может перемещаться ползунок 3 с экраном 4 (по нему определяется расстояние а). К концу бруска прикреплена рамка 5, в которую вставляют дифракционную решетку.

Порядок выполнения работы

1. Направить щель экрана на окно (люминесцентную лампу).

2. Смотря через дифракционную решетку на экран, направить прибор на источник света.

3. Перемещением экрана со шкалой по продольной линейке добиться четкого изображения на экране спектров 1 и 2 -го порядка (Наилучшее расстояние b для получения точных результатов для данного прибора в пределах 10-20 см).

4. Определить расстояние от нулевого деления шкалы экрана до середины полоски нужного цвета (расстояние а).

5. Измерить расстояние от решетки до экрана (b).

6. Опыт повторить 3 раза со спектрами 1 и 2-го порядка (по индивидуальному заданию преподавателя).

7. По формуле (8.4) вычислить λ.

8. Выбрав табличное значение волны из таблицы 8.1, во всех 3 опытах рассчитать абсолютную погрешность измерений по формуле: ∆ λ= | - λ| (8.4).

Таблица 1

Цвет	Границы, нм	Цвет	Границы, нм
Фиолетовый	380-450	Желто-зеленый	550-575
Синий	450-480	Желтый	575-585
Голубой	480-510	Оранжевый	585-620
Зеленый	510-550	Красный	620-760

9. Определить относительную погрешность измерений: λ = ∆ λ* 100% . (8.5)

10. Результаты измерений и вычислений занести в таблицу 8.2.

Таблица 2

№	d(м)	N	а (м)	b (м)	λ (м)	λ (%)	Цвет
1
2'
3

Контрольные вопросы

Вариант 1

1. Почему нулевой максимум дифракционного спектра белого света - белая полоса, а максимумы высших порядков - набор цветных полос?

2. Какова природа световых волн и звуковых волн?

3. Имеем графическое изображение красной, фиолетовой и желтой световой волны смотрите рисунок 8.2. Какой график, какой волне принадлежит?

Рисунок 8.2 - График изображения световых волн

Вариант 2

1.Какой вид имеет интерференционная картина в случае монохроматического света?

2.Частота 7,5 * 10¹⁴ Гц. Какому цвету соответствует эта частота?

3.Почему стоя за колонной в театре, мы слышим певца, но не видим его?

ЛАБОРАТОРНАЯ РАБОТА № 9

Наблюдение сплошного и линейчатых спектров

Цель: наблюдение сплошного спектра, выделение основных цветов спектра; наблюдать линейчатые спектры водорода, гелия и неона и выделение наиболее ярких линий спектров.

Оборудование: проекционный аппарат; спектральные трубки с водородом, неоном или гелием; высоковольтный индуктор; источник питания; штатив; соединительные провода, стеклянная пластина со скошенными гранями.

Подготовительные вопросы:

1. Какие виды спектров вы знаете?

2. В чём состоит главное отличие линейчатых спектров от непрерывных?

3. В чём состоит главное отличие линейчатых спектров от полосатых?

ХОД РАБОТЫ

1. Расположить пластину горизонтально перед глазом. Сквозь грани, составляющие угол 45°, наблюдать светлую вертикальную полоску на экране — изображение раздвижной щели проекционного аппарата.

2. Выделить основные цвета полученного сплошного спектра и записать их в наблюдаемой последовательности.

3. Повторить опыт, рассматривая полоску через грани, образующие угол 60°. Записать различия в виде спектров.

4. Наблюдать линейчатые спектры водорода, гелия или неона, рассматривая

5. светящиеся спектральные трубки сквозь грани стеклянной пластины. Записать наиболее яркие линии спектров.

6. Контрольные вопросы:

7. 1 .Является ли спектр лампы накаливания непрерывным?

8. Как изменяется линейчатый спектр при увеличении плотности атомарного газа?

ЛАБОРАТОРНАЯ РАБОТА № 10

ИЗУЧЕНИЕ ТРЕКОВ ЗАРЯЖЕННЫХ ЧАСТИЦ ПО ГОТОВЫМ

ФОТОГРАФИЯМ

Цель работы

1. Ознакомиться с одним из методов изучения заряженных частиц. 2.Закрепить и углубить знания по теме « Элементарные частицы».

Оборудование

1.Фотографии или рисунки косых столкновений частиц.

2.Транспортир.

3.Линейка.

4.Тонко заточенный карандаш.

Теория

В результате нецентрального (косого) соударения двух элементарных частиц каждая разделяется по траектории, выходящей из одной точки, поэтому образуется "вилка".

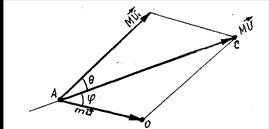
Рисунок 10.1 – Соударение двух элементарных частиц

На рисунке 10.1 показана импульсная диаграмма такого взаимодействия движущейся частицы и неподвижной. Здесь

М - масса движущейся частицы;

v , v₁ - скорость движущейся частицы до и после взаимодействия;

m- масса неподвижной частицы;

u - скорость движения неподвижной частицы после взаимодействия;

θ - угол рассеяния;

φ - угол отдачи;

М v и М v₁ - векторы импульсов налетающей частицы до и после взаимодействия;

mu - вектор импульса неподвижной частицы после взаимодействия; Используя закон сохранения энергии и теорему синусов можно вывести соотношение:

M / m = sin (θ + 2 φ) / sin θ , (10.1)

позволяющее решить ряд задач по трекам частиц на готовых фотографиях.

Порядок выполнения работы

1. Используя рисунок (фотографию), скопировать его на прозрачную бумагу, прикрепить в тетрадь скопированный трек налетающей частицы и продолжить его тонкими линиями.

2. Начертить прямолинейные участки треков взаимодействующих частиц, сохранив углы рассеяния θ и отдачи φ. Отметить эти углы и измерить транспортиром.

3. Записать массу m или М известной частицы в а.е.м. и, используя формулу (101), вычислить массу неизвестной частицы .

4. Зная массу и используя таблицу " Периодическая система элементов ", определить ядром какого атома является неизвестная частица. Назвать эту частицу.

5. Результаты измерений записать в таблицу 1.

Таблица 10.1

№	θ	φ	M (а.е.м.)	m (а.е.м.)	Вид частицы

Контрольные вопросы

Вариант 1

1. Что вам известно о протоне?

2. Дайте определение атомной единицы массы. Укажите ее соотношение с

килограммом.

3. Как узнать ядро какого атома приобретает большую кинетическую энергию после столкновения?

4. По какому принципу частицы делят на адроны и лептоны?

5. Какими частицами обмениваются нуклоны в ядре при взаимодействиях?

Вариант 2

1. Что вам известно об α- частице?

2. Какие частицы относятся к нуклонам?

3. По какой схеме распадается свободный нейтрон? Каково время его жизни?

4. Какой заряд и массовое число имеет электрон? Его обозначение в ядерных реакциях?

5. Какие законы сохранения действуют в ядерных реакциях?

Список использованных источников

1. Лабораторные занятия по физике : учеб. пособие / под ред. Л. Л. Гольдина. – М. : Наука, 1983. – 704 с.

2. Лабораторный практикум по физике. Часть 1. Физические измерения : учеб. пособие / под ред. В. И. Ивлева. – Саранск : Изд-во СВМО, 1999. – 50 с.

3. Соловьев В. М. Экспериментальные методы обработки результатов измерений – Л.: Изд-во Ленингр. ун-та, 1977. – 72 с.

4. Детлаф А.А., Яворский М.В. Курс физики.- М.:1989 г.

Номер опыта

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

19.01.2020