Министерство образования и науки Луганской Народной Республики

Индустриальный техникум ДонГТУ

 

                                       

 

 

 

 

                                                

Методические рекомендации

для самостоятельной работы

студентов

по дисциплине «Дискретная математика»

 

для студентов специальности

09.02.03 «Программирование в компьютерных системах»

 

 

 

 

Алчевск

2016

 

 

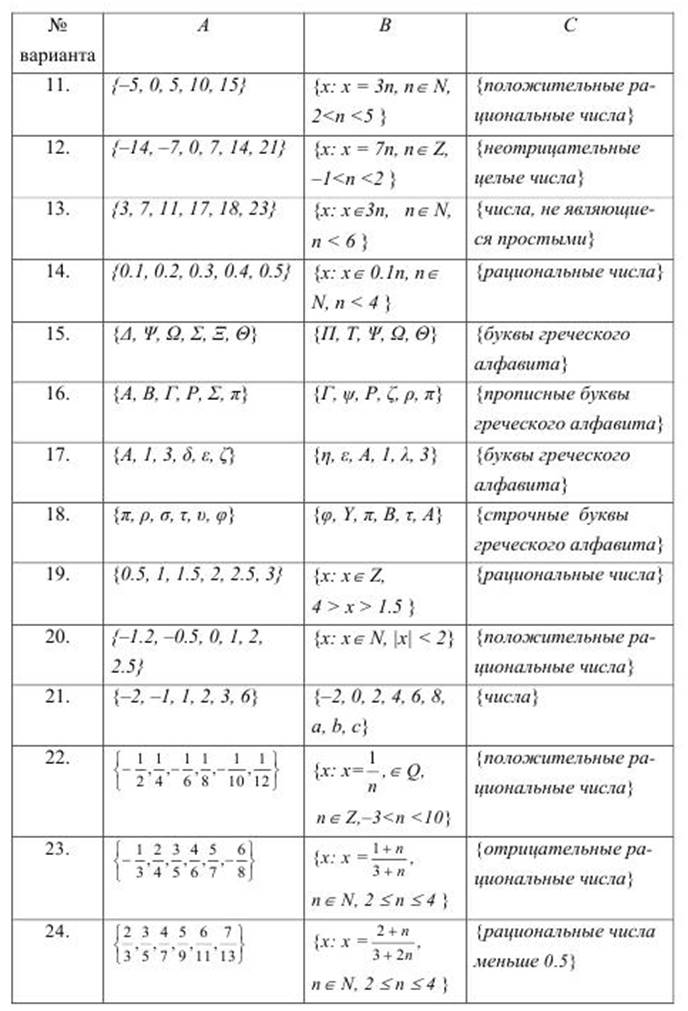
Разработала	_____________	Л.Л. Кузьмина  – преподаватель высшей категории, старший преподаватель
Рецензент	_____________	Л.С. Филоненко – преподаватель высшей категории

 

 

 

     

Утверждено на заседании Методического совета

__________Л.Л. Кузьмина  председатель Методического совета ИТ ДонГТУ

                 

 

 

 

 

 

Рассмотрено и одобрено на заседании цикловой комиссии

«Информатики и компьютерной техники»

Протокол от «___» ________  2016 г. № __

Председатель комиссии

_____________О.Ю. Ленкова

 

 

Содержание

 

Введение	4
Инструкция о модульно-рейтинговой системе текущего и итогового контроля уровня знаний студентов	7
Оценка элементов модулей дисциплины «Дискретная математика»	9
Модуль № 1	11
Модуль № 2	15
Модуль № 3	19
Модуль № 4	23
Модуль № 5	24
Варианты семестрового задания	27
Литература	44

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Для современных инженерно-технических задач необходимо использовать сложный математический аппарат и разные методы их решения. При этом часто приходиться встречаться с задачами, для которых аналитическое решение или вообще невозможно, или выражается такими громоздкими формулами, что использовать их для практических целей нецелесообразно.

Главная цель курса «Дискретная математика»: формировать знания, умения и навыки, необходимые для рационального использования средств современных информационных технологий при решении задач, дать математическое обеспечение для современных компьютерных и информационных технологий.

Содержание как всего курса, так и отдельных тем, изучается путем изучения потребностей специальной подготовки и профессиональной деятельности младших специалистов для данной  группы специальностей.                  

В результате систематического и добросовестного изучения материала студенты узнают о базовых математических моделях и алгоритмах, которые в дальнейшем позволят им профессионально формулировать и решать множество задач в конкретных областях информатики и вычислительной техники. Студенты овладеют основами знаний для абстрактного проектирования логических структур и вычислительных процессов на графах.

На изучение дисциплины отводится 216 часов, из них 112 – аудиторных занятий и 104 – на самостоятельную работу студента. Изучать материал следует систематически и в той последовательности, которая предусмотрена программой дисциплины.

Для полного и успешного изучения дисциплины запланированы следующие виды занятий:

1. Изучение материала по основным вопросам курса на лекционных занятиях

2.  Выполнение расчетных заданий.

3. Самостоятельное изучение отдельных вопросов с использованием этих методических рекомендаций и литературы, которую необходимо использовать для изучения дисциплины. Самостоятельная работа предусматривает подготовку студентов к практическим работам, практическим занятиям, контрольным работам, выполнению расчетных заданий, семестрового задания и тому подобное.

Организация самостоятельной работы студентов предполагает внедрение в деятельность таких приемов работы: смысловой переработки текстов, закрепления учебного материала, усвоения обобщенных способов решения заданий, приемы краткой, самой рациональной записи (выписывание, планы, тезисы, конспекты, общие приемы работ с книгой); общие приемы запоминания; концентрирование внимания на использовании студентами разных видов самоконтроля, поэтапную проверку своей работы, общие приемы поиска дополнительной информации (работы с библиографическими справками, каталогами, словарями).

Методические рекомендации к самостоятельной работе студентов содержат пять модулей, оценку каждого его элемента. Первый модуль раскрывает сущность алгебры множеств, второй модуль – логики Буля, третий модуль – логических функций, четвертый модуль – элементов теории графов, пятый модуль – теории бесконечных автоматов. Каждый модуль заканчивается защитой данного модуля по контрольным вопросам.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, то более детально разобрать вопрос по литературе, указанной в данной методике, или обратиться за консультацией к преподавателю.

Правила выполнения и оформления

семестрового задания:

-        студент должен выполнить семестровое задание согласно своего варианта;

-        семестровое задание следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний преподавателя;

-        решение задач следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач;

-        перед решением каждой задачи нужно выписать полностью условие;

-        решение задач оформлять обстоятельно и аккуратно, объясняя все действия;

-        семестровое задание, выполненное не по своему варианту, не засчитываются;

-        по получении проверенной работы студент должен исправить в ней все отмеченные ошибки и недостатки.

 

 

 

 

Инструкция

по модульной – рейтинговой системе

текущего и итогового контроля уровня знаний студентов

по дисциплине «Дискретная математика»

для специальности  «Разработка программного обеспечения»

 

Общее количество часов на дисциплина - 216; аудиторных – 112;

самостоятельных – 104 часов.  Дисциплина изучается два семестра.

Теоретический материал разбит на пять модулей. Каждый модуль – это завершенный раздел дисциплины.

Модуль 1 – Алгебра множеств

Модуль 2 – Логика Буля

Модуль 3 – Логические функции

Модуль 4 – Элементы теории графов

Модуль 5 – Теория бесконечных автоматов

Модульно-рейтинговая система предусматривает оценку знаний студентов по дисциплине

«5» – 90 - 100 баллов

«4» – 74 -  89 баллов

«3» – 60 – 73 баллов

Студенты, которые своевременно выполнили график учебного процесса и набрали 60 баллов и выше в течение семестра считаются успевающими.

Присутствие студента необходимо для сообщения ему суммарной оценки и занесения ее в зачетную книжку и ведомость.

К сдаче экзамена допускаются студенты, которые выполнили график самостоятельной работы и набрали определенное количество необходимых баллов, из возможных 50, но не менее 25. Такого количества достаточно для допуска к экзамену, согласно решения дисциплинарной комиссии.

Студенты, которые в течение семестра работали не ритмично, нарушали график учебного процесса и не набрали необходимого количества баллов, считаются неуспевающими. Такие студенты имеют возможность получить зачетные 60–100 баллов во время сессии. Для сдачи экзамена студент должен получить допуск.

Когда студент набирает 60 (и более) баллов по результатам работы в семестре, но не полностью выполнил график самостоятельной работы, то есть не отработал практическую работу или расчетное задание, то такому студенту не засчитывается весь модуль и он считается должником. Об этом предупреждается студент. Такой студент имеет право сдавать не весь материал дисциплины, а лишь ее часть, то есть задолженности по модулю. Для студента, который выполнил график самостоятельной работы, но не получил необходимое количество зачетных баллов по одному из модулей дисциплины, предоставляется возможность, во время сессии добрать это количество баллов, чтобы считаться успевающим.

 

 

 

 

 

 

 

Оценка элементов модулей дисциплины

«Дискретная математика»

 

 

 

Модуль №1

1.      Проработка  лекций  № 1 - 2

2.      Подготовка к выполнению письменного опроса № 1

3.      Подготовка к выполнению самостоятельной работы № 1

4.      Подготовка к выполнению самостоятельной работы № 2

5.      Подготовка к защите модуля № 1 по лекциями № 1 - 2

6.      Выдача семестрового задания, с. 27

 

1.      Проработать лекции № 1 - 2 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения,  термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более подробно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

2. Письменный опрос №1

1.      Напишите обозначение основных символов, используемых в теории множеств

2.      Что такое множество? Как его обозначить? Пример

3.      Как можно задать множество? Пример

4.      Какое множество называют счетным? Какое – пустым? Пример

5.      Что такое подмножество? Пример

6.      Сформулируйте основные свойства счетных множеств

7.      Какие соотношения (действия) между множествами вы знаете, перечислите их. Как они обозначаются?

8.      Какое множество можно назвать универсальным? Пример

9.      Какие операции (из аналогичных арифметических) нельзя производить с множествами?

10. Что такое диаграмма Эйлера? Проиллюстрируйте с помощью диаграмм Эйлера объединение и пересечение трех множеств

11. Дайте определение декартова произведения множеств (прямое произведение множеств). Пример

12. Поясните термин «мощность множества»

13. Сформулируйте понятие включения множеств. Пример

14. Сформулируйте понятие суммы множеств. Пример

15. Сформулируйте понятие произведения множеств. Пример

16. Сформулируйте понятие вычитания множеств. Пример

17. Сформулируйте понятие дополнения множества. Пример

18. Сформулируйте основные тождества коммутативности алгебры множеств

19. Сформулируйте основные тождества ассоциативности алгебры множеств

20. Сформулируйте основные тождества дистрибутивности алгебры множеств

21. Сформулируйте основные законы двойственности алгебры множеств

22. Сформулируйте основные законы поглощения алгебры множеств

23. Сформулируйте основные тождества алгебры множеств: объединения множества с пустым множеством, универсальным и своим дополнением

24. Сформулируйте основные тождества алгебры множеств: пересечения множества с пустым множеством, универсальным и своим дополнением

25. Дайте определение отображения множества А во множество В. Пример

26. Что такое сюръекция? Пример

27. Что такое инъекция? Пример

28. Что такое биекция? Пример

29. Дайте определение функции. Пример

30. Поясните термин «образ подмножества». Пример

31. Поясните термин «прообраз подмножества». Пример

32. Как определяется обратное отображение? Пример

3. Самостоятельная работа № 1

Для подготовки к этой самостоятельной работе нужно проработать лекции № 1-2, детально разобрать все приведеннеы на практических занятиях примеры. по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

Проверьте справедливость тождеств с помощью свойств и с помощью диаграмм Ейлера-вена.

U

U

4. Самостоятельная работа № 2

Для подготовки к этой самостоятельной работе нужно проработать лекции № 1-2, детально разобрать все приведеннеы на практических занятиях примеры. по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

Максимально упростите выражение своего варианта, воспользовавшись тождествами алгебры множеств. Затем с помощью диаграмм Эйлера-Вена сравните ваше упрощенное выражение с исходным.

5. Защита модуля № 1

Для защиты модуля № 1 студенту предоставляется расчетное индивидуальное задание, которое нужно выполнить и детально объяснить порядок выполнения действий.

Задание состоит из трех вопросов, например:

1. Выразить символично (используя знаки операций пересечения, объединения и дополнения) множества, заштрихованные на диаграммах Эйлера-Венна

а) 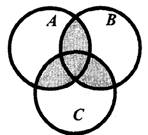 б)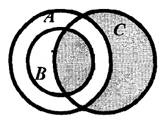

2. Нарисовать диаграмму Эйлера для четырех множеств A, B, C, D, образующих множество F, и изобразить штриховкой его область.

3. Докажите справедливость нижеприведенных тождеств любыми двумя способами из трех предложенных:

ü с помощью тождеств;

ü с помощью свойств;

ü с помощью диаграмм Эйлера – Венна.

Модуль №2

1.    Проработать лекции № 3 - 4

2.    Подготовка к выполнению письменного опроса № 2

3.    Подготовка к обязательной контрольной работе № 1

4.    Подготовка к выполнению самостоятельной работы № 3

5.    Подготовка к защите модуля № 2 по лекциями № 3 - 4

6.    Выполнение семестрового задания, с. 27

 

1.      Проработать лекции № 3 - 4 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

2. Письменный опрос №2

1.      Какие формулы называются тавтологиями? Противоречиями? Пример

2.      Что такое дизъюнкция? Как ее  задать с помощью диаграмм Эйлера?

3.      Что такое конъюнкция? Как ее  задать с помощью диаграмм Эйлера?

4.      Что такое разность? Как ее  задать с помощью диаграмм Эйлера?

5.      Что такое импликация? Как ее  задать с помощью диаграмм Эйлера?

6.      Что такое штрих Щеффера? Как его  задать с помощью диаграмм Эйлера?

7.      Что такое стрелка Пирса? Как ее  задать с помощью диаграмм Эйлера?

8.      Что такое симметрическая разность? Как ее  задать с помощью диаграмм Эйлера?

9.      Что такое эквивалентность? Как ее  задать с помощью диаграмм Эйлера?

10. Что такое дизъюнкция? Как ее  задать с помощью таблицы истинности?

11. Что такое конъюнкция? Как ее  задать с помощью таблицы истинности?

12. Что такое разность? Как ее  задать с помощью таблицы истинности?

13. Что такое импликация? Как ее  задать с помощью таблицы истинности?

14. Что такое штрих Щеффера? Как его  задать с помощью таблицы истинности?

15. Что такое стрелка Пирса? Как ее  задать с помощью таблицы истинности?

16. Что такое симметрическая разность? Как ее  задать с помощью таблицы истинности?

17. Что такое эквивалентность? Как ее  задать с помощью таблицы истинности?

18. Сформулируйте основные тождества коммутативности логики Буля

19. Сформулируйте основные тождества ассоциативности логики Буля

20. Сформулируйте основные тождества дистрибутивности логики Буля

21. Сформулируйте основные законы двойственности логики Буля

22. Сформулируйте основные законы поглощения логики Буля

23. Сформулируйте основные тождества логики Буля: объединения множества с пустым множеством, универсальным и своим дополнением

24. Сформулируйте основные тождества логики Буля: пересечения множества с пустым множеством, универсальным и своим дополнением

 

3. Обязательная контрольная работа№1

Контрольная работа состоит из трех задач и проводится в аудитории в течение двух академических часов:

ü  доказать аналитическим путем справедливость выражения, потом проверить с помощью таблиц истинности;

ü  упростить данное выражение;

ü  проверить справедливость выражения с помощью диаграмм Эйлера

Работа выполняется на листах со штампом. Каждая задача обязательно должна иметь объяснение к решению задачи. Перед контрольной работой студент должен повторить теоретический материал, рассмотреть примеры, которые приведены в учебниках и на практических занятиях.

4. Самостоятельная работа № 2

Для подготовки к этой самостоятельной работе нужно проработать лекции № 3-4, детально разобрать все приведеннеы на практических занятиях примеры. по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

Докажите справедливость ниже приведенного тождества любыми двумя способами из трех предложенных:

ü  аналитическим способом, то есть на основе формул взаимосвязи между логическими операциями;

ü  с помощью таблиц истинности;

ü  с помощью диаграмм Эйлера – Венна.

5. Защита модуля № 2

Для защиты модуля № 2 студентам предоставляется расчетное индивидуальное задание, которое нужно выполнить и детально объяснить порядок выполнения действий.

Доказать тождественность аналитическим путем и с помощью диаграмм Эйлера:

 

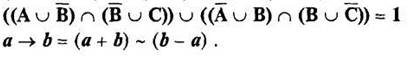
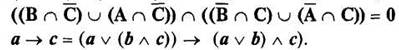
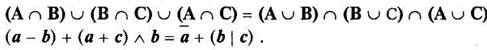
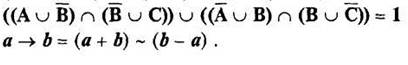
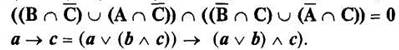
Модуль №3

1.       Проработка  лекций  № 5 - 9

2.       Подготовка к выполнению самостоятельной работы № 4

3.       Подготовка к выполнению самостоятельной работы № 5

4.       Подготовка к выполнению самостоятельной работы № 6

5.       Подготовка к выполнению письменного опроса № 3

6.       Подготовка к защите модуля № 3 по лекциями № 5 - 9

7.       Выдача семестрового задания, с. 27

 

1. Проработать лекции № 5 - 9 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения,  термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более подробно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

2. Самостоятельная работа № 4.

Для подготовки к этой самостоятельной работе нужно проработать лекции № 5-9, детально разобрать все приведеннеы на практических занятиях примеры. по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

Выполнить задание вида:

1. Для функции заданы номера наборов, на которых она равняется единице. Необходимо минимизировать эту функцию в ДНФ и КНФ методом карт Вейча.

f(0,3,5,7,8,11,12)=1

2. Минимизировать в ДНФ и КНФ с помощью карт Вейча не полностью определенную функцию, оптимально ее дополнив.

0*01101100011**0

3. Самостоятельная работа № 5.

Выполнить задание вида: провести логическое преобразование функции f в табличном виде и записать ее ДНФ и КНФ. Провести минимизацию функции методом карт Вейча.

4. Самостоятельная работа № 6.

Выполнить задание вида: для приведенных легенд запишите с использованием 4—6 различных букв клаузу, отвечающую тексту или контексту вашей легенды, для чего сформули­руйте необходимые посылки и два следствия: одно истинное, другое ложное. С помощью таблицы истинности найдите МНФ

5. Письменный опрос №3

1.      Что такое высказывание? Привести пример

2.      Как образуется логическая связка «отрицание». Привести пример.

3.      Как образуется логическая связка «дизъюнкция». Привести пример.

4.      Как образуется логическая связка «конъюнкция». Привести пример.

5.      Как образуется логическая связка «импликация». Привести пример.

6.      Как образуется логическая связка «эквивалентность». Привести пример.

7.      Какими союзами можно пользоваться в логике высказываний при описании «отрицания». Привести пример

8.      Какими союзами можно пользоваться в логике высказываний при описании «отрицания». Какие имеются особенности в высказываниях. Привести пример

9.      Какими союзами можно пользоваться в логике высказываний при описании «дизъюнкции». Какие имеются особенности в высказываниях. Привести пример

10. Какими союзами можно пользоваться в логике высказываний при описании «конъюнкции». Какие имеются особенности в высказываниях. Привести пример

11. Какими союзами можно пользоваться в логике высказываний при описании «импликации». Какие имеются особенности в высказываниях. Привести пример

12. Какими союзами можно пользоваться в логике высказываний при описании «эквивалентности». Какие имеются особенности в высказываниях. Привести пример

13. На чем строятся доказательства в логике высказываний в отличие от логики Буля?

14. Как оформляются утверждения в логике высказываний?

15. Закон рефлексивности. Пример

16. Закон антисимметричности. Пример

17. Закон транзитивности. Пример

18. Что такое клауза? Привести пример

19. Что предполагает аксиоматический метод доказательства высказываний?

20. Что предполагает конструктивный метод доказательства высказываний?

21. Основная аксиома логики высказываний

22. Что такое легенда? Привести пример

23. Аксиомы логики высказываний: отношения порядка, дистрибутивность.

24. Аксиомы логики высказываний: ассоциативность, коммутативность.

25. Что такое предикат. Понятие логики предикатов. Привести пример

26. Что означает понятие «однородная функция», «неоднородная функция».  Привести пример

27. Квантор общности. Что он означает? Привести пример

28. Квантор существования. Что он означает? Привести пример

29. Как можно выразить квантор существования через квантор общности?

30. Что такое одноместный, двухместный предикат. Привести пример

31. Что такое константа в логике предикатов? Привести пример

32. Что такое нульместный,  трехместный предикат. Привести пример.

6. Подготовка к защите модуля № 3 по лекциями № 5 - 9

Для защиты модуля № 3 нужно проработать лекции № 5-9, детально разобрать все приведенные на практических занятиях примеры. Если возникли вопросы, более подробно разобрать вопрос по литературе, которая указана в действующей методике, или обратиться за консультацией к преподавателю.

Для защиты модуля № 3 студентам предоставляется расчетное индивидуальное задание, которое нужно выполнить и детально объяснить порядок выполнения действий. Предоставляются легенды, нужно записать с использованием 4—6 разных букв клаузу, которая отвечает тексту или контексту легенды, сформулировать необходимые предпосылки и два следствия: одно истинное, другое ложное. С помощью таблицы истинности проверить сформулированные следствия.

 

Модуль №4

1.       Проработка  лекций  № 10 - 11

2.       Подготовка к выполнению письменного опроса № 4

3.       Подготовка к выполнению самостоятельной работы № 7

4.       Подготовка к защите модуля № 4 по лекциями № 10 - 11

5.       Выдача семестрового задания, с. 27

 

1. Проработать лекции № 10 - 11 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

2. Письменный опрос №4

1.      Что такое граф? Пример

2.      Какой граф называется ориентированным? Пример

3.      Какой граф называется неориентированным? Пример

4.      Что называется петлей? Пример

5.      Какие вершины называются смежными? Пример

6.      Какое ребро называется инцидентным? Пример

7.      Что такое степень вершины? Пример

8.      Что такое кратность пары вершин? Пример

9.      Что такое подграф? Пример

10. Что такое частный граф? Пример

11. Что называется путем в графе? Пример

12. Что называется длиной пути в графе? Пример

13. Что такое дерево? Пример

14. В чем заключается задача о коммивояжере? Пример

15. Способы решения задачи о коммивояжере

16. Каким  способом в дискретной математике решают задачу коммивояжере?

 

3. Самостоятельная работа № 7.

Для подготовки к этой самостоятельной работе нужно проработать лекции № 10-11, детально разобрать все приведеннеы на практических занятиях примеры. по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

Выполнить задание вида:

Для функции заданы номера наборов, на которых она равняется единице. Необходимо минимизировать эту функцию в ДНФ и КНФ методом карт Вейча и построить логическую схему устройства, реализующую логическую функцию  f(0,3,5,7,8,11,12)=1.

4. Подготовка к защите модуля № 4 по лекциями № 10-11

Для защиты модуля № 4 нужно проработать лекции № 10-11, детально разобрать все приведенные на практических занятиях примеры. Если возникли вопросы, более подробно разобрать вопрос по литературе, которая указана в действующей методике, или обратиться за консультацией к преподавателю.

Для защиты модуля № 4 студентам предоставляется расчетное индивидуальное задание, которое нужно выполнить и детально объяснить порядок выполнения действий.

Решение задач на построение графов методом ветвей и границ.

 

Модуль №5

1.    Проработать лекции № 12 - 13

2.       Подготовка к выполнению самостоятельной работы № 8

3.       Подготовка к обязательной контрольной работе № 2

4.       Подготовка к выполнению самостоятельной работы № 9

5.       Подготовка к защите модуля № 5 по лекциями № 12 - 13

6.       Сдача семестрового задания, с. 27

 

1. Проработать лекции № 12 - 13 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

2. Самостоятельная работа № 8.

Для подготовки к этой самостоятельной работе нужно проработать лекции № 12, детально разобрать все приведеннеы на практических занятиях примеры. по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

Выполнить задание вида:

Для функции заданы номера наборов, на которых она равняется единице. Необходимо минимизировать эту функцию в ДНФ и КНФ методом карт Вейча и построить логическую схему устройства, которое реализовывает логическую функцию.

3. Обязательная контрольная работа№2

Контрольная работа состоит из трех задач и проводится в аудитории в течение двух академических часов:

ü Минимизировать в ДНФ и КНФ с помощью карт Вейча неполность определенную функцию, оптимально дополнив ее;

ü Посторить логическую схему устройства, реализовувающего логическую функцию из задания 1;

ü проверить справедливость выражения с помощью диаграмм Эйлера

Работа выполняется на листах со штампом. Каждая задача обязательно должна иметь объяснение к решению задачи. Перед контрольной работой студент должен повторить теоретический материал, рассмотреть примеры, которые приведены в учебниках и на практических занятиях.

4. Самостоятельная работа № 9.

Выполнить задание вида: упростить перпеключательные схемы; по данному выражению постоить переключательную схему.

 

 

5. Подготовка к защите модуля № 5 по лекциями № 12-13

Для защиты модуля № 5 нужно проработать лекции № 12-13, детально разобрать все приведенные на практических занятиях примеры. Если возникли вопросы, более подробно разобрать вопрос по литературе, которая указана в действующей методике, или обратиться за консультацией к преподавателю.

Для защиты модуля № 5 студентам предоставляется расчетное индивидуальное задание, которое нужно выполнить и детально объяснить порядок выполнения действий.

Решение задач на построение и упрощение логических схем.

6. Семестровое задание

 

Задание 1.

 

Для заданных множеств А, В и С найти следующие множества:

, , , ,

 

Задание 2.

Решите следующие задания, используя диаграммы Эйлера-Венна

 

Задание 3.

В таблице Заданы номера наборов аргументов, на которых логическая функция принимает значения, равное единице. Необходимо минимизировать эту функцию двумя методами: Квайна и карт Вейча. Минимизацию провести в ДНФ и КНФ. Результаты сравнить.

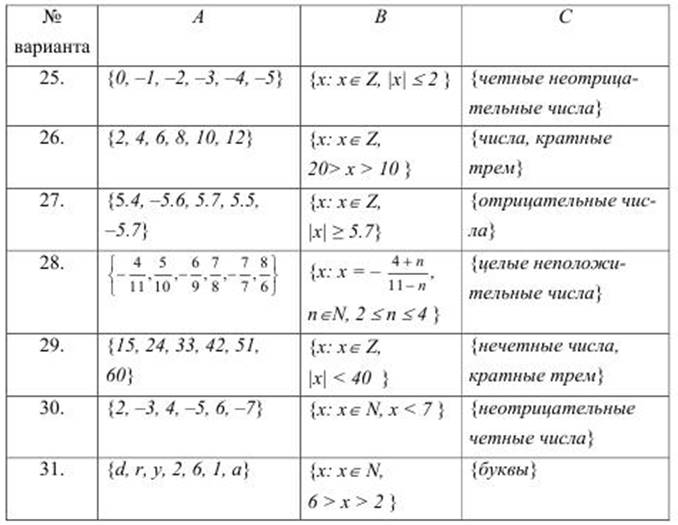
Задание 4.

Докажите или опровергните справедливость выражений с помощью диаграмм Эйлера-Венна и таблиц истинности

 

Вариант 1

, если

Вариант 2

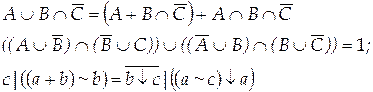
Вариант 3

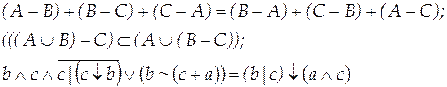
Вариант 4

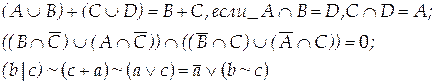
Вариант 5

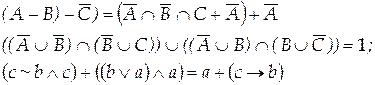
Вариант 6

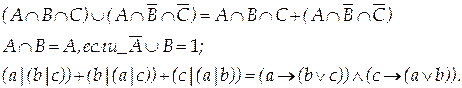
Вариант 7

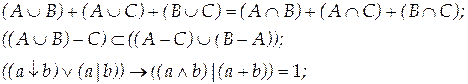
Вариант 8

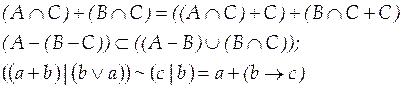
Вариант 9

 

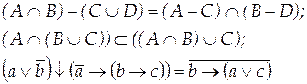
Вариант 10

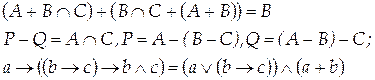
Вариант 11

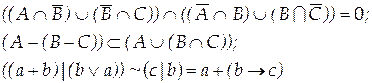
Вариант 12

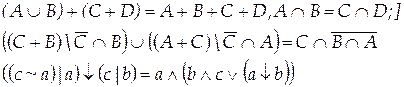
Вариант 13

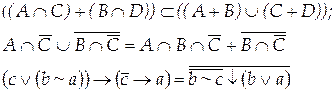
Вариант 14

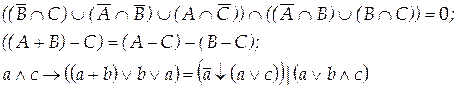
Вариант 15

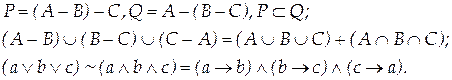
Вариант 16

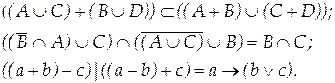
Вариант 17

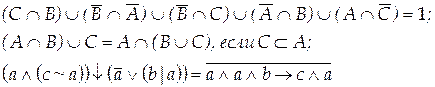
Вариант 18

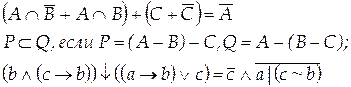
Вариант 19

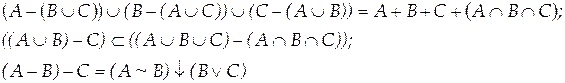
Вариант 20

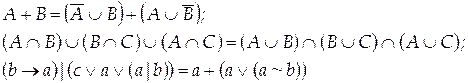
Вариант 21

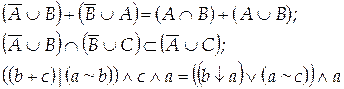
Вариант 22

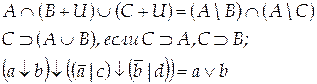
Вариант 23

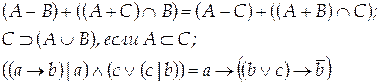
Вариант 24

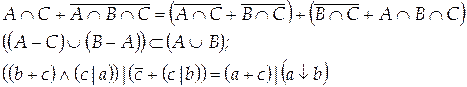
Вариант 25

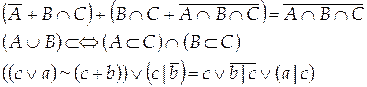
Вариант 26

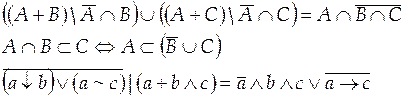
Вариант 27

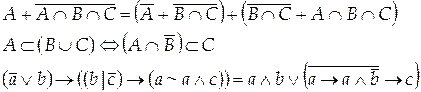
Вариант 28

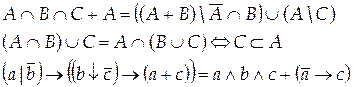
Вариант 29

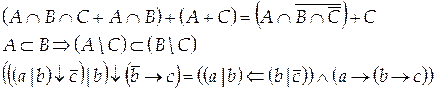
Вариант 30

 

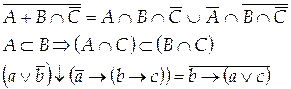
Задание 5.

 

Ниже приведены диаграммы Эйлера — Венна. Представьте заштрихован­ные и отдельно незаштрихованные области максимально компактными анали­тическими выражениями, в которых бы использовалось минимальное количест­во логических операций и букв. С этой целью сначала выразите все заштрихо­ванные области через конституенты-конъюнкты, а незаштрихованные — через конституенты-дизъюнкты.

 

1.                         2.                          3.

                         

 

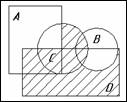
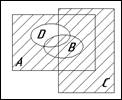
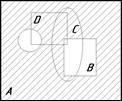
4.                         5.                          6.

                          

 

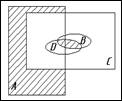
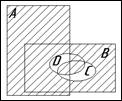
7.                         8.                          9.

 

 

10.                         11.                       12.

 

13.                         14.                       15.

 

16.                       17.                        18.

37

 

19.                         20.                         21.

 

22.                       23.                          24.

 

25.                       26.                          27.

           

 

 

 

 

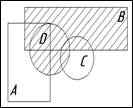
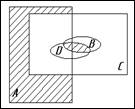
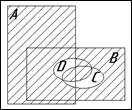
28.                         29.                       30.

 

 

Литература

1.      Акимов А.Е. Дискретная математика: логика, группы, графы. – М.: Лабораторная Базовых Известный, 2003. – 376 с.: ил.

2.      Гончарова Г.А., Мочалин А.А. Элементы дискретной математики: Учебное пособие. М.: ФОРУМ: ИНФРА-м, 2003. – 128 с.

3.      Компьютерная дискретная математика: Учебник/ М.Ф. Бондаренко, Н.В. Билоус. А.Г. Рут касс. – Харьков: «Компания СМИТ», 2004. – 480 с.

4.      Судоплатов С.В., Овчинникова. Элементы дискретной математики: Учебник. – М.: ИНФРА-м; Новосибирск: НГТУ, 2003. – 280 с. – (Серия «Высшее образование»)