Методические рекомендации к практическим работам по математике для 1 курса СПО

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Университетский колледж

МАТЕМАТИКА

Методические рекомендации к практическим работам

1 курса

Университетский колледж

Специальность

Вологда

2024

Математика: Методические указания по выполнению практических работ для студентов 1 курса. – Вологда: ВОГУ, 2024.

Методические указания разработаны с целью оказания помощи студентам при выполнении практических работ по математике. Рассмотрены теоретические и практические основы практических работ, приведены задания для самостоятельной работы.

Утверждено редакционно-издательским советом ВОГУ

Автор: С.В. Шутова, преподаватель высшей категории УК ВОГУ

Рецензент

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ».

1.     Возрастание и убывание функции.

     1.1 Критические (стационарные) точки.

Рассмотрим функцию y=f(x). Внутренние точки области определения функции называются критическими, если производная функции в этой точке равна нулю или не существует: f '(х) = 0.

Алгоритм нахождения критических точек:

1)    Найти область определения функции D(f);

2)    Найти производную функции f '(х);

3)    Найти нули производной и точки, в которых производная не существует f '(х)=0;

4)    Записать ответ.

Пример 1: Найти критические точки функции f(x)=.

Решение:

1)    D(f)=R

2)  f '(x)=

3)    f '(х)=0

  x=0                 (это уравнение корней не имеет)

4)     x=0 – критическая точка. Точек, в которых производная не существует, нет.       

Ответ: x=0.

Пример 2: Найти критические точки функции f(x)=.

Решение:

1)  D(f) = (

2)  f '(x)=

3)    f '(х)=0

            и     

4)  Критические точки:  ,  и  (точка, в которой производная не существует).

Ответ:  ,  , .

      1.2 Промежутки возрастания и убывания функции.

       Определение: Функция  называется возрастающей (убывающей) на промежутке [a;b), если для любых , принадлежащих данному промежутку, из неравенства  следует неравенство  ().

    Теорема 1: Если функция  дифференцируема на интервале (a;b) и  для всех то функция возрастает на интервале (a;b).

    Теорема 2: Если функция  дифференцируема на интервале (a;b) и  для всех то функция убывает на интервале (a;b).

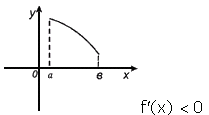
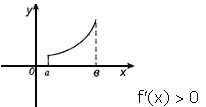
Алгоритм нахождения промежутков возрастания и убывания функции:

1)    Найти область определения функции D(f);

2)    Найти производную функции f '(х);

3)    Найти критические точки,  f '(х)=0;

4)    Определить знак производной на каждом из полученных промежутков, разделённых критическими точками на числовой прямой;

5)    Пользуясь теоремами возрастания и убывания, записать ответ.

Пример 3: Найти промежутки возрастания и убывания функции

.

Решение:

1)    D(f)=R

2)  f '(x)=

3)    f '(х)=0       

4)    Определяем знак производной на каждом из промежутков:

f '(x)     +                                  +             х

                         -1                  

     5) Функция возрастает при x [-;-1] и при х [;]

         Функция убывает при х [-1;].

Пример 4: Найти промежутки возрастания и убывания функции   f(x)=.

Решение:

1)  D(f) = (

2)  f '(x)=

3)    f '(х)=0

            и     

Критические точки:  ,  и  (точка, в которой производная не существует).

4)    Определяем знак производной на каждом из промежутков:

f '(x)    +                               +           х

             -1           0               1   

     5) Функция возрастает при х [-;-1] и при х [;]

         Функция убывает при х [-1;] и при х [;].

        2. Экстремумы функции.

       Определение: Критические точки, в которых функция достигает максимального или минимального значения на промежутке, называются точками экстремума.

      Теорема: Пусть функция f(x) дифференцируема на интервале (a;b), , и .

Тогда:

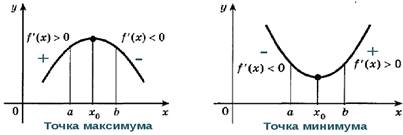
1)   если при переходе через стационарную точку  функции f(x) её производная меняет знак с «плюса» на «минус», то точка максимума функции f(x).

2)   если при переходе через стационарную точку  функции f(x) её производная меняет знак с «минуса» на «плюс», то точка минимума функции f(x).

Алгоритм нахождения точек экстремума функции:

1)     Найти область определения функции D(f);

2)    Найти производную функции f '(х);

3)    Найти критические точки, f '(х)=0;

4)    Определить знак производной на каждом из полученных промежутков, разделённых критическими точками на числовой прямой;

5)    Пользуясь теоремами максимума и минимума функции, записать ответ.

Пример5: Найти точки максимума и минимума функции .

Решение:

1)    D(f)=R

2)  f '(x)=

3)    f '(х)=0   

4)    Определяем знак производной на каждом из промежутков:

f '(x)     +                                 +             х

         f (x)                   

5)  В точке  производная поменяла знак с «плюса» на «минус», значит эта точка – точка максимума.

В точке  производная поменяла знак с «минуса» на «плюс», значит эта точка – точка минимума.

Ответ:

       3.Применение производной к построению графика функции.

      Построение графика функции необходимо начинать с исследования функции.

Алгоритм исследования и построения графика функции с помощью производной:

1)    Найти область определения функции;

2)    Определить четность (нечетность) функции:

если f(-x) = f(x), то функция чётная - график функции будет симметричен относительно оси ординат;

если f(-x) = - f(x), то функция нечётная - график функции будет симметричен относительно начала координат;

3)    Найти точки пересечения с осями координат:

с осью Оу: х = 0, у=f (0)

с осью Ох: у = 0, х находим из уравнения f(х) = 0;

Исследовать функцию при помощи производной:

4)    Найти производную функции и её критические точки;

5)    Найти промежутки возрастания и убывания функции;

6)    Найти точки экстремума и значения функции в этих точках;

Результаты исследования функции с помощью производной занести в таблицу.

7)    Найти дополнительные точки (при необходимости);

8)    Построить график.

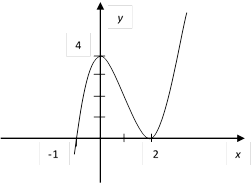
Пример6: Исследовать функцию  и построить её график.

Решение:

1)    Область определения функции - любое действительное число D(y)=R.

2)    Функция не является ни чётной, ни нечётной.

3)    Найдем точки пересечения графика функции с осями координат:

с осью Оy:   ,

точка пересечения: (0;4)

с осью Ох:

   Точки пересечения: (-1;0) и (2;0).

4)    Найдём производную функции и её критические точки:

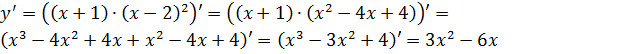
Критические точки: .

5)    Результаты исследования будем заносить в таблицу:

6)    По полученным точкам и данным таблицы, построим график функции:

Пример 7: Построить график функции .

Решение:

1)    Область определения функции – любое действительное число, кроме 0.

.

2)    Определим чётность (нечётность функции):

Функция является чётной, значит график этой функции будет  симметричен относительно оси ординат.

3)    Найдём точки пересечения графика функции с осями координат:

Так как . Таким образом, точек пересечения графика функции с осями координат нет.

4)    Найдем производную функции и критические точки:

             это уравнение корней не имеет, так как .

– стационарная точка (точка, в которой производная не существует).

        Для построения графика чётной функции достаточно исследовать свойства и построить её график при , а затем отразить его симметрично относительно оси ординат.

5)    Результаты исследования занесем в таблицу:

6)    Найдём дополнительные точки:

7)    Отметим данные точки на координатной плоскости и построим график функции:

                                         у

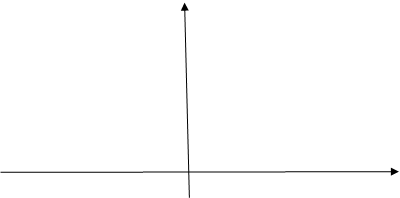                                        0           1                                  х

        4. Наибольшее и наименьшее значения функции.

        На практике часто приходится решать задачи, в которых требуется найти наибольшее или наименьшее значение из всех тех значений, которые функция принимает на отрезке.

Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке [a;b]:

1)  Найти производную функции f '(x);

2)  Найти критические точки, решив уравнение f '(x)=0;

3)  Найти значения функции на концах отрезка, то есть числа f(a) и f(b);

4)  Найти значения функции в тех критических точках, которые принадлежат интервалу (a;b);

5)  Из всех найденных значений выбрать наибольшее и наименьшее.

Пример 8: Найти наибольшее и наименьшее значения функции

                     на отрезке [-2;2].

Решение:

1)  Найдем производную: .

2)  Найдем критические точки. Решим уравнение: 0

                                             ;   

3)    Найдем значения функции на концах отрезка [-2;2]:

4)    Найдем значения функции в тех критических точках, которые принадлежат интервалу (-2;2):

Данному интервалу принадлежит только одна критическая точка x=1

5)    Из найденных значений выбираем наибольшее и наименьшее значения:

 .

Ответ: .

            При решении многих задач часто приходится находить наибольшее или наименьшее значение функции не на отрезке, а на интервале.

           Нередко встречаются задачи, в которых функция имеет на заданном интервале только одну стационарную точку: либо точку максимума, либо точку минимума. В этих случаях в точке максимума функция принимает наибольшее значение на данном интервале, а в точке минимума – наименьшее значение на данном интервале.

Пример 9: Число 36 записать в виде произведения двух положительных чисел, сумма которых наименьшая.

Решение: Пусть первый множитель равен , тогда второй множитель равен . Сумма этих чисел равна . По условию задачи  – положительное число. Таким образом, задача свелась к нахождению такого значения , при котором функция  принимает наименьшее значение на интервале .

1)     Найдем производную:

2)    Найдем стационарные точки:

На интервале есть только одна стационарная точка .

3)  Докажем, что точка   – точка минимума на интервале .

Для этого определим знак производной функции на промежуткахи .

          f '(x)                                 +             х

0                                                    6

             При переходе через точку  производная меняет знак с «минуса» на «плюс», поэтому  - точка минимума. Следовательно, наименьшее значение на интервале  функция  принимает в точке .

4)    Ответим на вопрос задачи.

           Требовалось число 36 записать в виде произведения двух положительных чисел. Первое число мы нашли , найдем второе:

          Ответ:  .

Контрольные вопросы для подготовки к практической работе:

1)    Какие точки называются критическими (стационарными)?

2)    Перечислите алгоритм нахождения стационарных точек функции.

3)    Сформулируйте достаточные условия возрастания или убывания функции.

4)    Перечислите алгоритм нахождения промежутков возрастания и убывания функции.

5)    Что такое экстремумы функции?

6)    Перечислите алгоритм нахождения точек экстремума функции.

7)    Перечислите алгоритм исследования и построения графика функции с помощью производной.

8)    Перечислите алгоритм нахождения наибольшего и наименьшего значений функции на отрезке, на интервале.

     Типовые задания для подготовки к практической работе:

1)    Найдите промежутки возрастания и убывания функции:

а) ;                      .

          2)  Найдите точки экстремума функции:

               а)            .

          3) Постройте график функции:

               а)       б)         .

          4) Найдите наибольшее и наименьшее значения функции:

              а) ;

              б)   на отрезке   [.

          5) Из всех прямоугольников, площадь которых равна 9 , найти прямоугольник с наименьшим периметром.

Практическая работа

Тема. Применение производной к исследованию функций и построению графиков

Цель: Отработать навыки использования производной для построения графиков функций и нахождения наибольшего и наименьшего значений функции.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ТЕМЕ «ИНТЕГРАЛ».

1.     Первообразная. Неопределенный интеграл.

       Определение: Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех х из этого промежутка F(x)' = f(x).

      Операцию нахождения производной для заданной функции называют дифференцированием. Обратную операцию нахождения первообразной для данной функции называют интегрированием. Для нахождения первообразных функций используют таблицу первообразных и правила интегрирования.

Таблица первообразных

       Правила интегрирования:

Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x) на некотором промежутке. Тогда:

1)  функция F(x)  G(x) является первообразной функции f(x)  g(x);

2)    функция aF(x) является первообразной функции af(x).

Пример 1: Найти одну из первообразных функции  f(x) =

Решение: Используя правила интегрирования и таблицу первообразных, находим одну из первообразных функции:

F(x) =.

Пример 2: Для функции f(x) = 2х+3 найти такую первообразную, график которой проходит через точку М(1;2).

Решение: Используя правила интегрирования и таблицу первообразных, находим все первообразные функции:

F(x) =

Найдём число , такое, чтобы график функции у =  проходил через точку М(1;2). Подставляя х=1, у=2, получаем 2=, откуда  Следовательно, F(x) = .

       Определение: Совокупность первообразных для функции f(x) называется неопределенным интегралом и обозначается символом .

, где

f(x) – подынтегральная функция

f(x)dx - подынтегральное выражение

C- произвольная постоянная

       Свойства неопределенного интеграла:

1.     Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:

.

2.     Постоянный множитель подынтегрального выражения можно выносить за знак интеграла:

.

        2. Вычисление интегралов методом непосредственного интегрирования.

        Этот способ вычисления интегралов предполагает такое преобразование подынтегральной функции, которое позволило бы использовать табличные значения первообразных.

Пример 3:  Вычислить

Решение: Для вычисления интеграла воспользуемся свойствами неопределенного интеграла и табличными значениями первообразных функций.

Пример 4:  Вычислить dx

Решение: Для вычисления интеграла сначала каждый член числителя разделим на знаменатель, затем воспользуемся свойствами неопределенного интеграла и табличными значениями первообразных функций.

5.

3.     Площадь криволинейной трапеции.

     Определение: Криволинейная трапеция – это фигура, ограниченная непрерывной кривой графика функции y=f(x), осью абсцисс и отрезками прямых х=а и х=b.

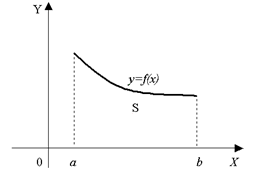
      Площадь криволинейной трапеции вычисляется с помощью определённого интеграла по формуле Ньютона-Лейбница:

S=.

Рассмотрим основные случаи расположения плоской фигуры и соответствующие формулы для вычисления  площадей.

1)    Плоская фигура на отрезке [a;b] расположена выше оси ОХ

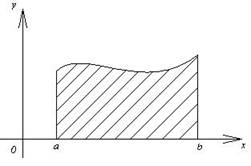
Площадь такой фигуры вычисляется по формуле

2)    Плоская фигура на отрезке [a;b] расположена ниже оси ОХ

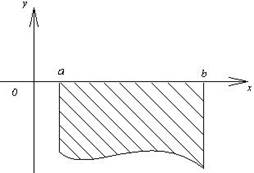
Площадь такой фигуры вычисляется по формуле

3)    Плоская фигура на отрезке [a;b] ограничена линиями графиков двух функций:  f(x) и g(x)

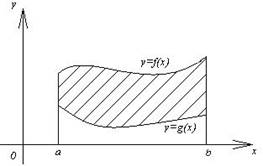
Площадь такой фигуры вычисляется по формуле  

4)    Плоская фигура на отрезке [a;b] разбита на части.

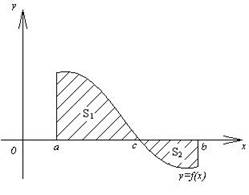
Площадь такой фигуры вычисляется как сумма площадей её частей:

Так как часть фигуры, на отрезке [c;b], находится ниже оси Ох. То площадь фигуры вычисляется по формуле

Алгоритм вычисления площади плоской фигуры:

1.     Построить графики линий, ограничивающие фигуру.

2.     Определить фигуру, площадь которой нужно найти.

3.     Выделить функции, ограничивающие криволинейную трапецию.

4.     Определить границы интегрирования ( отрезок [a;b] на оси Ох).

5.     Вычислить площадь плоской фигуры по формуле Ньютона-Лейбница.

Рассмотрим примеры вычисления определённых интегралов и площадей плоских фигур.

Пример 5: Вычислить интеграл

Решение: Определенный интеграл вычисляют по формуле Ньютона-Лейбница

, где F(x)-одна из первообразных функции f(x).

Пример 6: Вычислить интеграл  

Решение: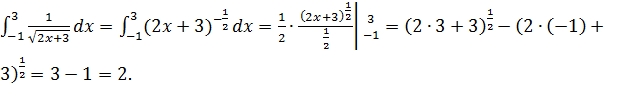

Пример 7: Вычислить интеграл

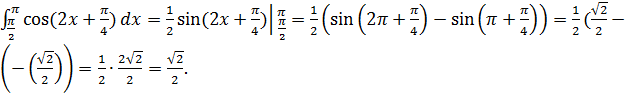
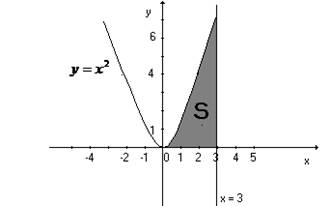
Пример 8: Найти площадь фигуры, изображённой на рисунке:

Решение:

1). Фигура, изображённая на рисунке, является криволинейной трапецией, ограниченной линиями  графиков функций:  y= , x=3 и осью Ох.

2). Границами интегрирования является отрезок [0;3].

3). Вычислим площадь фигуры по формуле Ньютона-Лейбница

Ответ: 9 кв.ед.

Пример 9: Вычислить площадь фигуры, ограниченной линиями:

y=, осями координат и прямой х = 2.

Решение: 1. Построим данные линии.

Графиком функции  y=является парабола парабола, ветви которой направлены вниз, вершина в точке (-1;4).

Графиком функции х = 2 является прямая, параллельная оси Оу.

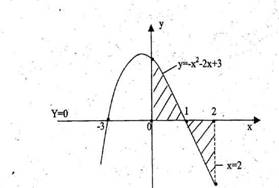
2.Определяем фигуру, площадь которой нужно найти.

Плоская фигура является криволинейной трапецией, которая состоит из двух частей.

3. Находим точки пересечения графика с осью Ох.

 у =

4.Определяем границы интегрирования.

Это два отрезка: [0;1] и [1;2].

5.Вычисляем площадь криволинейной трапеции.

Так как на отрезке [1;2] криволинейная трапеция находится ниже оси Ох, то на этом отрезке интеграл берем с противоположным знаком.

           S=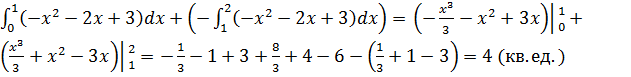

         Ответ: 4 кв.ед.

Пример 10: Вычислите площадь фигуры, ограниченной линиями:

f(x)= 0,5, g(x)=3-x,  x=-3, x=2.

Решение:

1.Строим данные линии.

Графиком функции  f(x)= 0,5 является парабола, ветви которой  направлены вверх, а вершина находится в точке (2;1). Точка пересечения параболы с осью Оу (0;3).

Графиком функции g(x)=3-x является прямая. Строим по двум точкам (2;1) и (0;3).

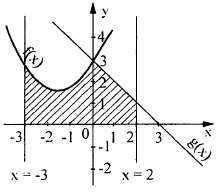
2.Определяем фигуру, площадь которой нужно найти.

Фигура является криволинейной трапецией, которая состоит из двух частей. Одна часть трапеции ограничена графиком функции f(x)= 0,5, а вторая графиком функции g(x)=3-x.

3.Графики функций пересекаются в точке (0;3).

4.Границы интегрирования: для первой части отрезок [-3;0] , для второй  [0;2].

5.Вычислим площадь криволинейной трапеции как сумму площадей её частей

(кв.ед.)

Ответ: 8,5 кв.ед.

Пример 11: Вычислить площадь фигуры, ограниченной линиями:

                     y=4x , y=5 ,  x=3 и осью Оу.

Решение:

1). Строим данные линии.

Графиком функции  y=4x является парабола, ветви которой направлены вниз.  Вершиной параболы является точка (2;4), нули функции  x= 0; 4.

Графиком функции  y=5 является прямая, параллельная оси Ох, проходящая через точку (0;5).

Графиком функции  x=3 является прямая, параллельная оси Оу, проходящая через точку (3;0).

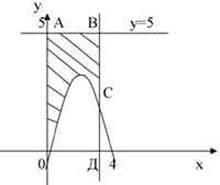
2). Определяем фигуру, площадь которой нужно найти.

Фигура является криволинейной трапецией, ограниченной сверху графиком функции  y=5 , а  снизу – графиком функции y=4x

3). Границами интегрирования является отрезок [0;3].

4). Площадь получившейся фигуры можно найти по формуле :

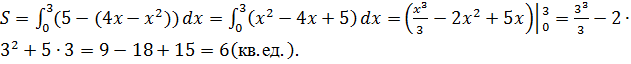
Ответ: 6 кв.ед.

Контрольные вопросы для подготовки к практической работе:

1.     Что называется первообразной?

2.     Что называется неопределенным интегралом?

3.     Что такое интегрирование?

4.     Сформулируйте свойства неопределенного интеграла.

5.     Что называется криволинейной трапецией?

6.     Как вычислить площадь криволинейной трапеции? Перечислите алгоритм.

7.     Что называется определенным интегралом и как его вычислить?

8.     Запишите формулу Ньютона-Лейбница.

Типовые задания для подготовки к практической работе:

1)    Найдите одну из первообразных функции:

а)  f(x)=       б)  f(x)=             в) f(x)=3

     2) Для функции f(x) найдите первообразную, график которой проходит через точку М:

         а) f(x)=4x+1, M(-2;5);         б) f(x)=sin2x, M(.

3)    Вычислите неопределенный интеграл:    

     а)  ;        б)  .

4)    Вычислите определенный интеграл:

а)   ;          б)   ;          в)  .

     5)  Найдите площадь криволинейной трапеции, изображенной на рисунке:

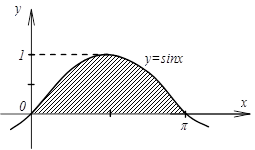
6) Найдите площадь фигуры, ограниченной линиями:

    а) ,     y=0,    x=0,   x=2.

    б) y = cosx ,    y=0,   x=,   x=.

Практическая работа

Тема: Интеграл. Площадь криволинейной трапеции.

Цель:  Отработать навыки вычисления интегралов функций и использования интеграла для нахождения площадей фигур.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ТЕМЕ «МНОГОГРАННИКИ. ПЛОЩАДЬ ПОВЕРХНОСТИ МНОГОГРАННИКОВ».

1.                     Многогранник.

Определение: Многогранник – геометрическое тело, ограниченное плоскими многоугольниками.

        Многоугольники, ограничивающие многогранник, называются гранями, их стороны – рёбрами, а вершины – вершинами многогранника. Отрезки, соединяющие две какие-нибудь вершины, не принадлежащие одной грани, называются диагоналями многогранника.

       Мы будем рассматривать только выпуклые многогранники, то есть такие, которые расположены по одну сторону от каждой своей грани.

2.                     Призма.

         Определение: Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами.

      Грани, которые находятся в параллельных плоскостях, называются основаниями призмы, а остальные грани – боковыми гранями призмы.

      В зависимости от основания призмы бывают треугольными, четырёхугольными, шестиугольными и другие.

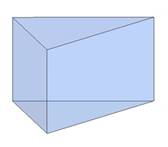
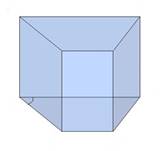
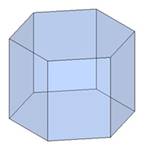
     Рисунок                                                                               

     Призма, боковые ребра которой перпендикулярны основаниям, называется прямой, в противном случае – наклонной.

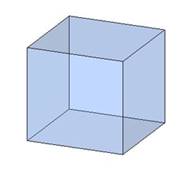
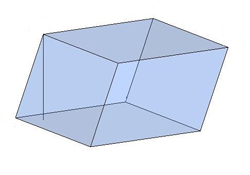
              Рисунок                                                                

        Прямая призма, у которой в основаниях лежат правильные n-угольники, называется правильной n-угольной призмой.

      Расстояние между основаниями призмы называется высотой призмы. Высота прямой призмы совпадает с боковым ребром.

Свойства призмы:

1.     Основания призмы являются равными многоугольниками.

2.     Боковые грани призмы являются параллелограммами.

3.     Боковые ребра призмы параллельны и равны.

      3. Параллелепипед

      Определение: Параллелепипед – это четырёхугольная призма, все грани которой являются параллелограммами.

      Параллелепипед, боковые ребра которого перпендикулярны к плоскостям оснований, называется прямым. В противном случае параллелепипед называется наклонным. Прямой параллелепипед, основания которого – прямоугольники, называется прямоугольным. Все грани прямоугольного параллелепипеда – прямоугольники.

     Свойства параллелепипеда:

1.     Противолежащие грани параллелепипеда попарно равны и параллельны.

2.     Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

3.     Середина диагонали параллелепипеда является его центром симметрии.

Виды параллелепипедов:  

      Свойства прямоугольного параллелепипеда:

1.     Все грани прямоугольного параллелепипеда – прямоугольники. Противолежащие грани попарно равны.

2.     Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:

3.     Все диагонали прямоугольного параллелепипеда равны.

4. Диагональное сечение призмы

     Диагональное сечение призмы – это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Каждое диагональное сечение содержит две диагонали призмы. Диагональное сечение прямой призмы является прямоугольником. Диагональное сечение наклонной призмы – параллелограмм.

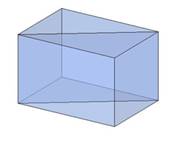
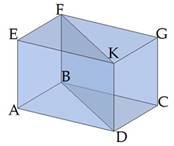
 Рисунок 

    У правильного шестиугольника диагонали бывают двух видов – короткие и длинные. В связи с этим, существует два вида диагональных сечений шестиугольной призмы:

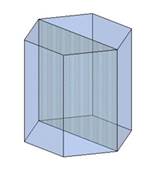
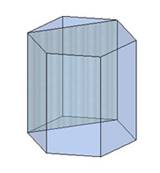
        Рисунок

       Как найти диагонали правильного шестиугольника, если известна длина его стороны. Учитывая то, что все углы правильного шестиугольника равны по 120, легко найти прямоугольный треугольник, в котором есть угол 30, и использовать соотношения в этом треугольнике.

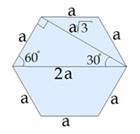
      Рисунок

          5. Углы, образованные диагональю призмы и элементами призмы.

        При решении задач очень важно уметь обозначать углы, образованные диагоналями призмы и элементами призмы. Рассмотрим различные случаи:

     6. Пирамида

       Определение: Пирамидой называется многогранник, в основании которого лежит n-угольник, а боковыми гранями являются треугольники с общей вершиной, которая называется вершиной пирамиды. Боковыми рёбрами пирамиды называются рёбра, по которым пересекаются боковые грани. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость её основания.

       Пирамида, основанием которой является правильный многоугольник, и вершина пирамиды проектируется в центр основания, называется правильной пирамидой. Боковые грани правильной пирамиды – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды называется апофемой.

       Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром. Все грани тетраэдра – равные равносторонние треугольники.

       Рассмотрим примеры правильных пирамид:

        Если боковые рёбра пирамиды с плоскостью основания образуют равные углы, то рёбра пирамиды равны, и вершина пирамиды проектируется в центр окружности, описанной около многоугольника основания.

      Главные зависимости для многоугольников, около которых можно описать окружность:

      Если боковые грани пирамиды с её основанием образуют равные двугранные углы, то все высоты боковых граней пирамиды равны (апофемы), и вершина пирамиды проектируется в центр окружности, вписанной в многоугольник основания.

      Главные зависимости для многоугольников, в которые можно вписать окружность:

      Формулы для вычисления радиусов описанных и вписанных окружностей правильных многоугольников, площадей:

       7. Усечённая пирамида.

       Определение: Усеченной пирамидой называется часть пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной основанию. Например, пирамида .

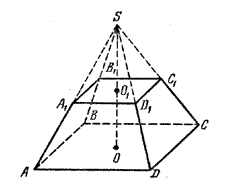
           Рисунок

        Основаниями усечённой пирамиды называются параллельные грани, где  – нижнее основание,  – верхнее основание. Высота усечённой пирамиды – отрезок прямой, перпендикулярный основаниям и заключённый между их плоскостями. На рисунке это . Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами.

       8. Площадь поверхности многогранника.

        Определение: Площадью полной поверхности многогранника называется сумма площадей всех его граней, а площадью боковой поверхности многогранника – сумма площадей его боковых граней.

Формулы для вычисления площадей поверхностей многогранников:

Рассмотрим примеры решения задач.

    Пример 1: Ребро куба равно 4 см. Найти:

                       1) диагональ грани куба;

                       2) диагональ куба;

                       3) площадь полной поверхности куба.

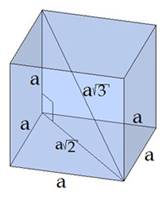Решение: Так как у куба все рёбра равны, то по теореме Пифагора можно получить формулу для вычисления диагонали грани куба: .

    Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. Тогда диагональ куба: . Можно получить формулу: . По условию задачи , тогда:

1) (см)

2)  (см)

3) ).

Ответ:  см,  см, .

       Пример 2: Найти диагональ и площадь полной поверхности прямоугольного параллелепипеда, если его измерения равны 16; 2; 8 см.

Решение: Диагональ прямоугольного параллелепипеда находим по формуле:

Площадь поверхности прямоугольного параллелепипеда найдем по формуле:

Ответ: ,  

         Пример 3: Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм и 3 дм, боковое ребро призмы равно 10 дм. Найдите площадь боковой и полной поверхности призмы.

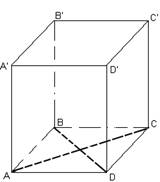 Дано: , O – точка пересечения диагоналей основания призмы.  , .

Найти: .

Решение:

    Используя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону ромба:

 Рассмотрим прямоугольный.

 дм

 дм

Боковое ребро прямой призмы является её высотой, найдем площадь боковой поверхности призмы:

Площадь полной поверхности пирамиды найдем по формуле:

Ответ:   , .

     Пример 4: Сторона основания правильной треугольной призмы равна 8 см, боковое ребро – 6см. Найти площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.

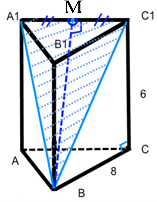Дано: – правильная треугольная призма, .  сечение, проходящее через сторону  и вершину  

Найти: .

Решение:

Сечением является равнобедренный треугольник , так как  как диагонали равных граней.

1) Рассмотрим  – прямоугольный, по теореме Пифагора:

2) Обозначим точкой М середину основания равнобедренного треугольника . BM – медиана и высота. Рассмотрим  – прямоугольный. По теореме Пифагора:  см

3) .

Ответ: .

      Пример 5: Диагональ правильной четырёхугольной призмы образует с плоскостью боковой грани  угол в 30 Найдите угол между диагональю и плоскостью основания.

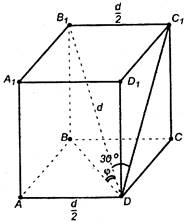                         Дано:. Диагональ  образует с плоскостью боковой грани угол .

Найти: .

Решение:

1) Рассмотрим – прямоугольный () с острым углом 30, тогда .

2) Найдем диагональ основания призмы  – квадрат со стороной, . Тогда диагональ квадрата .

3) Рассмотрим  – прямоугольный.

 , тогда .

Ответ:

     Пример 6: Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна 360  Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найти площадь боковой поверхности пирамиды.

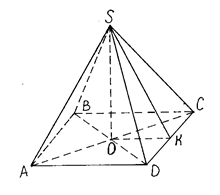Дано: – пирамида.  – параллелограмм, см, 36 см,  , 12 см – высота пирамиды.

Найти: .

Решение: Площадь боковой поверхности пирамиды равна сумме площадей всех боковых граней, которые попарно равны (по трём сторонам). Достаточно найти площади двух соседних граней.

1) По свойству параллелограмма:

.

В  проведём , тогда

2) Рассмотрим – прямоугольный. По теореме Пифагора:

 см

3) По теореме о трёх перпендикулярах , тогда

4) Аналогично найдем

90

По теореме Пифагора найдем :

 см

По теореме о трёх перпендикулярах , тогда

5) Найдем площадь боковой поверхности пирамиды:

Ответ: .

Контрольные вопросы для подготовки к практической работе:

1) Что называется многогранником? Перечислите основные элементы многогранника.

2) Какой многогранник называется призмой? Перечислите: основные элементы призмы, виды призм, свойства призмы. Что называется диагональным сечением призмы? Как построить диагональное сечение призмы?

3) Кокой многогранник называется параллелепипедом? Перечислите: основные элементы параллелепипеда, виды параллелепипедов, свойства.

4) Какой многогранник называется пирамидой? Перечислите: основные элементы пирамиды, виды пирамид, свойства.

5) Какой многогранник называется усечённой пирамидой? Перечислите: основные элементы усечённой пирамиды.

6) Что называется площадью полной  поверхности многогранника? Повторите формулы нахождения площадей поверхности многогранников.

Типовые задания для подготовки к практической работе:

1) Ребро куба равно 7 см. Найдите: диагональ грани куба, диагональ куба, площадь полной поверхности куба.

2) Найти диагональ и площадь полной поверхности прямоугольного параллелепипеда, если его измерения равны 12; 4; 6 см.

3) Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 см и 16 см. Площадь большей боковой грани равна 120 . Вычислите высоту призмы.

4) Диагональ прямоугольного параллелепипеда с плоскостью основания образует угол 45, стороны основания равны 12 см и 16 см. Вычислите высоту параллелепипеда.

5) Диагональ правильной четырёхугольной призмы равна 26 см и образует с боковой гранью угол 30. Вычислите площадь основания призмы.

6) Высота правильной треугольной призмы равна 5 см, площадь боковой поверхности равна 60 . Вычислите сторону основания призмы.

7) В правильной четырёхугольной призме площадь основания равна 144 , а высота равна 14 см. Найдите диагональ призмы и площадь полной поверхности.

8) В правильной треугольной пирамиде сторона основания равна 8 см, а апофема равна 13 см. Найдите площадь полной поверхности пирамиды.

9) Сторона основания правильной треугольной пирамиды равна 24 дм, а боковое ребро с плоскостью основания образует угол 30. Вычислите высоту пирамиды.

Практическая работа

Тема: Многогранники. Площадь поверхности многогранников.

Цель: Отработать навыки нахождения неизвестных элементов многогранника и использования формул для нахождения площади поверхности многогранника.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ТЕМЕ «ТЕЛА ВРАЩЕНИЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ ТЕЛ ВРАЩЕНИЯ».

       Конус, цилиндр и шар – это тела вращения, так как их можно получить вращением определённой фигуры вокруг некоторой оси.

       1. Цилиндр.

       Определение: Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Эти круги называются основаниями цилиндра. Отрезки, соединяющие соответствующие точки оснований – образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.

      Если образующие перпендикулярны основаниям, то цилиндр называется прямым цилиндром, иначе – наклонным. Прямой цилиндр можно получить, если вращать прямоугольник вокруг одной из его сторон (рисунок  )

                   Рисунок                                                                 Рисунок

        Мы будем рассматривать только прямые цилиндры. Основные элементы цилиндра:

1. Прямая – ось цилиндра.

2. Отрезок – высота цилиндра – это расстояние между основаниями цилиндра.

3. Отрезки  – образующие цилиндра, равны высоте цилиндра.

4. Отрезок  – радиус цилиндра – радиус основания цилиндра.

       Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым (рисунок  ). Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом, равный основаниям цилиндра (рисунок  ).

            Рисунок                                                                                    Рисунок

       За площадь боковой поверхности цилиндра принимается площадь её развёртки, которая является прямоугольником. Вычисляется по формуле:

, где  – радиус цилиндра, а   – высота цилиндра.

       Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Вычисляется по формуле:

.

       Рассмотрим примеры решения задач.

       Пример 1. Площадь боковой поверхности цилиндра равна , а диаметр основания равен 9 см. Найдите высоту цилиндра.

 Дано: Цилиндр, ,

Найти: h.

Решение:

Площадь боковой поверхности цилиндра вычисляется по формуле: , тогда

Найдем радиус цилиндра:

=

Ответ:

        Пример 2. Радиус основания цилиндра равен 5 см, а его образующая – 9 см. Найдите площадь осевого сечения.

Дано: Цилиндр,

Найти:

Решение:

Осевым сечением является прямоугольник

Ответ: .

        Пример 3. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.

 Дано: Цилиндр, , ,

Найти:

Решение:

Сечением цилиндра плоскостью, параллельной оси цилиндра, является прямоугольник .

Расстоянием от плоскости  до оси цилиндра является отрезок

Рассмотрим треугольник  – он равнобедренный с основанием , значит  – высота и медиана треугольника .

Треугольник  – прямоугольный, тогда по теореме Пифагора:

 – образующая цилиндра, равна его высоте.

.

Ответ: .

        Пример 4. Найдите стоимость металлической трубы, длина которой 10 м, а внутренний диаметр равен 30 см, если  трубы стоит 800 р.

Решение: Так как необходимо вычислить стоимость металлической трубы в форме цилиндра, то нужно найти площадь боковой поверхности цилиндра.

Вычислим стоимость трубы:

Ответ:

       2. Конус.

       Определение: Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Все образующие конуса равны друг другу.

 Конус – тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

Основные элементы конуса:

Точка P – вершина конуса

Круг с центром в точке О – основание конуса

Отрезок  АО – радиус конуса

Прямая PO – ось конуса

Отрезок PO – высота конуса

Отрезки PA и PB – образующие конуса, PA = PB.

Рисунок

      Рассмотрим сечения конуса различными плоскостями. Если секущая плоскость проходит через ось конуса (рисунок  ), то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Если секущая плоскость перпендикулярна к оси конуса (рисунок  ), то сечение конуса представляет собой круг с центром, расположенным на оси конуса.

Рисунок                                                                        Рисунок

       За площадь боковой поверхности конуса принимается площадь её развёртки, которая является круговым сектором. Вычисляется по формуле:

 , где  – радиус конуса,  – образующая конуса.

       Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания конуса. Вычисляется по формуле:

 .

       Определение: Усечённым конусом называется часть конуса, заключённая между его основанием и секущей плоскостью, параллельной основанию (рисунок  ).

        Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры,– высотой усечённого конуса. Часть конической поверхности, ограничивающая усечённой конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Все образующие усечённого конуса равны друг другу.

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям.

Основные элементы усечённого конуса:

Круг с центром в точке  – нижнее основание усечённого конуса.

Круг с центром в точке  – верхнее основание усечённого конуса.

Отрезок  – высота усечённого конуса.

Отрезок  – образующая усечённого конуса.

Рисунок

        Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую, то есть:

        Рассмотрим примеры решения задач.

        Пример 1. Высота конуса равна 57 см, а диаметр конуса равен 152 см. Найти образующую конуса.

Дано: Конус,  .

Найти: l

Решение:

Рассмотрим треугольник  – он прямоугольный, тогда по теореме Пифагора:

 см

 см.

Ответ: 95 см.

       Пример 2. Найти площадь полной поверхности выточенной детали в форме конуса, если площадь его осевого сечения равна , а высота изделия равна 10 см. Результат округлите до десятых.

       Для решения этой задачи можно воспользоваться чертежом из предыдущей задачи.

Дано: Конус, ,

Найти: .

Решение: Площадь полной поверхности конуса вычисляется по формуле , где  – образующая конуса,  – радиус основания конуса.

Осевым сечением конуса является равнобедренный треугольник , площадь которого равна , а его высота   Площадь равнобедренного треугольника можно найти по формуле:

, тогда подставляя известные величины, получим уравнение:

Для конуса отрезок  является диаметром, тогда можно найти радиус конуса:

Образующая конуса , её можно найти по теореме Пифагора из прямоугольного треугольника .

 дм.

Находим площадь полной поверхности выточенной детали:

Ответ:  .

       Пример 3. Высота конуса 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60, если плоскость сечения образует с плоскостью основания конуса угол 30.

Дано: Конус, , хорда,

Двугранный угол между плоскостью  и      плоскостью основания конуса равен .

Найти:

Решение:

Построим линейный угол двугранного угла. Проводим , строим отрезок . По теореме о трёх перпендикулярах . Так как  и , поэтому  – линейный угол двугранного угла и .

Сечением является равнобедренный треугольник , .

Рассмотрим треугольник  – прямоугольный с , тогда

.

Рассмотрим треугольник  – равносторонний, так как  и , тогда .– высота и медиана.

Рассмотрим треугольник  – прямоугольный, , .

Рассмотрим треугольник  – прямоугольный, ,.

Тогда , откуда , тогда .

.

Ответ: .

Скачано с www.znanio.ru