Методические указания предназначены для использования обучающимися при выполнении заданий по практическим занятиям и лабораторным работам по учебной дисциплине/междисциплинарному курсу ЕН.01 Математика по специальности/ профессии 22.02.07 Порошковая металлургия, композиционные материалы, покрытия . В методических указаниях предлагаются к выполнению практические работы, предусмотренные рабочей программой учебной дисциплины/ междисциплинарного курса.

ПРАВИТЕЛЬСТВО САНКТ-ПЕТЕРБУРГА

КОМИТЕТ ПО НАУКЕ И ВЫСШЕЙ ШКОЛЕ

Санкт-Петербургское государственное бюджетное профессиональное образовательное учреждение «Академия машиностроения имени Ж.Я. Котина»

УТВЕРЖДАЮ

Заместитель директора

по учебно-методической работе

_______________ Е.В.Щеглова

«______» _____________2018г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для практических занятий и лабораторных работ

по дисциплине/междисциплинарному курсу

_________________ЕН.01 Математика_____________

по специальности / профессии 22.02.07 Порошковая металлургия,

композиционные материалы, покрытия

__________________________2 (3)______________________

(курс, семестр)

Санкт-Петербург

2018г.

ОДОБРЕНО

Кафедральной комиссией/

предметной (цикловой) комиссией

общеобразовательных дисциплин

Протокол от «__» _ ___ 201 г. №____

Председатель: Козлов О.В.

Методические указания рассмотрены

Методическим советом

и рекомендованы для утверждения

протокол № ___ от _______________ г.

Организация-разработчик: СПБ ГБПОУ «АМК»

В методических указаниях предлагаются к выполнению практические работы, предусмотренные рабочей программой учебной дисциплины/ междисциплинарного курса.

Разработчик: преподаватель СПб ГБПОУ «АМК» преподаватель математики высшей категории Огур Л.И.

СОДЕРЖАНИЕ

1. Пояснительная записка. 4

2. Планирование практических занятий. 7

3. Критерии оценки выполненных заданий и степени овладения запланированных умений. 8

4 Общие методические рекомендации по организации и проведению

практических занятий /лабораторных работ. 8

5. Практического задания. 9

1. Пояснительная записка

Методические указания разработаны для практических занятий/лабораторных работ по учебной дисциплине/МДК _____ЕН.01 Математика____по специальности/ профессии _ 22.02.07 Порошковая металлургия, композиционные материалы, покрытия

в соответствии с Федеральным государственным образовательным стандартом среднего профессионального образования, утвержденным приказом Министерства образования и науки Российской Федерации от ___________ № _____.

Результатом освоения программы учебной дисциплины/ МДК является овладение обучающимися профессиональными (ПК) и общими (ОК) компетенциями

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК4.Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК8.Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ПК 3.1. Регулировать технологический процесс получения порошковых материалов на основе заданных параметров.

ПК3.4.Оформлять технологическую документацию с использованием информационно-компьютерных технологий.

В результате изучения учебной дисциплины/ МДК обучающийся должен:

уметь:

- анализировать сложные функции и строить их графики;

- выполнять действия над комплексными числами;

- вычислять значения геометрических и алгебраических величин;

- производить операции над матрицами и определителями;

-решать задачи на вычисление вероятности с использованием элементов комбинаторики;

- решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;

- решать системы линейных уравнений различными методами.

В результате освоения дисциплины обучающийся должен знать:

- основные математические методы решения прикладных задач;

- основные понятия и методы математического анализа, линейной алгебры, теорию комплексных чисел, теории вероятностей и математической статистики;

- основы интегрального и дифференциального исчисления;

- роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности

Результатом освоения программы общеобразовательной учебной дисциплины является достижение обучающимися следующих результатов:

• личностных:

− сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;

− понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

− развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;

− овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

− готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

− готовность и способность к самостоятельной творческой и ответственной деятельности;

− готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;

− отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;

• метапредметных:

− умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность;

− использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности;

− выбирать успешные стратегии в различных ситуациях;

− умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

− владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

− готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;

− владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

− владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;

− целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;

• предметных:

− сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

− сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

− владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;

− владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;

− сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

− владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;

− сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

− владение навыками использования готовых компьютерных программ при решении задач.

При разработке содержания практических работ учитывался уровень сложности освоения обучающимися соответствующей темы, общих и профессиональных компетенций.

Методические указания по учебной дисциплине/ МДК имеют практическую направленность и значимость. Формируемые в процессе практических занятий умения могут быть использованы обучающимися в будущей профессиональной деятельности.

Выполнение обучающимся практических /лабораторных работ по ЕН.01 Математика способствует:

развитию познавательных интересов и интеллектуальных способностей обучающихся;

воспитанию ответственного отношения к предмету.

Основными этапами практического занятия /лабораторной работы являются:

− проверка знаний обучающихся – их теоретической подготовленности к занятию;

− инструктаж, проводимый преподавателем;

− выполнение заданий, работ, упражнений;

− последующий анализ и оценка выполненных работ и степени овладения обучающимися запланированными умениями.

Методические указания включают:

− Планирование практических /лабораторных занятий;

− Общие методические рекомендации по организации и проведению практических работ/лабораторных занятий;

− Практические задания, сопровождающиеся указаниями для их выполнения;

− Критерии оценки выполнения работ и степени овладения обучающимися запланированных умений (освоенных компетенций).

2. Планирование практических занятий

/лабораторных работ

№ п/п	Наименование раздела, темы	Наименование практического/ лабораторного занятия	Кол-во часов
	Раздел № 1. Алгебра (Теория чисел)
1	Тема 1.2 Комплексные числа	Практическое занятие № 1	2
	Раздел 2. Математический анализ: Дифференциальное и интегральное исчисление
2	Тема 2.1. Предел функции. Вычисление предела с использованием первого и второго замечательных пределов.	Практическое занятие № 2	2
3	Тема 2.2. Производная. Производная сложной функции.	Практическое занятие №3	2
4	Тема 2.2. Производная. Решение примеров.	Практическое занятие №4	2
5	Тема 2.5 Исследование функций и построение графиков	Практическое занятие №5	2
6	Тема 2.7 Поиск оптимального решения	Практическое занятие №6	2
7	Тема 2.8 Неопределённый интеграл. Основные методы интегрирования.	Практическое занятие №7	2
8	Тема 2.9 Определённый интеграл. Интегрирование простейших функций.	Практическое занятие №8	2
9	Тема 2.10 Нахождение площадей .	Практическое занятие №9	2
10	Тема 2.10 Нахождение объёмов.	Практическое занятие №10	2
	Раздел 3. Линейная алгебра
11	Тема 3.1 Матрицы. Определители и их основные свойства.	Практическое занятие №11
12	Тема 3.2 Определители, вычисление определителей.	Практическое занятие №12	2
13	Тема 3.2 Определители, вычисление определителей. Правило вычисления определителей.	Практическое занятие №13	2
14	Тема 3.3 Системы линейных уравнений	Практическое занятие №14	2
15	Тема 3.4 Матрицы системы линейных уравнений.	Практическое занятие №15
16	Дифференцированный зачет	Практическое занятие №16	2

3. Критерии оценки выполненных заданий и степени овладения запланированных умений

1. Критерии оценки выполнения заданий по практическим занятиям /лабораторным работам:

Оценка	Требования к знаниям
отлично	Оценка «отлично» выставляется обучающемуся, если он глубоко и прочно усвоил программный материал, исчерпывающе, последовательно и логически стройно его излагает, умеет тесно увязывать теорию с практикой, свободно справляется с заданиями, причем не затрудняется с ответом при видоизменении вопросов; имеет необходимые практические навыки выполнения заданий.
хорошо	Оценка «хорошо» выставляется обучающемуся, если он твердо знает материал, не допуская существенных неточностей в ответе, в ходе выполнения практических заданий имеются незначительные погрешности, но в целом практические навыки по выполнению заданий сформированы.
удовлетворительно	Оценка «удовлетворительно» выставляется обучающемуся, если он имеет знания только основного материала, но не усвоил его деталей, допускает неточности, недостаточно правильные формулировки, нарушения логической последовательности в выполнении заданий , необходимые практические навыки работ с не сформированы, большинство заданий выполнено с ошибками.
неудовлетворительно	Оценка «неудовлетворительно» выставляется обучающемуся, который не знает значительной части программного материала, допускает существенные ошибки, неуверенно, с большими затруднениями выполняет практические работы. Как правило, оценка «неудовлетворительно» ставится обучающимся, которые не могут продолжить обучение без дополнительных занятий по соответствующей дисциплине.

4 Общие методические рекомендации по организации и проведению

практических занятий /лабораторных работ

Практические занятия/лабораторные работы по дисциплине /МДК проводятся в аудитории. Каждое практическое занятие/лабораторная работа начинается с организационного момента, включающего проверку посещаемости, готовности обучающихся к занятию.

Перед началом преподаватель ставит перед обучающимися задачи, проводит общий инструктаж по выполнению заданий (технике безопасности на рабочем месте).

В ходе выполнения заданий преподаватель направляет, консультирует обучающихся, проводит проверку знаний и умений, делает анализ выполнения задания. Занятие заканчивается оценкой работы обучающихся.

5. Практические задания

Практическое занятие № 1.

Комплексные числа

Цель занятия: Повторить комплексные числа

Задачи:

· учебная –повторить решение примеров с комплексными числами

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У2,З3,ОК01, ОК03, ПК3.1

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1. Тетрадь для практических работ

Ход практического занятия:

1.Для выполнения данных заданий необходимо повторить действия над комплексными числами.

2.На основе исходных данных решить примеры.

Теоретический материал:

Комплексные числа

Практическая работа №1: Действия над комплексными числами

1.Повторить определение комплексного числа в алгебраической форме.

Определение.

Комплексными числами называются числа вида а+bi, где а и b– действительные числа, а число i определяемое равенством i²=-1 (называемое мнимой единицей).

Два комплексных числа а₁+b₁i и а₂+b₂i называются равными, если а₁₌ а_2;b₁₌ b_2.

2.Алгебраическая форма комплексного числа записывается в виде:

z=a+bi,

где а- действительная часть,

b- мнимая часть комплексного числа.

Любое действительное число а содержится в множестве комплексных чисел, его можно записать а=а+аi; 1=1+0i; i=0+1i.

При а=0 комплексное число а+bi обращается в чисто мнимое число bi.

Комплексное число а-bi называется сопряженным с числом а+bi и обозначается z , т.е. ¯z= ^¯a+ ^¯bi= a-bi

Комплексные числа вида a+bi и -a-bi называются противоположными.

Модулем комплексного числа z=a+bi называется число √а₂+b₂

│Z │ =r=│ a+bi│ =√а₂+b₂

Модуль комплексного числа всегда есть действительное неотрицательное число │z│≥0, причем │z│=0.

Множество комплексных чисел обозначается буквой C. Множество комплексных чисел : R Ϲ C, → NCZCQCRCC.

Пример1. Вычисление модуля комплексного числа.

│Z │ =4-3

│Z │ =r=√16+9==√25=5

а=4; r=5; b=-3

Выполнение заданий.

Задания.

Действия на комплексными числами в алгебраической форме.

1.Сложение выполняется только по формуле:

Пример1:

Z₁=5+i

Z₂=-7-9 I => z₁+z₂=z

2.Вычитание комп. чисел вводятся как операция, обратная сложению:

Z₂-Z₁=> Z₂=a₂+b₂i =>z₂-z₁=(a₂ –a₁)+(b₂-b ₁) i

Пример2:

Z₁=3-4i

Z₂=10+5i

3.Умножение определяется по формуле: Z₁Z₂=(a₁+b₁i) (a₂+b₂i)=(a₁a₂- b₁b₂) + (a₁b₂+ a₂ b₁)i

Пример3:

Z₁=2+3i
Z₂=-1-I

1. Деление.│
Формула:

= + i

При делении на комплексное число достаточно умножить числитель и знаменатель дроби на число, сопряженное знаменателю, т.е на a₁-b₁_i

Пример4 : Даны комплементарные числа Z₁=3-4i. Выполнить деление

Z₂=10+5i

Пример 5: Найти комплексное число:

Пример 6: Найти аргумент комплексного числа 1) Z₁=1-i; 2) Z=-4

Контрольные вопросы

1.Дайте определение комплексного числа. 2.Определение мнимой единицы. 3.Как найти степень мнимой единицы? 4.Как изображаются комплексные числа геометрически? 5.Какие комплексные числа называются сопряженными, равными?

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Оформить отчёт о проделанной работе, который должен содержать исчерпывающие текстовые ответы на поставленные вопросы с решениями, пояснениями, результатами решения.

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

1.Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. – М.: Издательский центр «Академия»

2.Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студ. учреждений сред. проф. образования / М.И. Башмаков. -3-е изд., стер. - М.: Издательский центр «Академия»

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 2.

Предел функции. Вычисление предела с использованием первого и второго замечательных пределов.

Цель занятия: Повторить свойства предела, первый и второй замечательные пределы.

Задачи:

учебная – повторить свойства предела, первый замечательный предел и способы решения

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У3,З1,ОК04,ОК08,ПК3.4.

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

Тетрадь для практических работ

Ход практического занятия:

1. Для выполнения данного задания необходимо повторить свойства предела, первый и второй замечательные пределы.

2. На основе исходных данных решить задания.

Теоретический материал:

Свойства предела, первый замечательный предел и способы решения

Практическая работа №2: Предел функции. Вычисление предела с использованием первого и второго замечательных пределов.

Определение

Число А называется пределом последовательности a₁, а₂ ..., если, начиная с некоторого места, все члены этой последовательности будут сколь угодно мало отличаться от А. Обозначение: А = lim а_п .

n͢→∞

Выполнение заданий.

Примеры:

Определить

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 3.

Производная. Производная сложной функции.

Цель занятия: Повторить определение производной и таблицу производных функций.

Задачи:

учебная – повторить определение производной и таблицу производных функций

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У1,З1,З2,ОК01,ОК04,ПК3.1.

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2. Таблицы в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо повторить определение производной и таблицу производных функций

2. На основе исходных данных решить задания.

Теоретический материал:

Производная. Производная сложной функции.

Практическая работа №3: Производная. Производная сложной функции.

Понятие производной.

При решении различных задач механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=() получать новую функцию, которую называют производной функцией ( или просто производной) данной функции () и обозначают символом

y^'= ^' (x) или

Тот процесс, с помощью которого из данной функции () получают новую функцию ^' () , называют дифференцированием и состоит он из следующих трех шагов:

1) даем аргументу приращение Δ и определяем соответствующее приращение функции Δ у= ( + Δ)- ();

2) составляем отношение =

3) считая х постоянным, а Δ →0, находим lim , который

_Δх →0

обозначаем ^' (),как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения х, при котором мы переходим к пределу.

Определение

Производной y^'= ^' () данной функции y= () при данном называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится у нулю, если, конечно,этот предел существует, т.е. конечен.

Таким образом, ^' (x) = lim ,

_Δх →0

или у^'= lim

_Δх →0

Заметим, что если при некотором значении х, например при х=а, отношение

при Δ →0 не стремится к конечному пределу, то в этом случае говорят, что функция () при =a (или в точке =a) не имеет производной или не дифференцируема в точке =a.

Таблица производных .

Производные степенных функций	Производные тригонометрических функций	Производные обратных тригонометрических функций
$\left( c\right) '=0$	$\left( \sin x\right) '=\cos x$	$\left( \arcsin x\right) '=\dfrac {1}{\sqrt {1-x^{2}}}$
$\left( x^{a}\right) '=ax^{a-1}$	$\left( \cos x\right) '=-\sin x$	$\left( \arccos x\right) '=-\dfrac {1}{\sqrt {1-x^{2}}}$
$\left( a^{x}\right) '=a^{x}\ln a$	$\left( \tan x\right) '=\dfrac {1}{\cos ^{2}x}$	$\left( \arctan x\right) '=\dfrac {1}{1+x^{2}}$
$\left( \log_{a}x\right) '=\dfrac {1}{x\ln a}$	$\left( ctg x\right) '=-\dfrac {1}{\sin ^{2}x}$	$\left( arcctg x\right) '=-\dfrac {1}{1+x^{2}}$

$\left( c\right) =\left( const\right)$

Выполнение заданий.

Примеры:

1. у = 2х3 + Зх + 1

2. у = √3х+1.

3. y= ___x_____

х² +1

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 4.

Производная. Решение примеров.

Цель занятия: Способы решения всех видов производных

Задачи:

учебная – повторить способы решения сложных функций всех видов

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У1,З1,З2,ОК01,ОК03,ПК3.1.

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблицы в учебнике

Ход практического занятия:

2. На основе исходных данных решить задания.

Теоретический материал:

Производная. Решение примеров.

Практическая работа №4: Производная. Решение примеров.

Выполнение заданий.

Примеры:

1. у = (х+ 1)⁵

2. у = (2x+3)*(3x²+6x)

3. у = √6x-1

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 5.

Исследование функций и построение графиков

Цель занятия: научиться исследовать функцию и строить графики

Задачи:

учебная –научиться исследовать функцию и строить графики

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У1,З1,З2,ОК04,ОК08,ПК3.4.

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

Тетрадь для практических работ

Ход практического занятия:

1. Для выполнения данного задания необходимо научиться исследованию функций и построению графиков.

2. На основе исходных данных решить задания.

Теоретический материал:

Исследование функций и построение графиков

Практическая работа №5: Исследование функций и построение графиков

Выполнение заданий.

Задания.

Практические правила исследования функции на максимум и минимум с помощью первой производной. Необходимо придерживаться следующего алгоритма:

I. Найти производную f^'(x) функции f(x).

II. Найти критические точки функции y= f(x),т.е. точки, в которых f^'(x) обращается в нуль или терпит разрыв.

III. Исследовать знак производной f^'(x) в промежутках, на которые найденные критические точки делят область определения функции f(x). …………(Студенты должны продолжить.)

IV. …………(Студенты должны продолжить.)

Примеры:

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 6.

Поиск оптимального решения

Цель занятия: Поиск оптимального решения с помощью первой или второй производной

Задачи:

учебная – повторить исследование функций с помощью первой или второй производной

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У1,З1,З2,ОК01,ОК03,ПК3.1.

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

Тетрадь для практических работ

Ход практического занятия:

2. На основе исходных данных решить задания.

Теоретический материал:

Поиск оптимального решения

Практическая работа №6: Поиск оптимального решения

Выполнение заданий.

Примеры:

3) Найдите наименьшее и наибольшее значения функции

4) Закон прямолинейного движения тела задан уравнением

Найти максимальную скорость движения тела .

Контрольные вопросы

1.Изложите практические правила исследования функции на максимум и минимум с помощью первой производной.

2.Как исследуется функция на максимум и минимум с помощью второй производной?

3.Как находится наименьшее и наибольшее значения функции?

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 7.

Неопределённый интеграл. Основные методы интегрирования.

Цель занятия: Повторение неопределённого интеграла, основных методов интегрирования.

Задачи:

учебная – повторить определение неопределённого интеграла, основных методов интегрирования.

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У6,З4,ОК01,ОК03,ПК 3.1

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо повторить определение неопределённого интеграла, основных методов интегрирования.

2. На основе исходных данных решить задания.

Теоретический материал:

Неопределённый интеграл. Основные методы интегрирования.

Практическая работа №7: Неопределённый интеграл. Основные методы интегрирования

Повторить определение неопределенного интеграла и методы решения.

Выполнение заданий.

Примеры:

1. Вычислить ∫ sin² х dx .

2. Вычислить ∫sin 2x dx

3. Вычислить ∫(x³+4x²+5x+1) dx

4. Вычислить ∫ dx

Контрольные вопросы

1. Перечислите свойства первообразной.

2. Как связаны между собой две первообразные для одной и той же

функции?

3. Верно ли, что интеграл от любой степенной функции будет снова степенной функцией?

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 8.

Определённый интеграл. Интегрирование простейших функций.

Цель занятия: Повторение определённого интеграла и интегрирование простейших функций.

Задачи:

учебная – повторить определение интеграла и интегрирование простейших функций.

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У6,З4,ОК04,ОК08,ПК 3.4

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо повторить определённого интеграла и интегрирование простейших функций.

2. На основе исходных данных решить задания.

Теоретический материал:

Определённый интеграл. Интегрирование простейших функций.

Практическая работа №8: Определённый интеграл. Интегрирование простейших функций.

Повторить определение определенного интеграла и методы решения.

Выполнение заданий.

Примеры:

1.Скорость движения точки изменяется по закону v=(3t²+2t+1) (м/с).Найти путь пройденный точкой за 10 с от начала движения.

2. Тело брошено с поверхности земли вертикально вверх со скоростью v=(39,2-9,8t) (м/с). Найти наибольшую высоту подъема тела.

3. Вычислить определенный интеграл

4. Найти площадь одной арки синусоиды

^π

S = ∫₀ sin x dx

К данному примеру сделать схематический чертеж.

Контрольные вопросы

1. Как вычислить площадь плоской фигуры с помощью интеграла?

2. Назовите примеры физических величин, которые можно рассматривать как функции отрезка.

3. Что является плотностью работы как функции отрезка пути?

4. Что является плотностью перемещения как функции отрезка времени?

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 9.

Нахождение площадей.

Цель занятия: Повторение вычисления площади с помощью определенного интеграла

Задачи:

учебная – повторить вычисления площади с помощью определенного интеграла

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У6,З1,З4,ОК01,ОК03,ПК 3.1

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо повторить вычисления площади с помощью определенного интеграла

2. На основе исходных данных решить задания.

Теоретический материал:

Нахождение площадей.

Практическая работа №9: Нахождение площадей.

Выполнение заданий.

Примеры:

1. Найти площадь между дугами парабол у = х² и у = √х

К данному примеру сделать схематический чертеж.

2. Вычислить площадь фигуры, ограниченной данными линиями:

a) y²=x, y=0, x=1, x=4

b) y=x², y=0, x=2,x=3

c) y=x²,y=2x.

Контрольные вопросы

1. Какие вы знаете формулы для нахождения площади треугольника? 2.Что нужно знать, чтобы вычислить площадь фигуры с помощью интеграла?

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 10.

Нахождение объемов.

Цель занятия: Повторение вычисления объемов с помощью определенного интеграла

Задачи:

учебная – повторить вычисления объемов с помощью определенного интеграла

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У6,З1,З4,ОК01,ОК03,ПК 3.1

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо повторить вычисления объемов с помощью определенного интеграла

2. На основе исходных данных решить задания.

Теоретический материал:

Нахождение объемов.

Практическая работа №10: Нахождение объемов.

Выполнение заданий.

Примеры:

1.Вычислить объем тела, образованного вращением вокруг оси Оx фигуры, ограниченной параболой y²=2x, прямой x=3 и осью Оx.

2. Вычислить объем тела, образованного вращением вокруг оси Оx фигуры, ограниченной

осью Оx и полуволной синусоиды y= sin x ( 0 ≤x≤π)

3.Задача: сечение тела плоскостью, перпендикулярной к оси и проходящей через точку с абсциссой , является квадратом, сторона которого равна . Найти объем этого тела.

4. Вычислить объем тела, образованного вращением вокруг оси Оy фигуры, ограниченной параболой y=x², прямой x=4 .

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 11.

Матрицы. Определители и их основные свойства.

Цель занятия: Изучить матрицы, определители и их основные свойства.

Задачи:

учебная – изучить матрицы, определители и их основные свойства.

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У6,З1,З4,ОК04,ОК08,ПК 3.4

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо изучить матрицы, определители и их основные свойства.

2. На основе исходных данных решить задания.

Теоретический материал:

Матрицы, определители и их основные свойства.

Практическая работа №11: Матрицы, определители и их основные свойства.

Матрицы и операции над матрицами.

ОПРЕДЕЛЕНИЕ: Прямоугольная таблица чисел, состоящая из m - строк и n- столбцов, называется матрицей порядка m´n.

А=(а_ij)= a₁₁a₁₂…….a_1n

a₂₁a₂₂…….a_2n

………………

A_m1a_m2…….a_mn

Числа aij (вещественные или комплексные) называются элементами матрицы:

aij Î R или Z .

Первый индекс i обозначает номер строки, а второй индекс j - номер столбца, на пересечении этих строк и столбцов находится элемент aij .

Матрицей порядка 1´n является строка: А = (a1 а2 ....аn ).

Матрицей порядка m´1 является столбец:

a₁

A =

a₂

….

Если число строк матрицы равно числу ее столбцов то такая матрица называется квадратной порядка n´n , или матрицей n -го порядка.

Примеры простейших матриц: нулевая матрица О , единичная матрица Е , диагональная, верхняя и нижняя треугольная, блочная, симметричная, антисимметричная (кососимметричная), обратная, ортогональная, вырожденная и невырожденная,

эрмитова, ортогональная, унитарная, ....

Задание. Запишите примеры простейших матриц.

Однако, не всякие матрицы можно сложить и перемножить между собой, так как имеются ряд ограничений. Например, сложение матриц определено для матриц одинакового порядка, произведение матриц определено при условии, что число столбцов первой матрицы равно числу строк второй матрицы.

В линейной алгебре, кроме этих операций вводятся и другие очень важные операции:

транспонирование матрицы; прямая сумма матриц; след матрицы; определитель матрицы; эрмитово сопряжение матрицы; произведение Ли и произведение Иордана и др.

Операции над матрицами.

· Сложение матриц. При сложении матрицы A и матрицы B порядка m´n получается матрица C = (cij ) того же порядка:

A+ B =C , где cij = aij +bij

Свойства операции сложения:

A+ B = B + A

A+ (B + C) = (A+ B) + C

A+ O = A

· Умножение матрицы на число. При умножении матрицы A на число l

получается матрица D = (dij ) :

lA = D , где dij = laij

Свойства операции умножения:

l(A+ B) = lA+ lB

(a +b)A = aA+ bB

a(lA) = (al)A

Выполнение заданий

Задания. Сложить матрицы: A+B

2 -1 4 1

3 0 -3 -1

А= 5 8 , B= 2 3

2. A+2B

7 4 0 -7 -4 -1

-2 5 1 2 -5 0

А= , B=

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 12.

Определители, вычисление определителей.

Цель занятия: Изучить определители, вычисление определителей.

Задачи:

учебная – изучение определителей, вычисление определителей.

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У7,З1,З4,ОК01,ОК03,ПК 3.1

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо изучить определители, вычисление определителей.

2. На основе исходных данных решить задания.

Теоретический материал:

Определители, вычисление определителей

Практическая работа №12: Определители, вычисление определителей

1. ОПРЕДЕЛИТЕЛИ

Пусть дана матрица.

Число называется определителем второго порядка, соответствующим данной матрице, и обозначается символами (det A, ):

==-.

Определитель матрицы A размера 2x2 (определитель 2-го порядка) – это число, которое можно найти по правилу: произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали.

Определитель второго порядка содержит две строки и два столбца, числа , , , – элементы определителя. Правило вычисления определителя второго порядка можно представить схематически:

Количество строк и столбцов в определителе всегда совпадает. Кроме определителей второго порядка существуют определители 3-го, 4-го и т. д. порядков. Определитель 3-го порядка содержит три строки и три столбца:

Для вычисления определителя 3-го порядка существует несколько правил.

2. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ ТРЕТЬЕГО ПОРЯДКА

2.1.ПРАВИЛО ПРЯМОУГОЛЬНИКА

Для вычисления определителя надо повторить запись первого и второго столбцов. Проведем три левые диагонали, начиная с верхнего левого угла, и три правые диагонали. Три первые слагаемые получаются как результат произведения элементов, стоящих на каждой из левых диагоналей. Следующие три слагаемые получаются при умножении элементов, стоящих на каждой из правых диагоналей.Три последние произведения берутся с противоположным знаком.

Пример 1.

2.2. ПРАВИЛО ТРЕУГОЛЬНИКА

Перемножаются элементы, стоящие на левых диагоналях. Одна диагональ, главная, проходит через три элемента, и две диагонали побочные проходят через два элемента, третьим элементом для них является элемент, стоящий в вершине треугольника (схема 1). Аналогично находим произведения элементов, стоящих на правых диагоналях (схема 2). Эти произведения берутся с обратным знаком.

Пример 2.

2.3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ ПУТЕМ РАЗЛОЖЕНИЯ

ПО ЭЛЕМЕНТАМ СТРОКИ

Прежде чем перейти к следующему правилу вычисления определителя, введем понятие минора и алгебраического дополнения. В определителе

вычеркнем одну строку и один столбец, останется определитель второго порядка, который принято называть минором. Например, при вычеркивании первой строки и первого столбца получим минор

При вычеркивании “i”-й строки и “j”-го столбца получим минор . Через обозначим алгебраическое дополнение элемента . Алгебраическим дополнениемэлементаопределителя называется его минор, взятый со знакос «плюс», если суммаi+j - четное число, и со знаком «минус» если эта сумма нечетная т.е.

По свойствам определителя его можно представить в виде суммы:

что соответствует разложению определителя по элементам первой строки. Аналогично можно разложить по элементам любой строки или столбца.

Пример 3.

Вычислим определитель разложением по элементам строки. Для определенности выберем первую строку.

Тогда , , .

– получен вычеркиванием первой строки и первого столбца.

– получен вычеркиванием первой строки и второго столбца.

Тогда .

Вывод: Вычисление определителей. Определитель матрицы A размера 2x2(определитель 2-го порядка) – это число, которое можно найти по правилу:

(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).

Определитель матрицы A размера 3x3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:

Пример 4. Найти:

Решение. При нахождении определителя воспользуемся сначала формулой,а затем (для вычисления определителей 2-го порядка) формулой .

Выполнение заданий.

Примеры:

Вычислить определители:

2) ;

3) ;

Справка. Число i определяется равенством i²=-1. Называется мнимой единицей.

Контрольные вопросы

1.Что называется матрицей?

2. Что называется матрицей- строкой? Матрицей-столбцом?

3.Какая матрица называется единичной?

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Ответить на контрольные вопросы.

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 13.

Определители, вычисление определителей.

Цель занятия: Изучить определители, вычисление определителей. Правило вычисления определителей

Задачи:

учебная – изучение определителей, вычисление определителей.

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У7,З1,З4,ОК04,ОК08,ПК 3.4

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо изучить определители, вычисление определителей.

2. На основе исходных данных решить задания.

Теоретический материал:

Определители, вычисление определителей. Правило вычисления определителей.

Практическая работа №13: Определители, вычисление определителей. Правило вычисления определителей

Выполнение заданий

Задание 1. Вычислить определитель, разложив его по элементам первой строки:

Задание 2. Вычислить определитель, разложив его по элементам третьей строки:

Задание 3. Вычислить определитель по правилу треугольника и, разложив его по элементам первого столбца:

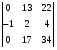
Задание 4. Вычислить определитель:

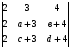
Задание 5. Вычислить определитель: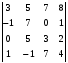

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 14.

Системы линейных уравнений

Цель занятия: Изучить системы линейных уравнений

Задачи:

учебная – изучение системы линейных уравнений

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У7,З1,З4,ОК01,ОК03,ПК 3.1

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо изучить системы линейных уравнений

2. На основе исходных данных решить задания.

Теоретический материал:

Системы линейных уравнений

Практическая работа №14: Системы линейных уравнений

Выполнение заданий

Примеры:

1. 2x-4y+9z=28

7x+3y-6z=-1

7x+9y-9z+5

2. 2x+3y+4z=15

x+y+5z=16

3x-2y+z=1

3. 3x+2y-5z=0

5x-2y-3z=0

x+ y+ z=1

4. 5x+y-3z= -2 4x+3y+2z=16 2x-3y+z=17

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 15.

Матрицы системы линейных уравнений

Цель занятия: Изучить матрицы системы линейных уравнений

Задачи:

учебная – изучение матриц системы линейных уравнений

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У7,З1,З4,ОК04,ОК08,ПК 3.4

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо изучить матрицы системы линейных уравнений

2. На основе исходных данных решить задания.

Теоретический материал:

Матрицы системы линейных уравнений

Практическая работа №15: Матрицы системы линейных уравнений

Матрица размера mхn– это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.

Например, рассмотрим матрицу А размерности 2 х 3:

В этой матрице две строки (m= 2) и три столбца (n= 3), т.е. она состоит из шести элементов _ij, где i- номер строки, j - номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается). А именно,a₁₁= 3;a₁₂= 0;a₁₃= -1;a₂₁= 0;a₂₂= 1,5;a₂₃= 5.

Матрицы А и В одного размера (mхn) называют равными, если они поэлементно совпадают, т.е.a_ij=b_ijдля, т.е. для любыхiиj(можно записать"i,j).

Матрица-строка– это матрица, состоящая из одной строки, а матрица-столбец– это матрица, состоящая из одного столбца.

Например, - матрица-строка, а.

Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n.

Например, - квадратная матрица второго порядка.

Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (a_ij,i=j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементыa₁₁= 3 иa₂₂= 5.

Диагональная матрица– это квадратная матрица, в которой все недиагональные элементы равны нулю. Например,- диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например,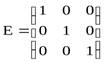- единичная матрица третьего порядка.

Матрица называется нулевой, если все ее элементы равны нулю.

Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например,- треугольная матрица третьего порядка.

Операции над матрицами

Над матрицами можно производить следующие операции:

1. Умножение матрицы на число. Произведением матрицы А на число l называется матрица В =lА, элементы которой b_ij=la_ijдля любых i и j.

Например, если, то.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой с_ij=a_ij+b_ijдля "i,j.

Например, если то

Отметим, что через предыдущие операции можно определить вычитание матриц одинакового размера: разность А-В = А + (-1)*В.

3. Умножение матриц. Произведением матрицы А размера mxn на матрицу В размера nxp называется такая матрица С, каждый элемент которой с_ijравен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е..

Например, если

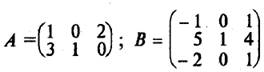, то размер матрицы-произведения будет 2 x 3, и она будет иметь вид:

В этом случае матрица А называется согласованной с матрицей В.

Подчеркнем, что сложение (вычитание) и умножение матриц определены не для любых двух матриц, а только для удовлетворяющим определенным требованиям к своей размерности. Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными).

Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами.

1) Коммутативный (переместительный) закон сложения:

А + В = В + А

2) Ассоциативный (сочетательный) закон сложения:

(А + В) + С = А + (В + С)

3) Дистрибутивный (распределительный) закон умножения относительно сложения:

l(А + В) = lА +lВ

А (В + С) = АВ + АС

(А + В) С = АС + ВС

5) Ассоциативный (сочетательный) закон умножения:

l(АВ) = (lА)В = А(lВ)

A(BС) = (АВ)С

Подчеркнем, что переместительный закон умножения для матриц в общем случае НЕ выполняется, т.е. AB ¹BA. Более того, из существования AB не обязательно следует существование ВА (матрицы могут быть не согласованными, и тогда их произведение вообще не определено, как в приведенном примере умножения матриц). Но даже если оба произведения существуют, они обычно разные.

В частном случае коммутативным законом обладает произведение любой квадратной матрицы А на единичную матрицу того же порядка, причем это произведение равно А (умножение на единичную матрицу здесь аналогично умножению на единицу при умножении чисел):

АЕ = ЕА = А

В самом деле,

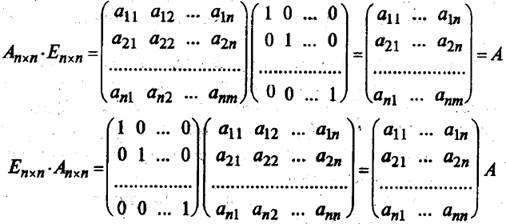
Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например,

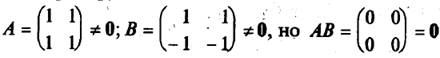
Выполнение заданий

Примеры:

3x₁-5x₂=13

2x₁-7x₂=81

5x₁-8x₂+x₃=2

2. 3x₁-2x₂+6x₃=-7

2x₁-x₂-x₃=-5

2x₁-3x₂+x₃=-7

3. x₁+4x₂+2x₃=-1

2x₁-4x₂= -5

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Практическое занятие № 16.

Цель занятия: Проверить уровень освоения изученного материала

Задачи:

учебная – контроль изученного материала

· воспитательная – воспитание аккуратности и внимательности при выполнении письменных работ

· развивающая – расширение кругозора, умение выделять главное в изученном материале

· сформировать У7,З1,З4, ОК01, ОК03,ОК04,ОК08, ПК 3.1,ПК 3.4

Время на выполнение работы:

2час

Оборудование, технические средства и инструменты:

1.Тетрадь для практических работ

2.Таблица в учебнике

Ход практического занятия:

1. Для выполнения данного задания необходимо изучить матрицы системы линейных уравнений

2. На основе исходных данных решить задания.

Теоретический материал:

Изученный материал за семестр

Практическая работа №16: дифференцированный зачет

1.Предел функции, область определения функции.

2.Основные теоремы о пределах. Способы решения.

3.Определение производной. Нахождение простейших табличных формул производной.

4.Геометрический смысл производной. Примеры.

5.Механический смысл производной. Примеры. 6.Производные основных элементарных функций. 7. Производные суммы, произведения и частного двух функций. 8. Производная степенной функции с натуральным показателем. 9. Производная тригонометрических функций. 10. Правило дифференцирования сложной и обратной функций. 11. Построение графиков функций с помощью производной. 12. Исследование функции с помощью производной. 13. Первообразная и неопределенный интеграл. 14. Основные свойства неопределенного интеграла. Таблица интегралов.

15.Геометрические приложения неопределенного интеграла.

16.Физические приложения определенного интеграла.

17. Методы интегрирования: непосредственное интегрирование, метод разложения, метод замены переменной. 18. Задача о площади криволинейной трапеции. 19. Свойства определенного интеграла. Формула Ньютона- Лейбница. 20. Определённый интеграл и его геометрический смысл. 21. Определённый интеграл и его физический смысл. 22. Способы вычисления определённого интеграла. 23. Вычисление площадей плоских фигур с помощью определённого интеграла. 24.Вычисление площади и объема вращения криволинейной трапеции. 25. Определение матрицы. Виды матриц. 26.Действия над матрицами. 27.Сложение матриц. 28.Умножение матриц. Свойства умножения матриц. 29. Вычисление определителя второго порядка. 30.Вычисление определителя третьего порядка. (Формулы Гауса и Крамера).

31.Элементы комбинаторики. 32.Элементы теории вероятностей и математической статистики. 33.Случайная величина. Закон ее распределения. 34.Математическое ожидание. 35.Дисперсия случайной величины, ее свойства. 36.Переход комплексного числа от тригонометрической формы к показательной форме. 37.Переход комплексного числа от показательной формы к тригонометрической форме. 38.Переход комплексного числа от показательной формы к алгебраической форме. 39. Переход комплексного числа от алгебраической формы к тригонометрической форме. 40.Переход комплексного числа от тригонометрической формы к алгебраической форме. 41. Комплексное число. Показательная форма. Примеры. 42. Комплексное число. Тригонометрическая форма. Примеры. 43. Комплексное число. Алгебраическая форма. Примеры.

Итоговое выступление преподавателя/подведение итогов:

Оформление результатов работы

Сформулировать выводы по результатам работы.

Сдать и защитить работу.

Список рекомендуемой литературы

Учебники и учебные пособия:

· Основные

3. Дадаян А.А. Математика: учебник – 3-е изд. М.: Форум, (Профессиональное образование.).

Скачано с www.znanio.ru

ПРАВИТЕЛЬСТВО САНКТ-ПЕТЕРБУРГА

ОДОБРЕНО Кафедральной комиссией/ предметной (цикловой) комиссией общеобразовательных дисциплин

СОДЕРЖАНИЕ

Пояснительная записка Методические указания разработаны для практических занятий/лабораторных работ по учебной дисциплине/МДК _____ЕН

− понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;…

При разработке содержания практических работ учитывался уровень сложности освоения обучающимися соответствующей темы, общих и профессиональных компетенций

Планирование практических занятий /лабораторных работ № п/п

Критерии оценки выполненных заданий и степени овладения запланированных умений 1

Практические задания Практическое занятие № 1

Z │ = r =│ a + bi │ =√а 2 + b 2

Пример4 : Даны комплементарные числа

Цель занятия: Повторить свойства предела, первый и второй замечательные пределы

Список рекомендуемой литературы

Тот процесс, с помощью которого из данной функции ( ) получают новую функцию ' ( ) , называют дифференцированием и состоит он из следующих трех…

Выполнение заданий. Примеры: 1

Практическое занятие № 4. Производная

Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студ

Итоговое выступление преподавателя/подведение итогов:

Выполнение заданий. Примеры: 3)

Задачи: учебная – повторить определение неопределённого интеграла, основных методов интегрирования

Сформулировать выводы по результатам работы

Скорость движения точки изменяется по закону v =(3 t 2 +2 t +1) (м/с)

Дадаян А.А. Математика: учебник – 3-е изд

Оформление результатов работы

Примеры: 1.Вычислить объем тела, образованного вращением вокруг оси

У6,З1,З4,ОК04,ОК08, ПК 3.4

Примеры простейших матриц: нулевая матрица

Итоговое выступление преподавателя/подведение итогов:

ОПРЕДЕЛИТЕЛИ Пусть дана матрица

Аналогично находим произведения элементов, стоящих на правых диагоналях (схема 2)

Тогда . Вывод: Вычисление определителей

Оформление результатов работы

Задание 1. Вычислить определитель, разложив его по элементам первой строки:

Практическое занятие № 14. Системы линейных уравнений

Итоговое выступление преподавателя/подведение итогов:

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией

Операции над матрицами Над матрицами можно производить следующие операции: 1

Коммутативный (переместительный) закон сложения:

О матрицах этого сказать нельзя, т

У7,З1,З4, ОК01, ОК03,ОК04,ОК08,

Определённый интеграл и его физический смысл

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

08.03.2020