Министерство образования и науки Луганской Народной Республики

Индустриальный техникум ДонГТУ

 

 

 

 

 

 

 

 

Методические рекомендации

для самостоятельной работы

студентов

по дисциплине «Теория вероятностей и

математическая статистика»

 

для студентов специальности

09.02.03 «Программирование в компьютерных системах»

 

 

 

 

Алчевск

2018

 

 

Разработала	_____________	Л.Л. Кузьмина  – преподаватель высшей категории, старший преподаватель
Рецензент	_____________	Л.С. Филоненко – преподаватель высшей категории

 

 

 

     

Утверждено на заседании Методического совета

__________Л.Л. Кузьмина  председатель Методического совета ИТ ДонГТУ

                 

 

 

 

 

 

Рассмотрено и одобрено на заседании цикловой комиссии

«Информатики и компьютерной техники»

Протокол от «___» ________  2018 г. № __

Председатель комиссии

_____________О.Ю. Ленкова

 

 

Содержание

 

Введение	4
Инструкция о модульно-рейтинговой системе текущего и итогового контроля уровня знаний студентов	7
Оценка элементов модулей дисциплины «Теория вероятностей и математическая статистика»	9
Модуль № 1	10
Модуль № 2	26
Модуль № 3	38
Варианты семестрового задания	46
Приложения	72
Литература	76

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Целью изучения курса «Теория вероятностей и математическая статистика» является формирование знания, умений и навыков, необходимых для изучения закономерностей массовых однородных случайных событий. Теория вероятности имеет непосредственный выход на прикладные задачи: определение надежности систем, анализ технологических процессов, проверка достоверности информации, планирования и организации производства и другие.

В настоящее время получение новой информации, новых знаний, переход от объекта к компьютеру невозможно без развитой методологии, которая раскрывает истинные возможности вычислительной техники.

Суть этой методологии заключается в единстве трех этапов «модель–алгоритм–программа». Кроме высококвалифицированных специалистов, разрабатывающих задачи, необходим широкий круг пользователей, которые способны раскрыть методологические возможности вычислительной техники при решении конкретных задач, обеспечить переход от академических приложений математического моделирования к отраслям массового производства.

Все знания и навыки, которые были получены при изучении дисциплины, могут быть использованы в процессе изучения специальных дисциплин, при выполнении курсового проекта, а также в практической работе на производстве.

На изучение дисциплины отводится 108 часов, из них 60 – аудиторных занятий и 48 – на самостоятельную работу студента. Изучать материал следует систематически и в той последовательности, которая предусмотрена программой дисциплины.

Для полного и успешного изучения дисциплины запланированы следующие виды занятий:

1. Изучение материала по основным вопросам курса на лекционных занятиях

2. Выполнения практических работ и расчетных заданий.

3. Самостоятельное изучение отдельных вопросов с использованием этих методических рекомендаций и литературы, которую необходимо использовать для изучения дисциплины. Самостоятельная работа предусматривает подготовку студентов к практическим работам, практическим занятиям, контрольным работам, выполнению расчетных заданий, семестрового задания и тому подобное.

Организация самостоятельной работы студентов предполагает внедрение в деятельность таких приемов работы: смысловой переработки текстов, закрепления учебного материала, усвоения обобщенных способов решения заданий, приемы краткой, самой рациональной записи (выписывание, планы, тезисы, конспекты, общие приемы работ с книгой); общие приемы запоминания; концентрирование внимания на использовании студентами разных видов самоконтроля, поэтапную проверку своей работы, общие приемы поиска дополнительной информации (работы с библиографическими справками, каталогами, словарями).

Методические рекомендации к самостоятельной работе студентов содержат три модуля, оценку каждого его элемента. В первом модуле рассмотренные задачи с элементами комбинаторики, непосредственного подсчета вероятности, задачи, где используются теоремы умножения и сложения, формулы полной достоверности и Бейеса, формулы Бернулли и теоремы Муавра-Лапласа.

Второй модуль посвящен случайным величинам. В нем рассматриваются способы задания дискретных и непрерывных случайных величин, их числовые характеристики, а также некоторые законы распределения вероятности дискретных и непрерывных случайных величин.

Третий модуль посвящен элементам математической статистики, в которой рассматриваются вариационные ряды, интервальные оценки параметров статистического распределения и методы расчета характеристик выборки.

Каждый модуль заканчивается защитой данного модуля по контрольным вопросам.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, то более детально разобрать вопрос по литературе, указанной в данной методике, или обратиться за консультацией к преподавателю.

Правила выполнения и оформления

семестрового задания:

-        студент должен выполнить семестровое задание согласно своего варианта;

-        семестровое задание следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний преподавателя;

-        решение задач следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач;

-        перед решением каждой задачи нужно выписать полностью условие;

-        решение задач оформлять обстоятельно и аккуратно, объясняя все действия;

-        семестровое задание, выполненное не по своему варианту, не засчитываются;

-        по получении проверенной работы студент должен исправить в ней все отмеченные ошибки и недостатки.

 

 

 

 

Инструкция

по модульной – рейтинговой системе

текущего и итогового контроля уровня знаний студентов

по дисциплине «Теория вероятностей и математическая статистика»

для специальности  «Разработка программного обеспечения»

 

Общее количество часов на дисциплина - 108; аудиторных – 60;

самостоятельных – 48 часов.  Дисциплина изучается один семестр.

Теоретический материал разбит на три модуля. Каждый модуль – это завершенный раздел дисциплины.

Модуль 1 – Случайные события

Модуль 2 – Случайные величины

Модуль 3 – Элементы математической статистики

Модульно-рейтинговая система предусматривает оценку знаний студентов по дисциплине

«5» – 90 - 100 баллов

«4» – 74 -  89 баллов

«3» – 60 – 73 баллов

Студенты, которые своевременно выполнили график учебного процесса и набрали 60 баллов и выше в течение семестра считаются успевающими.

Присутствие студента необходимо для сообщения ему суммарной оценки и занесения ее в зачетную книжку и ведомость.

К сдаче экзамена допускаются студенты, которые выполнили график самостоятельной работы и набрали определенное количество необходимых баллов, из возможных 50, но не менее 25. Такого количества достаточно для допуска к экзамену, согласно решения дисциплинарной комиссии.

Студенты, которые в течение семестра работали не ритмично, нарушали график учебного процесса и не набрали необходимого количества баллов, считаются неуспевающими. Такие студенты имеют возможность получить зачетные 60–100 баллов во время сессии. Для сдачи экзамена студент должен получить допуск.

Когда студент набирает 60 (и более) баллов по результатам работы в семестре, но не полностью выполнил график самостоятельной работы, то есть не отработал практическую работу или расчетное задание, то такому студенту не засчитывается весь модуль и он считается должником. Об этом предупреждается студент. Такой студент имеет право сдавать не весь материал дисциплины, а лишь ее часть, то есть задолженности по модулю. Для студента, который выполнил график самостоятельной работы, но не получил необходимое количество зачетных баллов по одному из модулей дисциплины, предоставляется возможность, во время сессии добрать это количество баллов, чтобы считаться успевающим.

 

 

 

 

 

 

 

Оценка элементов модулей дисциплины

«Теория вероятностей и математическая статистика»

Модуль №1

1.      Проработка  лекций  № 1 - 4

2.      Подготовка к выполнению практической работы № 1

3.      Подготовка к выполнению практической работы № 2

4.      Подготовка к выполнению практической работы № 3

5.      Подготовка к выполнению практической работы № 4

6.      Подготовка к выполнению практической работы № 5

7.      Подготовка к защите модуля № 1 по лекциями № 1 - 4

8.      Выдача семестрового задания, с. 46

 

1.      Проработать лекции № 1 - 4 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения,  термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

 [3] с. 3–52

2. Практическая работа № 1 по теме «Решения задач по комбинаторике»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 1-4

3. Практическая работа № 2 по теме «Использования теорем сложения вероятностей»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 4-9

4. Практическая работа № 3 по теме «Использование теорем сложения и умножения вероятностей»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 9-15

5. Практическая работа № 4 по теме Использование формул полной вероятности и Бейеса»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 15-20

6. Практическая работа № 5 по теме «Формула Бернулли. Локальная и интегральная теоремы Лапласа»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 20-24

7. Защита модуля № 1

Контрольные вопросы модуля № 1

Защита модуля проводится в письменном виде согласно вопросов по лекциям № 1 – 4

1.         Что является предметом теории вероятностей?

2.         Что такое «испытание»?

3.         Что такое «событие»?

4.         Что такое «случайное событие»?

5.         Что такое «вероятность события»?

6.         В чем заключается статистическое определение вероятности?

7.         При каких условиях можно применять классическое определение вероятности?

8.         Какова формулировка классического определения вероятности?

9.         Приведите несколько примеров достоверных, невозможных и случайных событий.

10.    Чему равна вероятность невозможного и достоверного событий?

11.    Дайте определение суммы и произведения событий. Примеры.

12.    Как понимают равенство двух событий? Примеры.

13.    Какие события называют противоположными? Примеры.

14.    Что обозначают слова “наугад”, ”произвольно”? Примеры.

15.    Что такое перестановки? Число всех возможных перестановок?

16.    Что такое размещение? Число всех возможных размещений?

17.    Что такое сочетания? Число всех возможных сочетаний?

18.    В чем заключается «правило суммы»?

19.    В чем заключается «правило произведения»?

20.    Что такое множество элементарных событий?

21.    Что такое сумма случайных событий?

22.    Что такое произведение случайных событий?

23.    Что такое разность событий?

24.    Что такое множество случайных событий?

25.    Что такое противоположное событие?

26.    Что такое несовместные события?

27.    Какова вероятность суммы двух совместных событий?

28.    Какие события образуют полную группу?

29.    Какова вероятность противоположного события?

30.    Что такое условная вероятность?

31.    Как выражается условная вероятность через безусловную?

32.    Как связаны условные вероятности двух независимых событий?

33.    Какова формула произведения событий?

34.    Чему равна вероятность появления хотя бы одного события из независимых в совокупности событий?

35.    Каковы условия задачи, определяемой формулой полной вероятности?

36.    Напишите формулу полной вероятности

37.    Каковы условия задачи, определяемой формулой Бейеса?

38.    Напишите формулу Бейеса.

39.    Объясните условие независимых испытаний

40.    Запишите формулу Бернулли

41.    Сформулируйте локальную предельную теорему Муавра-Лапласа

42.    Сформулируйте интегральную предельную теорему Муавра-Лапласа

Практические задания к зачету по модулю 1

1.    Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал различных 5 цветов?

2.    Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков: русского, английского, французского, немецкого, итальянского на любой из этих пяти языков?

3.    У одного человека есть 7 книг по математике, а у другого 9 книг.  Сколькими способами они могут обменять 2 книги одного на 2 книги другого?

4.    Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хоть бы один туз?

5.    В местком выбрано 10 человек. Из них надо выбрать председателя, заместителя председателя, секретаря и культорга. Сколькими способами это можно сделать?

6.    Из состава конференции, на которой присутствовало 52 человека, надо избрать делегацию из 5 человек. Сколькими способами это можно сделать?

7.    Из спортивного клуба, насчитывающего 30 членов, надо составить команду из 4 – х человек для участия в беге на 1000м. Сколькими способами это можно сделать? А сколькими способами можно составить команду из 4 – х человек для участия в эстафете 100 + 200 + 400 + 800?

8.     Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы из них было не менее 4 женщин. Сколькими способами это можно сделать?

9.    На студенческом вечере присутствует 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

10.           Сколькими способами можно выбрать 12 человек из 17, если  Иванов и Петров входят в число этих 17 и их нельзя избирать вместе?

11.           Сколькими способами можно переставить буквы в слове «логарифм» так, чтобы второе, четвертое и шестое места были заняты согласными буквами?

12.           Сколькими способами можно выбрать из слова «логарифм» две согласных и одну гласную букву? Та же задача, если среди выбранных есть буква «ф».

13.           Каким числом способов можно разбить колоду из 36 карт пополам так, чтобы в каждой пачке было по 2 туза?

14.            Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными?

15.           В вещевой лотерее разыгрывается 8 предметов. Первый подошедший к урне вытягивает из нее 5 билетов. Каким числом способов он может их вынуть, чтобы: 1) ровно 2 из них оказались выигрышными; 2) по крайней мере, 2 из них были выигрышными? Всего в урне 50 билетов.

16.            Из 15 солдат 3 необходимо отправить на разведку. Сколькими способами можно это сделать?

17.           В партии из 100 изделий 10 дефектных. Сколькими способами можно из 100 изделий извлечь 5 так, чтобы среди них было ровно 3 дефектных?

18.           В урне 5 белых и 7 черных шаров. Из урны вынимают сразу 3 шара. Сколькими способами их урны можно вынуть 2 белый и 1 черный шар?

19.           Некто купил карточку спортлото и отметил в ней 6 из имеющихся 49 номеров. Сколько есть способов угадать 3 выигрышных номера? 4 номера? 5 номеров? 6 номеров?

20.           В автомашине 7 мест. Сколькими способами можно 7 человек могут усесться в эту машину, если занять место водителя могут только 3 из них?

21.           Студенту необходимо сдать 4 экзамена в течение 10 дней. Сколькими способами можно составить ему расписание?

22.           Сколько существует различных автомобильных номеров, которые состоят из 5 цифр, если первая из них не равна 0? Если номер состоит из 1 буквы, за которой следуют цифры, отличные от 0?

23.           Энциклопедия состоит из 9 томов – с 1 по 9. Сколькими способами можно поставить ее на полке в беспорядке, т. е. так, чтобы тома не следовали один за другим в порядке возрастания их номеров?

24.           На железной дороге 50 станций. На каждом билете печатается название станции отправления и прибытия. Сколько различных билетов нужно отпечатать? Тот же вопрос, если каждый билет можно использовать в любом направлении, т. е. безразлично, с какой из 2 – х обозначенных на билете станций вы отправляетесь.

25.           Из группы в 20 солдат каждую ночь выделяется наряд, состоящий из 3 –х человек. Сколько подряд ночей командир может выделять наряд, не совпадающий ни с одним из предыдущих. Сколько раз при этом в наряд войдет Вилли Смит, который находится среди этих 20 солдат?

26.           Предприятие может предоставить работу по специальности токарь 4 – м женщинам, по специальности слесаря – пяти мужчинам и по специальности фрезеровщика – трем работникам, независимо от их пола. Сколькими способами можно заполнить эти места, если на них имеются 18 претендентов, среди которых 8 женщин и 10 мужчин?

27.           В лифт шестиэтажного дома сели 4 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом, начиная со второго, этаже. Определить вероятность того, что а) все вышли на равных этажах; б) по крайней мере двое сошли на одном этаже.

28.           В урне имеется 10 шаров: 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность того, что этот шар: а) белый, б) черный?

29.           Из слова «наугад» вынимается одна буква. Какова вероятность того, что это буква «я»? Какова вероятность того, что эта буква гласная?

30.           Брошены 2 монеты. Найти вероятность того, что выпадут два герба.

31.           Бросают игральную кость. Какова вероятность выпадения № 4 на верхней грани упавшей на стол кости? Какова вероятность выпадения номера, большего 4?

32.           При стрельбе была получена частота попадания 0,6. Сколько было сделано выстрелов, если было допущено 12 промахов?

33.           Брошены 2 игральные кости. Какова вероятность выпадения на двух костях в сумме не менее 9 очков? Какова вероятность выпадения 1 по крайней мере на одной кости?

34.           На шахматную доску из 64 клеток ставят наудачу две ладьи белого и черного цвета. С какой вероятностью они будут бить друг друга?

35.           Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбирают три и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «два»?

36.           Из последовательности 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 наудачу выбирают 2 числа. Какова вероятность того, что одно из них меньше 5, а другое больше 5?

37.           Ребёнок играет с четырьмя буквами равной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА».

38.           При наборе телефонного номера абонент забыл две последние цифры и набрал их на удачу, помня только, что эти цифры нечётные и равные. Найти вероятность того, что номер набран правильно

39.           В лотерее 100 билетов, из которых 20 выигрышных. Участник лотереи покупает 3 билета. Определить вероятность того, что он выиграл хотя бы один билет?

40.           Среди 25 экзаменационных билетов 5 «хороших». Два студента берут поочерёдно по одному билету. Найти вероятности следующих событий.

 А: первый студент взял хороший билет, (а второй или хороший или плохой).

 В: второй студент взял хороший билет, (а первый или хороший или плохой).

 С: оба студента взяли хороший билет.

41.           В партии из 50 изделий 5 бракованных. Из партии выбираются наугад 6 изделий. Определить вероятность того, что  среди этих 6 изделий 2 окажутся бракованными.

42.           В лифте 7 этажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит  на любом этаже, начиная со второго. Найти вероятность  следующих событий:

 А: все пассажиры выйдут на 4 этаже

 В: все пассажиры выйдут на одном этаже вместе

 С: все пассажиры выйдут на разных этажах.

43.           Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики  тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь две окрашенные стороны.

44.           Из полного набора костей домино на удачу берутся 5 костей. Найти вероятность того, что  среди них будет хотя бы одна с шестеркой.

45.           Из 10 билетов выигрышными являются 2. Определить вероятность того, что  среди взятых на удачу 5 билетов: а) 1 выигрышный; б) оба выигрышных; в) хотя бы один выигрышный.

46.           Десять книг на одной полке расставляются наудачу.  Определить вероятность того, что  рядом кажутся поставленными «Обломов», «Обрыв», «Обыкновенная история»?

47.            В колоде 36 карт четырёх мастей. После извлечения и возвращения одной карты колода перемешивается и снова извлекается одна карта. Определить вероятность того, что обе извлеченные карты одной масти?

48.           Буквенный замок содержит, на общей оси 5 дисков, каждый из которых разделён на 6 секторов с различными нанесёнными на них буквами. Замок открывается только в том случае, если каждый диск занимает одно определённое положение относительно корпуса замка. Определить вероятность открытия замка, если установлена произвольная комбинация букв.

49.           Из колоды карт (52 карты) наудачу извлекается 3 карты. Найти вероятность, что это будет тройка, семёрка и туз.

50.           Студент купил карточку спортлото и отметил в ней 6 из имеющихся 49 номеров. После этого в тираже разыгрываются 6 «выигрышных» номеров из 49. Найти вероятность, следующих событий:

А: верно угаданы 3 выигрышных номера из 6

Б: верно угаданы 4 выигрышных номера из 6

С: верно угаданы 36выйграшных номера из 6

Д: верно угаданы все 6 номеров.

51.           В урне 7 белых и 3 чёрных шара. Из урны одновременно вынимают 2 шара. Какое событие более вероятно: А = {шары одного цвета} или  В= {шары разных цветов}?

52.           Из ящика, содержащего 5 перенумерованных изделий, вынимают одно за другим все находящиеся в нём изделия. Найти вероятность того, что номера вынимаемых изделий будут идти по порядку 1, 2, 3, 4, 5.

53.           Из ящика содержащего 5 перенумерованных изделий, вынимают одно за другим все изделия находящиеся в нём. Каждое изделие после вынимания вкладываются обратно и перемешиваются с другими, а его номер записывается. Найти вероятность того, что  записана естественная последовательность номеров 1, 2, 3, 4, 5.

54.           Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность не сдать зачет, если после отказа отвечать на вопрос, преподаватель задает еще один вопрос?

55.           Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.

56.           Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель 0,7, для второго – 0,8. Какова вероятность попадания в волка (хотя бы при одном выстреле)? Как изменится результат, если охотники сделают по два выстрела?

57.           Вероятность попадания в цель первым стрелком 0,6, вторым 0,4. Стрелки выстрелили одновременно. Какова вероятность того, что один из них попадет в цель, а другой не попадет?

58.           В двух партиях 71 и 47% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:

a)    Хотя бы одно бракованное;

b)   Два бракованных;

c)    Одно доброкачественное и одно бракованное;

59.            Вероятность того, что цель поражена при одном выстреле, первым стрелком равна 0,61, вторым 0,55. Первый сделал 2, а второй 3 выстрела. Найти вероятность того, что цель не поражена.

60.           Определить вероятность того, что партия из 100 изделий, среди которых 5 бракованных, будет принята при испытании наудачу выбранной половины всей партии, если условиями приема допускается бракованных изделий не более 1 из 50.

61.            Разрыв электронной цепи происходит в том случае, когда выходит из строя хотя бы один из трех последовательно соединенных элементов. Определить вероятность того, что не будет цепи, если элементы выходят из строя с вероятностями 0,3; 0,4 и 0,6. Как изменится искомая вероятность, если первый элемент не выходит из строя?

62.           Определить вероятность того, что выбранное на удачу изделие является первосортным, если известно, что 4 % всей продукции являются браком, а 75% не бракованных изделий удовлетворяют требования первого сорта.

63.           Партия из 100 деталей подвергается выборочному контролю. Условием непригодности всей партии является наличием хотя бы одной бракованной детали среди 5 проверяемых. Какова вероятность для данной партии быть не принятой, если она содержит 5% неисправных деталей?

64.           Радист трижды вызывает корреспондента. Вероятность принятия вызова равна 0,2 для одного вызова; 0,3 для второго вызова; 0,4 для третьего вызова. Найти вероятность установления связи, если события, если события, состоящие в том, что данный вызов будет услышан, независимы.

65.           Производится стрельба по некоторой цели, вероятность попадания в которую при одном выстреле равна 0,2. Стрельба прекращается при первом попадании. Найти вероятность того, что будет произведено ровно 6 выстрелов.

66.           В приемнике имеется 6 радио ламп одного типа и 8 радиоламп другого типа. Вероятность выхода лампы из строя  в течении времени Т равна 0,002 для лампы первого типа  и 0,004 – для лампы второго типа. Какова вероятность того, что в течении этого времени выйдет  из строя хотя бы одна лампа?

67.           Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит 3 вопроса. Найти вероятность того, что студент знает:

а) все три вопроса;

б) только два вопроса;

в) только один вопрос экзаменационного вопроса.

68.           Три стрелка в одинаковых и независимых условиях  произвели по одному выстрелу по одной и той же цели. Найти вероятность того, что:

а) только один из стрелков попал в цель;

б) только два стрелка попали в цель;

в) все три стрела попали в цель.

69.           Для сигнализации об аварии установили 3 независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает:

а) только одно устройство;

б) только два устройство;

в) все три устройства.

70.           Вероятность того, что в течение дня произойдет неполадка станка, равна 0,03. Какова вероятность того, что в течение четырех дней  подряд

а) произойдет более трех неполадок;

б) менее двух неполадок;

71.           Из полной колоды карт (52) вынимаются четыре карты. Найти вероятность того, что все эти четыре карты будут разных мастей.

72.           Завод изготавливает определенного типа изделия, каждое из которых имеет дефект с вероятностью 0,1. Изделие осматривается одним контролером; он обнаруживает имеющийся дефект с вероятностью 0,95, а если дефект не обнаружен, пропускает изделие в готовую продукцию. Кроме того, контролер может по ошибке забраковать изделие, не имеющее дефекта; вероятность этого 0,02. Найти вероятность следующих событий:

А – изделие будет забраковано;

В – изделие будет забраковано, но ошибочно;

С – изделие будет пропущено в готовую продукцию с дефектом.

73.           При включении зажигания двигателя начинает работать с вероятностью 0,7.

1)   Найти вероятность того, что двигатель начнет работать при втором включении зажигания;

2)   Найти вероятность того, что для ввода двигателя в работу придется включить зажигание не более двух раз.

74.           Истребитель, вооружений двумя ракетами, посылается на перехват воздушной цели. Вероятность вывода истребителя в такое положение,  из которого возможно  атака цели, равна 0,6. Если истребитель выведен в такое положение, он выпускает по цели обе ракеты,  каждая из которых  независима друг от друга, выводятся в окрестность цели  с вероятностью 0,8. Если ракета выведена в окрестность цели, она поражает ее с вероятностью 0,98. Найти вероятность того, что цель будет поражена.

75.           Имеются две урны: в первой 3 белых шара и два черных, во второй четыре белых и четыре чёрных. Из первой урны перекладывают во вторую, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.

76.           Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? (считать, что мужчин и женщин одинаковое число). 

77.           На фабрике изготовляющей болты, первая машина производит 25, вторая – 35, третья – 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%.

78.           а) Какова вероятность того, что случайно выбранный болт дефектный?

79.           б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен второй машиной?

80.           Из 1000 ламп 100 принадлежат 1 – й партии, 250 – 2 – й партии, остальные – 3 –й партии. В 1 – й партии 6%, во 2 – й 5%, в 3 – й  4% бракованных ламп. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа бракованная.

81.            В первой урне 4 белых и 1 черный шар, во второй – 2 белых и 5 черных. Из первой урны во вторую переложено 3 шара, затем из второй урны извлечен один шар. Определить вероятность того, что выбранный из второй урны шар – белый.

82.           В альбоме 8 чистых и 10 гашёных марок. Из них наудачу извлекаются 3 марки (среди которых могут быть и чистые и гашёные), подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекаются 2 марки. Определить вероятность того, что эти 2 марки чистые.

83.           В магазин поступают однотипные изделия с трех завозов, причем первый завод поставляет 50%  изделий, второй 30%, третий завод 20% изделий. Среди изделий первого завода 70% первосортных, среди изделий второго завода 80% и среди изделий третьего завода 90% первосортных. Куплено одно изделия. Оно оказалось первосортным. Определить вероятность того, что купленное изделие оказалось изготовленным первым заводом.

84.           В тире имеется 5 ружей, вероятности попадания, из которых равны соответственно 0,5; 0,6; 0,7; 0,8; 0,9 .  Определить вероятность попадания, если стреляющий берет одно из ружей на удачу.

85.           Телеграфное сообщение состоит из сигналов “точка” и “тире”. Статистические свойства помех таковы, что искажаются в среднем 2/5  сообщений “точка” и 1/3 сообщений “тире”. Известно, что среди передаваемых сигналов “точка” и “тире” встречаются в соотношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если: а)принят сигнал “точка”;  б) принят сигнал “тире”

86.           13. В правом кармане имеются три монеты по 20 коп. и четыре монеты по 3 коп., а  в левом – шесть по 20 коп. и три – по 3 коп. Из правого кармана в левый, наудачу перекладываются пять монет. Определить вероятность извлечения из левого кармана после перекладывания монеты   в 20 коп., если монета берется наудачу?

87.           Известно, что 96% выпускаемой продукции удовлетворяет стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную – с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

88.             Для контроля продукции  из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других – все доброкачественные?

89.           На трех станках при одинаковых и независимых условиях изготовляются детали одного наименования. На первом станке изготовляют 10% , на втором – 30%, на третьем – 60% всех деталей  вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке; 0,8 -  если на втором станке и 0,9 – если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.

90.           В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны переложили во вторую наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется чёрным.

91.            Имеется десять одинаковых урн, из которых в девяти находится по два черных и два белых шара, а в одной - пять белых и один черный шар. Из урн, взятой наудачу, извлечён белый шар. Какова вероятность того, что шар извлечен из урны, содержащей пять белых шаров?

92.           Имеются две партии изделий по 12 и 10 штук, причём в каждой партии изделие бракованное. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается на удачу изделие из второй партии. Определить вероятность влечения бракованного изделия из второй партии.

93.           Для сигнализации о том, что режим работы автоматической линии станков отклоняется от нормального, используется индикатор, принадлежащий  с вероятностями 0,2; 0,3 и 0,5 к одному из трех типов, для которых вероятности срабатывания  при рушении нормальной работы линии равны соответственно 1, 0,75 и 0,4. От индикатора получен сигнал. К какому типу вероятнее всего принадлежит индикатор?

94.           Имеется три одинаковые с виду урны. В первой 5 белых и 5 черных шаров, во второй 0 белых и 7 черных, в третьей – только белые шары. Некто подходит наугад к одной из этих урн  и извлекает один шар. Найти вероятность того, что этот шар белый.

95.           Прибор может работать в двух режимах: 1) нормальном; 2) ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, ненормальный – в 20% Вероятность выхода прибора  из строя за время  в нормальном режиме равна 0,1, в ненормальном 0,7. Найти вероятность выхода прибора из строя за время.

96.           У рыбака имеются три излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он закладывает удочку на первом месте, рыба клюет с вероятностью 0,85, на втором месте – с вероятностью 0,8, на третьем – с вероятностью 0,9 Известно, что рыбак вышел на ловлю рыбы и рыба клюнула только один раз. Найти вероятность того, что он удил рыбу на первом месте.

97.           В группе из 10 студентов, пришедших на экзамен, 3 подготовленных на экзамены отлично, 4 хорошо, 2  - посредственно и один плохо. В Экзаменационных билетах имеются на все 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный на – 16, посредственно – 10, плохо – 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: а) отлично, б) плохо.

98.           Группа студентов состоит из 5 отличников, 10 хорошо успевающих и 10 занимающихся слабо. Отличники на предстающем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что он получит хорошую или отличную оценку.

99.           В автобусе едут 9 пассажиров. На следующей остановке каждый из них выходит с вероятностью 0,6. Кроме того, в автобусе с вероятностью 0,7 не выходит ни один пассажир, с вероятностью 0,3 появляется один новый пассажир. Найти вероятность того, что когда автобус снова тронется в путь после следующей остановки, в нем будет по-прежнему 9 пассажиров.

100.      Прибор состоит из двух узлов: работа каждого узла, безусловно, необходима для работы прибора в целом. Надежность (вероятность безотказной работы течение времени t) первого узла равна 0,9, второго 0,95. Прибор испытывался в течение времени t, в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.

101.      В цехе работают 20 станков. Из них 10 – марки А, 6 – марки В и 4 – марки С. вероятность того, что качество детали скажется отличным, для этих станков соответственно равна: 0,9; 0,8 и 0,7. Какой процент отличных деталей выпускает цех?

106. Среди изделий цеха 10% с дефектом. Изделия с одинаковой вероятностью могут попасть к одному из трёх контролёров. Вероятности определения дефекта каждым контролёром соответственно равно 0,9; 0,93; и 0,87. Определить вероятность того, что дефект будет обнаружен в цеху.

107.      Радиолампа принадлежит к одной из трёх партий с вероятностями 0,2; 0,3; и 0,5. Вероятность того, что лампа проработает Т ч., равна для этих партий 0,3; 0,6; и 0,8. Вычислить вероятность того, что лампа проработает Т часов.

108.      В случае аварии дежурный с равной возможностью может воспользоваться одной из трёх сигнализаций. Вероятности срабатывания сигнализации равны 0,9; 0,96 и 0,87.

а) Определить вероятность того, что сигнал об аварии будет получен. б) сигнал об аварии не получен. Определить вероятность того, что дежурный воспользуется вторым сигнализатором.

109.      На фабрике находится продукция  трёх фабрик. Продукция первой фабрики 10%, второй- 35% и третьей- 55%. Брак соответственно для каждой фабрики составляет: 1, 3 и 2%. Определить вероятность того, что наугад взятое изделие:

а) окажется стандартным;

б) окажется бракованным и изготовлено на первой фабрике.

110.      Для работы прибора необходима исправность обоих блоков, из которых он состоит. Вероятность безотказной работы в течении времени F для первого блока Р1, а для второго Р2. Прибор испытали Т часов, в результате он вышел из строя. Определить вероятность того, что отказал только первый блок.

111.      Вероятность появления успеха в каждом испытании равна 0,25. Какова вероятность того, что при 300 испытаниях успех наступит: а) равно 75 раз? Б) равно 85 раз?

112.      В первые классы должно быть принято 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика равна 0,515.

113.      Какова вероятность того, что в столбике 100 наугад отобранных монет число монет, расположенных «гербом » вверх, будет от 45 до 55?

114.      Производство даёт 1% брака. Какова вероятность того, что  из взятых на исследование 1100 изделий выбраковано будет не больше 17?

115.      Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших будет заключено между 790 и 830.

116.      Монета подбрасывается 8 раз. Какова вероятность того, что 6 раз она упадёт гербом вверх?

117.      Монета подбрасывается 6 раз. Какова вероятность того, что она упадёт гербом вверх не более 3 раз?

118.      Какова вероятность того, что при 100 бросаниях монеты герб появится от 40 до 60 раз?

119.      В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в цехе в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.

120.      Найти вероятность того , что событие А появится на пяти независимых испытаниях не менее 2 раз, если в каждом испытании вероятность появления события А равно 0,3?

121.      Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того , что событие А появится  хотя бы 2 раза.

122.      Монета подбрасывается 6 раз. Какова вероятность того, что  герб выпадет: а) менее 2 раз; б) не менее 2 раз.

123.      По каналу связи передаётся 7 сообщений. Каждое сообщение не зависимо от друг друга с вероятностью 0,1 искажается помехами. Найти вероятность следующих событий.

 А: = {из 7 сообщений ровно 3 будут искажаться помехами}

 В: = {не менее трех из 7 сообщений будут переданы неискаженными}

 С: = {не более половины всех передаваемых сообщений будут искажены}

 Д: = {все сообщения будут приняты без искажений}

 Е: = {не менее 2-х сообщений будут искажены}

124.      Цех завода выпускает шарики для подшипников. За смену производится п=1000 шариков. Вероятность того, что  один шарик окажется дефектом, равна 0,05. Причины дефектов для отдельных шариков не зависимы. Найти вероятность событий:

А:  к концу смены будет ровно 50 бракованных шариков;

В: число бракованных шариков будет колебаться от 30 до 70;

С: число бракованных шариков  не превысит 500.

125.      Техническое устройство С состоит из 5 узлов, каждый узел за время эксплуатации отказывает (выходит из строя) с вероятностью р= 0,4. Отдельные узлы отказывают независимо друг от друга. Если оказывается более трёх узлов, устройство не может работать, если откажет один узел или два узла, оно работает, но с понижением эффективностью. Найти вероятность событий:

А: в устройстве не отказал ни один узел

В: устройство не может работать

С: устройство работает с пониженной эффективностью.

126.      Вероятность выхода из строя изделия за время испытаний на надёжность р=0,05. Какова вероятность, что за время испытаний ста изделий выйдут из строя: а) ровно 5 изделий; б) не менее 5 изделий; в) не более 5 изделий; г) от 5 до 10 изделий.

127.      Имеются 100 станков одинаковой мощности, работающих независимо друг от друга в одинаковом режиме, при котором их привод оказывается включенным  в течении 0,8 всего рабочего времени. Какова вероятность того, что в произвольно взятый момент времени включенными окажутся ровно 80 станков? От 70 до 86 станков?

128.      В учебном заведении обучаются 730 студентов. Вероятность того, что день рождения наудачу взятого студента приходится на любой день года равна 1/365. Найти вероятность того, что на 1 января выпадет: а) день рождения 3-х студентов; б) не менее 4-х студентов.

129.      Вероятность выхода из строя за время Т одного конденсатора равна 0,2. Определить вероятность того, что за время Т из 100 конденсаторов выйдут из строя: а) ровно 20 конденсаторов; б) не менее 20 конденсаторов; в) менее 28 конденсаторов; г) от 14 до 26 конденсаторов.

130.      Вероятность того, что лампа останется исправной после 1000 часов работы, равна 0,2. Какова вероятность того, что хотя бы одна лампа из трех останется исправной после 1000 часов работы?

131.      Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,002. Поступило 1000 вызовов. Найти вероятность: а) 7 сбоев; б) не менее 7 сбоев; в) менее 7 сбоев; г) от 7 до 20 сбоев.

132.      На каждый лотерейный билет с вероятностью 0,1 может выпасть крупный выигрыш, с вероятностью 0,2 – мелкий выигрыш, и с вероятностью 0,7 билет может остаться без выигрыша. Куплено 15 билетов. Определить вероятность получения одного крупного и 2 мелких выигрышей.

 

Модуль №2

1.    Проработать лекции № 5 - 7

2.    Подготовка к выполнению практической работы № 6

3.    Подготовка к выполнению практической работы № 7

4.    Подготовка к выполнению практической работы № 8

5.    Подготовка к обязательной контрольной работе

6.    Подготовка к защите модуля № 2 по лекциям № 5 - 7

7.    Выполнение семестрового задания, с. 46

 

1.      Проработать лекции № 5 - 7 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения, термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

 [3] с. 52–65

2. Практическая работа № 6 по теме «Закон распределения

вероятностей дискретных случайных величин»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 25-31

3. Практическая работа № 7 по теме «Определения функции и  плотности распределения вероятностей»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 31-37

4. Практическая работа № 8 по теме «Вычисление вероятностей заданного отклонения»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 37-42

5. Обязательная контрольная работа

Контрольная работа состоит из трех задач и проводится в аудитории в течение двух академических часов. Работа выполняется на листах со штампом. Каждая задача обязательно должна иметь объяснение к решению задачи. Перед контрольной работой студент должен повторить теоретический материал, рассмотреть примеры, которые приведены в учебниках и на практических занятиях.

Задание к обязательной контрольной работе

1.      На сборку поступают детали с трёх автоматов. Первый даёт 25%, второй – 30% и третий  – 30% и третий – 45% деталей данного типа, поступающих на сборку. Первый автомат допускает 0,1% нестандартных деталей, второй – 0,2%, третий – 0,3%. Найти вероятность поступления на сборку нестандартной детали.

2.      Имеются две урны с шарами. В первой урне 34 белых и 6 черных, во второй 3 белых и 2 черных. Из первой урны наудачу извлекается один шар и перекладывается во вторую. Затем из второй урны извлекается шар. Найти вероятность того, что этот шар белый.

3.      Пусть в условии предыдущей задачи из второй урны извлечен белый шар. Какова вероятность того, что из первой урны во вторую был переложен белый шар?

4.      Имеются два набора деталей. Вероятность того, что деталь первого набора бракована, равна 0,01%, а второго – 0,02. Найти вероятность того, что взятая наудачу деталь из наудачу взятого набора качественная.

5.      Для сигнализации о том, что режим работы автоматической линии отклоняется от нормального, используется индикатор. Он принадлежит с вероятностями 0,2, 0,3 и 0,5 к одному из трёх типов, для которых вероятность срабатывания при нарушении нормальной работы равны соответственно 0,9, 0,7 и 0,6. Найти вероятность того, что наудачу взятый индикатор сработает при нарушении нормальной работы линии.

6.      Пусть в условиях предыдущей задачи от индикатора получим сигнал. Найти вероятность того, что индикатор принадлежит к первому типу.

7.      Имеются три урны с шарами. В первой урне 4 белых и 3 черных, во второй 5 белых и 2 черных, в третьей 2 белых и 5 черных. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар окажется белым.

8.      На двух автоматических станках изготовляются одинаковые детали. Известно, что вероятность изготовления детали высшего качества на первом станке равна 0,92, а на втором – 0,8. Изготовленные на обоих станках не рассортированные детали находятся на складе. Среди них деталей, изготовленных на первом станке, в три раза больше, чем на втором. Найти вероятность того, что наудачу взятая деталь будет высшего качества.

9.      Пусть в условиях предыдущей задачи наудачу взятая деталь окажется высшего качества. Найти вероятность того, что она изготовлена на втором станке.

10.Некоторое изделие может поступить для обработки в случайном порядке на один из трёх станков с вероятностями соответственно равными Р1=0,2; Р2=0,3; Р3=0,5. При обработке на первом станке вероятность брака равна 0,02, на втором – 0,3, на третьем -  0,05. Найти вероятность того, что поступившие в цех изделие после обработки окажется удовлетворяющим техническим условиям.

11.Пусть в условиях предыдущей задачи, поступившее в цех изделие после обработки оказалось удовлетворяющим техническим условиям. Какова вероятность того, что изделие обрабатывалось на третьем станке? 

12.В ящике имеются 5 деталей, среди которых могут быть и бракованные. Вынутая наугад  оказалось не бракованной. Найти вероятность того, что 3 детали в ящике не бракованные, а 2 бракованные, если предположить, что до опыта все гипотезы равновозможные. 

13.Радиолампа может принадлежать к одной из двух партий с вероятностями р₁=0,6 и р₂=0,4. Вероятности того, что лампа проработает заданное число часов, равны для этих партий соответственно 0,7 и 0,8. Определить вероятность того, что лампа проработает заданное число часов.

14.Пусть в условиях предыдущей задачи лампа проработает заданное число часов. Какова вероятность того, что она принадлежит к первой партии?

15.В ящике имеются 4 детали, среди которых могут быть и бракованные. Вынутая наугад деталь оказалась не бракованной. Определить вероятность того, что все детали в ящике не бракованные. (Предполагается, что до опыта все гипотезы равновозможны).

16.В первой коробке 20 деталей, из них 18 стандартных, во второй коробке 10 деталей, из них 7 стандартных. Из второй коробки наудачу взята деталь и переложена в первую. Найти вероятность того, что деталь, наудачу извлеченная из первой коробки, стандартна.

17.Пусть в условиях предыдущей задачи деталь, извлеченная из первой коробки, оказалась стандартной. Найти вероятность того, что из второй коробки переложена в первую стандартная деталь.

18.Детали, изготовленные цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Найти вероятность того, что годная деталь будет признана стандартной.

19.Имеются два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. найти вероятность того, что взятая наудачу деталь из наудачу взятого набора нестандартна.

20.Пусть в условиях предыдущей задачи взятая наудачу деталь из наудачу взятого набора оказалась нестандартной. Какова вероятность того, что она принадлежала первому набору?

21.На сборку поступают детали с трех автоматов. Первый дает 20%, второй 30% и третий 50% деталей данного типа, поступающих на сборку. Первый автомат допускает 0,2% брака деталей, второй – 0,3%, третий – 0,5%. Найти вероятность того, что взятая наудачу деталь стандартна.

22.В цехе три типа автоматических станков производят одни и те же детали. Станки первого типа производят 0,94 деталей отличного качества, второго – 0,9 и третьего – 0,85. Все произведенные в цехе за смену детали в не рассортированном виде сложены на складе. Определить вероятность того, что взятая наудачу деталь окажется отличного качества, если станков первого типа 5 штук, второго – 3 штуки, третьего – 2 штуки и производительность всех одинакова.

23.Пусть в условиях предыдущей задачи взятая наудачу деталь оказалась отличного качества. Найти вероятность того, что она была произведена на станке первого типа.

24.Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором – 10 белых и 10 черных, в третьем – 20 черных шаров. Из выбранного наудачу ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.

25.В ящик, содержащий две детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.

26.Пусть в условиях предыдущей задачи извлечена стандартная деталь. Найти вероятность того, что первоначально в ящике была одна стандартная и одна нестандартная деталь.

27.Детали для сборки изготавливаются на двух станках, из которых первый производит деталей в 4 раза больше второго. При этом брак составляет в выпуске первого станка 0,2, а в выпуске второго – 0,01. Взятая наугад деталь оказалась годной для сборки. Найти вероятность того, что она изготовлена на первом станке.

28.В группе спортсменов 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0,9, для велосипедистов – 0,8 и для бегуна – 0,6. найти вероятность того, что спортсмен, выбранный наудачу, выполнит квалификационную норму.

29.Пусть в условиях предыдущей задачи спортсмен выполнил квалификационную норму. Найти вероятность того, что это был велосипедист.

30.В двух урнах находятся белые и черные шары. В первой 3 белых и 2 черных, во второй 2 белых и 2 черных. Из первой урны наудачу вынимают один шар и перекладывают во вторую, а затем из второй урны наудачу извлекают один шар. Найти вероятность того, что этот шар будет белым.

31.Для участия в студенческих отборных соревнованиях выделено из первой группы курса 4, из второй 6, из третьей 5 студентов. Вероятность того, что студенты первой, второй и третьей групп попадут в сборную института, соответственно равна 0,9; 0,7; и 0,6. Найти  вероятность того, что студент, выбранный на удачу, в итоге соревнований попадет в сборную.

32.Пусть в условиях предыдущей задачи наудачу выбранный студент в итоге соревнований попал в сборную. Найти вероятность того, что это был студент первой группы.

33.В первом ящике содержатся 12 ламп, из них одна нестандартная; во втором 10 ламп, из них также одна нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.

34.Возле бензоколонки, стоящей на шоссе, проезжает в среднем 80% грузовых и 20% легковых автомашин. Вероятность того, что будет заправляться грузовая машина, равна 0,05, для легковой эта вероятность равна 0,1. Найти вероятность того, что выбранная наудачу машина будет заправляться.

35.В телевизионном ателье имеется 4 кинескопа разных типов. Вероятность того, что кинескоп выдержит гарантийный срок службы, соответственно равна 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп  выдержит гарантийный срок.

36.Пусть в условиях предыдущей задачи выбранный наудачу кинескоп выдержал гарантийный срок службы. Найти вероятность того, что это был кинескоп 1-го типа.

37.Распределение вероятностей непрерывной случайной величины задано функцией распределения

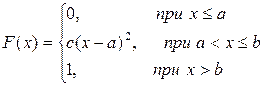
Требуется: а) найти значение с; б) плотность распределения вероятностей f(x);

в) построить график функций F(x) и f(x); г) вычислить М(х); D(x); s(x); д) Р.

Данные приведены в таблице

 

6. Защита модуля № 2

Контрольные вопросы к модулю № 2

Защита модуля проводится в письменном виде согласно вопросов по лекциям № 5 – 7

1.        Что называется случайной величиной? Примеры

2.        Какую случайную величину называют дискретной? Пример

3.        Какую случайную величину называют непрерывной? Пример

4.        Что называют законом распределения дискретной случайной величины?

5.        Что называют числовыми характеристиками случайной величины?

6.        Что такое математическое ожидание?

7.        Свойства математического ожидания

8.        Что является числовой характеристикой рассеяния случайной величины?

9.        Формула для вычисления дисперсии

10.  Свойства дисперсии

11.  Что называю среднеквадратическим отклонением случайной величины?

12.  Как найти среднеквадратическое отклонение дискретной случайной величины?

13.  Определение функции распределения. Пример

14.  Свойства функции распределения.

15.  График функции распределения. Пример

16.  Что называют плотностью распределения вероятностей непрерывной случайной величины?

17.  Как найти вероятность попадания непрерывной случайной величины в заданный интервал?

18.  Свойства плотности распределения

19.  Что называют математическим ожиданием непрерывной случайной величины?

20.  Что называют дисперсией непрерывной случайной величины?

21.  Как найти среднеквадратическое отклонение непрерывной случайной величины?

22.  Может ли при каком-либо значении аргумента:

а) функция распределения быть больше 1?

б) плотность распределения вероятности быть больше 1?

в) функция распределения быть отрицательной?

г) плотность распределения вероятности быть отрицательной?

23.  Почему f (x) носит название «плотность распределения вероятностей»?

24.  Что называют нормальным распределением?

25.  Какими параметрами определяется нормальное распределение?

26.  Чему равно математическое ожидание нормального распределения?

27.  Чему равна дисперсия нормального распределения?

28.  Чему равно среднеквадратическое отклонение нормального распределения?

29.  Какой график имеет нормальная кривая?

30.  Как вычислить попадание в заданный интервал нормальной случайной величины?

31.  Как вычислить вероятность заданного отклонения?

32.  Как используется правило трех сигм?

 

Практическое задание к зачету по модулю 2

1.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

2.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

3.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

4.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

5.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

6.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

7.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной сл. величины, заданной законом распределения

8.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

9.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной сл. величины, заданной законом распределения.

10.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

11.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое  отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

12.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

13.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое  отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

14.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

15.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной  случайной величины, заданной законом распределения.

16.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x) и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

17.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое  отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

18.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

19.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной  случайной величины, заданной законом распределения.

20.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

21.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

22.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

23.      Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

24.      По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

 

Модуль №3

                          1.  Проработать лекции № 8 - 10

                          2.  Подготовка к выполнению практической работы № 9

                          3.  Подготовка к выполнению практической работы № 10

                          4.  Подготовка к защите модуля № 3 по лекциям № 8 - 10

                          5.  Сдача семестрового задания, с. 46

 

1.      Проработать лекции № 8 - 10 по плану лекции.

При проработке лекции необходимо прочитать ее, выучить основные определения,  термины и формулы, ответить на контрольные вопросы, которые есть после каждой лекции. Если возникли вопросы, более плотно разобрать вопрос по литературе, указанной в действующей методике, или обратиться за консультацией к преподавателю.

 [3] с. 66–83

2. Практическая работа № 9 по теме «Расчет сводных характеристик выборки»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 42-47

3. Практическая работа № 10 по теме «Уравнение прямой линии регрессии по  сгруппированным данным»

Для данной работы нужно использовать методические рекомендации к выполнению практических работ, где дано объяснение выполнения работы, как ее оформить и варианты индивидуального задания, дать ответы на контрольные вопросы, которые есть в рекомендациях.

[4] с. 47-52

4. Защита модуля № 3

Контрольные вопросы модуля № 3

Защита модуля проводится в письменном виде согласно вопросов по лекциям № 8 – 10

1.          Задачи математической статистики.

2.   Что называется выборочной совокупностью?

3.   Что называют генеральной совокупностью?

4.   Что такое объем совокупности?

5.   Что называют статистическим распределение выборки?

6.   Что является эмпирической функцией распределения?

7.   Свойства эмпирической функции распределения

8.   Что называю полигоном частот?

9.   Что называю полигоном относительных частот?

10.     Что называю гистограммой частот?

11.     Что называю гистограммой относительных частот?

12.     Какая оценка называется несмещенной?

13.     Какая оценка называется смещенной?

14.     Какая оценка называется эффективной?

15.     Какая оценка называется состоятельной?

16.     Что называют генеральной средней?

17.     Что называют выборочной средней?

18.     Что называют генеральной дисперсией?

19.     Что называют генеральным средним квадратическим отклонением?

20.     Что называют выборочной дисперсией?

21.     Написать формулу для вычисления выборочной дисперсии

22.     Какую оценку называют интервальной?

23.     Что такое надежность оценки?

24.     Как находят доверительный интервал для оценки математического ожидания при известном σ?

25.     Как находят доверительный интервал для оценки математического ожидания при неизвестном σ?

26.     Как находят доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения?

27.     Как пользоваться справочными таблицами?

28.     Какие варианты называют равноотстоящими?

29.     Какие варианты называют условными?

30.     Что называют обычным эмпирическим моментом?

31.     Что называют начальным эмпирическим моментом?

32.     Что называют центральным эмпирическим моментом?

33.     Что называют условным эмпирическим моментом?

34.     Как выражаются обычные моменты через условные?

35.     Как выражаются центральные моменты через условные?

36.     Техника вычислений центральных моментов по условным с помощью метода произведений.

37.     Какие существуют виды зависимостей?

38.     Что называют статистической зависимостью?

39.     Что называют корреляционной зависимостью?

40.     Что называют условным средним?

41.     Какое уравнение называют выборочным уравнением регрессии?

42.     Какую функцию называют выборочной регрессией?

43.     Что является выборочной линией регрессии?

44.     Что называют выборочным коэффициентом регрессии?

45.     В чем заключается метод наименьших квадратов?

46.     Какую зависимость называют статистической?

47.     Какую зависимость называют корреляционной?

48.     Что называют условным средним?

49.     В качестве каких оценок принимают условные средние?

50.     Какое уравнение называют выборочным уравнением регрессии?

51.     Какую функцию называют выборочной регрессией?

52.     Что называют выборочной линией регрессии?

53.     Что называют выборочным коэффициентом регрессии?

54.     Как находятся параметры выборочного уравнения прямой линии регрессии по сгруппированным данным?

 

Практическое задание к зачету по модулю 3

1.           Построить график эмпирической функции распределения

хi	3	5	8	10
ni	3	4	7	9

2.           Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=8, =19,21, n= 36, γ=0,96

3.           Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n= 80, γ=0,99, =29,3, s =0,7

4.           Построить график эмпирической функции распределения

хi	8	9	13	20
ni	3	4	7	2

5.           Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=12, =13,45, n= 81, γ=0,98

6.           Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n= 20, γ=0,99, =45,2, s =0,8

7.           Построить график эмпирической функции распределения

хi	1	5	7	9
ni	2	4	8	3

8.           Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=7, =95,7, n= 144, γ=0,89

9.           Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n= 35, γ=0,99, =71,35, s =0,8

10.     Построить график эмпирической функции распределения

хi	3	7	13	15
ni	1	5	7	1

11.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=13, =62,45, n= 121, γ=0,77

12.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n= 90, γ=0,999, =14,23, s =0,6

13.     Построить график эмпирической функции распределения

хi	6	7	15	20
ni	3	7	5	2

14.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=11, =32,14, n= 81, γ=0,97

15.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=60, γ=0,999, =13,23, s =0,6

16.     Построить график эмпирической функции распределения

хi	4	8	9	11
ni	4	7	5	6

17.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=13, =22,14, n= 64, γ=0,78

18.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=50, γ=0,99, =43,23, s =0,7

19.     Построить график эмпирической функции распределения

хi	6	7	9	12
ni	3	5	7	1

20.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=7, =54,21, n= 64, γ=0,75

21.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=40, γ=0,999, =13,23, s =0,7

22.     Построить график эмпирической функции распределения

хi	1	5	7	13
ni	3	5	7	1

23.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=9, =50,21, n= 16, γ=0,85

24.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=19, γ=0,999, =43,23, s =0,8

25.     Построить график эмпирической функции распределения

хi	7	9	12	13
ni	1	3	4	2

26.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=12, =0,21, n= 144, γ=0,65

27.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=120, γ=0,999, =23,23, s =0,6

28.     Построить график эмпирической функции распределения

хi	2	4	6	14
ni	3	8	2	1

29.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=2, =10,21, n= 196, γ=0,99

30.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=14, γ=0,99, =13,25, s =0,7

31.     Построить график эмпирической функции распределения

хi	1	3	8	9
ni	5	10	1	2

32.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=12, =45,85, n= 4, γ=0,98

33.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=13, γ=0,999, =11,25, s =0,7

34.     Построить график эмпирической функции распределения

хi	2	3	8	11
ni	6	7	1	3

35.     Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя , объем выборки n. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью γ

σ=18, =15,85, n= 9, γ=0,88

36.     Количественный признак Х генеральной совокупности распределен нормально. При выборке объема n найдены выборочная средняя и «исправленной» среднее квадратическое отклонение s. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью γ

n=12, γ=0,99, =31,25, s =0,7

 

5. Семестровое задание

Правила оформления семестрового задания даны в введении данного методического пособия. Согласно своего варианта выполните следующие задания:

Вариант № 1

1.  В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

2.  Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки р=0,3. Определить вероятность того, что на соревнованиях спортсмен улучшит свой вариант, если разрешается делать две попытки.

3.  В первой урне содержится 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

 

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 2

1.  В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта на удачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.

2.  В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета.

3.  В каждый из трех урн содержится 6 черных и 4 белых шара. Из первой урны на удачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 3

1.  В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлечённых деталей нет бракованных.

2.  Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из пяти первых покупателей обувь этого размера будет необходима, по крайней мере, одному.

3.  Имеется две урны. В первой 4 белых и 6 чёрных шаров, во второй 5 белых и 5 чёрных шаров. Из первой урны во вторую перекладывается один шар. Шары перемешиваются, и затем из второй урны в первую перекладывается один шар. После этого из первой урны берут наугад один шар. Найти вероятность того, что он будет белым.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

 

Вариант № 4

1.  Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

2.  Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб».

3.  В ящике находится 6 новых теннисных мячей и 4 игранных. Из ящика наугад вынимается два мяча, которыми играют. После этого мячи возвращаются в ящик. Для следующей игры из ящика снова берут наугад два мяча. Найти вероятность того, что они будут новыми.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной сл. величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

 

Вариант №5

1.  В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных окажутся три женщины.

2.  Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятность того, что деталь содержится не более чем в трех ящиках.

3.  Имеются две урны. В одной из них находится шар, о котором известно, что он либо белый, либо черный. В другой урне находится 1 белый и 2 черных шара. Выбирается наугад одна из урн и вынимается из нее шар. Найти вероятность того, что извлеченный шар белый.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной сл. величины, заданной законом распределения.

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант №6

1.  В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.

2.  Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

3.  Стрелок А поражает мишень при некоторых условиях стрельбы с вероятностью p1=0,6, стрелок В – с вероятностью p2=0,5 и стрелок С -  с вероятностью p3=0,4. Стрелки дали залп по мишени, и две пули попали в цель. Какова вероятность того, что  С попал в мишень?

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое  отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 7

1.  В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажется два окрашенных изделия.

2.  Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка стрела равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

3.   В первой урне содержится 8 белых и 2 черных шара. Во второй урне 4 белых и 16 черных шаров. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взять ещё один шар. Найти вероятность того, что взять белый шар.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое  отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 8

1.  В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет годных.

2.  Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.

3.  В семье 5 детей. Найти вероятность того, что среди этих детей не более двух мальчиков. Вероятность рождения мальчика равна 0,51.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной  случайной величины, заданной законом распределения.

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x) и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 9

1.  В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажется хотя бы одно окрашенное изделие.

2.  Вероятность выбить 10 очков при одном выстреле равна 0,2; 9 очков равна 0,3; от 1 до 9 очков равна 0,7. Определить вероятность выбить не менее 9 очков и вероятность промаха.

3.   Найти вероятность того, что событие А появится не менее 3 раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое  отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

 

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 10

1.  Устройство содержит 5 элементов, из которых 2 изношены. При включении устройства включаются случайным образом 2 элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

2.  Студент знает 20 вопросов из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.

3.  Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадает к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной  случайной величины, заданной законом распределения.

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 11

1.  После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-м и 55-м километрами линии?

2.  В ящике 10 деталей, из которых 4 окрашены. Сборщик на удачу взял 3 детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

3.  В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95 , для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из взятой винтовки на удачу. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант №12

1.  Из полной колоды карт (52 карты) наугад извлекаются три карты. Найти вероятность того, что это будет тройка, семерка, туз.

2.  Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.

3.  В специализированную больницу поступает в среднем 50% больных с заболеванием К, 30% - с заболеванием L, 20% - с заболеванием M. Вероятность полного излечения болезни К равна 0,7; для болезней L и M эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 13

1.  Из десяти билетов выигрышными являются два. Определить вероятность того. Что среди взятых наудачу пяти билетов оба выигрышные.

2.  Устройство содержит два независимо работающих элемента. Вероятность отказа элементов соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

3.  Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятность попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,2, 0,4 и 0,3.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант №14

1.  Десять книг на одной полке расставляются наудачу. Определить вероятность того, что при этом три определенные книги окажутся поставленными рядом.

2.  Вероятность выигрыша по одному билету лотереи равна 0,1. Какова вероятность того, что лицо, имеющее 6 билетов выиграет по двум билетам?

3.  Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равны 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 15

1.  Среди электрических лампочек три нестандартные. Найти вероятность того, что две взятые одновременно электрические лампочки окажутся нестандартными.

2.  Вероятность того, что взятый наугад для испытаний образец шерстяной ткани выдержит установленную нагрузку, равна 0,8. Случайным образом отбираются четыре образца. Какова вероятность того, что хотя бы один из них выдержит указанную нагрузку?

3.  Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести (ничья во внимание не принимается)?

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения дискретной случайной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 16

1.  В урне имеется 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад 2 шара окажутся белыми.

2.  Имеется 5 билетов стоимостью 1 грн., три билета по 3 грн. и два билета по пять грн. Наугад берутся три билета. Определить вероятность того, что хотя бы два из этих билетов имеют одинаковую стоимость.

3.  Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения дискретной случайной величины заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 17

1.  Из пяти букв разрезной азбуки составлено слово «книга». Ребёнок не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получится слово «книга».

2.   Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трёх проверенных изделий только два изделия высшего сорта.

3.  Вероятность попадания по движущейся мишени принимается равной 0,7. Какова вероятность того, что из 20 выстрелов 15 окажутся удачными.

4.   Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения.

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 18

1.  В коробке содержится 6 одинаковых пронумерованных кубиков. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

2.   Предприятие выпускает 96% изделий качественных, из каждых 100 которых 75 являются изделиями первого сорта. Найти вероятность того, что наудачу взятое изделие окажется первого сорта.

3.   Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть не менее двух  партий из четырёх или не менее трёх партий из пяти (ничья во внимание не принимаются)?

4.   Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения дискретной случайной величины, заданной законом распределения 

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

 

Вариант № 19

1.  На стеллаже библиотеке в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет на удачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

2.  Вероятность попадания в цель первого стрелка равна 0,1, а вероятность второго стрелка равна 0,9. Определить вероятность того, что при выстреле обоих стрелков в мишени окажется одна пуля.

3.  Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,3.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной случайной величины, заданной законом распределения.

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант №20

1.  В ящике 10 одинаковых деталей, помеченных номерами 1, 2, … 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся детали № 1 и  № 2.

2.  Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности, попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7;

3.  В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы,  соответственно равны 0,8; 0,85; 0,9; 0,95. Найти  вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения дискретной случайной величины, заданной законом распределения.

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 21

1.  Имеется лабиринт с шестью разветвлениями пути. Из каждого разветвления идут два пути, причём один из них ведёт в тупик. Вычислить вероятность пройти по этому лабиринту, не заходя ни в один из тупиков.

2.  Для сигнализации об аварии установлены 2 независимо работающих устройства. Вероятность того, что при аварии  сработает первое устройство, равна 0,9, второе – 0,95. Найти вероятность того, что при аварии сработает хотя бы одно устройство.

3.  Рабочий обслуживает три станка, работающих независимо друг от друга. вероятность того, что в течение часа первый станок потребует внимания рабочего, равна 0,1, для второго такая вероятность равна 0,2, для третьего – 0,3. Какова вероятность того, что в течение часа хотя бы один станок потребует внимания рабочего.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант №22

1.  Брошена монета и игральная кость. Найти вероятность совмещения событий: «появился герб» и «появилось 4 очка».

2.  Три стрелка стреляют в одну мишень. При этом известно, что вероятность попадания с одного выстрела для первого стрелка равна 0,8, для второго – 0,7, для третьего – 0,6. Найти вероятность появления в мишени одной пробоины в результате одновременного выстрела всех трёх стрелков.

3.  На двух автоматических станках изготовляются одинаковые детали. Известно, что вероятность изготовления детали высшего качества на первом станке равна 0,92, а на втором – 0,8. Изготовленные на обоих станках не рассортированные детали находятся на складе. Среди них деталей, изготовленных на первом станке, в три раза больше, чем на втором. Найти вероятность того, что наудачу взятая деталь будет высшего качества.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 23

1.  В первой коробке 20 деталей, из них 18 стандартных, во второй коробке 10 деталей, из них 7 стандартных. Из второй коробки наудачу взята деталь и переложена в первую. Найти вероятность того, что деталь, наудачу извлеченная из первой коробки, стандартна.

2.  Пусть в условиях предыдущей задачи деталь, извлеченная из первой коробки, оказалась стандартной. Найти вероятность того, что из второй коробки переложена в первую стандартная деталь.

3.  Детали, изготовленные цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4, вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Найти вероятность того, что годная деталь будет признана стандартной.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 24

1.  Приборы одного наименования изготовляются двумя заводами, первый завод поставляет 60 % всех изделий, второй – 40%. Вероятность безотказной работы за время Т прибора, изготовленного первым заводом, равна 0,9, вторым – 0,8. Определить вероятность безотказной работы взятого наудачу прибора, поступившего на производство.

2.  Пусть в условиях предыдущей задачи взятый наудачу прибор проработал безотказно время Т. Каково вероятность того, что этот прибор изготовлен первым заводом?

3.  Пассажир может обратиться за получением билета в одну из двух касс. Вероятность обращения в каждую кассу зависит от их местоположения и равна соответственно 0,7 и 0,3. Вероятность того, что к моменту прихода пассажира билеты будут проданы, равна для первой кассы 0,8, для второй –0,4. Найти вероятность того, что, выбрав наудачу кассу, пассажир приобретет билет.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

 

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Вариант № 25

1.  Производится стрельба по цели. Цель состоит из трех частей, площади которых равны S₁, S₂, S₃, (S₁+S₂+S₃ = S). Для попавшего в цель снаряда вероятность попасть в ту или другую часть пропорциональна площади части. При попадании в первую часть цель поражается с вероятностью р₁, во вторую часть р₂, в третью – р₃. Найти вероятность поражения цели, если известно, что в нее попал один снаряд.

2.  На первом заводе на каждые 100 лампочек производится в среднем 90 стандартных, на втором 95, на третьем – 85, а продукция их составляет соответственно 50, 30, 20 процентов всех электрических лампочек, поставляемых в магазины данного района. Найти вероятность приобретения стандартной электрической лампочки.

3.  Пусть в условиях предыдущей задачи электрическая лампочка, приобретена в магазине данного района, оказалась стандартной. Найти вероятность того, что лампочка произведена на первом заводе.

4.  Вычислить числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение) и построить многоугольник распределения для дискретной величины, заданной законом распределения

5.  По заданному виду плотности вероятности f(x) случайной величины Х, принимающей значения в заданном интервале. Найти уравнение плотности f(x)  и функции распределения F(x). Построить графики этих функций, вычислить числовые характеристики непрерывной случайной величины.

6.  Дана корреляционная таблица.

 

Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.

Приложение 1

 

 

Приложение 2

Таблица значений функции

 

Продолжение приложения 2

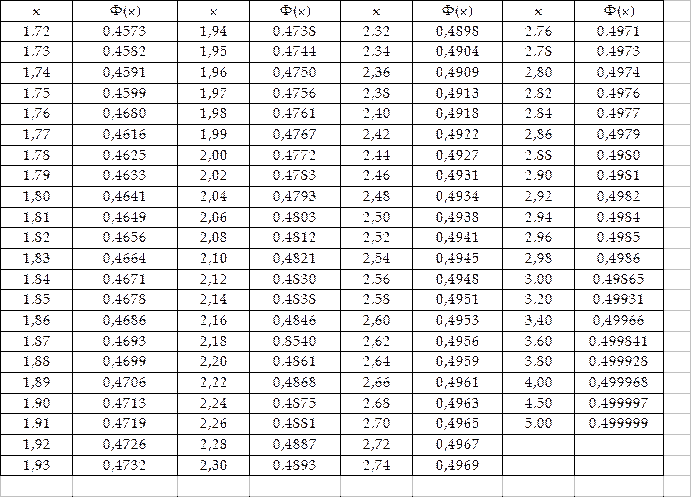Приложение 3

Таблица значений 

Приложение 4

 

Таблица значений

 

 

Литература

 

Базовая

1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебн. пособие для вузов.  - М: Высш.шк., 2003. – 479 с.:ил.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособие для вузов. М: Высш.шк., 2003. – 405 с.:ил.

3. Вентцель е.С. Теория вероятностей. Учебн. пособие для вузов. – М: Высш.шк., 2002. – 575 с.:ил.

Дополнительная

4. Вентцель е.С., Овчаров л.А. Теория вероятностей и ее инженерные приложения. Учебн. пособие для втузов. - М: Высш.шк., 2000. – 480 с.:ил.

5. Кромер н.Ш. Теория вероятностей. Учебн. пособие для вузов.  – М: ЮНИТИ-ДАНА, 2001. – 543 с.