Поделиться
Методические указания.docx
Министерство образования Красноярского края
Краевое государственное бюджетное профессиональное образовательное учреждение
«Зеленогорский техникум промышленных технологий и сервиса»
Техническая механика
Методические указания
по выполнению лабораторных и расчетно-графических работ
для студентов специальности 08.02.09 Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий
Раздел «Теоретическая механика»
Рассмотрено
на заседании ЦМК преподавателей
и мастеров п\о профессий техники
и технологии строительства
Председатель____________Т.В.Просвирнина
Протокол № ___от «____»__________2020 г
г. Зеленогорск, 2020
Пояснительная записка
Рабочей программой учебной дисциплины Техническая механика предусмотрено выполнение следующих практических занятий по разделу: «Теоретическая механика»:
Практическая работа № 1 Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способом;
Практическая работа №2 Определение главного вектора и главного момента системы сил графическим и аналитическим способом;
Практическая работа работа №3 Равновесие плоской системы сил. Уравнения равновесия и их различные формы. Балочные системы. Классификация нагрузок и виды опор. Определение реакций опор;
Практическая работа №4 Определение координат центра тяжести составного сечения;
Практическая работа №5. Определение параметров поступательного и вращательного движения точки.
В результате изучения дисциплины обучающийся должен уметь:
- определять координаты центра тяжести тел;
- выполнять расчеты на прочность и жесткость;
В результате освоения дисциплины обучающийся должен знать:
- виды деформации;
- законы механического движения и равновесия;
- методы механических испытаний материалов;
- методы расчета элементов конструкции на прочность;
- устойчивость при различных видах нагружения;
- основные типы деталей машин и механизмов.
Общие правила выполнения практических заданий
1. Каждый обучающийся после выполнения задания должен представить отчет о проделанной работе с анализом полученных результатов и выводом.
2. Отчет о проделанной работе следует оформить в тетради для практических занятий. Содержание отчета указано в описании выполнения практического задания.
3. Таблицы и рисунки следует выполнять с помощью чертежных инструментов.
4. В расчетах обязательно указывать буквенные обозначения величин и единицы измерения.
5. Расчет следует проводить с точностью до двух значащих цифр после запятой.
6. Если обучающийся не выполнил практическое задание. То он может выполнить его во внеурочное время, согласованное с преподавателем.
7. Оценку по практическому занятию обучающийся получает с учетом срока выполнения работы, если:
- расчеты выполнены правильно и в полном объеме;
- сделан вывод по результатам работы;
- обучающийся может пояснить выполнение любого этапа работы;
- отчет выполнен в соответствии с требованиями к выполнению практического задания.
ПРАКТИЧЕСКАЯ РАБОТА №5
Тема: . Определение параметров поступательного и вращательного движения точки
Цель работы: научиться определять кинематические параметры материальной точки, движущейся с ускорением, с учетом принципа Даламбера.
Необходимые материалы и оборудование:
Порядок выполнения задания:
1. По номеру в журнале выписать из таблицы величины исходных данных.
2. Выделить точку, движение которой рассматривается и изобразить на рисунке.
3. Определить (выявить) все активные силы и изобразить их, приложенными к точке на рисунке.
4. Освободить точку от связей, заменить связи их реакциями и также изобразить их на рисунке.
5. Изобразить на рисунке ускорение.
6. Добавить к рисунку силу инерции.
7. Рассмотреть образовавшуюся уравновешенную систему сил.
8. Определить искомую величину.
9. Сформулировать вывод.
Краткие теоретические сведения
Кинематика рассматривает механическое движение тела без учета причин, вызывающих это движение и устанавливает способы задания движения и определяет методы определения кинематических параметров движения.
Основные кинематические характеристики:
Траектория – линия, которую описывает материальная точка при движении в пространстве. Уравнение траектории у=f(х).
Пройденный путь – расстояние пройденное телом вдоль траектории. Движение тела можно задать двумя способами: Уравнение движения можно представить двумя способами: естественным (положение тела в каждый момент времени определяется по расстоянию, пройденным телом вдоль траектории от неподвижной точки, которая является началом отсчета) S= f(t); координатным (положение тела в каждый момент времени определяется её координатами в зависимости от времени) х= f(t), у= f(t)/
Скорость движения – векторная величина, характеризующая быстроту и направление движения по траектории в данный момент времени.
Скорость
величина векторная, направленная в любой момент времени по касательной к
траектории в сторону движения. Есть скорость средняя на пути 
. Есть скорость мгновенная -
скорость точки в данный момент времени. Она определяется как производная пути
по времени: 
.
Ускорение точки – векторная
величина, характеризующая быстроту изменения скорости по величине и
направлению. Среднее ускорение за промежуток времени: 
. Мгновенное ускорение - это
ускорение в данный момент времени. Определяется как первая производная скорости
по времени или вторая производная пути по времени 
.
Обычно рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное.
Нормальное ускорение 
характеризует изменение скорости по
направлению и определяется как 
, где 
- радиус кривизны траектории в данный
момент времени. Нормальное ускорение всегда направлено перпендикулярно скорости
к центру дуги.
Касательное ускорение 
характеризует изменение скорости по
величине и всегда направлено по касательной к траектории; при ускоренном
движении оно совпадает по направлению с вектором скорости, при замедленном
движении оно направлено противоположно направлению вектора скорости. Формула
для касательного ускорения:
.
Полное ускорение определяется как 
.
В зависимости от ускорения существуют следующие виды движения:
Равномерное – это движение с постоянной скоростью.
Для прямолинейного равномерного движения
- 
.
Для криволинейного движения - 
.
Уравнение движения 
.
Равнопеременное движение – это движение с
постоянным ускорением 
.
Для прямолинейного равнопеременного
движения 
.
Для криволинейного движения - 
.
Уравнение движения 
.
Уравнение скорости 
.
Неравномерное движение – это движение, при котором скорость и ускорение с течением времени изменяются.
Уравнение движения это уравнение третей 
и выше степени.
Кинематические графики.
Равномерное движение
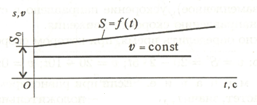
Равнопеременное движение
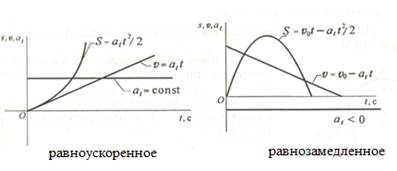
Простейшие виды движения твердого тела
Поступательное движение – это движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению. При поступательном движении все точки тела движутся одинаково.
Вращательное движение – это движение, при котором все точки тела описывают окружности вокруг общей неподвижной оси, которая называется осью вращения.
Для описания вращательного тела вокруг неподвижной оси используют угловые характеристики:
Угол
поворота тела 
. Измеряется в радианах. Уравнение
движения 
Угловая
скорость 
, определяет изменение угла поворота в
единицу времени. Измеряется рад/с. Угловая скорость определяется как первая
производная от угла поворота по времени 
.
Иногда
для оценки быстроты вращения используют угловую частоту вращения n, которая
оценивается в оборотах в минуту. Между угловой скоростью и частотой вращения
существует зависимость: 
.
Угловое
ускорение 
, определяет изменение угловой скорости во
времени. Измеряется рад/с2. Угловое ускорение определяется как
первая производная от угловой скорости по времени или вторая производная от
угла поворота по времени 
.
Частные случаи вращательного движения:
Равномерное
вращение – угловая скорость постоянна 
.
Уравнение
равномерного вращения 
.
Кинематические графики
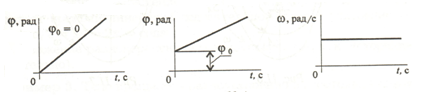
Равнопеременное вращение - угловое
ускорение постоянно 
.
Уравнение
равнопеременного вращения 
.
Угловое ускорение при ускоренном движении – величина положительная, угловая скорость возрастает.
Угловое ускорение при замедленном движении – величина отрицательная, угловая скорость убывает.
Кинематические графики
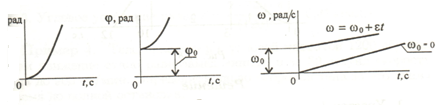
Скорости и ускорения точек вращающегося тела
Тело вращается вокруг точки О. Определим параметры
движения точки А, расположенной на расстоянии 
от оси вращения.
Путь точки А: 
;
Линейная скорость точки А:
.
Ускорение точки А: 
; 
.
Задание 1.
1. Определить вид движения на каждом участке по приведенному кинематическому графику.
2. Записать законы движения шкива на каждом участке. Параметры движения в конце каждого участка являются начальными параметрами движения на каждом последующем.
3. Определить полный угол поворота шкива за время вращения. Использовать формулу для перехода от угловой частоты вращения к угловому ускорению.
4.
Определить
полное число оборотов шкива, используя формулу 
.
5. Построить графики угловых перемещений и угловых ускорений.
6. Определить нормальное и касательное ускорения точки на ободе шкива в указанные моменты времени.
Задание 2.
1. Подставив заданные коэффициенты в общее уравнение движения, определить вид движения.
2. Определить уравнение скорости и ускорения груза.
Примеры решения задач
Задача
1.
Дано
уравнение движения точки: 
. Определить скорость точки в конце
третьей секунды движения и среднюю скорость за первые 3 секунды.
Решение.
1. Уравнение скорости
;
2. Скорость в конце
третьей секунды (
.
3. Средняя скорость 
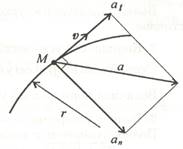Задача 2. Точка движется по
кривой радиуса 10 м согласно уравнению 
. Определить полное ускорение точки в
конце второй секунды движения и указать направление касательной и нормальной
составляющих ускорения в точке М и вид движения точки.
Решение:
1.
Касательное
ускорение определяется как 
.
2.
Уравнение
скорости: 
3.
Касательное
ускорение 
м/с2.
4. Касательное ускорение не зависит от времени, оно постоянно, следовательно, движение равноускоренное.
5.
Нормальное
ускорение: 
.
Скорость на
второй секунде будет равно: 
м/с.
Величина
нормального ускорения 
м/с2.
6.
Полное
ускорение: 
.
Полное ускорение в конце второй секунды:
м/с2.
7. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.
Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, так как касательное ускорение положительная величина.
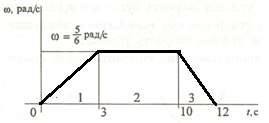Задача 3. По заданному
графику угловой скорости определить вид движения. Определить полное
число оборотов шкива за время движения. Построить графики угловых перемещений
и угловых ускорений шкива.
Решение:
1. Из графика определяем вид движения:
Участок 1 – скорость возрастает равномерно, движение равноускоренное;
Участок 2 – скорость постоянна - движение равномерное;
Участок 3 – скорость убывает равномерно – движение равноускоренное.
2.
Определяем
угловое ускорение: 
Участок
1 - 
рад/с; 
рад/с; 
рад/с2
Участок
2 - 
рад/с; 
рад/с; 
рад/с2;
Участок
3 - 
рад/с; 
рад/с. 
рад/с2.
3.
Определяем
угол поворота : 
; 
; 
.
Участок
1 - 
рад;
Участок
2 - 
рад;
Участок
3 – 
рад.
рад.
4. Определяем полное число оборотов шкива за время движения:
5. Строим графики угловых перемещений:
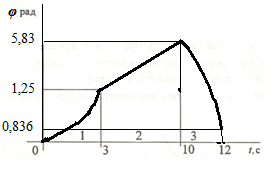Участок 1 - 
рад;
Участок
2 - 
рад;
Участок
3 – 
рад.
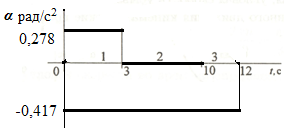
6. Строим графики угловых ускорений.
Участок
1 - 
рад/с2
Участок
2 - 
рад/с2;
Участок
3 - 
рад/с2.
Отчет о проделанной работе должен содержать:
1. Тема работы
2. Цель работы
3. Исходные данные из таблицы.
4. Решение заданий1,2.
5. Вывод.
Содержание задания:
По номеру в журнале из таблицы выписать условия четырех задач и выполнить решение. Сформулировать вывод.
Задание 1. Частота вращения шкива диаметром d меняется согласно
графику. Определить полное число оборотов шкива за время движения и среднюю
угловую скорость за это же время. Построить графики угловых перемещений и
угловых ускорений шкива. Определить ускорение точек обода колеса в момент
времени 
и 
. Данные для своего варианта взять в
таблице. Номер варианта соответствует порядковому номеру в журнале.
|
Параметры |
Вариант |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Номер схемы |
1 |
2 |
3 |
4 |
5 |
6 |
4 |
5 |
2 |
1 |
|
Диаметр шкива ,м |
0,2 |
0.3 |
0,4 |
0,6 |
0,5 |
0,8 |
0,7 |
0,9 |
0,2 |
0.3 |
|
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
3 |
|
|
8 |
9 |
8 |
9 |
8 |
6 |
9 |
8 |
9 |
6 |
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Номер схемы |
5 |
1 |
3 |
6 |
4 |
5 |
3 |
2 |
6 |
1 |
|
Диаметр шкива ,м |
0,4 |
0,6 |
0,2 |
0.3 |
0,4 |
0,6 |
0,5 |
0,8 |
0,7 |
0,9 |
|
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
|
|
8 |
9 |
8 |
9 |
8 |
6 |
9 |
8 |
9 |
6 |
|
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
Номер схемы |
6 |
3 |
1 |
4 |
2 |
5 |
3 |
4 |
1 |
3 |
|
Диаметр шкива ,м |
0,2 |
0.3 |
0,4 |
0,6 |
0,5 |
0,8 |
0,7 |
0,9 |
0,2 |
0.3 |
|
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
3 |
|
|
8 |
9 |
8 |
9 |
8 |
6 |
9 |
8 |
9 |
6 |
|
|
|
|
|
|
|
|
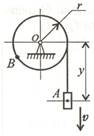Задание
2. Движение
груза А задано уравнением 
. Определить скорость и ускорение груза в
момент времени 
и 
, а так же скорость и ускорение точки В на
ободе барабана лебедки. Данные для своего варианта взять в таблице. Номер
варианта соответствует порядковому номеру в журнале.
Данные
|
Параметры |
Вариант |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
а, м/с2 |
2 |
0 |
3 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
|
b, м/с |
0 |
4 |
3 |
6 |
5 |
2 |
1 |
4 |
0 |
5 |
|
с, м |
3 |
4 |
2 |
0 |
1 |
3 |
5 |
2 |
1 |
0 |
|
r1, м |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,2 |
0,3 |
0,4 |
|
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
3 |
|
|
8 |
9 |
8 |
9 |
8 |
6 |
9 |
8 |
9 |
6 |
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
а, м/с2 |
3 |
4 |
2 |
1 |
0 |
3 |
4 |
0 |
2 |
1 |
|
b, м/с |
5 |
3 |
0 |
2 |
1 |
4 |
2 |
1 |
0 |
3 |
|
с, м |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
r1, м |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,2 |
0,3 |
0,4 |
|
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
3 |
|
|
8 |
9 |
8 |
9 |
8 |
6 |
9 |
8 |
9 |
6 |
|
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
а, м/с2 |
4 |
0 |
1 |
2 |
3 |
4 |
0 |
1 |
2 |
3 |
|
b, м/с |
0 |
1 |
2 |
3 |
4 |
5 |
0 |
1 |
2 |
3 |
|
с, м |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
|
r1, м |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,2 |
0,3 |
0,4 |
|
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
3 |
|
|
8 |
9 |
8 |
9 |
8 |
6 |
9 |
8 |
9 |
6 |
Контрольные вопросы:
1. Как определяется мгновенная скорость?
2. Формула касательного ускорения.
3. Запишите уравнение равномерного движения.
4. Какое направление имеет нормальное ускорение?
5. Формула для определения мгновенной скорости.
|
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
