УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛИПЕЦКОЙ ОБЛАСТИ

Г(О)Б ПОУ «ЗАДОНСКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»

 

 

Инструкционные карты 

 

для практических и лабораторных занятий  по дисциплине:

«Физика»

 

 

 

Автор: преподаватель физики Г.С. Акатова

 

 

 

 

 

 

 

 Задонск 2021

Пояснительная записка

Методические указания   по выполнению лабораторно - практических  работ  по  дисциплине Физика являются составной частью УМК по Физике  и предназначены для профессий среднего профессионального образования.

Цель методических рекомендаций по выполнению лабораторных работ по  дисциплине "Физика":

организация выполнения обучающимися  лабораторных работ, предусмотренных программой по физике,

формирование и закрепление навыков работы с лабораторным оборудованием,

 организация определения погрешности и числовой обработки результатов лабораторного эксперимента,

формирование навыков самостоятельной работы студентов со справочной литературой,

развитие внимательности и аккуратности при выполнении лабораторных работ,

формирование общеучебных и общепрофессиональных компетенций студентов.

Весь процесс выполнения лабораторных работ включает в себя теоретическую подготовку, ознакомление с приборами и сборку схем, проведение опыта и измерений, числовую обработку результатов лабораторного эксперимента и сдачу зачета по выполненной работе.

Теоретическая подготовка

Теоретическая подготовка необходима для проведения физического эксперимента, должна проводиться обучающимися в порядке самостоятельной работы. Ее следует начинать внимательным разбором руководства к данной лабораторной работе.

Особое внимание в ходе теоретической подготовки должно быть обращено на понимание физической сущности процесса.

Для самоконтроля в каждой работе приведены контрольные вопросы, на которые обучающийся обязан дать четкие, правильные ответы.

Теоретическая подготовка завершается предварительным составлением отчета со следующим порядком записей:

1.    Название работы.

2.    Цель работы.

3.    Оборудование.

4.    Ход работы (включает рисунки, схемы, таблицы, основные формулы для определения величин, а так же расчетные формулы для определения погрешностей измеряемых величин).

5.    Расчеты – окончательная запись результатов работы.

6.    Вывод.

Ознакомление с приборами, сборка схем

Лабораторные работы проводятся в учебном кабинете лицея, оснащенном всем необходимым техническим и лабораторным оборудованием. Перед началом каждым занятием проводится инструктаж по технике безопасности.

     Приступая к лабораторным работам, необходимо:

1)    получить у лаборанта приборы, требуемые для выполнения работы;

2)    разобраться в назначении приборов и принадлежностей в соответствии с их техническими данными;

3)    пользуясь схемой или рисунками, имеющимися в пособии, разместить приборы так, чтобы удобно было производить отсчеты, а затем собрать установку;

4)    сборку электрических схем следует производить после тщательного изучения правил выполнения лабораторных работ по электричеству.

Проведение опыта и измерений

При выполнении лабораторных работ измерение физических величин необходимо проводить в строгой, заранее предусмотренной последовательности.

Особо следует обратить внимание на точность и своевременность отсчетов при измерении нужных физических величин. Например,   точность измерения времени с помощью секундомера зависит не только от четкого определения положения стрелки, но и в значительной степени – от своевременности  включения и выключения часового механизма.

  Преподаватель принимает выполненную учащимся лабораторную работу в индивидуальном порядке. Хорошо выполненные работы следует рекомендовать для ознакомления всем учащимся. Для зачета, по окончании лабораторных работ, учащийся представляет надлежащим образом оформленную тетрадь.

   Целесообразно в конце занятия сообщать тему следующего практического занятия и указывать литературные источники. Учащиеся в таких случаях приходят с готовыми конспектами, и преподавателю остается дать лишь целевую установку занятия, распределить задания, показать технику выполнения. После этого учащиеся приступают к самостоятельной работе.

Критерии оценки практической работы.

Практические занятия оцениваются преподавателем, исходя из следующих критериев успешности работ:

1) соответствие содержания работы заданной теме и оформление в соответствии с существующими требованиями;

2) логика изложения, взаимосвязь структурных элементов работы;

3) объем, характер и качество использованных источников;

4) обоснованность выводов, их глубина, оригинальность;

5) теоретическая и методическая достаточность, стиль и качество оформления компьютерной презентации

Оценивая итоговое задание, преподаватель ставит отметку.

Оценка «5» (отлично) ставится, если обучающийся выполняет работу в полном объеме с соблюдением необходимой последовательности проведения опытов и измерений; самостоятельно и рационально монтирует необходимое оборудование; все опыты проводит в условиях и режимах, обеспечивающих получение правильных результатов и выводов; соблюдает требования правил безопасного труда; в отчете правильно и аккуратно выполняет все записи, таблицы, рисунки, чертежи, графики, вычисления; правильно выполняет анализ погрешностей.

- в отчете правильно и аккуратно выполнены все записи, таблицы, рисунки, чертежи, графики, вычисления;

- правильно выполнен анализ погрешностей.

«4» (хорошо) ставится в том случае, если были выполнены требования к оценке «5», но допущены недочеты или негрубые ошибки.

«3» (удовлетворительно) ставится, если результат выполненной части таков, что позволяет получить правильные выводы, но в ходе проведения опыта и измерений были допущены ошибки.

«2» (неудовлетворительно) ставится, если результаты не позволяют сделать правильных выводов, если опыты, измерения, вычисления, наблюдения производились неправильно.

Техника безопасности при выполнении практических занятий.

Перед началом практического занятия:

1. Внимательно прослушайте вводный инструктаж преподавателя о порядке и особенностях выполнения практического занятия.

2. Внимательно изучите методические указания к работе, которую выполняете и строго руководствуетесь.

3. Подготовьте рабочее место для безопасной работы: уберите его, если на нем находятся посторонние предметы;

4. Проверьте и подготовьте к работе, согласно методическим указаниям, необходимые инструменты и принадлежности.

Во время работы:

1. Выполняйте только ту работу, которая разрешена преподавателем.

2. За разъяснениями по всем вопросам выполнения практического занятия обращайтесь к преподавателю.

3. Будьте внимательны и аккуратны. Не отвлекайтесь сами и не отвлекайте других. Не вмешивайтесь в процесс работы других обучающихся, если это предусмотрено инструкцией

По окончании работы:

1. Наведите порядок на рабочем месте и сдайте его преподавателю;

2. Сдайте преподавателю учебную литературу и инструменты;

При выполнении работы строго запрещается:

1. Бесцельно ходить по кабинету и лаборатории.

2. Покидать помещение кабинета (лаборатории)  в рабочее время без разрешения преподавателя.

 

 

 

 

 

 

 

 

 

 

 

 

 

Раздел 2. Механика

Тема 2.1. Кинематика

Практическая работа № 1. «Расчет основных кинематических величин»

Цель: закрепить умения и навыки вычисления кинематических величин материальной точки, развитие умения анализировать, выделять главное, обобщать и систематизировать, применять знания на практике, систематизация полученных знаний по данной теме, отработка умений выполнять задания по образцу, применять полученные знания для решения физических задач.

Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы, линейка, карандаш.

Указание: Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы:

ü К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

ü Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

ü При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

ü Внимательно прочитать теоретическую часть и план решения задач.

ü Рассмотреть примеры решения задач.

ü Ответить на контрольные вопросы.

ü Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Теоретическая часть

Основные механические величины и их обозначения

Приставки и множители для образования десятичных кратных и дольных единиц

Кинематика – раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики - динамика.

Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движения рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).

Механическое движение - это изменение положения тела относительно других тел в пространстве с течением времени. В любом механическом движении всегда участвуют не менее двух тел. Одно из них условно принимают за неподвижное тело отсчета и по отношению к нему определяют механическое состояние всех остальных тел.  Материальная точка – тело, размеры и форму которого можно не учитывать при описании его движения и массу которого можно считать сосредоточенной в точке. Тело отсчета - тело, относительно которого определяется положение данного тела. Движение материальной точки характеризуют траекторией, длиной пути, перемещением, скоростью, ускорением. Траектория – это линия, вдоль которой движется тело в данной системе отсчета.

Путь – скалярная величина, равная длине участка траектории между начальным и конечным положением тела.

Радиус-вектор – вектор, соединяющий начало отсчёта с положением точки в произвольный момент времени.

При движении точки конец радиус-вектора описывает траекторию движения. На рис. линия М₁М₂ изображает участок r₁Dr траектории движения точки при изменении её радиуса-вектора r от значения r₀ в начальный момент времени t₀ до значения r в момент времени t.

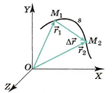Перемещение материальной точки за промежуток времени Dt=t-t₀ – вектор, равный разности радиусов-векторов, характеризующих конечное начальное  положения движущейся точки:. Перемещение (s) – вектор, направленный из начального в конечное положение движущейся точки.

 , мы можем записать два уравнения в координатной форме:

-для проекции на ось ОХ, - для проекции на ось ОY.

Если учесть, что , то эти уравнения можно переписать так: [s]=1м.

Расстояние, на которое смещается движущая точка от начального положения в конечное, определяет положительная скалярная величина – путь.

Путь – длина участка траектории, пройденного материальной точкой за данный промежуток времени. [l]=1м.

Поступательное движение тела – движение, при котором любая прямая, жестко связанная с движущимся телом и проведенная через две произвольные точки данного тела, остается параллельной самой себе.

Скорость является пространственно-временной характеристикой движения тела. Если, например, автомобиль проехал путь 500м за 20с, то можно предположить, что за секунду автомобиль проезжал 25м. Однако реально в течение первых пяти секунд он мог двигаться медленно, следующие 8с стоять, а последние 7с двигаться очень быстро. Поэтому путь, проходимый телом в среднем за секунду, характеризует среднюю скорость. Средняя скорость – скалярная  величина, равная отношению пути к промежутку времени, затраченному на его прохождение:

Средняя скорость, как и любая средняя величина, является достаточно приблизительной характеристикой движения. Например, водитель, двигаясь на автомобиле, не раз посмотрит на спидометр, показывающий скорость движения в данный момент времени (в данное мгновение) - мгновенную скорость. Чем меньше интервал времени, тем меньше за это время успевает измениться скорость, тем точнее её можно определить, момент времени. Мгновенная скорость - скорость движения тела в данный момент времени, или за бесконечно малый интервал времени. Мгновенная скорость тела направлена по касательной к траектории в сторону его движения.

Физический смысл: модуль мгновенной скорости численно равен расстоянию, которое может пройти тело за единицу времени, продолжая двигаться так же, как оно двигалось в данный момент времени.

 Скорость – векторная величина, определяющая быстроту движения и его направление в данный момент времени и равная отношению перемещения тела к промежутку времени, за который это перемещение произошло.

Скорости можно складывать, они складываются, как и все векторы геометрически

Закон сложения скоростей: Если тело движется относительно некоторой системы координат со скоростью  и сама система движется относительно другой системы координат со скоростью , то скорость тела относительно второй системы равна геометрической сумме скоростей  и

Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчёта, движущихся относительно друг друга.

Проекции скоростей складываются алгебраически:

При движении тел в одном направлении модуль относительной скорости равен разности скоростей.

При встречном движении тела сближаются с относительной скоростью, равной сумме их скоростей, поэтому встречное столкновение тел очень опасно.

Ускорением тела называют отношение изменения скорости тела ко времени, за которое это изменение произошло.

Ускорение характеризует быстроту изменения скорости:   (1)

Ускорение - векторная величина. Оно показывает, как изменяется мгновенная скорость тела за единицу времени.

По форме траектории механическое движение делится на два вида: криволинейное и прямолинейное.

 Криволинейным называется движение, траекторией которого является кривая линия. Прямолинейным называется движение, траекторией которого является прямая линия.

Путь равен модулю вектора перемещения только при прямолинейном движении в одном направлении. Если направление прямолинейного движения изменяется, то путь превосходит модуль вектора перемещения. Например, автобус, движущийся из пункта А в пункт В, а затем возвращается обратно в А, проходит путь 2l. При этом перемещение его относительно начальной точки равно 0. При криволинейном движении путь больше перемещения, т.к. длина дуги всегда больше перемещения. В зависимости от значения ускорения различают следующие виды движения:

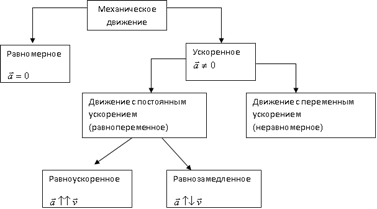
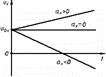Равноускоренным называется движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково. Зная начальную скорость тела и его ускорение, из формулы (1) можно найти скорость в любой момент времени:  (2)

Для этого уравнение нужно записать в проекциях на выбранную ось: v_x=v_0x+ a_xt

Графиком скорости при равноускоренном движении является прямая.

Перемещение и путь при прямолинейном равноускоренном движении

Предположим, что тело совершило перемещение за время t, двигаясь с ускорением. Если скорость изменяется от  до   и учитывая, что, , получим , .

Используя график скорости, можно определить пройденный телом за известное время путь - он численно равен площади заштрихованной поверхности.

Свободное падение тел

Движение тел в безвоздушном пространстве под действием силы тяжести называют свободным падением.

Свободное падение – это равноускоренное движение. Ускорение свободного падения в данном месте Земли постоянно для всех тел и не зависит от массы падающего тела: g = 9,8 м/с ².

Для решения различных задач из раздела "Кинематика" необходимы два уравнения:  и

Формула свободного падения тел: , , , где h - высота падения, g - ускорение свободного падения, g 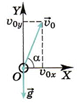= 10 м/с

С движением тел, получивших начальную скорость под углом к ускорению свободного падения или под углом к горизонту, приходится встречаться  довольно часто. Например, снаряд, выпущенный под углом к горизонту; ядро, которое толкнул спортсмен. Найдем траекторию тела, брошенного под углом к горизонту. Пусть из точки О брошено тело с начальной скоростью  под углом a к горизонту. (рис). Выберем оси координат так, чтобы векторы  и  были расположены в какой-либо координатной плоскости, например, в плоскости XOY. Ось OX направим горизонтально вправо, а ось OY - вертикально вверх. Начало координат выберем в точке бросания. Так как ускорение свободного падения с течением времени не изменяется, то движение тела в данном случае, как и любое движение с постоянным ускорением, можно описать уравнениями  (1) и  (2) Так как в начальный момент времени тело находилось в начале координат, то  и . Проекцию вектора на какую-нибудь ос можно выразить через модуль вектора и синус или косинус угла, который этот вектор образует с положительным направлением оси. Из рисунка видно, что , ,  и  . Поэтому уравнения (1) и (2) можно записать в виде (3) и (4). Для построения траектории точки необходимо из уравнений (3) и (4) найти значения координат x и y для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией. Получим зависимость y(x), для этого необходимо из уравнений (3) и (4) исключить время. Из (3) имеем . Следовательно,  или . Введём обозначения  и . Тогда получим квадратичную функцию , графиком которой является парабола (рис). Мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе. Определим дальность и максимальную высоту полёта тела. Дальность полета  (5). Время полета можно определить из (4). При падении тела y=0, то время полета . Подставив это выражение в уравнение (5), получим , после преобразования окончательно имеем . Время подъёма . Подставим в уравнение (4) и получим формулу максимальной высоты подъёма . Из формул (3) и (4) видно, что движение тела, брошенного под углом к горизонту, можно рассматривать как сумму двух независимых движений - равномерного движения вдоль оси OY. Скорость

Перемещение

 

Координата

Свободное падение

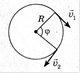Периодическое движение – движение, повторяющееся через определенный промежуток времени. Движение по окружности – периодическое движение, траекторий которого является окружность. Равномерное движение по окружности – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, т.е. проходит дуги равной длины. Угловое перемещение j - угол поворота радиуса-вектора точки за время Δt.  Линейная, или мгновенная скорость – это скорость, с которой тело движется по окружности.  Модуль линейной скорости можно определить отношением длины дуги окружности ко времени, за которое эта дуга пройдена. Угловая скорость – это скорость, модуль которой равен отношению угла поворота радиуса, соединяющего материальную точку с центром окружности, ко времени этого поворота. Угловая скорость обозначается символом ω; измеряется в СИ в рад/с., где φ - угол поворота радиуса. Направление вектора угловой скорости определяется по правилу буравчика (правого винта). Угловое ускорение ε – векторная величина, модуль которой равен отношению изменения угловой скорости ко времени её изменения.  Период вращения – это время, за которое тело совершает один полный оборот. . Период – величина скалярная, в СИ измеряется в секундах (с). Частота вращения – число вращений за единицу времени. .    Частота – скалярная величина, в СИ измеряется в (с-1). Центростремительное ускорение – это векторная величина, которая в каждой точке окружности направлена вдоль радиуса к центру окружности и численно равна отношению квадрата скорости и радиуса окружности.. Ускорение в СИ измеряется в (м/с²). Центростремительное ускорение характеризует изменение линейной скорости по направлению. При равномерном движении точки по окружности постоянно по модулю и направлению по радиусу к центру окружности.

Величина	Формула	Единица измерения
Частота и период обращения	;	с-1
Угловая скорость	;	рад/с
Угловое ускорение		рад/с2
Линейная скорость	; ;	м/с
Центростремительное ускорение		м/с2

 

 

 

 

 

 

 

 

 

 

План решения задач

1.1 Внимательно прочитать задачу, проанализировать условие, выписать числовые значения заданных величин.

1.2 Сделать схематический чертеж, отображающий описанное в задаче движение. Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения.

1.3 Выбрать систему координат, при этом координатные оси направить так, чтобы проекции векторов на них выражались, возможно, более простым образом. Отметить координаты движущегося тела в заданные и интересующие нас моменты времени, спроектировать векторы скоростей и ускорений на оси координат.

1.4 Составить для данного движения уравнения, отражающие математическую связь между проекциями векторов на оси координат. Составить уравнения, отражающие дополнительные условия задачи. Число уравнений должно быть равно числу неизвестных величин.

1.5 Решить составленную систему уравнений относительно искомых величин и получить ответ сначала в аналитическом виде (т.е. получить расчетные формулы).

1.6 Подставить в расчетные формулы вместо обозначений физических величин обозначения их единиц в СИ, произвести преобразования и убедиться, получаются ли в результате единицы искомых величин.

1.7 Подставить в расчетные формулы числовые значения физических величин и произвести вычисления. Оценить реальность полученного результата.

Примеры решения задач

1.     Моторная лодка проходит расстояние между А и В за 3 часа, а плот - за 12 часов. Сколько времени затратит моторная лодка на обратный путь?

Дано:	Решение:
t1=3 ч tпл=12 ч	Введем следующие обозначения: L – расстояние между А и В, vp – скорость течения реки, vл – собственная скорость лодки. Тогда скорость лодки по течению равна (vp + vл), против течения - (vp -vл). Используя формулу и условие задачи, получим:  (1)  (2)  (3) Выразим из (1) и (2) L и приравняем правые части полученных выражений:  ,  или . Тогда из (3)   (4) Из (1)  . Подставим полученное выражение для L в (4):  ч.                          Ответ: 6 ч
Найти:  t2 -?

2.     Тело движется равномерно вдоль оси Х. Со скоростью v=2 м/с противоположно положительного направления оси Х. Найдите положение тела в момент времени t₁=10 с после начала движения, если начальная координата x₀=5 м. Чему равен путь, пройденный телом? 

Дано:	Решение:
v=2 м/с t1=10 с x0=5 м	Из условия задачи видно, что физической моделью задачи является материальная точка, двигающаяся по прямой с постоянной скоростью. Математической моделью  такого процесса является математическое уравнение для координат материальной точки: . По условию задачи  и формула для координаты принимает вид: . Пройденный телом путь равен   . В этих уравнениях t – параметр, переменная величина. Уравнения показывают, как изменяется координата материальной точки и пройденный ею путь со временем t. Можно для большей ясности писать x(t) и s(t). Смотрим в условие задачи, что нам нужно найти. Координату и пройденный путь в момент времени t1. Надо подставить вместо t ее численное значение t1 и подсчитать численный ответ. Обратите внимание, t - переменная величина, а t1 – число.  Итак, мы имеем: .  Пройденный телом путь равен    Ответ: s=20м, x=-5 м.
Найти:  x -? s - ?

 

3.     Из пунктов А и В, расстояние между которыми l=55 км, одновременно начали двигаться с постоянными скоростями навстречу друг другу по прямому шоссе два автомобиля. Скорость первого автомобиля v₁=50 км/ч, а второго v₂=60 км/ч. Через сколько времени после начала движения автомобили встретятся? Найдите пути, пройденные каждым автомобилем за это время. 

Дано:	Решение:
l=55 км  v1=50 км/ч  v2=60 км/ч	Выберем начало отсчёта движения пункт А, тогда уравнение движения автомобиля, вышедшего из пункта А: . По условию задачи автомобили движутся навстречу друг другу, то для второго  и формула для координаты принимает вид: . Начальная координата для второго автомобиля  В этих уравнениях t – параметр, переменная величина. Уравнения показывают, как изменяется координата материальной точки и пройденный ею путь  со временем t. Подставим в эти уравнения числовые данные из условия задачи. Обратите внимание, t - переменная величина, а t1 – число.  Итак, мы имеем:  и . Так как при встрече , то . Решая данное уравнение получим время встречи . Пройденный автомобилем, двигающемся из пункта А,  путь равен    А второй автомобиль   Ответ: t=0,5 ч, s1=25км, s2=30км
Найти: t1-? s1-? s2-?

4.     Расстояние между двумя пунктами 1,5 км. Первую половину этого расстояния автомобиль проходит равноускорено, вторую – равнозамедленно с тем же по модулю ускорением.  Максимальная скорость автомобиля 54 км/ч.  Найти ускорение и время движения автомобиля между пунктами.

Дано:	СИ	Решение:
v= 54 км/ч	15 м/с	Для первой половины пути, учитывая, что v 0=0: , откуда выражаем а:  м/с2. Конечная скорость для первой половины пути , откуда время движения по первой половине пути  с Время движения по второй половине пути t2 будет равно  t1. Действительно,  учитывая,  что  конечная  скорость  для  второго  участка пути равна нулю, получаем: , т.е. . Следовательно, полное время движения автомобиля с Ответ: a=0,15м/с2, t=200 с
l =1,5 км	1500 м
Найти:
a - ? t - ?

 

5.     Автомобиль, находясь на расстоянии 50 м от светофора и имея в этот момент скорость 36 км/ч, начал тормозить. Определите положение автомобиля относительно светофора через 4 с после начала торможения, если ускорение автомобиля равно 2 м/с².

 

Дано:	СИ	Решение:
l=50 м
v0=36 км/ч	10 м/с
t=4 с
a=2 м/с2		Свяжем систему отсчёта с поверхностью земли, координатную ось ОХ направим по направлению движения автомобиля, за начало координат О примем точку, где находится светофор (рис). Уравнение координаты тела при равноускоренном движении имеет вид: где x0=- l, v0x =v0, ax=-a. подставляя выписанные значения в уравнение для координаты, получим:. Мы получили ответ в общем (аналитическом) виде. Теперь произведём вычисления: . Ответ: через 4 с после начала торможения автомобиль  будет находиться на расстоянии 26 м левее светофора.
Найти: x-?

 

6.     Тело, двигаясь равноускоренно из состояния покоя, за пятую секунду прошло путь 18 м. Чему равно ускорение и какой путь тело прошло за 5 с?

Дано:	Решение:
t5– t4= 1 с	Путь, пройденный телом за пятую секунду .  Отсюда , . Путь, пройденный телом за 5 секунд ,  . Ответ: 50 м, 4 м/с2.
s = 18 м
t = 5 с
Найти:  s5 - ?  a -?

 

7.     В последнюю секунду свободно падающее тело прошло половину своего пути. Сколько времени и с какой высоты падало тело?

Дано:	Решение:
	Путь, пройденный телом за все время падения: .  До последней секунды тело прошло путь  . Следовательно,  или. Отсюда . Высота падения    Ответ: »57 м, 3,4 с.
g = 9,8 м/с2
Найти:  t - ?  ℎ𝑛 - ?

8.     Колеса велосипеда диаметром 80 см вращаются, делая 120 об/мин. Определите линейную скорость колес автомобиля.

Дано:	СИ	Решение:
d=80 cм	0,8 м	Линейная скорость определяется по формуле , где ω – угловая скорость ,  . Итак, получили . Вычисления: .                Ответ: .
ν=120 об/мин	2 с-1
Найти: υ-?

9.     Ротор электродвигателя, имеющий частоту вращения 900 об/мин, после выключения остановился через 10 с. Считая вращение ротора равнозамедленным, определите: 1) угловое ускорение ротора после выключения электродвигателя; 2) число оборотов n, которое сделал ротор до остановки.

Дано:  v=900 об/мин  ω=0  t=10 с	СИ: 15 с-1	Решение:   Угловая скорость ω0, которую имел ротор до выключения двигателя: (1). Через время t он остановится, т.е. ω=0 (2). Угловое ускорение ε после выключения двигателя определяем по формуле: .  С учетом формул (1) и (2) получим:  (3). При равнозамедленном движении угловое перемещение ротора до остановки:  (4). Подставив в формулу (4) отношения (1) и (3), имеем:  (5). Число оборотов n равно: Вычисления: 1) : ; 2) Ответ:1) , 2) .
Найти: 1) ε-?  2) n - ?

10. Посадочная скорость пассажирского самолета 135 км/ч, а длина пробега его 500 м. Определить время пробега по посадочной полосе и ускорение самолета, считая движение равнозамедленным.

Дано:	СИ	Решение:
l=140 м		Относительная скорость движения обоих поездов . Следовательно, время, в течение которого мимо пассажирского Ɩ = 140 м  поезда пройдет товарный, определим по формуле: . Подставляем данные:   Ответ: 4 с.
v1 = 72 км/ч	20 м/с
v2 = 54 км/ч	15 м/с
Найти: t -?

11.           Длина минутной стрелки башенных часов равна 4,5 м. С какой линейной скоростью перемещается конец стрелки?  Какова угловая скорость движения стрелки?

Дано:	Решение:
l = 4,5 м	Период вращения минутной стрелки Т = 1 ч = 3600 с. Находим угловую скорость: .  Длина стрелки l является радиусом вращения конца стрелки, поэтому, линейная скорость  . Подставляем данные:   Ответ: , .
Найти: ω -?

Контрольные вопросы для самопроверки

1.    Что называется системой отсчёта? Что значит выбрать систему отсчёта? Какое тело называется телом отсчёта? Для чего необходимо выбрать систему координат?

2.    Что называют механическим движением? Что означает относительность движения? Привести пример.

3.    Что называют материальной точкой? Приведите пример.

4.    Что такое вектор перемещения? Что он характеризует? Как обозначают малые перемещение?

5.    Что такое траектория? Что означает, что траектория относительна? Существует ли понятие траектории для микрочастиц? Почему?

1.8 Что такое пройденный путь? Может ли пройденный путь совпадать с модулем вектора перемещения?

1.9 Что такое ускорение? Что показывает модуль ускорения?

1.10       Какие виды движения существуют? Дайте определение каждому виду.

Контрольные вопросы для самопроверки

1.    Какое движение называется периодическим? Какое периодическое движение называется движением по окружности?

2.    Какое движение называется равномерным движение по окружности?

3.    Что называется периодом вращения? Частотой вращения? Запишите формулы для вычисления периода и частоты вращения.

4.    Что называется угловой скоростью? Угловым ускорением? Запишите формулы для вычисления угловой скорости и углового ускорения.

5.    Что называется линейной скоростью?? Запишите формулы для вычисления линейной скорости.

6.    Что называется центростремительным ускорением? Что характеризует центростремительное ускорение? Запишите формулы для вычисления центростремительного ускорения.

Индивидуальные задания к практической работе №1

Вариант 1

1.    Тело переместилось из точки с координатами х₀=0, у₀=2м в точку с координатами х=4м, у₀= -1м. Сделать чертёж, найти перемещение и его проекции на оси координат.

2.    Стайер бежал по кольцевой дорожке радиусом 160 м. Определите длину пути и модуль перемещения стайера после прохождения им полукольца.

3.    Автомобиль проехал первую половину пути со скоростью 10м/с, а вторую половину пути со скоростью 15 м/с. Найти среднюю скорость автомобиля.

4.    Тело, свободно падающее из состояния покоя, в конце первой половины пути достигло скорости 20 м/с. Через сколько времени тело достигло Земли? Принять g = 10 м/с². Результат представить в единицах СИ и округлить до десятых.

5.    Конец минутной стрелки часов на Спасской башне Кремля передвинулся по дуге за 1 мин на 37 см. Определите длину минутной стрелки.

6.    С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40м, чтобы центростремительное ускорение было равно ускорению свободного падения?

Вариант 2

1.    Сколько времени длится разгон автомобиля, если он, двигаясь с ускорением 0,5м/с², увеличил свою скорость от 10м/с до 20м/с?

2.    Определить время подъема из метро пассажира, стоящего на движущемся эскалаторе, если по неподвижному эскалатору он поднимается за 120 с, а по движущемуся – за 30 с.

3.    Мотоциклист, двигаясь по хорошей дороге с постоянной скоростью 108 км/ч, проехал 4/7 всего пути. Оставшуюся часть пути по плохой дороге он проехал со скоростью 15 м/с. Какова средняя скорость мотоциклиста на всём пути?

4.    При свободном падении над поверхностью Земли в последние 2 с тело прошло 28 м. Сколько времени продолжалось свободное падение тела? Результат представить в единицах СИ и округлить до десятых.

5.    Рабочее колесо турбины Красноярской ГЭС имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?

6.    Период обращения платформы карусельного станка 4 с. Найти скорость крайних точек платформы, удаленных от оси вращения на 2 м.

Вариант 3

1.     В начальный момент времени жук находился в точке с координатами х₀=2м, у₀= -3м. Через некоторое время он переполз в точку с координатами х= -3м, у=2м. Начертите вектор перемещения и найдите его проекции на координатные оси.

2.     Тело свободно падает из состояния покоя с высоты 80 м.  Каково его перемещение в первую секунду падения?

3.     С балкона дома на высоте 5 м вверх подбросили мяч со скоростью 4 м/с. Какой будет скорость мяча через 0,4 с?

4.     Мотоциклист за первые два часа проехал 90 км, а следующие три часа двигался со скоростью 50 км/ч. Какова средняя скорость (в км/ч) на всем пути?

5.      

Вариант 4

1.     Тело свободно падает из состояния покоя с высоты 80 м.  Каково его перемещение в последнюю секунду падения?

2.     Координаты точки при равномерном прямолинейном движении на плоскости ХОУ за время t=2с изменилось от начальных значений x₀=6м и y₀= 8м до значений x=-2м, y=2м. Определить скорость движения точки. Изобразить вектор скорости.

3.     Первую четверть пути поезд прошел со скоростью 60 км/ч. Средняя скорость на всем пути оказалась равной 40 км/ч. С какой скоростью (в км/ч) поезд прошел оставшуюся часть пути?

4.     Камень падает с высоты, равной 20 м. Определите время падения камня, а также его конечную скорость.

5.     Минутная стрелка часов в 4 раза длиннее секундной. Определите отношение между линейными скоростями концов этих стрелок.

6.     Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.

Вариант 5

1.    Тело переместилось из точки с координатами x₁ = 1м, y₁ = 3м в точку с координатами x₂ = 4м, y₂= -1м. Сделать чертеж, определить перемещение тела и его проекции на оси.

2.    Сколько времени пассажир, сидящий у окна поезда, идущего со скоростью υ₁ = 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого υ₂ = 36 км/ч, а длина l = 150 м?

3.    Велосипедист проехал половину пути со скоростью 10 м/с, а половину оставшегося времени со скоростью 8 м/с, а затем до конца пути он ехал со скоростью 4 м/с. Определить среднюю скорость движения велосипедиста на всем пути. Результат представить в единицах СИ.

4.    Какова высота обрыва, если тело, брошенное вертикально вверх со скоростью 10 м/с через 3 с достигает подножия? Результат представить в единицах СИ. Принять g = 10 м/с².

5.     Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800м со скоростью 20 м/с?

6.    Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.

Вариант 6

1.    

y

В начальный момент времени жук находился в точке с координатами х₀=2м, у₀= -3м. Через некоторое время он переполз в точку с координатами х= -3м, у=2м. Начертите вектор перемещения и найдите его проекции на координатные оси.

2.     Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно земли. Если он сам идёт в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчёта, связанной с эскалатором.

3.     Хоккейная шайба пересекла ледяное поле длиной 60 м за 4 с и остановилась. Какую скорость сообщил шайбе хоккеист, ударив по ней клюшкой?

4.     Самолёт пролетел первую половину пути со скоростью 1100 км/ч, а оставшийся путь со скоростью 800 км/ч. Найдите среднюю скорость его полёта.

5.     За какое время колесо, имеющее угловую скорость 4π рад/с, сделает 100 оборотов?

6.     Ветряное колесо радиусом 2,0 м делает 40 оборотов в минуту. Найдите центростремительное ускорение концевых точек лопастей колеса.

Тема 2.2. Законы механики Ньютона

Практическая работа № 2. «Применение основных законов динамики»

Цель: раскрыть содержание законов Ньютона; закрепить умения и навыки решения задач на основные законы динамики, отработать умения выполнять задания по образцу, научиться применять полученные знания для решения физических задач.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы

1.     К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.     Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.     При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.     Внимательно прочитать теоретическую часть и план решения задач.

5.     Рассмотреть примеры решения задач.

6.     Ответить на контрольные вопросы.

7.     Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Динамика рассматривает законы движения тел и причины, которые его вызывают или изменяют. В основе динамики лежат законы Ньютона. Инерция – свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии воздействия на него других тел или их компенсации. Первый закон Ньютона: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока действие сил не изменит это состояние. (R = 0). Инерциальная система отсчета – система отсчета, в которой свободное тело движется равномерно и прямолинейно. Свободное тело – тело, на которое не действуют другие тела. Принцип Галилея: все законы механики сохраняются во всех инерциальных системах отсчета. Причиной изменения скорости движения тела является его взаимодействие с другими телами. Все тела обладают свойством, которое называется инертностью. Инертность – способность тела изменять свою скорость не мгновенно, а за определенный промежуток времени. Масса тела m – скалярная физическая величина, являющаяся мерой инертности тела. Единицей измерения массы является килограмм (кг).

Свойства массы:

1.              масса не зависит от того, движется тело или покоится (если v<<c);

2.              масса тела равна сумме масс его частей.

Сила F – векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате чего тело изменяет свою скорость (приобретает ускорение) или деформируется. Единицей измерения силы является ньютон (Н). сила характеризуется: точкой приложения; модулем; направлением в пространстве.

Принцип суперпозиции сил: если на тело действует несколько сил, то их можно заменить одной равнодействующей силой F, которая равна векторной сумме всех сил, действующих на тело. Равнодействующая сила определяется по правилам сложения векторов. Второй  закон  Ньютона:  ускорение,  сообщаемое   телу  данной  силой,  прямо пропорционально величине этой силы и обратно пропорционально массе тела:  или . Равнодействующая сил направлена в сторону ускорения.

Третий закон Ньютона: действия тел друг на друга всегда равны по величине и противоположны по направлению: 𝑭_𝟏= - 𝑭_𝟐 или 𝑚₁𝑎₁= - 𝑚₂𝑎_2. При этом силы лежат на одной прямой, одной природы и не компенсируют друг друга, т.к. приложены к разным телам (R ≠ 0).

Закон  всемирного  тяготения:  все  материальные  точки  притягиваются  друг  к  другу  с силой,  пропорциональной произведению их масс  и  обратно  пропорциональной  квадрату расстояния между ними: , где G – гравитационная постоянная, , m₁ и m₂ – массы тел, R - расстояние между телами. Силы лежат на одной прямой, соединяющей центры масс этих тел, и направлены навстречу друг другу. В первом приближении сила тяжести равна силе всемирного тяготения между телом массой m и Землей массой М. Она приложена к центру тяжести тела, направлена вертикально вниз и сообщает телу ускорение свободного падения g:. На высоте h над поверхностью Земли эти формулы имеют вид:  ; .   

Ускорение свободного падения зависит от: 1) R_Земли(географической широты): чем R_Земли ↑ (экватор), тем g ↓, 2) h – высоты тела над поверхностью Земли: чем h ↓, тем g ↓.

Для любого космического тела . Минимальная скорость, которую нужно сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите (ИСЗ) -  первая космическая скорость υ₁= 7,9 км/с. . Минимальная скорость, при которой тело преодолевает земное притяжение и становится спутником Солнца (орбита - парабола) –  вторая космическая скорость υ₂= 11,2 км/с.. Скорость, при которой тело преодолевает притяжение Солнца и покидает Солнечную систему – третья космическая скорость υ₃=16,7 км/с.

Гравитационное поле – форма материи, посредством которой осуществляется гравитационное взаимодействие. Гравитационная сила – сила взаимного притяжения тел массами m₁ и m₂, находящихся на расстоянии R друг от друга, определяемые по закону всемирного тяготения (практ. раб. № 4).

Сила тяжести – это гравитационная сила, с которой Земля притягивает к себе тела: , где  – ускорение свободного падения, .

Сила трения: возникает вдоль поверхности двух трущихся тел из-за деформации этих поверхностей и направлена вдоль поверхности против смещения.  Природа – электромагнитная.  , где N − сила реакции опоры всегда перпендикулярна поверхности, μ – коэффициент трения зависит от рода и состояния трущихся поверхностей и скорости движения. Величина безразмерная. Сила трения бывает: покоя, скольжения, качения и жидкое трение.  Если трение полезно –  его увеличивают (шурупы, песок, шиповки, рукавицы и т.д.), а если вредно –  уменьшают (подшипники, смазка, обтекаемая форма и т.д.).

Сила упругости –  сила, возникающая при деформации тел и стремящаяся восстановить первоначальные размеры и форму тела.  Природа –  электромагнитная. Деформация бывает упругая (растяжение -  сжатие, изгиб, сдвиг –  срез, кручение) и пластическая (не исчезает после прекращения воздействия. Для  упругой  деформации  выполняется  закон  Гука:  сила  упругости  прямо пропорциональна удлинению тела:  , где  k  –  жесткость тела, ∆Ɩ  –  его удлинение. Знак «−» указывает, что F_упр направлена противоположно смещению частиц тела.

Вес  тела  –  это  сила,  с  которой  тело,  вследствие  его  притяжения  к  Земле,  действует  на опору или подвес:  ,  где P  –  вес тела,  [𝑃]=H,    –  ускорение свободного падения,  .  В этом случае опора или подвес находятся в состоянии равномерного прямолинейного движения относительно Земли.  Однако вес может быть больше или меньше силы тяжести. Если опора или подвес движутся ускоренно вниз, то вес .

Если  опора  или  подвес  движутся  ускоренно  вверх,  то  вес  ,  тело  испытывает перегрузки. Если тело движется только под действием силы тяжести, то оно находятся в состоянии невесомости (Р = 0).

План решения задач

1.  Проанализировать условие задачи, понять физический процесс, рассматриваемый в ней, выяснить, какие силы действуют на интересующие нас тела.

2. Сделать схематический рисунок, изобразив на нем кинематические характеристики движения (ускорения и скорости), нарисовать векторы всех сил, действующих на каждое тело.

3. Для каждого тела в отдельности на основании второго закона Ньютона записать уравнения движения, связывающие проекции сил и ускорений, выбрав предварительно систему отсчета. При движении тела по  прямой  второй закон Ньютона  для  тела  имеет  вид: ,  где   – сумма  проекций всех сил, действующих на тело, на прямую, по которой происходит движение. При этом положительное направление отсчета удобно выбирать совпадающим с направлением ускорения. Если направление составляющей силы совпадает с направлением ускорения, то соответствующая проекция силы берется со знаком плюс, в противном случае - со знаком минус.

4. При решении задач, в которых рассматривается динамика равномерного движения по окружности, также целесообразно положительное направление координатной оси выбирать совпадающим с направлением ускорения, т.е. к центру вращения. Согласно  второму закону  Ньютона ,  где     –  сумма  проекций  всех  сил, действующих на тело, на радиус вращения. При этом, если проекция

силы направлена к центру вращения, ее нужно считать положительной, если от центра - отрицательной.

5. Полученные уравнения дополнить, если необходимо, выражениями для конкретных видов сил (сила трения скольжения, сила трения покоя, сила упругости, сила Архимеда) и решить полученную систему уравнений в общем виде, т.е. получить расчетные формулы.

6. Убедиться, получаются ли в результате единицы искомых величин. Подставить в расчетные формулы числовые значения физических величин и произвести вычисления.

Примеры решения задач

1.     Сила 100 Н сообщает телу ускорение 0,8 м/с². Определите массу тела, и силу, которая этому телу сообщит ускорение 1,2 м/с².

Дано: F1= 100 Н a1=0,8 м/с2 a2=1,2 м/с2	Решение: Массу тела определяем из второго закона Ньютона: . Откуда  (1). Сила F2, согласно второму закону Ньютона, будет   (2). Учитывая (2), получим . Вычисления   Ответ:
Найти:  m - ? F2 -?

 

2.     На вагон массой 20т, движущийся со скоростью54 км/ч, начинает действовать сила торможения, и он останавливается через 100 с. Определите: 1) ускорение, с которым он двигался; 2) путь, пройденный вагоном до остановки: 3) силу, действующую на вагон.

Дано:	СИ	Решение:
m = 20т v0 = 54км/ч t=100 с	2∙104 кг 15 м/с	На вагон действуют: сила тяжести , сила реакции опоры , сила трения . Вагон движется в горизонтальном направлении. За положительное направление оси ОХ примем направление движения вагона. Движение вагона равнозамедленное, векторы ускорения и скорости направлены в противоположные стороны. В векторной форме второй закон Ньютона имеет вид: . Проекция сил на ось OX:  или . Ускорение и путь, пройденный вагоном до остановки, найдем из уравнения кинематики: , откуда , так как v=0; . Вычислим искомые величины: 1) ; 2) ; 3)  Ответ: 1) 0,15м/с2; 2) 750 м; 3) 3кН.
Найти: 1) a -? 2) s -? 3) Fтр-?

3.     Какую скорость надо сообщить спутнику, чтобы вывести его на круговую орбиту на высоте 400км от поверхности Земли?

Дано:	СИ:	Решение: Спутник двигается вокруг Земли под действием только силы тяжести:  (1). Согласно второму закону Ньютона сила тяжести сообщает спутнику. Центростремительное ускорение: . Подставляем полученное выражение в (1):   или . Выражаем v:  Подставляем численные значения: Ответ: 7,66км/с.
h=400 км	м
Найти: v -?

4.     Определите силу гравитационного притяжения двух электронов, находящихся на расстоянии 1 нм.

Дано: mе = 9,1∙10-31 кг h = 1нм	СИ:   10-9 м	Решение: Сила гравитационного притяжения электронов определяется по закону всемирного тяготения    Подставляем численные значения: Ответ: .
Найти: F -?

5.     Вдоль оси ОХ движется тело массой 1 кг под действием силы 1 Н. определите силу трения, действующую на тело, если уравнение движения тела имеет вид: .

Дано: m=1 кг Fтяги=1 Н	Решение:                                 На тело действуют силы, изображенные на рис.                          Запишем второй закон Ньютона в векторной форме:  (1) Найдём проекции сил, входящих в уравнение (1) на ось OX. OX: . Отсюда . Ускорение найдем из его определения . По данному уравнению  имеем, что ускорение равно 0. Поэтому тело движется с постоянной скоростью 2м/с, тогда Ответ:  1H
Найти: Fтр-?

6.     Тело массой 2 кг падает в воздухе с ускорением 9,3 м/с². Определите силу сопротивления воздуха.

Дано: m = 2 кг а = 9,3 м/с2

Решение: На падающее в воздухе тело действуют: сила тяжести, направленная вертикально вниз и сила сопротивления воздуха, направленная противоположно движению тела, т.е. вертикально вверх.   (см. рис) Согласно второму закону Ньютона, имеем . Пусть положительное направление оси OY совпадает с направлением движения тела. Уравнение движения тела в скалярной фирме (в проекции на ось OY): . Отсюда   Вычислим искомую величину: Ответ: 1 Н.

Найти: F -?

7.                                                                           При помощи пружинного динамометра с ускорением 3 м/с², направленным вверх, поднимают груз массой 1кг.  Найти удлинение пружины динамометра, если ее жесткость 800 Н/м.

Дано:	Решение: Изобразим схему действующих на груз сил, прикладывая их к центру тяжести тела. Составим уравнение движения тела:. Запишем второй закон Ньютона в проекциях на ось OY: Учитывая, что и , получаем Выразим x: . Подставляем численные значения:.          Ответ: 3,2 см.
a = 3 м/с2 m= 2 кг k=800 H/м
Найти: x -?

Контрольные вопросы для самопроверки

1.     Какие системы отсчёта являются инерциальными? Можно ли считать инерциальными системами отсчета, неподвижно связанные Землёй?

2.     Сформулируйте первый закон Ньютона. В чем состоит явление инерции?

3.     Запишите второй закон Ньютона.

4.     Сформулируйте третий закон Ньютона. Как направлены силы взаимодействия?

5.     Что называется силой всемирного тяготения? Сформулируйте закон всемирного тяготения. В чем заключается физический смысл гравитационной постоянной?

6.     Какие силы называются гравитационными? Что называется силой всемирного тяготения?

7.     Что называется весом тела? Чем отличается сила тяжести от веса тела?

8.     Что называется перегрузкой и невесомостью?

9.     Какая сила называется силой упругости? Запишите закон Гука.

10. Какая сила называется силой трения? Перечислите виды трения. Запишите формулу для вычисления силы трения.

 

 

 

Индивидуальные задания к практической работе № 2

Вариант 1

1.    Трактор, сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 м/с². Какое ускорение сообщит тому же прицепу трактор, развивающий тяговое усилие 60 кН?

2.    С какой силой притягивают друг к другу две книги массой 200 г каждая, находящиеся на расстоянии 1 м друг от друга?

3.    К пружине длиной 10 см, жесткость которой 500Н/м, подвесили груз массой 2 кг. Какой стала длина пружины?

4.    Космическая ракета при старте с поверхности Земли движется вертикально с ускорением 20 м/с². Найти вес летчика-космонавта массой 80 кг в кабине при старте ракеты.

5.    На участке дороги, где установлен дорожный знак, изображенный на рисунке, водитель применил аварийное торможение. Инспектор ДПС обнаружил п следу колес, что тормозной путь равен 12 м. нарушил ли водитель правила движения, если коэффициент трения (резина по сухому асфальту) равен 0,6?

Вариант 2

1.    Тело массой 4 кг под действием некоторой силы приобрело ускорение 2 м/с². Какое ускорение приобретает тело массой 10 кг под действием такой же силы?

2.    Космический корабль массой 8т приблизился к орбитальной космической станции массой 20 т на расстояние 500 м. Найдите силу их взаимного притяжения.

3.    При помощи динамометра ученик перемещал деревянный брусок массой 200 г по горизонтально расположенной доске. Каков коэффициент трения, если динамометр показывал 0,6 Н?

4.    С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы пассажир на мгновение оказался в состоянии невесомости?

5.    На соревнованиях лошадей тяжелоупряжных пород одна из них перевезла груз массой 23 т. Найти коэффициент сопротивления, если сила тяги лошади 2,3 кН.

Вариант 3

1.    Определить ускорение свободного падения на высоте 100 км от поверхности Земли.

2.    Сила 60 Н сообщает телу ускорение 0,8 м/с². Какая сила сообщит этому телу ускорение 2 м/с²?

3.    При движении по горизонтальной поверхности на тело массой 54 кг действует сила трения скольжения 12 Н. Какой станет сила трения скольжения после уменьшения массы тела в 6 раз, если коэффициент трения не изменится?

4.    Какая сила упругости троса вызовет ускорение движение вверх груза массой m=1,3 кг с ускорением а=2 м/с²?

5.    Самолет выходит из пикирования, описывая в вертикальной плоскости дугу окружности радиусом 800 м. Скорость самолета в нижней точке траектории 200 м/с. Какую перегрузку испытывает летчик в этой точке?

Вариант 4

1.    Найдите силу гравитационного притяжения, действующую между Землёй и Солнцем, если масса Земли равна  кг, а масса Солнца - кг. Расстояние от Земли до Солнца  м.

2.     Боевая реактивная установка БМ-13 («катюша») имела длину направляющих балок 5 м, массу каждого снаряда 42,5 кг и силу реактивной тяги 19,6 кН. Найти скорость схода снаряда с направляющей балки.

3.     Две пружины жесткостью 0,3 кН/м и 0,8 кН/м соединены последовательно. На сколько сантиметров растянулась первая пружина, если вторая растянулась на 1,5 см?

4.     Чему равен вес тела массой m=0,5 кг при движении вниз с ускорением а=2,5 м/с²? Под действием, каких сил движется тело?

5.     На горизонтальной дороге автомобиль делает поворот радиусом 16 м. какую наибольшую скорость может развить автомобиль, чтобы его не занесло, если коэффициент трения колес о дорогу равен 0,4?

 Вариант 5

1.     Порожнему прицепу тягач сообщает ускорение а₁= 0,4 м/с², а гружёному а₂=0,1 м/с². Какое ускорение сообщит тягач обоим прицепам, соединенным вместе? Силу тяги тягача считать во всех случаях одинаковой.

2.     Определить ускорение свободного падения на расстоянии 9600 км от поверхности Земли.

3.    При сжатии пружины на 5 мм возникает сила упругости 10кН. Во сколько раз возрастет эта сила, если сжать пружину еще на 15 мм?

4.    При раскрытии парашюта скорость парашютиста уменьшается с 50 до 10 м/с за 1 с. Какую перегрузку испытывает парашютист?

5.   Мальчик массой 50 кг, скатившись на санках с горки, проехал по горизонтальной дороге до остановки путь 20 м за 10 с. Найти силу трения и коэффициент трения

Вариант 6

1.     Под действием некоторой силы тележка, двигаясь из состояния покоя, прошла путь 40 см. Когда на тележку положили груз массой 200 г, то под действием той же силы за то же время тележка прошла из состояния покоя путь 20 см. какова масса тележки?

2.  Найти силу гравитационного взаимодействия Земли и Луны, если масса Земли равна кг, масса Луны - кг, среднее расстояние от Луны до  Земли -   м.

3.     Вес космонавта на Земле 800 Н. Каков его вес в ракете при движении с ускорением 4g, направленным вертикально вверх?

4.     Жесткость пружины 900 Н/м. Груз какой массы надо подвесить к пружине, чтобы она растянулась на 3 см?

5.     Упряжка собак при движении саней по снегу может действовать с максимальной силой 0,5 кН. Какой массы сани с грузом может перемещать упряжка, если коэффициент трения равен 0,1?

Лабораторная работа № 1. Изучение особенностей силы трения (скольжения)

Цель работы:  выяснение зависимости силы трения скольжения от силы нормального давления, определение коэффициента трения дерева по дереву.

Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.

Теория

   Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.

Сила трения - это сила электромагнитной природы.

   Возникновение силы трения объясняется двумя причинами:

   1) шероховатостью поверхностей;   2) проявлением сил молекулярного взаимодействия.

  Силы трения всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, скольжения, качения.

   В данной работе исследуется зависимость силы трения скольжения от веса тела.

   Сила трения скольжения – это сила, которая возникает при скольжении предмета по какой-либо поверхности. По модулю она почти равна максимальной силе трения покоя. Направление силы трения скольжения противоположно направлению движения тела. Сила трения в широких пределах не зависит от площади соприкасающихся поверхностей. В данной работе надо будет убедиться в том, что сила трения скольжения пропорциональна силе давления (силе реакции опоры):  Fтр=μN, где μ - коэффициент пропорциональности, называется коэффициентом трения. Он характеризует не тело, а сразу два тела, трущихся друг о друга.        

Ход работы

1. Определите цену деления шкалы динамометра.

2. Определите массу бруска. Подвесьте брусок к динамометру, показания динамометра - это вес бруска. Для нахождения массы бруска разделите вес на g. Принять g=10 м/с².

2. Положите брусок на горизонтально расположенную деревянную линейку. На брусок поставьте груз 100 г.

3. Прикрепив к бруску динамометр, как можно более равномерно тяните его вдоль линейки. Запишите показания динамометра, это и есть величина силы трения скольжения.

4. Добавьте второй, третий, четвертый грузы, каждый раз измеряя силу трения. С увеличением числа грузов растет сила нормального давления.

5. Результаты измерений занесите в таблицу.

№ опыта	Масса бруска,  m1 , кг	Масса груза, m2 , кг	Общий вес тела  (сила нормального давления), Р=N=(m1+m2)g, Н	Сила трения, Fтр, Н	Коэффициент трения, μ	Среднее значение коэффициента трения, μср
1
2
3
4
5

6.Сделайте вывод: зависит ли сила трения скольжения от силы нормального давления, и если зависит, то как?

7. В каждом опыте рассчитать коэффициент трения по формуле: . Принять g=10 м/с².

    Результаты расчётов занести в таблицу.

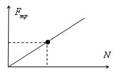8. По результатам измерений постройте график зависимости силы трения от силы нормального давления. При построении графика по результатам опытов экспериментальные точки могут не оказаться на прямой, которая соответствует формуле. Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы трения и силы нормального давления и вычислите коэффициент трения . Это и будет средним значением коэффициента трения. Запишите его в таблицу.

9. Исходя из цели работы, запишите вывод и ответьте на контрольные вопросы.

Контрольные вопросы.

1.     Что называется силой трения? Какова природа сил трения?

2.     Назовите основные причины, от которых зависит сила трения?

3.     Перечислите виды трения.

6.     Можно ли считать явление трения вредным? Почему?

Тема 2.3. Законы сохранения в механике. Статика

Практическая работа № 3 «Законы изменения и сохранения в механике»

Цели: закрепить умения и навыки решения задач на закон сохранения импульса тела, сформировать умения и навыки нахождения физической величины, её вывода   из формулы, закрепить умения и навыки решения задач на закон сохранения энергии, сформировать умения и навыки нахождения физической величины, её вывода   из формулы.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Импульс (количество движения) тела – это произведение массы тела на скорость его движения, т.е. величина

 . Единица измерения импульса тела .

Закон сохранения импульса тела: суммарный импульс замкнутой механической системы не изменяется в результате взаимодействия между телами системы:

Полный импульс системы до взаимодействия  равен полному импульсу системы  после взаимодействия  :  или  

Абсолютно неупругий удар - удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью. Импульс системы тел сохраняется 

Абсолютно упругий удар - удар, при котором сохраняется механическая энергия системы. Сохраняется импульс системы тел:  

Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.

 Абсолютно упругий удар тел m₁ и m_2, имеющих скорости :

Скорость тела m₁ после удара . Скорость тела  ₂ после удара

Энергия тела – физическая величина, показывающая работу, которую может совершить рассматриваемое тело (за любое, в том числе неограниченное время наблюдения). Тело, совершающее положительную работу, теряет часть своей энергии. Если же положительная работа совершается над телом, энергия тела увеличивается. Для отрицательной работы – наоборот.

Энергией называют физическую величину, которая характеризует способность тела или системы взаимодействующих тел совершить работу. Единица энергии в СИ 1 Джоуль (Дж).

 Кинетической энергией называется энергия движущихся тел. Под движением тела следует понимать не только перемещение в пространстве, но и вращение тела. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения (перемещения в пространстве и/или вращения). Кинетическая энергия зависит от тела, по отношению к которому измеряют скорость рассматриваемого тела. Кинетическая энергия Е_к тела массой m, движущегося со скоростью v, определяется по формуле .

Потенциальной энергией называется энергия взаимодействующих тел или частей тела. Различают потенциальную энергию тел, находящихся под действием силы тяжести, силы упругости, архимедовой силы. Любая потенциальная энергия зависит от силы взаимодействия и расстояния между взаимодействующими телами (или частями тела). Потенциальная энергия отсчитывается от условного нулевого уровня.

1.       Потенциальной энергией обладают, например, груз, поднятый над поверхностью Земли, и сжатая пружина.

2.       Потенциальная энергия поднятого груза Е_п = mgh.

3.       Кинетическая энергия может превращаться в потенциальную, и обратно.

Изменение энергии. Мерой изменения энергии системы тел ∆Е является работа А, совершаемая системой тел. (∆Е = А).

Механической энергией тела называют сумму его кинетической и потенциальной энергий. Поэтому механическая энергия любого тела зависит от выбора тела, по отношению к которому измеряют скорость рассматриваемого тела, а также от выбора условных нулевых уровней для всех разновидностей имеющихся у тела потенциальных энергий.

Механическая энергия характеризует способность тела или системы тел совершить работу вследствие изменения скорости тела или взаимного положения взаимодействующих тел.

Теорема о кинетической энергии: изменение кинетической энергии тела _∆Ек при переходе из одного положения в другое равно работе всех сил, действующих на тело:  

Потенциальная энергия – энергия, которая зависит от взаимного расположения тел или частей одного и того же тела.

Потенциальная энергия взаимодействия: ,   

Теорема о потенциальной энергии под действием силы тяжести:

Работа силы тяжести  

Потенциальная энергия упругодеформированного тела:  ; 

Полная механическая энергия равна сумме кинетической и потенциальной энергий:

Теорема о потенциальной энергии упругодеформированного тела:  

Работа силы упругости на замкнутой траектории равна нулю.

Внутренней энергией называется такая энергия тела, за счёт которой может совершаться механическая работа, не вызывая убыли механической энергии этого тела. Внутренняя энергия не зависит от механической энергии тела и зависит от строения тела и его состояния.

Закон сохранения и превращения энергии гласит, что энергия ниоткуда не возникает и никуда не исчезает; она лишь переходит из одного вида в другой или от одного тела к другому.

Закон сохранения механической энергии: если между телами системы действуют только силы тяготения и силы упругости, то сумма кинетической и потенциальной энергии остается неизменной, то есть механическая энергия сохраняется. В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔЕ=0 или Е_п0+Е_к0=Е_п+Е_к. Применим законы сохранения импульса и энергии к основным моделям столкновений тел

Абсолютно неупругий удар - удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью. Полная механическая энергия не сохраняется:

Изменение кинетической энергии системы после удара 

Знак «минус» свидетельствует об уменьшении кинетической энергии.

Абсолютно упругий удар - удар, при котором сохраняется механическая энергия системы.

Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.

Как решать задачи на применение законов сохранения в механике?

Студенты должны уметь, рассчитывать работу сил, значения потенциальной и кинетической энергии. Для расчета работы сил необходимо усвоить, что работа совершается только, когда на тело действует сила и под действием этой силы тело перемещается

1.    Внимательно, не торопясь, прочитайте условие задачи.

2.    Выберите систему отсчета.

3.    Выделите систему взаимодействующих тел.

4.    Сделайте рисунок. Определите импульсы всех тел системы до и после взаимодействия.

5.    Запишите закон сохранения импульса в векторной форме.

6.    Избавьтесь от векторов, взяв их проекции на координатные оси.

7.    Запишите закон сохранения импульса в скалярном виде.

8.    Выразите требуемую величину.

9.    Выполните вычисления.

Примеры решения задач

1.    Железнодорожную платформу массой 20 т, движущуюся по горизонтальному участку пути со скоростью 0,5 м/с, догоняет платформа массой 10 т, имеющая скорость 2 м/с. Определите скорость платформ после сцепления.

Дано:	СИ:	Решение
m1=20т		m1   m2   m1   m2   Изобразим систему тел до и сразу после столкновения. На втором рисунке учтём, что сцепленные платформы будут продолжать двигаться в туже сторону, в какую двигались до столкновения. Запишем выражение импульса системы до столкновения: . Запишем выражение импульса системы после столкновения: . По закону сохранения импульса приравняем оба выражения для импульса рассматриваемой системы тел: . Спроецируем векторное уравнение на ось Х и решим полученное скалярное уравнение относительно скорости v: Произведём вычисления:                               Ответ: 1м/с.
v01=0,5м/с
m2=10т  v02=2м/с	104 кг
Найти: v-?

2.    Граната, летевшая горизонтально со скоростью 10 м/с, разорвалась на два осколка массами 1 кг и 1,5 кг. Больший осколок после взрыва летит в том же направлении и его скорость 25 м/с. Определите направление движения и скорость меньшего осколка.

Дано:	Решение:
кг      кг      м/с  м/с
Найти:	′′  , , масса гранаты   Ответ:

3.    Камень брошен вертикально вверх со скоростью 16 м/с. На какой высоте кинетическая энергия камня будет равна его потенциальной энергии? Сопротивлением воздуха пренебречь.

Дано:	Решение: Применяя закон сохранения энергии: . Т.к. камень брошен с земли, то  и , ;           Следовательно, .       .                    Ответ:
Найти:

4.    На «американских горках» имеется мертвая петля. Ее радиус 10 м. С какой минимальной высоты h над дном петли должна начать двигаться тележка, чтобы удержаться на колее, если потерями энергии на трение можно пренебречь?

Дано: r=10 м	Решение:
	Чтобы удержаться на колее в верхней точке, тележка должна проходить ее по инерции. Следовательно, в верхней точке  и g, где . По закону сохранения энергии для замкнутой системы: ;  Отсюда минимальная высота над дном петли . В полученную формулу подставляем числовые данные Ответ: υ= 25м
Найти: h -?

5.    Две частицы массой m скреплены пружиной жесткости k. На них налетает третья частица массы m, которая движется вдоль оси пружины со скоростью v. Найдите максимальное сжатие пружины. Внешними силами пренебречь.

Дано: k, m, v	Решение:
	Разобьем процесс взаимодействия частиц и пружины на две стадии (рис.) 1. За состояние I примем исходное состояние системы: частица 1 движется со скоростью , остальные тела покоятся. В конечном состоянии II частица 1 налетела на частицу 2, но поскольку время соударения очень маленькое, то пружина еще не сжалась, шар 3 неподвижен. К этим состояниям можно применить законы сохранения импульса и механической энергии:   и , где  и  – скорости движения первой и второй частицы после соударения. Возведем первое уравнение в квадрат, тогда получим систему двух уравнений . Чтобы эти уравнения были совместны, необходимо, чтобы / Отсюда следует, что . Последнее означает, что после столкновения частица 1 остановится, а частица 2 придет в  движение со скоростью . 2. На второй стадии в начальном состоянии движется со скоростью  вторая частица. Конечное состояние III соответствует максимальному сжатию пружины, в котором пружина и частицы 2 и 3 движутся как одно целое со скоростью . Применим к ним законы сохранения импульса и механической энергии. , , где х – максимальное сжатие пружины. Решая эту систему уравнений, получим    Ответ:
Найти: h -?

ВНИМАНИЕ!

1.Если вы поняли, как решать задачи, то приступайте к самостоятельному решению.

2.Если возникли трудности с выполнением рисунка, то попробуйте подобрать его из предложенных ниже рисунков. (стр.28)

Если вы не уверены в правильности выбранного рисунка, то обратитесь за помощью к преподавателю.

3.Если вы не можете записать закон сохранения импульса для вашего случая, то попробуйте выбрать его из предложенных вариантов. (стр.28)

4. Если не уверены в правильности выбранной вами записи, то обратитесь за помощью к преподавателю.

1.

2.

3.

4.

5.

 

6.

Подберите вариант записи закона сохранения импульса:

1.        m₁₁ + m₂₂ = m₁₃ + m_{2 4}

2.        m₁₁ + m₂₂ = (m₁ + m₂)

3.        m₁₁ = m₂₂

4.        (m₁ + m₂) ₁ = m₂₂ + m₁

5.         m₁₁ = (m₁ + m₂)

Контрольные вопросы для самопроверки

1.    Сформулируйте закон сохранение импульса тела.

2.     Дайте определение импульса тела и реактивного движения.

3.    На каком законе основано существование реактивного движения? От чего зависит скорость, развиваемая ракетой?

4.    Что называется, механической работой? Приведите примеры, когда совершается механическая работа?

5.    Что называется, механической мощностью? В чём заключается её физический смысл?

6.    Сформулируйте закон сохранения энергии? Приведите примеры использования этого закона.

7.    Какое столкновение называют абсолютно неупругим? Приведите примеры.

6.    Какое столкновение называют абсолютно упругим? Приведите примеры.

7.    Какие законы сохранения выполняются при: а) абсолютно упругом ударе, б) абсолютно не упругом ударе?

8.    На каком законе основано существование реактивного движения? От чего зависит скорость, развиваемая ракетой

Индивидуальные задания к практической работе № 3

Вариант 1

1.     На тело массой 2 кг, движущегося со скоростью 1 м/с, начала действовать постоянная сила. Каким должен быть импульс этой силы, чтобы скорость тела возросла до 6 м/с?

2.     Два шара массами 2 и 8 кг движутся навстречу друг другу со скоростями 10 и 2 м/с соответственно.  С какой скоростью они будут продолжать движение при абсолютно неупругом ударе?

3.     Какую работу надо совершить, чтобы растянуть пружину жесткостью 40кН/м на 0,5 см?

4.     Тело массой m = 1 кг брошено c поверхности земли вертикально вверх с начальной скоростью v₀ = 19,6 м/с. Определить изменение потенциальной энергии тела за промежуток времени t = 2 с после броска.

5.     Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.

6.     При подготовке пружинного пистолета к выстрелу пружину жесткостью 1 кН/м сжали на 3 см. Какую скорость приобретет «снаряд» массой 45 г при выстреле в горизонтальном направлении?

Вариант 2

1.    Мальчик массой 20 кг, стоя на коньках, горизонтально бросает камень со скоростью 5 м/с. Чему равна скорость, с которой после броска поедет мальчик, если масса камня 1 кг?

2.    На тележку массой 100 кг, движущуюся равномерно по гладкой горизонтальной поверхности со скоростью 3 м/с, вертикально падает груз массой 50 кг. С какой скоростью будет двигаться тележка, если груз не соскальзывает с нее?

3.    Мальчик везёт санки с постоянной скоростью. Сила трения санок о снег равна 30 Н. Мальчик совершил работу, равную 30 Дж. Определите пройденный путь.

4.    Масса футбольного мяча в 3 раза больше, а скорость в 3 раза меньше хоккейной шайбы. Сравнить их кинетические энергии.

5.    Какова потенциальная энергия книги на столе относительно уровня пола? Масса книги 500г, высота стола 80 см, ускорение силы тяжести 10 м/c²?

6.    Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?

Вариант 3

1.     Вагон массой 10 т движется со скоростью 1 м/с и сталкивается с неподвижной платформой массой 5т. Чему равна скорость их совместного движения после того, как сработала автосцепка?

2.     Ракета, масса которой 2 т, летит со скоростью 240 м/с. От ракеты отделяется носовая часть массой 500 кг и при этом скорость отделившейся части возрастает до 300 м/с. Определите скорость оставшейся части ракеты.

3.     При открывании двери пружину жёсткостью 50 кН/м растягивают на 10 см. Какую работу совершает пружина, открывая дверь?

4.     Камень брошен вертикально вверх со скоростью 10 м/с. На какой высоте кинетическая энергия камня равна его потенциальной энергии?

5.     Спусковую пружину игрушечного пистолета сжали на 5 см, при вылете шарик массой 20 г приобрел скорость 2 м/с. Необходимо рассчитать, какова жесткость пружины

6.     Тело массой 0,5 кг брошено вертикально вверх со скоростью 4 м/с. Найти работу силы тяжести, изменение потенциальной энергии и изменение кинетической энергии при подъеме тела до максимальной высоты.

Вариант 4

1.    Тележка массой 40 кг движется со скоростью 4 м/с навстречу тележке массой 60 кг, движущейся со скоростью 2 м/с. После неупругого соударения тележки движутся вместе. В каком направлении и с какой скоростью будут двигаться тележки?

2.    С лодки массой 200 кг, движущейся со скоростью 1 м/с, ныряет мальчик массой 50 кг. Какой станет скорость лодки после прыжка мальчика, если он прыгает с кормы со скоростью 4 м/с?

3.    Спортсмен поднимает гирю массой 16 кг на высоту 2 м, затрачивая на это 0,8 с. Какую мощность при этом развивает спортсмен?

4.    Скорость свободно падающего тела массой 4 кг на некотором пути увеличилась с 2 до 8 м/с. Найти работу силы тяжести на этом пути.

5.    Пружина жесткостью 104 Н/м растянута на 4см. Какова потенциальная энергия упругой деформации пружины?

6.    С какой начальной скоростью надо бросить вниз мяч с высоты 5 м, чтобы он подпрыгнул на высоту в 2 раза большую? Считать удар о землю абсолютно упругим.

Вариант 5

1.    Первый вагон массой 45 т движется со скоростью 1,5 м/c и догоняет второй вагон массой 30 т, движущийся со скоростью 0,5 м/с. После столкновения второй вагон приобретает скорость 1 м/с. Какова скорость первого вагона после столкновения?

2.    С отплывающей от берега со скоростью 1,3 м/с лодки, масса которой вместе с человеком равна 250 кг, в горизонтальном направлении сбросили на берег груз. Чему равна масса груза, если скорость лодки увеличилась до 1,4 м/с?

3.    Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20 мг, при её падении с высоты 2 км?

4.    Найти кинетическую энергию тела массой 400 г, упавшего с высоты 2 м, в момент удара о землю.

5.    Снаряд, выпущенный вертикально вверх, достиг максимальной высоты 1 км. Какой скоростью он обладал на половине высоты?

6.    При подготовке пружинного пистолета к выстрелу пружину жесткостью 1 кН/м сжали на 3 см. какую скорость приобретает «снаряд» массой 45 г при выстреле в горизонтальном направлении?

Вариант 6

1.    Находившийся в годы войны на вооружении советских войск ручной пулемет конструкции Дегтярева (РПД) имел массу 9 кг, его пули были калибром 7,62 мм и массой 9 г; при выстреле пуля приобретала начальную скорость около 700 м/с. Определите скорость отдачи, которую приобретал при выстреле пулемет.

2.    С лодки массой 200 кг, движущейся со скоростью 1 м/с, ныряет мальчик массой 50 кг. Какой станет скорость лодки после прыжка мальчика, если он прыгает с носа со скоростью 2 м/с?

3.    С какой скоростью должна лететь бронебойная пуля массой 0,15 кг, чтобы обладать кинетической энергией 6,75 кДж?

4.    Тело массой 2кг, движущееся со скоростью 8м/с, сталкивается с телом массой 3кг, движущимся навстречу ему со скоростью 4м/с. Каково изменение кинетической энергии второго тела в результате столкновения, если столкновение абсолютно неупругое?

5.    При растяжении пружины на 20 см она приобрела потенциальную энергию упругодеформированного тела 20 Дж. Какова жесткость пружины?

6.     Тело брошено вертикально вверх с начальной скоростью v₀ =3 м/с. На какой высоте его кинетическая энергия будет равна потенциальной? Сопротивление воздуха не учитывать.

Тема 2.4. Механические колебания и волны

Практическая работа № 4 «Расчёт основных характеристик механических колебаний и волн»

Цели: закрепить умения и навыки вычисления параметров колебательного движения, характеристик механических колебаний, правильно оформлять решение задач, правильно давать ответ, в нужных единицах измерения, формирование знаний, умений и навыков при решении задач, анализировать задачу, отработка умений выполнять задания по образцу, обобщение и систематизация знаний по теме «Механические волны».

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. 

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Движения или процессы, которые точно или приблизительно повторяются через одинаковые промежутки времени, называются колебательными (или механическими колебаниями).

Среди них важную роль играют периодические движения.

Движение называют периодическими, если значения физических величин (например, смещения или скорости), изменяющиеся в процессе движения, повторяются через равные промежутки времени.

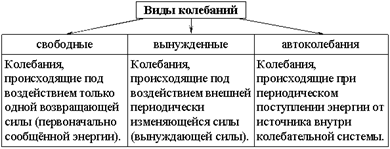
Полным колебанием называют один законченный цикл колебательного движения, после которого оно повторяется в том же порядке.

Колебательное движение основано на следующих кинематических характеристиках колебаний. К таковым относятся:

1.    Смещение x – отклонение тела (материальной точки) от положения равновесия (координата колеблющейся точки). Она зависит от времени и является одной из основных характеристик колебательного движения. Смещение равно расстоянию от положения равновесия точки до положения её в данный момент времени.  Амплитуда колебаний А – это максимальное расстояние x_m, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем первоначальным отклонением или толчком, которым маятник или груз на пружине был приведен в движение;

2.    период колебания Т – это минимальный промежуток времени, по истечении которого система возвращается в прежнее состояние, т. е. когда колеблющееся тело оказывается в том же положении и с прежним значением вектора скорости; иначе говоря, период колебания — это время, за которое совершается одно полное колебание , где п – число колебаний, a  t – время, за которое произошло п колебаний, ,  единица измерения:  (секунда);

3.    частота колебаний ν – это величина, показывающая  число полных колебаний, совершаемых в единицу времени , измеряется в герцах (Гц). Если частота равна 1 Гц, то, значит, за каждую секунду совершается лишь одно колебание, если 50 Гц, то за каждую секунду совершается 50 колебаний, и т.д. Частота и период – взаимообратные величины:  или

4.    циклическая частота ω - это число полных колебаний, совершаемых за время 2π сек, т.е.

.

Физический смысл циклической частоты заключается в том, что она показывает, какое число колебаний совершается за 2 π секунд, т. е. приблизительно за 6,28 с.

Измеряется циклическая частота в  рад/с или с^-1.

Гармонические колебания  –  колебания, при которых физическая величина периодически изменяется с течением времени по законам синуса или косинуса , A – амплитуда колебаний.

  Пружинный маятник – это колебательная система, представляющая собой совокупность некоторого тела и прикреплённой к нему пружины.

Для пружинного маятника, период равен: , где m – масса груза , k – коэффициент жесткости пружины  .

Период колебаний пружинного маятника зависит от массы колеблющегося тела и жесткости пружины.

Математический маятник - это материальная точка, подвешенная на невесомой и нерастяжимой нити, находящейся в поле тяжести Земли.

Математический маятник – это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити l много больше размеров подвешенного на ней тела, масса нити ничтожно мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Для математического маятника  ,  где  l – длина нити, ,   – ускорение свободного падения, .

Период колебаний математического маятника не зависит от его массы и амплитуды колебаний, он определяется лишь длиной маятника и ускорением свободного падения в том месте, где находится маятник.

Волновой процесс - процесс переноса энергии без переноса вещества. Волна - это колебания, распространяющиеся в пространстве с течением времени. При возбуждении волны происходит процесс распространения колебаний, но не перенос вещества. Возникшие в каком-то месте колебания воды, например, от брошенного камня, передаются соседним участкам и постепенно распространяются во все стороны, вовлекая в колебательные движения всё новые и новые частицы среды. Течение же воды не возникает, перемещаются лишь локальные формы её поверхности.

В результате внешнего воздействия на среду в ней возникает возмущение - отклонение частиц среды от положения равновесия.

Механическая (упругая) волна - процесс распространения механических колебаний в твердых, жидких и газообразных телах, т.е. в упругой среде.

Наличие упругой среды - необходимое условие распространения механических волн.

Упругая среда - это среда, состоящая из частиц, связанных друг с другом упругими силами.

Механические колебания возникают в любой среде, содержащей атомы или молекулы, если устойчивое равновесие частиц среды нарушается. Возникшее нарушение устойчивого равновесия не остается в пределах некоторой области, а вследствие того, что среда упругая и обладает инертными свойствами, передается в другие части среды.

Луч – это линия, касательная к которой в каждой точке совпадает с направлением распространения волны. Колебания частиц среды могут совершаться по направлению луча и перпендикулярно ему.

Различают поперечные и продольные волны.

Волны, в которых колебания происходят перпендикулярно направлению распространения волны, называются поперечными волнами.

Волны, в которых колебания происходят вдоль направления распространения волны, называются продольными волнами.

Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства.

Геометрическое место точек, до которых доходят колебания к моменту времени t, называют волновым фронтом.

Геометрическое положение точек, колеблющихся в одинаковой фазе, называют волновой поверхностью.

Любая волна характеризуется направлением распространения и скоростью.

Скорость распространения волны - это скорость перемещения любой точки волнового фронта (волновой поверхности) волны.

Вектор скорости v направлен по нормали к волновой поверхности в сторону распространения волны (в изотропной среде совпадает по направлению с направлением луча).

Скорость распространения волнового процесса v зависит от плотности среды ρ, в которой возникают волны.

Длина волны λ - кратчайшее расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.

Длина волны — расстояние, на которое распространяется фронт волны за период , где  - частота колебаний.

Период волны Т - время одного полного колебания ее точек.

Частота колебаний ν - частота источника волн, которая во всех средах, где может распространяться волна, постоянна.

Это объясняется тем, что при возникновении волн их частота определяется частотой колебаний источника волн.

Скорость распространения волн зависит от свойств среды. Поэтому волны одной и той же частоты имеют в разных средах имеют разную длину волны.

Бегущими называют волны, которые переносят в пространстве энергию.

Упругую волну называют гармонической, если соответствующие ей колебания частиц среды являются гармоническими.

Уравнение волны — уравнение, выражающее зависимость смещения колеблющейся частицы, участвующей в волновом процессе, от координаты ее равновесного положения и времени.

 - уравнение плоской поперечной волны, где y – смещение любой из точек среды с координатой x в момент t; v – скорость распространения колебаний в среде. Связь разности фаз Dj колебаний с расстоянием между точками среды, отсчитанным в направлении распространения колебаний: Dj = (2 p / l ) D x, где l – длина волны.

Из уравнения плоской волны вытекает, что:

1) амплитуда плоской волны А = const (мы рассматривали среду, не поглощающую энергию);

2) любая точка среды совершает гармонические колебания, фаза которых зависит от расстояния данной точке от источника колебаний.

Ухо человека воспринимает в виде звука колебания, частота которых лежит в пределах от 17 до 20 000 Гц. Такие колебания называют акустическими. Акустика - это учение о звуке. Звуковые волны - это упругие волны в среде, вызывающие у человека слуховые ощущения. Энергетической характеристикой звука, как и механической волны, является интенсивность I, или сила звука, которая зависит от энергии, ежесекундно переносимой через единичную площадку, расположенную перпендикулярно направлению распространения звуковой волны. Единица интенсивности звука — ватт на квадратный метр (Вт/м²).

Количество энергии, переносимой волной в единицу времени через единичную площадку, пропорционально квадрату амплитуды волны и квадрату частоты, следовательно, интенсивность, или сила звука данной частоты пропорциональна квадрату амплитуды.

Звук характеризуют громкостью, высотой и тембром.

Громкость звука — субъективная характеристика звука, связанная с его интенсивностью (амплитудой колебаний в звуковой волне). Единица громкости — бел (Б). Обычно пользуются единицей, в 10 раз меньшей, — децибелом (дБ).

Высота звука — качество звука, определяемое человеком субъективно на слух и зависящее от частоты звуковой волны. С ростом частоты высота звука увеличивается, т.е. звук становится выше.

Чем больше частота, тем меньше период колебаний, тем более высокий звук мы слышим.

 Характер акустического спектра и распределения энергии между отдельными частицами определяет своеобразие звукового ощущения, называемое тембром звука.

Примеры решения задач

1.    Какова масса груза, колеблющегося на пружине жесткостью 0,5 кН/м, если при амплитуде колебаний 6 см он имеет максимальную скорость 3 м/с?

Дано:	СИ	Решение:
k = 0,5 кН/м	500 Н/м	По закону сохранения для колебаний пружинного маятника: кинетическая энергия движения груза переходит в потенциальную энергию упругодеформированного тела . Из формулы выразим массу груза . Подставляем числовые значения:   Ответ:
v = 3 м/с
x = 6см	6×10-2 м
Найти: m -?

2.   Гармонические колебания  величины  x  описываются  уравнением  , м . Определите:  амплитуду  А  колебаний; циклическую частоту 𝜔₀;  частоту  колебаний  ν; период колебаний Т; 𝑥₁в момент времени

Дано:	Решение:
, м	Сравнив уравнение гармонических колебаний  с данным в задаче, находим А = 0,2 м; 𝜔0= 2𝜋 с−1; , откуда ν = 1 Гц; , откуда Т = 1 с. Подставив значение  в уравнение, данное в условии задачи, определяем 𝑥1: м. Ответ: А = 0,2 м; 𝜔0= 2𝜋 с−1; ν = 1 Гц; Т = 1 с; 𝑥1= 0 м
Найти: А,  𝜔0, ν, Т, 𝑥1- ?

3.    Напишите уравнение гармонических колебаний, если амплитуда колебаний A = 2 см, начальная фаза колебаний 𝜑₀= 30° и за t = 10 c совершается n = 20 полных колебаний.

Дано:	СИ	Решение:
A = 2 см	0,02 м	Уравнение гармонических колебаний имеет вид . Период колебаний Т – время, в течение которого совершается одно колебание: . Зная Т, определяем циклическую частоту: ,  или  . Уравнение данных гармонических колебаний будет иметь вид: , м  Ответ: , м
𝜑0=30°
t = 10 c
n = 20
Найти:  x(t) - ?

4.    Период колебаний математического маятника на Луне 𝑇_л=10с. Определите период колебаний Т этого  маятника на Земле. Ускорение свободного падения на Луне .

Дано:	Решение:
𝑇л=10с	Периоды колебаний математического маятника на Луне  𝑇л и Земле Т: ;  . Разделив второе уравнение на первое уравнение, получим: , откуда  . Подставляем числовые значения:         Ответ:
Найти:  x(t) - ?

5.    Математический маятник, длина нити которого 0,5 м, совершает гармонические колебания с амплитудой 5 см. Определите максимальную скорость колеблющейся материальной точки.

Дано:	СИ	Решение:
A = 5 см	0,05 м	Математический маятник совершает гармонические колебания по уравнению , где 𝜔0 – собственная циклическая частота, ; Т – период колебаний маятника, , следовательно, . Максимальная скорость материальной точки  . Вычисления:   Ответ:
l = 0,5 м
Найти:  𝜐max - ?

Вопросы для самоконтроля по теме:

1.    Что называется механическими колебаниями?

2.    Какие колебания называются гармоническими колебаниями? Записать уравнение гармонических колебаний.

3.    Дайте определения и запишите формулы для вычислений характеристик механических движений.

4.    Что называется математическим маятником? Записать формулу периода колебаний и циклической частоты математического маятника.

5.    Что называется пружинным маятником? Записать формулу периода колебаний пружинного маятника.

6.    Что называется волновым процессом?

7.    Какие волны называют упругими?

8.    Перечислите виды механических волн. Дайте определения каждому виду.

9.    Назовите характеристики волны. Какова связь между ними? Запишите, объяснив, связь между ними.

10. Какие волны называют звуковыми.

Индивидуальные задания к практической работе № 4

Вариант №1

1.    Найти массу груза, который на пружине жёсткостью 250Н/м делает 20 колебаний за 16 с.

2.    Девушка-горянка несёт на коромысле вёдра с водой, период собственных колебаний которых 1,6 с. При какой скорости движения девушки вода начнёт особенно сильно выплёскиваться из вёдер, если длина её шага 60 см?

3.    Координата колеблющегося тела изменяется по закону: х=5cos(πt+π/2). Определить амплитуду, циклическую частоту, частоту, период, начальную фазу колебаний.

4.    Если длину математического маятника уменьшить в 4 раза, то, как изменится частота его малых колебаний?

5.    Рыболов заметил, что за 10 с поплавок совершил на волнах 20 колебаний, а расстояние между соседними гребнями волн 1,2 м. Какова скорость распространения волны?

6.    При измерении глубины моря под кораблём с помощью эхолота оказалось, что моменты отправления и приёма ультразвука разделены промежутком времени 0,6 с. Какова глубина моря под кораблём? Скорость звука в воде 1400 м/с

Вариант №2

1)    Груз, подвешенный на пружине жёсткостью 600Н/м, совершает гармонически колебания. Какой должна быть жёсткость пружины, чтобы частота колебаний уменьшилась в 2 раза?

2)    Колебания математического маятника задано уравнением: х=5sin(πt+π/2), см.  Определить амплитуду, циклическую частоту, частоту, период, начальную фазу колебаний.

3)    Как нужно изменить длину математического маятника, чтобы период его колебаний уменьшить в 2 раза?

4)    Какова масса груза, колеблющегося на пружине жёсткостью 0,5 кН/м, если при амплитуде колебаний 6 см он имеет максимальную скорость 3 м/с?

5)        По поверхности воды в озере волна распространяется со скоростью 6 м/с. Каковы период и частота колебаний бакена, если длина волны 3м?

6)        Волна распространяется в упругой среде со скоростью 150 м/с. Определите частоту колебаний, если минимальное расстояние между точками среды, фазы которых противоположны, равно 0,75м.

Вариант №3

 Маятник совершил 50 колебаний за 25с. Определите период и частоту колебаний маятника.

 По графику гармонического колебания определите: амплитуду, период, частоту колебаний. Напишите уравнение данного колебания. 

t,с

10

12

8

6

4

2

-4

 

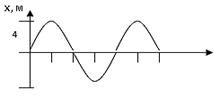
 Маятник длиной 1 м совершил 60 колебаний за 2 минуты. Найти ускорение свободного падения для данной местности.

 Груз, подвешенный на пружине жёсткостью 600Н/м, совершает гармонически колебания. Какой должна быть жёсткость пружины, чтобы частота колебаний уменьшилась в 2 раза?

 Определите, на каком расстоянии от наблюдателя ударила молния, если он услышал гром через 3 с после того, как увидел молнию.

 Определите длину волны, распространяющейся со скоростью 2 м/с, в которой за 20 с происходит 10 колебаний. 

Вариант № 4

1.    По графику гармонического колебания определите: амплитуду, период, частоту колебаний.  Напишите уравнение данного колебания.

 

 

 

5

4

2

3

1

          

t, c

                                                                          

-2

                                                                               

 

2.   Уравнение свободных колебаний пружинного маятника имеет вид . Определите циклическую частоту, частоту и период колебаний. Чему равна жёсткость пружины этого маятника, если масса груза 500г.

3.    Вычислите период и частоту свободных колебаний математического маятника, длина нити которого 1 м. Сколько времени будут длиться 10 колебаний этого маятника?

4.    Как изменится частота колебаний нитяного маятника длиной 0,5 м, если увеличить длину нити на 1,5 м?

5.    Звуковая волна распространяется со скоростью 346 м/с и частотой 1000 Гц. Определить длину звуковой волны.

6.    Длина морской волны равна 2 м. Какое количество колебаний за 10 с совершит на ней поплавок, если скорость распространения волны равна 6 м/с

Вариант №5

1.    Маятник совершил 180 колебаний за 72 с. Определите период и частоту колебаний маятника.

2.   Уравнение свободных колебаний математического маятника имеет вид . Определите циклическую частоту, частоту и период колебаний этого маятника. Чему равна длина его нити?

3.    По графику(рис.) определите амплитуду, период и частоту колебаний.

4.    Масса грузика, прикреплённого к пружине, равна 100 г. Определите период и частоту его свободных колебаний, если жёсткость пружины 40 Н/м. Сколько колебаний совершит этот пружинный маятник за 20 с?

5.    На озере в безветренную погоду с лодки сбросили тяжёлый якорь. От места бросания пошли волны. Человек, стоящий на берегу, заметил, что волна дошла до него через 50 с, расстояние между соседними горбами волн 50 см, а за 50 с было 20 всплесков о берег. Как далеко от берега находилась лодка?

6.    Какой путь пройдёт ультразвуковая волна длиной 5 см за 0,001 с, если генератор, испускающий эти волны, работает на частоте 1 МГц?

Вариант №6

1.    По графику (рис.) определите амплитуду, период и частоту колебаний.

2.    Амплитуда колебаний математического маятника А=10см. Наибольшая скорость маятника 0,5м/с. Определите длину такого маятника, если ускорение свободного падения равно 10 м/с² .

3.    На неизвестной планете маятник длиной 80 см совершил 36 полных колебаний за 1 мин. Чему равно ускорение свободного падения на этой планете?

4.    Пружинный маятник массой 0,16 кг совершает гармонические колебания. Какой должна стать масса этого маятника, чтобы период колебаний увеличился в 2 раза?

5.    Чему равна длина волны на воде, если скорость распределения волн равна 2,4 м/с, а тело, плавающее на воде, совершает 30 колебаний за 25 с?

6.    Под­вод­ная лодка всплы­ла на рас­сто­я­нии s=200 м от бе­ре­га, вы­зва­ла волны на по­верх­но­сти воды. Волны дошли до бе­ре­га за t=40 с, при­чем за сле­ду­ю­щие Δt=30 с было N=60 всплес­ков волн о берег. Ка­ко­во рас­сто­я­ние между греб­ня­ми со­сед­них волн λ?

Раздел 3. Молекулярная физика и термодинамика.

Методические указания к выполнению практической работы для студентов

1.     К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.     Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы.

Физические величины и их обозначения

Единицы тепловых величин и величин молекулярной физики в СИ

Рекомендации к решению задач по теме "Молекулярная физика"

a.       Внимательно проанализировать условие задачи.

b.      Если в задачах предлагается произвести расчёт параметров состояния идеальных газов, то:

а)   установить, какие параметры меняются, а какие - остаются постоян­ными;

б) сделать, если возможно, поясняющий рисунок, указав при этом, ка­кие параметры характеризуют каждое состояние;

в) для каждого состояния записать нужные соотношения, используя таблицы данной книги. Решить полученную систему уравнений отно­сительно искомой величины.

c.       Для решения графических задач следует воспользоваться графическим изображением на плоскости изопроцессов.

d.      Для решения задач о тепловом расширении тел необходимо:

а)   для каждого теплового состояния каждого тела записать соотноше­ние, пользуясь таблицами;

б) если в задаче рассматриваются и другие процессы, то добавить фор­мулы, отражающие эти процессы;

в) решить полученную систему уравнений относительно искомой вели­чины.

План решения задач

Для решения задачи можно рекомендовать следующую последовательность действий:

1.   Прочитав условие задачи, записать данные, ясно представить какие из параметров газа меняются, какие остаются постоянными.

2.   Записать уравнения Клапейрона-Менделеева для каждого состояния, приписывая соответствующие индексы изменяющимся параметрам.

3.   Записать математически все вспомогательные условия и решить полученную систему уравнений относительно неизвестной величины. При решении системы уравнений, можно использовать деление одного уравнения на другое, вычитание, сложение уравнений и т. д.

Если дана смесь газов, то уравнение Клапейрона-Менделеева записывают для каждого компонента. Давление смеси газов устанавливается законом Дальтона.

В задачах на газовые законы следует пользоваться только абсолютной температурой и сразу переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.

Тема 3.1. Основы молекулярно-кинетической теории

Практическая работа № 5. «Расчет параметров состояния идеального газа»

Цели: закрепить умения и навыки решения задач на законы сохранения в механике, сформировать умения и навыки нахождения физической величины, её вывода   из формулы.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

В основе молекулярно-кинетической теории лежат три основных положения:

1.    Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул

2.    Атомы и молекулы находятся в непрерывном хаотическом движении. Масса одной молекулы m₀ выражается формулой

 

Количеством вещества v называется отношение числа молекул N к числу Авогадро N_A :

 

Концентрацией молекул n называется отношение числа молекул N в объеме V к этому объему V:

 

Давление p можно выразить следующей формулой

 

Средняя кинетическая энергия                    где      k—постоянная Больцмана.

Газовые законы описывают изменение состояния идеального газа. Иными словами, газовый закон всегда связывает друг с другом параметры начального и конечного состояний идеального газа.

Для идеальных газов справедливы следующие законы:

1.     Закон Бойля — Мариотта описывает изотермический процесс:   при Т = const, m = const.

2.     Закон Шарля описывает изохорный процесс:  при V = const, m = const.

3.     Закон Гей-Люссака описывает изобарный процесс:   при р=const, m=const.

Газовые законы являются частными случаями объединенного газового закона: , где р₁, V₁, m₁, T₁ — параметры начального состояния идеального газа; р₂, V₂, m₂, T₂ — параметры конечного состояния идеального газа. Если в процессе перехода от начального состояния к конечному масса газа не изменяется (m₁= m₂), то объединенный газовый закон имеет вид:  - уравнение Клапейрона. В общем случае все газовые законы описываются уравнением со­стояния: - уравнение Клапейрона — Менделеева. Учитывая, что , получим ;  ,  получим .

При решении некоторых задач необходимо знание формулы закона Дальтона:  - давление смеси газов на стенки сосуда. Так как объем, занимаемый каждым компонентом смеси, одинаков,  то  ри этом уравнение Клапейрона — Менделеева для смеси газов: . Уравнение Клапейрона — Менделеева можно рассматривать как след­ствие основного уравнения МКТ:  .  После преобразований имеем .

Примеры решения задач

1.     Определить среднюю квадратичную скорость молекул аргона при нормальных условиях. Молярную массу аргона принять равной .

Дано:	Решение:
M=	Для определения средней квадратичной скорости воспользуемся формулой  (1), но  (2). Подставляя (2) в (1), получим.  Произведём числовые вычисления: . Ответ: .
Т=273К
Nа=
Найти: -?

2.     Определить начальную температуру газа, если при изохорном нагревании до температуры 580 К его давление увеличилось вдвое.

Дано:	Решение:
Т=580 К	Так как процесс изохорный, то запишем закон Шарля: . Учитывая условие задачи, подставим числовые значения в полученное уравнение и рассчитаем начальную температуру:          Ответ: Т0=290К
р=2р0
V=const
Найти: T0-?

3.   В баллоне вместимостью 0,1 м³ при температуре 250 К находится воздух под давлением . Определить объём этого воздуха при нормальных условиях.

Дано:	Решение:
V=0,1м3 Т=250 К р= р0=105Па Т0=273 К	Для решения задачи воспользуемся уравнением Менделеева-Клапейрона:  (1). Выразим из этой формулы объём воздуха при нормальных условиях:  (2). Для дальнейшего решения задачи нам неизвестна масса воздуха, которую можно найти из (1), используя начальные условия задачи: . Подставляя полученную формулу в (2), имеем: . Произведём вычисления, подставив числовые данные в полученную формулу: .                                                                                      Ответ: 0,22 м3.
Найти: V-?

4.     Какое давление производят пары ртути в баллоне ртутной лампы объёмом   при 300 К, если в ней  содержится 10¹⁸ молекул?

Дано:	Решение
Т=300 К N=1018	Для решения задачи воспользуемся формулой зависимости давления от температуры . Подставим в формулу числовые значения: . Ответ: 138 Па
Найти: р - ?

5.     Два сосуда, наполненных воздухом при давлениях р₁=0,8МПа и р₂=0,6МПа, имеют объёмы V₁=3л и V₂=5л. Сосуды соединяют трубкой, объёмом которой можно пренебречь по сравнению с объёмом сосудов. Найти установившееся давление р в сосудах. Температуру считать постоянной.

Дано:	СИ:	Решение
V1=3л V2=5л Т=const р1=0,8МПа р2=0,6МПа	м3	После соединения сосудов воздух, находившийся в каждом из них, распределится по объёму (V1+V2).  двух сосудов. Для воздуха, находившегося в первом сосуде по закону Бойля- Мариотта p1V1 = p/1(V1+ V 2) для воздуха, находившегося во втором сосуде, p2V2 = p/2(V1 + V2), где p/1 и p/2 - парциальные давления. Складывая эти равенства, получим p1V1 + p2V2 = (p'1+p'2)(V1 + V2). По закону Дальтона p = p/1+  p/2.  Таким образом, . Подставим в формулу числовые значения:   Ответ: 675кПа
	м3
	Па
	Па
Найти: р - ?

6.     В комнате объемом 50 м³ находится воздух при температуре 20°С и давлении 10⁵Па. Если температура воздуха повышается до 25°С, то через открытую форточку выйдет масса воздуха, равная ... (в кг).

Дано:	СИ:	Решение
V = 50 м3 t1 = 20°С t2 = 25°С		Уравнение Клапейрона-Менделеева для воздуха при двух разных температурах:  и . Из записанных уравнений выразим массы    и , тогда .  Молярную массу воздуха берем из справочных таблиц 0,029 кг/моль: Ответ: 1 кг
	293К
	298 К
Найти:  Δm-?

7.     И закрытом сосуде объемом 4 л находится газ под давлением 10⁵Па при температуре 27°С. После подкачивания газа его давление увеличилось в 2 раза, а температура возросла на 50°С. На сколько увеличилось число молекул газа?

Дано:	СИ:	Решение
t1=270C V=4л Δt=500С р1=10 5Па р2=2р1	27+273=300К	В моле любого вещества содержится одинаковое число частиц, равное числу Авогадро. Для того, чтобы найти, на сколько увеличилось число молекул, найдем на сколько увеличилось число молей газа после подкачивания. Запишем уравнение Клапейрона- Менделеева для первого состояния газа:   (1) После подкачивания масса газа увеличивается и уравнение состояния примет вид:  (2) Из уравнений (1) и (2) находим количество вещества газа до и после подкачивания:  (3)   (4) Вычтем из уравнения (4) уравнение (3): , тогда   Значение числа Авогадро и универсальной газовой постоянной берем из справочных таблиц:  , R=8,31  Дж/(кг∙моль). Подставляем числовые значения:  .            Ответ:
Найти:

Контрольные вопросы для самопроверки

1.    Какая теория называется молекулярно-кинетической теорией?

2.    Сформулируйте основные положения МКТ?

3.    Какое явление называется диффузией?

4.    Какое движение называется броуновским? Приведите примеры.

5.    Запишите формулу для вычисления количества частиц.

6.    Какое число названо постоянной Авогадро?

7.    Какую температуру называют абсолютной? Что такое абсолютный нуль?

8.    Запишите основное уравнение МКТ.

Индивидуальные задания к практической работе № 5

Вариант №1

1.     Подсчитайте, сколько молекул содержится в капле воды (Н₂О) диаметром d=1,0 мм при температуре t=23°C.

2.     В цилиндре дизельного двигателя автомобиля температура воздуха в начале такта сжатия была 50⁰С. Найдите температуру воздуха в конце такта, если его объём уменьшился в 17 раз, а давление возрастает в 50 раз.

3.     Из баллона выпустили 2 г газа, вследствие чего давление в нем снизилось на 10%. Определите емкость баллона, если плотность газа в начальный момент была 0,2 кг/м³. Температура газа в баллоне не менялась.

Вариант №2

1.     Один киломоль углекислого газа (СО₂) имеет молярную массу М=44,0 г/моль. Определите плотность углекислого газа и массу его молекулы при нормальных условиях (р = 1,01 10⁵ Па;Т₀ = 273К)

2.     На изделие, площадь поверхности которого 52 см², нанесен слой хрома толщиной 1мкм. Сколько атомов хрома в покрытии?

3.     Начальный объем газа составляет 60 л. Определите, каким будет объем этой массы газа, если абсолютная температура повысится от 300 К до 450 К, а давление уменьшится в 2 раза.

Вариант №3

1.   Вакуумный насос позволяет понижать давление до значения .  Определите, сколько молекул газа содержится в объеме V=1,0 см³ газа при данном давлении и температуре

2.     Сколько молекул содержится в сосуде емкостью 250 см³, если давление газа 566 мм рт.ст., а температура равна 100 °С?

3.     Какое давление рабочей смеси устанавливается в цилиндрах двигателя автомобиля, если к концу такта сжатия температура повышается с 50 до 250⁰С, а объём уменьшается с 0,75 до 0,12 л? Первоначальное давление равно 80 кПа.

Вариант №4

1.     Подсчитайте, сколько раз можно опоясать Землю по экватору цепочкой из молекул кислорода (О₂), содержащихся в объеме V=1,0см³ этого газа при нормальных условиях. Диаметр молекулы кислорода , радиус Земли R₃=6,410 км.

2.     Кислород находится в баллоне под давлением  Па. Температура в баллоне равна 47 °С. Какую плотность имеет кислород?

3.     Какая масса воздуха выйдет из комнаты, имеющий объем V=60 м³, в следствие повышения температуры от Т₁=280 К до Т₂=300 К при нормальном давлении?

Вариант №5

1.    Подсчитайте, сколько молекул газа содержится в баллоне емкостью V=60,0 л при температуре Т= 300 К и давлении р=5,0010 Па.

2.    Определите, какой будет абсолютная температура определенной массы идеального газа, если давление газа увеличить 4 раза, а объем уменьшить на 2 раза. Начальная температура газа равна 300 К.

3.    В баллоне объемом V=10 л содержится гелий под давлением р₁=1 МПа при температуре Т₁=300 К. После того как из баллона вышло 10 г гелия, температура в нем уменьшилась до Т₂=290 К. Определите давление гелия, оставшегося в баллоне.

Вариант №6

ü Найдите массу атома гелия (Не).

ü Плотность газа в баллоне газонаполненной электрической лампочки ρ = 0,9 кг/м³. Когда лампочка горит, давление газа в ней возрастает с  до . На сколько увеличится при этом средняя квадратичная скорость молекул газа?

ü В сосуде при температуре 27⁰С находится смесь азота и кислорода. С какой средней квадратичной скоростью движутся молекулы газа?

Тема 3.3. Основы термодинамики

Практическая работа №6. «Изучение газовых законов»

Цели: закрепить умения и навыки решения задач на газовые законы, сформировать умения и навыки нахождения физической величины, её вывода   из формулы, сформировать умения объяснять физические явления и решать задачи с помощью законов идеального газа.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы

1.     Рассмотрите теоретический материал по теме и примеры решения задач.

2.     Ответьте на контрольные вопросы.

3.    Решите самостоятельную работу. Выполнить задание соответствующего варианта.

Ход работы

Теоретическая часть

Изопроцессы – процессы, при которых масса газа и один из его термодинамических параметров остаются постоянными.

Шаблон формулировки процесса:

 Изо наз. процесс изменения данной массы газа при постоянном 

Т – « термос» - « теплый» - термический;

Р – « барос» - « тяжелый» -барический;

 V - « хорема» - « вместимость» - хорический.

Шаблон формулировки закона: При постоянной массе газа и неизменном ,  газа прямо

(обратно) пропорционально его

                                                     m = const,

 

Т= const Изотермический	Р = const Изобарический	Изохорический
Закон Бойля - Мариотта	Закон Гей - Люссака	Закон Шарля
=	=	=
V	T	T   V   T   P   P   P   P   V   T   P   T   V   P   P
В остальных случаях постоянный параметр перпендикулярен соответствующей оси
	T
T	V	T   V   V

Примеры решения задач:

  1. Какие процессы изменения состояния газа представлены на графике? Какой параметр постоянный, как называется процесс? Чей закон?

T   T   T   V   V   Р   Р
V = const Изохорический Шарля	P = const             Изобарический Гей - Люссака	T= const Изотермический Бойля - Мариотта

 2. Газ переведен из состояния 1 в состояние 2 . Какой это процесс? Как изменилось давление газа?                                     

 

 

 

3. Изобразить процесс в осях РV, PT                                                                                                     

					Р

 

 

 

 4. На сколько градусов надо охладить газ, имеющий температуру 0⁰С и объем 21 л, чтобы его объем при том же давлении стал 3 л?

Дано:   Газ Р= const Т1 = 00С V1 = 21 л V2 = 3 л	«СИ»   273К 21·103м3 3·103м3	1) Формулы:  ∆Т = Т1- Т2    =	2) Вычисления: Т2 =  =  = 39 (К)            ∆Т = 273 – 39 = 234 (К)
∆ Т- ?		Т2 =	Ответ: 234 К

5. Находившийся в закрытом баллоне газ нагрели от 300К до 360К, причем давление возросло на 8 атм. Определить первоначальное значение давления. Расширением баллона пренебречь.

Дано:   Газ V = const Т1 = 300 К Т2 = 360К ∆Р = 8 атм.	«СИ»       8·105м3	1) Формулы: Р2= Р1+∆Р    =       =	2) Вычисления:   Р1 =   =  = 4·106 = 4 МПа
Т- ?		Т2· Р1= Т1· Р1+ Т1·∆Р Р1 ·(Т2  –Т1) = Т1·∆Р    Р1 =	Ответ: 4 МПа

6) Кислородный баллон, содержащий 8 л 02 под давлением 6 атм. Соединился с пустым сосудом, после чего установилось давление 2 атм. Какова емкость присоединенного сосуда?

Дано:   02 Т= const V1 = 8 л Р1 = 6атм Роб = 2 атм	«СИ»   8·10 –3м3 6·105 Па 2·105 Па	1) Формулы:  Р1· V1=  Роб· Vоб V2 =  Vоб – V1  Vоб =	2) Вычисления:   Vоб =  = 24·103 (м3)   V2= (24 – 8)·10–3  =16 ·10–3  (м3)  = 16 (дм3)
V2 - ?			Ответ:16 дм3

Контрольные вопросы для самопроверки

1.    Что называется изопроцессом?

2.    Сформулируйте законы Бойля-Мариотта, Гей-Люссака, Шарля.

3.    Запишите уравнение Клапейрона-Менделеева.

Индивидуальные задания к практической работе № 6

Вариант №1

1.       При изохорном нагревании идеального газа, взятого при температуре 320К, его давление увеличилось от 1,4·10⁵ Па до 2,1·10⁵ Па. Как изменилась температура газа?

2.       На рисунке представлены графики замкнутых циклов. Вычертите диаграммы замкнутых циклов в координатах pV и VT

3.       Определите, до какой температуры нужно нагреть газ, взятый при температуре t₁=0 °C и постоянном давлении, чтобы его объем увеличился вдвое (V₂=V₁).

4.       При увеличении давления в 1,5 раза объём газа уменьшился на 30 мл. Найти первоначальный объём газа.

5.       Начертите графики изотермического  процесса в координатах P и V; P и T;T и V.

6.        В сосуде находится m=14 кг азота при Т=300 К и давлении р = 8,3*10⁴ Па. Определите объем V сосуда.

Вариант №2

1.       Газ находится в цилиндре с подвижным поршнем и при температуре 300 К занимает объём 250 см³. Какой объём (см³) займёт газ, если температура понизится до 270 К? Давление постоянно.

2.       Сосуд с газом под давлением 1,4·10⁵ Па соединили с пустым сосудом объемом 6 л. После этого в обоих сосудах установилось давление 10⁵ Па. Определить первоначальный объем при постоянной температуре.

3.       Начальный объем газа составляет 60 л. Определите, каким будет объем этой массы газа, если абсолютная температура повысится от 300 К до 450 К, а давление уменьшится в 2 раза.

4.       На рисунке представлены графики замкнутых циклов. Вычертите диаграммы замкнутых циклов в координатах pV и pT

5.       Начертите графики изобарного процесса в координатах P и V; P и T;T и V.

6.       При сжатии неизменного количества идеального газа объем уменьшился в 2 раза, а температура увеличилась в 2 раза. Определите, как изменилось давление газа .

Вариант №3

1.    На рисунке представлены графики замкнутых циклов. Вычертите диаграммы замкнутых циклов в координатах pV и pT

2.    Автомобильные шины накачены до давления 200 кПа при температуре 7⁰С. После нескольких часов езды температура воздуха в шинах поднялась до 42⁰С. Каким стало давление воздуха в шинах?

3.    Баллон, содержащий V₁=0,02 м³ воздуха под давлением р₁=410⁵ Па, соединяют с баллоном емкостью V₂=0,06 м³, из которого выкачан воздух. Найти давление р, которое установилось в сосудах. Температура постоянная.

4.    Газ при 300К и постоянном давлении занимает объем 250 м3. Какой объем займет та же масса газа, если температура понизилась до 270К?

5.    Начертите графики изохорного процесса в координатах P и V; P и T;T и V.

6.    В сосуде вместимостью  V=0,83 м ³находится m=2 кг азота при давлении р= 2*10⁵ Па. Определите температуру Т азота.

Вариант №4

1.    Какой объём займёт газ при температуре 77⁰, если при температуре 27⁰С его объём был 6 л?

2.    На рисунке представлены графики замкнутых циклов. Вычертите диаграммы замкнутых циклов в координатах VT и pT

3.    Баллон, содержащий 12 л кислорода при давлении 1МПа, соединяют с пустым баллоном вместимостью 3 л. Определите, какое давление установится в сосудах в процессе изотермического расширения газа.

4.    В изохорном процессе давление идеального газа увеличивается на 50 кПа. На сколько кельвин увеличится при этом температура газа, если первоначальное давление было 200 кПа, а первоначальная температура 300 К? Масса газа остаётся неизменной.

5.    Температура V₁=2 моль кислорода ,находящегося в сосуде, равна Т₁=300 К. Определите температуру Т₂ водорода, находящегося в сосуде той же вместимости при той же давлении, взятого в количестве V₂=2 моль.

6.    Идеальный газ сначала изобарно расширили, а затем изотермически сжали до прежнего объема. Изобразите эти процессы в координатах P и V; P и T; V и T.

Вариант №5

1.       Газ при постоянном давлении и температуре 300К занимает объем 250 см³. Какой объем займет та же масса газа, если температура повысится до 324 К?

2.       Определите, какой будет абсолютная температура определенной массы идеального газа, если давление газа увеличить 4 раза, а объем уменьшить на 2 раза. Начальная температура газа равна 300 К.

3.       Идеальный газ сжимают изотермически так, что объём газа изменяется в 1,4 раза, а давление на 200 кПа. Определите начальное давление газа.

4.       На рисунке представлены графики замкнутых циклов. Вычертите диаграммы замкнутых циклов в координатах VT и pT

5.       Идеальный газ сначала нагревался при постоянном давлении, потом его давление уменьшалось при постоянном объеме, затем при постоянной температуре объем газа уменьшился до первоначального значения. Построить график в координатных осях V-T.

6.       В баллоне емкостью 0,1 м3 содержится углекислый газ при температуре 30°С и давлении 2 МПа. Какой объем будет занимать этот газ при нормальных условиях?

Вариант №6

ь При температуре 27⁰С давление газа в закрытом сосуде (с постоянным объемом) было 75 кПа. Каким будет давление при температуре –13⁰С?

ь На рисунке представлены графики замкнутых циклов. Вычертите диаграммы замкнутых циклов в координатах VT и pT

ь При изобарном нагревании газа его объём увеличился вдвое по сравнению с объёмом при 0⁰С. На сколько градусов нагрели газ?

ь Газ изотермически сжали от объёма 6 л до объёма 4 л, при этом изменение давления равно 200 кПа. Определите начальное давление газа.

ь При изобарном охлаждении на 210 К объем газа уменьшился втрое. Каковы начальная и конечная температуры газа? Начертить график процесса в координатах (V, T).

ь  Определить плотность углекислого газа при температуре 330 К и давлении 300кПа.

Практическая работа № 7 «Изучение первого закона термодинамики».

Цель:  обобщение и систематизация знаний в рамках темы «Основы термодинамики», отработка умений и навыков выполнять задания по образцу, способности применять знания при решении конкретных задач, научиться самостоятельно устанавливать причину (изменение температуры) и следствие (изменение внутренней энергии), закрепить умения и навыки решения задач на первое начало термодинамики

Порядок выполнения работы:

ü К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

ü Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

ü При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

ü Внимательно прочитать теоретическую часть и план решения задач.

ü Рассмотреть примеры решения задач.

ü Ответить на контрольные вопросы.

ü Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы:

Теоретическая часть

Внутренняя энергия макроскопического тела равна сумме кинетических энергий беспорядочного движения всех молекул (или атомов) относительно центра и потенциальных энергий взаимодействия всех молекул друг с другом (но не с молекулами других тел).

Внутренняя энергия идеального газа прямо пропорциональна его абсолютной температуре.

Она не зависит от объема и других макроскопических параметров системы. Изменение внутренней энергии данной массы идеального газа происходит только при изменении его температуры:

Работа газа равна:  

Эту работу можно выразить через изменение объема газа. Начальный объем , а конечный , поэтому , где  - изменение объема газа.

При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают. В процессе расширения газ передает энергию окружающим телам.

Работа А, совершаемая внешними телами над газом, отличается от работы газа А^’ только знаком; А=А^’, так как сила F, действующая на газ, направлена против силы F^’, а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:

Закон сохранения энергии: энергия в природе не возникает из ничего и не исчезает; количество энергии неизменно, она только переходит из одной формы в другую.

Основу термодинамики составляют два закона (или начала).

Первое начало термодинамики: изменение внутренней энергии тела равно разности сообщенного телу количества теплоты и произведенной над ним механической работы ΔU=Q+A,

ΔU – изменение внутренней энергии, [ΔU] = Дж,

А – работа внешних сил (или газа), [A] = Дж,

Q – количество теплоты, [Q]= Дж.

ü    - изменение внутренней энергии для одноатомного газа (He)

ü    - изменение внутренней энергии для двухатомного газа (O₂, H₂, N₂)

ü     - внутренняя энергия для трех и более атомного газа (CO₂)

ü   , , если работа газа, , если работа внешних сил.

ü Количество теплоты, необходимого (выделяемого) для нагревания (при охлаждении) тела

, где c-удельная теплоемкость вещества.

Количество теплоты при плавлении (кристаллизации): , где λ – удельная теплота плавления.

Количество теплоты при парообразовании (конденсации): , где L – удельная теплота парообразования.

Применение первого закона термодинамики к изопроцессам

 Изотермический процесс: Т=const изменяется объем (V) и давление (p). Поскольку температура не изменяется, не изменяется и его внутренняя энергия, т.е. ΔU=0, тогда Q=A^’.

 Изохорный процесс. Объем газа остается постоянным, меняются его давление и температура, значит А^’=0, тогда Q=ΔU.

 Изобарный процесс. Давление остается постоянным, изменяются его объем и температура. Q=ΔU+A^’.

 Адиабатный процесс - процесс, происходящий без теплообмена с окружающими телами. ΔU=A^’.

Рекомендации к решению задач по теме «Изучение первого закона термодинамики»

Задачи об изменении внутренней энергии тел можно разделить на группы:

В задачах первой группы рассматривают такие явления, где в изолированной системе при взаимодействии тел изменяется лишь их внутренняя энергия без совершения работы над внешней средой.

1. Установить у каких тел внутренняя энергия уменьшается, а у каких – возрастает.

2. Составить уравнение теплового баланса (ΔU = 0), при записи которого в выражении Q =cm(t₂ – t₁), для изменения внутренней энергии, нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака.

3. Полученное уравнение решить относительно искомой величины.

4. Решение проверить и оценить критически.

В задачах второй группы рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел.

Результат такого взаимодействия: изменение внутренней энергии одного тела вследствие совершенной им или над ним работы:

а) выяснить причину изменения внутренней энергии тела;

б)   правильно записать первый закон термодинамики

в)   решив полученное уравнение, найти искомую величину.

 Установить у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом.

 Записать уравнение Q = ΔU + A^’ для тела, у которого изменяется внутренняя энергия, учитывая знак перед А и КПД рассматриваемого процесса.

 Если работа совершается за счет уменьшения внутренней энергии одного из тел, то А^’= -ΔU, а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то А^’ = ΔU.

 Найти выражения для ΔU и A^’.

 Подставляя в исходное уравнение вместо ΔU и A^’ их выражения, получим окончательное соотношение для определения искомой величины.

 Полученное уравнение решить относительно искомой величины.

 Решение проверить и оценить критически.

ь При расчетах все числовые значения должны быть выражены в меж­дународной системе единиц (СИ).

ь При расчетах руководствуйтесь правилами действий с приближенны­ми числами.

Первый закон термодинамики и изопроцессы

Примеры решения задач

1.    При изотермическом расширении идеальный газ совершает работу А=20Дж. Какое количество теплоты сообщено газу?

2.    Водород массой 4г, занимая первоначальный объем V₁=0,1м³, расширяется до объема V₂=1м³. Определите: 1) А₁-работу газа при изобарном процессе, 2) А₂ – работу газа при изотермическом процессе. Начальная температура газа Т₁=300К.

3.    Определите изменение внутренней энергии ΔU льда массой m=5 кг в процессе его таяния (плавления) при нормальных условиях.

Контрольные вопросы для самопроверки

1.    Что называется термодинамической системой?

2.     Какая энергия называется внутренней? Запишите формулу для вычисления внутренней энергии.

3.    Сформулируйте первый закон термодинамики. Дайте математическую запись первого закона термодинамики.

4.    Запишите первый закон термодинамики для изотермического процесса.

5.     Запишите первый закон термодинамики для изохорного процесса.

6.     Запишите первый закон термодинамики для изобарного процесса.

7.    Какой процесс называется адиабатным. Запишите первый закон термодинамики для адиабатного процесса

Индивидуальные задания к практической работе № 7

Вариант №1

1.    Для изобарного нагревания 800 моль газа на 500 К ему сообщили 9,4 МДж теплоты. Определите работу газа и изменение его внутренней энергии.

2.    Какова внутренняя энергия 20 моль одноатомного газа при 37С?

3.    При адиабатическом расширении температура гелия понизилась на 4⁰С, а совершённая им работа равна 498 Дж. Найти массу газа в граммах.

4.    Азот массой 280 г был нагрет при постоянном давлении на 100 К. Определите работу, которую совершает газ при расширении.

Вариант №2

1.     Какова внутренняя энергия 10 моль одноатомного газа при 27⁰С?

2.     Сколько моль одноатомного газа нагрели на 10 К, если количество подведённой теплоты равно 249 Дж? Процесс изохорный.

3.     В ходе изотермического расширения к одному молю идеального одноатомного газа подведено 43 Дж теплоты. Определить работу, совершённую газом.

4.     Температура азота массой 1,4 кг в результате адиабатного расширения упала на 20⁰С. Какую работу совершил газ при расширении?

Вариант №3

1.    При изобарном расширении газа была совершена работа 600 Дж. На сколько изменился объём газа, если давление газа было ?

2.    Как и на сколько изменилась внутренняя энергия газа, если при его адиабатном сжатии над ним была совершена работа 200 Дж.

3.    Сколько моль идеального одноатомного газа можно нагреть на 5 К, подведя к нему 41,5 Дж теплоты? Давление газа постоянно.

4.    При адиабатном расширении 128г кислорода О₂, находящегося при нормальных условиях (p₀=1,01×10⁵Па, T₁=273К), его температура уменьшилась в 2 раза. Найдите изменение внутренней энергии, работу расширения газа.

Вариант №4

1.    В процессе изобарного расширения газа была совершена работа, равная 400Дж. При каком давлении совершался процесс, если объём газа изменился с 0,3 м³ до 600 л?

2.    Чему равна внутренняя энергия 5 моль одноатомного идеального газа при температуре 47°С?

3.    В ходе изотермического расширения к одному молю идеального одноатомного газа подведено 43 Дж теплоты. Определить работу, совершённую газом.

4.    Найти начальную температуру 560 г азота, если при изобарном нагревании его до 97⁰С газ совершил работу 16,6 кДж. Молярная масса азота 28г/моль.

Вариант №5

1.    Если идеальный газ получил количество теплоты 100 Дж, и при этом внутренняя энергия газа увеличилась на 100 Дж, то газ в этом процессе какую работу совершил?

2.    Баллон вместимостью 20 л, содержащий гелий при температуре 27⁰С и давлении 300 кПа, охладили на 50 К. Найдите изменение внутренней энергии газа.

3.    В цилиндре под поршнем находится 1,25 кг воздуха. Для его нагревания на 4 ⁰С при постоянном давлении было затрачено 5 кДж теплоты. Определите изменение внутренней энергии воздуха. Молярная масса воздуха 0,029кг/моль.

4.    К некоторому количеству газа подвели 250 Дж тепла. Газ расширился при постоянном давлении 100 кПа на 0,001 м³. На сколько джоулей изменилась его внутренняя энергия?

Вариант №6

1.    Расширяясь при постоянном давлении, газ совершил работу 20 кДж. Чему было равно давление в газе, если объём газа при расширении увеличился на 0,2м³

2.    Идеальный газ получил количество теплоты 300 Дж и совершил работу 100 Дж. При этом как изменилась его внутренняя энергия?

3.    Газ, занимавший объём 20 л при нормальных условиях (p₀=1,01×10⁵Па, T₁=273К), был изобарно нагрет до 80⁰С. Определить работу расширения газа.

4.    Одноатомный идеальный газ массой 20 г при расширении без теплообмена совершил работу 249Дж. На сколько градусов изменилась температура газа?

Практическая работа № 8 «КПД тепловых двигателей. Модели тепловых двигателей».

Цель:  научиться решать задачи по образцу, анализировать задачу, обобщить и систематизировать знания по теме «Тепловые двигатели»

Порядок выполнения работы:

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы:

Теоретическая часть

Тепловой двигатель представляет собой устройство, превращающее внутреннюю энергию топлива в механическую.

Механическая работа в двигателе совершается при расширении рабочего вещества, перемещающего поршень в цилиндре. Для циклической работы двигателя необходимо возвращение поршня в первоначальное положение, т.е. сжатие рабочего вещества. Полная механическая работа А цикла складывается из работы расширения газа А_расш и работы А_сж, совершаемой силами давления газа при его сжатии. Так как при сжатии , то , поэтому .

Для получения положительной работы (A>0) давление газа при сжатии р_сж должно быть меньше его давления при расширении р_расш. Поэтому после расширения, при сжатии, газ должен быть охлаждён, т.е. приведён в контакт с холодильником – телом, имеющим более низкую температуру.

Необходимое условие для циклического совершения механической работы в тепловом двигателе – наличие нагревателя и холодильника.

Замкнутый процесс (цикл) – совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние. Эффективность преобразования внутренней энергии газа в механическую работу, совершаемую за цикл, оценивают с помощью коэффициента полезного действия.

Коэффициент полезного действия (КПД) – отношение работы, совершаемой двигателем за цикл, к количеству теплоты Q₁, полученному от нагревателя:

При замкнутом цикле количество теплоты Q₂ отдаётся холодильнику. Поэтому работа, совершаемая двигателем за цикл, не может быть больше работы .

КПД теплового двигателя всегда меньше единицы:

В 1828 г. Сади Карно предложил использовать для теплового двигателя цикл, состоящий из двух адиабатных и двух изотермических процессов, имеющий максимальный КПД:

Количество теплоты Q₁ подводится при изотермическом расширении 1-2 при температуре Т₁. При адиабатном расширении 2-3 газ охлаждается до температуры Т₂. Количество теплоты Q₂ отводится при изотермическом сжатии 3-4.

Тепловой двигатель - главный двигатель современной энергетики

Схема

 

 

 

Рабочее тело

                                                                                                            A^/=Q₁-Q₂

 

 

 

 

Коэффициент полезного действия теплового двигателя

                 

 

Цикл Карно

(для машины Карно)

 

1-2 - система заимствует тепло Q₁от нагревателя и производит работу против внешнего давления

2-3 - система совершает работу против внешнего давления и охлаждается

3-4 - над системой производится работа, и она отдаёт холодильнику количество теплоты Q₂

4-1 - над системой совершается работа и она нагревается

Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т1 и Т2 нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего вещества.

Примеры решения задач

1.    Температура нагревателя идеальной тепловой машины Т₁ =500 К, температура холодильника Т₂=300 К. Определите КПД тепловой машины η и теплоту Q₁, получаемую от нагревателя, если за один цикл машина совершает работу А=400Дж.

2.    Температура нагревателя идеальной тепловой машины 117⁰С, а холодильника 27⁰С. Количество теплоты, получаемое машиной от нагревателя за 1с, равно 60кДж. Вычислить КПД машины, количество теплоты, отдаваемое холодильнику в 1с и мощность машины.

3.    Идеальная холодильная машина, работающая по обратному циклу Карно, совершает за один цикл работу А=37 кДж. При этом она берет тепло от тела с температурой t₂= -10°C и передает тепло телу с температурой t₁=17°C. Найти КПД η цикла, количество теплоты Q₂, отнятое у холодного тела за один цикл, и количество теплоты Q₁, переданное более горячему телу за один цикл.

4.    Идеальная холодильная машина, работающая по обратному циклу Карно, передает тепло от холодильника с водой при температуре t₂=0°C кипятильнику с водой при температуре t₁=100°C. Какую массу m₂ воды нужно заморозить в холодильнике, чтобы превратить в пар массу m₁=1 кг воды в кипятильнике?

Контрольные вопросы для самопроверки

1.    Дайте определение теплового двигателя.

2.    Физический принцип работы теплового двигателя:

?   T1 – это ___________________;	?     ?             ?     ?
Т2 – это ___________________;
Q1 – это ___________________;
Q2 – это ___________________
A=Q1-Q2 – это _________________________________ ______________________________________________

3.    Что называется КПД теплового двигателя? Запишите формулы для вычисления КПД теплового двигателя и КПД теплового двигателя, работающего по циклу Карно.

Индивидуальные задания к практической работе № 8

Вариант №1

1.    КПД идеального теплового двигателя 40%. Газ получил от нагревателя 5кДж теплоты. Какое количество теплоты отдано холодильнику?

2.    Температура холодильника идеальной тепловой машины, работающей по циклу Карно и имеющей КПД 30%, 20 ⁰С. Какова температура нагревателя машины?

3.    Определить КПД тепловой машины, если количество теплоты, полученное от нагревателя, в 6 раз превышает количество теплоты, отданное холодильнику. Ответ дать в процентах.

4.    В двигателе внутреннего сгорания было израсходовано 0,5 кг горючего, теплота сгорания которого 46·106 Дж/кг при этом двигатель совершил 7·10⁶ Дж полезной работы. Каков его КПД?

5.    Какую среднюю мощность развивает двигатель мотоцикла, если при скорости движения 108 км/ч расход бензина составляет 3,7 л на 100 км пути, а КПД двигателя 25%?

Вариант №2

1-   В идеальной тепловой машине Карно, КПД которой 30%, газ получил от нагревателя 10 кДж теплоты. Какое количество теплоты машина отдала холодильнику?

2-   Чему равен максимальный КПД теплового двигателя, если температура нагревателя 455⁰С, а холодильника 273⁰С?

3-   Тепловая машина с КПД, равным 20%, совершает в каждом цикле работу А = 100 Дж. Сколько теплоты Q₁ получает при этом машина от нагревателя и сколько Q₂ отдает холодильнику?

4-   Какое количество воды можно вскипятить, затратив 800 г дров, если КПД кипятильника 30%, начальная температура воды 10 ⁰С?

5-   Междугородний автобус прошёл путь 80 км за 1 ч. Двигатель при этом развивал среднюю мощность 70 кВт при КПД, равном 25%. Сколько дизельного топлива, плотность которого 800 кг/м³, сэкономил водитель на рейсе, если норма расхода 40 л на 100 км пути?

Вариант №3

1.    Температура нагревателя идеальной тепловой машины 117⁰С, а холодильника 27⁰С. Найти КПД тепловой идеальной машины.

2.    В идеальной тепловой машине Карно газ получил от нагревателя 10 кДж теплоты. Какое количество теплоты машина отдала холодильнику? КПД тепловой машины 40%.

3.    Температура нагревателя идеальной тепловой машины 1170С, а холодильника 270С. Количество теплоты, получаемое машиной от нагревателя, равно 60 кДж. Вычислить КПД машины и количество теплоты, отдаваемое холодильнику

4.    Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q2 = 13,4 кДж. Найдите КПД цикла.

5.    Определить мощность электрического чайника, если в нём за 20 мин нагревается 1,5 кг воды от 20 до 10⁰⁰С при КПД равном 0,6. Удельная теплоёмкость воды равна.

Вариант № 4

1.    Определите температуру нагревателя идеальной тепловой машины, если температура холодильника 280 К, а КПД равен 30%.

2.    КПД идеальной тепловой машины 40%. За цикл она получает от нагревателя количество теплоты 1200Дж. Какую полезную работу она при этом совершает??

3.    Температура нагревателя идеальной тепловой машины 527⁰С, а температура холодильника 127⁰С. Определите количество теплоты, полученное машиной от нагревателя, если она совершила работу 700 Дж.

4.    Тепловая машина работает по циклу Карно, при этом 80% теплоты, полученной от нагревателя, передается холодильнику. За один цикл рабочее тело получает от нагревателя 6,3 Дж теплоты. Найдите работу и КПД цикла.

5.    Определить массу расходуемой нефти в тепловозе на 1кВ·ч, если КПД тепловоза 30%. Удельная теплота сгорания нефти 50 МДж/кг.

Вариант № 5

1.    Тепловая машина за цикл совершает работу 100 Дж и отдаёт холодильнику 400 Дж теплоты. Определите КПД тепловой машины и количество полученной от нагревателя теплоты.

2.    Идеальная тепловая машина, работающая по циклу Карно, получает от нагревателя 40кДж энергии. Какую работу она при этом произведёт, если температуры её нагревателя и холодильника соответственно равны 150 и 25⁰С?

3.    Температура холодильника тепловой машины 400 К, температура нагревателя на 200 К больше, чем у холодильника. Найти максимально возможный КПД машины.

4.    Вода массой 175 г подогревается на спиртовке. Пока вода нагрелась от t1=15 до t2=75 градусов Цельсия, масса спиртовки уменьшилась с 163 до 157 г Вычислите КПД установки.

5.    Тепловая машина работает с КПД 60%. Во сколько раз теплота, полученная при изотермическом расширении рабочего газа, больше теплоты, отданной при изотермическом сжатии

Вариант № 6

1.    Определите температуру нагревателя идеальной тепловой машины, если температура холодильника 280 К, а КПД равен 30%.

2.    В идеальной тепловой машине за счёт каждого килоджоуля энергии, получаемой от нагревателя, совершается работа 300 Дж. Определить КПД машины.

3.    В одном цикле работы теплового двигателя его рабочее тело получает от нагревателя количество теплоты 1,5 МДж. Какое количество теплоты оно отдаёт за цикл холодильнику, если КПД двигателя 0,2? Чему равна работа, совершаемая этим двигателем за один цикл?

4.    Старый двигатель совершил работу 220,8 МДж, при этом израсходовав 16 килограмм бензина. Вычислите КПД двигателя.

5.    Механическая лопата, приводимая в движение мотором мощностью 5 кВт, поднимает 180 т песку на высоту 6м в течение часа. Каков КПД установки?

Раздел 4. Электродинамика

Обозначение электрических и магнитных величин

 

 

Электрические и магнитные величины и их единицы в СИ

Наименование величины	Наименование единицы	Обозначение единицы
Сила электрического тока	Ампер	А
Электрический заряд	Кулон	Кл
Напряжённость электрического поля	Вольт на метр	В/м
Электрическое напряжение; электрический потенциал; разность электрических потенциалов; электродвижущая сила	Вольт	В
Электрическая ёмкость	Фарад	Ф
Магнитная индукция	Тесла	Тл
Магнитный поток	Вебер	Вб
Индуктивность	Генри	Гн
Электрическое сопротивление	Ом	Ом
Удельное электрическое сопротивление	Ом-метр

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Физические постоянные

 

Постоянная	Обозна­чение	Значение
Заряд электрона	е
Масса покоя электрона	те
Электрическая постоянная	ε0
Магнитная постоянная	µ0
Постоянная Фарадея	F	96485,31 Кл/моль

 

 

 

 

 

 

 

Тема 4.1. Электрическое поле

Практическая работа № 9.  «Расчет основных электростатических величин».

Цель: научиться решать задачи с использованием основного закона электростатики.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы:

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Электрический заряд - величина, характеризующая способность частицы вещества к электрическому взаимодействию.

В природе существует два рода электрических зарядов, условно названные положительными и отрицательными. Носителями электрических зарядов являются элементарные частицы, в частности частицы, входящие в состав атомов, - электрон (отрицательный заряд) и протон (положительный заряд).

Многочисленные опыты доказывают, что:

1.    при взаимодействии одноименные заряды отталкиваются, разноименные - притягиваются;

2.    существует наименьший возможный в природе заряд, называемый элементарным, который может быть  отрицательным (электрон е = -1,6×10^-19Кл) и положительным (протон q = +1,6×10^-19Кл);

3.    электрический заряд дискретен, это значит, что любой заряд, больший заряда электрона, кратен элементарному заряду;

4.    заряд инвариантен, то есть не зависит от скорости движения заряженной частицы, а значит, и от выбора системы отсчета.

Закон сохранения электрического заряда: в замкнутой системе алгебраическая сумма положительных и отрицательных зарядов остается неизменной при любых процессах в этой системе:

Сила взаимодействия между двумя покоящимися точечными зарядами определяется законом Кулона, установленным опытным путем.

Закон Кулона: сила взаимодействия между двумя неподвижными точечными электрическими  зарядами прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними, направлена вдоль прямой, соединяющей эти ряды, и зависит от среды, в которой заряды взаимодействуют: , где ε - относительная диэлектрическая проницаемость среды, , .

Закон Кулона справедлив:

1.    для точечных электрических зарядов;

2.    для тел, имеющих сферическую форму, на любом расстоянии между их центрами, если объемная или поверхностная плотность электрического заряда каждого из тел постоянна;

3.    при взаимодействии точечного и сферического электрических зарядов.

Если на данный электрический заряд q действует несколько точечных зарядов q₁, q₂,..., q_n, то сила  по принципу суперпозиции равна векторной сумме сил, действующих на заряд q со стороны каждого заряда в отдельности: . Так как электрический заряд дискретен, то , где е=1,6×10^-19Кл; N=1,2,3…

Поверхностная плотность электрического заряда σ – величина, равная отношению величины  электрического заряда к площади его распределения: , где q – величина электрического заряда, S  – площадь заряженной поверхности.

Электростатическое поле -

вид материи, осуществляющий взаимодействие между электрически заряженными частицами.

Напряженность поля

(силовая характеристика эл. поля)

 

                                                                                                  

- отношение силы, с которой поле действует на точечный заряд, к этому заряду.

                                          
                                               величина векторная

Направление вектора совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, де­йствующей на отрицательный заряд.

Модуль напряженности поля точечного заряда

 

Вектор напряженности поля в заданной точке

 

 

 

Принцип суперпозиции полей

Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых , ,  и т.д., то результирующая напряженность поля в этой точке равна:

 

Электрическое поле. Теорема Гаусса.

 Линии напряжённости

 

Аналогия между электрическим полем и полем тяготения

 

 

 Электрические заряды могут быть как положительными, так и отрицательными, а гравитационные массы всегда положительны

Потенциал и разность потенциалов

 Потенциал - энергетическая характеристика поля.

W_P~q - для любого электростатического поля

Потенциалом электростатического поля называют отношение потенциальной энергии заряда в поле к этому заряду.

скаляр

                               

 

Потенциал поля в произвольной точке определяется как алгебраическая сумма потенциалов, создаваемых отдельными точечными зарядами

Не зависит от выбора нулевого уровня отсчета

Разность потенциалов (напряжение)

 

 

Эквипотенциальные поверхности - поверхности равного потенциала.

Две характеристики электростатического поля

 

 

Связь между характеристиками (для однородного поля)

              1   d      2

 

Напряженность электрического поля направлена в сторону убывания потенциала

 

Некоторые формулы электростатики

Некоторые формулы электростатики

 

План решения задач

Задачи по электродинамике условно можно разделить на следующие типы:

I тип. Задачи о точечных зарядах и системах, сводящихся к ним.

Решение таких задач основано на применении закона Кулона и его следствий с учетом законов механики. Рекомендуемая последовательность действий:

1. Расставить силы, действующие на точечный заряд, помещенный в электрическое поле, и записать для него условия равновесия или уравнение динамики материальной точки.

2. Выразить силы электрического взаимодействия через заряды и характеристики поля и подставить в исходное уравнение.

3. Если при взаимодействии происходит перераспределение электрических зарядов, то следует добавить уравнение закона сохранения электрического заряда.

4. Полученную систему уравнений решить относительно неизвестной величины.

II тип. Задачи на расчет полей, созданных точечными зарядами, решаются с учетом принципа суперпозиции полей.

Особое внимание следует обращать на векторный характер напряженности и помнить, что знак перед потенциалом определяется знаком заряда, создающего поле.

III тип. Задачи о заряженных телах, размерами которых нельзя пренебречь.

Если речь идет о плоских конденсаторах, то:

1.     следует установить тип соединения: выяснить, какие конденсаторы соединены последовательно, какие – параллельно:

2.     составить уравнения, связывающие заряды и напряжение на конденсаторах. Следует учесть, что, если плоский конденсатор подключить к источнику питания, зарядить его, а затем отключить, то при изменении емкости конденсатора вследствие раздвижения (сближения) пластин, внесения (удаления) диэлектрика, заряд на конденсаторе не меняется. Если конденсатор подключен к источнику постоянного напряжения, то при всех указанных выше изменениях емкости, напряжение между обкладками конденсатора остается неизменным. В случае если между обкладками конденсатора вставляют (вынимают) незаряженную металлическую пластину, не замыкающую конденсатор, область диэлектрика между обкладками уменьшается (увеличивается) на объем этой пластины, как если бы мы сближали (раздвигали) обкладки конденсатора;

3.     в плоском конденсаторе одну пластину можно рассматривать как тело с зарядом q, помещенное в однородное электрическое поле с некоторой напряженностью, созданное другой пластиной.

IV тип. Смешанные задачи, представляющие собой произвольную комбинацию всех типов задач с применением законов различных разделов физики.

При решении задач любого типа следует учитывать:

1.     напряженность электрического поля внутри заряженного проводника равна нулю. Поверхность проводника является эквипотенциальной. Потенциал во всех точках внутри проводника равен потенциалу на его поверхности;

2.     положительные электрические заряды движутся в электрическом поле из области с большим потенциалом в область с меньшим потенциалом. Отрицательные заряды перемещаются в противоположном направлении;

3.     потенциал земли и всех тел, соединенных проводником с землей, принимается равным нулю. 

Рекомендации к решению задач по теме «Электродинамика»

1.    Прочитайте условие, уточните термины и формулировки, содержа­щиеся в тексте.

2.    Сделайте краткую запись условия задачи, выразите заданные величины в единицах СИ.

3.    Решение задач о точечных зарядах основано на применении законов механики с учётом закона Кулона и вытекаю­щих из них следствий.        

4.    Следует помнить, что соотношение F=qE справедливо не только для точечного заряда, но и для заряженных протяжённых тел (сфера, плоскость, нить).

5.    Особое внимание следует обратить на векторный характер напря­жённости Е и помнить, что знак перед потенциалом φ определяется знаком заряда, создающего поле.

6.    Полезно иметь в виду, что положительные заряды, представленные самим себе, движутся в электрическом поле от точек с большим потенциалом к точкам, где потенциал меньше.

7.    При решении задач помните, что потенциал, разность потенциалов и работа по перемещению заряда в электрическом поле могут прини­мать как положительные, так и отрицательные значения.

8.    Потенциал Земли и всех тел, соединённых проводником с Землёй, принимается равным нулю.

9.    Составив необходимое количество уравнений, нужно получить решение в общем виде.

10. Получив решение в общем виде, проверьте правильную ли оно имеет размерность.

11. При расчётах руководствуйтесь правилами действий с приближён­ными числами.

Примеры решения задач

1.   Если расстояние между двумя точечными зарядами уменьшить на 50 см, то сила взаимодействия увеличится в 2 раза. Заряды находятся на расстоянии... (в м).

Дано:	СИ:	Решение
Δr=50 см F2=2F1	0,5 м	Сила кулоновского взаимодействия между зарядами, находящимися на расстоянии r: . При уменьшении расстояния на Δr (r2= r-Δr): ,  или . Извлекая квадратный корень из левой и правой части, получаем: Ответ: 1,75 м
Найти: r-?

2.   Модуль вектора напряженности поля на расстоянии 5 м от заряда равен 150 В/м. Потенциал электрического поля на расстоянии 10 м от этого заряда равен...(в В).

Дано:	Решение
r1=5м r2=10м E1=150В/м	Используя выражения для модуля напряженности и потенциала электростатического поля,  создаваемого точечным зарядом, получаем: , . Разделив первое выражение на второе, получим: . Отсюда, подставляя числовые данные в полученную формулу: .                                Ответ: 375 В
Найти: φ2-?

3.   Шарик массой т=1г с зарядом q=5•10^-8 Кл переместился из точки А, потенциал которой φ_А=600В, в точку В, потенциал которой равен нулю. Чему была равна его скорость в точке А, если в точке В она стала равна 0,4 м/с?

Дано:	СИ:	Решение
m=1г φА=600В φВ=0 v2=0,4м/с		Согласно закону сохранения энергии работа сил электрического поля равна изменению кинетической энергии шарика  или ;  откуда . Проверим правильность вывода формулы: . Подставим в формулу числовые значения:  . Ответ: 0,32 м/с
Найти: v1 - ?

4. Найдите силу, действующую на заряд q₂=-l ×10^-6Кл, если заряды q₁=l×10^-7Кл и q₃=2×10^-7Кл расположены в воздухе, а расстояние АВ=ВС=10 см.

Дано:	СИ:	Решение
АВ=ВС=10см q2=Кл q3=Кл q1=Кл	0,1м	На заряд q2 действуют заряды q1 и q3 с силами, вектор которых  и . Равнодействующая этих сил   направлена в сторону большей силы  и по модулю равна разности их модулей. По закону Кулона находим модули сил F1 и F3:  и    Подставим в формулу числовые значения:  ,  . Равнодействующая ,   Ответ: 0,1 Н
Найти: F - ?

5.   Какой заряд появится у каждого из трёх одинаковых шариков после того, как их приведут в соприкосновение и раздвинут, если начальные заряды шариков были равны соответственно 6 нКл, -4 нКл и 7 нКл?

Дано:	СИ:	Решение
q1=6нКл q2=-4нКл q3=7нКл	Кл	По закону сохранения электрического заряда  Так как шарики по условию одинаковые, то при соприкосновении и дальнейшем раздвижении, они получили одинаковый заряд, который равен среднему арифметическому значению зарядов: . Подставим в формулу числовые значения:   Ответ: 3нКл
	Кл
	Кл
Найти:  q- ?

2.    Два одинаковых металлических шарика с зарядами -120мкКл и +40мкКл привели в соприкосновение и развели на расстояние 10см. Сила взаимодействия шариков равна... (в кН).

Дано:	СИ:	Решение
q1=-120мкКл q2=40мкКл r1= 10 см	Кл	Шарики одинаковые, следовательно, они имеют одинаковые емкости и после соприкосновения заряды на шариках окажутся равными. По закону сохранения электрического заряда  При дальнейшем раздвижении, они получили одинаковый заряд, который равен среднему арифметическому значению зарядов: . Подставим в формулу числовые значения: . Силу взаимодействия шариков определим по закону Кулона:  . Ответ: 1440Н
	Кл
	0,1 м
Найти:  F - ?

3.    В однородном электрическом поле с напряженностью 200В/м находится в равновесии пылинка с зарядом 10^-7 Кл. Масса пылинки в граммах равна...

Дано:	Решение
E=200 В/м q=10-7 Кл	На заряженную пылинку в однородном электрическом поле действуют две силы: сила тяжести  Fтяж  и сила F со стороны  электрического  поля:  и . Пылинка будет находиться в равновесии, если эти силы равны по модулю и противоположны по направлению. . Подставим в формулу числовые значения: . Ответ: 0,002г
Найти:  m - ?

4.    Потенциал электрического поля на расстоянии 10 м от уединенного положительного точечного заряда равен 50В.  Модуль вектора напряженности поля на расстоянии 5 м от заряда ранен...(в В/м)

Дано:	Решение
r1=10 м r2= 5 м φ=50 В	Потенциал электрического поля, создаваемого точечным зарядом на расстоянии r1 от заряда:  (1). Напряженность электрического поля, создаваемого точечным зарядом на расстоянии r2 от заряда:  (2). Разделим уравнение (2) на уравнение (1): . Подставим в формулу числовые значения: /м. Ответ: 20 В/м
Найти:  m - ?

5.    Определите ускорение, которое сообщает электрону электрическое поле напряжённостью 2кН/Кл. Сравните это ускорение с ускорением свободного падения. Удельный заряд электрона  Кл/кг

Дано:	СИ:	Решение
E=2кН/Кл Кл/кг	Н/Кл	Электрон, попав в электрическое поле, получает ускорение, которое можно вычислить из равенства сил:  (1). Это соотношение следует из третьего закона Ньютона (см рис). Кулоновскую силу можно вычислить из определения напряжённости:  (2), динамическую силу – из второго закона Ньютона:  (3). В проекциях формулу (1) с учетом (2) и (3) запишем:. Отсюда , учитывая, что , подставим в полученную формулу числовые значения:  . Полученное ускорение электрона превышает ускорение свободного падения в раз.           Ответ: ; .
Найти: a- ?

Контрольные вопросы для самопроверки

1.   Что называется электрическим зарядом? Чем определяется электрический заряд тела?

2.   В чем состоит закон сохранения заряда?

3.   В чем сходство и различие закона всемирного тяготения и закона Кулона?

4.   Что такое электрическая постоянная и чему она равна в СИ?

5.   Какие поля называются электростатическими?

6.   Что такое напряженность электрического поля?

7.   В чем состоит принцип суперпозиции электрических полей?

8.   Чему равна напряженность поля точечного заряда?

9.   Дайте определение потенциала электростатического поля.  Какова связь между потенциалом и напряженностью электростатического поля?

Индивидуальные задания к практической работе № 9

Вариант №1

1)    Два одинаковых металлических шарика, заряд, одного из которых первоначально равен -5мкКл, соприкасаются и затем разводят снова. Заряд одного из шариков после соприкосновения равен 3 мкКл. Определить заряд второго шарика до соприкосновения.

2)    Какая сила действует на заряд 12 нКл, помещённый в точку, в которой напряжённость электрического поля равна 2 кВ/м?

3)    Определите модуль силы взаимодействия электрических зарядов q₁=0,66×10^-7Кл и q₂= 1,1×10^{- 7}Кл в воде на расстоянии r₁= 3,3см. На каком расстоянии их следует поместить в вакууме, чтобы сила взаимодействия осталась прежней?

4)    В некоторой точке поля на заряд 10-7Кл действует сила 4·10^-3 Н. Найти напряженность поля в этой точке и определить заряд, создающий поле, если точка удалена от него на 0,3 м.

5)    Два положительных заряда q и 2q находятся на расстоянии 10 мм. Заряды взаимодействуют с силой 7,2*10^-9 Н. какова величина зарядов?

Вариант №2

1.    При сообщении металлическому шару, находящемуся в воздухе, заряда 10^-9Кл его потенциал оказался равным 18 кВ. Определить радиус шара.

2.    Два одинаковых точечных заряда взаимодействуют в вакууме с силой 0,1 Н. Расстояние между зарядами равно 6 м. Найдите модуль этих зарядов.

3.    Одинаковые металлические шарики, заряженные одноимённо зарядами q и 4q, находятся на расстоянии 0,5 м друг от друга. Шарики привели в соприкосновение. На какое расстояние x надо их развести, чтобы сила взаимодействия осталась прежней?

4.    Пылинка массой 10^-8 г, имеющая заряд 1,6·10^-17 Кл, находится в однородном электрическом поле. Определите напряженность поля, если сила тяжести пылинки уравновешивается действием на нее электрического поля.

5.    Какова разность потенциалов двух точек электрического поля, если при перемещении заряда 2·10^-19 Кл между этими точками полем совершена работа 8·10^-9 Дж?

Вариант №3

1.     На расстоянии 9 см от центра металлического шара с зарядом 2 нКл и радиусом 3 см находится точечный заряд -6 нКл. Чему равен потенциал шара?

2.    В некоторой точке поля на заряд 0,1 мКл действует сила 4 мН. Найдите напряженность поля в этой точке.

3.    Два электрических заряда, один из которых в три раза больше другого, находясь в вакууме на расстоянии r₁= 30 см, взаимодействуют с силой, модуль которой F₁= 30 Н. Определите величины этих электрических зарядов. На каком расстоянии в воде они будут взаимодействовать с силой, в три раза большей?

4.              В однородном электрическом поле электрон движется с ускорением 3,2 ·10¹³ м/с². Определить напряженность поля, если масса электрона равна 9,1·10^-31кг.

5.   Конденсатору емкостью 10 мкФ сообщили заряд 4 мк Кл. Какова энергия заряженного конденсатора?

Вариант № 4

Заряд 5 нКл находится в электрическом поле с напряженностью 2кН/Кл. С какой силой поле действует на заряд?

Найдите потенциал шара радиусом 10см, если на расстоянии 10 м от его поверхности потенциал электрического поля равен 20В.

Проводящий шарик, несущий электрический заряду q₁=1,8×10^{- 8}Кл, привели в соприкосновение с такими же двумя шариками, один из  которых имел электрический заряд q₂= -3,0×10^-8Кл, а другой был не  заряжен. Как распределятся электрические заряды между шариками? С какой по модулю силой будут взаимодействовать два из них в вакууме на расстоянии r = 5,0 см один от другого?

Металлическому шару радиусов 3 см сообщили заряд 16 нКл. Найти потенциал поля на поверхности шара.

Заряды и 2·10^-12 Кл находятся на расстоянии 30 см друг от друга. Найти потенциал точки, которая находится на линии, соединяющей заряды, в 10 см от первого и 20 см от второго зарядов.

Вариант №5

1)    С какой силой отталкиваются два электрона, находящиеся в вакууме друг от друга на расстоянии 2×10^-8 см?

2)    Два одинаковых электрометра имеют электрические заряды: -30 мкКл и +10 мКл соответственно. Каким будет заряд у каждого электрометра, если их соединить металлическим стержнем на изолирующей ручке?

3)    Определите напряжённость электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды q₁=10нКл   и q₂=-8нКл и находящейся на расстоянии r=8см от отрицательного заряда. Расстояние между зарядами l=20см.

4)    Какую работу нужно совершить, чтобы переместить заряд 5* Кл между двумя точками электрического поля с разностью потенциалов 1600 В?

5)    На каком расстоянии от заряда Кл напряженность поля равна 300 Н/Кл?

Вариант №6

На каком расстоянии от точечного заряда +10^-8 Кл, находящегося в воздухе, напряжённость электрического поля окажется равной 10^-9 Н/Кл?

Два отрицательных точечных заряда q₁=-9нКл и q₂=-36нКл расположены на расстоянии l=3м друг от друга. Когда в некоторой точке поместили третий заряд q₃, то все заряды оказались в равновесии. Найдите заряд q₃.

В однородном электрическом поле электрон движется с ускорением, равным 32 м/с². Определите напряженность поля, если масса электрона равна 9,1×10^-31кг.

Какую работу совершает поле при перемещении заряда 20 нКл из точки с потенциалом 700 В а точку с потенциалом 200 В?

Расстояние между двумя точечными зарядами +6·10 ^-12 и – 4нКл равно 12 см. Найти напряженность поля в средней точке между зарядами.

Практическая работа № 10. «Проводники и диэлектрики в электрическом поле»

Цель: научиться решать задачи по образцу, анализировать задачу, обобщить и систематизировать знания по теме «Проводники и диэлектрики в электрическом поле. Конденсаторы», сформировать умения и навыки  нахождения электрической ёмкости, её выражение из формулы.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы:

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. К проводникам относят металлы, растворы солей, щелочей, кислот, плазму, тело человека и т.д.

В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах - ионы, в плазме - и электроны, и ионы.

Заряженные частицы, способные свободно перемещаться в проводнике под влиянием электрического поля, называются свободными зарядами.

Наличие в проводнике свободных зарядов приводит к тому, что даже при наличии внешнего электрического поля внутри проводника напряжённость поля равна нулю. Если бы напряжённость электрического поля была бы отлична от нуля, то поле приводило бы свободные заряды в упорядоченное движение, т.е. в проводнике существовал бы электрический ток. Для электростатических явлений поле внутри проводника равно нулю.

Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.

Свойства заряженного проводника во внешнем электрическом поле:

1)      Электростатического поля внутри проводника нет.

2)      Силовые линии электростатического поля вне проводника перпендикулярны его поверхности.

3)      Весь статический заряд проводника сосредоточен на его поверхности

 

 

 

 

Проводники в электростатическом поле

(металлы)

Диэлектрики - это вещества, у которых электроны внешних оболочек атома не могут свободно перемещаться по объему диэлектрика под действием сколь угодно малого внешнего поля.   

К диэлектрикам относят газы, некоторые жидкости (дистиллированную воду, бензол, масла и др.) и твёрдые тела (стекло, фарфор, слюда и др.)

У диэлектрика (изолятора) электрические заряды, а точнее, электрически заряженные частицы - электроны и ядра в нейтральных атомах связаны друг с другом. Они не могут, подобно свободным зарядам проводника, перемещаться под действием электрического поля по всему объёму тела. Свободные заряды в диэлектрике отсутствуют, поэтому диэлектрик практически не проводит электрический ток.

Диэлектрики в электростатическом поле

Электрическим диполем называют систему двух равных по модулю, но противоположных по знаку зарядов, находящихся на некотором расстоянии друг от друга

Диэлектрики в электростатическом поле

1. Внутри диэлектрика средний связанный электрический заряд равен 0.

2. Внутри диэлектрика существует электрическое поле (поле в диэлектрике слабее внешнего поля).

для неполярных диэлектриков мало зависит от температуры

для полярных диэлектриков с ростом температуры заметно уменьшается

Диэлектрическая проницаемость среды — физическая величина, показывающая, во сколько раз модуль напряженности электрического поля Е внутри однородного диэлектрика меньше модуля напряженности поля Е₀ в вакууме, созданного теми же свободными зарядами.

 

 

 

 

Потенциальность электростатического поля

Всякое электростатическое поле, независимо от того, создается оно в вакууме или в веществе, является полем потенциальным.

A₁₃₂=A₁₄₂ - работа не зависит от формы траектории

А₂₄₁= -А₁₄₂

A₁₃₂+A₂₄₁=A₁₃₂₄₁=0 - работа по любому замкнутому контуру равна 0

 

 

 

          работа при перемещении заряда в

                                       электростатическом поле                                      

 

 

 

потенциальная энергия заряда в однородном

электростатическом поле

Электроёмкость –

1.    характеризует способность двух проводников накапливать электрический заряд;

2.    не зависит от q и U;

3.    зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.

Электроёмкость

 

 

Конденсаторы

 

 

Батареи конденсаторов

 

 

Примеры решения задач

Два заряда Кл и Кл расположены в керосине на расстоянии 0,4 м друг от друга. Определить силу, с которой они взаимодействуют. Диэлектрическая проницаемость керосина равна 2,1.

Дано:	Решение
r=0,4м q2=Кл  q1=Кл ε=2,1	По закону Кулона находим модуль силы F:  Подставим в формулу числовые значения: Ответ: Н
Найти: F - ?

2.    Два точечных заряда q₁=3 нКл и q₂=7 нКл находятся в дистиллированной воде на расстоянии 70 см. Какую работу нужно совершить, чтобы сблизить их до расстояния 20 см?

Дано:	СИ:	Решение
q1=3нКл q2=7нКл r1= 70 см r2=20 см ε=81	Кл	Работа по сближению зарядов совершается против сил поля и не зависит от способа сближения зарядов. Искомая работа равна изменению потенциальной энергии поля. Будем считать заряд q1 неподвижным. Заряд q2 перемещается в электростатическом поле, создаваемым точечным зарядом q1. Потенциал электростатического поля, создаваемого точечным зарядом q1 на расстоянии r1от заряда:  (1).  Потенциал электростатического поля, создаваемого точечным зарядом q1, на расстоянии r2 от заряда:  (2).  Работа сил электростатического поля по перемещению заряда q2  из точки 1 в точку 2: , . Учитывая формулы (1) и (2), получаем: . Подставим в формулу числовые значения: . Ответ: 8,33×10-9 Дж.
	0,7м
	0,2м
Найти: A- ?

3.    Плоский воздушный конденсатор подключен к источнику постоянного напряжения 3кВ. Площадь каждой из обкладок 80 см², расстояние между обкладками 2,5 см. В пространство между обкладками конденсатора вводится металлическая пластина толщиной 1см. Какую энергию расходует источник при внесении пластины?

Дано:	СИ:	Решение
U=3кВ S=80см2 d= 2,5 см  l = 1 см	В	При внесении незаряженной металлической пластины в поле конденсатора пространство, занимаемое полем, уменьшается на объем пластины, так как напряженность электрического поля внутри пластины равна нулю. Емкость конденсатора увеличивается, как если бы его пластины сблизили. Конденсатор подключен к источнику постоянного напряжении, следовательно, изменение емкости приведет к изменению) заряда на обкладках конденсатора и по цепи пройдет некоторый заряд. Работа источника при прохождении через него заряда:, , где  – первоначальный заряд на конденсаторе, – заряд после увеличения емкости конденсатора. Т. к. конденсатор воздушный и плоский, то , (2). Подставим эти выражения в формулу для работы источника: . Подставим в формулу числовые значения: .                               Ответ: 8,33×10-9 Дж.
	10-2 м
Найти: A- ?

4.    Площадь каждой пластины плоского конденсатора 401см². Заряд пластин 1,42 мкКл. Найти напряженность поля между пластинами.

Дано:	СИ:	Решение
q=1,42мкКл S=401см2 d= 2,5 см  l = 1 см		,  . Подставим в формулу числовые значения: . Ответ: 4000 кВ/м.
	10-2 м
Найти: Е - ?

Контрольные вопросы для самопроверки

1.    Какие вещества называются проводниками, какие – диэлектриками? Привести примеры.

2.    Каков физический смысл диэлектрической проницаемости?

3.    Что представляют собой электрические диполи?

4.    Что называют электростатической индукцией?

5.    Что называется конденсатором? Электрическая ёмкость конденсатора, энергия заряженного плоского конденсатора

6.    Какие соединения конденсаторов существуют?

Индивидуальные задания к практической работе № 10

Вариант №1

1.    Заряд, равный  Кл, помещён в спирт на расстоянии 5 см от другого заряда. Определить значение и знак другого заряда, если заряды притягиваются с силой -0,45Н. Диэлектрическая проницаемость спирта равна 26.

2.    Точечный заряд q=10^-7Кл помещен в центре полого непроводящего шара, относительная диэлектрическая проницаемость которого ε=3. Внешний радиус шара R₁=1м. Радиус полости R₂=0,5м. Вычислите напряженность и потенциал поля в точке, удаленной от центра полости на расстояние r=2м.

3.    При перемещении заряда между точками с разностью потенциалов 1 кВ поле совершило работу 40 мкДж. Чему равен заряд?

4.    Найдите ёмкость плоского конденсатора, состоящего из двух круглых пластин диаметром 20 см, разделённых парафиновой прослойкой толщиной 1 мм. Диэлектрическая проницаемость парафина 2,1.

5.    Ёмкость одного конденсатора в 9 раз больше ёмкости другого. На какой из этих конденсаторов надо подать большее напряжение, чтобы их энергия была одинаковой? Во сколько раз большее?

6.    Найдите общую ёмкость С_общ батареи из двух параллельно соединённых конденсаторов емкостями С₁=6мкФ и С₂=8мкФ.

Вариант №2

1.    Какую разность потенциалов необходимо создать, чтобы сообщить ядру гелия зарядом Кл кинетическую энергию Дж?

2.    В центре сферы радиусом R=8см находится точечный заряд q₁=10нКл. По сфере распределен равномерно заряд q₂=-4q. Найти напряженность и потенциал поля на расстоянии r= 2R от центра сферы.

3.    На сколько увеличится потенциальная энергия взаимодействия зарядов 250мкКл и 400мкКл при изменении расстояния между ними с 10 до 20 см?

4.    Наибольшая ёмкость школьного конденсатора 58мкФ. Какой заряд он накопит при его подключении к полюсам источника постоянного напряжения 50В?

5.    Расстояние между пластинами плоского конденсатора ёмкостью 2 мкФ, подключённого к источнику напряжением 1В, увеличивают в 2 раза. Как изменится энергия электрического поля конденсатора?

6.    Определите общую ёмкость С_общ батареи из двух последовательно соединённых конденсаторов емкостями С₁=5пФ и С₂=10пФ.

Вариант №3

1.    Два заряда по Кл, разделённые слоем слюды, взаимодействуют с силой Н. Определите толщину слоя слюды, если её диэлектрическая проницаемость равна 8.

2.    Точечный заряд q=10^-7Кл помещен в центре полого непроводящего шара, относительная диэлектрическая проницаемость которого ε=3. Внешний радиус шара R₁=1м. Радиус полости R₂=0,5м. Вычислите напряженность и потенциал поля в точке, удаленной от центра полости на расстояние r= 0,75м.

3.    Найдите потенциал шара радиусом 10см, если на расстоянии 10 м от его поверхности потенциал электрического поля равен 20В.

4.    Конденсатору ёмкостью 10 мкФ сообщили заряд 4 мкКл. Какова энергия заряженного конденсатора?

5.    Площадь каждой пластины плоского конденсатора равна 520см² . На каком расстоянии друг от друга надо расположить пластины в воздухе, чтобы ёмкость конденсатора была равна 46 мкФ?

6.    Определите общую ёмкость С_общ батареи из двух последовательно соединённых конденсаторов емкостями С₁=6пФ и С₂=8пФ

Вариант № 4

1.    Заряд в  Кл в керосине на расстоянии 0,005 м притягивает к себе второй заряд с силой  Н.  Найдите величину второго заряда. Диэлектрическая проницаемость керосина равна 2.

2.    В центре сферы радиусом R=8см находится точечный заряд q₁=10нКл. По сфере распределен равномерно заряд q₂=-4q. Найти напряженность и потенциал поля на расстоянии r=R/2 от центра сферы.

3.    Ёмкость одного шара 8мкФ, а потенциал 1000В. Ёмкость второго шара 2мкФ, потенциал – 1000В. Сколько энергии выделится в проводнике, которым соединяют шары?

4.    До какой разности потенциалов нужно зарядить конденсатор ёмкостью 100 мкФ, чтобы энергия его электрического поля стала равна 1 Дж?

5.    Ёмкость первого конденсатора 0,5мкФ, а второго – 5000 пФ. Сравнить напряжения, которые надо подавать на эти конденсаторы, чтобы накопить одинаковые заряды.

6.    Найдите общую ёмкость С_общ батареи из двух параллельно соединённых конденсаторов емкостями С₁=10мкФ и С₂=5мкФ.

Вариант №5

1.    Какую работу надо совершить, чтобы перенести заряд 10^-16Кл из бесконечно удаленной точки, потенциал которой равен нулю, в точку поля которой равен 10В? 

2.    Точечный заряд q=10^-7Кл помещен в центре полого непроводящего шара, относительная диэлектрическая проницаемость которого ε=3. Внешний радиус шара R₁=1м. Радиус полости R₂=0,5м. Вычислите напряженность и потенциал поля в точке, удаленной от центра полости на расстояние r= 0,25м.

3.    Какую работу совершает однородное электрическое поле напряжённостью 200 В/м при перемещении заряда 4 мкКл на 4 см в направлении, противоположном направлению силовых линий?

4.     Чему равна энергия заряженного конденсатора, если его ёмкость равна 10пФ, а заряд равен 1 мкКл?

5.     Ёмкость одного конденсатора 200пФ, а другого – 1 мкФ. Сравнить заряды, накопленные на этих конденсаторах при их подключении к полюсам одного и того же источника постоянного тока.

6.    Определите общую ёмкость С_общ батареи из двух последовательно соединённых конденсаторов емкостями С₁=5пФ и С₂=8пФ.

Вариант №6

1.    Два заряда по Кл, разделённые слюдой толщиной 1см, взаимодействуют с силой Н. Определить диэлектрическую проницаемость среды.

2.    Напряжённость электрического поля в керосине уменьшается в 2 раза. Определите силу взаимодействия двух зарядов в керосине, если в вакууме она равна Н.

3.    Какую работу совершает электрическое поле при перемещении заряда 1мкКл из точки с потенциалом 5 кВ в точку с потенциалом –5 кВ?

4.    Какой заряд можно накопить на конденсаторе ёмкостью 1 мкФ, если его зарядить до напряжения 100В?

5.    Во сколько раз изменится ёмкость конденсатора при уменьшении рабочей площади пластин в 2 раза и уменьшении расстояния между ними в 3 раза?

6.    Найдите общую ёмкость С_общ батареи из двух параллельно соединённых конденсаторов емкостями С₁=6мкФ и С₂=10мкФ.

Тема 4.2. Законы постоянного тока

Практическая работа № 12 «Расчет электродинамических величин и электрических цепей»

Цель: научиться решать задачи по образцу, анализировать задачу, обобщить и систематизировать знания по теме, сформировать умения и навыки нахождения физической величины, её выражение из формулы, закрепить знания по вычислению основных электродинамических величин, сформировать умения и навыки нахождения физической величины, её выражение из формулы.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы:

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Электрический ток - направленное движение свободных зарядов. В электрических цепях применяют различные способы соединения сопротивлений: последовательное, параллельное и смешанное. Последовательным называется соединение, при котором конец одного проводника соединяется с началом другого и т.д.

При таком соединении проводников:

1) сила тока во всех участках цепи одинакова:

2)  падение напряжения в цепи равно сумме падений напряжений на отдельных участках

3)  общее  сопротивление  цепи,  состоящей  из  последовательно соединенных  проводников,  равно  сумме  сопротивлений  отдельных проводников:  

Параллельным называется соединение, при котором начала проводников соединяются в один узел, а их концы - в другой.

При таком типе соединения:

сила тока в неразветвленной части цепи равна сумме сил токов, текущих в разветвленных участках цепи:

падение напряжения на всех параллельно соединенных проводника одинаково:

величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям всех параллельно включенных проводников: . , где n – число одинаковых сопротивлений, т.е.

Закон Ома для полной цепи: ,где ε – ЭДС источника тока, [ε]=В, R-внешнее сопротивление  [R]=Ом,  r – внутреннее сопротивление или сопротивление источника тока [r]=Ом.

План решения задач

При решении задач данного раздела можно использовать следующие основные алгоритмы:

1. Начертить схему и указать на ней все элементы.

2. Установить, какие элементы цепи включены последовательно, какие – параллельно.

3. Расставить токи и напряжения на каждом участке цепи и записать для каждой точки разветвления (если они есть) уравнения токов и уравнения, связывающие напряжения на участках цепи.

4. Используя закон Ома, установить связь между токами, напряжениями и э.д.с (ε).

5. Если в схеме делают какие-либо переключения сопротивлений или источников, уравнения составляют для каждого режима работы цепи.

6. Решить полученную систему уравнений относительно неизвестной величины.

7. Решение проверить и оценить критически.

Расчет силы тока производится с использованием законов Ома для участка цепи и для полной цепи.

При решении задач на расчет работы, мощности и теплового действия тока, прежде всего, необходимо установить, идет ли речь о мощности, выделяемой на участке цепи или о полной мощности в цепи или же о мощности во внешней цепи источника и правильно выбрать формулы для расчета мощности. Решая задачи на мощность, выделяемую во внешней цепи, желательно помнить, что она будет максимальной, когда внешнее сопротивление цепи будет равно сопротивлению источника. Этим результатом можно пользоваться как готовым и значительно сократить вычисления.

При расчете теплового действия тока следует использовать закон Джоуля-Ленца . Когда участок цепи не  содержит источников тока, то можно использовать формулу , .      

Формулы  и , определяющие работу сил поля и количество теплоты, выделившейся  на  участке цепи, можно применить независимо от того, есть ли на этом участке источник ЭДС или нет.

Если на участке нет источника ЭДС, эти формулы тождественны. Если же участок содержит источник тока, величины А и Q окажутся разными.

Примеры решения задач

Сила тока и плотность тока

1.       Определите число n электронов, которые проходят через поперечное сечение проводника площадью S=1мм² за t=2 мин, если плотность тока в проводнике j=150А/см

Дано:	СИ	Решение:
S=1мм2	10-6м2	Число электронов, проходящих через поперечное сечение проводника, равно отношению электрического заряда, прошедшего через данное поперечное сечение, к заряду электрона:  (1). Учитывая, что  (2), получим за время t через сечение проводника пройдет . Ответ: 1,2×1021.
t=2 мин	120с
j=150А/см2	1,5×102 А/м2
Найти: n -?

2.       Если плотность тока при физиопроцедуре 0,1 мА/см², а площадь электродов 24 см², то заряд, проходящий через участок ткани человека за 5 мин, равен... (в Кл).

Дано:	СИ	Решение:
S=24см2		Количество заряда, проходящего через участок ткани человека, равно произведению силы тока на время прохождения электрического заряда: . Плотность тока по определению: . Для вычисления заряда получаем формулу: q = jSt. При подстановке числовых значений см2 можно не переводить в м2, т.к. эта единица измерения сокращается. Подставляем числовые значения:                       Ответ: 0,72Кл.
t=5 мин	300с
j=0,1мА/см2	0,1×10-3 А/см2
Найти: q -?

3.       При никелировании изделия в течение 1 часа отложился слой никеля толщиной l=0,01 мм. Определить плотность тока, если атомная масса никеля М_а = 0,0587 кг/моль, валентность n = 2.

Дано:	СИ	Решение:
l=0,01 мм	10-5 м	По закону Фарадея, масса выделившегося никеля равна:, где , S – площадь покрытия никелем. Тогда: , откуда получаем формулу: . Подставляем числовые значения:   Ответ: .
t= 1 час	3,6×104с
Ма=0,0587кг/моль
ρ=8,9×103кг/м3
F=9,65×104 кг/моль
n = 2
Найти: j  -?

Соединение проводников

4.       К сети напряжением U=200В присоединены два резистора. При их последовательном соединении I₁=4,4А, а при параллельном - I₂= 27,5А. Определите сопротивление R₁ и R₂ резисторов.

Дано:	Решение
U = 200В I1=4,4А I2= 27,5А	При последовательном соединении ; , откуда . При параллельном соединении: , , откуда  . Подставим в полученную формулу числовые значения:   и   Ответ: R1=50 Ом, R 2=8 Ом
Найти: R1 - ? R2 -?

5.       Имеются две лампы на напряжение U=220B, одна из которых рассчитана на мощность P₁=60Bт, а другая - на Р₂=100Вт. Сопротивление, какой лампы больше и во сколько раз?

Дано:	Решение
P1 = 60 Вт P2 = 100 Вт U = 220В= const	При постоянном напряжении удобно применить формулу . Откуда . Тогда ;  и . Подставим в полученную формулу числовые значения:    Ответ: 1,7.
Найти: - ?

6.       Проводники сопротивлением 3 Ом и 4 Ом соединены параллельно. Если через сопротивление 3 Ом протекает ток 0,2 А, то через сопротивление 4 Ом протекает ток.. .(в А).

Дано:	Решение
R1 = 3 Ом R2 = 4 Ом I1 = 0,2 А	При параллельном соединении: . По закону Ома: . Выражаем I2: Подставим в полученную формулу числовые значения:    Ответ: 0,15 А.
Найти:  I2 - ?

Контрольные вопросы для самопроверки

                                                               i.      Что понимают под электрическим током?

7.     

8.    Какое соединение сопротивлений называют последовательным? параллельным? Чему равно сопротивление цепи при этих соединениях?

Индивидуальные задания к практической работе № 12

Вариант №1

1.    Через лампу накаливания проходит ток 0,8 А. Сколько свободных электронов проходит через поперечное сечение волоска лампы в 1 с?

2.    До какой температуры нужно нагреть медный проводник, имеющий температуру 0°С, чтобы его сопротивление увеличилось в 3 раза? Температурный коэффициент сопротивления меди 4,3×10³К^-1.

3.    На рисунке показан участок цепи постоянного тока, содержащий 3 лампочки накаливания. Сопротивление каждой лампочки 6 Ом. Определите сопротивление всего участка цепи.

4.    Гирлянда из 10 одинаковых лампочек, соединённых параллельно, включена в сеть напряжением 220В и потребляет ток силой 2,5 А. Определить сопротивление одной лампочки.

Вариант №2

1.    Определите плотность тока, протекающего по константановому проводнику длиной 5 м, при напряжении 12 В.

2.    Сопротивление угольного проводника при температуре 0⁰С равно 15 Ом, а при температуре 220⁰С – 13,5 Ом. Определить температурный коэффициент сопротивления угля.

3.    Два резистора соединены параллельно. Сила тока в первом резисторе 0,5 А, во втором — 1 А. Сопротивление первого резистора 18 Ом. Определите силу тока на всем участке цепи и сопротивление второго резистора.

4.    Резисторы с сопротивлениями R₁=2Ом, R₂=3Ом, R₃=5Ом соединены по схеме, изображенной на рисунке. Найдите общее сопротивление этой цепи.

Вариант №3

1.    Обмотка реостата сопротивлением 84 Ом выполнена из никелиновой проволоки с площадью поперечного сечения 1 мм² . Какова длина проволоки?

2.    По нити накала лампочки карманного фонаря протекает ток силой 0,3А. Напряжение на полюсах батарейки 4,5 В. Найти энергию, израсходованную на нагревание нити накала лампочки за 100 с.

3.    Во сколько сопротивление R₁ при последовательном соединении 10 резисторов (n=10) сопротивлением по R=10 Ом больше, чем их сопротивление R₂ при параллельном соединении?

4.    В сеть напряжением U=24В подключили два последовательно соединённых резистора. При этом сила тока составила I₁=0,6А. Когда резисторы подключили параллельно, суммарная сила тока стала равной I₂=3,2А. Определить сопротивления резисторов.

Вариант № 4

1.    Определите сопротивление медного провода, если при силе протекающего в нем тока 10А напряжение на его концах равно 4 В.

2.    Сопротивление вольфрамовой нити электрической лампочки при 10⁰С равно 50 Ом. До какой температуры была нагрета нить, если её сопротивление стало равным 550 Ом? Температурный коэффициент равен 0,0048 К^-1.

3.     Напряжение в сети 120 В. Сопротивление каждой из двух электрических ламп, включенных в эту сеть, равно 240 Ом. Определите силу тока в каждой лампе при последовательном и параллельном их включении.

4.    На рисунке изображена схема соединения резисторов, у которых R_l=3Ом, R₂=6Ом, R₃=4Ом. Найдите общее сопротивление всей цепи.

Вариант №5

1.    Рассчитайте силу тока в лампочке, имеющей сопротивление 400 Ом, если напряжение на ее зажимах 120 В.

2.    Алюминиевая проволока при 0°С имеет сопротивление 4,25 Ом. Каково будет сопротивление этой проволоки при 200°С? Температурный коэффициент сопротивления алюминия 4×10^-3К^-1.

3.    Какие сопротивления  можно получить, имея три резистора по 6 Ом каждый?

4.    Чему равно общее сопротивление участка цепи, изображенного на рисунке, если сопротивление каждого из четырех резисторов равно 2 Ом.

Вариант №6

1.    Какова сила тока в проводнике, через поперечное сечение которого за 2 с проходит 12×10¹⁹электронов? Заряд электрона равен 1,6×10^-19Кл.

2.    Сопротивление платиновой проволоки при температуре 20°С равно 20 Ом, а при температуре 500°С равно 59Ом. Найдите значение температурного коэффициента сопротивления платины.

3.    Определить плотность тока, протекающего по константановому проводнику, длиной 5м, при напряжении 12В?

4.    Двигатель мощностью 30 Вт, рассчитанный на напряжение 15 В, необходимо подключить к источнику тока, составленному из батареек с ЭДС 1,5 В и внутренним сопротивлением 0,5 Ом. Сколько батареек следует включить в последовательную цепь?

Практическая работа № 12 «Расчет электродинамических величин и электрических цепей»

Цель: научиться решать задачи по образцу, анализировать задачу, обобщить и систематизировать знания по теме, систематизировать и закрепить приобретенные знания при решении задач по теме «Законы постоянного тока».

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы:

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Электрический ток-это упорядоченное движение заряженных частиц. Силой тока (I) называется величина, численно равная электрическому заряду, проходящему через сечение проводника в единицу времени: .

Если сила тока со временем не меняется, то ток называется постоянным. Для возникновения и существования электрического тока в веществе необходимо, во-первых, наличие свободных заряженных частиц; во-вторых, необходима сила, действующая на них в определённом направлении. Сопротивление однородного цилиндрического проводника, длиной l и площадью поперечного сечения S,  изготовленного  из  материала  с удельным сопротивлением ρ, определяется выражением: . 

Экспериментально  установленную  зависимость  силы  тока  I  от напряжения U и электрического сопротивления R участка цепи называют законом Ома для участка цепи: . Сила тока I прямо пропорциональна напряжению U и обратно пропорциональна электрическому сопротивлению R участка цепи.

Закон Ома для полной цепи: ,где ε – ЭДС источника тока, [ε]=В, R-внешнее сопротивление  [R]=Ом,  r – внутреннее сопротивление или сопротивление источника тока [r]=Ом.

При упорядоченном движении заряженных частиц электрическое поле совершает работу, её принято называть работой тока. Работа тока  Мощность тока равна отношению работы тока за время к этому интервалу     времени. P=A/ t=IU=U² /R.

Примеры решения задач

Сопротивление проводника

1.     Сопротивление вольфрамовой нити лампы накаливания при температуре +20⁰С равно 20 Ом, а при 3000⁰С – 250 Ом. Определите температурный коэффициент сопротивления вольфрама.

Дано:	Решение
R0 = 20 Ом R = 250 Ом t 0= +200С t = 30000С	Воспользуемся формулой зависимости сопротивления от температуры: . Откуда . Тогда . Подставим в полученную формулу числовые значения:   Ответ: 0,004 К-1 .
Найти: α- ?

Закон Ома для участка цепи без ЭДС

2.     Электрическая цепь, состоящая из резисторов R₁=100 Ом, R₂=200 Ом и R₃=300 Ом, подключена к двум источникам постоянного напряжения U₁ и U₂=100В. При каком напряжение U₁ сила тока I₁ через резистор R₁ будет равна нулю?

Дано:	Решение:
R1=100 Ом	Если через резистор R1 ток не идет, т.е. I1=0, следовательно, I1R1=0. Тогда напряжение U3 на резисторе R3 должно быть равно U1, т.е. (1). В этом случае резисторы R2 и R3 включены последовательно. Поэтому сила тока во всех частях цепи одинакова: . Падение напряжения  , откуда следует, что  (2) Учитывая, что  имеем, . После преобразования получим . Подставляем числовые значения: .              Ответ: 60 В
R2=200 Ом
R3=300 Ом
U2=100 В
Найти: I1 -? U1 -?

3.     Рассчитать силу тока, проходящую по медному проводу длиной 100м, площадью поперечного сечения 0,5мм², если к концам провода приложено напряжение 6,8B.

Дано:	Решение:
l=100 м	Сила тока по закону Ома равна  (1), сопротивление проводника можно вычислить из  его определения  (2). Подставим формулу (2) в (1) и после преобразования получим . Подставляем числовые значения: Ответ: 2 А
S=0,5 мм2
U=6,8 В
Найти: I -?

Закон Ома для полной цепи

4.     Определите силу тока короткого замыкания I_KЗ батареи, ЭДС которой ξ = 15 В, если при подключении к ней резистора сопротивлением R=3 Ом сила тока в цепи составляет I=4А

Дано:	Решение:
ξ = 15В	Силу тока короткого замыкания определяем по формуле  (1), где r-внутреннее сопротивление батареи. Согласно закону Ома, для полной цепи:   (2). Подставим формулу (2) в формулу (1): Подставляем числовые значения: Ответ: 20 А
R=3Ом
I=4А
Найти: I кз-?

5.     Источник тока с ЭДС 220 В и внутренним сопротивлением 2 Ом замкнут проводником сопротивлением 108 Ом. Определить падение напряжения внутри источника тока.

Дано:	Решение
ξ = 220В r = 2 Ом R = 108 Ом	При вычислении падения напряжения внутри источника тока удобно применить формулу закона Ома для участка цепи, т.к. : . Откуда . В данной формуле неизвестна сила тока, для её вычисления воспользуемся законом Ома для полной цепи: . Тогда . Подставим в полученную формулу числовые значения:   Ответ: 2,2 В
Найти: u- ?

6.     Амперметр с внутренним сопротивлением 2 Ом, подключен к зажимам батареи, показывает ток 5А. Вольтметр с внутренним сопротивлением 150 Ом, подключенный к зажимам этой же батареи, показывает напряжение 12В. Чему равен ток короткого замыкания?

Дано:	Решение
U = 12 В I = 5 А R а = 2 Ом	1) К батарее подключен амперметр:  (1), где ξ - ЭДС, r - внутреннее сопротивление батареи.  2) К батарее подключен вольтметр: он показывает напряжение, равное напряжению  на  зажимах  батареи, т.к. внешнее сопротивление состоит только из Rв:  (2). Ток короткого замыкания определяется формулой:  (3). Из формулы (1) следует  и подставляем в (2):  . . Тогда .  Полученные выражения для r  и  подставляем в (3):   Подставим в полученную формулу числовые значения:     Ответ: 29,6 А
R в = 150 Ом
Найти: Iкз - ?

7.     Батарея с внутренним сопротивлением 2 Ом и ЭДС 6 В замкнута проводником с сопротивлением 8 Ом.  Какое количество теплоты выделится в проводнике за 1 секунду?

Дано:	Решение
ξ = 6 В t = 1 с r = 2 Ом	Количество теплоты, выделяющееся в проводнике, определяется законом Джоуля-Ленца: . По закону Ома для полной цепи:  .Тогда .   Подставим в полученную формулу числовые значения:     Ответ: 2,88 А
R  = 8 Ом
Найти: Q - ?

Контрольные вопросы для самопроверки

1.     Что называют силой тока?

2.     Сформулируйте закон Ома для участка цепи без ЭДС.

3.     Как зависит сопротивление проводника от его длины, площади, поперечного сечения и материала?

4.     Как зависит сопротивление проводника от температуры?

5.     Что называют электродвижущей силой источника тока?

6.     Сформулируйте закон Ома для полной цепи.

Индивидуальные задания к практической работе № 13

Вариант №1

1.    Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 50 м и площадью поперечного сечения 1 мм², если напряжение на зажимах реостата 45 В. Удельное сопротивление никелина равно 0,4 (Оммм/м²).

2.    ЭДС источника тока 5 В. К источнику тока присоединили лампу сопротивлением 12 Ом. Найдите напряжение на лампе, если внутреннее сопротивление источника 0,5 Ом.

3.    Гальванический элемент дает на внешнее сопротивление 4 Ом ток 0,2 А. Если же внешнее сопротивление 7 Ом, то элемент дает ток 0,14 А. Какой ток даст элемент, если его замкнуть накоротко?

4.    Две спирали одинакового сопротивления включаются в цепь: один раз последовательно, другой раз параллельно. В каком случае в цепи выделяется большее количество теплоты и во сколько раз?

5.    Две электрические лампочки включены в сеть параллельно. Сопротивление первой лампочки равно 360 Ом, второй 240 Ом. Какая из лампочек потребляет большую мощность и во сколько раз?

Вариант №2

1.    Реостат изготовлен из никелиновой проволоки длиной 15 м. Напряжение на зажимах реостата 18 В, сила тока равна 3 А. Вычислите площадь поперечного сечения проволоки. Удельное сопротивление никелина равно 0,4 (Оммм²/м).

2.    К источнику тока, ЭДС которого 6 В, подключен проводник сопротивлением R₁ = 4 Ом, в результате чего амперметр показал силу тока 1 А. Какой станет сила тока, если проводник R₁ заменить проводником сопротивлением 2 Ом?

3.    Участок цепи состоит из стальной проволоки длиной 2 м и площадью поперечного сечения 0,48 мм², соединенной последовательно с никелиновой проволокой длиной 1 м и площадью поперечного сечения 0,21 мм². Какое напряжение надо подвести к участку, чтобы получить силу тока 0,6 А?

4.    Железная и медная проволоки ,одинаковых длин и сечений, соединены последовательно и включены в сеть. Найти отношение количеств теплоты, выделившихся в каждой проволоке.

5.    При ремонте электрической плитки спираль была укорочена на 0,1 первоначальной      длины. Во сколько раз изменилась мощность плитки?

Вариант №3

1.    Электрическую лампу сопротивлением 240 Ом, рассчитанную на 120 В, надо питать от сети с напряжением 220 В. Какой длины нихромовый проводник с площадью поперечного сечения 0,55 мм² надо включить последовательно с лампой?

2.    Дуговая печь потребляет ток 200 А от сети напряжением 120 В через ограничивающее сопротивление 0,2 Ом. Найти мощность, потребляемую печью.

3.    Кабель состоит из двух стальных жил площадью поперечного сечения 0,6 мм² каждая и четырех медных жил площадью сечения 0,85 мм² каждая. Каково падение напряжения на каждом километре кабеля при силе тока 0,1 А?

4.     Электромотор питается от сети с напряжением 220 В. Сопротивление обмотки мотора 2 Ом. Сила потребляемого тока 10 А. Найти потребляемую мощность.

5.    В цепи, состоящей из реостата и источника тока ζ= 6 В и внутренним сопротивлением r = 2 Ом, идет ток I₁ = 0,5 А. Какой ток I₂ пойдет при уменьшении сопротивления реостата в три раза?

Вариант № 4

1.    По медному проводнику с поперечным сечением 1 мм² течёт ток с силой 10 А. Определите среднюю скорость упорядоченного движения (скорость дрейфа) электронов в проводнике.

2.    ЭДС источника тока 4В, к его полюсам подсоединили резистор сопротивлением 8Ом, в результате чего, в цепи установилась сила тока 0,4А. Определите сопротивление источника.

3.     Напряжение в сети 120 В. Сопротивление каждой из двух электрических ламп, включенных в эту сеть, равно 240 Ом. Определите силу тока в каждой лампе при последовательном и параллельном их включении.

4.    Для определения ЭДС и внутреннего сопротивления источника тока к его выходу подключили реостат. При некотором положении ползунка реостата сила тока в цепи была 1,5А, а напряжение 4,5В. При другом положении – ток 2А, напряжение 3В. Какими оказались ЭДС и внутреннее сопротивление источника?

5.    Опасным для жизни человека является поражение электрическим током более 20мА. Какое напряжение может представлять опасность для жизни человека, если сопротивление тела человека при поврежденной коже около 1000 Ом?

Вариант №5

1. Электрическая цепь состоит из трёх последовательно соединенных кусков провода одинаковой длины, сделанных из одного материала, но имеющих разные сечения: S₁ = 1 мм², S₂ = 2 мм², S₃ = 3 мм². Напряжение на концах цепи 11 В. Найти напряжение на каждом проводнике.

2. Электропечь должна давать 0,1 МДж теплоты за 10 мин. Какова должна быть длина нихромовой проволоки сечением 0,5 мм², если печь предназначена для сети с напряжением 36 В?

3. 3.Какова ЭДС элемента, если при измерении напряжения на его зажимах вольтметром с внутренним сопротивлением 20 Ом получили 1,37 В, а при замыкании элемента на 10 Ом получили ток 0,132 А?

4.    Конфорка профессиональной электроплиты состоит из двух нагревательных элементов сопротивлением 150 Ом и 100 Ом, которые с помощью пакетного переключателя могут соединяться либо каждый отдельно, либо оба параллельно, либо оба последовательно. Какое количество теплоты выделяется в каждом случае за 1 ч? Напряжение питания конфорки 220 В.

5.    При напряжении 110 В, подведенном к резистору, сила тока в нем равна 5 А. Какова будет сила тока в резисторе, если напряжение на нем увеличить на 10 В?.

Вариант №6

1.    К полюсам источника тока с ЭДС 8В подсоединили проводник с сопротивлением 30 Ом. При этом напряжение на концах проводника стало равным 6В. Чему равно внутреннее сопротивление источника?

2.    Генератор питает 50 ламп сопротивлением 300 Ом каждая. Напряжение на зажимах генератора 128В, его внутреннее сопротивление 0,1 Ом, а сопротивление подводящей линии 0,4 Ом. Найти силу тока в линии, ЭДС генератора, напряжение на лампах и падение напряжения на внутренней части цепи.

3.    Источник постоянного тока с ЭДС ζ = 12 В и внутренним сопротивлением г = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Определить силу тока в цепи I, падение напряжения U_R на внешнем участке и падение напряжения U_r на внутреннем участке цепи.

4.    Источник тока с ЭДС равной 24 В и внутренним сопротивлением 1 Ом замкнут на резистор с сопротивлением 20 Ом. К  зажимам источника тока подключен так же конденсатор емкостью 1,2 мкФ. Найти заряд на конденсаторе.

5.    Конфорка профессиональной электроплиты состоит из двух нагревательных элементов сопротивлением 150 Ом и 100 Ом, которые с помощью пакетного переключателя могут соединяться либо каждый отдельно, либо оба параллельно, либо оба последовательно. Какая мощность будет выделяться в конфорке в каждом из случаев? Какое количество теплоты выделяется в каждом случае за 1 ч? Напряжение питания конфорки 220 В.

Лабораторная работа №2. Изучение последовательного и параллельного соединения проводников

Цель работы: установить на опыте зависимость силы тока от напряжения и сопротивления. Экспериментальная проверка законов последовательного и параллельного соединений проводников:

1)ознакомиться с приборами для проведения этой лабораторной работы                            

2) научиться соединять резисторы последовательно и параллельно

3) научиться измерять и рассчитывать сопротивление при последовательном и параллельном соединении резисторов

   Оборудование: амперметр лабораторный, вольтметр лабораторный, источник питания, набор из трёх резисторов сопротивлениями 1 Ом, 2 Ом, 4 Ом, реостат, ключ замыкания тока, соединительные провода.

Ход работы.

Теоретическая справка.

   Электрический ток - упорядоченное движение заряженных частиц.  Количественной мерой электрического тока служит сила тока.

   Сила тока – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:  I =

  В Международной системе единиц СИ сила тока измеряется в амперах [А].    [1A=1Кл/1с]

   Прибор для измерения силы тока Амперметр. Включается в цепь последовательно

   Напряжение – это физическая величина, характеризующая действие электрического поля на заряженные частицы, численно равно работе электрического поля по перемещению заряда из точки с потенциалом φ₁ в точку с потенциалом φ₂:  U=     Единица напряжения – Вольт [В]  [1B=1Дж/1Кл]

   Прибор для измерения напряжения – Вольтметр.  Подключается  в цепь параллельно тому участку цепи, на котором измеряется разность потенциалов.

   Величина, характеризующая противодействие электрическому току в проводнике, которое обусловлено внутренним строением проводника и хаотическим движением его частиц, называется электрическим сопротивлением проводника.  Электрическое сопротивление проводника зависит от размеров и формы проводника и от материала, из которого изготовлен проводник.   R=       В СИ единицей электрического сопротивления проводников служит Ом [Ом].

   Графическая зависимость силы тока I от напряжения U - вольт-амперная характеристика

   Закон Ома для участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.   I =

 Ход работы.

  1. Для выполнения работы соберите электрическую цепь из источника тока, амперметра, реостата, проволочного резистора сопротивлением 2 Ом и ключа. Параллельно проволочному резистору присоедините вольтметр (см. схему).

   

2 Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи. Включите ток. При помощи  реостата доведите напряжение на зажимах проволочного резистора до 1 В, затем до 2 В и до 3 В. Каждый раз при этом измеряйте силу тока и результаты записывайте в табл. 1.

Напряжение, В
Сила тока, А

 3. По данным опытов постройте график зависимости силы тока от напряжения. Сделайте вывод.

   4. Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах. Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.

Сопротивление участка, Ом
Сила тока, А

1.       По данным опытов постройте график зависимости силы тока от сопротивления. Сделайте вывод.

2.       Изучение последовательного и параллельного соединений проводников

1 часть: изучение последовательного соединения

1. Заполните  пропуски в формулах последовательного соединения

U=U₁…U₂              R=R₁….R₂              

2         Соберите цепь для изучения последовательного соединения по схеме:

3  Измерьте силу тока. Поочерёдно включая вольтметр к первому резистору, ко второму резистору и ко всему участку, измерьте напряжение. Результаты измерений занесите в таблицу

I, A	U1 B	U2 B	U B	R1 Ом	R2 Ом	R Ом

 4 Вычислите сопротивления и занесите результаты в таблицу

R₁= =….Ом         R₂=         R=   

5 Проверьте формулы (см пункт 1) последовательного соединения по данным таблицы

6 Посмотрите на резисторы и запишите:   R₁=….Ом         R₂=….Ом

7 Вычислите рассчитанное сопротивление при последовательном соединении R=R₁+R₂=….Ом

8 Сравните измеренное и рассчитанное сопротивления при последовательном соединении

2 часть: Изучение параллельного соединения

1 Заполните пропуски в формулах параллельного соединения

I=I₁….I₂                  

2 Cоберите цепь для изучения параллельного соединения

3 Замкните цепь и измерьте силу тока и напряжение на участке при параллельном соединении

Запишите:       I= ….….A              U=………B

4 Пользуясь измеренными данными вычислите сопротивление участка при параллельном соединении

         R=………Ом   (измеренное сопротивление)

5 Посмотрите на резисторы и запишите     R₁=…….Ом         R₂=………Ом

6 Вычислите по формуле  (см пункт1) сопротивление при параллельном соединении

        ……….Ом    (рассчитанное сопротивление)

7 Сравните рассчитанное и измеренное сопротивления при параллельном соединении

8 Сделать вывод

Контрольный вопрос

Как соединяются потребители электроэнергии в квартирах? Почему?

Лабораторная работа №3 Определение ЭДС и внутреннего сопротивления источника напряжения

Цель работы:  экспериментальное  определение ЭДС источника и его внутреннего сопротивления, установление зависимости силы тока от внешнего сопротивления, определить КПД электрической цепи.

Оборудование: источник тока, амперметр, вольтметр, реостат, проволочный резистор, ключ, соединительные провода.

Описание работы: Измерив силу тока в цепи и напряжение на клеммах источ­ника при двух различных значениях внешнего сопротивления и записав в обоих случаях закон Ома для полной цепи, получим    ε =U₁ + I₁r ,  ε =U₂ + I₂r  где ε — ЭДС источника, r — внутреннее сопротивление источника,    I₁     и U₁    — значения силы тока и напря­жения при одном внешнем сопротивлении цепи,    а  I₂     и U₂ — при другом.

Написанные соотношения являются системой двух линейных уравнений с двумя неизвестными   ε  и r. Решая эту систему, получим ε = (I₁ U₂- I₂ U₁)/( I₁ -   I₂ ), 

r = (U₂ - U₁)/( I₁ -   I₂)

Теоретическая справка.

Закон Ома для полной цепи - сила тока прямо пропорциональна ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где ε – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Электродвижущей силой (ЭДС) источника тока называют работу, которая требуется для перемещения единичного заряда между его полюсами.

КПД электрической цепи — это отношение полезного тепла к полному: η =  =   

Ход работы

Задание 1. Определение ЭДС источника и его внутреннего сопротивления

1.  Соберите электрическую цепь по изображенной на рисунке схеме.

2.  Установите ползунок реостата примерно в среднее положение, из­мерьте силу тока  I₁ и напряжение U₁.

3.  Передвинув ползунок реостата, измерьте 1₂ и U₂.

4.  По приведенным выше форму­лам вычислите r  и ε.

5.  Результаты измерений и вычислений запишите в таблицу, помещенную в тетради для лабораторных работ. Ниже приведен образец этой таблицы.

 

6.       Запишите в тетради для лабораторных работ вывод: что вы измеряли и какой получен результат.

Задание 2. Определение КПД электрической цепи

1)​ Начертите в тетради схему работы.

2)​ При разомкнутой цепи вольтметр,  подклю​ченный  к полюсам источника показывает значение ЭДС источника  ε =

3)​ При замыкании ключа снимите показания силы тока в цепи I =   и напряжения на полюсах источника U= .

4) Вычислите сопротивление цепи: R=

5)​ Используя закон Ома для полной цепи    ,  определите внутреннее сопротивление источника тока:

6) Вычислите КПД электрической цепи по формуле: η =   

    7)​ Сделать вывод по работе.                          

Контрольные вопросы

1. Какие силы принято называть сторонними?

2. Что называют электродвижущей силой?

3. Сформулируйте закон Ома для полной цепи.

4. Выполните  тест.

I.  При напряжении на концах проводника 2 В сила тока 0,8 А. Какое напряжение на этом проводнике при силе тока 0,2 А?

1. 1,6 В; 2. 1,2 В; 3. 0,6 В; 4. 0,5 В.

На рисунке  изображен график зависимости силы тока от напряжения.

II.  При каком напряжении на проводнике сила тока равна 2 А?

1. 2 В; 2. 1,6 В; 3. 1,2 В; 4. 0,8 В; 5. 0,4 В.

III.  Какова сила тока в проводнике при напряжении на нем 1,2 В?

1. 10 А; 2. 8 А; 3. 6 А; 4. 4 А; 5. 2 А.

IV. Напряжение на электрической лампе 220 В, а сила тока в ней 0,5 А. Определите сопротивление лампы.

I. 110 Ом; 2. 220 Ом; 3. 0,002 Ом; 4. 440 Ом.

V.    Выразите 2500 Ом в килоомах.

I. 0,0025 Ом; 2. 2,5Ом; 3. 250Ом; 4. 2500 Ом.   

VI.  Сила тока в нагревательном элементе чайника 2,5 А, а сопротивление 48 Ом. Вычислите напряжение на нагревательном элементе чайника .

1.120 В; 2.19,2 В; 3.0,05 В; 4.220 В; 5. 127 В

Тема 4.3. Магнитное поле

Практическая работа № 13 «Расчет силы Ампера и силы Лоренца»

Цель: закрепить умения и навыки вычисления величин с использованием закона Ампера, силы Лоренца.

Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы

1.     К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.     Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.     При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.     Внимательно прочитать теоретическую часть и план решения задач.

5.     Рассмотреть примеры решения задач.

6.     Ответить на контрольные вопросы.

7.     Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Сила, действующая на прямолинейный проводник с током, помещенный в магнитное поле, называется силой Ампера.

Закон Ампера: модуль силы Ампера равен произведению силы тока I, протекающего в проводнике, на модуль вектора магнитной индукции В, на длину проводника l и на синус угла α между вектором В и проводником с током. Величина силы, действующей со стороны магнитного поля на проводник длиной l, по которому идет ток силой I, определяется по формуле Ампера:

, где B - модуль магнитной индукции, [В] =Тл, l – длина проводника [l] = м, I – сила тока, [I] =A.

Направление силы Ампера определяются правилом левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции входила ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90⁰ большой палец покажет направление силы, действующей на отрезок проводника.

Сила, действующая на электрический заряд, движущийся в магнитном поле, называется силой Лоренца. Модуль силы Лоренца равен произведению абсолютного значения движущегося заряда q на скорость его движения v, на модуль вектора магнитной индукции В и на синус угла α между векторами В и v. Величина силы, действующей со стороны магнитного поля на заряженную частицу, определяется по формуле Лоренца:

 , где q – заряд частиц, ν – скорость движения частиц, В – магнитная индукция.

Направление силы Лоренца определяется по правилу левой руки: если левую руку расположить так, чтобы четыре пальца указывали направление скорости движения заряженной частицы, перпендикулярная к скорости составляющая вектора магнитной индукции входила в ладонь, то отогнутый на 90° большой палец укажет направления силы, действующей на положительный заряд и направление, противоположное направлению силы Лоренца, действующей на отрицательный заряд.

На заряженную частицу, движущуюся в однородном магнитном поле перпендикулярно линиям индукции магнитного поля, действует постоянная по модулю и направлению сила Лоренца, направленная перпендикулярно вектору скорости. Под действием силы Лоренца заряженная частица движется по окружности постоянного радиуса. Окружность лежит в плоскости, перпендикулярной к вектору магнитной индукции, а сила Лоренца является центростремительной. Радиус окружности R, по которой движется частица, определяется из условия:   , где R – радиус окружности [R] =м,  m – масса частиц,  [m] = кг, q – модуль заряда частицы, [q] = Кл.

Время, за которое частицы делают полный оборот (период обращения) равно: , R –  радиус окружности [R]  = м, m – масса частиц, [m] = кг, q -  модуль заряда частицы, [q] = Кл.

Отклонение заряженной частицы, движущейся перпендикулярно силовым линиям магнитного поля, используется для определения знака заряда частицы.

Если  вектор скорости заряженной частицы составляет угол α с направлением вектора магнитной  индукции  В  однородного поля, то частица движется по винтовой линии.  Радиус витка R: . Шаг витка h равен:

 

Примеры решения задач

·       Определите силу, действующую на проводник длиной 20 см помещенный в магнитное поле, индукция которого 5 Тл, если сила тока в проводнике 10 А и он образует угол α = 30° с направлением поля.

Дано:	СИ	Решение:
I=10 А		На проводник с током со стороны магнитного поля действует Ампера: . Подставляем числовые значения:   Ответ: .
α=300
l=20 см	0,2 м
B = 5Тл
Найти: Fa  -?

·       Пылинка массой 10 мг, зарядом 10 мкКл в магнитном поле с индукцией 5 Тл описала окружность радиусом 6 м. Скорость пылинки равна... (м/с).

Дано:	СИ	Решение:
m= 10 мг	10-5 кг	На заряженную пылинку в магнитном поле действует сила Лоренца. Сила Лоренца является центростремительной:. Выразим скорость движения частицы .  Подставляем числовые значения:   Ответ: .
q= 10 мкКл	10-5 Кл
R = 6 м
B = 5Тл
Найти: v  -?

·       С какой скоростью вылетает α-частица из радиоактивного ядра, если она, попадая в однородное магнитное поле с индукцией 1 Тл перпендику­лярно магнитным линиям, движется по дуге окружности радиуса 0,5 м?

Дано:	Решение:
В=1 Тл α=900 R=0,5 м	Из формулы ð . О заряде α-частицы мы узнаем то, что она содержит два протона, а о ее массе - по молярной массе гелия: М = 4×10-3 кг/моль. Так как , то скорость . Подставив числовые значения мы получаем, что скорость равна , что составляет около 1/10 скорости света. Ответ: 2,4 ×107 м/с.
Найти: v-?

·       Нихромовая проволока длиной l = 0,2 м подвешена на тонких невесомых нитях в однородном магнитном поле с индукцией В = 0,1Тл. На какой угол α отклонится эта проволока, если к ее концам приложить напряжения U= 0,5В.

Дано:   В=0,1 Тл l = 0,2 м U= 0,5В	Решение:
	На проволоку действует три силы: сила Ампера, сила тяжести и сила натяжения невесомых нитей. Т. к. проволока находится в равновесии, геометрическая сумма сил, действующих на нее, равна нулю. . Из геометрических построений следует, что: ,  (1) Модуль силы тяжести: , где ρ - плотность нихрома; S– площадь сечения нихромовой проволоки. Ток, протекающий по проволоке, можно рассчитать по закону Ома для участка цепи: , где  – удельное сопротивление нихрома. Подставим выражение силы тяжести и  силы тока в формулу (1) и получим: , ρR=1,1×10-6Ом×м; ρ=8,4×103кг/м3. Найдем угол  α: Ответ: .
Найти: α -?

Контрольные вопросы для самопроверки

1.    Что представляет собой магнитное поле? Как можно его обнаружить? Какими свойствами оно обладает?

2.    Что называют вектором магнитной индукции? Какой характеристикой поля она является?

3.    Какие линии называются линиями магнитной индукции?

4.    Какая сила называется силой Лоренца?  Сформулируйте правило левой руки?

5.    Какая величина называется силой Ампера? В чём заключается закон Ампера?

6.    В чём состоит отличие силы Лоренца от силы Ампера?

Индивидуальные задания к практической работе № 13

Вариант №1

1.    Прямолинейный проводник с током помещен в однородное магнитное поле с индукцией 2 Тл. Определите силу, с которой действует магнитное поле на проводник, если его длина 10 см, сила тока в проводнике 5 А и проводник составляет с направлением индукции магнитного поля угол 30°.

2.    Определите величину силы Лоренца, действующей на протон с индукцией 80 мТл, со скорость протона 200 км/с перпендикулярно линиям магнитной индукции.

3.     В однородное магнитное поле индукцией 10 мТл перпендикулярно линиям индукции влетает электрон с кинетической энергией 4,8×10^-15 Дж. Каков радиус кривизны траектории движения электрона в магнитном поле?

4.    Проводник с длиной 30 см расположен горизонтально в направлении восток – запад. С какой силой и в каком направлении действует на проводник однородное магнитное поле с индукцией В=5·10-2 Тл направленное в южном направлении под углом 0° к горизонту. Ток величиной 10 А направлен в восточном направлении.

5.    В однородном магнитном поле с индукцией 0,01Тл находится прямой проводник длиной 8см, расположенный перпендикулярно линиям магнитного поля. По проводу течет ток 2А. Под действием силы Ампера проводник переместился на расстояние 5 см. Найти работу, совершенную при этом силой Ампера.

Вариант №2

1.    Проводник длиной 1,5 м с током 2 А помещен в однородно магнитное поле с индукцией 0,1 Тл. Найти силу, действующую на проводник с током, если вектор магнитной индукции перпендикулярен направлению тока.

2.    Пылинка с зарядом 0,2 Кл влетает в вакууме в однородное магнитное поле со скоростью 500 м/с перпендикулярно линиям магнитной индукции. Величина индукции магнитного поля равна 6 Тл. Определите силу, действующую на пылинку.

3.    Электрон движется в однородном магнитном поле с индукцией 0,2 Тл по винтовой линии. Определите скорость электрона, если радиус винтовой линии 3 см, а шаг 9 см.

4.    Электрон в однородном магнитном поле с индукцией 2мТл описывает окружность радиусом 2см. Найти скорость электрона.

5.    Определите силу Ампера, действующей с индукцией с индукцией 0,1 Тл с силой тока 20 А, если длина проводника 14 см.

Вариант №3

1.    Определите длину активной части проводника, помещенного в магнитное поле с индукцией 400 Тл, если при силе тока 2,5 А на него действует сила 100 Н. Проводник расположен под углом 30⁰ к линиям магнитной индукции.

2.    Электрон влетел в однородное магнитное поле индукцией 5 мТл перпендикулярно линиям магнитной индукции со скоростью 10 Мм/с. С какой силой действует поле на электрон? Какую линию он опишет?

3.    Электрон влетает в магнитное поле перпендикулярно линиям индукции со скоростью 10⁷ м/с. Найдите индукцию поля, если электрон описал в поле окружность радиусом 1 см (m_е = 9,1×10 ^-31 кг, е =  -1,6 ×10 ^-19 Кл).

4.    Электрон и протон влетают в магнитное поле с одинаковыми по модулю скоростями. Вектор скорости электрона перпендикулярен вектору магнитной индукции, а вектор скорости протона – параллелен. Чему равно отношение сил, действующих со стороны магнитного поля на электрон и протон.

5.    Определите силу тока, если магнитная индукции равна 50 мТл, сила Ампера 40 мН, длина проводника 8 см

Вариант № 4

1.    На прямолинейный проводник с током 14,5 А в однородном магнитном поле с индукцией 0,34 Тл действует сила 1,65 Н. Определить длину проводника, если он расположен по углом 60⁰к силовым линиям поля.

2.    В однородное магнитное поле с индукцией 0,085 Тл влетает электрон со скоростью 46 Мм/с, направленной перпендикулярно силовым линиям. Определить силу, действующую на электрон в магнитном поле и радиус окружности, по которой он движется.

3.    Протон в однородном магнитном поле с индукцией 0,01Тл описал окружность радиусом 10 см.  Найдите скорость движения протона (m_р = 1,67 ×10 ^-27 кг, е+=1,6×10 ^-19 Кл).

4.    Вычислить индукцию магнитного поля проводника длиной 1м, если по нему течет ток в 1А и на него действует сила со стороны магнитного поля в 1Н.

5.    Найти кинетическую энергию электрона, движущегося по дуге окружности радиусом 60 см в однородном магнитном поле с индукцией 0,12 мкТл.

Вариант №5

1.    На прямой проводник длиной 2 м и с током 50 А в однородном магнитном поле под углом 30⁰ к линиям индукции действует сила 5 Н. Найти индукцию магнитного поля.

2.    Электрон влетает в однородное магнитное поле в вакууме со скоростью 10 Мм/с, направленной перпендикулярно линиям индукции. Найти силу, действующую на электрон со стороны магнитного поля, если индукция поля равна 2 Тл.

3.    Пылинка, заряд которой 10^-5Кл и масса 1 мг, влетает в однородное магнитное поле с индукцией 1 Тл и движется по окружности. Сколько оборотов сделает пылинка за время 3,14с?

4.    Электрон движется в однородном магнитном поле индукцией 4 мТл. Найти период  обращения электрона.

5.    Проводник длиной 0,2 м помещен в однородное магнитное поле с индукцией 2 Тл перпендикулярно линиям магнитной индукции. Найти силу тока в проводнике, если со стороны магнитного поля на него действует сила 2 Н.

Вариант №6

1.    Определите силу Ампера, действующей с индукцией с индукцией 0,1 Тл с силой тока 20 А, если длина проводника 14 см.

2.    Электрон влетает в однородное магнитное поле с индукцией 1,4 мТл в вакууме со скоростью 500 км/с перпендикулярно линиям магнитной индукции. Определите силу, действующую на электрон, радиус окружности, по которой он движется.

3.    Протон в магнитном поле индукцией 0,01 Тл описал окружность радиусом 10 см. Найти скорость протона.

4.    Определите длину активной части проводника, помещенного в магнитное поле с индукцией 400 Тл, если при силе тока 2,5 А на него действует сила 100 Н. Проводник расположен под углом 300 к линиям магнитной индукции.

5.    В однородном магнитном поле, индукция которого равна 0,2014 Тл, по окружности равномерно вращается протон. Определите радиус окружности, если скорость протона равна 3200 км/с.

Тема 4.4. Электромагнитная индукция

Практическая работа № 14 «Электромагнитная индукция. Закон электромагнитной индукции»

Цели: сформировать умения и навыки нахождения физической величины, её выражение из формулы, закрепить умения и навыки вычисления величин с использованием закона электромагнитной индукции.

Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. На выполнение практической отводится два академических часа.

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Электромагнитная индукция - явление возникновения электрического тока в катушке из проводника при изменении магнитного поля. Электрический ток, возникающий в результате электромагнитной индукции, называется индукционным.

Опыты показали, что индукционный ток в катушке можно получить различными способами: можно вдвигать магнит в катушку или выдвигать его из катушки, можно надевать катушку на магнит или снимать её с магнита.

Анализируя результаты своих опытов, Фарадей установил, что

Индукционный ток возникает всегда, когда изменяется пронизывающий контур магнитный поток. Сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения отклонение стрелки гальванометра (сила тока), тем больше, чем больше скорость движения магнита, или скорость движения катушек.

Работу этих сторон них сил характеризуют электродвижущей силой индукции. При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): . ξ не зависит от свойств контура: .

Закон Фарадея (закон электромагнитной индукции): ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

ЭДС не является силой в Ньютоновом смысле. ξ_i возникает при изменении магнитного потока Ф, пронизывающего контур.

  – ЭДС индукции.

  – ЭДС индукции в контуре, содержащем N витков провода.

  – ЭДС индукции при движении одного из проводников контура (так, чтобы менялся Ф). В этом случае проводник длиной l, движущийся со скоростью v становится источником тока

 – ЭДС индукции в контуре, вращающемся в магнитном поле со скоростью ω.

Опыт показывает, что   направление индукционного тока всегда определяется общим правилом, называемым правилом Ленца.

Правило Ленца: индукционный ток имеет такое направление, что созданное им магнитное поле оказывает компенсирующее действие на изменение магнитного поля, вызывающее данный индукционный ток, препятствует происходящим измене­ниям магнитного поля.

При возрастании магнитного потока , т.е. ЭДС индукции вызывает ток такого направления, при котором его магнитное поле уменьшает магнитный поток через контур; при уменьшении магнитного потока , т.е. магнитное поле индукционного тока увеличивает убывающий магнитный поток через контур.

Электродвижущая сила в цепи - это результат действия сторонних сил, т.е. сил неэлектрического происхождения. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца, под действием которой происходит разделение зарядов, в результате чего на концах проводника появляется разность потенциалов. ЭДС индукции в проводнике характеризует работу по перемещению единичного заряда вдоль проводника.

Явление электромагнитной индукции лежит в основе действия электротехнических генераторов. Если равномерно вращать проволочную рамку в однородном магнитном поле, то возникает индукционный ток, периодически изменяющий своё направление. Даже одиночная рамка, вращающаяся в однородном магнитном поле, представляет собой генератор переменного тока. Более сложные генераторы обычно являются улучшенными вариантами такого устройства.

Экспериментально   установлено,    что индукция магнитного поля в каждой точке пространства вокруг проводника с током пропорциональна силе тока в нем. Отсюда следует, что магнитный поток через контур прямо пропорционален силе тока в проводнике:   (1)

Коэффициент пропорциональности L между силой тока I и магнитным потоком Ф через контур называется индуктивно­стью контура.

Индуктивность L – это физическая величина, зависящая от площади, охватывае­мой контуром, формы контура, свойств среды, в которой на­ходится контур.

Важно: Единица индуктивности в Международной системе называется генри (Гн). Из выражения (1) следует:  (2)  .

Контур, в котором электрический ток силой 1 ампер создает магнитный поток 1 вебер, обладает индуктивностью 1 генри.

Индуктивность контура зависит от его геометрической формы, размеров и магнитных свойств среды, в которой он находится в вакууме или воздухе:   (3), где N – общее число  витков соленоида, μ₀ – магнитная постоянная. Учитывая, что объём соленоида , а  – число витков, приходящихся на единицу длины, формулу (3) можно переписать

Величину, равную отношению индуктивности контура в однородной среде к индуктивности контура в вакууме, называют магнитной проницаемостью среды  

Магнитная проницаемость среды – безразмерная величина

Если контур, состоящий из проводника 2 (рис.), поместить вблизи контура 1 с током, изменяющимся с течением времени, то в проводнике 2 будет зарегистрировано индуцированное электрическое поле.

Явление возникновения индуцированного электрического поля в проводниках, находящихся вблизи других проводников, по которым протекает изменяющийся во времени электрический ток, называют взаимной индукцией

ЭДС взаимной индукции определим по закону электромагнитной индукции: , где DФ₂₁ - поток магнитной индукции, который создаётся магнитным полем тока, протекающего по контуру и пронизывающего площадь поверхности, охватываемой контуром 2. Магнитный поток Ф₂₁ пропорционален току I₁, протекающему по первому контуру: . Коэффициент L₂₁ называют взаимной индуктивностью контуров 1 и 2.

Взаимная индуктивность контуров 1 и 2 зависит от размеров, геометрической формы, относительной проницаемости среды и взаимного расположения контуров, выражается в тех единицах, что и индуктивность, генри (Гн)

Согласно закону электромагнитной индукции изменение магнитного потока через контур индуктивностью L в результате изменения силы тока в контуре ΔI должно вызывать появление ЭДС индукции, равной   (4)

Явление возникновения ЭДС индукции, вызванной измене­ниями силы тока в самом контуре, называется самоиндукцией, а возникающую ЭДС – ЭДС самоиндукции.

Из выражения (4) можно дать еще одно определение еди­ницы индуктивности.

Индуктивностью 1 генри обладает кон­тур, в котором при равномерном изменении силы тока на 1 ам­пер за 1 секунду возникает ЭДС самоиндукции 1 вольт.

По правилу Ленца ЭДС самоиндукции при уменьшении силы тока в контуре действует в направлении поддержания силы то­ка неизменной, при увеличении силы тока в контуре ЭДС са­моиндукции препятствует увеличению силы тока.

Как определять направление индукционного тока?

Из ряда опытов следует, что в разных случаях направление индукционного тока может быть различным: отброс стрелки гальванометра в некоторых опытах происходило в одну сторону, а в других - в противоположную. Найдем общее правило, по которому определяем направление индукционного тока.

Если приближать магнит к ведущего кольца, то оно начнет отталкиваться от магнита. Это отталкивание можно объяснить только тем, что в кольце возникает индукционный ток, обусловленный ростом магнитного потока через кольцо, а кольцо с током взаимодействует с магнитом.

 

 Иначе говоря, если магнитный поток через контур увеличивается, то направление индукционного тока в контуре такой, что вектор магнитной индукции созданного этим током поля направлен противоположно вектору магнитной индукции внешнего магнитного поля.

В случае же удаления магнита в проводящем кольце возникает индукционный ток такого направления, что кольцо притягивается к магниту. Или иначе: если магнитный поток через контур уменьшается, то направление индукционного тока таково, что вектор магнитной индукции созданного этим током поля направлен так же, как вектор магнитной индукции внешнего магнитного поля.

Общим в этих исследованиях является то, что индукционный ток имеет такое направление, что созданный им магнитный поток всегда пытается компенсировать ту изменении магнитного потока, вызвавшего этот ток.

Эта закономерность называется правилом Ленца, потому что она была установлена опытным путем российского физика Эмилем Христиановичем Ленцем через два года после открытия Фарадеем явления электромагнитной индукции.

Часто бывает удобнее воспользоваться другим формулировкой правила Ленца: во всех случаях электромагнитной индукции токи и силы направлены так, чтобы противодействовать причине их возникновения.

Правило Ленца имеет глубокий физический смысл - оно выражает закон сохранения энергии. Для создания индукционного тока необходима энергия, следовательно, следует выполнить дополнительную работу внешних сил. После приближения магнита к контуру или отдаления его от контура всегда возникает сила, препятствующая движению. Чтобы преодолеть это противодействие, выполняется работа.

Алгоритм решения задач

Во время решения задач на правило Ленца следует придерживаться такого алгоритма:

1) определить направление вектора  магнитной индукции внешнего магнитного поля;

2) из условия задачи выяснить, увеличивается или уменьшается магнитный поток, пронизывающий контур;

3) определить направление вектора  магнитной индукции магнитного поля индукционного тока: если магнитный поток увеличивается, то ; если уменьшается, то ;

4) определить направление индукционного тока, воспользовавшись правилом правой руки

Примеры решения задач

1.    За 5 мс магнитный поток, пронизывающий контур, убывает с 9 до 4 мВб. Найти ЭДС индукции в контуре.

Дано:	СИ	Решение:
Δt = 5 мс	5×10-3 с	ЭДС индукции найдём из закона электромагнитной индукции . Подставляем числовые значения:   Ответ:
Ф1 = 9 мВб	9×10-3 Вб
Ф2= 4 мВб	4×10-3 Вб
Найти: ξ -?

2.    Магнитный поток через контур из проволоки с сопротивлением 4 Ом равномерно увеличился от нуля до  6×10^-4 Вб.  Какой заряд при этом прошел через поперечное сечение проводника?

Дано:	Решение:
R=4 Ом	При равномерном изменении магнитного потока, пронизывающего контур, сила тока, протекающего в проводнике постоянна. Следовательно: . Найдем силу тока в цепи. По закону Фарадея: , – время изменения магнитного потока. По закону Ома для полной цепи сила тока: , где  R – сопротивление проводника, являющееся в данной задаче общим сопротивлением цепи. Окончательно получаем общую формулу:,  Подставляем числовые значения:   Ответ: .
Ф1=0
Ф2=6×10-4 Вб
Найти: q -?

3.    Замкнутый проводник с сопротивлением R = 3 Ом поворачивается в магнитном поле так, что магнитный поток через площадь, ограниченную проводником, возрос с Ф₁ = 0,002 Вб до Ф₂ = 0,005 Вб. Какой заряд прошел через поперечное сечение проводника за время поворота?

Дано:	Решение:
Ф1=0,002 Вб Ф2=0,005 Вб R =3 Ом	Средняя ЭДС индукции за время поворота по формуле , где Δt - время поворота. По закону Ома средняя сила тока в проводнике тогда равна . Заряд, прошедший по проводнику за время Δt, можно всегда найти как произведение средней силы тока на промежуток времени его протекания:  . Подставив числовые значения мы получаем, что заряд равен   Ответ: 1 мКл
Найти:q-?

4.    Найти скорость изменения магнитного потокав соленоиде из 2000 витков при возбуждении в нём ЭДС индукции 120 В.

Дано:	Решение:
ξ=120 В N =2000	Обобщение закона электромагнитной индукции на случай соленоида с N витками имеет вид:  (1), где ξ – ЭДС индукции,   – модуль скорости изменения магнитного потока сквозь каждый виток. Из формулы (1) следует искомое выражение для скорости изменения магнитного потока: . Подставив числовые значения мы получаем, что заряд равен Ответ:
Найти: -?

5.    Сила тока в обмотке соленоида, содержащего 1500 витков, равна 5 А. Магнитный поток через поперечное сечение соленоида составляет 200 мкВБ. Определите энергию магнитного поля в соленоиде.

Дано:	СИ	Решение:
I = 5 А		Энергия магнитного поля в соленоиде вычисляется по формуле . Магнитный поток можно вычислить как , где Ф1 – магнитный поток одного витка соленоида. Из последней формулы выразим индуктивность . Подставим эту формулу в формулу вычисления энергии магнитного поля и получим: . Подставляем числовые значения:   Ответ:
Ф1 = 200 мкВб	2×10-4 Вб
N=1500
Найти: W -?

6.    Обмотка электромагнита, находясь под постоянным напряжением, имеет сопротивление 15 Ом и индуктивность 0,3 Гн. Определите время, за которое в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике.

Дано:	Решение:
R = 15 Ом	Количество теплоты, которое выделяется в обмотке электромагнита по условию равна энергии магнитного поля  количество теплоты можно найти по закону Джоуля-Ленца (1) Энергия магнитного поля равна  . (2) Приравнивая правые части формул (1) и (2), получим , так как U=const, то из последней полученной формулы выразим время . Подставляем числовые значения:   Ответ:
L = 0,3 Гн
Q=W
Найти: t -?

7.   Сила тока в контуре меняется по закону , где t – время, в секундах. Если при t=0 магнитный поток равен 0,2 Вб, то в конце пятой секунды он равен...(в Вб).

Дано:	Решение:
0	В  начальный  момент  времени  магнитный  поток: . В произвольный момент времени: . Отношение магнитных потоков: . Значение силы тока в момент времени t0=0: . В момент времени t = 5 с: . Произведём вычисления:   Ответ:

Контрольные вопросы для самопроверки

1.       Какое явление называется электромагнитной индукцией?

2.       Сформулируйте закон электромагнитной индукции.

3.       Сформулируйте правило Ленца.

4.       Какое явление называется самоиндукцией?

5.       Что называется индуктивностью?

Индивидуальные задания к практической работе № 14

Вариант №1

1.    В проводнике длиной 10см необходимо создать ЭДС индукции в 1В. С какой наименьшей скоростью необходимо перемещать этот проводник в магнитном поле с индукцией 0,2Тл?

2.    Сколько витков должна содержать катушка с площадью поперечного сечения 50 см^2, чтобы при изменении магнитной индукции от 0,2 до 0,3 Тл в течение 4 мс в ней возбуждалась ЭДС 10 В?

3.    Найти ЭДС индукции в проводнике с длиной активной части 0,25 м, перемещающемся в однородном магнитном поле индукцией 8 мТл со скоростью 5 м/с под углом 30⁰ к вектору магнитной индукции.

4.    В однородном магнитном поле, индукция которого равна 3·10² Тл поворачивают рамку площадью 90 см². Определить индукционный заряд, который пройдет через сечение проводника рамки с сопротивлением 0,1 Ом, если в начале поворота рамки ее плоскость была перпендикулярна, а в конце поворота параллельна вектору индукции.

5.    Определите индуктивность катушки, если при силе тока 6,2 А ее магнитное поле обладает энергией 0,32 Дж.

6.     Сколько витков должна иметь катушка, чтобы при изменении магнитного потока внутри неё от 0,024 до 0,056 Вб за 0,3 с в ней создавалась средняя ЭДС индукции, равная 10В?

Вариант №2

1.   Магнитный поток через контур из проволоки с сопротивлением 4 Ом равномерно увеличился на . Какой заряд при этом прошел через поперечное сечение проводника?

2.    За 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает с 9 до 7 мВб. Определите ЭДС индукции в соленоиде, а также силу индукционного тока в нем, если сопротивление равно 2 Ом.

3.    По горизонтальным рельсам, расположенным в вертикаль­ном магнитном поле с индукцией 0,01 Тл, скользит проводник длиной l=1 м с постоянной скоростью 10 м/с. Концы рельсов замкнуты на сопротивление R=2 Ом. Какое количество теплоты выделяется в сопротивлении за 1 с? Сопротивлением рельсов и движущегося проводника пренебречь.

4.    Найти ЭДС индукции в проводнике с длиной активной части 0,25 м, перемещающемся в однородном магнитном поле индукцией 8 мТл со скоростью 5 м/с под углом 30⁰ к вектору магнитной индукции.

5.    При помощи реостата равномерно увеличивают силу тока в катушке со скоростью 2 А/с, индуктивность катушки 200 мГн. Чему равна ЭДС самоиндукции в катушке?

6.    Какая ЭДС самоиндукции возникает в катушке индуктивностью 68 мГн, если ток в 3,8 А исчезает в ней за 0,012 с?

Вариант №3

1.    С какой скоростью надо перемещать проводник, длина активной части которого 1 м, под углом 60⁰ к линиям индукции магнитного поля, чтобы в проводнике возбуждалась ЭДС индукции 1 В? Индукция магнитного поля равна 0,2 Тл.

2.    Сколько витков провода должна со­держать обмотка на стальном сердечнике с поперечным сечением 50 см², чтобы в ней при изменении магнитной индукции от 0,1 до 1,1 Тл в течение 5 мс возбуждалась ЭДС индукции ξ_i = -100 В? Поле считать перпендикулярным виткам.

3.    В однородном магнитном поле с индукцией 0,1 Тл распо­ложен плоский проволочный виток, площадь которого 10³ см², а сопротивление равно 2 Ом. Плоскость витка перпендикулярна си­ловым линиям. Виток замкнут на гальванометр. Когда виток повер­нули, то через гальванометр прошел заряд 2,5мКл. На какой угол повернули виток?

4.    Сколько витков должна содержать катушка с площадью поперечного сечения 50 см² , чтобы при изменении магнитной индукции от 0,2 до 0,3 Тл в течение 4 мс в ней возбуждалась ЭДС 10 В?

5.    При равномерном уменьшении в течение 0,1 с силы тока в катушке от 10 А до нуля в ней возникла ЭДС самоиндукции 60 В. Определите индуктивность катушки.

6.    Определить энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3·10^-3Вб. Число витков в катушке 120.

Вариант № 4

1.    Найти величину средней ЭДС, возникающей при размыкании тока в электромагните с индукцией 1,6 Тл, если число витков равно 1000, а поперечное сечение обмотки магнита 30 см². Время размыкания тока 1 мс.

2.    Какую длину активной части должен иметь проводник, чтобы при перемещении его со скоростью 15 м/с перпендикулярно линиям индукции поля в нём возбудилась ЭДС индукции 3 В? Магнитная индукция поля равна 0,4 Тл.

3.    Какой заряд пройдёт через поперечное сечение витка, сопротивление которого 0,03 Ом, при уменьшении магнитного потока внутри витка на 12 мВб?

4.    За 5 мс магнитный поток, пронизывающий контур, убывает с 9 до 4 мВб. Найти  ЭДС индукции контура.

5.    Индуктивность катушки 0,1 мГн. При какой силе тока энер­гия магнитного поля будет равна 0,2 мДж?

6.    В катушке возникает магнитный поток 0,015 Вб, если по её виткам проходит ток 5 А. Сколько витков содержит катушка, если её индуктивность 60 мГн?

Вариант №5

1.    Ток 600 мА создает в контуре магнитный поток 20 мВб. Определить индуктивность контура и энергию магнитного поля контура.

2.    С какой скоростью надо перемещать проводник длиной 20 см перпендикулярно силовым линиям однородного магнитного поля, чтобы на концах проводника возникла ЭДС индукции 0,05 В? Индукция магнитного поля 0,5 Тл.

3.    В магнитное поле индукцией 0,1 Тл помещен контур, выполненный в форме кругового витка радиусом 3,4 см. Виток сделан из медной проволоки, площадь поперечного сечения которой 1 мм². Нормаль к плоскости витка совпадает с линиями индукции поля. Какой заряд пройдёт через поперечное сечение витка?

4.    Определить ЭДС индукции возникающей в проводнике длиной 60 см движущегося со скоростью 25 м/с в магнитном поле с индукцией 5·10^-4 Тл перпендикулярно направлению индукции.

5.    Найдите энергию магнитного поля соленоида, в котором при силе тока 10 А магнитный поток составляет 0,5 Вб.

6.    Чему равна индуктивность катушки с железным сердечником, если за время 0,5 с ток в цепи изменился с 10 до 5 А, а наведённая при этом на концах катушки ЭДС равна 25 В?

Вариант №6

1.    Проволочный виток площадью 2м² расположен перпендикулярно ли­ниям магнитной индукции однородного магнитного поля. Величина маг­нитной индукции равна 0,04 Тл. За время 0,01 с магнитная индукция спада­ет до нуля. Найдите ЭДС индукции в витке.

2.    Прямолинейный проводник длиной 86 см движется со скоростью 14 м/с в однородном магнитном поле с индукцией 0,025 Тл. Определить угол между векторами индукции поля и скорости, если в проводнике индуцируется ЭДС, равна 0,12 В.

3.    В магнитное поле индукцией 0,1 Тл помещен контур, выполненный в форме кругового витка радиусом 3,4 см. Виток сделан из медной проволоки, площадь поперечного сечения которой 1 мм². Нормаль к плоскости витка совпадает с линиями индукции поля. Какой заряд пройдёт через поперечное сечение витка при исчезновении поля?

4.    Определить индуктивность катушки, если при изменении силы тока в ней со скоростью 5 А/с ЭДС самоиндукции равна 120 В.

5.    В катушке индуктивностью 0,6 Гн сила тока равна 20 А. Какова энергия магнитного поля этой катушки? Как изменится энергия поля, если сила тока уменьшится вдвое?

6.    Поток магнитной индукции через площадь поперечного сечения катушки, имеющей 1000 витков, изменился на 0,002 Вб в результате изменения тока с 4 до 20 А. Найти индуктивность катушки.

Лабораторная работа № 4. Изучение явления электромагнитной индукции

Цели работы: исследование явления электромагнитной индукции,  определение на опыте зависимости силы и направления индукционного тока в катушке, знакомство с принципом действия трансформатора, определение коэффициента трансформации.

Оборудование: миллиамперметр, проволочная катушка, дуго­образный и полосовой магниты, источник тока, две катушки с сердечником, реостат, ключ, соединительные провода, трансформатор лабораторный разборный, вольтметры переменного  тока.

Описание работы

Индукционный ток в замкнутом контуре возникает при изме­нении магнитного потока через площадь, ограниченную контуром. В данной работе магнитный поток изменяют следующими спосо­бами:

1. изменяя во времени магнитное поле, в котором находится неподвижный контур — например, вдвигая магнит в катушку или выдвигая его из катушки;

2. перемещая этот контур (или его части) в постоянном маг­нитном поле (например, надевая катушку на магнит).

Ход работы

1. Одну из катушек без сердечника подключите к зажимам миллиампер­метра. Надевайте и снимайте катушку с северного полюса дугообразного маг­нита с различной скоростью.

2. Для каждого случая замечайте максимальное значение силы индукционного тока и его направление (по отклонению стрелки миллиамперметра). Запишите вывод.

3. Переверните магнит и наденьте катушку на его южный по­люс, а затем снимите её. Повторите опыт, увеличив скорость ка­тушки. Обратите внимание на показания миллиамперметра, в ча­стности, на направление отклонения стрелки прибора. Запишите выводы.

4. Сложите два магнита (полосовой и дугообразный) одноимен­ными полюсами и повторите эксперимент с разной скоростью дви­жения катушки относительно магнитов. Запишите вывод.

2 часть работы:

5. Соберите установку, схе­матически изображенную на рисунке.

6. Проведите следующие опыты.

а)  Поставьте ползунок ре­остата в положение, соответ­ствующее минимальному со­противлению. Замкните цепь ключом. Запишите, что вы на­блюдали при замыкании цепи.

б)  Разомкните цепь. Запишите, что вы наблюдали при размы­кании цепи.

б)  Разомкните цепь. Запишите, что вы наблюдали при размы­кании цепи.

в)  При замкнутой цепи изменяйте положение ползунка реос­тата и наблюдайте за показаниями миллиамперметра. Запишите, что вы наблюдали.

г)  Какие явления, наблюдаемые в этом опыте, помогают по­нять принцип действия трансформатора? Запишите свой ответ.

7. Определите первичную обмотку и две вторичные клеммы.

8. Присоедините первичную обмотку к сети переменного тока напряжением 36  В и измерьте напряжение на одной из вторичных обмоток.

9. Вычислите коэффициент трансформации.

10. Проделайте аналогичные действия для другой вторичной обмотки.

11. Присоедините одну из вторичных обмоток к сети переменного тока напряжением 4 В и измерьте напряжение на первичной обмотке.

12. Вычислите коэффициент трансформации.

13. Полученные данные запишите в таблицу.

10.  Запишите выводы из эксперимента.

Таблица

U	U1	U2	K1 = U1/U	K2 = U2 /U
4 В
36 В

Контрольные вопросы

1.  В чем заключается явление электромагнитной индукции?

2.  Какой ток называют индукционным?

3.  Сформулируйте закон электромагнитной индукции. Какой

формулой он описывается?

4.  Как формулируется правило Ленца?

5.  Какова связь правила Ленца с законом сохранения

энергии?

6. В чем заключается принципом действия трансформатора?

7.  Какой ток называют индукционным?

8. Что такое коэффициент трансформации?

9. Виды коэффициента трансформации.

Тема 4.5. Электромагнитные колебания

Практическая работа № 15. Переменный электрический ток. Трансформаторы

Цель: формирование знаний, умений и навыков при решении задач, анализировать задачу, отработка умений выполнять задания по образцу, обобщение и систематизация знаний по теме «Переменный ток», выявить умение студентов работать с уравнениями колебаний электрических величин, т.е. умение определять по уравнению параметры колебания.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. 

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Переменный ток – ток, изменяющийся во времени, является вынужденным электрическим колебанием.

При равномерном вращении плоской рамки площадью S, состоящей из N витков, в однородном магнитном поле с индукцией В в рамке возбуждается ЭДС индукции: , где  – амплитуда колебаний ЭДС. Если напряжение, подводимое в цепь, не содержащую индуктивности и емкости, изменяется по закону:  или . Тогда сила тока:  или

Сопротивление такой цепи называется активным:  где U – действующее значение напряжения, I – действующее значение силы тока: , .

Зная мгновенные значения u(t) и i(t), можно вычислить мгновенную мощность p(t) = u(t)i(t), которая, в отличие от цепей постоянного тока, изменяется с течением времени. С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
p(t) = u(t)i(t) = i²(t)R = I_o²Rsin²ωt. Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно. Перепишем формулу для мощности по-другому: р=ui=U_oI_osin²ωt=(1/2)U_oI_o(1−cos2ωt)=U_oI_o/2 − (U_oI_o/2)cos2ωt (*).

Выделяемая в цепи переменного тока мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между напряжением и силой тока.

Первое слагаемое не зависит от времени. Второе слагаемое − переменная составляющая − функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю. Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле

P_cp = U_oI_o/2 = I_o²/R. Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока. Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток. Поскольку для постоянного тока P_пост =I²R,то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока I_д = I_o/√2.Аналогично можно ввести действующее значение и для напряжения U_д = U_o/√2.Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения: P = U_дI_д = I_д²R = U_д²/R, I_д = U_д/R.

Трансформатор – устройство, применяемое для повышения или понижения напряжения переменного тока.

Трансформатор состоит из замкнутого стального сердечника, собранного из пластин, на который надеты две (иногда и более) катушки с проволочными обмотками. Одна из обмоток, называемая первичной, подключается к источнику переменного напряжения. Другая обмотка, к которой присоединяют нагрузку, т.е. приборы и устройства, потребляющие электроэнергию, называется вторичной.

Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в сердечнике появляется переменный магнитный поток, которым возбуждается ЭДС индукции в витках каждой обмотки. В первичной обмотке, имеющей N₁ витков, полная ЭДС индукции е₁ равна . Во вторичной обмотке полная ЭДС индукции е₂ равна  (N₂ - число витков этой обмотки) Отсюда следует, что . (1)

Обычно активное сопротивление обмоток трансформатора мало, и им можно пренебречь. В этом случае модуль напряжения на зажимах первичной обмотки примерно равен модулю суммарной ЭДС индукции: (2).

При разомкнутой вторичной обмотке трансформатора ток в ней не идёт, и имеет место соотношение  (3).

Мгновенные ЭДС е₁ и е₂ изменяются синфазно (одновременно достигают максимума и одновременно проходят через нуль). Поэтому их соотношение в формуле (1) можно заменить отношением действующих значений 𝜉₁ и 𝜉₂ этих ЭДС или, учитывая равенства (2) и (3) отношением действующих значений напряжений U₁ и U₂:  (4)

Величина k называется коэффициентом трансформации. Он равен отношению напряжений в первичной и вторичной обмотках трансформатора.

При k>1 трансформатор является понижающим, а при k<1 - повышающим.

Уменьшение амплитуды колебаний результирующего магнитного потока, казалось бы, должно, в свою очередь, уменьшить ЭДС индукции в первичной обмотке. Это, однако, не произойдёт, так как согласно формуле (2) . Поэтому при замыкании цепи вторичной обмотки автоматически увеличится сила тока в первичной обмотке. Его амплитуда возрастает таким образом, что восстановится прежнее значение амплитуды колебаний результирующего магнитного потока.

Увеличение силы тока в цепи первичной обмотки происходит в соответствии с законом сохранения энергии: отдача электроэнергии в цепь, присоединённую к вторичной обмотке трансформатора, сопровождается потреблением от сети такой же первичной обмоткой.

Мощность в первичной цепи при нагрузке трансформатора, близкой к номинальной, примерно равна мощности во вторичной цепи:   (5) отсюда  (6)

Это означает, что, повышая с помощью трансформатора напряжение в несколько раз, мы во столько же раз уменьшаем силу тока (и наоборот).

Следовательно, токи в обмотках трансформатора обратно пропорциональны напряжениям, а значит, и числам витков. Поэтому обмотку высшего напряжения всегда делают из большего числа витков провода меньшего сечения, тогда как обмотку низшего напряжения выполняют из меньшего числа витков провода большего сечения.

Любой КПД определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой. Учитывая, что работа равна отношению мощности ко времени, для трансформатора можно записать формулу КПД через мощность:      η = P₂ / P₁

Так как КПД трансформатора примерно 94-98%, то Р₂ немного меньше чем Р₁.

По числу фаз трансформаторы разделяют на однофазные и трехфазные. По назначению различают силовые (предназначенные для передачи и распределения электрической энергии) и специальные (сварочные, измерительные, печные, испытательные, инструментальные и т. д.) трансформаторы.

По способу охлаждения классификация такова: трансформаторы с воздушным, масляным, а также с масляным и принудительным воздушным охлаждением.

Колебательный контур представляет собой электрическую цепь, состоящую из конденсатора С и индуктивности L, соединенных между собой. Если сопротивление контура R =0, то такой колебательный контур называют идеальным.

Колебательный контур - электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора ёмкостью С и резистора сопротивлением R (рис. 1).

Колебательный контур предназначен для возбуждения и поддержания электромагнитных колебаний, сопровождающихся периодическим изменением электрических величин (зарядов, токов) и взаимны­ми превращениями электрического и магнитного полей.

1.        

2.       Рис. 1

Если в колебательном контуре отсутствует внешняя ЭДС, то в нем возникают свободные электромагнитные колебания, сопровождающиеся периодическими превращениями энергии электрического поля в энергию магнитного поля, и наоборот.

Период незатухающих собственных колебаний, возникающих в колебательном контуре, определяется по формуле . Эту формулу называют формулой Томсона.

Циклическая частота собственных электромагнитных колебаний . В идеальном колебательном контуре колебания происходят по закону , где q₀ - максимальный заряд на обкладках конденсатора; ω - циклическая частота собственных колебаний; ω₀ - начальная фаза.

Периодическое изменение заряда на обкладках конденсатора вызывает переменную разность потенциалов - переменное напряжение U и переменный электрический ток I: , где  - амплитуда напряжения.

Учитывая, что электрический ток характеризует скорость изменения заряда на обкладках конденсатора, можно записать: , где  - амплитуда тока.

Таким образом, по гармоническому закону изменяется не только заряд на обкладках конденсатора, но и напряжение и сила тока в контуре, т.е. возникают свободные электромагнитные колебания.

Отсюда вытекает, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на π/2.

Следовательно, ток достигает максимального значения в те моменты времени, когда заряд (напряжение) на обкладках конденсатора равен нулю, и наоборот.

Из закона сохранения энергии следует, что при R = 0 (потери на джоулеву теплоту отсутствуют) полная энергия колебательного контура W в каждый данный момент времени равна сумме энергий электрического поля конденсатора и магнитного поля катушки : . Очевидно, что максимальное значение энергии электрического поля заряженного конденсатора равно максимальному значению энергии магнитного поля катушки , где q_m и 1_т — амплитуды заряда и силы тока. Энергия электрического поля конденсатора полностью превращается в энергию магнитного поля катушки

Резонанс – явление резкого возрастания амплитуды вынужденных колебаний, при совпадении частоты внешней периодической силы с собственной частотой колебаний системы. ω₀= ω= 1/

Алгоритм решения задач

1 Задачи, в которых рассматриваются процессы в колебательном контуре: определяется связь между величинами емкости, индуктивности и параметрами возникших колебаний.

2 Для идеального колебательного контура справедлив закон сохранения энергии.

3 Все задачи, в которых задана аналитическая или графическая зависимость от времени ЭДС ξ , силы тока I, напряжения U и заряда q решаются точно так же, как и задачи такого типа на механические колебания.

4 Задачи на расчет цепей переменного тока решаются по закону Ома.

Примеры решения задач

1.     Частоту вращения проволочной рамки в однородном магнитном поле увеличили в 3 раза. Во сколько раз изменится частота переменного тока в рамке и ЭДС индукции.

Решение: При равномерном вращении рамки в однородном магнитном поле частота переменного тока в рамке равна частоте вращения рамки. Поэтому частота переменного тока увеличится также в з раза. ЭДС индукции, возникающая при вращении рамки, , где B – индукция магнитного поля, S – площадь рамки. Следовательно, он также увеличатся в 3 раза.

Ответ: частота переменного увеличится в 3 раза; ЭДС индукции увеличится в 3 раза.

 

2.     Амплитуда силы тока в контуре 1,4 мА, а амплитуда напряжения 280 В. Найти силу тока и напряжение в тот момент времени, когда энергия магнитного поля катушки равна энергии электрического поля конденсатора.

 

Дано:	СИ	Решение:
Im=1,4 мА Um=280В Wм=Wэ		Полная энергия колебательного контура равна: , где Im, Um – амплитудные значения силы тока и напряжения. В момент, когда энергия магнитного поля катушки равна энергии электрического поля конденсатора, закон сохранения энергии имеет вид  , причем  , тогда  и  .  Ответ: раз меньше соответствующих амплитуд силы тока и напряжению.
Найти: Iд -? Uд-?

3.     Рамка площадью 200 см² вращается с частотой 8 с^-1 в магнитном поле индукцией 0,4 Тл. Написать уравнения Ф = Ф(t) и e = e(t), если при t = 0 нормаль к плоскости рамки перпендикулярна линиям индукции поля. Найти амплитуду ЭДС индукции

Дано:	СИ	Решение:
S=200 см2 ν=8 с-1 B=0,4 Тл		Запишем общее выражение для потока магнитной индукции через поверхность, ограниченную рамкой: , здесь B – индукция магнитного поля, S – площадь рамки, ν – частота ее вращения, φ – фаза. Из условия задачи, при t=0 угол между нормалью к плоскости рамки и индукцией магнитного поля равен 900, находим . Таким образом, уравнение Ф = Ф(t) имеет вид:  . Согласно закона электромагнитной индукции, ЭДС индукции определятся формулой , а уравнение e = e(t) имеет вид . Из этого уравнения следует, что амплитуда ЭДС индукции равна 0,4 А.             Ответ: , , ξм=0,4 В
Найти: Ф = Ф(t);  e = e(t)

 

4.     Понижающий трансформатор с коэффициентом трансформации, равным 10, включен в сеть напряжением 220 В. Каково напряжение на выходе трансформатора, если сопротивление вторичной обмотки 0,2 Ом, а сопротивление полезной нагрузки 2 Ом?

Дано:	Решение:
U=220 В k=10 R=2 Ом R=0,2 Ом	Используя коэффициент трансформации, найдём ЭДС, индуцируемую во вторичной обмотке: . Запишем теперь закон Ома для полной цепи вторичной обмотки , где r – сопротивление вторичной обмотки, R – сопротивление полезной нагрузки. Тогда сила тока в цепи вторичной обмотки . Напряжение на выходе трансформатора равно падению напряжения на сопротивлении полезной нагрузки  . Вычисления:   Ответ:
Найти: Uв -?

7.    Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t в соответствии с уравнением . Записать уравнение , выражающее зависимость силы тока от времени. Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока.

Дано:	Решение:
	Мгновенное значение силы тока  . Период колебаний определяется из условия  , откуда . Частота колебаний связана с периодом соотношением  , откуда  . Амплитуда колебаний заряда , согласно общему виду уравнения гармонических колебаний заряда , равна 10-6 Кл, а амплитуду силы тока Im можно рассчитать по формуле мгновенного значения силы тока i(t) и она равна .  Ответ: , T= 002 с, 𝜈=5кГц, qm=1мкКл, Im=31,4мА
Найти:   Т-? n - ? -? -?

8.    Амплитуда силы тока в контуре 1,4 мА, а амплитуда напряжения 280 В. Найти силу тока и напряжение в тот момент времени, когда энергия магнитного поля катушки равна энергии электрического поля конденсатора.

Дано:	СИ	Решение:
Im=1,4 мА Um=280В Wм=Wэ		Полная энергия колебательного контура равна: , где Im, Um – амплитудные значения силы тока и напряжения. В момент, когда энергия магнитного поля катушки равна энергии электрического поля конденсатора, закон сохранения энергии имеет вид  , причем  , тогда  и  .  Ответ: раз меньше соответствующих амплитуд силы тока и напряжению.
Найти: Iд -? Uд-?

9.    В колебательном контуре индуктивность катушки равна 0,2 Гн, а амплитуда колебаний силы тока 40 мА. Найти энергию электрического поля конденсатора и магнитного поля кату в тот момент, когда мгновенное значение силы тока в 2 раза меньше амплитудного значения.

Дано:	СИ	Решение:
Im=40 мА L=0,2 Гн Im=2i		Зная индуктивность катушки и амплитудное значение силы тока, можно найти полную энергию колебательного контура: . Энергия магнитного поля катушки, когда ток вдвое меньше амплитудного значения, равна . Теперь энергию электрического поля конденсатора можно найти из закона сохранения энергии . Подставим числовые значения в полученные формулы ,  и Ответ: ,
Найти: Wм -? Wэ -?

Вопросы для самоконтроля по теме:

1.    Какие колебания называются электромагнитными?

2.    Что называют колебательным контуром? 

3.    Какие колебания называют свободными электромагнитными колебаниями? Каким образом возникают свободные колебания в колебательном контуре? От чего зависит период свободных колебаний в контуре?

4.    Запишите закон сохранения энергии в идеализированном колебательном контуре (R=0).

5.    Какой ток называется переменным? Чему равна промышленная частота переменного тока?

6.    Что называется действующими значениями силы тока и напряжения переменного тока?

7.    Какое устройство называется трансформатором? Как он устроен? Что является основной характеристикой трансформатора?

Индивидуальные задания к практической работе № 15

Вариант №1

1.    Амплитудные значения напряжения и тока на резисторе соответственно равны U_m=100 В, I_m=2 А. Какая средняя мощность выделится резисторе этой цепи?

2.    В сеть переменного тока частотой 50 Гц и напряжением 220 В включают конденсатор ёмкостью 4 мкФ. Найдите амплитудное и действующее значения силы тока в цепи конденсатора.

3.    Напряжение нах первичной обмотки трансформатора 110 В, сила тока в ней 0,1 А. Напряжение на концах вторичной обмотки 220В, сила тока в ней 0,04 А. Чему равен КПД трансформатора?

4.    Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?

5.    Заряд q на пластинах конденсатора колебательного контура изменяется с течением времени t в соответствии  с уравнением  . Записать уравнение зависимости силы тока от времени  Найти период и частоту колебаний в контуре, амплитуду колебаний заряда и амплитуду колебаний силы тока.

6.    Амплитуда силы тока в контуре 1,4 мА, а амплитуда напряжения 280 В. Найти силу тока и напряжение в тот момент времени, когда энергия магнитного поля катушки равна энергии электрического поля конденсатора.

Вариант №2

1.    Найдите активное сопротивление электрической лампы, включенной в цепь переменного тока с действующим напряжением 220 В, если при этом на ней выделяется средняя мощность 200 Вт.

2.    Действующее значение напряжения и силы переменного тока в резисторе равны соответственно 10 В и 0,5 А. Найдите амплитуды напряжения и силы тока, среднюю мощность, выделяющуюся на резисторе.

3.    Трансформатор, содержащий в первичной обмотке 840 витков, повышает напряжение с 220 до 660 В. Каков коэффициент трансформации? Сколько витков содержится во вторичной обмотке?

4.    Как изменится период и частота собственных колебаний контура, если его индуктивность увеличить в 10 раз, а ёмкость уменьшить в 2,5 раза?

5.    В идеальном электрическом колебательном контуре ёмкость конденсатора 2 мкФ, а амплитуда напряжения на нём 10 В. Определите максимальное значение энергии магнитного поля катушки.

6.    В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Конденсатор какой ёмкости надо включить в эту цепь, чтобы осуществлялся резонанс?

Вариант №3

1.   ЭДС, возникающая в рамке при вращении её в однородном магнитном поле, изменяется по закону . Определить амплитудное значение ЭДС, действующее значение ЭДС, период и частоту тока, мгновенное значение ЭДС при 0,01с.

2.    На какое напряжение надо рассчитывать изоляторы линии передачи, если действующее напряжение 430 кВ

3.    Первичная обмотка понижающего трансформатора включена в сеть переменного тока с напряжением U₁ = 220 В. Напряжение на зажимах вторичной обмотки U₂ = 20 В, ее сопротивление R₂ = 1 Ом, сила тока в ней I = 2 А. Найдите коэффициент трансформации.

4.    Найти период Т и частоту ν колебаний в контуре, состоящем из конденсатора емкостью С = 800 пФ и катушки индуктивностью L = 2 мкГн.

5.    В колебательном контуре конденсатор емкостью 50 кФ заряжен до максимального напряжения 100 В. Определите резонансную частоту колебаний в контуре, если максимальная сила тока в контуре равна 0,2 А. Активное сопротивление равно нулю.

6.   Уравнение колебаний напряжения (в СИ) . Определите амплитудное и действующее значения напряжения, период и частоту колебаний.

Вариант № 4

1.    Амплитуда колебаний напряжения на участке цепи переменного тока равна 50 В. Чему рано действующее значение напряжения на этом участке цепи?

2.    Понижающий трансформатор с коэффициентом трансформации 10 включен в сеть с напряжением 127 В. Сопротивление вторичной обмотки 2 Ом, сила тока 3 А. Определить напряжение на клеммах вторичной обмотки. Потерями энергии в первичной обмотке пренебречь.

3.    В цепь переменного тока частотой 200 Гц включили катушку индуктивностью 2 Гн, амплитуда силы тока равна 10А. Найдите действующее значение напряжения.

4.   Электрический заряд конденсатора в цепи переменного тока изменяется с течением времени по закону . Определить амплитуду заряда, циклическую и линейную частоты, период, фазу и начальную фазу колебаний.

5.    Определить период и частоту собственных колебаний контура, если индуктивность катушки равна Гн, а конденсаторы в контуре соединены параллельно и их электроёмкости равны  .

6.    В цепь переменного тока включены конденсатор емкостью 2 мкФ и катушка индуктивностью 0,005 Гн. При какой частоте тока в этой цепи будет резонанс?

Вариант №5

1.    В сеть переменного тока с действующим напряжением 220 В включено активное сопротивление 55 Ом. Определить действующее и амплитудное значение силы тока

2.    Сколько витков имеет рамка площадью 500 см², если при вращении ее с частотой 20 с 1 в однородном магнитном поле индукцией 0,1 Тл амплитудное значение ЭДС равно 63 В.

3.    Трансформатор с коэффициентом трансформации 10, имеет в первичной цепи напряжение 220 В. Во вторичной цепи, сопротивление которой 2 Ом, течет ток 4 А. Рассчитайте напряжение на выходе трансформатора. Потерями в первичной обмотке пренебречь.

4.   Напряжение на участке цепи изменяется с течением времени по закону . Определите амплитуду напряжения, циклическую и линейную частоты, период, фазу и начальную фазу колебаний.

5.    Определить период и частоту собственных колебаний контура, если индуктивность катушки равна 0,05 Гн, а конденсаторы в контуре соединены последовательно и их электроёмкости равны  .

6.    Максимальный заряд конденсатора в колебательном контуре 6 мкКл. Индуктивность катушки 3 мГн, электроёмкость конденсатора 2 мкФ. В некоторый момент времени сила тока в колебательном контуре равна 0,024 А. Определите заряд на конденсаторе в этот момент времени.

Вариант №6

1.    В рамке, равномерно вращающейся в однородном магнитном поле, индуцируется ток, мгновенное значение которого выражается формулой . Определить амплитудное и действующее значения силы тока, период и частоту тока, мгновенное значение силы тока при 0,05 с.

2.    Амплитуды напряжения и силы переменного тока в резисторе равны соответственно 28 В и 0,14 А. Найдите действующие значения силы тока и напряжения, а также среднюю мощность, выделяющуюся на резисторе.

3.    Трансформатор повышает напряжение с 220 В до 1,1 кВ и содержит 700 витков в первичной обмотке. Определите коэффициент трансформации, число витков во вторичной обмотке.

4.    В электрическом колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5 мА, а амплитуда напряжения на конденсаторе 2 В. Определите напряжение на конденсаторе в тот момент, когда сила тока будет равна 3 мА.

5.    Определить силу тока в колебательном контуре в момент полной разрядки конденсатора, если энергия магнитного поля катушки равна Кл, максимальное напряжение на его обкладках 500 В?

6.    Каков диапазон частот свободных колебаний в контуре, если его индуктивность можно изменять в пределах от 0,1 до 10 мкГн, а емкость — в пределах от 40 до 4000 пФ?

Практическая работа № 16. «Конденсатор и катушка в цепи переменного тока»

Цель: закрепить знания студентов о существовании сопротивления только в цепи переменного тока – это емкостное и индуктивное сопротивления, отработка умений и навыков решать задачи на вычисление ёмкостного и индуктивного сопротивлений, анализировать задачу, выполнять задания по образцу.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. 

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

В цепи с переменным током принято различать активное R и реактивное X сопротивления. Первым из них обладают те элементы цепи, в которых электрическая энергия необратимо пре­образуется во внутреннюю, а вторым — те элементы, в которых подобного преобразования не происходит.

Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком. Переменный же ток может идти по цепи, содержащий конденсатор.

При включении конденсатора в цепь переменного тока  (см рис) на его обкладках возникает переменное напряжение (1). Через диэлектрик, разделяющий обкладки конденсатора, электрические заряды проходить не могут. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в подведенных к нему проводах появляется переменный ток.

Колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на π/2 или переменный ток в цепи с емкостью опережает напряжение по фазе на π/2 (рис)

Это происходит потому, что при периодической зарядке конденсатора в цепи течет переменный ток, достигающий максимального значения в те моменты времени, когда напряжение равно нулю. Для такой цепи выполняется закон Ома не для мгновенных, а для амплитудных значений.

Чтобы найти сопротивление конденсатора переменному току, сопоставим выражение (3) с формулой сопротивления, получаемой на основе закона Ома. Мы видим, что . Если цепь, в которую включен конденсатор, обладает сопротивлением Х_C называемым емкостным

Физическая величина, обратная произведению циклической частоты тока на электроемкость конденсатора, называется емкостным сопротивлением:  

В этом случае, как мы знаем, сопротивление цепи переменному току является реактивным. С учетом этого определения соотношение можно переписать в виде .

Ёмкостное сопротивление обратно пропорционально емкости и круговой частоте переменного тока

Пусть в цепь переменного тока с . Включена катушка индуктивности, т. е. катушка со значительной индуктивностью L и пренебрежимо малым активным сопротивлением R (рис).

Колебания напряжения на катушке опережают по фазе колебания силы тока в ней на π/2 или переменный ток в цепи с индуктивностью отстает по фазе от напряжения π/2 (рис)

Это происходит потому, что при увеличении силы тока ЭДС самоиндукции вызывает индукционный ток, препятствующий увеличению основного тока, вследствие этого сила тока достигает максимального значения позже, чем напряжение. В этом случае, как известно, сопротивление цепи переменному току является реактивным.

Физическая величина, равная произведению циклической частоты тока на индуктивность катушки, называется индуктивным сопротивлением:  С учётом этого определения .

Возникновение индуктивного сопротивления обусловлено явлением самоиндукции: появляющееся при колебаниях силы тока в катушке вихревое электрическое поле препятствует тем изменениям тока, которые его вызвали.

Индуктивное сопротивление пропорционально индуктивности и круговой частоте

Рассмотрим полную цепь переменного тока, содержащую последовательно включённые резистор сопротивлением R, катушку индуктивностью L  и конденсатор ёмкостью C, к которой приложено переменное напряжение . Амплитуда силы тока .

Амплитуда силы переменного тока пропорциональна амплитуде напряжения и обратно пропорциональна полному сопротивлению цепи.  Полным сопротивлением цепи переменного тока называют величину  или

Если индуктивное сопротивление цепи оказывается равным емкостному, то в цепи наблюдается резонанс, при этом реактивное сопротивление цепи равно нулю. Полное сопротивление цепи равно активному сопротивлению. Тогда закон Ома примет вид .

Примеры решения задач

1.    В цепь переменного тока частотой 50 Гц последовательно включены резистор сопротивлением 100 Ом и конденсатор ёмкостью 22 мкФ. Определите, какая доля напряжения, приложенного к цепи, приходится на падение напряжения на конденсаторе.

Дано:	Решение:
𝜈=50 Гц R = 100 Ом C=22 мкФ	Амплитудное значение напряжение можно найти из закона Ома  . Так как в контуре имеются только резистор и конденсатор, то полное сопротивление вычисляется по формуле . Так как реактивное сопротивление конденсатора вычисляется , где  – циклическая частота. Амплитуда напряжения на конденсаторе вычисляется по закону Ома . Тогда отношение падение напряжения на конденсаторе к напряжению, приложенному к цепи, . Подставим числовые данные из условия задачи    Ответ:
Найти: -?

2.    В цепи переменного тока с частотой ω=314 рад/с вольтметр показывает нуль при L=0,2 Гн. Определите ёмкость конденсатора.

Дано:	Решение:
ω=314 рад/с UV=0 L=0,2 Гн	По условию задачи UV=0, так как катушка и конденсатор соединены последовательно, то общее напряжение будет равно: . Так как вольтметр внешней цепи показывает 0, то и сопротивление , тогда  и  . Подставим числовые данные из условия задачи  Ответ: 50 мкФ.
Найти: C -?

Вопросы для самоконтроля по теме:

1.     Какое сопротивление называется активным? Запишите закон Ома для цепи с активным сопротивлением.

2.     Какое сопротивление называется реактивным?

3.     Что называется ёмкостным сопротивлением? Запишите формулы для вычисления ёмкостного сопротивления и закона Ома для цепи с ёмкостным сопротивлением.

4.     Что называется индуктивным сопротивлением? Запишите формулы для вычисления индуктивного сопротивления и закона Ома для цепи с индуктивным сопротивлением.

5.     Запишите формулы для вычисления полного сопротивления и закон Ома для цепи переменного тока.

Индивидуальные задания к практической работе № 16

Вариант №1

1.    Колебательный контур состоит из конденсатора с емкостным сопротивлением X_C = 2,5 кОм и катушки индуктивности, индуктивное сопротивление которой X_L = 2 кОм. Найдите полное сопротивление контура.

2.    В цепь колебательного контура, содержащего последовательно соединенные резистор сопротивлением 40 Ом, катушку индуктивностью 0,36 Гн и конденсатор ёмкостью 26 мкФ, подключено внешнее переменное напряжение с амплитудным значением 180 В и частотой 314 рад/с. Определите амплитудное значение силы тока в цепи.

3.    В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Конденсатор какой ёмкости надо включить в эту цепь, чтобы осуществился резонанс?

4.    При какой частоте переменного тока емкостное сопротивление конденсатора электроемкостью 1 мкФ равно 3,2 кОм?

 Вариант №2

1.    В цепь колебательного контура, содержащего катушку индуктивностью 0,2 Гн и активным сопротивлением 9,7 Ом, а также конденсатор ёмкостью 40 мкФ, подключено внешнее переменное напряжение с амплитудным значением 180 В и частотой 314 рад/с. Определите амплитудное значение силы тока в цепи.

2.    Генератор, частота которого составляет 32 кГц и амплитудное значение напряжения 120 В, включен в резонирующую цепь, ёмкость которой 1 нФ. Определите амплитудное значение напряжения на конденсаторе, если активное сопротивление цепи 5 Ом.

3.    Катушка индуктивностью 0,2 Гн включена в сеть переменного тока с частотой 50 Гц. Чему равно индуктивное сопротивление катушки?

4.    Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.

Вариант №3

1.    Колебательный контур, подключенный к генератору, содержит резистор, сопротивление которого R = 5 Ом, катушку индуктивностью L = 5 Гн и конденсатор. Определите электроемкость конденсатора, при которой в контуре при частоте 1 кГц возникает резонанс.

2.    Электрическая цепь состоит из катушки индуктивностью L = 0,2 Гн, конденсатора емкостью С = 0,1 мкФ и резистора сопротивлением R = 367 Ом Найдите индуктивное сопротивление X_L, емкостное сопротивление X_C и полное сопротивление контура Z при частоте тока.

3.    Индуктивность контура 0,17мГн. Какова должна быть электроёмкость контура, чтобы он резонировал на частоту электромагнитных колебаний 10⁶ Гц?

4.    При увеличении частоты от 50 Гц до 60 Гц, ёмкостное сопротивление конденсатора с постоянной ёмкостью уменьшилось на 10 Ом.  Найдите электроёмкость конденсатора.

Вариант № 4

1.    В цепь колебательного контура, содержащего катушку индуктивностью 0,2 Гн и активным сопротивлением 9,7 Ом, а также конденсатор ёмкостью 40 мкФ, подключено внешнее переменное напряжение с амплитудным значением 180 В и частотой 314 рад/с. Определите амплитудное значение амплитудное значение напряжения на конденсаторе.

2.     Катушка индуктивностью L = 10мГн обладает активным сопротивлением 10 Ом. При каком значении частоты переменного тока индуктивное сопротивление катушки будет в 10 раз больше ее активного сопротивления?

3.    Резонанс в колебательном контуре наступает при частоте 5,3кГц. Определить индуктивность катушки, если ёмкость конденсатора 6мкФ.

4.    Конденсатор включен в цепь переменного тока стандартной частоты. Напряжение в сети 220 В. Сила тока в цепи этого конденсатора 2,5 А. Какова емкость конденсатора

Вариант №5

1.    В цепь колебательного контура, содержащего катушку индуктивностью 0,2 Гн и активным сопротивлением 9,7 Ом, а также конденсатор ёмкостью 40 мкФ, подключено внешнее переменное напряжение с амплитудным значением 180 В и частотой 314 рад/с. Определите амплитудное значение напряжения на катушке.

2.    При каких частотах переменного тока конденсатор ёмкостью 1 мкФ имеет сопротивление X_C1=3 кОм и X_C2=30 Ом?

3.    В колебательном контуре конденсатор ёмкостью 10нФ заряжен до максимального напряжения 40В. Найти резонансную частоту колебаний в контуре, если амплитуда колебаний силы тока в нём равна 2мА.

4.    Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 2,5 А. Какова индуктивность катушки.

Вариант №6

1.    К генератору переменного тока с частотой v = 100 Гц подключены катушка индуктивностью L = 0,5 Гн, конденсатор емкостью С = 4 мкФ и резистор сопротивлением R = 54 Ом. Сила тока в цепи I = 0,5 А Найдите полное сопротивление цепи и максимальное напряжение.

2.    В цепи переменного тока (см рис) с частотой 50 Гц вольтметр показывает нуль при значении ёмкости 20 мкФ. Определите индуктивность катушки.

3.    Электроёмкость контура 300пФ. Какова должна быть индуктивность контура, чтобы он резонировал на частоту электромагнитных колебаний 10⁶ Гц?

4.     Каково сопротивление конденсатора емкостью 4 мкФ в цепях с частотой переменного тока 50 и 400 Гц?

Тема 4.6 Электромагнитные волны

Практическая работа № 17 «Расчет основных характеристик электромагнитных волн»

Цель: отработка умений и навыков решать задачи по теме: «Электромагнитные волны», правильно оформлять решение задач, правильно давать ответ, в нужных единицах измерения, анализировать задачу, выполнять задания по образцу.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения. 

Порядок выполнения работы

1.    К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.    Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3.    При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4.    Внимательно прочитать теоретическую часть и план решения задач.

5.    Рассмотреть примеры решения задач.

6.    Ответить на контрольные вопросы.

7.    Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Электромагнитное поле – это порождающие друг друга переменные электрические и магнитные поля.

Теория электромагнитного поля создана Джеймсом Максвеллом в 1865 г. Он теоретически доказал, что: любое изменение со временем магнитного поля приводит к возникновению изменяющегося электрического поля, а всякое изменение со временем электрического поля порождает изменяющееся магнитное поле.  Эти поля имеют вихревой характер: силовые линии порождающего поля концентрический охвачены силовыми линиями порождаемого поля. Электромагнитное поле - это особая форма материи - совокупность электрических и магнитных полей. Переменные электрические и магнитные поля существуют одновременно и образуют единое электромагнитное поле. Оно материально:

1. проявляет себя в действии, как на покоящиеся, так и на движущиеся заряды;
2. распространяется с большой, но конечной скоростью;
3. существует независимо от нашей воли и желаний.

Процесс распространения в пространстве переменных электрических и магнитных полей в результате взаимного порождения магнитного поля электрическим и электрического поля магнитным называется электромагнитной волной. Электромагнитная волна является поперечной

Электромагнитные волны излучаются колеблющимися зарядами. При этом существенно, что скорость движения таких зарядов меняется со временем, т. е. они движутся с ускорением. Главное условие возникновения электромагнитной волны — ускоренное движение электрических зарядов. Для распространения электромагнитной волны не требуется среда, скорость с электромагнитной волны в вакууме равна 300000 км/с.

Электромагнитные волны не могут распространяться в проводящей среде, так как из-за наличия свободных электрических зарядов электрическое поле внутри проводников всегда равно нулю.

Электромагнитные волны обладают рядом свойств:

1.   Излучаются ускоренно движущимися зарядами, причем, чем больше их ускорение, тем быстрее изменяется напряжённость поля.

2.   Электромагнитные волны могут распространяться не только в различных средах, но и в вакууме.

3.   Скорость в вакууме электромагнитной волны совпадает со скоростью света 300 000 км/с (м/с).

4.   Скорость электромагнитных волн в веществе ниже, чем скорость света в вакууме.

5.   При переходе электромагнитной волны из одной среды в другую частота волны не изменяется.

6.   Электромагнитные волны могут поглощаться веществом.

7.   Электромагнитные волны преломляются и отражаются.

8.   Электромагнитная волна поперечна.

9.   Электромагнитные волны обладают дифракцией и интерференцией. Дифракция – это явление огибания препятствия. Интерференция – явление, возникающее при сложении когерентных электромагнитных волн. Когерентными называются колебания с одинаковой частотой и постоянной разностью фаз.

Расстояние, на которое перемещается электромагнитная волна за время, равное одному периоду колебания, называется длиной волны λ

Если v — скорость распространения электромагнитной волны в однородной среде, Т - ее период, 𝜈 — частота, а λ— длина, то λ = vT или λ=v/𝜈. Для вакуума λ₀=сТ или .

Если волна переходит из вакуума в среду с диэлектрической проницаемостью ε и магнитной μ, то длина волны уменьшается: , где λ₀ — длина волны в вакууме.

Для образования интенсивных электромагнитных волн необходимо создать электромагнитные колебания достаточно высокой частоты.

Чтобы увеличить частоту колебаний и тем самым повысить интенсивность электромагнитного излучения контура, Герц уменьшил индуктивность и емкость контура, раздвинув пластины конденсатора. Наконец, он реализовал так называемый открытый колебательный контур (вибратор Герца).

Открытый колебательный контур (вибратор Герца) - прямолинейный проводник с искровым промежутком посередине, обладающий очень малой емкостью и индуктивностью.

Примеры решения задач

1.    Колебательный контур радиопередатчика содержит конденсатор переменной ёмкости от 10 нФ до 0,1 нФ и катушку индуктивностью 1 мк Гн. Определите, в каком диапазоне длин волн работает радиопередатчик.

Дано:	СИ	Решение:
C1=10 нФ L= 1мкГн C2=0,1 нФ		Радиоволны распространяются в воздухе со скоростью света c. Длина волны  , или , где Т – период колебаний колебательного контура радио передатчика (). 1) Если С1=10-8 Ф, то ;  . 2) Если С2=10-10 Ф, то  ;   Ответ: .
Найти:-?

2.    Колебательный контур радиопередатчика, содержащий катушку индуктивностью 5 мкГн, настроен на приём электромагнитных волн длиной 1 м. определите ёмкость С конденсатора, включенного в этот колебательный контур.

Дано:	СИ	Решение:
λ=1 м L=5 мкГн		Длина электромагнитной волны: , откуда (1), где с – скорость распространения электромагнитных волн. Чтобы приёмник регистрировал электромагнитные волны, длина которых λ, его колебательный контур должен иметь период колебаний (1) или  (2) Приравняв правые части формул (1) и (2), получим , откуда  . Подставим числовые данные из условия задачи  Ответ:
Найти: C -?

 

3.    Радиолокатор испускает импульсы частотой 5 кГц. Длительность каждого импульса 40 мкс. Определите наибольшую дальность обнаружения цели в воздухе S₁ (ε₁=1; μ₁=1) и в воде S₂ (ε₂=81; ).

 

Дано:	СИ	Решение:
Δt=40 мкс 𝜈=5 кГц ε1=1; μ1=1 ε2=81;		Дальность обнаружения цели определяем по формуле: , где v – скорость  электромагнитной волны в среде; t – время распространения сигнала от локатора до цели:  (2), так как время распространения сигнала от локатора до цели равно времени распространения отражённого сигнала от цели до локатора. 1.   Если цель расположена в воздухе, то  (3), где с – скорость электромагнитной волны в воздухе и в вакууме . 2.   Если цель расположена в воздухе, то  (3), где . – скорость электромагнитной волны в воде. Тогда  Вычисления:   ; Ответ:
Найти: Wм -? Wэ -?

Вопросы для самоконтроля по теме:

1.    Что называется электромагнитной волной?

2.    Какова скорость распространения электромагнитных волн? От чего зависит скорость распространения?

3.    Что называют длиной волны? Может ли электромагнитная волна распространяться в вакууме?

4.    Какие характеристики электрического и магнитного полей периодически изменяются в электромагнитной волне? Каким образом?

5.    Что такое открытый колебательный контур?

6.    На какие виды делятся электромагнитные волны?

Индивидуальные задания к практической работе № 17

Вариант №1

1.     Колебательный контур радиопередатчика содержит конденсатор переменной ёмкости от 10нФ до 0,1нФ и катушку индуктивностью 1мкГн. Определите, в каком диапазоне длин волн работает радиопередатчик.

2.     Катушка приёмного контура радиоприёмника имеет индуктивность 1 мкГн. Какова ёмкость конденсатора, если идёт приём станции, работающей на длине волны 1000 м?

3.     Каким может быть максимальное число импульсов, посылаемых радиолокатором за 1 с, при разведывании цели, находящейся на расстоянии 30 км от него?

4.     На какую длину волны настроен радиоприёмник, если приемный контур обладает индуктивностью 2 мГн и ёмкостью 500 пФ?

 Вариант №2

1.    В радиоприёмнике один из коротковолновых диапазонов может принимать передачи, длина волны которых 24 – 26 м. Найти частотный диапазон.

2.    Радиолокатор работает на волне 15 см и даёт 4 000 импульсов в 1 с. Длительность каждого импульса 2 мкс. Сколько колебаний содержится в каждом импульсе и какова глубина разведки?

3.    В радиоприёмнике катушка имеет индуктивность 0,05 Гн. Какова должна быть ёмкость переменного конденсатора, чтобы принимать передачу радиостанции «Маяк», работающей на частоте 545 кГц?

4.    Сколько колебаний происходит в электромагнитной волне с длиной волны 300м и даёт 4000 импульсов в 1с.

Вариант №3

1.    Станция работает на длине волны 60м. Сколько колебаний несущей частоты происходит в течение одного периода звуковых колебаний с частотой 5кГц?

2.    Электрическая цепь состоит из катушки индуктивностью L = 0,2 Гн, конденсатора емкостью С = 0,1 мкФ и резистора сопротивлением R = 367 Ом Найдите индуктивное сопротивление X_L, емкостное сопротивление X_C и полное сопротивление контура Z при частоте тока 5МГц.

3.    Определить длину волны, на которую настроен входной контур радиоприёмника, если амплитуда заряда на обкладках конденсатора равна 10^-12 Кл, а амплитуда силы тока 10^-5А.

4.    На каком расстоянии от антенны    радиолокатора находится объект, ели отражённый от него радиосигнал возвратиться обратно через 200мкс?                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                

Вариант № 4

1.    Сколько колебаний происходит в электромагнитной волне с длиной волны 300 м за время, равное периоду звуковых колебаний с частотой 2000Гц?

2.    Радиостанция работает на частоте 100 МГц. Считая, что скорость распространения электромагнитных волн в атмосфере равна скорости света в вакууме, найдите соответствующую длину волны.

3.    Контур радиоприёмника настроен на радиостанцию, частота которой 6 МГц. Как нужно изменить ёмкость переменного конденсатора колебательного контура приёмника, чтобы он был настроен на длину волны 50 м?

4.    Контур радиоприёмника настроен на радиостанцию, частота которой 6 МГц. Как нужно изменить ёмкость переменного конденсатора колебательного контура приёмника, чтобы он был настроен на длину волны 50 м? радиолокатора 2 мс. Найти наибольшую глубину разведки.

 

Вариант №5

1.     Наименьшее расстояние от Земли до Сатурна 1,2 Тм. Через какой минимальный промежуток времени может быть получена ответная информация с космического корабля, находящегося в районе Сатурна, на радиосигнал, посланный с Земли?

2.     Определить длину волны, на которую настроен входной контур радиоприёмника, если амплитуда заряда на обкладках конденсатора равна 10^-12 Кл, а амплитуда силы тока 10^-5А, промышленной частоты.

3.     Радиосигнал, посланный на Венеру, был принят на Земле через 2,5 мин после его посылки. Определите расстояние от Земли до Венеры в момент локации?

4.     Колебательный контур состоит из катушки с индуктивностью  Гн, параллельно включённой с конденсатором, ёмкость которого меняется    от  до 10^-8 Ф. На какие длины волн он рассчитан?                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                

Вариант №6

1.     На каком расстоянии от антенны радиолокатора находится объект, если отражённый от него радиосигнал возвратиться обратно через 200 мкс?

2.     Колебательный контур радиоприёмника, содержащий катушку индуктивностью 5мкГн, настроен на приём электромагнитных волн длиной 1м. Определите электроёмкость конденсатора, включённого в колебательный контур промышленной частоты.

3.     Радиостанция «Ленинград» работает на волне λ=4,44 м. На какую электроёмкость должен быть настроен конденсатор, чтобы принимать эту радиостанцию? Индуктивность катушки приёмника равна .

4.     Колебательный контур состоит из катушки индуктивностью 1 мГн и двух последовательно соединённых конденсаторов ёмкостью 500 и 200 пФ. На какую длину волны настроен этот колебательный контур?

Тема 4.7 Геометрическая и волновая оптика

Практическая работа № 18 «Построение изображений в линзах»

Цель: закрепить умения и навыки вычисления показателя преломления среды, определения углов падения и преломления, а также построения изображения с помощью тонкой линзы и вычисления ее основных характеристик.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.  На выполнение практической отводится два академических часа.

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Линза - прозрачное тело, ограниченное двумя сферическими поверхностями. На рис. приведены условные обозначения линз: 1 - собирающая линза, 2 - рассеивающая линза. Главным фокусом линзы (F) - называется точка на главной оптической оси, в которой собираются после преломления в линзе лучи, параллельные друг другу и главной оптической оси линзы. Линза имеет два главных фокуса, расположенных на фокусном расстоянии от оптического центра линзы. У собирающей линзы фокусы действительные, у рассеивающей – мнимые. Побочным фокусом линзы называется точка, в которой пересекаются после преломления в линзе лучи, идущие до линзы параллельно друг другу. Побочные фокусы линзы расположены в фокальной плоскости, которая перпендикулярна главной оптической оси и проходит через главный фокус. Иллюстрация для собирающей линзы

Оптическая сила линзы - величина, обратная фокусному расстоянию , где F - фокусное расстояние, единицы измерения [м]; D - оптическая сила, единицы измерения - диоптрии [дптр]. Для построения изображения в линзах используют три «удобных» луча.

1.    Луч, проходящий через оптический центр линзы, не преломляется.

2.    Луч, распространяющийся параллельно главной оптической оси линзы, после преломления проходит через главный фокус линзы.

3.    Луч, выходящий из главного фокуса линзы, после преломления распространяется параллельно главной оптической оси.

Линза может быть ограничена выпуклыми сферическими поверхностями (двояковыпуклая линза, рис. 1, а), выпуклой сферической поверхностью и плоскостью (плосковыпуклая линза, рис.1, б), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза, рис. 1, в). Эти линзы посередине толще, чем у краев, и все они называются выпуклыми.

  

Рис. 1                        Рис. 2

Линзы, которые посередине тоньше, чем у краёв, называются вогнутыми. На рис. 2 изображены три вида вогнутых линз: двояковогнутая - а, плосковогнутая - б и выпукло-вогнутая - в.

Выпуклые линзы являются собирающими.

Собирающие линзы - линзы, преобразующие параллельный пучок световых лучей в сходящийся.

Вогнутые линзы являются рассеивающими. Рассеивающие линзы - линзы, преобразующие параллельный пучок световых лучей в расходящийся.

В дальнейшем для простоты мы будем рассматривать преломление световых лучей тонкими линзами.

Тонкая линза - линза, толщина которой пренебрежимо мала по сравнению с радиусами кривизны её поверхности.

Линзы характеризуют: главной оптической осью О₁О₂ - линией, соеди­няющей центры кривизны поверхностей линзы, оптическим центром О - точкой, лежащей на пересечении главной оптической оси и линии, соединяющей концы параллельных радиусов r₁ и r₂, проведенных из обоих центров кривизны

Формула тонкой линзы , a - расстояние от предмета до линзы (АВ), f - расстояние от линзы до изображения (A^’B^’),  F- фокус, или фокусное расстояние.

Оптическая сила линзы (D)  или .

Увеличение линзы (Г)  или , H – высота изображения (A^’B^’), h – высота предмета (АВ)

Фотоаппарат представляет собой замкнутую светонепроницаемую камеру. Изображение фотографируемых предметов создается на фотопленке системой линз, которая называется объективом. Специальный затвор позволяет открывать объектив на время экспозиции. Особенностью работы фотоаппарата является то, что на плоской фотопленке должны получаться достаточно резкими изображения предметов, находящихся на разных

расстояниях. В плоскости фотопленки получаются резкими только изображения предметов, находящихся на определенном расстоянии. Наводка на резкость достигается перемещением объектива относительно пленки. Изображения точек, не лежащих в плоскости резкой наводки, получаются нерезкими в виде кружков рассеяния. Размер d этих кружков может быть уменьшен путем диафрагмирования объектива, то есть уменьшения относительного отверстия a / F (рис.). Это приводит к увеличению глубины резкости.

Фотоаппарат

Проекционный аппарат предназначен для получения крупномасштабных изображений. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D) на удаленном экране Э (рис.). Система линз K, называемая конденсором, предназначена для того, чтобы сконцентрировать свет источника S на диапозитиве. На экране Э создается действительное увеличенное перевернутое изображение. Увеличение проекционного аппарата можно менять, приближая или удаляя экран Э с одновременным изменением расстояния между диапозитивом D и объективом O.

Проекционный аппарат

Законы отражения света.

Первый закон отражения: лучи, падающий и отражённый, лежат в одной плоскости с перпендикуляром к отражающей поверхности, восстановленным в точке падения луча.

Второй закон отражения: угол падения равен углу отражения (см. рис.).

α — угол падения, β — угол отражения.

Законы преломления света. Показатель преломления

Первый закон преломления: луч падающий, луч преломленный и перпендикуляр к границе раздела двух сред в точки падения луча лежат в одной плоскости (см. рис.)

 Второй закон преломления: отношение синуса угла падения к синусу угла преломления для данных двух сред и для данной длины волны есть величина постоянная и называется показателем преломления второй среды относительно первой: , где n_1,2 - относительный показатель преломления. , где n₁ - абсолютный показатель преломления первой среды, n₂ - абсолютный показатель преломления второй среды. , . с - скорость света вакууме, , υ₁ - скорость света в первой среде, υ₂ - скорость света во второй среде.

Полное отражение: если свет переходит из оптически более плотной среды в оптически менее плотную, то при выполнении условия α > α₀, где α₀ — предельный угол полного отражения, свет вообще не выйдет во вторую среду. Он полностью отразится от границы раздела и останется в первой среде. При этом закон отражения света даёт следующее соотношение: .

План решения задач

1.Задачи на законы отражения и преломления

При решении задач на построение и движение изображения предмета в плоском зеркале необходимо учитывать, что предмет и его изображение расположены симметрично относительно плоскости зеркала. Для построения изображения всего предмета достаточно найти изображение его крайних точек. В полученном чертеже возникают подобные треугольники, что позволяет записать пропорции из отношений их соответствующих сторон. Если предмет расположен не напротив зеркала, то необходимо продолжить плоскость зеркала и перенести крайние точки предмета симметрично на другую сторону от нее. При переходе через границу раздела двух сред с разными показателями преломления необходимо, как правило, сделать чертеж и изобразить ход лучей, учитывая, в более или менее плотную среду переходит свет. Если луч проходит несколько таких границ раздела, то соответствующий чертеж должен быть сделан для каждой из них. Затем записывается закон преломления для каждого перехода луча и, при необходимости, дополнительные геометрические соотношения, следующие из условия конкретной задачи.

2.Задачи на построение и расчеты в тонких линзах

1) Для построения изображения в линзах достаточно знать ход трех «удобных» лучей после преломления в линзах, описанных выше. Для построения изображения в собирающей линзе необходимо учесть, где относительно фокусов линзы расположен предмет. Если предмет расположен за двойным фокусным расстоянием (за 2F), то его изображение будет действительным, обратным, уменьшенным и расположенным между F и 2F. Такой случай реализуется в фотоаппарате. Если предмет расположен между F и 2F, то его изображение будет действительным, обратным, увеличенным и расположенным за 2F. Такое изображение используется в киноаппарате и проекционном аппарате. При помещении предмета между линзой и ее главным фокусом его изображение становится мнимым, прямым, увеличенным. Такое изображение мы наблюдаем в лупе. Для рассеивающей линзы качество изображения не зависит от того, где относительно линзы расположен предмет. В любом случае его изображение мнимое, прямое, уменьшенное. Если закрыть часть линзы непрозрачным экраном, то характеристики изображения не изменятся, однако его яркость уменьшится, т.к. в формировании изображения будет участвовать меньшее количество лучей. При построении изображения в системах линз необходимо строить цепочку изображений: изображение, даваемое первой линзой, является предметом для следующей, и так далее до окончательного изображения. Часто в построениях возникает понятие побочного фокуса линзы. Для нахождения побочных фокусов необходимо провести фокальную плоскость, которая проходит через главный фокус линзы перпендикулярно ее главной оптической оси.

2) Для проведения расчетов необходимо правильно записать формулу линзы, т.е. правильно выбрать знаки перед F, d и f. Название оптического прибора при этом дает нужную информацию о типе применяемых линз и характере изображения в них. Если используется система линз, то необходимо учесть, где располагаются «промежуточные» изображения, т.е. соотнести значения F, d, f и расстояния между линзами. Часто в задачах данного типа используется также формула для увеличения.

Примеры решения задач

1.     От предмета высотой 3 см получили с помощью линзы действительное изображение высотой 18 см. Когда предмет передвинули на 6 см, то получили мнимое изображение высотой 9 см. Определите фокусное расстояние и оптическую силу линзы.

Дано:	Решение:
h =3 см H=18см H1=9см a =6 см	Увеличение во первом случае: , выражаем . Запишем для первого случая формулу линзы и учтем полученное соотношение между d1 и f1: (1). Аналогично, увеличение во втором случае  и . Записывая формулу линзы во втором случае, учитываем, что изображение мнимое, поэтому перед  ставим знак минус:  . По условию , следовательно, . (2) Из (1) и (2) следует  и . Из (1) находим F: .    Ответ: 12 см и8,33 дптр.
Найти: F –? D -?

2.     Расстояние между двумя точечными источниками света 24 см. Где между ними надо поместить собирающую линзу с фокусным расстоянием 9 см, чтобы изображение обоих источников получилось в одной и той же точке?

Дано:	Решение:
l=24 см F=9 см	Так как изображения двух источников должны находиться в одной точке, то одно изображение будет действительным, а другое - мнимым. Предположим, что изображение первого источника будет мнимым, а второго - действительным:. Выразим из этих формул f1 и f2и учтем, что f 1=f 2:  ; ;  . По условию  и . Получаем  или  . Решаем квадратное уравнение: . Если d1 = 18 см, от d2 = 24 - 18 = 6 см. Если d1 = 18 см, от d2 = 24 - 6 = 18 см., следовательно, линза должна находиться на расстоянии 6 см от одного источника и 18 см от другого. Ответ: 18 см и 6 см
Найти: d1 –? d2 -?

5.    Если фотографировать движущийся объект, то расстояние, на которое он переместится во время экспозиции, оставляет размытость изображения на пленке. С какой скоростью может перемещаться объект перпендикулярно главной оптической оси объектива с фокусным расстоянием 7 см, на расстоянии 10 м от него, чтобы размытость не превышала 0,14 мм при времени экспозиции 1,4 мс?

Дано:	СИ	Решение:
F=7см t= 1,4 мс d=10 м l= 0,14 мм	с	За время экспозиции движущийся предмет перемещается на расстояние S= vt. Размытость l -  – это изображение расстояния S, откуда  Формула линзы . Выражаем f и подставляем в формулу для скорости: ; . Делаем подстановку числовых значений Ответ: 14,2 м/с
Найти: v -?

6.    Вертикальный колышек высотой 1 м, поставленный вблизи уличного фонаря, отбрасывает тень длиной 0,8 м. Если передвинуть колышек на 1 м дальше от фонаря в той же плоскости, то он отбрасывает тень длиной 1,25 м. На какой высоте подвешен фонарь?

Дано:	Решение:
h =1 м l1 =0,8м d =1м l2 =1,25 м	Обозначим расстояние от колышка до фонаря х. Из рис. видно, что треугольники ОАВ и CDB подобны, следовательно, . Выразим из этой формулы x: . После перемещения колышка образовались подобные треугольники OAB1 и C1D1B1. Поэтому  или . Подставляя в полученное выражение х, находим высоту, на которой подвешен фонарь .                                      Ответ: 3,2 м.
Найти: Н- ?

7.    Столб вбит в дно реки, и 1 м столба возвышается над водой (рис). Найти длину тени столба на поверхности и на дне реки, если высота солнца над горизонтом 30°, глубина реки 2 м, показатель преломления воды 1,33, показатель преломления воздуха равен 1.

Дано:	Решение:
h1 =1 м h2=2 м α =300 n=1,33	Тень на поверхности реки l1: . Тень на дне реки:  и . Угол преломления β находится из закона преломления:. Выражаем , учитывая, что : . Следовательно, . Находим .  Ответ: 1,73 м и 3,45 м.
Найти: l1–? l2 -?

8.    Луч света падает из воздуха на поверхность воды под углом 30°. Как измениться угол преломления света, если угол падения увеличить на 15°?

Дано:	Решение:
α=300 Δα=150 n=1,33 l= 0,14 мм	Показатель преломления . В нашем случае:  Зная  α и Δα, определим γ и γ1 ;   . Делаем подстановку числовых значений  Следовательно: Ответ: 9 0
Найти: γ1-γ- ?

1.     Луч света падает под углом 40° на плоскопараллельную пластину толщиной 1 см. Проходя через пластину, он смещается на 2,3 мм. Определить показатель преломления вещества плоскопараллельной пластинки.

Дано:	СИ	Решение:
j=400 AC=2,3 мм d=0,14 мм		Из ∆ADB определим АВ:  , а из ∆АСВ:   (1). По тригонометрическим формулам имеем . (2) Перепишем формулу (1) следующим образом .  Подставим в полученную формулу (2) и получим  , . Разделим обе части на cos j. Следовательно: . . Ответ: 1,36
Найти: n- ?

9.         У призмы с преломляющим углом 45° показатель преломления стекла равен 1,6. Каким должен быть наибольший угол падения луча на грань призмы, чтобы при выходе луча из призмы наступило полное отражение?

Дано:	Решение:
γ=450 n=1,6	Полное отражение наступит тогда, когда луч будет падать на грань АВ под углом, равным или большим предельного угла полного отражения. Предельный угол полного отражения определяется из соотношения: , следует . Зная угол j0 можно найти r1 из ∆ MNO: . Так как . Ответ: угол падения луча на грань АВ не должен превышать 10°10´
Найти: j- ?

Контрольные вопросы для самопроверки

1.    Что называют линзой? тонкой линзой?

2.    Какие линзы называют собирающими, а какие рассеивающими? Что такое главная оптическая ось, главный фокус линзы и побочный? Как построить изображение в линзах?

3.    Записать формулу тонкой линзы, пояснить смысл входящих величин и правило знаков. Что такое оптическая сила линзы? Что такое увеличение и как его определить?

4.    Какие оптические приборы Вы знаете? Поясните принципы их действия.

5.    Сформулируйте закон прямолинейного распространения света.

6.    Объясните на основе этого закона солнечные и лунные затмения.

7.    Что такое угол падения луча? Угол отражения? Угол преломления?

Индивидуальные задания к практической работе № 18

Вариант №1

1.    Постройте изображение данного предмета в линзе. Какое это изображение?

2.    Найти фокусное расстояние линзы, если известно, что действительное изображение предмета, находящегося на расстоянии 30 см от линзы, получается на таком же расстоянии от неё.

3.    Предмет находится на расстоянии 60 см от собирающей линзы с фокусным расстоянием 10 см. На каком расстоянии от линзы получено изображение? Найти увеличение.

4.    Угол падения луча на поверхность подсолнечного масла 60⁰, а угол преломления 36⁰. Найти показатель преломления масла.

5.    Предмет, освещённый маленькой лампочкой, отбрасывает тень на стену. Высота предмета 0,03 м, высота его тени 0,15м. Во сколько раз расстояние от лампочки до предмета меньше, чем от лампочки до стены?

6.    Как изменится угол между падающим на плоское зеркало и отражённым лучами при увеличении угла падения на 13⁰?

Вариант №2

.

1.    Постройте изображение данного предмета в линзе. Какое это изображение?

2.    Главное фокусное расстояние линзы - 10 см. Предмет находится на расстоянии 12 см от линзы. Найти расстояние изображения до линзы.

3.    Какое увеличение даёт фонарь, если его объектив с главным фокусным расстоянием 18 см расположен на расстоянии 6 м от экрана?

4.    На стеклянную пластину падает луч света. Каков угол падания, если угол между отраженными и преломленными тучами равен 90⁰?

5.    Угол между плоским зеркалом и падающим лучом увеличили на 6⁰. Что произойдет при этом с углом между падающим и отражённым лучами?

6.    Маленькая лампочка освещает экран через непрозрачную перегородку с круглым отверстием радиусом 0,2 м. Расстояние от лампочки до экрана в 6 раз больше расстояния от лампочки до перегородки. Каков радиус освещённого пятна на экране?

Вариант № 3

1.    Постройте изображение данного предмета в линзе. Какое это изображение?

2.    Найти оптическую силу и фокусное расстояние двояковыпуклой линзы, если изображение предмета, помещённого в 24 см от линзы, получается на расстоянии 0,4 от неё. Найти увеличение линзы.

3.    Фокусные расстояния линз 5 м и -40 м. Определите оптическую силу каждой линзы.

4.    Водолаз определял угол преломления луча в воде. Он оказался равным 30⁰. Под каким углом к поверхности воды падают лучи света, если показатель преломления воды 1,33?

5.    Луч света падает на плоское зеркало. Угол между падающим и отражённым лучами равен 36⁰. Определите угол между падающим лучом и зеркалом.

6.    Тень от столба в два раза длиннее его высоты. Под каким углом к горизонту в этот момент находится Солнце?

Вариант № 4

1.    Постройте изображение данного предмета в линзе. Какое это изображение?

2.    Свеча находится на расстоянии 12,5 см от собирающей линзы, оптическая сила которой равна 10 дптр. На каком расстоянии от линзы получится изображение?

3.    Главное фокусное расстояние объектива проекционного фонаря 15 см. Диапозитив находится на расстоянии 15,6 см от объектива. Какое линейное увеличение даёт фонарь?

4.    Луч света переходит из воды с показателем преломления 1,33 в стекло с показателем преломления 1,7. Определить угол падения луча, если угол преломления равен 45⁰.

5.    Луч света падает на плоское зеркало. Угол между падающим лучом и зеркалом равен 35⁰. Определите угол между падающим и отраженным лучами.

6.    К потолку комнаты высотой 3 м прикреплена лампа накаливания. На высоте 2 м от пола параллельно ему расположен непрозрачный прямоугольник размерами 2х1 м². Центр лампы и центр прямоугольника лежат на одной вертикали. Определите длину диагонали прямоугольной тени на полу.

Вариант № 5

1.    Постройте изображение данного предмета в линзе. Какое это изображение?

2.    Главное фокусное расстояние рассеивающей линзы – 12 см. Изображение предмета находится на расстоянии 9 см от линзы. Чему равно расстояние от предмета до линзы?

3.     Фотоаппаратом «Зоркий» с фокусным расстоянием 5 с сделан снимок автомашины высотой 1,6 м. С какого расстояния сделан снимок, если высота автомашины на снимке 4 мм?

4.    Луч света при переходе изо льда в воздух падает на поверхность льда под углом 30⁰. Определить угол преломления луча в воздухе, если показатель преломления льда 1,31.

5.    Луч света падает на плоское зеркало. Угол падения уменьшили на 17⁰. Что произойдет с углом между отражённым лучом и зеркалом?

6.    К потолку комнаты высотой 4 м прикреплена лампа накаливания. На высоте 3 м от пола параллельно ему расположен круглый непрозрачный диск диаметром 2 м. Центр лампы и центр диска лежат на одной вертикали. Каков диаметр тени на полу?

Вариант № 6

1.    Постройте изображение данного предмета в линзе. Какое это изображение?

2.    Пред­мет вы­со­той 3 см на­хо­дит­ся на рас­сто­я­нии 40 см от со­би­ра­ю­щей тон­кой линзы. Опре­де­лить вы­со­ту изоб­ра­же­ния, если из­вест­но, что оп­ти­че­ская сила линзы со­став­ля­ет 4 ди­оп­трии.

3.    Свеча находится на расстоянии 15см от собирающей линзы с оптической силой 10дптр. На каком расстоянии от линзы следует расположить экран для получения четкого изображения свечи?

4.    Определите угол преломления γ луча, направленного из воздуха в вещество с показателем преломления n = 1,5, если угол отражения ß = 45°

5.    Тень на экране от предмета, освещённого точечным источником света, имеет размеры в 3 раза больше, чем сам предмет. Расстояние от источника света до предмета равно 1 м. Определите расстояние от предмета до экрана.

6.    Луч света падает на плоское зеркало. Угол между падающим и отраженным лучами равен 24⁰. Определите угол между отраженным лучом и зеркалом.

Тема 6.1. Квантовая оптика

Практическая работа № 19 «Фотоэффект. Законы фотоэффекта»

Цель: повторить законы фотоэффекта, уметь, закрепить умения и навыки решения задач на использование формулы Эйнштейна.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.  На выполнение практической отводится два академических часа.

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Эйнштейн в 1905 г. создал квантовую теорию света, согласно которой не только излучение света, но и его распространение происходит в виде потока световых квантов — фотонов, энергия которых определяется соотношением (1), а масса(2).

Фотон - элементарная частица главной оптической оси и проходит через главный фокус. Иллюстрация для собирающей линзы. Фотоны не существуют в состоянии покоя, их масса и энергия покоя равна нулю.

Выражение для энергии фотона  (3). Обладая энергией, фотон должен обладать и импульсом р. Для фотона, имеющего нулевую массу энергия равна . Отсюда импульс фотона получаем .(4) Направление импульса фотона совпадает с направлением светового луча. Учитывая, соотношение , формулу (4) можно переписать (5). Из формул следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом.

Основные законы фотоэффекта:

1.     Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).

2.     Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.

3.     Для каждого вещества существует красная граница фотоэффекта – наименьшая частота света ν_min (наибольшая длина волны λ_max), при которой возможен фотоэффект. При ν<ν_min (λ>λ_max) фотоэффект не наблюдается ни при какой интенсивности света.

Существует три вида фотоэффекта:

внешний – вырывание связанных электронов из вещества падающим светом;

внутренний – изменение концентрации носителей тока в веществе, следовательно, изменение электрической проводимости данного вещества под действием света;

вентильный – возникновение под действием света ЭДС в системе, содержащей контакт двух различных полупроводников или полупроводника или металла.

Фотоэлектроны – электроны, выбиваемые с металлических пластин светом. Фототок – ток, образованный фотоэлектронами.

Для того чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение U_з. При U=Uз ни один из электронов, даже обладающий при вылете из катода максимальной скоростью v_мах, не может преодолеть задерживающего поля  и достигнуть анода. Измерив, задерживающее напряжение, можно найти максимальное значение кинетической энергии электронов, вырываемых светом из катода: .

Задерживающее напряжение U_зад – напряжение, при котором работа задерживающего электрического поля равна максимальной кинетической энергии фотоэлектронов.

Согласно опытам, задерживающее напряжение, следовательно, и максимальная кинетическая энергия фотоэлектронов не зависят от мощности светового излучения, но возрастают с увелечением частоты света.

Установлена также безынерциальность фотоэффекта: он возникает мгновенно при облучении вещества, если n=n₀. При вылете из металла энергия каждого электрона уменьшается на определенную величину, которую называют работой выхода (А_вых). Работа выхода — это работа, которую необходимо затратить, чтобы удалить электрон из металла. Кинетическая энергия фотоэлектронов при этом станет равной нулю. Из уравнения Эйнштейна получаем, что  (6) и есть красная граница фотоэффекта для данного металла.

Красная граница зависит лишь от работы выхода электрона, т.е. от химической природы вещества и состояния его поверхности. Работа выхода электрона из металла зависит от природы вещества.

Выражение (1) можно представить в виде: , где l₀ - максимальная длина волны падающего света (соответствует минимальной частоте n₀), при которой фотоэффект ещё возможен.

Фотоэффект применяется в различных областях науки и техники.

Примеры решения задач

1.    Какую максимальную кинетическую энергию имеют фотоэлектроны при облучении железа светом с длиной волны 200 нм? Красная граница фотоэффекта для железа 288 нм.

Дано:	СИ:	Решение:
= 288 нм		Для вычисления кинетической энергии фотоэлектронов воспользуемся уравнением Эйнштейна для фотоэффекта , учитывая, что . Откуда . Подставим формулу для нахождения частоты в уравнение Эйнштейна  . По определению кинетической энергии . Объединяя две последние формулы получим: . Подставим в данную формулу числовые данные и получим:   Ответ:
=200 нм
h=
Найти: Ек -?

2.       Возникнет ли фотоэффект в цинке  под действием облучения, имеющего длину волны 450 нм?

Дано:	СИ:	Решение:
А=4,2эВ		Для ответа на вопрос задачи необходимо вычислить красную границу, при которой наступает фотоэффект и сравнить полученную длину волны с данной: если , фотоэффект наблюдаться не будет, если   – фотоэффект наблюдается. . Откуда . Подставим в данную формулу числовые данные и получим: Так как 295 нм˂450нм, т.е. , то фотоэффект наблюдаться не будет Ответ: не будет
=450 нм
h=
Найти: λmax -?

3.    Какова максимальная скорость электронов, вылетающих при освещении ультрафиолетовым светом с частотой 10¹⁵ Гц металлического проводника с работой выхода 3,11 эВ?

Дано:	СИ:	Решение:
ν=1015 Гц		Для вычисления скорости электрона воспользуемся уравнением Эйнштейна для фотоэффекта. Откуда . Подставим в данную формулу числовые данные и получим: Ответ:
Aв=3,11эВ	Дж
mэ = кг h=
Найти: v-?

4.    Фотоэффект у данного металла начинается при частоте излучения Гц. Найдите частоту падающего света, если вылетающие с поверхности металла фотоэлектроны полностью задерживаются сеткой, потенциал которой относительно металла составляет -3В.

Дано:	Решение:
ν min= Гц	По минимальной частоте определим работу выхода, согласно . Далее по задерживающему напряжению определим максимальную кинетическую энергию электронов, согласно формуле: . Подставив эти формулы в уравнение Эйнштейна , Подставим  числовые данные и получим:  . Подставив числовые данные окончательно получим: Ответ:
Uз=-3В
e = Кл h=
Найти: ν -?

5. При облучении цезия с длиной волны 0,4 мкм максимальная скорость вылетающих фотоэлектронов равна 660 км/с. Каков наименьший импульс фотона, который ещё может вызвать фотоэффект в цезии?

Дано:	СИ:	Решение:
λ=0,4 мкм	м	Минимальный импульс можно найти по формуле:. Найдём минимальную необходимую энергию фотона: . Работу выхода найдем из формулы Эйнштейна как разность между энергией фотона со диной волны, данной в задаче, и возникающей при этом кинетической энергии электрона:  , учитывая, что. Тогда . Зная энергию предельно допустимого фотона, найдём его импульс:  Подставим в данную формулу числовые данные и получим: Ответ:
v=660 км/с	м/с
h= с= м/с mэ = кг
Найти: pmin-?

Контрольные вопросы для самопроверки

1.    Запишите формулу Планка, пояснив смысл его квантовой гипотезы. В чём заключается гипотеза Планка?

2.    Что называется фотоном?

3.    Что называется фотоэффектом? При каком условии возникает фотоэффект?

4.     Назовите виды фотоэффекта. Дайте определения каждому виду фотоэффекта.

5.    Сформулировать законы фотоэффекта Столетова.

6.    Запишите уравнение Эйнштейна для внешнего фотоэффекта.

7.    В чем заключается безынертность фотоэффекта?

8.    От каких факторов зависит работа выхода электрона из вещества? 

Индивидуальные задания к практической работе № 30

Вариант №1

1.     При облучении алюминиевой пластины фотоэффект начинается при наименьшей частоте 1,03 ПГЦ. Найдите работу выхода электронов из алюминия

2.     Найти энергию фотона, если максимальная кинетическая энергия фотоэлектронов равна 1,2 эВ. Работа выхода электронов для данного вещества равна 3,6 эВ.

3.     Какую разность потенциалов надо приложить к фотоэлементу, чтобы задержать поток фотоэлектронов, испус­каемых калием при облучении его ультрафиолетовым светом с длиной волны 330 нм? Работа выхода для калия равна 2,15 эВ.

4.     Определите максимальную кинетическую энергию фотоэлектронов калия при освещении лучами с длиной волны 400 нм, если работа выхода электронов у калия равна 2,26 эВ.

Вариант №2

1.    Вычислите энергию кванта излучения фиолетового света, если его длина волны в вакууме равна 400 нм.

2.    Определить максимальную кинетическую энергию электронов, выбиваемых с поверхности металла фотонами с энергией 4,6 эВ. Работа выхода электронов из металла равна 1,8 эВ.

3.    При освещении металлической пластинки мо­нохроматическим светом задерживающая разность потенциалов равна 1,6 В. Если увеличить частоту света в 2 раза, задерживаю­щая разность потенциалов равна 5,1 В. Определить работу выхода электрона.

4.   Работа выхода для цинка равна Возникает ли фотоэффект под действием излучения, имеющего длину волны 0,45 мкм?

Вариант № 3

1.     Определить энергию фотона, соответствующего излучению с длиной волны 0,495 мкм.

2.     Работа выхода электронов из металла равна 6,6 • 10^-19 Дж. Найти красную границу фотоэффекта.

3.     Поверхность металла освещается квантами све­та с энергией 4 эВ. Определить максимальную скорость вырываемых электронов, если работа выхода электронов 1,125 эВ. Массу электрона принять равной 9,2 • 10^{-31 кг.}

4.     Работа выхода электронов из кадмия равна 4,08 эВ. Какой должна быть длина волны излучения, падающего на кадмий, чтобы при фотоэффекте максимальная скорость фотоэлектронов была равна ? Масса электрона .

Вариант № 4

1.    Определите энергию кванта зелёного света, длина волны которого в вакууме 510 нм.

2.    Красная граница фотоэффекта 250 нм. Какова работа выхода электрона из этого металла?

3.    Длина волны ультрафиолетового света, падаю­щего на металлическую пластинку, уменьшилась с 250 до 125 нм. Во сколько раз увеличилась максимальная кинетическая энергия вылетающих электронов, если работа выхода равна 3,3 эВ?

4.   Натриевую пластинку облучают светом, длина волны которого . Определите скорость фотоэлектронов, если работа выхода натрия равна .

Вариант № 5

1.   Определите частоту электромагнитного излучения, энергия кванта которого равна .

2.    Когда ультрафиолетовый свет с длиной волны 165 нм падает на металлическую пластинку, максимальная кине­тическая энергия испускаемых электронов равна 3 эВ. Чему равна работа выхода электронов из металла?

3.    Фотоны с энергией 2,1 эВ вызывают фотоэф­фект с поверхности цезия. На сколько нужно увеличить энергию фотонов, чтобы максимальная кинетическая энергия фотоэлектронов увеличилась в 3 раза? Работа выхода электрона с поверхности цезия равна 1,9 эВ.

4.    Каким наименьшим напряжением полностью задерживаются электроны, вырванные ультрафиолетовыми лучами с длиной волны 300 нм из вольфрамовой пластины, если работа выхода равна ?

Вариант № 6

1.    Вычислите энергию кванта излучения красного света, если его длина волны в вакууме равна 750 нм.

2.    При освещении металлической поверхности фотонами с энергией 6,2 эВ обнаружено, что фототок прекра­щается при величине задерживающей разности потенциалов, равной 3,7 В. Определить работу выхода элек­тронов из металла.

3.    Определите максимальную скорость вылета фотоэлектронов из калия, работа выхода электронов которого равна 2,26эВ, при освещении его ультрафиолетовым излучением с длиной волны 200 нм. Масса электрона .

4.    Красная граница фотоэффекта у натрия, напылённого на вольфраме, равна 590 нм. Определите работу выхода электронов.

Практическая работа № 31 «Энергия связи. Дефект массы. Законы радиоактивности, закон радиоактивного распада»

Цель: закрепить умения и навыки вычисления энергии связи ядра, а также правильного написания ядерной реакции с использованием законов сохранения массового и зарядового чисел (ЗСМЗЧ) и вычисления энергетического выхода ядерной реакции, закрепить умения и навыки решения задач по теме: «Радиоактивные излучения», правильного оформления решения задач.

Оборудование: тетрадь для практических работ, ручка, методические   рекомендации по выполнению работы, линейка, работы, линейка, карандаш.

Указание: практическая работа состоит из двух частей –  теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.  На выполнение практической отводится два академических часа.

Порядок выполнения работы

1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.

2.  Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.

3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы

4. Внимательно прочитать теоретическую часть и план решения задач.

5. Рассмотреть примеры решения задач.

6. Ответить на контрольные вопросы.

7. Получить и выполнить индивидуальные задания

На выполнение практической отводится два академических часа.

Ход работы

Теоретическая часть

Энергия связи – минимальная энергия, необходимая для совершения работы по расщеплению ядра против ядерных сил.

Измерение масс ядер показывает, что масса ядра меньше суммы масс составляющих его нуклонов, т.е. при образовании ядра из нуклонов происходит уменьшение их массы, потеря некоторой ее части. Специальная теория относительности объясняет это явление: уменьшение суммарной массы нуклонов при образовании из них ядра можно объяснить выделением энергии связи.

Если обозначить Е_св энергию, выделяющуюся при образовании ядра, то соответствующая ей масса  характеризует уменьшение суммарной массы при образовании ядра из составных частиц. Если ядро с массой М_я образовано из Z протонов с массой т_р и из А-Z нейтронов с массой т_п, то . Величину Δm называют дефектом массы. Она может служить мерой энергии связи. Энергия связи ядра равна той энергии, которой выделяется при образовании ядра из отдельных частиц: Энергия связи – это энергия, которая необходима для расщепления ядра на составляющие его частицы. .

Введем понятие энергии связи отдельного нуклона в ядре, т.е. удельной энергии связи e_св Удельная энергии связи -  физическая величина, равная работе, которую нужно совершить для удаления нуклона из ядра.

Ядерными реакциями называют изменения атомных ядер при взаимодействии их с элементами частицами или друг с другом. Например,  Энергетическим выходом ядерной реакции называется разность энергий покоя ядра и частиц до реакции и после реакции. Энергетический выход ядерной реакции можно определить:

1) по дефекту массы ядерной реакции;

2) по разности суммарной энергии связи образующихся и исходных ядер.

Реакции, сопровождаемые выделением энергии, называются экзотермическими, а поглощением энергии - эндотермическими.

Радиоактивность – это самопроизвольное превращение неустойчивого изотопа одного химического элемента из основного или возбужденного состояния в изотоп другого элемента, сопровождающееся испусканием элементарных частиц и электромагнитной энергии. Такие ядра или соответствующие атомы называют радиоактивными. Само явление называется радиоактивным распадом. Радий имеет относительную атомную массу, равную 226, и занимает в таблице Д.И. Менделеева клетку под номером более 83 являются радиоактивными. Различают естественную и искусственную радиоактивность.

Естественная радиоактивность - радиоактивность, наблюдаемая у неустойчивых изотопов, существующих в природе.

Искусственная радиоактивность - радиоактивность изотопов, полученных искусственно при ядерных реакциях.

Естественной радиоактивностью называют самопроизвольное превращение одних атомных ядер в другие, которое сопровождается испусканием определенных частиц и электромагнитного излучения.

Естественную радиоактивность наблюдают, как правило, у тяжелых ядер, располагающихся в конце Периодической системе Менделеева, за свинцом. Однако имеются и легкие естественно-радиоактивные ядра: изотопы калия, углерода, рубидия, и редкоземельных элементов     патана, самарии, лютеция. Нестабильными, или радиоактивными, являются тяжёлые ядра с зарядовым числом Z>83 или массовым числом A>209, которые могут спонтанно распадаться.

Радиоактивный распад - радиоактивное (самопроизвольное) превращение исходного (материнского) ядра в новые (дочерние) ядра.

Причиной радиоактивного распада является нарушение баланса между количеством Z протонов и N нейтронов в ядре. Ядра, содержащие избыточное число протонов, освобождаются от  этого избытка в результате a-распада.

Альфа-распад (a-распад)- спонтанное превращение радиоактивного ядра в новое ядро с испусканием a - частицы. Ядра, содержащие избыточное число нейтронов, уменьшают их число в результате b-распада.

Бета (минус) - распад (b-распад)- спонтанное превращение радиоактивного ядра в новое ядро с испусканием электрона и антинейтрино.

При a - распаде радиоактивное (материнское) ядро X превращается в новое (дочернее) ядро Y, испуская при этом a-частицу (ядро атома  -  Z=2; A=4). С учётом законов сохранения электрического заряда и числа нуклонов запишем уравнение α - распада:

Гамма – излучение (g-распад) - электромагнитное излучение, возникающее при переходе ядра из возбуждённого в более низкие энергетические состояния.

При b^--распаде радиоактивное (материнское) ядро X превращается в новое (дочернее) ядро Y с испусканием электрона (сначала испускаемые электроны при таком распаде назвали бета-лучами). В результате бета-распада образуется элемент с порядковым номером в таблице Менделеева, большим на единицу: , где - антинейтрино.

Электрон и антинейтрино не входят в состав ядра атома, а рождаются в процессе b-распада. Появление новых частиц в ходе ядерных реакций отражает их фундаментальное свойство - взаимопревращаемость

Радиоактивность элемента не зависит от того, является ли он химически чистым или находится в составе какого-либо химического соединения. Радиоактивность представляет собой внутриядерный процесс.

Если в начальный момент времени t =0 имеется N₀ радиоактивных атомов, то в момент времени t число оставшихся радиоактивных атомов , Т_1/2 - период полураспада.

Период полураспада - промежуток времени, за который распадётся половина первоначального числа атомов.

Зная число N нераспавшихся атомов и их начальное число, можно найти число атомов N_расп, распавшихся к моменту времени t: .

Скорость изменения любой физической величины со временем определяется как производная от этой величины в определённом направлении равна производной по времени от соответствующей величины. Скорость радиоактивного распада определяется , называется активностью радиоактивного  вещества. Активность радиоактивного вещества - число распадов радиоактивных ядер за 1 с. Единицей активности является беккерель 1 Бк = 1 расп./с = 1 с^-1. Величину τ = 1/λ называют средним временем жизни радиоактивного изотопа. Значения λ и τ не зависят от внешних условий, а определяются лишь свойствами атомного ядра. 1 беккерель - активность радиоактивного вещества, в котором за 1с происходит один распад.

Чем быстрее распадаются ядра, тем меньше период полураспада, значит, тем больше активность вещества. Активность пропорциональна числу нераспавшихся атомов, которое убывает с течением времени. Следовательно, активность одного грамма радия равна Бк. Эта величина часто используется на практике в качестве единицы активности кюри (1Ки): . Промежуток времени t=1,44Т_1/2 характеризует среднее время жизни радиоактивного изотопа.

Примеры решения задач

1.     Определите энергетический выход ядерной реакций   .

1 способ

1) определить массу ядра и частиц m₁ до реакций

2) определить массу ядра и частиц m₂ после реакций

3) определить изменение массы  

4) рассчитать изменение энергии:

До реакции

После реакции:  

Энергия поглощается, т.к. .

2 способ

Дано:	Решение:
EN =104,653 МэВ	Энергия связи равна нулю, поэтому . Подставим в данную формулу числовые данные и получим:  Ответ:
EHe = 28,2937 МэВ
EO =131,754 МэВ
Найти: Е -?

2. Чему равна энергия связи ядра изотопа натрия ? Масса ядра равна 22,9898а.е.м.

Дано:	Решение:
mp=1,007276 аем mn=1,008665 аем с2 = 931,5 МэВ/аем	В изотопе натрия имеется 11 протонов и 23 - 11 = 12 нейтронов. По формуле  вычислим энергию связи атома натрия. Подставим в данную формулу числовые и табличные данные и найдём энергию связи:   Ответ: 0,18 МэВ.
Найти: Eсв -?

3. Какая вторая частица образуется в ходе реакции ?

Решение:

Сумма верхних индексов исходных ядер равна 5. Следовательно, массо­вое число неизвестной частицы равно 5-4=1; зарядовые числа уравнены и без участия неизвестной частицы, следовательно, ее заряд равен нулю. Эта частица - нейтрон  и реакция примет вид: .

 Ответ: нейтрон.

4.     Дан график зависимости числа нераспавшихся ядер ртути от времени. Чему равен пери­од полураспада этого изотопа  ртути (в минутах)?

Решение:

Начальное число ядер (60 единиц по оси орди­нат) поделим на два: получим 30. Посмотрим, где отметка 30 пересечет нашу кривую, и прочтем абс­циссу этой точки (примерно 7,5 минут). Можно для проверки взять времена, соответствующие любым другим вдвое отличающимся количествам ядер, например, 40 и 20 единиц. Промежуток времени между ними 11,5 - 4 = 7,5 минут.

Ответ: 7,5 минут.

5.     За один год осталось 25% некоторого исходного радиоактивного элемента. Определите период полураспада этого элемента.

Дано:	Решение:
t =1 год N=0,25N0	Закон радиоактивного . Разделив обе части равенства на N0, получим . Подставим числовые значения . Решаем уравнение относительно Т1/2. . . Отсюда,  Тогда  . Ответ: 0,5 года
Найти: Т1/2 -?

6.     Определите, сколько ядер в 1 г радиоактивного стронция  распадается в течение одного года, период полураспада стронция 27 лет.

Дано:	Решение:
t =1 год Т1/2=27 лет m=10-3 кг	Количество распавшихся ядер определяется по формуле .(1) Для определения числа атомов, содержащихся в 1 г стронция, используем соотношение: . (2), где - постоянная Авогадро,  – молярная масса изотопа стронция. Используя закон радиоактивного  (3), где N0 – начальное число неравпавшихся ядер в момент времени t=0, N – число нераспавшихся ядер в момент времени t.  Подставив в формулу (1) выражения (2) и (3), получим . Подставим числовые значения . Ответ:
Найти: Nрас -?

7.      В начальный момент времени активность некоторого радиоактивного элемента составляла А₀=200Бк. Определите его активность А через промежуток времени , равный двум периодам полураспада.

Дано:	Решение:
А0=200Бк	Активность радиоактивного изотопа изменяется по  / Подставим данные из условия задачи . Ответ:
Найти: А -?

 

Контрольные вопросы для самопроверки

1.    Что называют массовым числом? зарядовым числом?

2.    Что определяет порядковый номер химического элемента в Периодической системе Д.И. Менделеева?

3.    Что такое дефект масс и как его определяют?

4.    Что такое ядерная реакция?

5.    Какие реакции называются эндотермическими? экзотермическими?

6.    Что называется радиоактивностью?

7.    Какую радиоактивность называют естественной?

8.    Что называют радиоактивным распадом?

9.    Что называют периодом полураспада?

10. Запишите, закон радиоактивного распада.

11. Что называют активностью распада? Запишите формулу для вычисления активности.

Индивидуальные задания к практической работе № 20

Вариант №1

1.    Определите энергию связи и удельную энергию связи нуклонов в ядре изотопа , если , , и масса ядра атома изотопа 15,99492 а.е.м.

2.    Сколько протонов и нейтронов содержит ядро изотопа ?

3.    Определите энергетический выход следующей ядерной реакции . Атомные массы изотопов лития, водорода и бериллия соответственно равны 7,01601 а.е.м., 2,01410 а.е.м. и 8,00531 а.е.м.

1.    Определите среднее время жизни радиоактивного стронция, если его период полураспада равен 27 лет.

2.    Период полураспада ядер изотопа радия 1600 лет. Определите число распавшихся ядер за время 3200 лет, если начальное число ядер 10^9.

4.    Активность некоторого радиоактивного элемента за время 32 дня уменьшилась в n=4 раза. Определите период полураспада этого элемента.

Вариант №2

1.   Определите энергию связи и удельную энергию связи ядра атома изотопа, если , , и  — соответственно массы протона, нейтрона и ядра.

2.    Сколько протонов и нейтронов содержит ядро изотопа ?

3.    Определите энергию, выделяющуюся в следующей ядерной реакции. Какая это реакция: экзо- или эндотермическая? Атомные массы изотопов лития, гелия и бора равны соответственно 7,01601 а.е.м., 4,0026 а.е.м. и 10,01294 а.е.м.

4.    Период полураспада радия равен 1600 лет. Определите среднее время жизни радиоактивного ядра.

5.    Период полураспада ядер изотопа йода 8 сут. Определите число распавшихся ядер за время 80 сут, если начальное число ядер 10^9.

6.    Активность некоторого радиоактивного элемента за 18 дней уменьшилась в n=8 раз. Определите период полураспада этого элемента.

Вариант № 3

1.   Определите энергию связи и удельную энергию связи нуклонов в ядре трития (, , .)

2.    Сколько протонов и нейтронов содержит ядро изотопа ?

3.    Вычислите энергетический выход ядерной реакции . Атомные массы изотопов углерода, водорода и азота равны соответственно 7,01601 а.е.м., 1,00783 а.е.м. и 14,003242 а.е.м.

4.    Период полураспада радия равен 50,2 года. Определите среднее время жизни радиоактивного ядра.

5.    Период полураспада радиоактивного аргона равен 110 мин. Определите время, в течение которого распадается 75% начального количества атомов.

6.    Определите период полураспада некоторого радиоактивного изотопа, если его активность уменьшилась 2 2,2 раза за 5 суток.

Вариант № 4

1.    Определить энергию связи и удельную энергию связи нуклонов в ядре изотопа углерода: , если , , .

2.    Сколько протонов и нейтронов содержит ядро изотопа ?

3.    Какая энергия выделяется при ядерной реакции  (, , )

4.    Определить период полураспада некоторого радиоактивного вещества, среднее время жизни атомов 1с.

5.    Во сколько раз уменьшается число радиоактивных ядер за время, равное четырём периодам полураспада?

6.    Активность изотопа углерода  ₆С¹⁴ в древних деревянных предметах составляет 4/5 активности этого изотопа в свежевырубленных деревьях. Период полураспада этого изотопа равен 5570 годам. Определить возраст древних предметов.

Вариант № 5

1.    Определите энергию связи и удельную энергию связи нуклонов в ядре изотопа урана , если , , и  — соответственно массы протона, нейтрона и ядра.

2.    Сколько протонов и нейтронов содержит ядро изотопа ?

3.    Определите энергию, выделяющуюся при термоядерной реакции , (, , , )

4.    Определить период полураспада радиоактивного нуклида, если среднее время его жизни составляет 1,44 ч.

5.    Чему равен период полураспада одного из изотопов франция, если за 6 с количество ядер этого изотопа уменьшается в 8 раз?

6.    Активность радиоактивного элемента уменьшилась в 4 раза за 8 сут. Найти период полураспада.

Вариант № 6

1.    Определите энергию связи и удельную энергию связи нуклонов в ядре изотопа радия , если , , и  — соответственно массы протона, нейтрона и ядра.

2.    Сколько протонов и нейтронов содержит ядро изотопа ?

3.   Определите выделяется или поглощается энергия при ядерной реакции , (, , ).

4.    Определите среднее время жизни радиоактивного нуклида, если его период полураспада составляет 100 сут.

5.    Сколько процентов радиоактивных ядер кобальта останется через 3 дня, если период полураспада данного изотопа составляет 18 ч?

6.    Активность некоторого изотопа в начальный момент времени составляла 100 Бк. Определите активность этого изотопа по истечении промежутка времени, равного половине периода полураспада.

 

 

Скачано с www.znanio.ru