МИНИСТЕРСТВО ОБРАЗОВАНИЯ ИРКУТСКОЙ ОБЛАСТИ

ГБПОУ ИО «ИРКУТСКИЙ ТЕХНИКУМ ТРАНСПОРТА И

СТРОИТЕЛЬСТВА»

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

 И ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

ДЛЯ ОБУЧАЮЩИХСЯ ПО ЗАОЧНОЙ ФОРМЕ 

по  дисциплине «Математика»

Специальность 23.02.01 Организация перевозок и управление на транспорте (автомобильном)  (заочное отделение)

Иркутск, 2015 г.

Рассмотрено на заседании ДЦК протокол  № ___  от «___»_______2015 г.

Председатель ДЦК  _________________

Организация-разработчик: ГБПОУ ИО «Иркутский техникум транспорта и строительства»

Разработчик: Котлярова Анастасия Сергеевна, преподаватель первой квалификационной категории 

Утверждена  на заседании методического совета  Протокол  № ___     от  «___»__________ 2015 г. 

Заместитель директора по ОД  ______________

СОДЕРЖАНИЕ

1.     ВВЕДЕНИЕ

 Контрольная работа представляет собой форму студенческой самостоятельной работы. Написание контрольной работы предусмотрено учебным планом. Ее результат оценивается по пятибалльной системе и является допуском к экзаменационной сессии.

Разделы учебного курса:

•      Дифференциальное и интегральное исчисление.

•      Обыкновенные дифференциальные уравнения.

•      Ряды.

•      Комплексные числа.

•      Основы теории вероятности и математической статистики.

2.     ТРЕБОВАНИЯ К НАПИСАНИЮ КОНТРОЛЬНОЙ РАБОТЫ

1.   В процессе изучения математики, обучающийся должен выполнить одну контрольную работу. Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному  материалу, соответствующему этому заданию. 

2.   Контрольная работа должна быть оформлена в соответствии с настоящими  требованиями. Работа, выполненная без соблюдения этих требований, не засчитывается и возвращается обучающемуся для переработки.

3.   Контрольную работу следует выполнить в отдельной тетради, чернилами синего  цвета, оставляя поля для замечаний рецензента.

4.   На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, учебное заведение, специальность, номер группы, название дисциплины (Математика), контрольная работа, номер варианта. В конце работы следует поставить дату ее выполнения и расписаться.

5.   Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь. При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса. Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа π, е и т. д.

6.   Срок проверки контрольной работы 10 рабочих дней. Обучающиеся обязаны сдавать письменные контрольные работы не позднее, чем за    30 дней до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.

7.   После получения прорецензированной работы обучающийся должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и предоставить работу для повторной проверки. В связи с этим рекомендуется при выполнении контрольной работы оставить в конце тетради несколько чистых листов для внесения исправлений и дополнений впоследствии.

8.   В случае незачета работы и отсутствия прямого указания рецензента на то, что обучающийся может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.

9.   При представленных на повторную проверку исправлениях обязательно должны находиться прорецензированная работа и рецензия на нее. Вносить исправления в сам текст работы после ее рецензирования запрещается. 

10.        Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять.

11.        На экзамен обучающийся должен явиться с контрольной работой и рецензией на выполненную контрольную работу. Без предъявления преподавателю прорецензированной контрольной работы обучающийся к экзамену не допускается.

3. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

3.1. Дифференциальное и интегральное исчисление.

1.  Найти производные функций одной переменной.

1.         f x x³ 2x7⁴ ; 

2.         f (x)  cos(3x² 1); 

3.         f x cosx³ 2x

4.         f (x)  6sin³ x; 

5.         f (x) 3ctg2x² 1;

6.         f (x)  x² 1    x² 3;

7.         f (x)  sinx  2cosx; 

8.         f (x)  tg3x² 2;   

9.         f (x) tg²4x;   

10.     f (x)  x³  2 x² 1² . 

2.  Решить задачи.

1.а) Точка движется по закону s 2t³ 5t² 32. Найти величину скорости и ускорения в момент t=3 с, если путь измеряется в метрах.

  б) Сторона квадрата равна 10 дм. Найти приближенное приращение его площади при увеличении стороны на 0,1 дм.

2.а) Тело вращается вокруг оси по закону 12t t² . Найти угловую скорость вращения в момент t=1 c; угловое ускорение в момент t.

   б) Шар радиуса R=20 см был нагрет, в результате чего его объем увеличился на 40,5

см³. Вычислить приближенно удлинение радиуса шара.

3.а) Определить скорость движения точки в конце третьей секунды, если путь, пройденный точкой в t секунд, выражается формулой s t³ t² 2 и измеряется в

метрах.

   б) Сторона куба, равная 0,7 м, удлинилась на 5 см. На сколько при этом приближенно увеличится объем куба?

4.а) Температура тела Т изменяется в зависимости от времени t по закону T t³ 12t . С какой скоростью нагревается это тело в момент t=4 c?

   б) Шар радиуса R=15 дм был нагрет, в результате чего длина радиуса увеличилась на 1 см. Найти  приближенное значение приращения объема шара.

5.а) Количество электричества, протекшее через проводник за t секунд, определяется по формуле Q 3t³  2t 1. Найти силу тока в конце четвертой секунды.

   б) В прямоугольном параллелепипеде с квадратным основанием сторона основания равна 40 дм, а высота равна 20 дм. На сколько приближенно увеличится его объем, если сторону основания удлинить на 0,2 см? 1 ³ 5 x²  6x . Найти, в какие моменты времени

6.а) Тело движется по закону s  x 

                                                                                     3         2

скорости движения тела равны нулю?

   б) Радиус основания конуса равен 20 дм, а высота равна 25 дм. На сколько приближенно увеличится его объем, если радиус основания увеличить на 0,05 дм?

7.а) Угол поворота шкива определяется из уравнения t² 3t 5, где t время в секундах. Найти среднюю угловую скорость в промежутке времени от t=4 до t=6 и угловую скорость в момент t=6.

   б) Куб со стороной а=20 см был нагрет, в результате чего сторона его увеличилась на 0,01 см. найти приближенное значение приращения объема куба.

8.а) Тело вращается вокруг оси, причем закон изменения угла  в зависимости от времени t определяется уравнением  2t²  3t  2. Найти угловую скорость вращения тела в момент t=3.

   б) Сторону куба, равную 0,6 м, удлинили на 1 см. На сколько при этом приближенно увеличится объем куба?

9.а) Тело движется по закону s 5t 9t² t³ . Найти максимальную скорость движения тела.

   б) в конусе радиус основания равен 25 дм, а высота его равна 2 дм. На сколько приближенно увеличится его объем, если радиус основания удлинить на 0,1 см?

10.а) Тело, брошенное вертикально вверх со скоростью v0 м/с, движется по закону s  v₀t  4.9t² , где время t – в секундах, а путь s – в метрах. Найти скорость движения и ускорение в момент t; в конце третьей секунды, если v0=100 м/с.

     б) Шар радиуса R=20 дм был нагрет, в результате чего длина радиуса увеличилась на

0,3 см. Найти приближенное значение приращения объема шара.

3. Найти пределы функций, не пользуясь правилом Лопиталя.

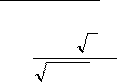
                                              2x² 3x1                                         3x² 5x 2

1.                            a) lim 3x2 x 4         ;        б)limx2 2x2 x6 ; x   

2 x

              в)         lim                   ;                                

x4 6x15

                                               5x²  2x1                                              2x² 15x 25

2. 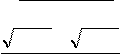                           а) limx 2x₂ x3 ;                          б)     xlim5               54xx₂   ;

9x 9x

            в) limx0             ₂                        ;                                   

x  6x

                                        3 2xx²                                                                                           4x² 7x3

3.                            а) limx       x2               ;        б) xlim1        2 ;

                                      4x1                                                          2x x1

3x3

  в) lim;         x1       8x3

 2                                            2

                                           3x 5x 4                                                   2x 9x9

4. 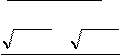                           а) limx x3 x1 ;     б) limx3 x2 5x 6 ;

5x 3x

          в) limx1           xx₂    ;                   

                                         2x² x 4                                                     5xx²  4

5.                            а) lim^x 3x 4x2 ;     б) limx4 2            ;

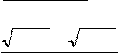x  2x8 7  x  7  x

                          в) lim;                                               

                               x0                  5x

 2                                        2

                                           x  7x1                                                        x  2x 8

6. 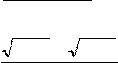                           а) lim^x       3x2        ;        б) xlim2 2x2  5x 2;

                                              x 3

4  x  4  x

            в) limx0                ₂                     ;                                   

3x  x

                                         3x² 5x 4                                                   3x²  2x1

7. 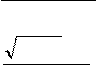                           а) lim^x 2x2 x1 ;  б) lim^x1 x2  4x3 ;

x² 7 3

                в) limx4 x₂  4x ;                                         

                                          2x³  2x1                                                      6xx²

8.                            а) lim^x3x2  4x 2 ;          б) xlim33x₂ 8x3;  3x3

                       в) lim;                                                  

                                x1        8x3

5 2x3x²            x³ 1  9.  а) limx x₂ x 3 ;  б) limx1 5x2  4x1; 4xx

              б) lim4     ₂               ;                                            

x x 16

                                          x² 3x 4                                                     x²  2x8

 10.  а) lim^x 2x₃ 5x1;                        б) limx2 8x₃          ; 

2x

                            б) lim;                                              

^x0 10 x 10 x

4. Задана функция y=f(x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.

                                      x  4,    x 1,

1.                        f (x) ^x²  2, 1 x 1,



                                    _2x,                   x 1.

                                      x  2,         x 1,    

2.                        f (x) ^x² 1, 1 x 1,



_

 x,

5.                        f (x) x2,



_x 1,

 x,



6.                        f (x) sin x,



_x  2,

x  0, 0  x  2, x  2. x  0,

0  x , x .

5.    Исследовать функцию и построить ее график. y  2x1,

1.                                       x5 

         2 x

2.                                       y    , x3

x2  6

3.                                       y    , x2 1

x

4.                                       y _ 2 3x ,

x1

² 8

yx 

5.                                       x ,

8

6.                                       y    2 ,

16x x

7.                                       y 2      ,

x _ 4

x

8.                                       y  ³ ₂ 4 ,

x

x3

9.                                       y    2 ,

1_ x

x

10.                                   y ² 1.

x

6.    Найти неопределенные интегралы. 

1.

           a)     e^{cos2 x} sin2xdx;            б)    xarctgxdx;

2.

                                           x²dx                               ^x ln1e^x dx;

a)     ^   ;        б)      _x3 _{ 4}6               e          

3.

                a)    1x2dxx6 ;            б)          x2xdx;



4.

                                             dx                                     x arccosx

   а) sin2 x2ctgx1;  б)  dx;

5. 

sin2xdx

  а)  ₃ ^;  б) x arccos_x dx; sin x

7.

arcsin xdx

              а) ;               б) xlnx^[1] ^[2]^[3]dx;

             а)  3 83sin x;                  б) xln xdx; 

7.    Вычислить определенные интегралы.



1

5x1

4.    x2  2x1dx.

0



5.    sin2xcos² xdx. 

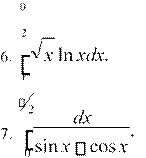
1

8.        xln1xdx. 

0 1

dx

9.         x2 x1. 

0

10.    .

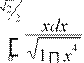8.        Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

3.2.  Обыкновенные дифференциальные уравнения.

9.        Найти решение дифференциального уравнения первого порядка, удовлетворяющее указанному начальному условию. Сделать проверку.

1.      2x2xy²     2 x² y  0,  у(1) = 0.

2.      xy ^| + xe^y/x – y = 0,   y(1) = 1 .

3.      20xdx – 3ydy = 3x²ydy – 5xy²dx,  y(1) = 1.

4.      xy ^| = y ln (y/x),  y(1) = e.

5.      3(x²y + y)dy + 9 y²dx = 0,  y(0) = 0.

6.      xy ^| + y = x + 1,  y(1) = 0.

7.      y ^|cosx = (y + 1)sinx,  y(0) = 0.

8.      xy ^| - y = x² y²,  y(1) = 0.

9.      y ^| - y/x = x²,  y(1) = 0.

10.  y ^| + ycosx = sin2x,  y(0) = 0.

3.3. Ряды.

10.    Выяснить, какие из данных рядов сходятся и какие расходятся.

1.          n1 nn425.       

2.          n1 ln(nn22).   

3.          n1 n3n 5.   

4.          n1 (23nn)!.

 n3

5.          ^n1 _en .               

6.          n1 nln23 n.        

7.           3n 2.   

n1 n5



8.          n1 (3n)!.

9.          n1 32nn21n.  

                                 nn

10.      n1 (n 2)!.

11.    Определить область сходимости данных рядов.

1.           n1 (nnn11)! xn.      

2.           n1 n(n5n 2) xn.       

3.           n1 (nnn1)n xn. 

                               3nn       n

4.           n1 (n 2)2 x .   

5.           n1 (n2nn2) xn.           

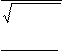
6.            4n xn. n_1 n(n1)

7.           n1 2n(nn1) xn.  

8.           n1 2n(nn(n1)3) xn.   

9.            n 5n              xn.

                      n1          2 (2n1)

10.       n1 n(nn32) xn.

3.4. Комплексные числа.

12.    Выполнить действия в алгебраической форме и представить полученный результат в тригонометрической форме.

2

                                 1         3

                                   i       

1.                   2i44 2i  _;

2.                   i⁹ 1i⁹ 1 ;

1i

i 1³

3.                   i12 i31 ; 

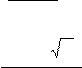3i15 i 32

4.                   i₉ ^₂       ; 

5.                   23ii103i ; 

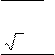 3 i³

6.                   i22 i ; 

i2 ^{i 3}3

7.                   1 25                  ;  _i

2

8.                   12i8i 3i ;

i8 3i11

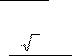9.                   1 2i₁₉ ; 

 3 i39

                        10.       i₂₀ _i     .

3.5. Основы теории вероятностей и математической статистики.

13.    решить задачи.

1.      а) Сколькими способами из группы, включающей 25 учащихся, можно выбрать актив группы в составе старосты и профорга? 

    б) В урне находится 7 красных и 6 синих шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара красные. 

2.      а) Найти количество всех трехзначных чисел, состоящих из чисел 1,2,3,4,5. 

     б) Набирая номер телефона, абонент забыл три последние цифры, и помня только, что они различны, набрал их наудачу. Какова вероятность, что он набрал нужные цифры.

3.      а) Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек. 

    б) К концу дня в магазине осталось 60 арбузов, из которых 50 спелых Покупатель выбирает 2 арбуза. Какова вероятность, что оба арбуза спелые?

4.      а) Сколько всего игр должны провести 20 футбольных команд в однокруговом чемпионате? 

    б) Девять книг, из которых 4 одинаковые, а остальные различны, расставлены наудачу на одной полке. Найти вероятность того, что эти 4 книги окажутся поставленными рядом.

5.      а) В   третьем   классе   изучается   10   предметов.   В   понедельник   4   урока.

Сколькими способами можно составить расписание на этот день

     б) В партии из 24 деталей 6 бракованных. Из партии выбирают наугад  детали. Найти вероятность того, что они все будут бракованными.

6.      а) Сколькими способами можно из 20 человек назначить двух дежурных, из которых один старший?

    б) Карточка «Спортлото» содержит 49 чисел. В тираже участвуют 6 чисел. Какова вероятность того, что будет верно угадано 4 числа?

7.      а) В подразделении 30 солдат и 3 офицера. Сколькими способами можно выделить патруль, состоящий из 3 солдат и одного офицера?

    б)  Из группы, состоящей из 10 юношей и 8 девушек, выбирают по жребию дежурных.

Какова вероятность того, что все выбранные окажутся юношами?

8.      а) Из 8 различных цветков нужно составить букет так, чтобы в него входило не менее 2 цветков. Сколько существует способов для составления такого букета?

    б)  Студент знает 20 из 25 вопросов программы. Вычислить вероятность того, что студент знает 2 вопроса из билета.

9.      а) Сколькими способами можно выбрать четырёх человек на четыре различные должности из девяти кандидатов на эти должности?

    б) В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что 4 наугад выбранных билета будут выигрышными?

10.  а) Из 7 бегунов и 3 прыгунов нужно составить команду из 5 человек, в которую должен входить хотя бы один прыгун. Сколькими способами это можно сделать?

      б) В партии из 10 деталей имеются 3 нестандартных. Найти вероятность того, что 3 наудачу взятые детали

14.  Задана непрерывная  случайная величина  Х  своей плотностью распределения  f(x).  Требуется:

1)      определить коэффициент А;

2)      найти функцию распределения F(x);

3)      схематично построить графики функций f(x)  и  F(x);

4)      вычислить математическое ожидание и дисперсию  X;

5)      определить вероятность того, что Х  примет значение из интервала (а, b).

                                                                          

1.      f(x) =  A0sinпри2x xпри 0 или0 xx4_, .        a = ₆ ; b =  .

                                                                             4

                                       2x

                                  Ae             при x 0,

2.      f(x) =                    a = 1; b =+ .

_ 0 при x 0.

                                     ²

3.      f(x) = ^_ Ax  при 0  x1,         a =0,5; b  = 2.

 0 при x 0 или x 1.

                                                                        

                                 Acos2x           при 0 x ^[9] ,         a = ^_; b =  ^ .

                                     2x

                                Ae           при x 0,

5.  f(x) = 

                      0

          a = - ; b = 1. при x 0.



10.  F(x) = ^_



1 Ae^2x                  при x 0,

         a = - 1; b =+ .

0 при x 0.

4. СПИСОК ВОПРОСОВ К ЭКЗАМЕНУ

1.          Функция. 

2.          Производная и дифференциал функции.

3.          Область определения функции.

4.          Неопределенный интеграл. Свойства неопределенного интегала. Основные методы интегрирования.

5.          Определенный интеграл, его свойства. 

6.          Приложения определенного интеграла для решения геометрических задач.

7.          Определение комплексного числа.  Алгебраическая форма комплексного числа. 

8.          Натуральная степень мнимой единицы.

9.          Комплексная плоскость. Геометрическая иллюстрация сложения и вычитания комплексных чисел в алгебраической форме.

10.      Действия над комплексными числами в алгебраической форме.

11.      Тригонометрическая форма комплексного числа. 

12.      Действия над комплексными числами в тригонометрической форме. Формула Муавра.

13.      Основные понятия комбинаторики. Комбинации перестановки, размещения, сочетания.

14.      Бином Ньютона. Свойства биноминальных коэффициентов.

15.      События. Виды событий. Определения  вероятностей.

16.      Теоремы сложения теории вероятностей.

17.      Теоремы умножения теории вероятностей.

18.      Формулы полной вероятности и Баейса.

19.      Дискретная случайная величина и её числовые характеристики.

20.      Функция распределения дискретной случайной величины.

21.      Непрерывные случайные величины. Математическое ожидание и дисперсия непрерывной СВ.

5. ПРИМЕРНЫЕ ПРАКТИЧЕСКИЕ ЗАДАНИЯ К ЭКЗАМЕНУ

1.        Найти производную функции:  у = sin x ^cosx . sin x  cosx

2.        Найти производную сложной функции:  у = ln ctg3x.

3.        Исследовать функцию на монотонность, экстремумы у =  x³-x² + 4  и построить схематичный график.

4.        Скорость прямолинейного движения тела ^ 2t² t см/с. Найти путь тела, пройденного за 6 с, считая S0  0см.

1

5.        Вычислить интегралы способом замены переменной 53x³dx

0



6.        Вычислить интегралы способом замены переменной ^2_1sin_cosx_xdx

0

7.        Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у²=х+2, х=0, х=9 и у=0.

3 i17

8.        Выполнить действия:   i₁₂                

9.        Выполнить действия в показательной форме, а результат записать в алгебраической 

                     _i3^ 10

 .





10.    .Выполнить действия  в тригонометрической форме , а результат записать в

алгебраической   3(cos^+ i sin^)²  

                                                              3             3

11.    Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная 0,8, второго – 0,9. найти вероятность того, что взятая наугад деталь окажется стандартной.

12.    В урне имеется 4 шара с номерами от 1 до 4. Вынули два шара. Случайная величина

X - сумма номеров шаров. Построить  ряд  распределения  случайной величины  X .

13.    Бросают три игральные кости. Какова вероятность того, что выпавшие цифры будут попарно различными?

14.    Решить уравнение: 2Сxx21 Ax32

15.    ДСВ задана рядом распределения. Закончить ряд распределения, найти числовые

                                                хⁱ            2      3     5    6

характеристики:

                                                p_i        0.2   0.3   ?   0,1

16.    Построить многоугольник распределения и найти числовые характеристики ДСВ по

            ряду распределения. x_i  4      6     10

                                                          p_i           ?     0,3   0,5

17.    ДСВ задана рядом распределения. Закончить ряд распределения, найти числовые

                               характеристики:.                    Построить    многоугольник    распределения    и

график функции распределения.

6. БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основные источники:  

1.Богомолов Н.В. Математика: Учебник для ссузов. М.: Дрофа, 2006. 

2. Богомолов Н.В.  Сборник  задач  по  математике:  Учебное  пособие  для ссузов. М.: Дрофа, 2007.

3.Григорьев С.Г. Математика: учебник для студентов сред. проф. учреждений / С.Г. Григорьев, С.В. Задулина; под ред. В.А. Гусева. – 2-е изд., стер. – М.: Издательский центр «Академия», 2009. – 384 с.:

4.Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2012. – 573 с. 5.  Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2009. – 352 с.

6. Спирина. М.С. Теория вероятностей и математическая статистика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2010. – 352 с.

7.Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям: Учебное пособие, 7-е изд., доп.- СПб.: Издательство «Лань», 2002. –432 с. – (Учебники для вузов. Специальная литература).

8. Выгодский М.Я. Справочник по высшей математике. -М.: Наука, 1987.

9.Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Справочное пособие по высшей математике. Т.1: Математический анализ: введение в анализ, производная, интеграл. – М.: Едиториал УРСС, 2004. – 360 с. Интернет ресурсы:  

1.   Единое   окно доступа      к        образовательным          ресурсам.   Электронная библиотека      [Электронный     ресурс].      —      Режим        доступа: http://window.edu.ru/window, свободный. — Загл. с экрана.

2.   Российская национальная библиотека [Электронный ресурс]. — Режим доступа: http:// nlr.ru/lawcenter, свободный. — Загл. с экрана. 

3.   Электронные библиотеки России /pdf учебники студентам [Электронный ресурс].— Режим доступа: http://www.gaudeamus.