Методика преподавания математики в условиях ЕГЭ

Методика преподавания математики в условиях ЕГЭ       

Цены растут, зарплата в течении ряда лет не повышается, а требования к подготовке выпускников в условиях сдачи ЕГЭ, ГИА повышаются.

Количество часов, отводимое, на изучение предмета осталось прежним (скорее уменьшилось: с 6 до 5 часов).

В такой ситуации работающий учитель пребывает в состоянии постоянного стресса.

Как в условиях огромной перегрузки современного преподавателя обеспечить достойный уровень обучения?

В пятых, шестых классах одним из главных направлений обучения является устный счёт. Нужно постараться научить детей как можно больше вычислений производить в уме, используя законы арифметики.

67 х 5 = (67 х 10) : 2 = 335

360 х 4 = (360 х 2) х 2 = 1440

360 х 8 = (360 х 4) х 2 = 2880

360 х 16 = (360 х 8) х 2 = 5760

Если ученик производит более сложные вычисления в уме (сложение, вычитание, умножение, деление многозначных чисел), то у доски разрешаю не писать столбики  вычислений. Психологический эффект воздействия таких «особенных» учеников на своих одноклассников сильнее, чем подробное решение.

Хороши и устные упражнения столбиками:

8,1 х 4 | 32,4

-11,6   |20,8

:2         |10,4   

+3,1     |13,5

В это время ребята встают, и устный счёт проходит стоя, своего рода небольшая физическая разрядка. Если ответил правильно, можно сесть по желанию, но в основном ребята продолжают стоя отвечать на вопросы.

Стараюсь проводить физические зарядки: «похлопали, потопали, покрутились во все стороны, посмотрели друг на друга и т.д.». Так как внимание к середине урока рассеивается и нужна тренировка, научить работать детей в течении  длительного времени.

В этом году провожу развёрнутый анализ всех контрольных работ (в тематическом планировании отводится урок обобщения перед контрольной работой и после урок анализа контрольной работы, где выставляю всем ученикам отметки). К доске вызываю учеников, получивших «2» и «3», на дом задаётся контрольная работа другого варианта, затем вновь проверка. Нагрузка возрастает, но толк в этом есть.

В конце года итоговые контрольные работы проводились в форме ГИА в 5-8 классах и ЕГЭ в 10 классе. На работу отводилось два урока в среднем звене и четыре урока в десятом классе. Каждому ученику были распечатаны варианты работ в виде книжечки. Они были использованы на уроках повторения, в домашних заданиях, на тренировочных, самостоятельных работах. Показательны и итоги, в каждом классе составлен рейтинг учащихся, «5», «4», «3», «2» - разных достоинств, это конечно приближает детей к атмосфере ЕГЭ.

Одна из главных задач подготовки детей к экзамену является психологическая. Детей нужно научить мыслить, в условиях экзаменационного стресса мыслить плодотворно в течении длительного времени (4 часа продолжается экзамен). Контрольные работы провожу в строгой дисциплинарной атмосфере, парты расставляются по классу от стены до стены, с большим расстоянием между ними и между рядами. Используя возможность рассадить за дополнительные парты, предлагаю 4 варианта заданий.

Ребята привыкают к такой жёсткой атмосфере с младших классов. Это вносит элемент особого урока, значимости контроля и на уроках многие начинают серьёзнее работать, так как на контрольной работе приходится рассчитывать только на себя.

Часто на контрольных работах дети задают вопросы по формулировке и оформлению задания: чертить рисунок или нет, сколько действий в решении задачи, находить величину или нет? И нередко учитель тем самым подсказывает алгоритм решения задачи. Поэтому на ЕГЭ ученик попадает в трудное положение, так как чётко уяснить, что требуется найти в задаче, составить план её выполнения является одним из основных этапов решения. Считаю лучшим из вариантов проведения контрольных работ – раздать тексты и предоставить полную свободу действий.

Излишнее внимание на оформление (не то количество клеток отсчитал от штампа, зачеркивания на титульном листе и т.д.) считаю недопустимым.

Геометрические задачи на ЕГЭ занимают немалую часть текста. Научить хорошо решать задачи по геометрии в условиях двухчасовой нагрузки в неделю – трудное дело. Большим подспорьем в этом – устные задачи. Пока ребята готовят домашние задачи на центральной доске, на боковой, стараюсь, как можно больше начертить рисунков к задачам, решаемые в устной форме. Без оформления геометрическая задача становится как ребус, идеи к задачам рассказывают ребята. В работе над одной задачей участвуют 2-3 ученика, решение происходит быстро, ребята получают оценки.

На уроках геометрии стараюсь решать большое количество задач. Для этого приходится выбирать одну задачу с полным оформлением, в остальных на чертеже отмечаем данные и сразу записываем короткое решение. Решение задачи стараемся оформить на математическом языке.

BSє (BCS)

BS║a              => BS║KN

(BCS)∩a=KN

Задача.

Точка L лежит на стороне AB параллелограмма ABCD, так что AL: LB = 3:4. Прямая CL пересекает луч DA в точке K, а площадь треугольника AKL равна 36. Найдите площадь параллелограмма ABCD.

Решение:

                                                              B                                          C

           K                                 A                                       D

∆ AKL ~ ∆ BCL, k = AL : LB = AK : BC = 3 : 4, AK = 3y, BC = AD = 4y, AL = 3x, LB = 4x,

SAKL =   ·3x · 3y · sinα = 36, xy · sinα = 8

SABCD = 7x · 4y · sin(180°-α) = 28xy sinα = 28 · 8 = 224.

Ответ: 224.

Задача.

Найдите площадь треугольника ABC, если его стороны AB и AC равны соответственно 12 и 18, а биссектриса AM отсекает от него треугольник ABM, площадь которого равна 20.

Решение:

                                                      А

                             B 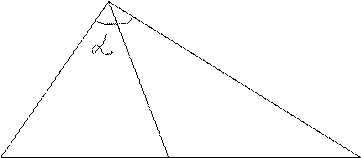C

                                                                         M

SAMB =   · 12 · AM · sinα = 20, AM sinα =  

SAMC =  · 18 · AM · sinα = 9 ·  = 30

SABC = 20 + 30 = 50.

Ответ: 50.