Методика решения задач по кинематике

МетоДика решения заДач.

(Алгоритмы)

Усвоить курс физики — это значит не только достаточно ясно и глубоко овладеть системой знаний, но и уметь применять их на практике. Однако это умение не приходит само собой, этому нужно учить. Особое место в этом смысле занимает решение задач.

Решение задач в школьном курсе физики имеет большое значение для конкретизации знаний учащихся, привития им умения видеть общее в его различных проявлениях. Решение задач также способствует более глубокому и прочному усвоению физических законов, развитию логического мышления, сообразительности, вызывает общий интерес к физике.

Содержание физических задач расширяет круг знаний учащихся • о явлениях природы и техники, знакомит их с различными профессиями.

Решение задач одно из важных средств повторения, закрепления, проверки и оценки знаний учащихся.

Как показывает практика, навыки учащихся в решении задач за последние годы возросли, но в ряде случаев продолжают еще оставаться недостаточными. Особенно это относится к решению задач по механике.

В связи с этим в данных рекомендациях будет рассмотрен наиболее рациональный координатный способ решения задач в ряде разделов механики и даны алгоритмы решения задач.

I МетоДика решения заДач по кинематике.

Одну и ту же задачу часто можно решить несколькими способами.

Рассмотри примеры:

Задача 1.1.

По наклонной доске бросили снизу вверх небольшой шарик. В точке, находящейся на расстоянии ЗОсм. от начала пути, шарик побывал дважды через 1 с. и через 2 с после начала движения. Определить начальную скорость и ускорение движение шарика, считая ускорение постоянным.

Решение 1-е

Сделаем схематический чертеж. Начальное положение шарика обозначим точкой А, положение шарика, находящееся от начала пути на 30 см., - точкой В и крайнее верхнее положение шарика на наклонной плоскости — точкой С. Рис 1.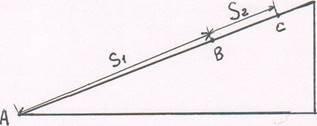

На участке АС шарик движется равнозамедленно до полной остановки в (.) С, а затем равноускоренно в противоположном направлении. обозначим отрезок АВ через Sl, отрезок ВС через S2 и время через tl и t2. По условию Sl=30 см.=0,З м, tl=1c, t2=2c.

Тогда время t2 - tl, шарик затратил на то, чтобы дважды пройти путь S2, двигаясь вверх и вниз. Так как ускорение шарика при движении вверх и вниз по наклонной плоскости одинаково, то, очевидно, что путь S2 он пройдет за

время

2

Таким образом, время подъема шарика из (.) А в (.) С

tn=tl+

                       2                2

     Поскольку          , то можно составить уравнение

а

(1) а  2

где - скорость шарика в (. ) А;

а — ускорение шарика

Для участка пути Sl, можно составить второе уравнение s=Votj-      (2)     2

Решая совместно уравнения (1) и (2), найдем и а:

2Sl tlt2   tlt2

Подставляя численные значения, получим [4=0, 45 ^м ; а=0,Зм 2

Решение 2-е.

           Преобразуем чертеж. Укажем на нем векторы начальной с орости          и

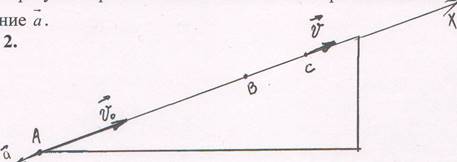ускорение а . Рис 2.

Движение шарика вдоль наклонной плоскости является равнопеременным. В векторной форме кинематическое уравнение такого

2

   движения имеет вид: S = sо +    

2

Чтобы использовать это уравнение для решения задачи, надо записать его в скалярном виде. Для этого направления вверх по наклонной плоскости будем считать положительным. Тогда, спроектировав на выбранное

at2 направление все векторы, получим S = S + Vot —  2

Из условия задачи So=O; S=Sl, при t=tl и S=Sl при t=t2

Учитывая это, можно записать: Sl = V0tl —

                                                                                               2                           2

Решая совместно эти уравнения, найдем tlt2   t2tl

Откуда  а=0,З м/с²

В чем разница этих двух решений одной задачи? В первом случае полнее вскрывается сущность отдельных этапов движения, для второго решения характерен более общий подход к описанию движения.

Второй вариант решения можно оформить иначе. Выберем систему координат, которую наиболее удобно взять в виде одной оси Х, положительное направление которой совпадает с начальным направлением движения шарика, а начало отсчета — с (.) А (см. рис. 2).

Тогда для данной системы координат уравнение движения будет таким:

at

2

Согласно условию задач x=Sl, при t=tl и t=t2 at12      

      Следовательно, Sl = Votl —           = vot2

                                                               2                            2

Решая совместно эти уравнения, получаем 2Sl tlt2  tlt2

откуда  а=0,З м/с²

З

В этом варианте решения определяется зависимость координаты движущегося тела от времени. Отсюда и название метода решения задач — координатный.

Координатным методом в кинематике решаются задачи, в которых по известному перемещению и ускорению надо найти начальную скорость, время движения или, наоборот, по известной начальной скорости и ускорению.

 величину перемещения и времени, за которое произошло перемещение.  Решение проводят по следующему алгоритму:

1.     Выбор системы координат. Координатные оси следует выбирать таким образом, чтобы нахождение проекций векторных величин, входящих в условие задачи, и координат точек осуществлялось максимально просто.

2.     Определение значений координат, соответствующих начальному положению тела.

З. Определение начального значения скорости и ускорения относительно всех осей координат.

4.     Составление уравнений, связывающих отдельные кинематические характеристики в соответствии с условиями задач.

5.     Решение системы этих уравнений относительно искомых величин в общем, виде.

6.     Перевод единиц измерения физических величин в одну систему. Подстановка числовых данных в полученное решение.

7.     Анализ решения.

Для примера рассмотрим следующую задачу Задача 1.2.

Рис З.

Одно тело брошено с поверхности Земли вертикально вверх с некоторой начальной скоростью [⁷01, а другое падает с высоты h м без начальной скорости (У02=0). Движения начались одновременно и проходят по одной прямой. Найти начальную скорость первого тела, если известно, что через t=2 с после начала движения расстояние между телами S=2 м. Решение.

h=40 м t=2 с

1.     В данной задаче в качестве системь координат достаточно одной оси ОУ с началом отсчета в точке бросания тела и направленной вертикально вверх.

2.     В начальный момент времени первое тело находится в начале координат (Ут=О), второе — в (.) (Yn=h)

З. Начальная скорость бросаемого тела направлена вертикально вверх, ускорение для обоих тел направлено вертикально вниз.

4.     Уравнение движения первого и второго тела: Ур     (1)

                                                                                                          УА- gt2          (2)

2

5.     Расстояние между телами равно разности их координат: S=Y2-Yl (3)

6.     Решая совместно уравнения (1), (2) и (З), получаем S=h_ gt2 _ V01t+g-t2 =h- V01tl, откуда n—S

                                                                                                                                               40 —2             

7.     Подставляя численные значения, найдем [⁷01 =

2

8.     Анализ решения. Спустя 2 с после начала движения первое тело буде 10-22 на высоте с координатой У

2

10-22 второе Уг=40 2

Разница высот

Следовательно, задача решена правильно.

Алгоритм координатного метода можно считать во многих случаях наиболее рациональным, облегчающим решение основной задачи кинематики.

П МетоДика решения задач по Динамике.

При изучении динамики решаются задачи, в которых ускорение создается различными силами: Силами упругости гравитационными силами, силами трения и другими, действующими совместно или в отдельности.

Чтобы добиться сознательного усвоения учащимися вопросов динамики, необходимо решать задачи в порядке возрастания их сложности:

1.     Задачи на движение тел под действием сил, направленных по одной прямой.

2.     Задачи на движение тел под действием сил, направленных под углом друг к другу.

Решение задач по динамике целесообразно проводить по следующему алгоритму:

1.     Записать кратко условие задачи.

2.     Определить систему координат. Установить, в каком направлении могут двигаться тела, о которых говорится в задаче, какова их возможная траектория; дать схематический чертеж к задаче и указать на нем все векторные величины.

З. Составить уравнение второго закона Ньютона для каждого из тел системы. Число уравнений должно быть равно числу неизвестных.

Недостающие уравнения обычно составляются на основании формул кинематики.

4.     Решить систему уравнений в общем виде.

5.     Выразить физические величины в одной системе единиц.

6.     Произвести вычисления и проанализировать полученный ответ.

В качестве примера рассмотрим решение следующей задачи.

Задача 2.1.

 По наклонной плоскости с углом наклона L скользит вниз брусок массой т. Найти его ускорение, если коэффициент трения бруска о плоскость равен

Решение

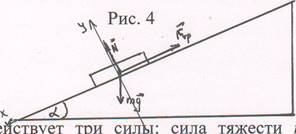2. На брусок де ствует три сил т: сила тяжести rng , сила реакции плоскости л^т и сила трения F тр.

З. Запишем второй закон Ньютона в виде двух скалярных уравнений: mgsinL-gN=max (в проекции на ось ОХ) N-mgcosL=0 (в проекции на ось ОУ) 4. Исключая из этих уравнений N, получим mgsinL-gmgcosL=max откуда

Учитывая, что ах=а, окончательно запишем:

5. Анализ этого выражения показывает, что при отсутствии трения

Если тело движется равномерно (а=О), то коэффициент трения g=tgL

III МетоДика решения задач по статике.

В основном, в школьном курсе физике по этой теме решают задачи на равновесие тел под действием сил, лежащих в одной плоскости. Поэтому для решения задачи достаточно использовать условие равновесия тела, заключающиеся в следующим:

Е =O•, Е Fy=o•, Е

При решении задач предлагаю использовать такой алгоритм:

1.    Записать кратко условие задачи.

2.    Сделать чертеж, указать силы, действующие на тело: реакции связей, внешние силы, силы трения и т.д. Выбрать оси координат ОХ и ОУ и найти проекции всех сил.

З. Составить уравнение равновесия для проекций сил на оси координат: Е =O•, Е Fy=o•,

4. Составить уравнение моментов сил. Для этого нужно выбрать точку, относительно которой будут рассматриваться моменты приложенных сил.

Данную точку лучше всего выбрать таким образом, чтобы через нее проходило наибольшее число линий действия неизвестных сил, тогда их, моменты будут равны нулю, и уравнение будет более простым.

5.     Решить полученную систему уравнений.

6.     Выразить все величины в одной системе единиц.

7.     Найти численные значения и проверить правильность результатов.

Примечания:

1.     Если тело, находящееся в равновесии, имеет одну неподвижную ось вращения, то можно ограничиться лишь составлением уравнения моментов. Раскладывать силы по осям координат в этом случае не нужно.

2.     Иногда при решении задач на равновесие тел, не имеющих закрепленной оси вращения, можно ограничиться только составлением уравнения моментов и не использовать уравнения проекций сил. Во всех таких случаях нужно лишь удачно выбрать точку, относительно которой определяются моменты.

З. Если линии действия всех сил на тело пересекаются в одной точке, то достаточно составить лишь уравнения проекций сил.

Для примера рассмотрим задачу.

Задача 3.1.

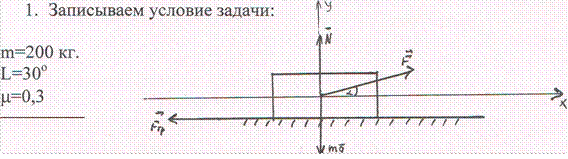
Тело массой 200 кг. перемещается равномерно по горизонтальной поверхности под действием силы F, направленной под углом 30⁰ к горизонту. Определить эту силу, если коэффициент трения тела о поверхность при движении џ=0, З

          Решение                                              Рис 5.

m=200 кг.

L=3C

2. Сделаем чертеж и изобразим силы, действующие на тело. Выбираем систему координат, согласно рис. 5. Т.к. линии действия всех сил персекаются в одной (.) 0 и по условию задачи тело движется равномерно, т.е. находится в равновесии, то для решения задачи достаточно составить уравнения для проекций сил.

З. Запишем уравнение равновесия для проекций сил на ось ОХ и на ось

ОУ

FsinL+N-mg=O (ОУ) (2)

Т.к. число уравнений равно двум, а число неизвестных (F ;Fmp N) равно

трем, то недостающее уравнение составим на основании того, что (З)

Таким образом, получаем систему уравнений:

FcosL-Fmp=O

FsinL+N-mg=O

ЏТ=О

4.     Решим данную систему уравнений. Исключив из последних двух уравнений ТЫ, получим систему из 2-х уравнений

FcosL-Fmp=O

FsinL+ тр -mg=0

Исключив из этой системы Fтр, придем к одному уравнению

                FcosL                                     gmg

Fs inL+ , откуда F= џ sinL = cos L

5.     Подставляя значения величин, получим F=588H

IV Методика решения задач по теме

«Импульс тела. Закон сохранения импульса»

Задачи по этой теме в школьном курсе физики решаются с

случаем закона сохранения импульса — одного из фундаментальных законов физики, справедливого в инерциальной системе координат для любой замкнутой системы тел.

Векторное уравнение закона сохранения импульса эквивалентно трем скалярным:

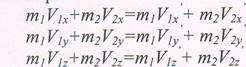
Т.к. оси координат х, у, z могут быть выбраны произвольно, то это означает, что сумма проекций импульса тел системы на любое направление является постоянной. В связи с этим закон сохранения импульса можно применять и для незамкнутой системы. В данном случае постоянной будет сумма проекций импульсов системы на направление, в котором внешние силы не действуют или уравновешиваются.

Закон сохранения импульса целесообразнее применять в тех задачах, в которых силы взаимодействия между телами системы являются переменными и сложным образом зависят от времени. В данных задачах, составляя уравнение закона сохранения импульса, мы исключаем из рассмотрения эти силы, чем упрощаем нахождение ответа.

Следует заметить, решению задач на применение закона сохранения импульса должен предшествовать анализ возможности применения этого закона.

При решении задач предлагаю использовать следующий алгоритм:

1.     Записать кратко условие задачи.

2.     Сделать чертеж, где для каждого тела системы изобразить векторы импульса в начале и в конце взаимодействия с другими телами системы.

З. Выбрать систему координат; установить положительное направление осей; найти проекции векторов импульсов.

Примечание: Оси координат необходимо выбирать так, чтобы приходилось делать минимум разложений и чтобы, по крайней мере, вдоль одной из осей не действовали внешние силы.

4.     Составить уравнения закона сохранения импульса тел в проекциях на оси ОХ и ОУ.

Если направление вектора 111 V или его составляющей совпадает с направлением оси координат, то его проекция берется со знаком (+), если нет — то со знаком (-). Если направление импульса неизвестно, то его проекцию можно считать положительной.

5.     Если число неизвестных более одного, то исходя из данных задачи, необходимо составить недостающие уравнения, используя для этого формулы кинематики или других разделов физики.

6.     Решить полученную систему уравнений.

7.     Найти численное значение неизвестного. проверить полученный ответ, проанализировать его.

В качестве примера рассмотрим задачу.

Задача 4.1.

Человек массой 60 кг. прыгает под углом 10⁰ к горизонту с неподвижной тележки массой 30 кг., стоящей на рельсах. При этом тележка перемещается на 2 м. Считая коэффициент трения при движении 0, 1., найти скорость, которую развивает человек при прыжке. Рельсы расположены в горизонтальной плоскости.

Решение.

1.     Записываем условие задачи: Рис.б пч=60 кг

0 кг

L=100

S=2M

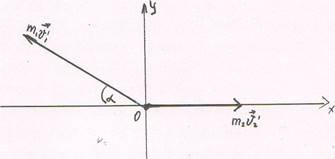
2.     На рис. 6 изобразим векторы импульсов человека и тележки после взаимодействия. До взаимодействия их импульс были равны 0. Т.к. процесс взаимодействия человека и тележки проходил быстро, то можно считать, что их скорости при взаимодействии изменились практически мгновенно и в направлении движения тележки систему тел в момент взаимодействия можно считать замкнутой.

З. Точку пространства, где находился человек в момент прыжка, возьмем за начло координат. Оси ОХ и ОУ направим соответственно вправо и вверх. Проекции импульсов на ось ОХ будут 17'llV rcosL и 1112V 2

4.     Составим уравнение закона сохранения импульса в проекциях на ось ОХ (в этом направлении в момент взаимодействия система

 (1)

5.     Т.к. в уравнении (1) два неизвестных, то на основании формула кинематики составляем еще одно уравнение =2aS. используя второй закон ньютона и определение силы трения, получим а=Етр 31712 g _—gg тогда 2ggS (2)

                                                             1712

2ggS

6.     Решая совместно, уравнения (1) и (2), получаем Щ =

 cos L

7.     Определяем численное значение V'l

зо 2-0,1 .9,8-2

zl,02 (08)

60 • cosL

Очевидно, это выражение для V'l не имеет смысла при L=90⁰

Методика решения задач с использованием закона сохранения энергии

Уравнение (Ею-Епј=А) закона сохранения и превращения энергии позволяет решить многие задачи школьного курса механики. Особенно удобно использовать закон сохранения при решении задач, где:

1.     Даются два механических состояния или положения тела в пространстве при равнопеременном движении.

2.     Рассматриваются два состояния или положения тела (или системы тел) в процессе неравномерно-переменного движения.

Во многих задачах уравнение, составленное на основании закона сохранения энергии, вместе с уравнением второго закона Ньютона и уравнением закона сохранения импульса составляют полную систему уравнений, описывающих данный процесс.

Задачи на применение закона сохранения энергии в механике предлагаю решать по следующему алгоритму

1.     Записать кратко условие задачи.

2.     Сделать схематический чертеж.

З. Установить начальное и конечное положение тела (системы тел).

4.     Выбрать систему координат и уровень отсчета потенциальной энергии.

5.     Изобразить на чертеже все внешние силы, действующие на тела в произвольной точке траектории, скорости тел и высоты тел над уровнем отсчета потенциальной энергии в начальном и конечном

положениях.

6.     Составить уравнение закона сохранения энергии.

       Примечание.         

Если система замкнута, то работа внешних сил равна 0 и уравнение примет вид Еп2-Ет=0. Если при переходе системы тел из начального положения в конечное на тело действовали внешние силы, то составляется равенство Еп2-Епј=А , где А — работа внешних сил.

7.     Если количество неизвестных величин больше числа составленных уравнений, то к ним следует добавить уравнения, составленные на основе второго закона Ньютона, закона сохранения импульса или кинематические уравнения.

8.     Решить систему уравнений относительно искомых величин.

9.     Произвести вычисления и проверить ответ. В качестве примера рассмотрим решения задачи.

Задача 5.1.

Некоторая сила толкает тело массой 16 кг. Вверх по наклонной плоскости длиной 3,1 м. И с углом наклона 30⁰ . Скорость тела у основания наклонной плоскости 0,6 м/с, а у ее верхнего края 3,1 м/с. Чему равна работа, произведенная силой, если коэффициент трения тела о наклонную плоскость 0, ? Сила направлена вдоль наклонной плоскости.

1.   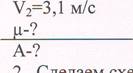   Запишем кратко условие задачи:

Решение m=16 кг

д=зоо vro,6 м/с

2.      Сделаем схематический чертеж (рис 7).

З. Начальное положение — (.) А; конечное — (.) В

4.     За уровень отсчета потенциальной энергии берем основание наклонной плоскости.

5.     Внешними силами в данной задаче будут и , с которой тянут тело вверх. Кроме того на тело действуют mg и л^т .

6.     Составляем уравнение закона сохранения энергии: Еп2-Епј=А, где Ею полная м.энергия тела в начальный момент;

      112—      =mgh- полная механическая энергия тела в конечный момент.

2

А=А Г А тр =А Г F тр •,• • А— работа внешних сил.

Следовательно, Г тр

2  2 m(V2² —

                     откуда Ай+ rngh=Fmp                                 (1)

2

7.     В уравнении (1), помимо Ау; неизвестно h и Fmp. Сила трения

           Т.к. N=mgcosL, то           mgcosL            (2)

            h= sinL                                               (З)

8.     Подставив в уравнение (1) значение       из (2) и 11 из (З), получим

 rn(V22 -V2)¹ + rng sinL+ mg cosL или+g (sinL+gcosL)] 2     2

9.     Произведем вычисления:

4=16 30⁰ +0,  (Дж). Полезно показать, 2 что задачи данного типа можно решить, используя уравнение второго закона  Ньютона.