


А. Ю. ]ћишенцев А. Е Коробейников
МЕТОДЫ И МОДЕЛИ
ЦИФРОВОЙ ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
Санкт-Петербург
Издательство Политехнического университета
удк 004.92•, 004.932•, 004.05
ББК 32.973.26-04•, 32.973.26-018.2
Г85
Рецензенты:
Доктор физико-математических наук, профессор, директор Санкт-Петербургского филиала Федерального государственного бюджетного учреждения науки Института земного магнетизма, ионосферы и распространения радиоволн им. Н. В. Пушкова
Российской академии наук Ю. А. Копытенко
Доктор технических наук, профессор, декан факультета информатики и вычислительной техники Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Поволжский государственный технологический университет» И. Е Сидоркина
Тришенцев А. Ю. Методы и модели
цифровой обработки изображений / А. Ю. Гришенцев, А. Г. Коробейников. — СПб. :
Изд-во Политехн. ун-та, 2014.![]()
Монография посвящена некоторым методам и моделям обработки функциональных изображений, научным основам построения средств компьютерной графики, методов геометрического моделирования проектируемых объектов и синтеза виртуальной реальности. Наряду с фундаментальными методами рассмотрены авторские, нашедшие успешное применение в практике. В работе приведено значительное количество практических примеров, реализованных на языке С++ и в среде MatLab. Книга может быть интересна студентам, аспирантам и инженерам, специализирующимся в области цифровой обработки.
Редактор Л. Е Позднякова
Компьютерная верстка М. В. Герасимова
Предисловие . ... . .. . . .. . ... . .. . . .. . ...
. .. . . . . ...![]()
1. Формат цифровых изображений .![]()
1.2. Физиологические
особенности восприятия информации ![]() 10
10
1.3. Тензорное поле — формат
представления многомерных цифровых сигналов.. . . .. . ... . .. . . .. . ... .
.. . . .. . ... ... . .. . . .. . ..![]()
1.4. О
цветовых пространствах ![]() 17
17
1.5. Форматы
цифровых изображений....................![]() . 23
. 23
1.6. Программные
преобразования цветовых пространств ![]() 27
27
1.7. Модель
классификации изображений............................ ![]() .
.![]() . 27
. 27
2.2. Измерение
машинного времени![]() 35
35
2.3. Цифровые
сигнальные процессоры![]() 38
38
2.4. Графические
процессоры![]() 40
40
2.5. Модели
разработки программного обеспечения ![]() 41
41
2.7. Практическое применение оптимизации
вычислений на базе преобразования форматов ![]() 52 2.8. Оптимизация вычислительных
циклов . . .. . ... . .. . . .. . ... . .. . . .. . ... . . . . .. . . 54
52 2.8. Оптимизация вычислительных
циклов . . .. . ... . .. . . .. . ... . .. . . .. . ... . . . . .. . . 54
3.1. Управление диапазоном значений сигналов ![]() 56 3.2. Масштабирование
и трансформация многомерных сигналов . . . .. . ... . .. . . .. . ... . .. . .
.. . ... . .. . ..
56 3.2. Масштабирование
и трансформация многомерных сигналов . . . .. . ... . .. . . .. . ... . .. . .
.. . ... . .. . ..![]() .
60
.
60
3.3. Классификация
шума .![]() 62
62
3.6. Адаптивные фильтры шума ![]() 71
71
4 Содержание
![]()
3.7. О коррекции некоторых искажений
оптоэлектронных систем.........................................................![]() 72
72
4.1. Линейные
системы![]() 79
79
4.2. Понятие
свёртки![]() . 80 4.3. Программная реализация свёртки..............................................
82
. 80 4.3. Программная реализация свёртки..............................................
82
4.4. Примеры обработки многомерных
сигналов с помощью свёртки ![]() 84
84
4.5. Декомпозиция
и синтез в линейных системах![]() 86
86
4.6. Фурье-декомпозиция
и синтез ![]() 87
87
4.8. О
фурье-преобразовании многомерных сигналов . ![]() . 91
. 91
4.9. Свёртка как результат произведения спектров сигналов. ... ... ... 98
4.10. Дискретное косинусное преобразование
![]() 98
98
|
4.1 1.
Вейвлет-преобразование |
|
|
4.12. Преобразование
Лапласа |
|
|
4.13.
4.14. О неопределённости при спектральных преобразовашшх |
|
|
сигналов............... 5. Способ декомпозиции п-мерных сигналов по базису |
|
|
прямоугольных всплесков . |
|
|
5.1. Формальное
описание способа |
|
5.2. Декомпозиции для одномерного случая![]()
|
5.3. Декомпозиция
двумерного сигнала |
116 |
|
5.4. Свойства и особенности преобразования 6. Предпосылки к формированию компактного вида цифровых |
118 |
|
сигналов
....................................... |
124 |
|
6.1. Общие принципы и классификация 6.2. Частотно-пространственные области концентрации |
124 |
|
информации
6.3. Предпосылки к исключению избыточной информации на |
125 |
|
базе
частотно-дифференциального анализа |
127 |
|
6.4. Сжатие
битовых последовательностей без потерь |
130 |
5 Содержание
![]()
7.1. Анализ дифференциальной структуры
и формирование паттерна краевых условий цифрового сигнала![]()
|
7.2. Восстановление сигнала методом конечных
разностей 7.3. Сжатие многомерных цифровых сигналов на базе анализа |
138 |
|
их дифференциальной структуры . 7.4. Повышение эффективности сжатия с учётом специфики |
139 |
|
цифрового
сигнала. .. . . .. . ... . .. . . .. . ... . .. . . .. . .. . . .. . ... . ..
. 7.5. Вычислительная оптимизация МКР путем отыскания |
144 |
|
промежуточного
решения 7.6. Практические результаты сжатия с помощью анализа |
149 |
|
дифференциальной
структуры |
152 |
|
8. Распознавание образов .. . .. . . .. . ... . .. .
. .. . ... . .. . . .. . .. . ... . .. . |
160 |
|
8.1. Задача распознавания образов. .. . ... .
.. . . .. . ... . .. . . .. . ... . . |
160 |
|
8.2. Оценки подобия . . .. . ... . .. . . .. .
... . .. . . .. . ... |
161 |
|
8.3. Анализ
спектра для распознавания образов |
165 |
|
8.4. Классификация образов ... . .. . . .. .
... . .. . . .. . ... . .. . . . |
168 |
|
8.5. Морфологический анализ. .. . . .. . ... .
.. . . .. . ... . .. . . .. . .. . .. . . . |
173 |
|
8.6. Нейронные сети . . .. . ... . .. . . .. . ... . .. . . .. . ... . . . . .. . ... . .. . . .. . ... . .. . . .. . ... . .. . .. . ... 175 |
|
|
Заключение . . ... . .. . . .. . ... . .. . . .. .
... . .. . . . . ... . .. . . .. . ... . .. . . .. . ... |
|
|
Список литературы.. . ... . .. . . .. . ... . .. . .
.. . ... . .. . .. . |
|

ПРЕДИСЛОВИЕ
Присущая человеку жажда знания является одной из движущих сил развития цивилизации.
В наше время информационные технологии получили особое значение. С конца ХХ—начала ХХТ вв. благодаря повсеместному распространению электронных вычислительных средств (ЭВС) произошли значительные изменения на самых различных уровнях организации и управления ресурсами, в том числе информационными. Широкие круги общества получили доступ практически к любой информации. Исследователи имеют возможность решать задачи, требующие одновременной работы множества мощнейших вычислительных систем. Стимулированные потребительским спросом значительно трансформировались и развились области знаний, связанные с информационными технологиями. Появились свежие инженерные решения, сформировались новые научные направления. Тенденции развития современных вычислительных устройств предполагают применение таких технологий, как параллельные и облачные вычисления. Доступность существенных объёмов памяти и рост тактовой частоты процессоров позволяют решать практические задачи с помощью методов, которые ранее вследствие вычислительной затратности не могли быть решены на существующих вычислительных платформах. Благодаря современным решениям, например GPGPU (General-Purpose Graphics Processing Units), реализующим неграфические вычисления на графических процессорах, обыкновенный персональный компьютер способен оперативно обрабатывать ресурсоемкие задачи.
Цифровые сигналы в большинстве случаев являются результатом преобразования информации, получаемой от аналоговых датчиков, а в некоторых случаях полностью производятся (синтезируются) цифровыми устройствами. Цифровая обработка сигналов (ЦОС), по сравнению с аналоговой, во многих случаях позволяет существенно поднять качественный уровень передачи, хранения и преобразования данных.
Повышение многообразия цифровых устройств и увеличение потока информации, требующей обработки, передачи и хранения, определяют актуальность исследований и анализа методов цифровой обработки сигналов и, в частности, цифровых изображений. Существенная часть инженерных, научных задач решается методами обработки изображений [4, 81, 125]. Возможность визуализации процесса и результатов обработки данных,
т.е. синтез цифровых графических изображений, является стандартным функционалом современных приложений [101, 159, 164, 166].
Предисловие
В данной монографии рассмотрены некоторые элементы теории ЦОС, изучены аспекты нового научно-практического направления формализации и обработки цифровых сигналов, в первую очередь графических изображений, как полевых структур.
Практическая ценность монографии заключается в анализе некоторых современных принципов ЦОС, подробном рассмотрении алгоритмов и программ, реализованных на языке С++ и в программной среде MatLab.
Значительная часть исследований выполнена на базе Университета ИТМО (Санкт-Петербург), Санкт-Петербургского филиала Института земного магнетизма, ионосферы и распространения радиоволн им. Н. В. Пушкова РАН (ИЗМИРАН). Результаты исследований востребованы в проектах Национального научного центра <<Никитский ботанический сад» (НБС, Крым), Санкт-Петербургского государственного политехнического университета (СПбГПУ), Государственного научного центра <<Арктический и антарктический научно-исследовательский институт» (ААНИИ).
Монография рассчитана на специалистов в области цифровой обработки сигналов, она может быть полезна студентам и аспирантам.
Гришенцев А. Ю. выражает благодарность своим учителям
Л. И. Иванову, Ю. П. Пирогову, К. Г. Короткову, А. Г. Коробейникову
Формат цифровых изображрений зачастую определяется архитектурой вычислительной машины, в первую очередь — организацией памяти и доступа к ней. Совместимость вычислительных систем подразумевает возможность работы с несколькими распространёнными форматами. Существует значительное число широко распространённых форматов, стандартных и являющихся практически (de faclo, т.е. <<на деле») стандартными, что, в свою очередь, требует множества их взаимных преобразований.
Для получения эффективных результатов при разработке программного обеспечения средствами ЭВС необходимо учитывать не только особенности форматов данных, но и восприятие их человеком.
Термин («изображение» часто используют для обозначения художественного образа, например, литературное изображение, графическое изображение и т.д.
Изображение — объект, образ, явление, в той или иной степени подобное (но не идентичное) изображаемому или сам процесс их создания.
Изображением (ооразом) в математическом смысле называют результат функционального преобразования. Преобразование (отображение) множества Х в множество У обозначают f : Х У . Если для каждого х Е Х существует единственный элемент у Е У , то у— Г (х) . Для некоторого прообраза Z Х множество f(Z) есть изображение, или образ [6].
Говоря о цифровых изображениях, имеют в виду цифровые (дискретные) образы. В контексте этой работы цифровыми изображением (или изображением) называются цифровые сигналы, полученные в результате некоторых отображений. В большинстве случаев рассматривается частный случай цифровых сигналов — цифровые графические изображения. Отметим, что цифровые сигналы в большинстве случаев являются образами реальных физических процессов; могут иметь только дискретные, в заданном диапазоне, значения; всегда имеют конечную область определения. Следует отметить, что цифровые графические изображения являются частным случаем многомерных цифровых сигналов.
В качестве объекта обработки и исследования в работе используются цифровые графические изображения, поскольку:
![]() они составляют наиболее значимый объём
цифровой информации, накопленной человечеством;
они составляют наиболее значимый объём
цифровой информации, накопленной человечеством; ![]() графические изображения
удобны для восприятия человеком;
графические изображения
удобны для восприятия человеком;
![]() несмотря на то что рассматриваемые методы
применимы к самому широкому классу цифровых сигналов, изначально они
создавались для обработки именно цифровых графических изображений.
несмотря на то что рассматриваемые методы
применимы к самому широкому классу цифровых сигналов, изначально они
создавались для обработки именно цифровых графических изображений.
Изначально превалирующее большинство сигналов существует в аналоговом виде. Зарегистрированные приёмниками, они могут быть преобразованы в цифровой вид с помощью аналого-цифрового преобразователя (АЦП). Критерием корректного преобразования аналогового сигнала в цифровой вид является возможность его восстановления с заданной точностью. Основополагающим законом, позволяющим производить такие преобразования, является опубликованная в 1933 г. теорема Котельникова [82], таюке называемая теоремой отсчётов, повторно «открытая» в 1949 г. Клодом Шенноном.
Теорема Котельникова гласит: любую функцию x(t) , состоящую из частот от нуля до f , можно передавать с любой точностью при помощи чисел, следующих друг за другом через секунд, такая последователь-
ность образует дискретные отсчёты с частотой
дискретизации 2f![]()
В 1999 г. Международный научный фонд Эдуарда Рейна (Германия) признал приоритет В. А. Котельникова , наградив его в номинации <<фундаментальные исследования» премией «за впервые математически точно сформулированнуко и доказанную в аспекте коммуникационных технологий теорему отсчётов» [83].
Во множестве практических задач цифровой обработки сигналов конечным объектом восприятия информации является человек. Например, с особенностями физиологического восприятия изображений связаны форматы, параметры и принципы графического отображения цифровых сигналов, в частности, цветовые схемы, частота обновления кадров, гамма-коррекция, разрешение оптико-электронных приборов и др.
В исследованиях Э. Вебера показано, что определяющим связь между интенсивностью ощущения и силой раздражения воспринимается не абсолютный, а относительный прирост силы раздражителя (света, воздействующего на сетчатку глаза; звука, воспринимаемого органами слуха; груза, давящего на кожу):
![]() Владимир Александрович Котельников (24 августа, 1908, Казань
— 11 февраля 2005, Москва) — инженер и учёный.
Владимир Александрович Котельников (24 августа, 1908, Казань
— 11 февраля 2005, Москва) — инженер и учёный.
Эрнст Генрих Вебер (24 июня 1795, Виттенберг — 26 января 1878, Лейпциг) — психофизиолог и анатом, брат физика Вильгельма Вебера.
![]() const
const
где Р, ДР величина и приращение раздражителя. Минимальный прирост ощущения определяется как
![]()
где с — коэффициент пропорциональности. Проинтегрировав выражение (1 .2) и полагая, что величина S = 0 (ощущение) при минимальном значении абсолютного порога Рпи.п , можно записать:
![]() — cln lpl — cln = cln
— cln lpl — cln = cln![]()
Перейдя к десятичному основанию логарифма при помощи подстанов-
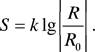
Разнообразные раздражители принято классифицировать по модаиьносп1и [102], различают световые, механические, химические, осмотические, электрические, тепловые и другие раздражители. Все раздражители подразделяют на адекватные и неадекватные по отношению к конкретной ткани, в частности, к рецепторному аппарату. Адекватным называют раздражитель, к восприятию воздействия которого ткань в ходе эволюции приспособилась. Адекватность раздражителя проявляется в том, что его пороговая величина значительно ниже, чем у неадекватных раздражителей.
Значительная разница в восприятии адекватных и неадекватных раздражителей свойственна сенсорным системам всех органов чувств [104]. Сенсорные системы образованы: рецепторами, реагирующими на сигналы внешней и внутренних сред организма; чувствительными нервными волокнами, проводящими сигналы от рецепторов в центральную нервную систему (ЦНС); структурами ЦНС, которые анализируют эти сигналы.
В соответствии с модальностью адекватного раздражителя, разнообразные рецепторные аппараты подразделяют на:
![]() фоторецепторы (обеспечивают восприятие
света),
фоторецепторы (обеспечивают восприятие
света), ![]() механорецепторы (ответственны за
восприятие механических раздражителей, в том числе виброакустических),
механорецепторы (ответственны за
восприятие механических раздражителей, в том числе виброакустических),
— хеморецепторы (получают информацию о химических
свойствах окружающей среды). К хеморецепторам относятся обонятельные и
вкусовые, а также некоторые рецепторы внутренних органов (интероцепторы), ![]() терморецепторы
(воспринимают изменение температуры окружающей среды),
терморецепторы
(воспринимают изменение температуры окружающей среды), ![]() осморецепторы (реагируют
на изменение осмотического давления).
осморецепторы (реагируют
на изменение осмотического давления).
Нами рассмотрены далеко не все рецепторные аппараты человека, присутствующие в большом количестве во всех органах и тканях. По расположению рецепторных аппаратов различают экстерорецепторы, обращённые во внешнюю среду, и интерорецепторы, реагирующие на процессы во внутренней среде организма. У экстерорецепторов выражена специализация — высокая избирательная чувствительность к адекватным раздражителям. Из-за большой разницы в порогах адекватных и неадекватных раздражителей большинство экстерорецепторов принято считать приспособленными к восприятию стимулов одной модальности. Например, фоторецепторы глаза начинают воспринимать свет с минимальным потоком световой энергии порядка 10 17 —10 18 Вт, ощущение вспышки можно вызвать механическим воздействием на глаз (явление механического фосфена), для этого необходима энергия порядка 10 Вт, следовательно, разница между световым (адекватным) и механическим (неадекватным) раздражителем составляет порядка 1013 —1014 раз.
В. О. Самойлов отмечает, что чувствительность фоторецепторов человека необычайно высока [104]. Возбуждение палочки происходит при поглощении одного кванта света, человек способен ощущать такой свет, который приводит к возбуждению не менее 5—10 палочек, поглощающих соответствующее число фотонов. Пороги чувствительности одного порядка были получены различными исследователями. С. И. Вавилово установил порог в 9 фотонов (к примеру, С. Гехт — 6 фотонов, Н. И. Пинегин — 2 фотона), такие результаты исследования позволили ему сделать вывод о том, что зрительный анализатор человека близок по своим характеристикам к идеальному прибору. Диапазон воспринимаемой яркости человеком 10 —106 кд•м- , что соответствует 12 порядкам, а по некоторым оценкам — 14.
Фоторецепторы сосредоточены на сетчатке глаза, каждый глаз человека содержит примерно 1.25 • 108 палочек и .5•106 колбочек. Фактически фоторецепторная система человека является дискретной. Зрительный нерв содержит порядка 106 волокон, по ним в мозг направляются сигналы от 130• 106 фоторецепторов. Один аксон ганглиозной клетки в среднем соби-
![]()
- Сергей Иванович Вавилов (12 марта 1891, Москва — 25 января 1951, Москва) — советский физик, основатель научной школы физической оптики в СССР, академик (1932) и президент АН СССР (с 1945 года). Лауреат четырёх Сталинских премий.
рает информацию от множества рецепторных клеток. Все фоторецепторы, посылающие сигналы к этой ганглиозной клетке, составляют её рецепторное поле. Число рецепторных полей, образованных палочками, гораздо больше числа колбочковых полей. Каждая колбочка, находящаяся в центральной ямке жёлтого пятна сетчатки, связана с одной ганглиозной клеткой, что определяет наилучшую разрешающую способность центрального колбочкового зрения. Ганглиозные клетки, к которым сигналы приходят от палочек, получают сигналы от многих тысяч палочек. Поэтому разрешающая способность палочкового зрения существенно ниже колбочкового, при этом первое обеспечивает максимальную чувствительность. Палочковое зрение называют скотопическим, световая чувствительность скотопического зрения, по ощущениям зрительного восприятия, примерно на три порядка выше колбочкового (фотопического).
 Первичный механизм
возбуждения палочек светом связан со сложными превращениями высокомолекулярного
соединения (родопсрша) в фоторецепторной мембране. Максимумы спектра поглощения
родопсина приходятся на длину волны Х=498 (видимое излучение) и 278 нм
(ультрафиолетовое, невидимое, излучение). Поглощение в видимом диапазоне
приводит к возбуждению родопсина и последующему восприятию света, ультрафиолетовое
(УФ) излучение не может возбудить родопсин, поскольку оно практически полностью
поглощается преломляющитуш средами глаза. Спектр поглощения родопсина хорошо
(«приспособлен» к восприятию достаточно широкой области солнечного излучения,
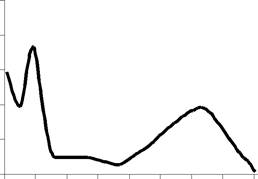
но лучше всего этот зрительный шпмент поглощает в зелёной части спектра (рис. 1
. 1 D — оптическая плотность родопсина). В процессе эволюции организм приобрёл
зрительные пигменты, эффективно воспринтмающие ту область спектра, которой
принадлежит значительная доля отфильтрованного атмосферой излучения абсолютно
чёрного тела при Т=6000 К, что близко к температуре поверхности Сојшца. D, о.е.
8 6
Первичный механизм
возбуждения палочек светом связан со сложными превращениями высокомолекулярного
соединения (родопсрша) в фоторецепторной мембране. Максимумы спектра поглощения
родопсина приходятся на длину волны Х=498 (видимое излучение) и 278 нм
(ультрафиолетовое, невидимое, излучение). Поглощение в видимом диапазоне
приводит к возбуждению родопсина и последующему восприятию света, ультрафиолетовое
(УФ) излучение не может возбудить родопсин, поскольку оно практически полностью
поглощается преломляющитуш средами глаза. Спектр поглощения родопсина хорошо
(«приспособлен» к восприятию достаточно широкой области солнечного излучения,
но лучше всего этот зрительный шпмент поглощает в зелёной части спектра (рис. 1
. 1 D — оптическая плотность родопсина). В процессе эволюции организм приобрёл
зрительные пигменты, эффективно воспринтмающие ту область спектра, которой
принадлежит значительная доля отфильтрованного атмосферой излучения абсолютно
чёрного тела при Т=6000 К, что близко к температуре поверхности Сојшца. D, о.е.
8 6
4
2
240 320 400 440 нм
Рис. 1.1. Спектр поглощения родопсина
С функционированием колбочек, сосредоточенных в центральной ямке сетчатки, связана предельная острота зрения человека. Благодаря существованию колбочковых пигментов трёх типов человек обладает цветным зрением. В результате у человека и приматов присутствуют колбочки трёх типов, условно названные «красными», «зелёными», «синими», каждая из которых характеризуется содержанием особого пигмента. Пигмент «красных» колбочек имеет фиолетовый цвет и потому называется йодопсином (от гр. 0600 — фиолетовый), «красные» колбочки способны хорошо поглощать свет в жёлто-красной области солнечного спектра (Xz562 нм). Максимум поглощения пигмента («зелёных» колбочек приходится на iz500 нм, пигмент «синих» колбочек лучше всего поглощает фиолетовые и синие лучи с максимумом поглощения на iz449 нм. Спектры поглощения колбочковых пигментов приведены на рис. 1.2 (р — относительное поглощение излучения; 1 — «синие», 2 — «зеленые», З — («красные»).
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 60 40
20
Рис. 1.2. Спектр поглощения колбочек
Строение органов зрения и слуха человека чрезвычайно сложно, им свойственны различные способы передачи и преобразования сигналов как в цифровом, так и в аналоговом виде. Например, пространственная структура расположения фоторецепторов на сетчатке дискретна, в результате проекции изображения фотосенсорная система в каждый момент времени способна формировать образ воспринимаемой информации с некоторым конечным разрешением (возбуждение импульсов в нейронной сети таюке обладает свойствами дискретности).
1.3. Тензорное поле — формат представления многомерных цифровых
Все физические процессы происходят в четырёхмерном пространственно-временном континууме — окружающий нас мир имеет три пространственные координаты и одну временную. В некоторых случаях могут возникать задачи обработки данных (сигналов), рассматриваемых в пространствах, имеющих более четырёх измерений.
Формализация способа записи многомерных сигналов требует особого внимания. Каждый элемент многомерного сигнала может быть представлен множеством значений, причём мощность этого множества может не соответствовать размерности пространства, в котором рассматривается цифровой сигнал. Элементы цифрового сигнала могут быть представлены скалярными и векторными величинами, а сигналы могут быть рассмотрены в различных координатных пространствах. Такое многообразие представлений цифровых сигналов требует определённой систематизации. Возможность несовпадения мерности пространства, в котором рассматривается сигнал, и мерности пространства значений сигнала, не позволяет априори считать сигналы векторными или скалярными полями.
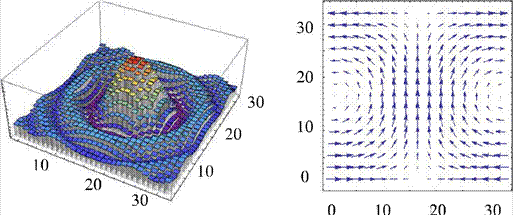
Для формального описания цифровых сигналов наиболее подходит тензорное поле (рис. 1.3, а — тензор нулевого ранга, скаляр, б — тензор первого ранга, вектор в двумерном пространстве—плоскости), когда каждому элементу, характеризуемому набором координат в пространстве сигнала, ставится в соответствие тензор одного типа. Такой подход позволит обобщить множество действий на базе определённых операций над тензорами.
 200
200
0
а
Рис. 1.3. Двумерные дискретные тензорные поля
Будем называть многомерной систему, объекты которой
исследуются в конечномерном пространстве, допускающем размерность п 2![]()
Для обозначения размерности пространства, в котором рассматриваются сигналы, будем использовать упорядоченное ортонормированное множество = r r ) . Запись f(Rl ) означает, что сигнал рассматривается в п -мерном пространстве. Цифровые сигналы обозначим следующим образом: f[ro, 73 , ...,rn 1] , или f[R"] . Очевидно, что одномерные сигналы могут рассматриваться как частный случай. Значению сигнала в каждой точке пространства ставится в соответствие тензор Х типа (р, q) , т.е. р раз ковариантный и q раз контравариантный. Обозначать тензоры будем индексы ili, ...i называют ковариантными (соответствукот ковариантным координатам х. в каждом базисе е и ), jljy..jq— контра-
вариантными (соответствуют контравариантным координатам х-11.12 -14 в каждом базисе е . Сумму (p+q) называют рангом, или валентностью, тензора. Тензор будем рассматривать в произвольном (необязательно евклидовом) вещественном К -мерном линейном пространстве Lk .
Частным случаем тензора нулевого ранга является скаляр х . Тензору первого ранга (с единичной валентностью) соответствует ковариантный вектор х. или контравариантный х] В большинстве случаев для записи цифровых сигналов достаточно скаляров и векторов (см. рис. 1.3).
В формализации тензорного исчисления используются краткие записи групповых операций с однотипными слагаемыми — соглашения. Представим выражение, составленное из сомножителей, которые снабжены конечным числом индексов — нижних и верхних. При этом все индексы обозначены различными символами. Если в выражении два одинаковых индекса: один верхний, а другой нижний, то по этим индексам выполняется суммирование. Например, для выражения
![]() = Ebimxm
= Ebimxm
краткая форма записи будет иметь вид:
![]() = bimxm
= bimxm
![]() где у. — координаты ковариантного вектора
первого ранга; — координаты контравариантного вектора первого ранга; Ь
координаты ковариантного вектора второго ранга (матрицы).
где у. — координаты ковариантного вектора
первого ранга; — координаты контравариантного вектора первого ранга; Ь
координаты ковариантного вектора второго ранга (матрицы).
Мы не будем рассматривать все формальные определения и операции тензорного исчисления [22, 67], поскольку это выходит за рамки работы.
Большинство физических законов можно выразить шафференциальными соотношениями между физическими величинами, являющимися тензорными полями [94]. Цифровые сигналы соответствуют образам некоторых реальных физических процессов или виртуальных моделей, по этой причине тензорные исчисления являются удобным способом обработки цифровых сигналов, соответствующих отображению реальных физических.
Применение тензорного исчисления к многомерным цифровым сигналам позволяет формализовать некоторые особенности сигналов, а операции над тензорами — расширить операционное пространство, доступное для действий с ними.
Зрительная система человека воспринимает информацию покомпонентно, любой цвет может быть получен в результате синтеза, т.е. комбинщий суммы или разности компонентов различной интенсивности. Обычно используют три компонента — базовые цвета: красный, зелёный и синий, или RGB (Red, Green, Blue). С точки зрения формирования цветопередачи цветовые модели можно разделить на аддитивные, разностные и смешанные. Например, модель RGB является аддитивной; СМУК — разностной; а YCbCr — смешанной, в которой компонент У — аддитивный, СЬ и Cr — разностные.
В настоящее время имеется множество моделей цветовых пространств и их вариаций, а соответственно — средств обработки и воспроизведения цветных изображений. На базе цветовых моделей формируют цветовое пространство, которое можно рассматривать как геометрическое, в котором задана система координат, связанная с цветовой моделью. Наиболее распространены трёхкомпонентные цветовые модели и пространства. В практике ЦОС для представления цветовых пространств наиболее широко используется прямоугольная, реже — цилиндрическая система координат. В цифровых сигналах число возможных значений каждого компонента определяет совокупное возможное количество цветовых оттенков, например, при восьмиразрядном представлении каждого компонента в трёхмерном цветовом пространстве — 256, общее число цветов 2563 = 16777216 , такого цветового разнообразия вполне достаточно для визуализации большинства цветных изображений.
Исследованиями и стандартизацией цветопередачи, в том числе в области цветоощущения, занимаются следующие организации:
— International Commission оп Illumination, или СIЕ — Международная комиссия по освещению, официальный сайт: http://cie.co.at/;
— ISO, International 0rganization for Standartization — Международная организация стандартизации, официальный сайт: http://www.iso.org/;
— ITU, International Telecommunication Union — Международный союз электросвязи, официальный сайт: http://www.itu.int/;
![]() Всероссийский научно-исследовательский
светотехнический институт им. С. И. Вавилова, официальный сайт:
http://www.vnisi.ru/.
Всероссийский научно-исследовательский
светотехнический институт им. С. И. Вавилова, официальный сайт:
http://www.vnisi.ru/.
Эти организации разработали ряд стандартов и рекомендаций по классификации и использованию цветовых пространств.
Рассмотрим некоторые цветовые пространства и методы взаимного преобразования их моделей. Следует отметить, что широко используемые дискретные реализации моделей цветовых пространств не обеспечивают передачу всего спектра оттенков, воспринимаемых человеком (поскольку большинство моделей не охватывают спектра, кроме того, при дискретной реализации непрерывный аналоговый спектр интерпретируется как линейчатый). Однако для решения большинства задач отображения графической информации вполне достаточно возможностей существующих моделей.
Линейное цветовое пространство CIE хуУ предложено Международной комиссией по освещению, модель цветового пространства CIE хуУ построена на основании зрительных особенностей восприятия «среднего наблюдателя». Цветовое пространство CIE ХУУ является трёхмерным, по оси х расположен цветовой градиент от синего до красного, по оси у — от синего до зелёного, по оси У распределены значения интенсивности элементов цветовой плоскости ху. На рис. 1.4 (http://members.eunet.at/cie) выделена область, очерченная линиями красного и фиолетового, внугри нее находятся все видимые человеком цвета. Эта диаграмма получена в результате длительных исследований способностей цветоощущения человека. В центре диаграммы находится оцененная статистически для «среднего наблюдателя» точка равных интенсивностей цветовых компонентов, соответствующая белому цвету, а при движении по оси У— различной интенсивности оттенка серого. На рис. 1.4 отображена графическая интерпретация соотношения CIE хуУ с цветовыми моделями NTSC, RGB.
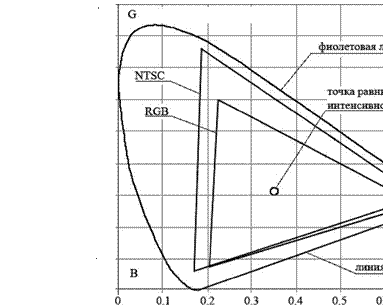
Рис. L4. Соотношение цветовых пространств RGB, NTSC на плоскости СГЕ ху
Все оттенки в модели RGB формируются путём сложения трёх
компонентов с различной интенсивностью, поэтому RGB является аддитивной.
Сочетание компонентов равной интенсивности даёт различные оттенки серого цвета:
от чёрного до белого. ![]() построена с учётом трёхкомпонентного
цветового восприятия человека и учитывает физиологические особенности, она
наиболее широко используется в электронных устройствах визуализации цветной
графической информации. Трёхкомпонентное цветовое пространство во многих
случаях позволяет эффективно производить обработку и анализ графической
информации, поэтому на работу с данными в цветовом пространстве RGB
ориентированы многие вычислительные устройства и программное обеспечение.
построена с учётом трёхкомпонентного
цветового восприятия человека и учитывает физиологические особенности, она
наиболее широко используется в электронных устройствах визуализации цветной
графической информации. Трёхкомпонентное цветовое пространство во многих
случаях позволяет эффективно производить обработку и анализ графической
информации, поэтому на работу с данными в цветовом пространстве RGB
ориентированы многие вычислительные устройства и программное обеспечение.
СМУК-модель (Суап — голубой, Magenta — пурпурный, Yellow ![]() жёлтый
и дополнительный цвет Ь1асК — чёрный, или Кеу c010r) является подтиножеством
модели RGB и используется в основном для цветной триадной печати на белой
поверхности. Модель СМУК, в отличие от RGB, является разностной, это означает,
что получение требуемого оттенка основывается на вычитании из белого (цвета
поверхности печати) соответствующей комбинации СМУК. Чёрный цвет необходим для
возможности изменения яркостной составляющей и получения некоторых оттенков.
Число доступных цветовых оттенков для модели СМУК существенно меньше, чем,
например, для RGB. Отображение цвета в пространстве СМУК существенно зависит от
яркости и белизны поверхности печати.
жёлтый
и дополнительный цвет Ь1асК — чёрный, или Кеу c010r) является подтиножеством
модели RGB и используется в основном для цветной триадной печати на белой
поверхности. Модель СМУК, в отличие от RGB, является разностной, это означает,
что получение требуемого оттенка основывается на вычитании из белого (цвета
поверхности печати) соответствующей комбинации СМУК. Чёрный цвет необходим для
возможности изменения яркостной составляющей и получения некоторых оттенков.
Число доступных цветовых оттенков для модели СМУК существенно меньше, чем,
например, для RGB. Отображение цвета в пространстве СМУК существенно зависит от
яркости и белизны поверхности печати.
Трёхмерная базовая модель YUV применяется в аналоговом
телевизионном вещании. Будучи производной от ![]() YUV содержит три
компонента: У определяет общий уровень яркости, аддитивный компонент, а U и V —
цветоразностные. Яркость рассчитывается путём взвешивания интенсивностей
красного, зелёного и синего, разностные компоненты формируются путём вычитания
яркости из синего и красного. Обратную совместимость форматов цветного и
черно-белого телевизионных сигналов обеспечивает яркостная составляющая,
обрабатывать которую возможно вне зависимости от цвета: например, производить
изменение динамического диапазона, в частности, гамма-коррещию. Цветовое
пространство, построенное на базе
YUV содержит три
компонента: У определяет общий уровень яркости, аддитивный компонент, а U и V —
цветоразностные. Яркость рассчитывается путём взвешивания интенсивностей
красного, зелёного и синего, разностные компоненты формируются путём вычитания
яркости из синего и красного. Обратную совместимость форматов цветного и
черно-белого телевизионных сигналов обеспечивает яркостная составляющая,
обрабатывать которую возможно вне зависимости от цвета: например, производить
изменение динамического диапазона, в частности, гамма-коррещию. Цветовое
пространство, построенное на базе ![]() (при диапазонах значений У = 0—1, U =
(при диапазонах значений У = 0—1, U = ![]() 0.6—0.6
и V = —0.64.6), содержит значительно больше цветовых оттенков, чем RGB при
допустимых значениях для всех компонентов 0—1. Компоненты цветового
пространства, прошедшие гамма-коррещию, будем обозначать как Y'U'V' , взаимное
преобразование R',G',B' в Y'UV' и обратно можно выполнять с помощью следующих
выражений:
0.6—0.6
и V = —0.64.6), содержит значительно больше цветовых оттенков, чем RGB при
допустимых значениях для всех компонентов 0—1. Компоненты цветового
пространства, прошедшие гамма-коррещию, будем обозначать как Y'U'V' , взаимное
преобразование R',G',B' в Y'UV' и обратно можно выполнять с помощью следующих
выражений:
![]() У' = 0.299R'
У' = 0.299R' ![]() +
0.114В',
+
0.114В',
U' = -0.147R'
- 0.289G' + 0.436В' = 0.429(В'![]()
V' = 0.615R'
- 0.515G' - 0.100В' = 0.877(R'![]()
и
 0.581V',
0.581V',
![]() цветового пространства, используемая для
цифрового видео, разработана в рамках рекомендации ITU-R ВТ.601-7 от 03/2011 [1
53],
цветового пространства, используемая для
цифрового видео, разработана в рамках рекомендации ITU-R ВТ.601-7 от 03/2011 [1
53], ![]() построена на базе
построена на базе ![]() Компоненты
цветового пространства, прошедшие гамма-коррекцию, будем обозначать как
Y'Cb'Cr' , взаимное преобразование R',G',B' в Y'Cb'Cr' и обратно можно
производить с помощью выражений [155] :
Компоненты
цветового пространства, прошедшие гамма-коррекцию, будем обозначать как
Y'Cb'Cr' , взаимное преобразование R',G',B' в Y'Cb'Cr' и обратно можно
производить с помощью выражений [155] :
У! = 0.257R' + 0.504G' + 0.098В' +16,
О. - 0.291G' + 0.439В' +128,
G' = 1.164(У' -16) -0.813(Cr' -128) -0.З92(СЬ' -128), ![]() В' = 1.164(У' -16) +
В' = 1.164(У' -16) + ![]() -128).
-128).
Для преобразования значений, описывающих цвет без гаммакоррекции, используемого, например, в цифровом телевидении, в пространствах YCbCr и RGB, применяют следующие выражения:
У = 0.299R+O.587G+O.114B,
СЬ = -0.16874R - 0.33126G + 0.5В + 128,
Cr = 0.5R +128 и
R = У + 1.4020-179.456,
G = У - 0.34414СЬ - 0.71414Cr +135.45984, В = У + 1.772СЬ - 226.816.
Вариация распространённая в компьютерных системах, цифровом телевидении, также применяется при компрессии графических изображений:
= +16,
СЬ = -0.101R - 0.338G + 0.439В +128,
Cr = 0.439R - - 0.040В +128 и
16414У709 + 1.79237СЬ - ![]() -
247.909, G = 1.16414У709 -0.5З4ЗО8СЬ - 0.213096Cr + 77.0414,
-
247.909, G = 1.16414У709 -0.5З4ЗО8СЬ - 0.213096Cr + 77.0414,![]()
16414У709 + 0.000987185Cb + 2.11358Cr - 289.291.
специфична для ![]() изображений, это
расширение содержащее дополнительный канал черного (Ь1асК) цвета. происходит
эффективнее, если информация о цвете и информация о яркости изображения
преобразуются независимо друг от друга.
изображений, это
расширение содержащее дополнительный канал черного (Ь1асК) цвета. происходит
эффективнее, если информация о цвете и информация о яркости изображения
преобразуются независимо друг от друга.
![]() разработанная на базе рекомендаций ITU601
и ITU709 [1 53, 1 54], применяется для кодирования цветных фотографий. Модель
содержит яркостную составляющую (У) и две цветоразностные С 1 и С2.
Отображаемый спектр цветовой модели
разработанная на базе рекомендаций ITU601
и ITU709 [1 53, 1 54], применяется для кодирования цветных фотографий. Модель
содержит яркостную составляющую (У) и две цветоразностные С 1 и С2.
Отображаемый спектр цветовой модели ![]() несколько шире спектра, воспроизводимого
большинством средств визуализации графической информации. При разработке
PhotoYCC решалась задача максимального сохранения цветовых свойств, сравнимых с
полученными при использовании высококачественной цветной фотоплёнки. Взаимное
преобразование в цветовых пространствах R',G',B' в PhotoYC'C' данных, прошедших
гамма-коррекцию, при нормировании R', G',B' в диапазоне 0—1 производят с
помощью выражений [155] :
несколько шире спектра, воспроизводимого
большинством средств визуализации графической информации. При разработке
PhotoYCC решалась задача максимального сохранения цветовых свойств, сравнимых с
полученными при использовании высококачественной цветной фотоплёнки. Взаимное
преобразование в цветовых пространствах R',G',B' в PhotoYC'C' данных, прошедших
гамма-коррекцию, при нормировании R', G',B' в диапазоне 0—1 производят с
помощью выражений [155] :
У! = 0.213R' + 0.419G' + 0.081В',
0.131R' ![]() +0.612, су = 0.373R'
+0.612, су = 0.373R' ![]() 0.537.
0.537.
В связи с тем что возможности ![]() несколько шире, чем у
несколько шире, чем у ![]() преобразование
из первого цветового пространства во второе обычно производится с учётом
специфики средств воспроизведения, например, компания Intel [155] предлагает
следующий вариант с гаммакоррекцией в качестве возможного для
электронно-лучевых мониторов:
преобразование
из первого цветового пространства во второе обычно производится с учётом
специфики средств воспроизведения, например, компания Intel [155] предлагает
следующий вариант с гаммакоррекцией в качестве возможного для
электронно-лучевых мониторов:
![]() R' = 0.981У +
R' = 0.981У + ![]() 0.537),
0.537),
где уровни значений Y,Cl и С2 ограничены диапазоном 0—1.
УСоСд-модель была разработана для повышения эффективности сжатия цветных изображений, она содержит яркостную (У) и две цветоразностные составляющие: Со — смещённый оранжевый и Сд — смещённый зелёный. Взаимное преобразование с RGB производится в соответствии с выражениями [158] :
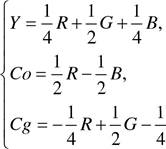 в
в
и
В=У-С0-Сд.
УСоСд-модель имеет несколько больший потенциал для отображения цветовых отгенков, чем RGB, поэтому при взаимных преобразованиях УСоСд в RGB часть информщии может быть безвозвратно утрачена.
Модели цветового пространства HSV (Ние — оттенок, Lightness — яркость, Saturation — насыщенность) и HLS (Ние — отгенок, Saturation — насыщенность, Value значение) разработаны как «интуитивно понятные» в манипуляциях с цветами и основаны на некоторых принципах восприятия цвета человеком. Для геометрической интерпретации данных цветовых пространств наиболее часто используют цилиндрические координаты.
Модель CIE XYZ разработана Международной комиссией по освещению. Компонент У определяет яркость, а Х и Z — оттенок цвета. Для геометрической интерпретации этой цветовой модели обычно используют прямоугольную систему координат. В положительную область пространства CIE XYZ, ограниченную значениями 0—1 по осям, могут быть отображены все видимые цвета. Кроме того, значительная часть цветов из куба, вписанного в пространство CIE XYZ, выходит за диапазон воспринимаемых человеком цветов.
Для отображения R', G',B' в CIEXYZ (при ограничении значений Х ,
![]() У, Z диапазоном 0—1) и обратно
используют следующие выражения [1 66]: Х = 0.412453R' + 0.35758G' + 0.180423В',
У, Z диапазоном 0—1) и обратно
используют следующие выражения [1 66]: Х = 0.412453R' + 0.35758G' + 0.180423В',
У = 0.212671R' + 0.71516G' + 0.072169В',
Z = 0.019334R' + 0.119193G' + 0.950227В',
и
R = 3.240479Х -1.53715У - 0.498535Z,
0.969256Х + 1.875991У + 0.041556Z, В! - 0.055648Х - 0.20404ЗУ +1.05731 И.
Рассмотренные взаимные преобразования
цветовых пространств возможно интерпретировать как тензорные операции. Для
преобразования пространств достаточно использовать операцию сложения и свёртки
тензоров. Запишем операцию свёртки двух тензоров: ti = di , где 1. тензор
второго ранга, матрица преобразований; и тензоры первого ранга, векторы ![]() и
di — цветовых пространств. Следует отметить, что в приведённых преобразованиях
цветовых пространств векторы vm и d не являются взаимно
контравариантным и ковариантным, т.е. d T и d поскольку тензоры
второго ранга t. не являются метрическими. Напомним, что для метрического
тензора должно выполняться условие t. mi симметрия относительно главной
диагонали матрицы.
и
di — цветовых пространств. Следует отметить, что в приведённых преобразованиях
цветовых пространств векторы vm и d не являются взаимно
контравариантным и ковариантным, т.е. d T и d поскольку тензоры
второго ранга t. не являются метрическими. Напомним, что для метрического
тензора должно выполняться условие t. mi симметрия относительно главной
диагонали матрицы.
Принципы построения современных вычислительных машин определяют физические основы преобразования информации в них. Световой импульс, передающий информацию по оптоволоконному кабелю; заряд, хранящийся в ячейке памяти; или токи, протекающие через логические элементы интегральных схем, — всё это, с точки зрения современной физики, разновидности электромагнитного поля. Различные виды преобразования электромагнитной энергии являются основой современной цифровой техники. Большинство вычислительных машин работает с дискретными величинами, представленными при помощи особым способом модулированного электромагнитного поля. Можно заметить, что наряду с цифровыми вычислительными машинами существуют аналоговые (АВМ).
Основной единицей информации в цифровых ЭВМ является бит, на
базе которого формируются более крупные единицы информации. Бит — это неделимый
квант информации, способный принимать лишь одно из двух состояний: или![]()
Используемые для ЦОС вычислительные системы строятся на базе цифровых сигнальных процессоров, которые, в свою очередь, можно разделить на процессоры с фиксированной и плавающей точкой. Различие между этими разновидностями вычислительных устройств состоит в возможности обрабатывать различные числовые типы на аппаратном уровне. Первые предназначены для обработки целочисленных форматов, при этом они могут обрабатывать форматы чисел с плавающей точкой за счёт специальных подпрограмм. Процессоры с плавающей точкой могуг обрабатывать данные в формате с плавающей точкой и целочисленные (например, для организации счётчиков). Многие современные процессоры с фиксированной точкой имеют гибридную структуру и содержат интегрированные (математические) сопроцессоры, позволяющие производить вычисления в формате с плавающей точкой.
Отдельного внимания заслуживают технологии параллельных вычислений. Обобщённая модель классификации по признакам параллелизма в вычислительной архитектуре предложена М. Флинном в 1970-х гг.
(табл. 1.1).
Таблица 1.1. Классификация параллелизма в вычислительных системах по М. Флину
|
Поток данных |
Поток команд |
|
|
одиночный (Single Instruction) |
множественный (Multiple Instruction) |
|
|
Одиночный (Single Data) |
окод (SISD) |
мкод (MISD) |
|
Множественный (Multiple Data) |
ОКМД (snvfI) |
ГУЖМД (MIMD) |
Многие современные вычислительные системы в той или иной степени используют технологии параллелизма, поэтому однозначно отнести конкретную ЭВС к какому-либо типу (см. табл. 1.1) не всегда возможно
![]()
В большинстве современных компьютеров основной массив оперативной памяти представляет собой линейное адресное пространство и имеет одно адресное измерение, поэтому одним из базовых типов данных, непосредственно связанных с архитектурой вычислительных машин, является массив. Адресное пространство линейно, при этом большинство цифровых устройств может одновременно обращаться к различным адресам памяти. Массив позволяет упорядоченно располагать в памяти вычислительной машины данные, состоящие из множества элементов одного типа, индексируя каждый элемент идентификатором. В самом простом случае элементом массива является ячейка памяти с уникальным адресом, адрес ячейки соотносится с индексом элемента массива с учётом смещения (табл. 1.2).
Таб-тица 1.2. Расположение данных в памяти ЭВМ
|
Индекс массива а[] |
Адрес |
Значение |
|
|
|
|
|
|
ОхООЕЗ97З2 |
0х01 |
|
|
ОхООЕЗ97З |
0xFF |
|
|
0х00ЕЗ97ЗО |
0хА0 |
|
|
|
|
В случае одномерных цифровых сигналов номер отсчёта сигнала соответствует адресу ячейки памяти, с учётом смещения и разрядности (формата) хранения сигнала в памяти ЭВМ. Если сигнал многомерный, то его необходимо отображать на одномерную память, при такой процедуре применяют многомерные массивы, или массивы массивов.
Как было показано ранее, цифровые сигналы удобно рассматривать в виде тензорного поля, причём в большинстве случаев тензор имеет ранг «нуль» (скаляр) или «единица» (вектор). Если тензор имеет нулевой ранг, значение элемента сигнала сохраняется в виде единственного числа, если единичный — в виде массива или структуры.
Рассмотрим пример создания структуры описания цветового пространства (листинг 1.1), которую можно рассматривать как тензор первого ранга — в трёхмерных цветовых пространствах, например RGB и YCbCr. Директива препроцессора #pragma раск (push, 1) устанавливает плотность упаковки данных в структуре в 1 байт, а директива #pragma раск
(рор) возвращает установки компилятора по умолчанию. В связи с тем что в языке С++ для трёхбайтных элементов не предусмотрен специальный тип, в случае использования объединений (ип±оп) в памяти будет помещено объединеште длиной в четыре, при типе 1опд int — в шесть байт [100]. Таким образом, по адресу элемента объединения хранятся четырёхбайтное целое представление цветового значения элемента (тензор нулевого ранга) и покомпонентная структура C010rSpace (тензор первого ранга), такой подход позволяет проводить быстрые преобразования типов данных, а следовательно, и тензорных полей цифровых сигналов. Дия хранения полноцветного изображения требуется 24 бита на каждый пиксел, в примере (листинг 1.1) задействовано 32 бита, для экономии адресного пространства (используется только 24 битов на пиксел) достаточно исключить union.
Лиспзинг 1.1. Структура вектора цветового пространства RGB и YCbCr (С++)
![]()
/ / цв а товая палитра RGB
/ / покомпонентное представление, в скобках указаны компоненты
/ / палитр (RGB) и (YCbCr) соответств а
нно struct C010rSpace { uchar byteLo; / / компонент![]() (У) является
младшим байтом (Lower) uchar byteAv; / / компонент
(У) является
младшим байтом (Lower) uchar byteAv; / / компонент![]() (СЬ) является ср о
дним байтом
(СЬ) является ср о
дним байтом
(Avaraga)
![]()
4
Отметим, что для разных компиляторов и вычислительных платформ длина типов может различаться, поэтому для определённости часто используют явное указание длины, например, вместо int применяют тип int32.
uchar byt a Hi; / компонент (В ) ( Cr) является старшим байтом
![]()
/ / объединение для быстрого преобразования вектора в скаляр и об— ратно union UC010rSpace { C010rSpace rgb; uint питЬ;
#pragma рас К (рор)
![]()
Рассмотрим листинг программы выделения памяти для поля цифрового сигнала (листинг 1.2). В качестве примера возьмём статическое изображение с количеством оттенков 16 777 215 (0xFFFFFF), для сохранения элементов изображения будем использовать ранее созданную структуру C010rSpace (СМ. ЛИСТИНГ 1.1).
Иистинг 1.2. Выделение памяти для полноцветного изображения (С++)
![]()
/ / выделяем память
#pragma рас К (push, 1)
/ / объявля а м указатель на двум а рный массив изображения C010rSpace* * data 0;
/ / iHeight высота изображения (число строк)
/ / iwidth ширина изображения (длина строк
(столбцы) ) data=new C010rSpac a * [iHeightj ![]() for (int i=O; i<iH a
ight; i++) { data [ i ] =new C010rSpace [i\Nidth] ; memset (data [1] , 0,
for (int i=O; i<iH a
ight; i++) { data [ i ] =new C010rSpace [i\Nidth] ; memset (data [1] , 0,
![]() siz=of
(C010rSpace) ) ; / / инициализация
siz=of
(C010rSpace) ) ; / / инициализация
#pragma рас К (рор)
/ / используем выделенную память
/ / чистим память for (int i=O;
i<iHeiqht; ![]() de1ete [ ] data [ i j ;
de1ete [ ] data [ i j ;
![]()
Дефрагментация, возникающая при многократном выделении и очистке памяти, может способствовать утечке ресурсов и снижению быстродействия. Поэтому следует использовать существующие в рамках стандартной библиотеки (С++) интеллектуальные указатели и алгоритмы сборки мусора, позволяющие эффективно использовать адресное пространство эвм.
Взаимные преобразования цветовых пространств выполняют с помощью как программных, так и аппаратных средств. Рассмотрим вариант программного преобразования на примере RGB в YCbCr (вариация Y709CbCr) в соответствии с выражением (1.11), на базе операций с плавающей точкой (листинг 1.3), используемый тип данных C010rSpace подробно рассмотрен ранее (см. листинг 1.1).
Лисупинг L3. Преобразование значения из цветового пространства RGB в YCbCr, вычисления в формате с плавающей точкой (С++)
![]()
C010rSpac a х; / / объявляем структуру типа C010rSpac a
/ / с плавающей точкой f10at R , G, В;
В= (f10at) x.byteHi; / / компонент У
x.byt a Lo= (uchar) f100r (0.183*R+O . 614*G+O . 062*В+1о) ; / / компонент СЬ x.byt aAv= (uchar) f100r (—0 . 101 . 338*G+O . 439*В+128) ; / / компонент Cr
![]()
Очевидно, что преобразование, выполненное подобным образом, будет не самым эффективным решением с точки зрения использования вычислительных ресурсов. Требуются двойное преобразование форматов из unsrgned char в f10at и обратно, три умножения и три сложения, операция округления в формате с плавающей точкой для каждого из каналов. Как будет показано далее, подобные преобразования возможно значительно оптимизировать за счёт применения вычислений на базе формата с фиксированной точкой.
Разнообразие цифровых графических изображений, форматов их хранения, способов визуализации и обработки требует упорядочивания по общим и отличительным признакам. Классификация графических объектов является непременным фактором выбора оптимальных средств и методов их обработки, хранения и анализа.
В первую очередь, все цифровые изображения можно разделить
на две группы: статические, т.е. неизменные во времени, и динамические ![]() меняющиеся.
Динамические изображения обычно называют видеорядом или компьютерной анимацией
(частный случай компьютерной графики). Большинство динамических изображений
формируется из совокупности упорядоченных кадров, при этом каждый кадр является
статическим изображением.
меняющиеся.
Динамические изображения обычно называют видеорядом или компьютерной анимацией
(частный случай компьютерной графики). Большинство динамических изображений
формируется из совокупности упорядоченных кадров, при этом каждый кадр является
статическим изображением.
Статические и динамические изображения могут иметь различную размерность. В действительности прообразы большинства сигналов являются бесконечномерными явлениями. До сих пор не найден эффективный способ описания структуры таких комплексных явлений [1 1 7], поэтому на практике применяют значительно упрощённые, ограниченные техническими возможностями и необходимостью, способы отображения реальных прообразов в образы цифровых сигналов. В зависимости от размерности сигнала различают 1D, 2D, 3D и т.д. изображения. В динамических изображениях одно или несколько измерений соответствует времени. Современные графические системы таюке работают с изображениями 4D, 5D и более [123]. Причиной увеличения мерности изображения является стремление к реалистичности передачи визуальной информации. Например, к классу 4D относят динамическше трёхмерные изображения. Дальнейшее увеличение мерности определяется числом и степенью свободы оптических регистраторов изображения. Различают способы формирования изображения с одной (single-view) и с множества точек (multi-view). Достаточно продолжительное время разрабатываются системы визуализации трехмерных статических и динамических изображений в пространстве. Существует ряд решений, которые возможно применять для практических целей, однако сдерживающим фактором является колоссальный объём информации, необходимой для генерации многомерных изображений — образов реального мира. В современных условиях широко распространены псевдотрёхмерные изображения и устройства визуализации простых графических объектов в трёхмерном виде (3D и 4D). Псевдотрёхмерные изображения формируются за счёт особенностей стереоскопического зрения человека. Основой обычно служит двумерное изображение, которое расщепляется на две части при помощи специальных оптических устройств или методов цифровой обработки сигналов.
По особенностям цветопередачи изображения можно разделить на:
![]() монохроматические, каждый пиксел такого
изображения представляется одним битом;
монохроматические, каждый пиксел такого
изображения представляется одним битом;
— полутоновые, каждый пиксел изображения обычно может иметь
2 п значений от 0 до 21 — 1 , обозначающих опенки серого
или иного цвета, в ряде систем некоторые значения из этого диапазона могут
нести специальную информацию, например, о мигании пиксела с заданной частотой
или прозрачности (т.н. альфа-канал); ![]() цветные изображения с различными цветовыми
схемами позволяют передавать информацию о цвете: различают дискретно-тоновые
изображения (число цветовых оттенков существенно ограничено) и с непрерывным
тоном (значительное число оттенков — распространённые цифровые цветовые схемы
позволяют передать до 16 777 216 цветовых оттенков, что при просмотре создаёт
впечатление непрерывности цветовой палитры).
цветные изображения с различными цветовыми
схемами позволяют передавать информацию о цвете: различают дискретно-тоновые
изображения (число цветовых оттенков существенно ограничено) и с непрерывным
тоном (значительное число оттенков — распространённые цифровые цветовые схемы
позволяют передать до 16 777 216 цветовых оттенков, что при просмотре создаёт
впечатление непрерывности цветовой палитры).
По способу представления графических объектов изображения можно разделить на:
![]() векторные, когда изображение
рассматривается как совокупность графических примитивов (такие изображения
характерны для научнотехнической документации, компьютерной графики);
векторные, когда изображение
рассматривается как совокупность графических примитивов (такие изображения
характерны для научнотехнической документации, компьютерной графики); ![]() растровые,
когда изображение рассматривается как совокупность отдельных пикселов,
расположенных в определённом порядке (такие изображения характерны для цифровых
фотографий).
растровые,
когда изображение рассматривается как совокупность отдельных пикселов,
расположенных в определённом порядке (такие изображения характерны для цифровых
фотографий).
Возможна классификация изображений по наличию и уровню шума, например, для цифровых фотографий характерен шум, а синтетические изображения, полученные при помощи компьютерной графики, могут вовсе не содержать шумов. Характер шума таюке может различаться, например, шумы на снимках ЯМ[Р-томографа и фотографии космической обсерватории. Шумы могут возникать на различных этапах преобразования информации, поэтому способ и условия получения изображения определяют характер шумов.
Графические изображения можно классифицировать по способу
цветопередачи. Многие снимки изначально выполнены в невидимом спектре, например
инфракрасном, ультрафиолетовом, рентгеновском, радиочастотном. Для визуализации
таких снимков применяют функциональное преобразование образов, полученных в
невидимом диапазоне, к образам в видимом диапазоне. Цвета в таких изображениях
называются ложными и соответственно говорят <<изображения в ложных
цветах>> (@lse color), про изображения в реальных цветах говорят «в
истинных ![]() (true color). В некоторых случаях замену
цветов выполняют из-за особенностей технологического процесса или для лучшего
восприятия информации.
(true color). В некоторых случаях замену
цветов выполняют из-за особенностей технологического процесса или для лучшего
восприятия информации.
Существуют классификации по способу получения и области применения изображений, смысловой нагрузке: аэрофотоснимки, космические фотографии, медицинские, чертежные, текстовые, кинематографические, мультипликационные и пр.
В соответствии с типом изображения и его особенностялли применяют различные методы обработки и сжатия, используют разные форматы хранения, принципы визуализации. Метощ работы с изображением и ряд
зо
других количественных и качественных характеристик можно рассматриватъ как классификационные признаки.
Наиболее сложные системы классификации изображений, или
системы компьютерного зрения, являются частью области знаний, относящейся к
распознаванию образов.
Несмотря на гиперскоростное развитие в сфере информационных технологий за последние 50—60 лет, актуальным остается высказанное в 1995 г. замечание Н. Вирта: «программы становятся медленнее более стремительно, чем компьютеры становятся быстрее». С учётом постоянно растущего объёма данных, требующих обработки, и более жёстких требований к функциональным возможностям программного обеспечения оптимизация программного кода является очень актуальным направлением современных исследований. В основе работы любой вычислительной машины лежит заданная последовательность действий, называемая алгоритмом.
АЛГОРИТМ — это точный набор инструкций, определяющих способ решения некоторой задачи. Алгоритм обладает следующими свойствами:
![]() дискретность — содержит конечное число
определённых действий (шагов);
дискретность — содержит конечное число
определённых действий (шагов); ![]() детерминированность — в каждый момент
времени его состояние (текущее действие) должно однозначно определяться;
детерминированность — в каждый момент
времени его состояние (текущее действие) должно однозначно определяться; ![]() исполнимость
— алгоритм должен содержать только те инструкции, которые может реализовать
исполнитель;
исполнимость
— алгоритм должен содержать только те инструкции, которые может реализовать
исполнитель; ![]() результативность — работа алгоритма
должна заканчиваться получением определённых результатов, являющихся решением
задачи с корректно поставленными условиями (исходными данными);
результативность — работа алгоритма
должна заканчиваться получением определённых результатов, являющихся решением
задачи с корректно поставленными условиями (исходными данными); ![]() массовость —
алгоритм должен обеспечивать решение некоторого класса сходных задач, т.е.
должен быть применим к различным наборам исходных данных, удовлетворяющих
условиям задачи, на решение которой ориентирован.
массовость —
алгоритм должен обеспечивать решение некоторого класса сходных задач, т.е.
должен быть применим к различным наборам исходных данных, удовлетворяющих
условиям задачи, на решение которой ориентирован.
Способ — определённый порядок последовательных действий, направленных на достижение цели и обладающих всеми свойствами алгоритма: дискретность, определённость (детерминированность), результативность, массовость. Обычно алгоритм является более формальным, с точки зрения обозначений, выражением способа.
МапоД — совокупность способов, объединённых некоторой методологией (концептуальным обобщением) и направленных на достижение цели. Соответственно метод также обладает всеми свойствами алгоритма.
Машинно-независимые алгоритмы разрабатываются на
гипотетическом компьютере, так называемой машине с произво-иьным Доступом к
памяти (Random Access Machine), или ЕАМ-машине [110]. Принципы и условия работы
![]() следующие:
следующие:
![]() любая простая команда исполняется в
точности за один шаг;
любая простая команда исполняется в
точности за один шаг;
![]() циклы, подпрограммы не считаются простыми
командами и требуют некоторого конечного числа шагов (состоят из конечного
числа простых операций);
циклы, подпрограммы не считаются простыми
командами и требуют некоторого конечного числа шагов (состоят из конечного
числа простых операций); ![]() каждое обращение к памяти занимает ровно
один шаг, объем памяти
каждое обращение к памяти занимает ровно
один шаг, объем памяти ![]() не ограничен, всё адресное пространство
линейно и полностью доступно в любой момент времени исполнения программы.
не ограничен, всё адресное пространство
линейно и полностью доступно в любой момент времени исполнения программы.
С помощью ![]() можно оценить вычислительную слотсность
алгоритма как число шагов, требуемое для решения задачи при любом наборе
данных. Время исполнения алгоритма
можно оценить вычислительную слотсность
алгоритма как число шагов, требуемое для решения задачи при любом наборе
данных. Время исполнения алгоритма ![]() вычисляется по общему количеству шагов
исполнения программы. RAMмашина является моделью
вычисляется по общему количеству шагов
исполнения программы. RAMмашина является моделью ![]() реальных
вычислительных машин, поэтому позволяет произвести только приблизительную
оценку вычислительной сложности алгоритма. В отличие от абстрактных RAMмашин
практически используемые вычислительные машины являются сложными техническими
устройствами с большим разнообразием архитектур, работающими в многозадачных
режимах и производящими параллельные вычисления. Поэтому для наиболее
эффективной реализации алгоритма конкретной ЭВМ требуется доработка, а иногда —
полная переработка с целью оптимизации вычислений и использования ресурсов.
Следовательно, процедуры оценки вычислительной сложности алгоритма для
реальных
вычислительных машин, поэтому позволяет произвести только приблизительную
оценку вычислительной сложности алгоритма. В отличие от абстрактных RAMмашин
практически используемые вычислительные машины являются сложными техническими
устройствами с большим разнообразием архитектур, работающими в многозадачных
режимах и производящими параллельные вычисления. Поэтому для наиболее
эффективной реализации алгоритма конкретной ЭВМ требуется доработка, а иногда —
полная переработка с целью оптимизации вычислений и использования ресурсов.
Следовательно, процедуры оценки вычислительной сложности алгоритма для ![]() и
реальных ЭВС различаются.
и
реальных ЭВС различаются.
Принято рассматривать три оценки вычислительной сложности алгоритма на входном наборе данных размером п. :
![]() наихудший случай — функция, определяемая
максимальным количеством шагов, требуемых для завершения алгоритма;
наихудший случай — функция, определяемая
максимальным количеством шагов, требуемых для завершения алгоритма; ![]() наилучший
случай — функция, определяемая минимальным количеством шагов, требуемых для
завершения алгоритма;
наилучший
случай — функция, определяемая минимальным количеством шагов, требуемых для
завершения алгоритма; ![]() средний случай — функция, определяемая
средним количеством шагов, требуемых для завершения алгоритма.
средний случай — функция, определяемая
средним количеством шагов, требуемых для завершения алгоритма.
Как для различных входных наборов данных размером п = const может быть различная вычислительная сложность? Рассмотрим пример решения системы уравнений:
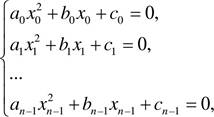
где Di =b.2 —4qq, i = ![]() ,
при D 20 требуются действия с действительными числами, а при D. < 0 — с
комплексными. Следовательно, на входном наборе данных размером п = const
понадобится различное число действий, например, при D. 0, i =
,
при D 20 требуются действия с действительными числами, а при D. < 0 — с
комплексными. Следовательно, на входном наборе данных размером п = const
понадобится различное число действий, например, при D. 0, i = ![]() вычислительная
сложность будет меньше, чем при D. < 0, i =
вычислительная
сложность будет меньше, чем при D. < 0, i = ![]() . Отметим, что мы лишь
сравниваем вычислительную сложность, не используя критерии («наилучший» или
<<наихудший>>, т.к. наилучший случай может быть реализован в
конкретном алгоритме только для некоторого множества наборов данных: например, в
для = 1, Ь. = 0, с. = 0, i =
. Отметим, что мы лишь
сравниваем вычислительную сложность, не используя критерии («наилучший» или
<<наихудший>>, т.к. наилучший случай может быть реализован в
конкретном алгоритме только для некоторого множества наборов данных: например, в
для = 1, Ь. = 0, с. = 0, i =![]() может быть реализован наилучший
вычислительный случай „у. = 0, i = 0,...,п—1
может быть реализован наилучший
вычислительный случай „у. = 0, i = 0,...,п—1 ![]()
Вычислительную сложность можно выразить с помощью функций, зависящих от размеров входного набора данных п . Для различных алгоритмов сложность таких функций может значительно различаться, кроме того, функции могут содержать множественные условия, зависящие от набора данных, в общем случае применение таких функций на практике затруднено. Вычислительная сложность ј(п) оценивается при помощи асимптотических функций, записываемых в асимптотической нотации (0(.. .), Q(.. .), 0(.. .)), которые формально определяются [110] следующим образом:
![]() f(n) = О(д(п)) означает, что существует
функция f(n) , ограниченная сверху функцией д(п) , с точностью до постоянного
множителя с = const , иными словами, существует такое значение с, для которого
f(n) = О(д(п)) означает, что существует
функция f(n) , ограниченная сверху функцией д(п) , с точностью до постоянного
множителя с = const , иными словами, существует такое значение с, для которого ![]() с •
д(п) при достаточно большом значении п ;
с •
д(п) при достаточно большом значении п ; ![]() f(n) = С)(д(п))
означает, что функция f(n) ограничена СНИЗУ функцией д(п) , с точностью до
постоянного множителя с = const , иными словами, существует такое значение с,
для которого f(n) сд(п) при достаточно большом значении п ;
f(n) = С)(д(п))
означает, что функция f(n) ограничена СНИЗУ функцией д(п) , с точностью до
постоянного множителя с = const , иными словами, существует такое значение с,
для которого f(n) сд(п) при достаточно большом значении п ; ![]() f(n) =
О(д(п)) означает, что функция f(n) ограничена сверху функцией д (п) и
ограничена снизу функцией д(п) , с точностью до постоянных множителей q = const
и = const соответственно. Иными словами, существуют такие значения с, для
которых С2Д(п) f(n) qg(n) при достаточно большом значении п .
f(n) =
О(д(п)) означает, что функция f(n) ограничена сверху функцией д (п) и
ограничена снизу функцией д(п) , с точностью до постоянных множителей q = const
и = const соответственно. Иными словами, существуют такие значения с, для
которых С2Д(п) f(n) qg(n) при достаточно большом значении п .
В основном наибольший интерес представляет f(n) = О(д(п)) ![]() верхняя
граница (рис. 2.1), на основе данной функции выполняют сравнение алгоритмов,
оценку требуемых вычислительных мощностей и т.п.
верхняя
граница (рис. 2.1), на основе данной функции выполняют сравнение алгоритмов,
оценку требуемых вычислительных мощностей и т.п.
|
|
|
|
О(д(п)) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Ап)
Ап)
Рис. 2.1. Верхняя и нижняя границы
функции вычислительной сложности алгоритма![]()
В табл. 2.1 приведены данные о времени вычислений на ЭВС,
выполняющей миллиард операций в секунду, т.е. время исполнения одной операции
10 с (отметим, что один год соответствует![]()
Таблица 2.L Оценка времени вычислений для некоторых распространённых асимптотических функций
|
|
log2 (п) , с |
|
2 |
З |
2П,с |
|
101 |
4-10_9 |
33-10_9 |
100-10_9 |
10 |
10 |
|
102 |
7-10—9 |
—9 |
10-10 |
ш—3 |
10'l |
|
103 |
10-10_9 |
9.97-10 |
-3 10 |
|
10292 |
|
104 |
14-10—9 |
132.9-10 |
0.1 |
103 |
10ЗОО 1 |
|
|
17-10_9 |
1.66 • 10—3 |
10 |
106 |
1030093 |
|
ш |
20-10 9 |
19.93-10—3 |
103 |
109 |
10301020 |
Сократить время исполнения вычислительных задач возможно путем оптимизации вычислительных алгоритмов или повышения быстродействия ЭВС.
Объединение высокоскоростной магистралью множества высокопроизводительных процессоров позволяет получать системы, называемые суперкомпьютерами. Быстродействие в таких системах достигается за счёт распараллеливания задачи на множество подзадач, соответственно требуются специальные алгоритмы и методы, на базе которых создаётся программное обеспечение для суперкомпьютеров. Для оценки реального быстродействия ЭВС применяют внесистемную единицу Flops (Floating point 0Perations per Second), показывающую, сколько операций с плавающей запятой в секунду выполняет данная вычислительная система.
Следует отметить, что в своих работах Бремерманн [137] показал существование некоторого вычислительного предела и трансвычислительных задач, для решения которых требуется обработка более чем 1093 бит.
Решение трансвычислительных задач может быть осуществлено компьютером размером с Землю, время вычисления будет равно времени ее существования. Существование практических трансвычислительных задач показывает, что имеется некоторое множество проблем, которые невозможно преодолеть только за счёт наращивания вычислительной мощности. Возможно, решение таких задач станет реальным с развитием математики, появлением новых вычислительных методов или совершенно новых областей знаний, использующих неизвестные пока принципы получения и обработки информации. Возможно, решение данных задач лежит в области иных концептуальных подходов, доступных в будущем, в соответствии с которыми трансвычислительные задачи в современной постановке могут, например, вовсе утратить свою актуальность.
Практический интерес при реализации алгоритмов цифровой обработки сигналов и вычислениях представляет время расчётов на вычислительной машине. Значительно варьирующаяся архитектура вычислительных машин не позволяет получить универсальной зависимости машинного времени от вычислительной сложности, ведь современные машины позволяют распараллеливать решаемые задачи, производить вычисления, применяя специальные сопроцессоры. В свою очередь, учет особенностей архитектуры компьютера, использование специальных процессорных инструкций позволяет добиться наилучших результатов оптимизации алгоритмов и программ для вычислительного устройства определённого типа. Особенно критично время вычислений при обработке сигналов в реальном масштабе времени, например, в операционных системах реального времени или специальных аппаратнопрограммных комплексах [34, 80, 92].
Таким образом, время вычисления одной и той же задачи сильно зависит от многих факторов. Поэтому для оценки практических затрат машинного времени применяют измерения. В частности, разработаны специальные тесты, позволяющие измерять время вычислений. Следует отметить, что многие тесты разработаны самими производителями вычислительных устройств (процессоров, чипсетов, сопроцессоров, памяти и др.), одной из целей таких тестов является демонстрация преимущества своих изделий над аналогами. Этот фактор может повлиять на объективность выводов, поэтому для более точной оценки желательно использовать вычислительные тесты от различных производителей, учитывающие архитектуру и особенности вычислительного устройства.
Машинное время обычно определяется как разность времени начала и времени завершения расчётов. Однако такой подход не всегда может дать приемлемый результат, особенно для современных сложных вычислительных систем. Дело в том, что большинство вычислительных систем являются многозадачными и могут выполнять некоторое множество расчётов одновременно или создавать видимость такой одновременности, квантуя машинное время и распределяя его между конкурирующими процессами. Ситуации, когда все вычислительные ресурсы предоставлены одному процессу и необходимо определить время его выполнения, достаточно тривиальны. Поэтому рассмотрим некоторые особенности расчёта машинного времени в многозадачных операционных системах (ОС) на примере ОС семейства UNIX и Windows. Внутри вычислительной системы «существует» несколько «времён»: пользовательское (затраченное на исполнение машинных инструкций, образующих процесс), системное (затраченное на выполнение машинных инструкций ядром от имени процесса, т.е. на исполнение системных вызовов процесса) и машинное (время работы вычислительной системы). Сумму пользовательского и системного времени часто называют процессорным временем [115].
В ОС UNIX любой процесс может вызвать функцию times (struct tms *buffer) , параметром которой является указатель на структуру tms (листинг 2.1). Функция times возвращает общее время, соответствующее времени от момента запуска процесса.
Значения типа с1осК содержат время, измеряемое в тактах (ticks). Для перевода этого значения в секунды необходимо воспользоваться функцией sysconf, с помощью вызова с параметром sc CLk тск можно получить количество тактов в секунду (частоту) для данной платформы.
Листинг 2. 1. Структура tms (UNIX, С)
![]()
|
struct tms { |
|
|
с 1 ос К t tms utimo |
пользовательское время |
|
с 1 ос К t tms stima |
системное время |
|
с 1 ос К t tms cutime ; |
пользовательское время для зав а ршения потомка |
|
с 1 ос К t tms cstime; |
системное время для завершившегося потомка |
![]()
В ОС Windows информацию о временных характеристиках процесса
можно получить с помощью функции GetProcessTimes, о временных характеристиках
потока — с помощью GetThreadTimes (в Windows 9х отсутствуют), о времени системы
— с помощью GetSystemTim- (листинг 2.2). Функции ![]() и GetThreadTimes в
случае успеха возвращают значение, отличное от нуля, при неудаче код ошибки
можно узнать при помощи функции G a tLastError, функция
GetSystemTime ничего не возвращает [120, 122, 161].
и GetThreadTimes в
случае успеха возвращают значение, отличное от нуля, при неудаче код ошибки
можно узнать при помощи функции G a tLastError, функция
GetSystemTime ничего не возвращает [120, 122, 161].
Лиспзинг 2.2. Функция GetProcessTimes (Windows, С++)
BOOL ![]() WINAPI
WINAPI
LPFILETIME 1pExitTime,
LPFILETIME 1pkerne1Time,
LPFILETIME lpUserTime
/ / Функция GetThreadTimes
BOOL WINAPI GetThreadTimes (
HANDLE hThread,
![]() LPFILETIME
LPFILETIME![]()
LPFILETIME 1pkern a 1Time,
LPFILETIME 1pUs a rTime
/ / Функция GetSystemTime
дескриптор процесса указат а ль на структуру FILETIME, которая получа а т время создания процесса . Указат а ль на структуру FILETIME, которая получает время выхода из потока . Если выход из потока не выполнен, то содержание этой структуры не опр а д а лено. Указат а ль на сшрукшуру FILETIME, которая получает значение системного вр а мени, т . е .
выполн а ния процесса в р а жим— ядра . Указатель на структуру FILETIME, которая получает значение пользовательского времени, т . е . времени выполнения процесса в пользовательском режиме .
дескриптор потока указатель на структуру FILETIME, которая получает время создания потока. Указатель на структуру FILETIME, которая получает время выхода из потока . Если выход из потока не выполнен, то содержание этой структуры не определено .
Указатель на структуру FILETIME, которая получает количество системного вр а мени, т . е .
выполнения потока в р а жиме ядра . Указатель на структуру FILETIME, которая получаеш количество пользовательского вр а мени, т . е . выполнения потока в пользовательском режиме .
void GetSyst a mTime (
LPSYSTEMTIME 1pSystemTima![]()
/ / 64-битная структура FILETIME typedef ![]() FILETIME
{
FILETIME
{
DWORD dwLowDateTime;![]()
DWORD dwHighDateTime;![]()
} FILETIME, *PFILETIME;
Указатель на структуру SYSTEMTIME, которая получает текущую дату и время сис т емы .
и указатель *PFILETIME
32 младших бита
32 старших бита
![]()
Используя описанные системные функции, можно получить объективные характеристики времени выполнения вычислительного процесса или его части. На основе полученных данных возможно делать выводы о затратах машинного времени для осуществления расчётов.
Следует отметить, что использование рассмотренных в листингах 2.1 и 2.2 функциональных средств не может заменить полноценного анализа программы, выполняемого разработчиком-оптимизатором с помощью профилировщиков — специальных приложений для анализа производительности программ; отладчиков — программ, позволяющих контролировать и управлять исполнением кода; дизассемблеров — программ, позволяющих преобразовать машинный код в набор инструкций языка ассемблера.
Снижению времени вычислений и вычислительных затрат в общем способствует специализация различных вычислительных машин на аппаратном уровне. Для преобразования цифровых сигналов предназначены цифровые сигнальные процессоры (ЦСП, Digital Signal Processor). Отличительными особенностями ЦСП являются [74] :
![]() специальные процессорные команды,
выполняющие за один такт операцию сложения с накоплением;
специальные процессорные команды,
выполняющие за один такт операцию сложения с накоплением; ![]() специфическая
архитектура, в особенности разделение памяти данных и программ в соответствии с
гарвардской или супергарвардской архитектурой;
специфическая
архитектура, в особенности разделение памяти данных и программ в соответствии с
гарвардской или супергарвардской архитектурой; ![]() возможность
векторно-конвейерной обработки при помощи генераторов адресных
последовательностей и кольцевых буферов в памяти, предоставляющих непрерывный
доступ к обновляющимся данным и исключающих переполнение;
возможность
векторно-конвейерной обработки при помощи генераторов адресных
последовательностей и кольцевых буферов в памяти, предоставляющих непрерывный
доступ к обновляющимся данным и исключающих переполнение; ![]() определённое
время (в тактах) выполнения команд и их последовательностей, что позволяет
встраивать процессоры в системы реального времени и создавать кластеры ЦСП;
определённое
время (в тактах) выполнения команд и их последовательностей, что позволяет
встраивать процессоры в системы реального времени и создавать кластеры ЦСП;
![]() организация циклов с автоматической
проверкой условия завершения;
организация циклов с автоматической
проверкой условия завершения; ![]() возможность одновременной выборки двух
операндов;
возможность одновременной выборки двух
операндов; ![]() таблицы готовых значений некоторых
функций, например, sin(), cos() и т.д.
таблицы готовых значений некоторых
функций, например, sin(), cos() и т.д.
Следует отметить, что современные тенденции развития микропроцессорной техники направлены на интеграцию различных архитектур и концепций на базе одного кристалла. Например, современные процессоры общего назначения, выпускаемые корпорациями Intel и AMD, содержат интегрированные сопроцессоры (графические, математические), специальные наборы инструкций ММХ, SSE (SSE2, SSE3) и 3DNow (3DNow2) соответственно, реализующие возможности ЦСП.
Наиболее широко ЦСП применяются для решения следующих задач:
![]() кодирование, мультимедийная обработка
аудио- и видеоданных;
кодирование, мультимедийная обработка
аудио- и видеоданных; ![]() производство и проектирование техники
(анализаторы спектра, генераторы сигналов, системы локации, робототехника и
др.);
производство и проектирование техники
(анализаторы спектра, генераторы сигналов, системы локации, робототехника и
др.);
— распознавание образов (речи, звуков,
графических образов и др.); ![]() многоскоростная обработка цифровых
сигналов.
многоскоростная обработка цифровых
сигналов.
Реализации ЦСП различаются типом обрабатываемых данных: с фиксированной или с плавающей точкой. На практике различие типов данных проявляется в значении отношения сигнал/шум. Для формата с плавающей точкой характерен приблизительно в 3000 раз меньший шум квантования, чем для формата с фиксированной точкой [1 12].
Разрядность ЦСП также определяет возможности процессора (наиболее распространены 16- и 32-разрядные ЦСП). Быстродействие ЦСП зависит от ряда факторов, связанных со временем обращения к памяти и временем выполнения машинных инструкций (арифметических и логических операций). Немаловажным фактором, определяющим конечное время выполнения тех или иных задач, является оптимизация программного кода под конкретный вид процессора. Производители ЦСП предоставляют библиотеки оптимизированного программного кода, ориентированные на выполнение множества стандартных задач (свёртка, быстрое преобразование Фурье и др.).
Возможно синтезировать многопроцессорные системы при помощи объединения нескольких ЦСП с выделенными линиями связи «точкаточка» через общую глобальную память или при помощи ячеистых структур.
Графические процессоры ГП (Graphics Processing Unit, GPU) ![]() специфические
вычислительные устройства, ориентированные на графический ренДеринг (синтез
изображений). Вычислительная мощность новейших ГП обеспечила новые возможности
их применения для неграфических вычислений, например, многопоточное решение
систем дифференциальных уравнений.
специфические
вычислительные устройства, ориентированные на графический ренДеринг (синтез
изображений). Вычислительная мощность новейших ГП обеспечила новые возможности
их применения для неграфических вычислений, например, многопоточное решение
систем дифференциальных уравнений.
Первые графические процессоры, работающие в составе персональных вычислительных машин, выполняли функцию буфера кадров, периодически выводя отображение определённой области памяти на экран монитора (само изображение формировалось центральным процессором). Поскольку во многих случаях центральный процессор не мог обработать всю необходимую графическую информацию за время между обновлениями кадров, предварительно кадр (или его часть) формировался в буфере, не пересекающемся с отображаемой областью видеопамяти, а затем готовые данные копировались в видеопамять. Такой подход применяется во многих системах компьютерной графики.
Совершенствование вычислительных технологий и спрос на высококачественные встроенные графические системы определили развитие ГП как самостоятельную технологию решения специфических задач синтеза изображений. Основной целью ГП является разгрузка центрального процессора и расширение графических возможностей персонального компьютера.
Архитектура современных ГП значительно варьирует. Основной парадигмой их построения является распараллеливание вычислений. Синтезирование графической информации требует обработки значительных объёмов данных, причём в силу специфики данные могут быть обработаны в параллельном режиме ограниченным числом команд. Таким образом, основу архитектуры ГП составляет множество работающих параллельно простых вычислительных ядер. Совместимость различных ГП достигается с помощью специального интерфейсного программного обеспечения (драйверов графических устройств). Дополнительные программные библиотеки (0penGL, DirectX) [20] позволяют связывать низкоуровневый программный и аппаратный интерфейс графического устройства с системой функций синтеза и обработки двух- и трёхмерных графических примитивов.
Значительная мощность ГП позволила использовать их для неграфических вычислений (General-purpose Graphics Processing Units, GPGPU), активно развивающихся благодаря повышению арифметической точности вычислений на ГП. Технологии неграфических вычислений представлены достаточно большим набором программных интерфейсов:
— 0penCL — Фреймворк от разработчиков Apple Inc., khronos Group (http://www.khronos.org/opencl]) ;
![]() CUDA (Compute Unified Device
Architecture) — решение от Nvidia (http://www.nvidia.com/);
CUDA (Compute Unified Device
Architecture) — решение от Nvidia (http://www.nvidia.com/);
![]() DirectCompute составная часть DirectX от
Microsoft (http://www.microsoft.com/);
DirectCompute составная часть DirectX от
Microsoft (http://www.microsoft.com/);
![]() AMD FireStream технология неграфических
вычислений от компании AMD (http://www.amd.com/).
AMD FireStream технология неграфических
вычислений от компании AMD (http://www.amd.com/).
Поддержка неграфических вычислений на базе ГП лидерами индустрии информационных технологий во многом определяет перспективы данного направления. Следует отметить, что пакет MATLAB (с 2010 г.) поддерживает технологию неграфических вычислений на ГП в компоненте Parallel Computing Toolbox [159].
Процессор, т.е. вычислительное ядро ЭВС, управляется потоком машинных кодов, образованных последовательностью нулей и единиц. Первичной моделью, или «семантическим интерфейсом» разработки, программного обеспечения является язык ассемблера. Ассемблер обеспечивает взаимно-однозначное соответствие между операторами и командами процессора. Ассемблер, при высокой квалификации разработчика, позволяет получить наиболее эффективный код для данного процессора, при переносе которого на друтую вычислительную платформу (например, построенную на базе процессора того же типа, но с другой моделью адресации интерфейсных портов или ОЗУ) может потребоваться существенная доработка кода, вплоть до написания всей программы заново. С учётом многообразия процессоров, вычислительных архитектур и операционных систем, постоянной конкуренции разработчиков программного обеспечения применение ассемблера является очень затратным технологическим процессом. Однако следует отметить, что во многих разработках в сфере оборонной промышленности, бортовых вычислительных устройств авионики и космонавтики, в микрокомпьютерах промышленных и бытовых устройств успешно используется ассемблер. Таким образом, в индустрии программного обеспечения применение ассемблера могут себе позволить только очень консервативные разработчики, удаётся удерживающие рынок сбыта за счёт добротных, компактных и быстрых программ или владения монопольным правом на их производство. Некоторые задачи возможно решить только средствами ассемблера. Например, большинство компиляторов языков С++, Fortran не могут «напрямую» использовать технологии SIMD (Single Instruction, Multiple Data одна команда, множество источников данных), исключение составляет компиляторы от Intel [28].
Для снижения трудозатрат на разработку, отладку и оптимизацию вместо ассемблера используют языки более высокого уровня с целью создания более «человекопонятного» программного кода с меньшей зависимостъю от архитектуры конкретной ЭВС. На сегодняшний день существует множество альтернативных подходов — от применения низкоуровневых языков до транслируемых языков разработки и виртуальных машин, практически абстрагированных от конкретной платформы.
Рассмотрим несколько различных уровней управления ЭВС:
![]() непосредственное управление ЭВС набором
машинных кодов;
непосредственное управление ЭВС набором
машинных кодов; ![]() применение ассемблера с последующей
компиляцией в машинный код;
применение ассемблера с последующей
компиляцией в машинный код; ![]() применение низкоуровневых языков (С, С++,
Fortran, Pascal и др.) с последующим преобразованием для конкретной операционной
системы и аппаратной платформы;
применение низкоуровневых языков (С, С++,
Fortran, Pascal и др.) с последующим преобразованием для конкретной операционной
системы и аппаратной платформы; ![]() применение высокоуровневых транслируемых
языков (BASIC, РНР и др.), которые переводятся в машинный код непосредственно в
момент исполнения;
применение высокоуровневых транслируемых
языков (BASIC, РНР и др.), которые переводятся в машинный код непосредственно в
момент исполнения; ![]() применение специальных виртуальных
вычислительных сред (Matlab, Matematica, Scilab, FreeFem++, Ch SoftIntegration
и др.).
применение специальных виртуальных
вычислительных сред (Matlab, Matematica, Scilab, FreeFem++, Ch SoftIntegration
и др.).
Применение виртуальных машин позволяет создавать требуемую виртуальную аппаратную и операционную среду, в рамках которой возможно использовать любой из перечисленных подходов.
Рассмотрим процесс разработки программного обеспечения как технологический цикл. Принято выделять несколько моделей жизненного цикла программного обеспечения. Разработка программного обеспечения может иметь каскадный или ип1ерационный (циклический) характер. При каскадном сначала формируются требования (техническое задание на разработку) в полном объёме, затем осуществляется поэтапная разработка. Причём завершение этапа означает переход к последующему этапу без возврата к предыдущему, что, вообще говоря, во многих случаях достаточно затруднительно. Особенные сложности такой подход вызывает в крупномасштабных проектах.
В соответствии с ГОСТ 34.601-90 выделяют следующие стадии и этапы создания автоматизированных систем, в том числе программного обеспечения (табл. 2.3). Данный стандарт ориентирован в большей степени на каскадный характер разработки.
Таблица 2.3. Стадии и этапы создания ПО
|
Стадии |
Этапы разработки |
|
Формирование требований к ПО |
Обследование объекта и обоснование необходимости создания ПО |
|
Формирование требований пользователя к ПО |
|
|
Оформление отчета о выполненной работе и заявки на разработку ПО (тактико-технического задания) |
|
|
Разработка концепции по |
Изучение объекта |
|
Проведение необходимых научно-исследовательских работ |
|
|
Разработка концепций ПО и выбор варианта, удовлетворяющего требованиям пользователя |
|
|
Оформление отчета о выполненной работе |
|
|
Техническое задание |
Разработка и утверждение технического задания на создание ПО |
|
Эскизный проект |
Разработка предварительных проектных решений по системе и ее частям |
|
Разработка документации на ПО и ее части |
|
|
Технический проект |
Разработка проектных решений по системе и ее частям |
|
Разработка документации на ПО и ее части |
|
|
Разработка и оформление документации на поставку изделий для комплектования ПО и (или) технических требований (технических заданий) на их разработку |
|
|
Разработка заданий на проектирование в смежных частях проекта объекта автоматизации |
|
|
Рабочая документация |
Разработка рабочей документации на систему и ее части |
|
Разработка или адаптация программ |
|
|
Ввод в действие |
Подготовка объекта автоматизации к вводу ПО в действие |
|
Подготовка персонала |
|
|
Комплектация ПО поставляемыми изделиями (программными и техническими средствами, программнотехническими комплексами, информационными изделиями) |
Более новый ГОСТ Р ИСО/МЭК 12207-2010, соответствующий международному стандарту ISO/IEC 12207:2008, выделяет несколько процессов жизненного цикла: основные, вспомогательные, организационные. Данный стандарт больше ориентирован на итерационный тип разработки: на каждом этапе получается работоспособный продукт с заложенной в него возможностью развития (эволюции). Целью последующих этапов является эволюция полученных на предыдущих этапах результатов. Каждый этап является проектом, содержащим все стадии жизненного цикла, соответствующие каскадной модели (см. табл. 2.3). Итерационный подход обеспечивает <<обозримость>> каждого этапа разработки, позволяет эффективнее производить тестирование, предоставляет возможность промежуточного согласования проекта с заказчиком. Итерационная концепция разработки хорошо согласуется с объектно-ориентированным программированием и предоставляет больше возможностей для повторного использования кода.
Кроме организационной модели жизненного цикла программного обеспечения существует ряд других, связанных с принципами проектирования и особенностями разработки, заложенными в языковые конструкции:
![]() модель шаблонов
проектирования;
модель шаблонов
проектирования; ![]() функциональная модель;
функциональная модель; ![]() объектно-ориентированная
модель;
объектно-ориентированная
модель; ![]() аспектно-ориентированная модель;
аспектно-ориентированная модель; ![]() модель
бизнес-логики;
модель
бизнес-логики; ![]() модель структуры данных.
модель структуры данных.
Многообразие моделей, связанных с разработкой программного обеспечения, обусловлено сложностью программных проектов и необходимостью систематизации на всех этапах жизненного цикла, что позволяет использовать ранее созданный программный код, вести подробное документирование и в результате сократить затраты ресурсов на разработку.
Например, парадигма «модель—вид—контроллер>>
(Model—View ![]() Contr011er) позволяет создавать
приложения, в которых интерфейсная часть (в частном случае, визуализация
графического интерфейса или межпрограммное взаимодействие) минимально зависит
от бизнес-логики вычислительного ядра. Такой подход существенно способствует
повторному использованию программного кода и переносу, например, в другую
операционную систему.
Contr011er) позволяет создавать
приложения, в которых интерфейсная часть (в частном случае, визуализация
графического интерфейса или межпрограммное взаимодействие) минимально зависит
от бизнес-логики вычислительного ядра. Такой подход существенно способствует
повторному использованию программного кода и переносу, например, в другую
операционную систему.
В начале 2000-х гг. появилась аспектно-ориешпированная модель разработки программного обеспечения, согласно которой сквозная функциональность выделяется в отдельную сущность. В ней используется понятие «аспект» — программный модуль, оформленный в виде функций и(или) классов и реализующий сквозную функциональность.
Актуальной задачей на сегодняшний день является разработка интерфейсной части программного обеспечения, в частности, и информационно-управляющих систем — в целом. Под интерфейсной частью мы понимаем некоторую часть системы (например, программного обеспечения), являющейся подсистемой взаимодействия с другими системами. Особенности интерфейсной части программного обеспечения, её соответствия распространённым стандартам во многом определяет возможности использования, а соответственно и распространения.
Когда выбраны аппаратная архитектура и средства разработки программного обеспечения, возникает ряд задач: оптимизация кода, отладка, сопровождение, контроль версий, документирование, рефакторинг.
Многие современные интегрированные среды разработки (IDE, Integrated Deve10pment Environment), такие как Inte11 Para11e1 Studio, Embarcadero RAD Studio, Microsoft Visual Studio, Qt Creator, Eclipse, NetBeans, Xcode содержат практически полный подключаемый или встроенный инструментарий для решения задач на всех стадиях разработки.
Хороший стиль разработки программного обеспечения определяется следующими принципами: максимально возможное исключение повторяющегося кода, полное документирование и комментирование, применение проверенных практикой паттернов и шаблонов, в том числе для выделения и очистки памяти и обработки исключительных ситуаций.
Комментирование и документирование позволяют менять команду разработчиков, поддерживать код по окончании разработки и предоставлять его сторонним разработчикам. Великий русский путешественник и исследователь Н. М. Пржевальский говорил: «у путешественника нет памяти», поэтому регулярно вёл путевые заметки. Разработчик программного обеспечения, подобно путешественнику, памяти не имеет. Если нет надлежащих комментариев и документации, код, написанный пять лет и даже неделю назад, может превратиться в головоломку для автора и потребовать значительного времени и усилий для ее разгадки.
Многие разработчики и их сообщества стараются придерживаться определённых стилей программирования, построенных на едином форматировании кода; осмысленном и синтаксически обоснованном присвоении имён переменным, функциям, классам; комментировании кода. Сам код обычно создаётся с использованием некоторых паттернов и достаточно универсальных библиотек, возможно от сторонних разработчиков. Такой код при некоторых навыках легко читается, и его многие части не требуют отдельного внимания. Принципиальным плюсом этого подхода является возможность сосредоточить внимание на уникальных для данной программы решениях (которые, в большинстве случаев, могут занимать лишь малую часть от всего объёма кода). Однако унификация приводит к недостаточной оптимизации кода под конкретные задачи, а значит и сравнительно невысокому быстродействию. Рефакторинг доработка программного кода до более удобного для восприятия вида без изменения функциональности программы — имеет особое значение.
Оптимизация программ является отдельной задачей разработки
программного обеспечения [28]. Касперски К. в книге <<Техника оптимизации
программ» [73] предлагает выполнять оптимизацию: ![]() на уровне структур
данных и алгоритмов их обработки;
на уровне структур
данных и алгоритмов их обработки; ![]() на уровне планирования потоков машинных
команд;
на уровне планирования потоков машинных
команд; ![]() на уровне компиляции, выбор и сравнение
качества оптимизации различными компиляторами;
на уровне компиляции, выбор и сравнение
качества оптимизации различными компиляторами; ![]() работы с периферией
(жесткие и лазерные диски, коммуникации, параллельные и последовательные порты,
видеоподсистема); —параллельных вычислений.
работы с периферией
(жесткие и лазерные диски, коммуникации, параллельные и последовательные порты,
видеоподсистема); —параллельных вычислений.
Наиболее ощутимые результаты дает оптимизация на уровне структур данных и алгоритмов их обработки [109]. Решение множества практических задач облегчают библиотеки, содержащие наиболее совершенные алгоритмические решения [1 10, 112].
Существенную помощь в вопросах оптимизации могут оказать ПРОФИИИРОВЩИКИ — специальные пакеты программ, предназначенные для анализа программного кода во время выполнения (в частности, VTune, CodeAnalyst, AQtime). Профилировщик помогает выявлять затратные (времени исполнения, потреблению памяти, количеству вызовов) фрагменты кода и принимать решения по оптимизации программ. Задача профилировки сопряжена с задачами Дизассемблирования и обратного инжиниринга, т.е. анализа и разбора машинного кода. Мощным программным пакетом, предназначенным для решения задач обратного инжиниринга, является IDA (Interactive DisAssemb1er).
При разработке программного обеспечения требуются доработка, улучшение, расширение функционала и другая модификация кода. Изменения могут затронуть весь код или некоторую его часть. При этом необходимо управлять версиями (при этом требуется особая аккуратность, поскольку риск ошибки разработчика достаточно высок) и выполнять акп1уализацию. Современные средства разработки содержат интегрированные сторонние или собственные системы управления версиями (VCS, Version Control System).
Единицей измерения информации и самым малым объектом хранения и передачи двоичной информации является бит. Следующей после бита единицей информации является байт, содержащий в своём составе несколько битов. Наиболее распространённая архитектура современных ЭВС ставит в соответствие одному байту восемь упорядоченных (0—7) битов. На языке ассемблера байт обозначается директивой БВ. Далее в иерархии машинных форматов находятся слово (в ассемблере WORD или DW), состоящее из шестнадцати бит, или двух байт, и Двойное слово (в ассемблере DnORD или DD), состоящее из тридцати двух бит, или четырёх байт. Информация об обозначениях типа данных, диапазона допустимых значений, разрядности для некоторых базовых типов, принятых в языке С++ приведена в табл. 2.4.
![]() Таблица
2.4. Типы данных С++
Таблица
2.4. Типы данных С++
|
Тип С++ |
Псевдоним (Alias) |
Разрядность, бит |
Диапазон |
|
|
минимум |
максимум |
|||
|
Ьоо1 |
Ьоо1 |
8 |
true или fa1se |
|
|
char (int8) |
|
8 |
- 128 |
127 |
|
unsigned char |
unsigned int8 |
8 |
0 |
255 |
|
short int |
|
16 |
- 32768 |
32767 |
|
unsigned short int |
unsigned |
16 |
0 |
65535 |
|
1опд int |
int32 |
32 |
2 147483648 |
2147483647 |
|
unsigned long int |
unsigned int32 |
32 |
0 |
4294967295 |
|
|
int64 |
64 |
-2Е+6З |
(2Е6З)-1 |
|
|
unsigned int64 |
64 |
0 |
(2Е64)-1 |
|
f10at |
|
32 |
З.4Е-З8 |
З.4Е+З8 |
|
double |
|
64 |
1.7Е-ЗО8 |
1.7Е+ЗО8 |
|
lon double |
|
80 |
З.4Е-49З2 |
З.4Е+49З2 |
Следует учитывать, что различные компиляторы могут по-разному трактовать определения некоторых типов, в зависимости от разрядности аппаратной платформы (8, 16, 32, 64 и т.д.), настройки компилятора и т.д. Поэтому в некоторых случаях целесообразно явно указывать размер и тип, например, вместо short int, использовать int16.
Проанализировав табл. 2.4, можно выделить формат чисел с плавающей точкой и целочисленный формат (рис. 2.2).
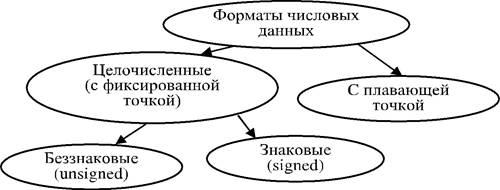
Рис. 2.2. Классификация базовых форматов числовых данных
В каком формате предпочтительно обрабатывать и хранить информацию, в частности, цифровые сигналы? У каждого формата есть свои преимущества и недостатки. Формат с плавающей точкой в некотором смысле можно считать «аналоговым», он обладает широким диапазоном значений, возможностью сохранения дробных величин с высокой точностью. К недостаткам формата относится то, что:
![]() вычисления выполняются относительно
медленно;
вычисления выполняются относительно
медленно; ![]() сигналы от большинства датчиков после АЦП
переводятся в целочисленный формат;
сигналы от большинства датчиков после АЦП
переводятся в целочисленный формат; ![]() большинство «(потребителей» цифровых
сигналов, в том числе устройства визуализации, воспроизведения звука, требуют
данных в целочисленных форматах, для чего необходимо преобразование форматов.
большинство «(потребителей» цифровых
сигналов, в том числе устройства визуализации, воспроизведения звука, требуют
данных в целочисленных форматах, для чего необходимо преобразование форматов.
На рис. 2.3 приведены две схемы обработки сигналов (ФТФ —
формат с фиксированной точкой; ПТФ — формат с плавающей точкой; АЦП ![]() аналогово-цифровой
преобразователь; ЦАП — цифро-аналоговый преобразователь). Схема а обеспечивает
высокое быстродействие, но накладывает некоторые, порой недопустимые,
ограничения на процедуру преобразования; схема б позволяет производить самые
разнообразные цифровые преобразования сигнала, но существенно снижает
быстродействие на этапах обработки сигнала в формате с плавающей точкой и
преобразования форматов.
аналогово-цифровой
преобразователь; ЦАП — цифро-аналоговый преобразователь). Схема а обеспечивает
высокое быстродействие, но накладывает некоторые, порой недопустимые,
ограничения на процедуру преобразования; схема б позволяет производить самые
разнообразные цифровые преобразования сигнала, но существенно снижает
быстродействие на этапах обработки сигнала в формате с плавающей точкой и
преобразования форматов.
|
|
Обработка |
ФТФ |
ЦАП |
а АЦП

Рис. 2.3. Схемы обработки цифровых сигналов
Возможным решением задачи повышения быстродействия является использование схемы, приведённой на рис. 2.4 (Ф1 — ФТФ, совместимый с ЦАП и АЦП; Ф2 — Ф ТФ, позволяющий произвести требуемые преобразования). В этой схеме все операции выполняются в целочисленных форматах, а требуемая точность достигается за счёт увеличения числа разрядов, фактически за счёт перехода к формату с фиксированной точкой.

Рис. 2.4. Альтернативная схема цифровых преобразований сигналов
Например, в большинстве цветовых схем на каждый цветовой канал изображения выделяется восемь бит. Сложение двух или более восьмибитных элементов в формате типа unsign a d char может привести к переполнению расчетных регистров, ячеек памяти. Использование переменных большей разрядности позволяет, гарантированно не вызывая переполнения (до определённого значения суммы), производить сложение: например, формат unszgned int10 позволяет выполнять сложение до 256 элементов типа unsign a d char.
В целочисленной арифметике умножение на число, кратное степени двух, может быть выполнено с помощью поразрядного сдвига влево. При операциях над сигналами, каждый дискретный элемент которых представлен в формате unsrgned char, действия в формате unsigned int16 могут вызвать переполнение уже при втором умножении, в unscgned int32 — при четвёртом. Можно заключить, что при использовании целочисленных форматов для операции умножения необходимо ограничивать результаты после выполнения соответствующего числа операций. Практическая реализация такого ограничения зависит от особенностей конкретной программно-аппаратной платформы и способа решения задачи.
Наиболее затратной с точки зрения потребления вычислительных ресурсов является операция деления. В целочисленной арифметике деление на число, кратное степени двух, может быть выполнено с помощью поразрядного сдвига вправо. Заметим, что деление можно с заданной степенью точности реализовать с помощью операций сдвига и сложения. При делении в целочисленной арифметике может возникать существенная потеря точности за счёт отбрасывания дробной части.
Обобщим сказанное в формальной записи. В цифровой обработке преимущественно используется умножение с последующим суммированием, например, свёртка, быстрое преобразование Фурье, фильтр скользящего среднего реализуется на базе умножения с последующим суммированием. Пусть по схеме (рис. 2.4) необходимо в ФТФ выполнить умножение с последующим суммированием N некоторых значений oq на коэффициенты сј .
![]()
где — число в ФТФ; с — число в ПТФ• S — численный результат суммы в ПТФ.
Для исключения переполнения, когда все од. = 0 N—1, имеют максимальную величину, необходимо ограничить число элементов N и значения коэффициентов с. .
Ограничить значение N при необходимости можно, разделив сумму (2.1) на:
![]() s=E uc
s=E uc![]()
i=()
Ограничить значения с возможно, например, при помощи нормирования:

Далее, с учётом Ф ТФ, в котором будет
производиться умножение с суммированием, необходимо принять решение: сколько
знаков после точки должно быть учтено. Пусть значимое число знаков будет К,
тогда коэффициент h возможно вычислить как ![]() 1016k = 16k,
где Ох — префикс 16-ричной системы счисления. Основание степени 16 обеспечивает
некоторую избыточность, по сравнению с основанием десятичной системы счисления,
повышая точность вычислений. В общем случае при h=2к (К — целое число) операции
умножения и деления на h легко выполнить с помощью сдвига влево и вправо на
log2h бит, для h= 16 k
1016k = 16k,
где Ох — префикс 16-ричной системы счисления. Основание степени 16 обеспечивает
некоторую избыточность, по сравнению с основанием десятичной системы счисления,
повышая точность вычислений. В общем случае при h=2к (К — целое число) операции
умножения и деления на h легко выполнить с помощью сдвига влево и вправо на
log2h бит, для h= 16 k ![]()
![]() умножение с. « 4k = (0х10К ) ;
умножение с. « 4k = (0х10К ) ; ![]() деление
с. 4k / (0х1 о к у, где << и >> — операторы поразрядного
сдвига влево и вправо соответственно.
деление
с. 4k / (0х1 о к у, где << и >> — операторы поразрядного
сдвига влево и вправо соответственно.
Таким образом, получим результирующее выражение для операций умножения с последующим суммированием:
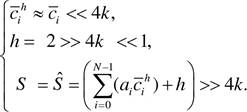 (2.4)
(2.4)
При вычислениях в машинных системах неизбежны ошибки, вызванные дискретностью всех форматов данных в цифровых ЭВС. Причиной ошибок при дискретных вычислениях является необходимость постоянного округления промежуточных и конечных результатов.
К ошибкам приводит и то, что в форматах для записи чисел с плавающей точкой длины мантиссы и экспоненты постоянны. Числа с меньшим значением экспоненты имеют меньший шаг дискретизации. Вычисления с одновременным использованием чисел разного порядка могут вызвать существенные ошибки.
Принято различать случайные и нараспшющие ошибки (рис. 2.5). Первые компенсируют друг друга и обычно их влияние на результаты вычислений не столь существенно. В некоторых случаях случайные ошибки можно существенно уменьшить при помощи повторных вычислений с последующей обработкой, например, аппроксимацией наилучшего значения.
Нарастающие ошибки приводят к регулярному искажению результатов и не могут быть устранены повторными вычислениями, для борьбы с ними необходимо применять, например, алгоритм Кэхэна.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нарастающая |
|
ои-шбка |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайная |
ошибка |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5. Случайная и нарастающая ошибки
В листинге 2.3 приведён программный код, генерирующий
нарастающие и случайные ошибки, при последовательном многократном сложении
err+=dlt получается значение, отличное от результата единовременного вычисления
![]() (step)
(с умножением). При малых значениях step преобладает случайная ошибка,
нарастающая отсутствует, с увеличением st a p влияние нарастающей
ошибки увеличивается, и при достаточно больших step она значительно превалирует
над случайной. График (рис. 2.5) сгенерирован с помощью программы (см. листинг
2.3), необходимо обратить внимание, что некоторые компиляторы способны
«разворачивать» подобный код и оптимизировать, поэтому результаты расчётов
могут различаться для различных компиляторов при включённой опции оптимизации.
(step)
(с умножением). При малых значениях step преобладает случайная ошибка,
нарастающая отсутствует, с увеличением st a p влияние нарастающей
ошибки увеличивается, и при достаточно больших step она значительно превалирует
над случайной. График (рис. 2.5) сгенерирован с помощью программы (см. листинг
2.3), необходимо обратить внимание, что некоторые компиляторы способны
«разворачивать» подобный код и оптимизировать, поэтому результаты расчётов
могут различаться для различных компиляторов при включённой опции оптимизации.
Мистинг 2.3. Генератор ошибок округления (С++)
![]()
f10at d1t; / / величина приращения
f10at err 0 . 0; / / ошибка ![]() i ; / / счётчики int st a p 150; / / число шагов
последовательного сложения randomize ( )
i ; / / счётчики int st a p 150; / / число шагов
последовательного сложения randomize ( )![]()
/ / последовательное сложение
![]()
err+=d1t;
/ / объединенное вычитание с умножением
![]()
При разработке программного обеспечения для снижения влияния ошибок округления на результаты вычислений необходимо учитывать вычислительные особенности платформы и языка реализации.
![]()
![]()
![]() 2.7. Практическое применение
оптимизации вычислений
2.7. Практическое применение
оптимизации вычислений
Оптимизированный вариант преобразования данных из цветового
пространства RGB в YCbCr (вариация Y709CbCr) в соответствии с выражением
(1.11), построен на базе рассмотренных ранее принципов целочисленных вычислений
(листинг 2.4). Для перевода в ФТФ использовался множитель К = 2 = 1 048 576 ,
соответственно для окрутления к ближайшему целому можно использовать добавление
величины 0.5 К ![]()
Ииспшнг 2.4. Преобразование значения из цветового пространства RGB в YCbCr
![]()
C010rSpace х;
R— (int) x.byt a Lo; G— (int) x.byt a Av; В— (int) x
.byt a Hi; const int ![]() / / h=524288,• / / компонент (У)
/ / h=524288,• / / компонент (У)
x.byteAv= (uchar) (abs (—105906*R—
![]()
/ / компон а нш (Cr)
![]()
Сравнения преобразований на базе вычислений ПТФ и ФТФ (рис. 2.6), показали, что время операций было сокращено более чем в восемнадцать раз. Подобное повышение скорости вычислений иллюстрирует эффективность перехода (при возможности) к Ф ТФ даже при наличии математического сопроцессора.
![]() 2.00
2.00
1.50
1.00
0.50
0
Рис:. 2.6. Скорость вычисления преобразования цветовых пространств, изображение размером 4000х2000
Обратные преобразования из YCbCr в RGB можно выполнить в соответствии с выражением (1.12), реализованным в ФТФ (листинг 2.5, для уменьшения искажений вследствие окрутления к целому применены поправочные коэффициенты).
Лисптнг 2.5. Преобразование значения из цветового пространства YCbCr в RGB
![]()
C010rSpac a х;
int У, Cb, Cr; У= (int) x .byteLo;
Cb= (int) x.byteAv;
/ / поправочные коэффициенты const
int h1=354615; const int h2=614460; / / компонент ( R ) x.byteLo= (uchar) (abs![]()
![]()
/ / компонент (G) x.byteAv= (uchar)
(abs ![]() / / компонент (В)
/ / компонент (В)
![]()
Следует отметить, что в программах (листинги 1.3, 2.4, 2.5) в результате целочисленных округлений преобразования становятся нелинейными, следствие нелинейности — искажения и частичная потеря информации, визуально незаметная, но, возможно, критичная для технических приложений. При множественных взаимных преобразованиях искажения могут накапливаться. Исключить или уменьшить их можно, изменив алгоритм и добавив некоторые условия, это приведет к замедлению вычислений (особенно заметному для циклов попиксельной обработки изображения). Поэтому часто применяют «оперативные методы коррекции», в частности, для «повышения однозначности» взаимного преобразования листинге 2.5 введены поправочные коэффициенты (h1 и h2).
Приведённые в данном труде вычисления машинного времени производились на компьютере, построенном на базе процессора Core2Duo Е8500, с эффективной тактовой частотой 3,16 ГГц, частотой процессорной шины 1 .333 ГГц, кэш-памятью второго уровня размером 6 МБ, в среде 0S Windows ХР и Windows-7.
2.8. Оптимизация вычислительных циклов
Способ организации выделенного адресного пространства может существенно повлиять на эффективность вычислений [73]. В листинге 2.6 сравниваются способы перебора двумерного массива. Результаты работы программы для массива data размером 8192х8192 приведены на рис. 2.7. Очевидно, что скорость цикла перебора по столбцам, вложенного в цикл перебора по строкам, примерно в два раза выше, чем у другой пары вложенных циклов. Здесь надо отметить, что понятия «строка» и («столбец» достаточно условны, ведь память ЭВС линейна. В соответствии с последовательностью выделения памяти (листинг 1 .2) соседние элементы строки расположены по соседним адресам в физической памяти, а элементы столбцов удалены друг от друга. Следовательно, при проходе по строке более эффективно используются преимущества быстродействующей кэшпамяти, логика предсказания и меньше обращений к более медленной оперативной памяти.
Заметим, что быстрее заполнять фрагменты памяти возможно с помощью функций стандартной библиотеки С, таких как тетсру, mems a t•, или С++: например, инициализацией вектора (std: :vector) при объявлении. При решении более сложных задач, выбрав оптимальную последовательность перебора, можно существенно повысить быстродействие исполняемой программы.
Лисптинг 2.6. Сравнение способов перебора элементов двумерного массива (С++)
![]()
/ / заполнение двумерного массива изображения data
/ / знач а нием, сод а ржащимся в t a mp
UColorSpace temp; / / проход по столбцам
![]()
/ / проход по строкам for (uint i=O;
i<iHeiqht; i++) ![]() temp . питЬ= (i+j ) ; data [1] [ј ] =temp . rqb;
temp . питЬ= (i+j ) ; data [1] [ј ] =temp . rqb;
/ / проход по строкам for (uint i=O;
i<iHeiqht; ![]() / / проход по столбцам for (uint j=O;
/ / проход по столбцам for (uint j=O; ![]() temp . питЬ= (i+j ) ; data [ i ] [ј ]
=temp . rgb;
temp . питЬ= (i+j ) ; data [ i ] [ј ]
=temp . rgb;
![]()
0 Перебор по строкам, вложен в перебор по столбцам
Перебор по столбцам, вложен в перебор по строкам
![]() 1.00
1.00
0.80
0.60
0.40
0.20
0
Порядковый номер теста Рис. 2.7. Время выполнения теста:
способ перебора элементов двумерного массива
Оптимизация программы может обеспечить существенное повышение скорости обработки данных.
Искажения присущи практически всем цифровым сигналам, они могут существенно осложнить обработку и анализ изображений, а таюке восприятие их человеком. Поэтому необходимо бороться с различными видами искажений на всех этапах получения и преобразования изображения. Причиной возникновения искажений может быть:
![]() несовершенство приёмных устройств,
например, неидеальная форма линз оптических камер, дефекты ПЗС-матриц и т.д.;
несовершенство приёмных устройств,
например, неидеальная форма линз оптических камер, дефекты ПЗС-матриц и т.д.; ![]() аддитивное
и мультипликативное добавление шумов при передаче по линиям радиосвязи или
существенное затухание сигнала в линиях связи;
аддитивное
и мультипликативное добавление шумов при передаче по линиям радиосвязи или
существенное затухание сигнала в линиях связи; ![]() искажение сигнала во
время обработки, например, при масштабировании и повороте изображения.
искажение сигнала во
время обработки, например, при масштабировании и повороте изображения.
Искажения проявляются преимущественно в частотной или в пространственной области представления сигнала или одновременно в обеих областях. Исходя из специфики проявления искажений, с учётом причин их возникновения, следует выбирать способы устранения. В подавляющем большинстве случаев полностью исключить искажения невозможно, да и на практике достаточно частичного их устранения.
С искажениями следует бороться на всех этапах получения и преобразования сигнала, и в первую очерет, необходимо понять причины их возникновения. Вследствие многообразия видов искажений важнейший этап борьбы с ними — выбор адекватной математических моделей системы формирования изображений и объекта изображения. Задачу устранения искажений можно отнести к классу обратных задач цифровой обработки сигналов.
В ЭВС преобразования значений элементов, образующих сигнал, могут приводить к переполнениям, потере точности, смещению плотности распределения величины сигнала, следствием этого могут быть искажения. Результаты преобразования сигналов может существенно искажать использование различных числовых форматов (см. табл. 2.4).
Округление значений при переходе от формата с плавающей точкой к формату с фиксированной точкой. Наиболее распространено округление:
![]() в меньшую сторону (получение наибольшего
целого, не превышающего х
в меньшую сторону (получение наибольшего
целого, не превышающего х![]()
![]()
— в большую сторону (получение наимењшего целого, не меньшего х ):
![]() - Г лх]Л
- Г лх]Л![]()
![]() до ближайшего целого:
до ближайшего целого:
w[x] = lf[x] + 0.5ј или w[x] = [f[x] —
0.51![]()
Переход в беззнаковую область. При преобразованиях сигналов
в форматах со знаком с плавающей и/или с фиксированной точкой возможно
возникновение как положительных, так и отрицательных значений. При переходе к
беззнаковым форматам можно воспользоваться добавлением константы (например,
абсолютной величины минимального отрицательного значения) или определением
модуля (рис. З. 1): w[x] = Г [х] + const const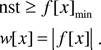
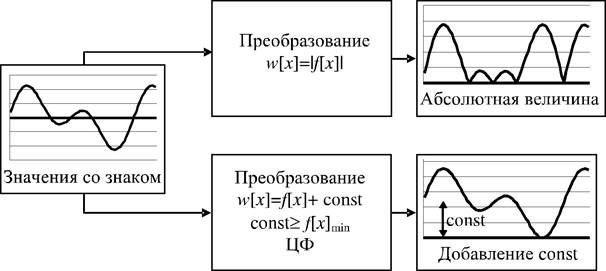
Рис. 3.1. Преобразование в беззнаковый формат
Очевидно, что полученные результаты различны, но каждый из описанных подходов может быть полезен в определённой ситуации. Например, при визуализации изображений, отсчёты которых (со значительной амплитудой — как положительной, так и отрицательной) важно различать, может быть полезным преобразование в беззнаковый формат путём вычисления абсолютной величины. С другой стороны, при определении абсолютной величины исходная форма сигнала утрачивается, это может быть недопустимо, особенно если требуется дальнейшая обработка.
Расширение и нормирование Динамического Диапазона сигнала
часто необходимо выполнять в ходе более сложных преобразований или как
самостоятельную задачу ЦОС. Примером может быть HDR (High Dynamic Range) способ
расширения динамического диапазона, применяемый для обработки фото- и
видеоизображений. Один из способов реализации HDR предполагает совместное
использование нескольких образов одного объекта, при этом каждый образ наиболее
эффективно передаёт области изображения с некоторым выбранным диапазоном
значений интенсивности светоизлучения (отражённого или собственного). ![]() применяют
в обработке разнообразных снимков — от медицинских до космических,
3Dмоделировании, телевидении высокой чёткости (High-Deftnition Television) и
др.
применяют
в обработке разнообразных снимков — от медицинских до космических,
3Dмоделировании, телевидении высокой чёткости (High-Deftnition Television) и
др.
На базе расширения и нормирования динамического диапазона реализуют так называемую гамма-коррекцию — изменение динамического диапазона сигнала с помощью степенной функции, применительно к графической информации она позволяет:
![]() эффективно использовать устройства
визуализации изображений (мониторы, проекторы и др.) — яркость элементов
визуализации практически всех устройств не линейно зависит от уровня сигнала, а
пропорциональна некоторой степенной функции (с показателем у);
эффективно использовать устройства
визуализации изображений (мониторы, проекторы и др.) — яркость элементов
визуализации практически всех устройств не линейно зависит от уровня сигнала, а
пропорциональна некоторой степенной функции (с показателем у); ![]() корректировать
изображения для печати — вследствие особенностей печатающих устройств и
различных расходных материалов может требоваться значительная предварительная
обработка изображений (преобразование цветового пространства, гамма-коррекция);
корректировать
изображения для печати — вследствие особенностей печатающих устройств и
различных расходных материалов может требоваться значительная предварительная
обработка изображений (преобразование цветового пространства, гамма-коррекция);
![]() повышать
контрастность некоторой области изображения это может быть необходимо при
обработке различных графических объектов, например, медицинских и космических
снимков.
повышать
контрастность некоторой области изображения это может быть необходимо при
обработке различных графических объектов, например, медицинских и космических
снимков.
На рис. 3.2 приведён пример нелинейной трансформации динамического диапазона.
Когда результаты прямого и обратного преобразования выходят за диапазон допустимых значений или не могут быть сохранены с приемлемой точностью из-за дискретного разрешения формата, взаимно-однозначное обратное преобразование невозможно, это практически всегда приводит к частичной потере информации.
Рассмотрим некоторые особенности функции преобразования (рис.
3.2) при различных значениях предела отношения: ![]() расширение
динамического диапазона:
расширение
динамического диапазона:
Aw(x) ![]() lim
lim
![]() ширина диапазона неизменна:
ширина диапазона неизменна:
Aw(x)
![]()
![]() сужение динамического диапазона:
сужение динамического диапазона:
Aw(x)
() < lim
![]() сужение и инверсия динамического
диапазона:
сужение и инверсия динамического
диапазона:
Aw(x)
—1< lim
![]() инверсия динамического диапазона при
неизменной ширине:
инверсия динамического диапазона при
неизменной ширине:
Aw(x)
![]()
![]() расширение и инверсия динамического
диапазона:
расширение и инверсия динамического
диапазона:
Aw(x) lim <—1![]()
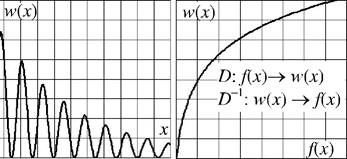
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 3.2. Преобразование динамического диапазона
(гамма-коррекция)
Нормирование динамического диапазона выполняется для того, чтобы значения сигнала не превышали допустимых, часто процедуры расширения или сужения диапазона совмещают с нормированием, исходя из требований к результату синтеза функции преобразования.
Согласно рекомендации ITU-R ВТ. 709 [154], в цветовом пространстве RGB для визуализации графической информации на электронных устройствах отображения (дисплеях, проекторах и пр.) гамма-коррекция выполняется в соответствии с выражением:
< 0.018,
R ' — 4.5R, R' = 1.099R045 -0.099,
и
(7' = 4.5G, G' = 1.099G045 -0.099, в! — 4.5В в' = 1.099В045 -0.099,
где R,G,B — исходные значения цветовых составляющих, заданные в диапазоне 0—1, R',G',B' — результаты гамма-коррекции в диапазоне 0—1.
Большинство цифровых сигналов требует различных преобразований, под которыми в общем случае имеются в виду отображения сигналов. Рассмотрим некоторые виды геометрических преобразований.
Наиболее простым видом преобразования является сдвиг, т.е.
изменение положения некоторого образа, более сложным — поворот. Сдвиг сигнала
f(Xl ![]() можно осуществить добавлением к
координатам некоторой величины (смещения) Д Д Д
можно осуществить добавлением к
координатам некоторой величины (смещения) Д Д Д![]()
![]() + ДрХ2 + + дп) =
+ ДрХ2 + + дп) =![]()
Операция сдвига может быть востребована, например, при центрировании некоторого образа. При сдвиге происходит только смещение сигнала, его форма неизменна, если не было выхода за область определения сигнала.
Операция поворота (рис. 3.3) осуществляется путем преобразования координат, в результате умножения координат на матрицу поворота (поворачивающую матрицу). Например, поворот координат в двумерном пространстве осуществляется с помощью выражения:
cos и — sin и ![]()
—sinu
cosu ![]()
![]() где , 12 исходные, а
хр 2 — результирующие координаты; угол поворота.
где , 12 исходные, а
хр 2 — результирующие координаты; угол поворота.
Исходное изображение Поворот на 45 0

Рис. 3.3. Поворот изображения (с масштабированием)
В трёхмерном пространстве обычно используют три поворачивающие матрицы. Следует отметить, что при визуализации результатов трёхмерного моделирования зачастую выполняется поворот не изображения, а наблюдателя (или камеры) — некоторой точки в виртуальном пространстве, относительно которой моделируется вся сцена. В этом случае применяют характеристику «угол Эйлера», или ее интерпретацию для данного виртуального пространства. Углы Эйлера описывают поворот абсолютно твёрдого тела в пространстве:
![]() вращение
вокруг оси Х ( — угол крена):
вращение
вокруг оси Х ( — угол крена):
![]() 1 0 0
1 0 0
R 0 cosu —sin и 0 sinu cosu ![]() вращение вокрут оси У
(Р — угол тангажа):
вращение вокрут оси У
(Р — угол тангажа):
![]()
![]() cosp 0
cosp 0
Rо 1
У
sinp 0 cos р
— вращение вокруг оси Z (у — угол рыскания):
![]()
![]() cos у
—siny 0
cos у
—siny 0
Rsiny cosy 0
0 0 1
При повороте, как и при некоторых других преобразованиях, вследствие дискретности цифрового сигнала, значения исходных координат могут не попасть точно (в целочисленном виде) в значения новых координат. Кроме того, сигнал может быть растянут или сжат, поэтому в большинстве случаев фактические значения необходимо пересчитывать. Исходя из желаемых результатов и возможностей следует выбрать подход к пересчёту значений сигнала при преобразованрш координат. Во многих случаях, например для графических изображений, хороший результат даёт аппроксимащи (рис. 3.4).
|
лхз,уз] |
ЛХ5,У5] |
|
|
|
Рис. 3.4. Аппроксимация значения сигнала
Значение сигнала f[xs, уз] в точке (х, , уз) аппроксимируется относительно точек (м, у) , (х, , )'2), (хз, уз) и ( Ч, )74) .
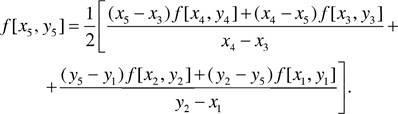
Достаточно распространено аффинное преобразование геометрических цифровых сигналов, т.е. линейное отображение на себя, при котором прямые отображаются в прямые:
![]()
Например, аффинные преобразования для двумерного пространства могуг быть описаны следующей системой уравнений: х ' = тих + тру + пиз,
(3.20) у ' = тих + 11122 у + 11123 , где х, у — исходные координаты точки; х ', у ' координаты, полученные в результате аффинных преобразований; 111ij — коэффициенты аффин-
ных преобразований: М в Коэффициенты матрицы М
![]() т22 23 определяют результат
аффинных преобразований и соответственно — отображения исходного сигнала.
Очевидно, что сдвиг, поворот и масштабирование являются частными случаями
аффинных преобразований.
т22 23 определяют результат
аффинных преобразований и соответственно — отображения исходного сигнала.
Очевидно, что сдвиг, поворот и масштабирование являются частными случаями
аффинных преобразований.
Весьма распространена задача коррекции геометрических искажений вызванных, например, несовершенством передающего тракта оптоэлектронного приёмника или особенностями положения объекта, регистрируемого фото- или видеоприёмником.
К шумам обычно относят некоторую часть сигнала, в той или иной степени препятствующую восприятию (распознаванию, анализу, выделению) полезной информации. В некоторых случаях шум сам по себе является полезной информацией, например, исследование реликтового излучения Вселенной позволяет оценивать её параметры (возраст, температуру и т.д.). Радиостанции, излучая сигналы сложной модуляции, порождают гармонические компоненты, которые, проходя на частоты вещания других радиостанций, могут восприниматься как шумы. Таким образом, один и тот же сигнал в некоторых случаях может быть отнесен к шумам, а в друтих — к полезной информации.
Шумы присутствуют практически во всех цифровых сигналах. Возможно выделить характерные признаки, отличающие различные виды шума.
1. Плотность распределения амплитуды, согласно которой шум может считаться гауссовым, максвелловским, равномерным и пр.
2. Спектральная плотность шума определяется характерной формой спектра, т.е. частотным составом шума. Наиболее распространённые виды шума: белый — со сплошным равномерным спектром в выделенном диапазоне частот, а таюке его разновидности (розовый, красный, серый и т.д.); шумы, имеющие линейчатый спектр. Для полупроводниковой аппаратуры характерны фликкер-шум (имеет розовый спектр) и дробовой шум.
З. Пространственная и временная плотность распределения шума. Например, пространственная неоднородность плотности шумов может возникнуть в результате синтеза (путём склейки) нескольких сигналов, полученных при различных условиях.
4. Регулярные и нерегулярные (случайные) шумы: например, регулярность пространственных шумов в цифровых фотоснтлках может быть вызвана дефектами оптики или ПЗС-матрицы (такие шумы называют локальными), периодические шумы во времени в той же ПЗС-матрице могуг быть вызваны периодически возгшкающей электромагнитной помехой. Спрогнозировать появление нерегулярных или случайных шумов достаточно сложно.
5. Шумы естественного (тепловой шум, шум атмосферных электромагнитных явлений и т.д.) и антропогенного происхождения (шумы, вызванные работой электроустановок, загрязнением атмосферы и т.д.).
6. Стационарные и нестационарные шумы, так же как и стационарные и нестационарные случайные процессы, характеризуется изменением вероятностных характеристик с течением времени [106].
Для снижения уровня шума на этапе аналоговой обработки и аналого-цифровых преобразований применяют малошумящие полупроводниковые схемотехнические элементы, охлаждение токоведущих и оптических элементов, стабилизацию питающих напряжений, экранирование и ряд других мер, которые можно отнести к аппаратным решениям. Программные решения можно рассматривать как другой вид шумоподавления.
Вследствие многообразия причин возникновения шума не существует универсальных фильтров, детектирующих и подавляющих все виды шумов, поэтому выделяют несколько принципиально различных подходов к программному или аппаратно-программному снижению уровня шума.
Многие фильтры шума работают по принципу подавления области
частот, в которой шум наиболее проявляется. Недостатком частотной фильтрации
может быть потеря значимой информации. Например, при фильтрации случайных шумов
в двумерном изображении с помощью выбранной разновидности однородного фильтра
(скользящего среднего) на базе операции свёртки с функцией рассеяния точки
(ФРТ) З![]()
![]()
или
![]() (3.22)
(3.22)
вследствие усреднения значений и подавления высокочастотных составляющих спектра контрастные границы различных объектов на изображении размываются. Поэтому требуется определить допустимые потери полезной информации, т.е. выявить диапазон частот, подавление которых уменьшит шум, не вызвав существенного искажения полезного сигнала.
Следует отметить, что подавление высоких частот в спектре сигнала с помощью операторных преобразований может привести к появлению низкочастотного шума, который в некоторых случаях визуально более заметен, чем высокочастотный.
В работе [140] Де Хаан предлагает оригинальный свёрточный фильтр, в котором в качестве значения центрального элемента используется взвешенная сумма пикселов, следующих через один.
Основанный на избыточности информации метод снижения шумов может дать очень хорошие результаты, при этом существенной проблемой является значительное время вычислений и увеличение необходимых объёмов информации.
В соответствии с теоремой Ляпунова [97] для подчиняющихся одному закону распределения независимых случайных величин Х1 , Х, ..., Х
![]()
с математическим ожиданием т и дисперсией о , при неограниченном увеличении п ( 71 ) закон распределения суммы
 (3.23) мало отличается от нормального.
(3.23) мало отличается от нормального.
![]() Александр Михайлович Ляпунов (25 мая 1857, Ярославль — 3
ноября 1918, Одесса)
Александр Михайлович Ляпунов (25 мая 1857, Ярославль — 3
ноября 1918, Одесса) ![]() математик и механик, член-корреспондент Петербургской Академии наук
(1900); академик (1901). Ученик П. Л. Чебышева.
математик и механик, член-корреспондент Петербургской Академии наук
(1900); академик (1901). Ученик П. Л. Чебышева.
Практическим следствием теоремы Ляпунова является то, что сложение случайных некоррелированных шумов не приводит к увеличению суммарного шума, имеющего нормальную плотность распределения. Теорема остаётся справедливой и для суммы случайных некоррелированных величин с неодинаковыми законами распределения при некоторых дополнительных условиях, которые, как правило, выполняются на практике для рассматриваемых случайных величин. Как показывает опыт, сумму порядка десяти слагаемых можно считать нормально распределённой [97]. В практических задачах цифровой обработки сигналов для сокращения вычислительных затрат по возможности ограничиваются тремя-пятью слагаемыми.
Хорошим примером является передача сигнала малой мощности в радиоэфире с шумами, такая задача может возникать при передаче данных со спутника. При достаточно протяжённых радиотрассах и практически постоянной передаче различных данных (телеметрических, космических снимков и т.д.), мощность спутниковых радиопередатчиков существенно ограничена мощностью доступного источника питания. Способ распознавания слабого сигнала на фоне шума — многократная передача повторяющихся фрагментов (пакетов), накопление пакетов со сложением на принимающей стороне. Если математическое ожидание шума в каждом пакете близко к нулю (или другой константе), то математическое ожидание суммарного шума таюке будет близко к нулю (или константе), причем чем больше пакетов, тем ближе. При этом математическое ожидание суммы пакетов будет стремиться к незашумлённому значению сигнала, умноженному на число пакетов. При некотором числе принятых и сложенных пакетов уровень сигнала превысит уровень шума на величину, достаточную для распознавания. Непременным условием эффективной фильтрации является отсутствие корреляции между шумами различных пакетов. Реализация рассмотренного способа проиллюстрирована в листинге 3.1, а результаты её выполнения — на рис. 3.5. Теоретически фильтрация за счёт накопления позволяет выделять сигнал с любым сколь угодно малым отношением сигнал/шум.
Лисптинг 3.1. Подавление случайного шума за счёт накопления пакетов
(MATLAB)
![]()
c1ear а 11; удаление переменных c10se а 11; % закрытие всех окон
% очистка командного окна
![]() 0 опр а д а ление
исходных данных
0 опр а д а ление
исходных данных
![]() 100; 0 число ошсчешов сигнала и шума
nnoise=100; D число накопленных пакетов
100; 0 число ошсчешов сигнала и шума
nnoise=100; D число накопленных пакетов ![]() D задание сигнала data=sin (—х:2*х/
(size—1) : х) •
D задание сигнала data=sin (—х:2*х/
(size—1) : х) •
а=4; D амплитуда шума nois a =zeros (size, nnocse) • D начальная инициализация матрицы % формирование матрицы пакетов,
![]() % образованной
векторами суммы (сигнал + шум) for
% образованной
векторами суммы (сигнал + шум) for
+data ( : ) —а; end
![]() D накопление пакетов
resu1t=zeros (size, nnoise) D начальная инициализация
D накопление пакетов
resu1t=zeros (size, nnoise) D начальная инициализация
![]() D непосредственно цикл суммирования
зашумлённых пакетов
D непосредственно цикл суммирования
зашумлённых пакетов ![]() для наглядности фильтрации пакеты суммируются
в матрицу,
для наглядности фильтрации пакеты суммируются
в матрицу, ![]() каждый последующий вектор матрицы
каждый последующий вектор матрицы ![]() образован
большим числом пакетов for : nnoise resu1t ( : ,
образован
большим числом пакетов for : nnoise resu1t ( : , ![]() end
end
![]()
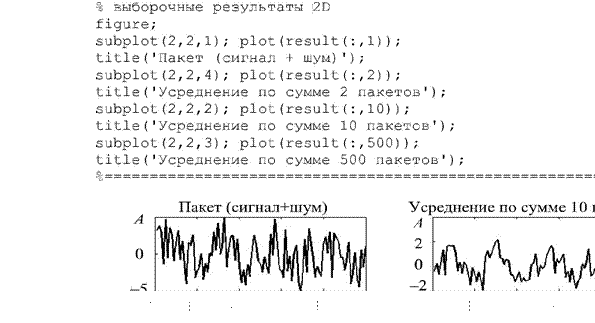
Усреднение по сумме 500 пакетов Усреднение по сумме 2 пакетов
![]() о 20 40 60 80
i
о 20 40 60 80
i 
Рис. 3.5. Подавление случайного шума за счёт накопления пакетов
Подход с накоплением информации можно применять для
фильтрации щшамических изображений. В большинстве случаев такие изображения
состоят из последовательности кадров![]()
![]() +1)... , при этом
соседние кадры мало отличаются друг от друга, исключением могут быть кадры,
соответствующие резкой смене сцены. Данную особенность динамических изображений
можно использовать для фильтрации случайных шумов (обычно достаточно 3—5 кадров
последовательности). Преодолеть возникающее при такой фильтрации размытие
границ движущихся объектов отчасти позволяет использование адаптивных фильтров
и/или автоматизированный анализ распознавания движения.
+1)... , при этом
соседние кадры мало отличаются друг от друга, исключением могут быть кадры,
соответствующие резкой смене сцены. Данную особенность динамических изображений
можно использовать для фильтрации случайных шумов (обычно достаточно 3—5 кадров
последовательности). Преодолеть возникающее при такой фильтрации размытие
границ движущихся объектов отчасти позволяет использование адаптивных фильтров
и/или автоматизированный анализ распознавания движения.
Фильтрация за счёт накопления информации неэффективна для подавления регулярных шумов, поскольку они коррелирутот между собой. Для подавления регулярного шума можно использовать способы, основанные на получении тестовых (калибровочных) сигналов, а таюке применять адаптивные фильтры. Например, для определения в радиоэфире шумов регулярной природы (гармонические составляющие радиосигналов, помехи от электрооборудования и т.д.) можно производить приём сигнала в период, когда радиопередатчик, связанный с данной частотой, соблюдает радиомолчание или посылает заранее известный (калибровочный, тестовый) сигнал — таким образом возможно идентифицировать регулярные шумы. В некоторых устройствах распознавания голоса фильтрацию шумов производят на основе данных, полученных в промежутках между словами. Выявление собственного регулярного шума фото- и видеоаппаратуры можно производить с помощью специальных тестовых снимков.
Термин стохастический резонанс впервые использован в работах
1981—1982 гг. [132, 133] при изучении периодичности ледниковых периодов и их
моделировании с помощью бистабильного осциллятора. Явление стохастического
резонанса свойственно мультистабильным (обычно метастабильных областей немного
— две-три) и нелинейным системам. В работах [132, 133] показано, что по
периодичности с ледниковыми периодами совпадают колебания эксцентриситета
Земли. Модельные расчёты показали, что сами по себе они не могут вызвать столь
существенных изменений климата, но при введении дополнительной («случайной»
силы были получены условия, достаточные для преодоления потенциального барьера
(точки бифуркации) и перевода климатической системы в состояние ледникового
периода и выхода из него. Последующие исследования описанного явления позволили
выявить его наличие в процессах, происходящих в самых различных системах. В
1983 г. стохастический резонанс бьш исследован в триггере Шмидта [144], а в
1988 г. — в кольцевом лазере [160], в 1991—1994 гг. ![]() в магнитных [146,
148], биологических и прочих системах. Есть основание полагать, что
биологические системы в ходе эволюции приспособились использовать неустранимый
внутренний и внешний шум для выделения полезного сигнала [142, 156, 168].
Явление стохастического резонанса в различных системах обобщено в работе [8], в
частности, рассмотрены особенности синхронизации фазы, поведение ансамблей
систем, которым оно свойственно, а также информационные и энтропийные
характеристики резонанса.
в магнитных [146,
148], биологических и прочих системах. Есть основание полагать, что
биологические системы в ходе эволюции приспособились использовать неустранимый
внутренний и внешний шум для выделения полезного сигнала [142, 156, 168].
Явление стохастического резонанса в различных системах обобщено в работе [8], в
частности, рассмотрены особенности синхронизации фазы, поведение ансамблей
систем, которым оно свойственно, а также информационные и энтропийные
характеристики резонанса.
Замечательным примером бифуркации является развитие массовых средств телекоммуникаций (проводная телефония, Интернет, мобильная связь и др.). Новые телекоммуникационные системы интегрируются в социум, сначала являясь достоянием лишь малой части общества, но, стремительно развиваясь, переходят на новый, массовый, уровень. При этом наблюдаются изменения как в социуме, например, появление новых возможностей для общения, трудовых вакансий, инфраструктур и т.д., так и в системе технического оснащения и данных, спрос рождает предложение, а массовый спрос рождает лавину предложений. Таким образом системы переходят на новый информационно-организационный уровень, т.е. меняется упорядоченность системы. Скачок социальной системы на новый информационный уровень стал очевиден с появлением сети Интернет, которая обеспечивает доступ практически к любой информации, наработанной человечеством, стирая границы между слоями общества, языковые преграды и расстояния.
Бифуркация непосредственно связана с уединёнными волнами — солитонами. Бифуркации солитонов впервые были обнаружены в численных экспериментах Лонге—Хиггинса как характеристика гравитационнокапиллярных волновых процессов на глубокой воде [2, 157]. Наличие солитонов свойственно информационным системам. Например, передача информации в биологических нейронных сетях осуществляется при помощи уединённых электрохимических волн. В вычислительных системах примером солитона служит некоторая программа, например компьютерный вирус, распространение которой может спровоцировать переход всей вычислительной системы в новое состояние, т.е. вызвать бифуркацию.
Бифуркация проявляется при стохастическом резонансе, когда в нелинейных системах сложение полезного сигнала с шумом приводит к усилению первого. Стохастический резонанс может возникать в нелинейных системах, имеющих несколько стабильных или метастабильных состояний, переход между которыми осуществляется в точках бифуркщии. При поступлении в такую систему некоторого полезного сигнала f(x) , недостаточного для ее возмущения и преодоления потенциального барьера — точки бифуркации, особую роль может сыграть шум п(х) определённой интенсивности, такой, что его суммарной мощности с полезным сигналом (f(x) + п(х)) будет достаточно для преодоления точки бифуркации. При
повышении мощности шума переход из одного состояния системы в другое происходит всё более хаотично, так что выходной сигнал становится независимым от полезного сигнала. В работе [8] также показана зависимость поведения системы от спектра шума. Таким образом, в системах, которым свойственен стохастический резонанс, шум может усилить полезный сигнал.
Другой вариант преодоления потенциального барьера в условиях недостаточной исходной энергии возможен в квантовых системах при туннельном эффекте, когда частица обладает одновременно волновыми и корпускулярными свойствами [1 17].
Модель стохастического резонанса рассмотрена в листинге 3.2. Полезный сигнал на входе системы не превышает 30 0 -0.з;+0.з от порогового значения перехода системы в относительно устойчивые состояния
—1 и +1 , следовательно, без дополнительного фактора (которым является
шум) система не может перейти из одного состояния в друтое. Устойчивость системы (запотушнание прежнего состоякшя) обеспечивается рекурсией для случаев, когда суммарной амплитуды сигнала и шума недостаточно для преодоления порогов. Результаты выполнения программы представлены на
![]()
Лиспшнг 3.2. Модель стохастического резонанса в нелинейной системе (MATLAB)
![]()
c1ear а 11; удаление переменных c10se а 11; закрытие всех окон очистка командного окна
![]() D определени а исходных
данных npoint=1000;
D определени а исходных
данных npoint=1000;![]() 0 число точек данных
0 число точек данных
![]() (1 : npoint)
(1 : npoint)![]() 0
вектор точек отсчёта
0
вектор точек отсчёта ![]() npoint) • вектор сигнала noise=O . 5*randn
(npoint, 1) • вектор шума data=sig+noise; 0 сумма (сигнал+шум)
npoint) • вектор сигнала noise=O . 5*randn
(npoint, 1) • вектор шума data=sig+noise; 0 сумма (сигнал+шум)
resu1t=zeros (npoint, 1 ) • подготовка вектора результатов
resu1t ![]() 0
начальное состояние системы
0
начальное состояние системы
![]() собственно модель нелинейной сист емы
собственно модель нелинейной сист емы ![]() с запоминанием предыдущего состояния
(рекурсией) for : npoint
с запоминанием предыдущего состояния
(рекурсией) for : npoint
e1seif data (i) <—1 resu1t (i) e1sa resu1t (i) =resu1t (i—1) —data (i—1) +data (i) ; end end
![]()
Полезный сигнал Сумма (сигнал+шум)
![]()
![]() 0
0
а
Выход системы Случайный шум
![]() 0
0
г
Рис. 3.6. Модель стохастического резонанса
Интересным примером стохастического резонанса, рассмотренным в [173], является сложение видеосигнала со случайным шумом некоторой интенсивности. Нелинейными элементами системы в этом случае будуг устройство визуализации (монитор, принтер с нелинейным динамическим щдапазоном) и зрительная система наблюдателя.
Стохастический резонанс в бистабильной системе можно описать аналитической моделью вида [61 ]: du(x)
![]() (З
.24)
(З
.24)
dx где и(х) выходной сигнал бистабильной системы; w(x) — нелинейная характеристика системы; f(x) и п(х) — сигнал и шум на входе системы.
Аттрактор Лоренца (или странный аттрактор) таюке относится к аналитической интерпретации стохастического резонанса в системах со случайными процессами, характерными для бистабильных систем, существующих в реальных физических процессах, например, в слое жидкости, подогреваемой снизу.
Достаточно хорошие результаты подавления шума обеспечивают адаптивные фильтры. Из названия понятно, что фильтры такого типа имеют некоторые способности к адаптации, т.е. позволяют производить фильтрацию с учётом щшамично изменяющихся особенностей сигнала.
Рассмотрим адаптивный фильтр (рис. 3.7), реализованный по
классической схеме [106]. На вход фильтра поступает зашумлённый сигнал ![]() —
f(x) + п(х) , в суммирующий узел поступают отфильтрованный и(х) и опорный —d(x)
сигналы. На основании сигнала ошибки А(х) = и(х) + (—d(x)) рассчитываются или
корректируются коэффициенты фильтра Н. В результате работы системы адаптивной
фильтрации получаем сигнал и(х) или сигнал ошибки Д(х) . В качестве опорного
сигнала используют шум или полученный ранее полезный сигнал. Например,
адаптивный фильтр, встроенный в систему распознавания голоса, может
рассматривать в качестве опорного сигнала шум в паузах между словами.
Периодически обновляя опорный сигнал, фильтр перестраивается (адаптируется) в
соответствии с изменяющимися характеристиками входного сигнала и шума. Задача
адаптивной фильтрации состоит в минимизации значения А(х) [56].
—
f(x) + п(х) , в суммирующий узел поступают отфильтрованный и(х) и опорный —d(x)
сигналы. На основании сигнала ошибки А(х) = и(х) + (—d(x)) рассчитываются или
корректируются коэффициенты фильтра Н. В результате работы системы адаптивной
фильтрации получаем сигнал и(х) или сигнал ошибки Д(х) . В качестве опорного
сигнала используют шум или полученный ранее полезный сигнал. Например,
адаптивный фильтр, встроенный в систему распознавания голоса, может
рассматривать в качестве опорного сигнала шум в паузах между словами.
Периодически обновляя опорный сигнал, фильтр перестраивается (адаптируется) в
соответствии с изменяющимися характеристиками входного сигнала и шума. Задача
адаптивной фильтрации состоит в минимизации значения А(х) [56].
—d(x)
![]() Опорный
Опорный
Алгоритм адаптации
Рис. З. 7. Блок-схема адаптивного фильтра
Адаптивная фильтрация нашла применение в различных научнопрактических приложениях, связанных с обработкой и анализом отражённых сигналов, например, в различных видах локации. Различают несколько видов адаптивной фильтрации: адаптивный фильтр Винера, алгоритм наименьших квадратов Уидроу—Хопфа, рекурсивные и статистические схемы.
При сканировании неровно положенный лист или корешок книги могуг исказить изображение. Фотоснимки могут содержать искажения, вызванные дефектами преломляющей системой объектива камеры. При фотографировании из космоса близкой к сферической поверхности планеты и отображении её на плоскость ПЗС-матрицы также будут возникать искажения. Подобные искажения могут быть особенно критичны для систем распознавания образов. Любой сигнал, несущий образ некоторого реального объекта, искажён, поскольку создание абсолютной копии возможно лишь на квантовом уровне.
При получении цифровых сигналов с помощью оптических систем возникают специфические искажения — аберрации, т.е. отклонения луча в реальной оптической системе от направления луча в идеальной. Качество оптической системы определяется её аберрациями, различают [ 12] :
— сферическую аберрацию (в частности,
наклонного пучка лучей); ![]() отступление от условия синусов;
отступление от условия синусов;
— меридиональную и сагиттальную кому (коматическую аберрацию);
— аберрации косых лучей; ![]() астигматизм;
астигматизм; ![]() кривизну
поля;
кривизну
поля;
— дисторсию; ![]() хроматизм положения;
хроматизм положения; ![]() хроматизм
увеличения;
хроматизм
увеличения;
— хроматическую разность сферических аберраций;
— хроматическую аберрацию наклонного пучка лучей.
В отдельную категорию выделяют искажения, свойственные непосредственно ПЗС-матрицам. Например, блуминг — это процесс перетекания заряда с более сильно освещённых пикселов к соседним, менее освещённым. Блуминг проявляется в виде вертикальных полос, расположенных выше и ниже яркого объекта с малыми угловыми размерами.
Устранять искажения желательно на стадии формирования сигнала за счет повышения качества оптоэлектронной системы. Если оптоэлектронная система не может обеспечить приемлемого качества цифрового сигнала, непосредственно к цифровым сигналам применяют специальные численные методы коррекции. Одним из распространенных видов искажений является оптическая дисторсия, проявляющаяся в том, что при прохождении света через реальную оптическую систему положение точек, образующих изображение, смещается относительно того положения, которое должно быть в идеальной оптической системе. Радиальная дисторсия обусловлена сферической поверхностью линз объектива, а тангенциальная — неперпендикулярностью главной оптической оси к плоскости изображения и прохождением главной оптической оси не через центр кадра [33].
Связь координат точек, полученных в реальной (х, у) и идеальной
(хо , уо) системах, может быть выражена следующими уравнениями:
Хо = Х +
![]()
(3.25)
Уо = У+б ![]()
При этом суммарное влияние радиальной и тангенциальной шсторсии определяется как
б = х kl(r2 ![]() 164
) + + 2XYI)2,
164
) + + 2XYI)2,
(3.26) б = у k1(r2 r02) К2 (r4 ![]() r04
) +2ХУР1 + (Р
r04
) +2ХУР1 + (Р![]()
![]() где
Кр К, ирр коэффициенты радиальной и тангенциальной дистор-
где
Кр К, ирр коэффициенты радиальной и тангенциальной дистор-
сии; r —расстояние до точки; ro — расстояние до точки нулевой дисторсии.
Отметим, что в общем случае к Дисторсии относят разнообразные искажения, связанные с изменением формы сигнала. Например, реактивные свойства электронных устройств, обусловленные наличием емкостей и индуктивностей, способствуют «сглаживанию» аналогового сигнала, т.е. фактически производят подавление высокочастотной составляющей.
В цифровых сигналах, полученных с помощью оптических систем, скорректировать дисторсию возможно с помощью уравнений, подобных (3.26), коэффициенты которых определяют опытным путём при помощи специальных тестовых изображений [27, 88, 151, 176]. В работах представлены [26, 76] интересные предложения по решению задач калибровки оптических систем и устранения искажений при помощи нейронных сетей.
rm(lqrm + Кут4 )
![]() (3.27)
(3.27)
![]()
![]() ¯ (k1rm2 + кут4 )
¯ (k1rm2 + кут4 )
где /q, .k2 коэффициенты сферической аберрации, постоянные для каждой оптической системы; f — фокусное расстояние; r радиус диафрагмы.
В случае коматической аберрации, в отличие от сферической, ФРТ несимметрична по направлениям, при этом радиус функции рассеяния точки можно оценить [1 1 6], например, при помощи выражения:
![]() Br(3r: + ry2 ) (3.28)
З где В — коэффициент комы, постоянный для каждой оптической системы; r —
расстояние от точки до главной оптической оси М, rx и r, зрачковые координаты
крайнего луча.
Br(3r: + ry2 ) (3.28)
З где В — коэффициент комы, постоянный для каждой оптической системы; r —
расстояние от точки до главной оптической оси М, rx и r, зрачковые координаты
крайнего луча.
В случае сферической аберрации ФРТ может быть заменена двумерной функцией распределения Гаусса. Пакет MATLAB предлагает специальные инструменты для выполнения операции обратной свёртки (листинг 3.3) [134, 150].
Лисупинг 3.3. Моделирование: размытие и коррекция (MATLAB)
![]()
c1ear а 11; удаление переменных c10se
а 11; ![]() о закрытие всех окон
о закрытие всех окон ![]() о очистка командного окна
о очистка командного окна
% формирование исходного изображения
Image=checkerboard (В) • ![]() функция
рассеяния точки
функция
рассеяния точки
![]() 0 искаж а ние
изображ а ния: размытие и шум те=0 ; D медиана шума de=O . 0001;
дисперсия шума
0 искаж а ние
изображ а ния: размытие и шум те=0 ; D медиана шума de=O . 0001;
дисперсия шума
Blurr a dNoisy=imnoise (imfilter (Image, PSF) , ' gaussian ' , те, de) ; Blurr a dNoisy=imfilter (Imaq a , PSF) •
![]() 0 восстановление
изображения обратной свёрткой ni=15; ЧИСЛО итераций
0 восстановление
изображения обратной свёрткой ni=15; ЧИСЛО итераций
ReIm=deconvlucy (BlurredNoisy, PSF, ni , sqrt (de) ) ;
![]() 0 визуализация результатов figure;
colormap (Gray) , subplot (2 , 2 , 1 ) ; imshow (Image) ; title ( ' Исходное
изображение ' ) • subp10t (2 , 2 , 2 ) ; imshow (B1urredNoisy) , tit1e ( '
Искажённое изображение ' ) • subp10t (2 , 2 , З) ; imagesc (PSF) ; tit1e ( '
Функция рассеяния точки ' ) • subp10t (2, 2 , 4 ) ; imshow (R a Im)
0 визуализация результатов figure;
colormap (Gray) , subplot (2 , 2 , 1 ) ; imshow (Image) ; title ( ' Исходное
изображение ' ) • subp10t (2 , 2 , 2 ) ; imshow (B1urredNoisy) , tit1e ( '
Искажённое изображение ' ) • subp10t (2 , 2 , З) ; imagesc (PSF) ; tit1e ( '
Функция рассеяния точки ' ) • subp10t (2, 2 , 4 ) ; imshow (R a Im) ![]() tit1e ( ' Восстановленное изображение
' )
tit1e ( ' Восстановленное изображение
' )
На рис. 3.8 приведены результаты выполнения программы (см. листинг 3.3). Очевидно, что при повышении резкости изображения полного восстановления не происходит, это связано с потерей части информации при свёртке.
Соответственно при размытии, обусловленном оптической системой, условиями приёма или обработки сигнала, с помощью обратной свёртки таюке невозможно получить качество <<неискажённого» сигнала, но в некоторых случаях возможно повысить качество сигнала до уровня, достаточного для дальнейшей обработки и анализа.
Исходное изображение Искажённое изображение

Функция рассеяния Восстановленное точки изображение
|
|
|
Рис. 3.8. Устранение сферической аберрации
Астигматизм — явление, при котором лучи одного и того же пучка, идущие по отношению друг к друту в двух взаимно перпендикулярных плоскостях, после преломления в оптической системе не собираются в одну точку, а образуют две точки (иногда более).
Кривизна поля изображения — аберрация, в результате которой изображение плоского объекта, перпендикулярного оптической оси объектива, лежит на поверхности, вогнутой либо выпуклой к объективу.
В общем случае можно рассматривать следующую линейную модель оптического приёмника (рис. 3.9). На вход оптического приёмника поступает некоторый сигнал f(x, у) , первым входным модулем модели является оптическая система (ОС) образованная совокупностью оптических преобразователей (системой линз, зеркал, призм, фильтров и т.д.); следующим элементом является детектор оптического сигнала (ДОС), например, ПЗС-матрица; затем аналоговый сигнал преобразуется, например, усиливается; далее сигнал преобразуется в цифровой вид при помощи модуля АЦП. Элементы системы (ОП — оптический преобразователь; АП — аналоговый преобразователь, ДОС) обладают собственной импульсной характеристикой ФРТ (PSF). В результате на выходе приёмника будет дискретный сигнал f[x, у] , являющийся цифровым образом исходного сигнала, свёрнутого с импульсными характеристиками модулей модели:
(х,
у) ![]() *PSF у),
*PSF у),
(3.29) f[x, у] - АЦП и(х, у) ![]()

Рис:. 3.9. Модель оптического приёмника
Учитывая специфику импульсной характеристики ка;кдого модуля, возможно производить коррекцию сигнала. Подобный приём рассмотрен в [125]. На практике измерение полной ФРТ является достаточно сложной задачей, т.к. необходимо учитывать влияние пространственной дискретизации, эффекты, связанные со смещением изображения в процессе интегрирования сигнала детектором. Таюке существует вероятность изменения ФРТ с течением времени и в результате физических воздействий на оптический приёмник, например, изменение влажности, температуры, давления, химического состава окружающей среды и пр.
Любое приёмное устройство, кроме пространственных, вносит искажения в энергетические характеристики сигнала. Например, цвета изображения, полученного при помощи фотоаппарата, не будут в точности соответствовать истинным цветам объекта фотографирования. Причина этих искажений состоит в том, что приёмник регистрирует отклик на исходный сигнал, в свою очередь, отклик синтезируется датчиком в результате воздействия на него исходного сигнала. Сам датчик при этом обладает определенными физическими характеристиками, например, спектром поглощения. В результате принятый сигнал будет содержать информацию не только об исходном сигнале, но и обо всём приёмном тракте. Искажения сигнала возможно рассматривать с точки зрения преобразования энергии.
Для цифрового графического изображения цвет — это лишь набор некоторых цифровых кодов, но, преобразовав эти коды в электронные импульсы и подав на устройство визуализации (например, монитор), можно получить цветную картинку, которая будет дополнительно искажена влиянием особенностей конкретного устройства визуализации. При регистрации цифровых сигналов принято говорить не об абсолютных энергетических характеристиках, а об относительных и условных, принятых в системе
данного приёмно-измерительного устройства и зарегистрированных в результате отклика датчиков устройства на внешний сигнал.
В специализированной литературе [33, 63] можно найти
разнообразные способы коррекции различных искажений, в зависимости от типа
приёмного устройства и условий приёма сигнала. Практическая реализация
значительной части таких корректирующих способов ориентирована на конкретные
устройства, поэтому их рассмотрение выходит за рамки данного труда.
Декомпозиция и синтез наиболее распространённые операции цифровой обработки сигналов. Многие методы анализа данных и распознавания образов построены на способах декомпозиции и синтеза. Современные методы компрессии, такие как JPEG (разработчик Joint Photographic Experts Group) [84, 105, 112], MPEG (Moving Picture Experts Group) [108, 153, 154], используют декомпозицию и синтез на базе дискретного косинусного или вейвлет-преобразования.
Системы называются ЛИНеЙНЫМИ, если они обладают свойствами однороДности и аддитивности.
Аддитивность системы F означает, что при
воздействии на её вход суммы сигналов Jl[R n ] + f2[Rn ]
на выходе возникает сигнал щ [R “ ] + щ [Ю] , причём щ [РК П ] есть
результат воздействия сигнала fl[R"] , а l12[R" ] — сигнала 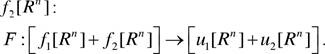
Однородность системы F означает, что входной сигнал .f[W] вызовет ответную реакцию системы, т.е. выходной сигнал:
![]() = hf[P]
= hf[P] ![]() где h
=const в общем случае может быть собственной многомерной импульсной
характеристикой системы h[W] , тогда выражение (4.2) будет иметь вид:
где h
=const в общем случае может быть собственной многомерной импульсной
характеристикой системы h[W] , тогда выражение (4.2) будет иметь вид:
![]()
операция ( * ) называется свёрткой, её мы рассмотрим далее.
Таким образом, линейная система подразумевает преобразования сигналов путём их сложения и/или умножения на константу (массив констант), в общем случае — свёртку с собственной импульсной характеристикой системы, в противном случае система не является линейной. Любую линейную систему можно представить в виде совокупности подсистем, производящих умножение сигналов на константу и сложение. Линейным системам свойственна коммутативность, т.е. если для преобразования сигнала используется цепочка последовательно соединённых линейных систем, то порядок соединения не влияет на результат.
Превалирующее число задач ЦОС можно решить выполняется с помощью операций, осуществляемых линейными системами. Нелинейные системы в большинстве случаев можно представить в виде совокупности линейных систем. В отличие от линейных систем, на выходе нелинейных возникают частотные компоненты, не входящие в частотные спектры исходных сигналов [78].
Свёртка является математической бинарной операцией, формирующей из двух входных сигналов один, один сигнал на входе операции называют импульсной характерисп1икой системы, другой — входным сигналом (рис. 4.1). Свёртку можно описать выражением:
![]()
где f[R H ] - входной сигнал; h[R"] — импульсная характеристика систеМЫ; u[R Yl ] выходной сигнал.

Рис. 4.1. Блок-схема свёртки
Согласно определению, импульсной характеристикой h[W] называется реакция линейной дискретной системы на цифровой единичный импульс Л) [R п ] , поданный на вход при нулевых начальных условиях.
Переходной характеристикой g[R"] называется реакция линейной дискретной системы на сигнал перехода (между двумя соседними отсчетами) из нулевых уровней в единичные Л 1 [ R 'l ] или из единичных в нулевые
Ло [ ] , поданный на вход этой
системы при нулевых начальных условиях: ![]() fh[P]
fh[P] ![]()
Свёртка может быть применена для самых разнообразных преобразований цифровых сигналов, с ее помощью можно произвести декомпозицию и синтез. Свёртку можно рассматривать как один из видов корреляционного анализа, например, она может помочь в распознавании заранее известных образов изображения, которые используются в качестве импульсных характеристик системы.
В дискретном виде свёртку одномерного сигнала можно описать уравнением:
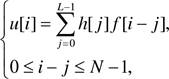
где h[] — импульсная
характеристика системы размером L , f[] входной сигнал размером N ; — выходной
сигнал (результат свёртки) размером N+L—1![]()
В двумерном случае уравнение свёртки (4.6) будет иметь вид:
 нал
No
нал
No
В случае п -мерного сигнала уравнение свёртки будет иметь вид:
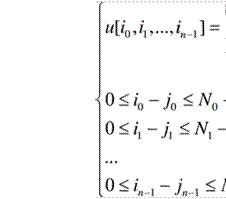 тл,л,.
тл,л,.![]()
Свёртка просто реализуется программно, при этом ее вычислительная сложность может быть достаточно большой.
Вычислительную сложность алгоритма свёртки можно оценить как:
Из выражения (4.9) видно, что сложность вычислений зависит от размерности пространства, размеров входного сигнала и импульсной характеристики. Уменьшение вычислительной сложности возможно благодаря снижению размеров импульсной характеристики системы. При постоянстве размеров импульсной характеристики в соответствии с асимптотической нотацией выражение (4.9) можно сократить:
![]()
Свёртка удовлетворяет следующим
законам: ![]() переместительный:
переместительный:
![]()
![]() сочетательный:
сочетательный:
![]()
— распределительный:
![]()
Рассмотрим программную реализацию свёртки в одномерном случае (листинг 4.1). Массив data [ ] содержит исходный одномерный сигнал, размерность массива data [ ] - sd. Массив pu1se [ ] содержит импульс, которым производится свёртка, размер массива pu1se [ - sp. Результат помещается в массив resu1t [ ] размером sd+sp-1.
Листинг 4.1. Одномерная свёртка сигнала (С++)
![]()
/ / цикл по сигналу
![]()
/ / цикл по импульсу
for (int j=O; ![]() resu1t [i+j
] +=data [ i ] *pu1se
resu1t [i+j
] +=data [ i ] *pu1se![]()
![]()
Рассмотрим свёртку двумерного сигнала — изображения No с импульсной характеристикой L0 х Ll . Отметим, что двумерные импульсные характеристики системы в дискретном виде принято называть функцией рассеяния точек (ФРТ).
Фрагмент программы, производящей свёртку двумерного сигнала,
приведен в листинге 4.2. Массив data2d[j [ ) содержит исходный двумерный
сигнал, размерность массива data2d[] [1- sdY И sdX ПО строкам И столбцам
соответственно. Массив pu1se2d[j [1 содержит ФРТ, с которой производится
свёртка, размер массива pu1se2d [ ] [ spY и spx по строкам и столбцам
соответственно. Результат помещается в массив ![]() [ ] [ ] размером
sdY+spY-1 И sdX+spX-1.
[ ] [ ] размером
sdY+spY-1 И sdX+spX-1.
Лисптинг 4.2. Двумерная свёртка сигнала (С++)
![]()
/ / выполн а ние свёртки /
/ циклы по сигналу for (int iyd=O; iyd<sdY; iyd++) { for (int ixd=O; ![]() ixd++)
{
ixd++)
{
![]() / циклы по импульсу ФРТ for (int
iyp=O; iyp<spY; iyp++) { iy=iyd+iyp; for (int ixp=O; ixp<spX; ixp++) {
ix=ixd+ixp; resu1t2d [iy] [ix]
/ циклы по импульсу ФРТ for (int
iyp=O; iyp<spY; iyp++) { iy=iyd+iyp; for (int ixp=O; ixp<spX; ixp++) {
ix=ixd+ixp; resu1t2d [iy] [ix] ![]() [ixpj *data2d [iyd] [ixd] ;
[ixpj *data2d [iyd] [ixd] ;
![]()
На практике цифровые сигналы зачастую являются многоканальными, например, изображения в формате RGB содержат три цифровых канала, поэтому свёртку в большинстве случаев выполняют для каждого из них. По каждому каналу может быть использована своя ФРТ, связанная, например, с особенностями восприятия человеком различных цветов в силу специфики анатомического строения глаза или с особенностями самого изображения.
Очевидно, что из-за специфики цифровых сигналов — ограниченности разрядной сетки и дискретности значений при свёртке, как и при многих других преобразованиях, возможны потеря значимой информации и выход за допустимый диапазон значений. Например, для цветовой палитры RGB, по каждому каналу, диапазон значений 0—255, дискретный шаг равен единице. Эти особенности необходимо учитывать при разработке и реализации вычислительных алгоритмов, производить нормировку динамического диапазона.
Быстродействие алгоритма может быть обеспечено вычислениями
в целочисленных форматах и совмещением в едином циклическом пакете свёртки по
всем каналам цифрового сигнала. Как было сказано, вычислительная сложность
алгоритма зависит от размеров исходного сигнала и ФРТ. Для обработки изображений
в большинстве случаев достаточно ФРТ размером 3х3 или 5х5 ![]()
Размеры полученного в результате свёртки сигнала больше размеров исходного сигнала и импульсной характеристики, при этом в большинстве случаев интерес представляет центральная часть, которая может быть получена путём вырезания из результирующего сигнала части, совпадающей по размерам с исходным сигналом.
Свёртка является одним из самых распространённых способов обработки цифровых сигналов, она используется для обработки статических и динамических изображений. Вычисление корреляции на базе свёртки может быть полезно, например, при распознавании образов. Например, при фрактальном сжатии изображений и вычислении автокорреляции на базе свёртки возможно найти самоподобные элементы.
В цифровой обработке сигналов свёртка используется очень широко — самостоятельно и как составная часть некоторых методов. Свёртка является своеобразным математическим обобщением, с её помощью можно решать множество задач преобразования сигналов. На базе свёртки, выбирая различные импульсные характеристики, можно реализовать значительное количество прочих операций, рассмотрим некоторые из них.
Для двумерного непрерывного (аналогового) сигнала f(x, у) произ-
![]()
водные в направлениях х и у вычисляются соответственно каки Гх
![]() Переходя к дискретному образу f[x, у]
непрерывной функции
Переходя к дискретному образу f[x, у]
непрерывной функции
Гу
![]() полагаем, что ее приращения имеют значения:
Гј(х, у) f[X+ 1, у] — f[x, у] и Гј(х, у) f[x, У +1] —f[x, у] приращение
аргументов дх = Гу z Ах = Лу = 1 , тогда производные сигнала f[x, у] :
полагаем, что ее приращения имеют значения:
Гј(х, у) f[X+ 1, у] — f[x, у] и Гј(х, у) f[x, У +1] —f[x, у] приращение
аргументов дх = Гу z Ах = Лу = 1 , тогда производные сигнала f[x, у] :
![]() в направлении х
в направлении х
![]()
Гх
![]() в направлении у
в направлении у
![]()
Гу
Производные сигнала f[x, у] можно вычислить с помощью свертки
с ФРТ:
![]()
![]()
![]()
![]() — в
направлении х о о оо о о
— в
направлении х о о оо о о
1 -1или1 —1 0
![]() в направлении у
в направлении у
![]()
![]()
![]() о о оо
о о оо
1 0 или h[x, у]о
-1 оо
Вычислить сумму производных по направлениям
Гх Гу
можно с помощью свёртки с ФРТ:
1 —2 0 или h[x, у] = 0 2
![]() Вычислим производные
второго порядка
Вычислим производные
второго порядка ![]() и
и ![]() для Гх2 Гу2
для Гх2 Гу2
![]()
![]() f[x, у] с
помощью свёртки с ФРТ:
f[x, у] с
помощью свёртки с ФРТ:
0 1
или h[x, у] = 0 -2
о 1
Для функции f[x, у] получим суммы производных второго порядка:
![]()
![]() 0 1 0
0 1 0
0 1 0
С помощью свёртки можно выполнить вычисления производных и более высоких порядков, например, решить уравнения в частных производных на массиве граничных условий.
Свёртка позволяет реализовать разнообразные фильтры, причём для высокочастотных достаточно использовать ФРТ небольших размеров.
Высокочастотный фильтр подчёркивания
границ на базе ФРТ 3х З![]()
![]()
![]() 0.125 0.125
-0.125
0.125 0.125
-0.125
-0.125 2 -0.125
-0.125 -0.125 -0.125
а на базе ФРТ 5х5 реализует фильтр повышения контрастности изображения:
0.0125 ![]() 0.1 2
0.1 2 ![]() 0.1
0.1 ![]() 0.0125 (4.20)
0.0125 (4.20)
На рис. 4.2 приведён пример использования свёртки с ФРТ (4.20) для повышения контрастности фрагмента снимка поверхности Земли, полученного со спутника AQUA.

Рис. 4.2. Повышение контрастности спутникового снимка Земли с помощью свёртки: а — исходное изображение; о — свёртка выполнена один раз, в — дважды
Свёртка сшналов находит пртленение в самом широком спектре научно-технических и прикладных задач. На базе концептуальной сущности свертки можно реализовать различные математические методы обработки и анализа п-мерных сигналов.
Декомпозиция в линейных системах — представление одного, сколь угодно сложного, сигнала в виде суммы нескольких, относительно простых:
![]()
![]() операция декомпозиции; f[R" ] исходный
сигнал;
операция декомпозиции; f[R" ] исходный
сигнал; ![]() и [ R 'i ] — множество элементов (от 0 до
р —1) декомпозиции исходного сигнала в п -мерном пространстве.
и [ R 'i ] — множество элементов (от 0 до
р —1) декомпозиции исходного сигнала в п -мерном пространстве.
Обратный декомпозиции процесс D восстановления сигнала путём суммирования элементов называется синтезом:
Р-1
![]() (4.22)
(4.22)
Декомпозицию и синтез сигнала можно выполнять в пространстве и/или времени. Цель преобразований и особенности сигнала определяют способ декомпозиции и синтеза.
Одной из классических операций декомпозиции и синтеза одномерного сигнала является преобразование Фурье 6.
Взаимно-ортогональные функции синуса и косинуса, выступающие
в качестве компонентов фурье-декомпозиции, называют баЗИСНЬШИ функциями
преобразования Фурье. Различают преобразование Фурье непрерывных и дискретных функций
[З 1![]()
Для непрерывной функции f(x) , заданной в замкнутом промежутке
(6,6 + 2тс) и не имеющей в нём либо имеющей ограниченное число экстремумов, ряд Фурье сходится всюду и его сумма равна f(x) для всякого значения х е (6,6 + 21) , на концах промежутка (6,6+ 2тс) сумма ряда имеет значение —(f(6) + f(2n)) . Косинусные и синусные коэффициенты ряда Фурье могут быть вычислены в соответствии с выражениями [5] :
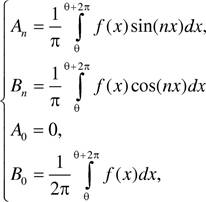 (4.23)
(4.23)
где f(x)— функция
разложения, А , В — коэффициенты ряда Фурье с индексом п![]()
Обратное преобразование Фурье (синтез) может быть выполнено с помощью выражения:
f(x) = Во + Е Дт sin(nx) + Вп cos(nx) (4.24)
![]() Жан Батист Жозеф Фурье (21 марта 1768, осер — 16 мая 1830,
Париж) — математик и физик.
Жан Батист Жозеф Фурье (21 марта 1768, осер — 16 мая 1830,
Париж) — математик и физик.
Если период равен не 21, а произвольному Т , то функцию f(x) следует рассматривать на интервале (6,6 + Т) при этом выражения (4.23) и (4.24) приобретут вид:
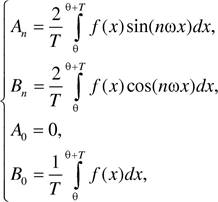 (4.25)
(4.25)
|
f(x) = Во +
Е Ап sin(nox) + Вп cos(nox) где о = — . Используя формулы Эйлера [22]: |
(4.26) |
![]() cos(nx) =
cos(nx) = ![]()
2
(4.27) sin(nx) — ![]() 2Ј
2Ј
![]() —1 , можно записать преобразование Фурье
на множестве ком-
—1 , можно записать преобразование Фурье
на множестве ком-
плексных чисел.
Для обратного преобразования Фурье получим:
![]()
![]() jncox ¯.Јпох¯Јпох
jncox ¯.Јпох¯Јпох
етох + Во,
![]() 2 2 далее с учётом (4.25) и (4.26) можно записать: вп
jAn 1
2 2 далее с учётом (4.25) и (4.26) можно записать: вп
jAn 1
![]() f(x) cos(nox) — jsin(nox) dx
f(x) cos(nox) — jsin(nox) dx
2
![]() 7
7
Леонард Эйлер (4 апреля 1707, Базель,
Швейцария — 7 сентября 1783, Санкт-Петербург) ![]() математик, внёсший значительный вклад
в развитие математики, механики, физики, астрономии и ряда прикладных наук.
математик, внёсший значительный вклад
в развитие математики, механики, физики, астрономии и ряда прикладных наук.
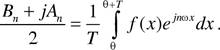
Согласно работе [5] :
вп jAn ![]() из выражения для можно
получить выражение для
из выражения для можно
получить выражение для
2
Вн + jAn ![]() заменив п на —п , при
этом если первый коэффициент обозна-
заменив п на —п , при
этом если первый коэффициент обозна-
![]() 2 чить через Сп , то второй должен быть обозначен как С
2 чить через Сп , то второй должен быть обозначен как С ![]() постояннЬ1й
член можно записать в виде: Во
постояннЬ1й
член можно записать в виде: Во
Следовательно, для преобразования Фурье на множестве комплексных чисел можно записать:
|
f(x) где комплексные коэффициенты Фурье: |
С еЈпох |
(4.28) |
![]() 1
1
(4.29)
Для дискретных функций, заданных в виде отсчётов, выражения
(4.25) и (4.26) можно записать в виде:
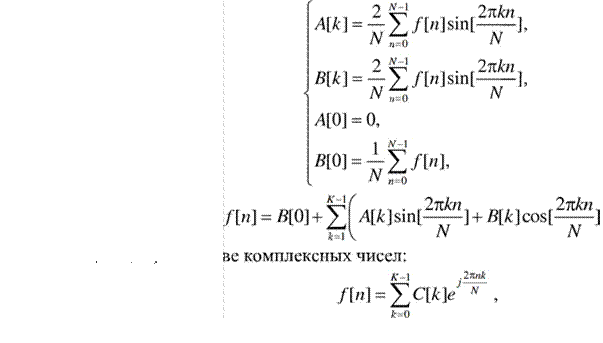
2лпк
![]() Елте (4.33)
Елте (4.33)
Схожесть выражений для обратного (4.32) и прямого (4.33) преобразования именуют дуальностью преобразования Фурье.
Описанный способ получения частотных коэффициентов может быть применён в случае разложения функции в более общие ряды декомпозиции по системе ортогональных базисных функций.
Отметим, что в соответствии с теоремой Парсеваля энергия
функции f(x) , представленной во времени или пространстве, равна интегральной
составляющей энергии частотного спектра F f(x)![]()
![]() flF
f(x) df
flF
f(x) df ![]() (4.34)
(4.34)
где F f(x) — непрерывное преобразование Фурье сигнала f(x) .
Для дискретного преобразования Фурье Е [К] сигнала f[n] выражение (4.17) будет иметь вид:
1V-1 1V-1
Ef2[n]- EF2[k] (4.35)
В практических целях используют быспзрое преобразование Фурье (БПФ). Идея БПФ была сформулирована Гауссом много раньше, чем появилась возможность практической реализации с помощью технических средств. Вторую жизнь в идею вдохнули Дж. Кули и Дж. Тьюки в 1965 г. [139]. Вычислительная сложность алгоритма БПФ оценивается:
![]() (4.36) где п— размер массива для
преобразования Фурье.
(4.36) где п— размер массива для
преобразования Фурье.
В современных системах ЦОС БПФ — один из наиболее используемых методов. Существует множество модификаций БПФ, некоторые из них ориентированы на специальные типы данных, другие универсальные. Способы практического применения и особенности различных видов преобразования Фурье подробно рассмотрены, например, в работах [85, 95, 112, 114] и др.
Оконное преобразование Фурье выполняется выбором некоторого
периода Т = (tmin тах) для функции Jf (x) , заданной в интервале х
min' тах) причём Т с Х ![]()
![]() Парсеваль Марк-Антуан (27 апреля 1755, Розьер-о-Салин — 16
августа 1836, Париж)
Парсеваль Марк-Антуан (27 апреля 1755, Розьер-о-Салин — 16
августа 1836, Париж) ![]() математик.
математик.
Гаусс Иоганн Карл Фридрих (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген) — математик, астроном и физик.
![]() f(x)w(x —
f(x)w(x —![]() (4.37)
(4.37)
где w(x— т) некоторая оконная функция, т — переменная, определяющая сдвиг окна, прочие обозначения те же, что и в предыдущем разделе. С помощью оконного преооразования Фурье можно получить образ функции f(x) в фазовом пространстве. Следует отметить, что в качестве оконных обычно используют функции, имеющие всплески: некоторый однополярный ограниченный и быстро затухающий по мере удаления от области наибольшей амплитуды.
Рассмотрим примеры таких функций:
![]() прямоугольное окно (окно Дирихле):
прямоугольное окно (окно Дирихле):
![]() min ' тах min т
min ' тах min т ![]() где [ лкп , — область окна;
где [ лкп , — область окна; ![]() окно
Хемминга:
окно
Хемминга:
2лх
w(x) = 0.54— 0.46 cos (4.39) х
где Х — длина интервала
[О,хт х], в котором задано окно, значения, не входящие в [О х плах] нулевые; ![]() окно
Блекмана:
окно
Блекмана:
2лх w(x) = 0.42 — 0.5 cos + 0.08 cos ![]() (4.40)
х х
(4.40)
х х ![]() окно Ханна:
окно Ханна:
2лх w(x) = 0.5 1—cos х
Для преобразования многомерных сигналов необходимо полностью или фрагментарно отобразить одномерные сигналы на одномерное пространство. Рассмотрим более подробно вариант фурье-преобразования двумерного сигнала, применяемого, например, для обработки цифровых графических изображений. Цифровой образ графического изображения рассмотрим в виде матрицы чисел (скалярного поля, каждый элемент — тензор нулевого ранга) размером Х х У . В случае полноцветного изображения (когда каждый элемент является вектором, т.е. тензором первого ранга) преобразование необходимо выполнять, рассматривая тензорное поле
первого ранга как совокупность тензорных полей нулевого ранга. Для матрицы скалярного поля изображения:
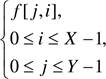 (4.42)
(4.42)
произведём разделение на векторы. Полученные векторы длиной У (содержащие члены ряда Фурье в виде комплексных чисел) подвергнем фурье-декомпозиции. Далее выполним конкатенацию полученных векторов так, чтобы при движении к центру вектора частота повышалась, результирующий вектор, состоящий из векторов реальной и мнимой части, запишем в ( (Х ХУ) -матрицу P[j,i] . Затем матрицу P[j,i] разделим на векторы длиной Х , с последующей фурье-декомпозицией, конкатенацией и записью результата в массив F[j,i] .
Последовательное выполнение указанных преобразований обеспечивает декомпозицию двумерного сигнала f[j,i] на волны, образованные гармоническими функциями (sin и cos), характеризуемые частотой, амплитудой и вектором направления (рис. 4.3).

Рис. 4.3. Элемент декомпозиции двумерного сигнала
Рассмотрим пример реализации декомпозиции Фурье двумерного цифрового сигнала (листинг 4.3). Программа MATLAB позволяет производить декомпозицию и синтез изображения, а также фильтрацию (подавление) некоторого диапазона выделенных частот и визуализацию результатов (высокочастотные составляющие располагаются ближе к центру, низкочастотные — на периферии, нумерация элементов массивов в MATLAB начинается с единицы).
Листинг 4.3. Фурье-декомпозиция цифрового изображения (MATLAB)
![]()
|
c1ear а 11; |
|
|
c10se а 11; |
0 закрытие всех окон |
![]() 0 очистка командного окна
0 очистка командного окна
![]() 0 загрузка изображения imgRGB imread(
' image .bmp ,
0 загрузка изображения imgRGB imread(
' image .bmp , ![]() 0 получ а ние размера изображения sz=size (imgRGB) •
0 получ а ние размера изображения sz=size (imgRGB) •
S у SZ (1) •![]() о высота
о высота
S х sz (2) •![]() о ширина
о ширина
![]() 1 р— 10;
1 р— 10;![]() о параметр
управления филь трацией 0 преобразование изображения в градации серого
imgGray=im2doub1e (rgb2gray (imgRGB) ) ;
о параметр
управления филь трацией 0 преобразование изображения в градации серого
imgGray=im2doub1e (rgb2gray (imgRGB) ) ;
-6 последовательное транспонирование матрицы изображения
![]() 0 и преобразование Фурь а
0 и преобразование Фурь а
![]() 0 сначала в горизонтальном, а затем в
вертикальном направлении RF=fft ( fft (imgGray) .
0 сначала в горизонтальном, а затем в
вертикальном направлении RF=fft ( fft (imgGray) .![]()
![]() 0 или в вид а одной
функции y=fft2 (imgGray)
0 или в вид а одной
функции y=fft2 (imgGray)![]()
% фильтр производит подавление выделенных часшош
![]() . (sy—1p) , (1р+1) : (sx—1p) )
. (sy—1p) , (1р+1) : (sx—1p) ) ![]() % обратно— преобразование imgRes=ifft
(ifft (RF) .
% обратно— преобразование imgRes=ifft
(ifft (RF) .![]()
![]() 0 или в вид а одной
функции imqRes=ifft2 (RF) ;
0 или в вид а одной
функции imqRes=ifft2 (RF) ;
![]() 0 визуализация
результатов
0 визуализация
результатов ![]() 0 исходное изображение figure ( 'Name' ,
'Origina1 image ' ) ; colormap (Gray) imaqesc (imqGray) ,
0 исходное изображение figure ( 'Name' ,
'Origina1 image ' ) ; colormap (Gray) imaqesc (imqGray) ,
![]() 0 вещественная часть
спектра figure ( 'Name' , 'Rea1 part ' ) • colormap (Gray) imaqesc (real (RF) )
;
0 вещественная часть
спектра figure ( 'Name' , 'Rea1 part ' ) • colormap (Gray) imaqesc (real (RF) )
;
![]() 0 мнимая часть спектра
0 мнимая часть спектра
![]() ' Imaginary part ; c010rmap (Gray) ;
imagesc (imag (RF) ) ;
' Imaginary part ; c010rmap (Gray) ;
imagesc (imag (RF) ) ; ![]() о амплитуда figur a ( 'Name , ' Amp1itud a ) ;
c010rmap (Gray) ; imagesc (abs (RF) ) ;
о амплитуда figur a ( 'Name , ' Amp1itud a ) ;
c010rmap (Gray) ; imagesc (abs (RF) ) ; ![]() 0 фаза
0 фаза


Рис. 4.4. Фурье-преобразование (а) столбцов матрицы изображения f[j, i] и (б) строк матрицы Р[ј, i] : I — мнимая часть, 2 — реальная часть, З — амплитуда, 4 — фаза спектра; в — восстановленное изображение; г — подавленные элементы спектра изображения на примере фазы F[j, i] (l — сохранено 100, 2 — 75, З — 44,
4 — 12 элементов спектра)
Рассмотренный принцип последовательных преобразований Фурье можно применять для сигналов любой размерности, существенным достоинством такого подхода является возможность распараллеливания процесса преобразования, что очень актуально для современных многопоточных вычислительных систем. В работе [112] подробно рассмотрено, как с помощью многомерного фурье-преобразования можно осуществить быструю свёртку и корреляцию многомерных сигналов, что может быть полезно для проблемы распознавания образов.
Рассмотрим стеганографическое встраивание информации в частотную область фурье-образа графического сигнала. В качестве контейнера используем стандартное тестовое изображение [178], уменьшенное до размеров 128х 128 (<<128.bmp»), встраивать будем тестовое изображение, уменьшенное до 64х 64 (<<64.bmp>>). Все преобразования выполнены в программе MATLAB (листинг 4.4). В начале программы происходит загрузка исходных изображений: контейнера (рис. 4.5, а) и встраиваемого (рис. 4.6, а). Затем выполняется их фурье-преобразование и встраивание спектра изображения (рис. 4.6, а) в спектр (рис. 4.5, а). Встраивание происходит в область высоких частот. На рис. 4.7 приведены спектр контейнера до (а) и после встраивания (б), а таюке спектр контейнера и встроенного изображения с искажениями (в). Искажения возникают в результате преобразования спектра заполненного контейнера в изображение при отсечении мнимой части. Следующим действием в программе является сохранение контейнера в виде изображения с последующим чтением и извлечением содержимого (рис. 4.6, б). В завершение происходит визуализация и сохранение результатов в файл.
Лиспшнг 4.4. Встраивание информации в частотную область
![]()
clear а 11; ![]() удаление переменных
close а 11;
удаление переменных
close а 11; ![]() 0 закрытие всех окон
0 закрытие всех окон
![]() D очистка командного окна
D очистка командного окна
![]() 0 загрузка исходного изображения
контейнера imgRGBcont
0 загрузка исходного изображения
контейнера imgRGBcont![]() imread( ' 128 .bmp ' ) ;
imread( ' 128 .bmp ' ) ; ![]() 0 загрузка изображения для встраивания imgRGBemb
0 загрузка изображения для встраивания imgRGBemb![]() imread ( ' 64 .bmp ' ) ;
imread ( ' 64 .bmp ' ) ;
![]() 0 получение размера изображений
sz=size (imgRGBcont) • D контейнер syc=sz ( 1 ) ; высота sxc=sz (2) • ширина
sz=size (imgRGBemb) • 0 встраиваемое sye S 2 (1) • 0 высота sxe S 7 (2) • 0
ширина
0 получение размера изображений
sz=size (imgRGBcont) • D контейнер syc=sz ( 1 ) ; высота sxc=sz (2) • ширина
sz=size (imgRGBemb) • 0 встраиваемое sye S 2 (1) • 0 высота sxe S 7 (2) • 0
ширина
![]() фурье—образ контейнера
фурье—образ контейнера
RFC fft2 (rgb2gray (imgRGBcont) ) ;
Ecupa1.,1Ea 0 Moro 1-4306paxeH1,1A
REE fft2 (rgb2qray (imgRGBemb) ) ;
(sxc—sxe+2) / 2) : (
(sxc+sxe) / 2) ( (syc—sye+2) 12) : ( (syc+sye) 12) )![]()
![]() (sxe) , (1)
:
(sxe) , (1)
: ![]() 00
oöpaTHoe npeoöpa30BaHme imgRes= (ifft2 (RE C) ) ; 0
B03HMKÆ-10BeÆ-1me MHMMoj'1 qacTM B curl Hane M30—
00
oöpaTHoe npeoöpa30BaHme imgRes= (ifft2 (RE C) ) ; 0
B03HMKÆ-10BeÆ-1me MHMMoj'1 qacTM B curl Hane M30—
6paxeHMA imgRes=reaI (imgRes) 0 nonepA MHOOPMaUMM (oncegeHMe MHMMOÜ qac rm,f)
![]() coxpaHeHMe
1-430ÖpaxeHMA zar10J7HeHHOT7 0 K0HmeÜHepa imwrite (mat 2
gray (abs (imgRes) ) imageRes . bmp '
coxpaHeHMe
1-430ÖpaxeHMA zar10J7HeHHOT7 0 K0HmeÜHepa imwrite (mat 2
gray (abs (imgRes) ) imageRes . bmp ' ![]()
![]() 3arn pys«a
M30ÖpaxeHMA zar10J7HeHHOT7 0 K0HmeÜHepa imgRGBsteg imread
( ' imageRes . bmp ,
3arn pys«a
M30ÖpaxeHMA zar10J7HeHHOT7 0 K0HmeÜHepa imgRGBsteg imread
( ' imageRes . bmp , ![]() oypbe—oöpaz M30ÖpaxeHM51
3ar10JTHeHHOTl O K0HTeÜHepa
oypbe—oöpaz M30ÖpaxeHM51
3ar10JTHeHHOTl O K0HTeÜHepa
RES fft2 (imgRGBsteg) ,
![]() 0
M3BJ1eqeHMe com o pxvnuor•o K0Hmej1H o pa imgExtract
0
M3BJ1eqeHMe com o pxvnuor•o K0Hmej1H o pa imgExtract ![]() ifft2
(sxc—sx o +2) / 2) : ( (sxc+sxe) / 2)
ifft2
(sxc—sx o +2) / 2) : ( (sxc+sxe) / 2) ![]() sy n +2)
/ 2) : ( (syc+sy o ) /2) ) ) ;
sy n +2)
/ 2) : ( (syc+sy o ) /2) ) ) ;
![]() 0 BOCC rraHOEJ1eHMe
BCTPO O HHOI'O M306paxeHMA imgCont ifft2 (RES) ;
0 BOCC rraHOEJ1eHMe
BCTPO O HHOI'O M306paxeHMA imgCont ifft2 (RES) ;
![]() 0 El.,f3yaJIM3aUMfi p o s yr1BTaT0B
0 El.,f3yaJIM3aUMfi p o s yr1BTaT0B
1 magesc (
imgRGBcont) ![]()
![]() pesyneuau E cupab1EaHb1A (Sari051HeHHb1j1
R0Huej1Hep) figure ( 'Name ' ' Container full ' ) • colormap (Gray) ,
pesyneuau E cupab1EaHb1A (Sari051HeHHb1j1
R0Huej1Hep) figure ( 'Name ' ' Container full ' ) • colormap (Gray) ,
1 magesc (abs (imgCont) ) •
1 mwrit= (mat 2 gray (abs (imgCont) ) , 1 mageRes . bmp bmp![]()
![]() c,
aMnnmnyma cneKupa san0JIHeHH011 0
c,
aMnnmnyma cneKupa san0JIHeHH011 0 ![]() figure (
'Name ' , 'Amplitude J ) ; colormap (Gray) ;
figure (
'Name ' , 'Amplitude J ) ; colormap (Gray) ;
1 mage sc
(log (abs (RE C) ) ) ; imwrite (mat 2 gray (log (abs (RFC) ) ) , imageAmp . bmp
' , 'b![]()
![]() 0
aMFIJIMTyma cneærpa 3aF10JIHeHÆ-1cr1 0 1-cowre1hHepa
nocne q rreHMA—3a11MCM figure ( 'Name ' , 'Araplitude r o write
' ) ;
0
aMFIJIMTyma cneærpa 3aF10JIHeHÆ-1cr1 0 1-cowre1hHepa
nocne q rreHMA—3a11MCM figure ( 'Name ' , 'Araplitude r o write
' ) ;
![]() 0 %
colormap (Gray)
0 %
colormap (Gray) ![]() 1 mage sc (log (abs (RES) ) ) ; imwrite (mat 2
gray (log (abs (RES) ) ) ,
1 mage sc (log (abs (RES) ) ) ; imwrite (mat 2
gray (log (abs (RES) ) ) , ![]() pe3YJ1b rra rr
1,43BneqeHMA figure ( 'Name ' , 'Extract image ' ) , colormap (Gray) ; imagesc
(abs (imgExtract) ) ; imwrite (mat 2 gray (abs (imgExtract) ) ima g e Amp rw .
bmp ,
pe3YJ1b rra rr
1,43BneqeHMA figure ( 'Name ' , 'Extract image ' ) , colormap (Gray) ; imagesc
(abs (imgExtract) ) ; imwrite (mat 2 gray (abs (imgExtract) ) ima g e Amp rw .
bmp , ![]()
' extract . bmp '

Рис. 4.5. Контейнер:
а — исходный вид; б — со встроенным изображением
На рис. 4.5, б видна высокочастотная рябь. Сравнив рис. 4.6, а и б, можно заметить искажения во встраиваемом изображении, вызванные отсечением мнимой части при обратном фурье-преобразовании заполненного контейнера и потерей информации о фазе гармонических составляющих. Избежать потери информации позволит метод дискретного косинусного преобразования, используемого для форматов JPEG, NfPEG.

а исходное; б — извлечённое из контейнера
Рис. 4. 7. Фурье-спектр:
а — исходного изображения; б — контейнера со встроенным изображением; в — контейнера со встроенным изображением и частичными искажениями
Одно из важных свойств свёртки — возможность её выполнения с помощью операции произведения спектра исходного сигнала f[W] и спектра импульсной характеристики h[R n ] :
![]() (4.43)
(4.43)
где F и Н — прямое фурье-преобразование сигнала f[R 11 ] и импульсной характеристики h[W] соответственно; х операция произведения спектров; F — оператор обратного преобразования Фурье.
Произведение спектров предполагает следующие вычисления:
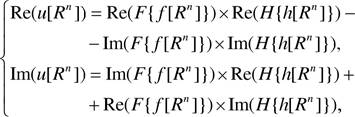 (4.44)
(4.44)
где Re и Im — вещественные и мнимые составляющие.
Дискретное косинусное преобразование (ДКП) — один из стандартных видов частотной декомпозиции по базису гармонических функций. В отличие от преобразования Фурье, в ДКП используются только косинусные функции и все преобразования происходят в области вещественных чисел, что возможно за счёт искусственного симметрирования сигнала, при котором мнимая (синусная) часть спектра обращается в нуль [112]. Для одномерного ДКП набор базисных функций описывается уравнениями вида:
b[x] = cos![]() (4.45)
(4.45)
где К = О, ![]() частотный
коэффициент базисных составляющих, Х
частотный
коэффициент базисных составляющих, Х ![]() размер (число дискретных элементов)
вектора, х номер отсчёта
размер (число дискретных элементов)
вектора, х номер отсчёта
![]()
Одномерное ДКП можно выполнить в соответствии с выражением:
![]() (2х + 1)Кл
(2х + 1)Кл
Е [К] = w(k)(4.46)
где f[x] — элемент предназначенного для ДКП вектора размером Х отсчётов, функция w(k) может принимать следующие значения:
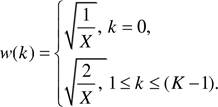
Двумерное ДКП преимущественно используется в алгоритмах сжатия статических (JPEG) и динамических изображений (NWEG). Основой такого ДКП является совокупность базисных функций, описываемых урав-
нением:
![]() (2х + 1)КТ
(2х + 1)КТ
b[x, у] = cos cos(4.47) 2х где К, р — частотные коэффициенты базисных составляющих, Х, У— размеры преобразуемого пространства. Наиболее распространённым решением является разделение пространства изображения f[...] на блоки размером 8х8 , 16х16 и 32х32 пикселов и выполнение ДКП для этих блоков в отдельности. Например, для случая разделения изображения на блоки 8х8 элементы Х = 8 и У = 8 . При этом х и у пробегают возможные значения х, у = 0—7. Поскольку в большинстве случаев размеры изображения значительно превосходят размеры блоков (Х дкп изображений фактически является одной из разновидностей многомерного оконного преобразования.
Двумерное ДКП возможно осуществить следующим образом:
![]() (2Х + 1)k7t (2х +
1)Кл cos (4.48)
(2Х + 1)k7t (2х +
1)Кл cos (4.48)
На рис. 4.8 графически представлены базисные функции двумерного ДКП для блока размером 8х8 , цифры отражают распространённую конфигурацию записи коэффициентов, полученных в результате прямого ДКП. Очевидно, что с увеличением значений К, р возрастает частота. На рисунке приведены оси х и у , в элементе с координатами х = 0, у = 0 сохраняется значение постоянной составляющей, а в элементе х = 7, у = 7 — значение составляющей, содержащей наибольшую частоту по двум направлениям.

Рис. 4.8. Графическое представление базисных функций двумерного ДКП
Рассмотрим вейвлет-преобразование [123, 126]. Вейвлетом называют (действительную или комплексную) функцию д (х) :
g(x)dx = const (4.49)
быстро затухающую при х ±оо Наиболее распространены вейвлеты,
+00 для которых выполняется условие g(x)dx = 0, такие функции осцилли-
руют относительно оси х и вклады в интегральную сумму положительных и отрицательных значений компенсируют друг друга.
Вейвлет должен обладать условием допустимости, т.е. характеризоваться конечной энергией:
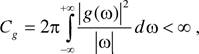
где о собственная частота вейвлета.
На базе д (х) получают семейство функций:
g(x,q,u)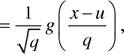
где и определяет сдвиг функции д (х) , q определяет масштабирование: q<1 — сжатие, q>1 — растяжение. Функцию д(х) , порождающую семейство д(х, ц, и) , при q и и = 0 принято называть мап1еринским вейвлетом.
На основе семейства функций (4.51) строится интегральное вейвлетпреобразование:
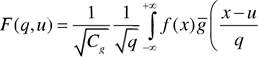 dx (4.52)
dx (4.52)
т.е. выполняется отображение исходного сигнала f(x) в фазовое пространство, это позволяет выполнить оконное преобразование Фурье, которое можно рассматривать как разновидность вейвлет-преобразования.
Для ортогональных и биортогональных вейвлет-преобразований справедлив аналог теоремы Парсеваля о равенстве энергии сигнала, выраженного в частотной или пространственной области:
![]() С +00 2
dudq (4.53)
С +00 2
dudq (4.53)
В листинге 4.5 приведён пример программы вейвлет-преобразования сигнала в среде MATLAB, в качестве материнского использован вейвлет «мексиканская шляпа>> (Mexican Hat Wavelet, mexh). Результатом исполнения программы является диаграмма (рис. 4.9), соответствующая распределению энергии вейвлетов.
Листинг 4.5. Вейвлет-преобразование (MATLAB)

![]() 0 задание парам а тров и
сигнала для преобразования
0 задание парам а тров и
сигнала для преобразования
|
|
длина |
|
step (2*pi) /siza |
шаг |
|
х —pi : step : (pi—step) ,
% вейвлет—преобразование |
вектор аргумента вектор значений |
|
sca1es |
0 вектор значений масштабирующей пе— |
|
coefs cwt (у, sca1es, 'mexh' ) |
расчёт вейвлеш—коэффициентов |
![]() coIormap (gray (64) ) ;
палитра: от т а нки с о рого wscaIogram ( ' imaqe ,
coefs, scal=s
coIormap (gray (64) ) ;
палитра: от т а нки с о рого wscaIogram ( ' imaqe ,
coefs, scal=s
а 
х10—3
![]() 20
20
15 б
10
5
Рис. 4.9. Результат выполнения программы (листинг 4.5).
а — график исходного сигнала; б — распределение энергии вейвлет-коэффициентов,
т.е. отображение сигнала в фазовое пространство (q — масштабный коэффициент вейвлета, х — номер отсчёта)
Вейвлет-преобразование эффективный инструмент обработки и
Множество реальных физических процессов описывается гармоническими и экспоненциальными функциями. Поэтому существенное значение для математического описания реальных систем имеет преобразование
10
.Јапласа . Двустороннее преобразование Лапласа позволяет получить изо-
![]() Пьер-Симон Лаплас (23 марта 1749, Кальвадос — 5 марта 1827,
Париж) — математик, физик и астроном; известен работами в области небесной
механики, дифференциальных уравнений, один из создателей теории вероятностей.
Пьер-Симон Лаплас (23 марта 1749, Кальвадос — 5 марта 1827,
Париж) — математик, физик и астроном; известен работами в области небесной
механики, дифференциальных уравнений, один из создателей теории вероятностей.
бражение F(p) непрерывной функции f(x) в
интервале (![]() на
на
![]()
![]() (4.54)
(4.54)
где р = 0+ јо — комплексный аргумент изображения, называемый оператором, о действительное число, о крутовая частота. Функция f(x) должна удовлетворять условиям Дирихле, т.е. за любой конечный промежуток иметь конечное число разрывов первого рода и конечное число максимумов и минимумов. Смысл преобразования Лапласа позволяет раскрыть выражение (4.54) в виде:
![]() е JOX dx .
е JOX dx .
Исходный сигнал f(x) умножается на экспоненциальный множитель е—ОХ в результате получается выражение f(x)e , умножение по-
¯ Јох
лученного выражения на е с последующим интегрированием:
![]()
позволяет получить комплексное
фурье-преобразование сигнала вида ![]() f(x)e
f(x)e![]()
Таким образом, преобразование Лапласа является совокупностью
преобразований Фурье для произведений исходного сигнала f(x) на
экспоненциальный множитель е . Пространственно преобразование Лапласа можно
представить в виде тензорного поля на ![]() заданной комплексными
координатами (о, јо) , каждая точка которого соответствует некоторой
комплексной величине F(o, о)
заданной комплексными
координатами (о, јо) , каждая точка которого соответствует некоторой
комплексной величине F(o, о)![]()
Обрапшое преобразование Лапласа имеет следующий вид:
00 +ix
1
![]() (4.57)
(4.57)
2тсј 60 —ioc
где р = 00 + јо![]()
Преобразование Лапласа позволяет с помощью операторного отображения переходить от дифференциальных и интегральных уравнений к
обыкновенным алгебраическим [60, 64, 69]. Рассмотрим односторонний случай, удовлетворяющий казуальным системам, производная
![]() будет иметь вид: dx
будет иметь вид: dx
![]()
здесь L f'(x)
обозначает преобразование Лапласа функции f'(x) ![]() Проинтегрировав
выражение (4.58) по частям, получим:
Проинтегрировав
выражение (4.58) по частям, получим:
![]() + р
+ р ![]() = pF(p) — Г (0) .
(4.59)
= pF(p) — Г (0) .
(4.59)
0
Для производной высших порядков в общем случае можно записать:
L
(х) = ![]() 2 f'(0)
2 f'(0) ![]()
(4.60)
![]() (п—1)
(п—1)
для случая f(0) = 0![]()
![]()
Отметим, что в выражении (4.61) слагаемое pF(p) соответствует широко применяющемуся в электротехнике преобразованию Карсона— Хевисайда:
![]() (4.62)
(4.62)
0
особенность которого — одинаковая размерность изображения и оригинала.
В одностороннем случае (Р(х) = ![]() имеет следующий вид:
имеет следующий вид:
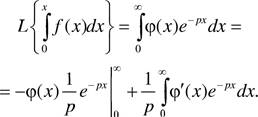 (4.63)
(4.63)
С учётом того, что функция и первое слагаемое (4.63)
![]() = 0 , а второе
= 0 , а второе ![]()
окончательно изображение интеграла будет иметь вид:
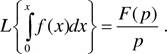 (4.64)
(4.64)
Преобразование Лапласа широко пртленяется при решении задач электротехники, ядерной физики, механики, сопротивления материалов и др.
В результате преобразования Лапласа импульсной характеристики
можно получить полную характеристику системы, исследуя только нули,
т.е. точки, где F(o,o) =0, и полюсы — точки, где F(o,o) = оо
а
б  х
х
Лм)
 х
х
Рис. 4.10. Графические образы исходных функций f(x) и их полюсы, построенные на
Одной из важнейших характеристик любой системы является устойчивость. Систему можно считать:
![]() устойчивой, когда её полюсы расположены в
левой
устойчивой, когда её полюсы расположены в
левой![]()
1
кости (рис. 4.10, а) f(x) = е X sin(x)
, ![]() = F(p) -
= F(p) -![]()
![]() условно устойчивой, когда полюсы
расположены на оси јо (0=0)
условно устойчивой, когда полюсы
расположены на оси јо (0=0)
(рис. 4. Ш, 6) f(x) , ![]() = F(p) -
= F(p) -![]()
![]() неустойчивой, если полюсы расположены в
правой
неустойчивой, если полюсы расположены в
правой![]()
1
(рис. 4.10, в) f(x) = е х sin(x)
, L{f(x)} = F(p) —![]()
Успюйчивость многополюсной системы определяется положением полюса, имеющего наибольшее значение о. Таким образом, критерием устойчивости системы является положение всех полюсов в левой полуплоскости.
4.13. Z-npe06pa30BaHue
Z-npe06pa30€aHue позволяет получить отображение дискретного
сигнала f[x] на ![]() Дискретное
Дискретное ![]() описывается
выражением:
описывается
выражением:
Јо
![]() где z=re так же как и преобразование Лапласа,
позволяет исследовать отклик системы с импульсной характеристикой f[n] на
гармонические осцилляции, нарастающие и затухающие экспоненциально с различными
скоростями.
где z=re так же как и преобразование Лапласа,
позволяет исследовать отклик системы с импульсной характеристикой f[n] на
гармонические осцилляции, нарастающие и затухающие экспоненциально с различными
скоростями.
Учитывая, что z = reЈо выражение (4.65) можно записать в виде:
¯Јох
(4.66)
таким образом, можно рассматривать как
совокупность преобразований Фурье для произведений некоторого дискретного
сигнала f[n] на экспоненциальный множитель r![]()
На рис. 4.11 приведены примеры исходных импульсных
характеристик систем .f[n] и положения полюсов и нулей 7-преобразований.
Критерием устойчивости системы является расположение всех полюсов, полученных в
результате ![]() импульсной характеристики, внутри
окружности единичного радиуса, расположение полюсов на линии окружности
единичного радиуса является признаком условно устойчивой системы, в ином случае
система считается неустойчивой.
импульсной характеристики, внутри
окружности единичного радиуса, расположение полюсов на линии окружности
единичного радиуса является признаком условно устойчивой системы, в ином случае
система считается неустойчивой.
|
|
Im |
|
|
|
|
|
|
![]() лих]
лих]
а х
|
|
Im |
|
|
|
|
|
|
б 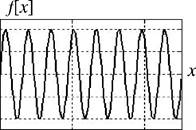
|
|
Im |
|
|
|
|
|
|
лих]
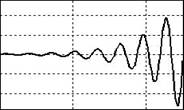 х
х
система а — устойчива, б — условно устойчива (генератор), в — неустойчива
Для удобства сравнения характеристик различных фильтров используют определяемую согласно теореме Котельникова нормированную частоту f , позволяющую привести спектр рассматриваемого сигнала к основ-
ной полосе частот 0; —![]()
2
![]() о
о
= — = от (4.67)
![]() частота
дискретизации; f — реальная частота; о = 27!f реальная круговая частота. Таким
образом, основная полоса частот сводится к диапазону f е 0; 0.5 и б Е 0; л
[108]. На
частота
дискретизации; f — реальная частота; о = 27!f реальная круговая частота. Таким
образом, основная полоса частот сводится к диапазону f е 0; 0.5 и б Е 0; л
[108]. На ![]() положение точки
положение точки
определяется утлом поворота о относительно начала координат и положительного направления вещественной оси, причём обычно используют нормированную круговую частоту о , таким образом ограничивают угол поворота сб Е —я; тс охватывающий положительные и отрицательные
частоты.
Наиболее широко ![]() применяется при анализе и синтезе
бесконечной импульсной характеристики фильтров.
применяется при анализе и синтезе
бесконечной импульсной характеристики фильтров.
В 1927 г. Гейзенберг 1 1 выдвинул предположение, что существует фундаментальный закон природы, объясняющий некоторые, парадоксальные с точки зрения классической физики, явления квантового мира. Этот закон он назвал ПРИНЦИПОМ неопределённости, который ограничивает применение к микрообъектам классических понятий и представлений [1 17].
Количественно этот принцип выражается в виде соотношений неопределённостей. Первое из них можно записать в виде:
дхдрх 2лћ (4.68) где Ах и Арх — неопределённость
координаты х и проекции импульса ![]() ћ = 1.05457160•10 Дж•с — универсальная
постоянная Планка . В общем случае соотношение Робертсона—Шрёдингера выражает
неопределённость значений любых двух переменных, которые не коммутируют друг с
другом. Под неопределённостью понимают минимально возможную погрешность
результатов одновременного измерения величин, связанных соотношением (4.68),
такие погрешности в квантовой механике считаются не следствием несовершенства
измерительной техники, а принципиальным законом, описывающим количественный
смысл соотношения неопределённостей.
ћ = 1.05457160•10 Дж•с — универсальная
постоянная Планка . В общем случае соотношение Робертсона—Шрёдингера выражает
неопределённость значений любых двух переменных, которые не коммутируют друг с
другом. Под неопределённостью понимают минимально возможную погрешность
результатов одновременного измерения величин, связанных соотношением (4.68),
такие погрешности в квантовой механике считаются не следствием несовершенства
измерительной техники, а принципиальным законом, описывающим количественный
смысл соотношения неопределённостей.
В качестве иллюстрации неопределённости Гейзенберг приводил пример [152] с воображаемым микроскопом, с помощью которого исследователь измеряет положение и импульс электрона, отражающего падающей на него фотон и тем обнаруживающего своё присугствие. Энергия фотона описывается уравнением Е = ћо , где о круговая частота излучения
2лс о = 271f . Если фотон имеет малую длину волны (где с — скорость
о света) и, следовательно большой импульс, то положение электрона может быть измерено вполне точно, при этом фотон рассеивается случайным образом, передавая электрону значительную и неопределенную долю своего импульса. Если у фотона большая длина волны и малый импульс, он мало изменяет импульс электрона, но рассеяние будет определять положение
![]() Гейзенберг Вернер Карл (5 декабря 1901, Вюрцбург — 1 февраля
1976, Мюнхен) — физик-теоретик, один из создателей квантовой механики; лауреат
Нобелевской премии по физике (1932).
Гейзенберг Вернер Карл (5 декабря 1901, Вюрцбург — 1 февраля
1976, Мюнхен) — физик-теоретик, один из создателей квантовой механики; лауреат
Нобелевской премии по физике (1932).
- Планк Макс Карл Эрнст Людвиг (23 апреля 1858, Киль —
4 октября 1947, Гёттинген) ![]() физик-теоретик, основоположник квантовой теории, член Берлинской АН
(1894).
физик-теоретик, основоположник квантовой теории, член Берлинской АН
(1894).
электрона очень неточно. В результате произведение неопределённостей в координате и импульсе остаётся не меньшим постоянной Планка.
Гейзенберг не сформулировал точное математическое выражение для принципа неопределённости, а использовал принцип как эвристическое количественное соотношение.
Неопределенность, замеченная в явлениях квантового мира,
проявляется и в других областях. В теории и практике цифровой обработки сигнала
известно, что чем уже сигнал во временной области, тем шире его образ в
частотной области, и наоборот. Вообще говоря, единичный импульс относится к
классу так называемых пар преобразований Фурье. Если некоторому сигналу [ (х)
во времени в частотной области соответствует образ F f(x) , то в частотной
области спектр, имеющий форму сигнала f(x) , во временной области будет
представлен образом F f(x) ![]()
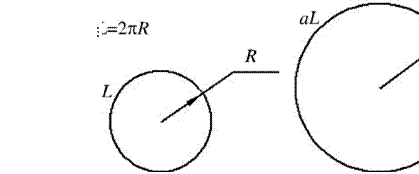
Рис. 4.12. Заданная окружность как мера
В преобразовании Лапласа используются две меры — экспоненциальная и гармоническая, формальная запись которых имеет вид (4.55); в вейвлет-преобразовании базовой мерой служит материнский вейвлет (в практических расчетах возможно выбрать наиболее подходящий). Заметим, что многие процессы в окружающем мире подчинены гармоническим и экспоненциальным законам, поэтому преобразование Лапласа находит применение во многих моделях, описывающих явления реального мира. Таким образом, выбор меры является основой для снижения неопределённости.
Согласно парадоксу Эйнштейна—Подольского—Розена (ЭПР) [143], изменение физической величины одной частицы в квантовой механике должно приводить к изменению вероятности распределения другой частицы, сцепленной с первой, причём со скоростью, которая может превышать скорость света. Такое поведение квантовых частиц согласуется с принципом Паули 1 ' (принципом запрета) который был сформулирован в 1925 г. для электронов и в дальнейшем распространён на все частицы с полуцелым спином. Парадокс ЭПР подтвержден экспериментально: в 1997 г. была осуществлена передача поляризационного состояния фотона [135, 136], а в 2004 г. — телепортация квантового состояния атома.
Успех эксперимента в области квантовой телепортации означает, что в качестве меры для определения состояния системы может быть использована система, связанная с ней набором квантовых чисел.
Во многих практических приложениях цифровой обработки сигналов качество результата может существенно зависеть от выбранной меры, поэтому на этапе разработки цифровых систем выбор принципов и способов преобразования, и следовательно меры, является ключевым.
Паули Вольфганг Эрнст (25 апреля 1900, Вена — 15 декабря 1958, Цюрих) физик, лауреат Нобелевской премии.
Необходимость повышения быстродействия вычислительных систем за счёт оптимизации и применения новых алгоритмов стимулирует поиски новых способов, позволяющих выполнять частотный синтез и декомпозицию. В настоящей главе рассмотрен предложенный автором способ декомпозиции цифровых сигналов по базису прямоугольных всплесков, эффективность которого подтверждена при решении ряда задач распознавания образов. По результатам разработки и исследования способа получен патент на изобретение [49].
Способ декомпозиции [49] по базису прямоугольных всплесков (БПВ) ориентирован на цифровые (дискретные) сигналы [37], образованные совокупностью прямоугольников (рис. 5.1). Таким образом, наилучшей мерой для цифровых сигналов могут быть прямоугольные функции или их некоторые объединения, являющиеся разновидностью вейвлетов.
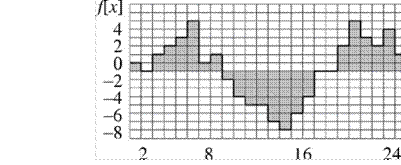
Рис. 5.1. Дискретность цифрового сигнала f[x]
Декомпозиция по БПВ [45] позволяет получить спектр п-мерного цифрового сигнала и локализовать его в пространстве и (или) времени, фактически отображая цифровой сигнал в фазовое пространство. Эта задача решается в ходе прямого преобразования (декомпозиции) путем последовательных итеративных вычислений в соответствии с выражением:
![]()
где Sk — спектральный компонент остаточного сигнала .
Значение индекса К соответствует протяжённости (периоду) взаимно перпендикулярных и параллельных элементов спектральных компонентов, при К = К сигнал является исходным. Сумма полученных в ходе прямого преобразования спектральных компонентов Sk соответствует обратному преобразованию (синтезу):
Разложение п-мерного сигнала на спектральные компоненты происходит не по выбранному заранее, а по формируемому для данного сигнала п-мерному базису (базисной функции), образованному взаимно параллельными и перпендикулярными (для п > 1 ) элементами исходного сигнала.
Рассмотрим предлагаетуњјй способ на примере сутгнала, кажщй элемент которого является тензором нулевого ранга, т.е. скаляром (такой сигнал образует скалярное поле, которое является частньлл случаем тензорного). В качестве примера скалярных полей можно указать: поле распределения температуры, плотности, электростатического потекщиала, поле яркости и т.д. Есгш сшнал не является скалярньпл полем, дпя дальнейшей декомпозш_црш его необхощтмо разложить на некоторое ограниченное множество скалярных полей. Как уже было показано ранее, двумерный сигнал цифрового изображения в пространстве RGB являегся тензорным полем, причём каждому элементу срп-нала соответствует тензор первого ранга, т.е. трёхмерный векгор, образованный компонентами RGB. Такой сигнал можно рассматривать как совокупность трёх скалярных полей — по отдельности для каждого щСгового компонента.
Дискретную структуру, имеющую размерность, равную размерности исходного сигнала с отличной от нуля амплитудой (высотой), будем называть элементарным всплеском. В направлении выделения протяжённость элементарного всплеска может иметь любое отличное от нуля значение, но не более размера исходного сигнала в этом направлении, по другим направлениям размеры элементарного всплеска равны единице дискретизации соответствующих направлений.
Разделение исходного сигнала Л на спектральные компоненты
происходит начиная с самых протяжённых элементарных всплесков. В каждой
последующей итерации, согласно (5.1), протяжённость элементарного всплеска на
единицу меньше, чем в предыдущей. При выделении из исходного сигнала взаимно
перпендикулярных всплесков учитывается принцип суперпозиции волн, т.е. сложения
их амплитуд в месте пересечения. Поэтому последовательность обхода направлений
для выполнения условия однозначности разложения должна быть одинаковой при
формировании каждого спектрального компонента Sk ![]()
Преобразования многомерного и одномерного сигнала различаются тем, что в первом случае нет заранее выбранного многомерного материнского вейвлета — базисной функции [41]. Такая функция формируется из элементов исходного сигнала, отдельно для каждой спектральной составляющей, совокупность которых образует спектр сигнала (они могуг обладать уникальной конфигурацией и в общем случае не выражаться через взаимные линей-
Спосоо ДеКОМПОЗИЦИИ п-јиерных СИГНаЛОВ по oa3LlCV прямоугольных всплесков 113
![]()
ные преобразования). В таком контексте понятие («материнский вейвлет» может быть применено по отношению к элементарному всплеску.
Приведем обобщённый алгоритм формирования спектральных
составляющих (прямое преобразование) для N -мерного скалярного поля в системе
координат ![]() , -хл, . Используемая в
алгоритме формулировка «определенность К сигнала в заданном направлении»
означает, что подлежащтђ декомпозиции исходный сш-нал тлеет в этом направлении
размер не менее К
, -хл, . Используемая в
алгоритме формулировка «определенность К сигнала в заданном направлении»
означает, что подлежащтђ декомпозиции исходный сш-нал тлеет в этом направлении
размер не менее К
1.
На поле исходного сигнала выбирают начальную величину К = тах(Х1
, ху... , хл,) как значение максимальной протяженности существующих в значений
сигнала (определенности) в направлениях координатных осей „у , х2![]()
(В последующих пунктах алгоритма последовательно в порядке
обхода направлений ![]() выделяют перпендикулярные и параллельные
элементарные всплески. )
выделяют перпендикулярные и параллельные
элементарные всплески. )
2.
Задают начальные координаты выделения из сигнала элементарных
всплесков п![]()
З. Проверяют определённость сигнала в выбранном направлении: если х не меньше К , то переход к п. 4, иначе — к п. 6.
4. Выделяют вдоль направления х элементарные всплески протяженностъю К , всплеск должен удовлетворять следующим условиям:
![]() границами считаются элементы, имеющие либо
нулевое значение, либо отличное его по знаку (в случае знакопеременного
сигнала);
границами считаются элементы, имеющие либо
нулевое значение, либо отличное его по знаку (в случае знакопеременного
сигнала); ![]() амплитуда элементарного всплеска
определяется как минимальное значение амплитуды между границами всплеска;
амплитуда элементарного всплеска
определяется как минимальное значение амплитуды между границами всплеска;
— единичная протяжённость по всем направлениям
положения, кроме х ![]()
5.
Локализованные (см. п. 4) элементарные всплески вычитают из
остаточного сигнала и добавляют к спектральной составляющей Sk в соответствии С
выражением = .fk — Sk ![]()
6. Если , то п = п+1 и переход к п. З, иначе — к п. 7.
7. Если значение К >1, то К = К—1 и переход к п. 2, иначе — окончание алгоритма.
Рассмотренный алгоритм позволяет производить декомпозицию многомерных сигналов по базису прямоугольных всплесков.
Декомпозиция по базису прямоугольных всплесков (5.1) и синтез (восстановление) сигнала из элементов декомпозиции (5.2) образуют систему операций, называемую преобразованием по базису прямоугольных всплесков (далее преобразование по БПВ).
![]()
Рассмотрим примеры декомпозиции одномерного сигнала. Приведенный на рис. 5.2 пример ( И 2 — исходный сигнал, fo — нулевой остаточный сигнал, А — амплитуда сигналов и спектральных составляющих) демонстрирует возможность применения предложенного способа:
![]() если положить, что ось х характеризует
время, то совокупность компонентов у, S , S , S1 в каждый отдельный момент
времени позволяет получить спектр сигнала, при этом не нужно производить
вычисления спектра в сдвигаемом окне, как это требуется при
фурье-преобразовании для получения отображения сигнала на фазовую плоскость;
если положить, что ось х характеризует
время, то совокупность компонентов у, S , S , S1 в каждый отдельный момент
времени позволяет получить спектр сигнала, при этом не нужно производить
вычисления спектра в сдвигаемом окне, как это требуется при
фурье-преобразовании для получения отображения сигнала на фазовую плоскость; ![]() используя
предложенный способ, возможно выполнять декомпозицию всего сигнала или любого
выбранного фрагмента, получая в результате отображение сигнала в фазовое
пространство, а в случае одномерного сигнала — на фазовуко плоскость (х, S ) .
используя
предложенный способ, возможно выполнять декомпозицию всего сигнала или любого
выбранного фрагмента, получая в результате отображение сигнала в фазовое
пространство, а в случае одномерного сигнала — на фазовуко плоскость (х, S ) .
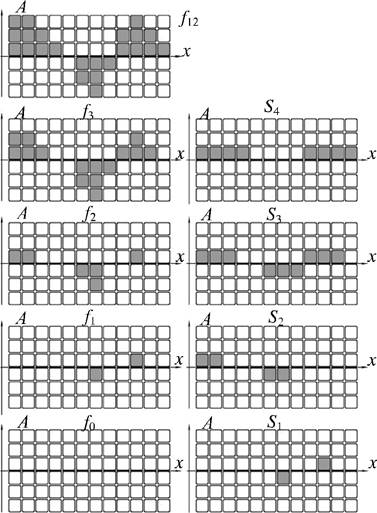
Рис. 5.2. Последовательное разложение на спектр одномерного сигнала
Спосоо ДеКОМПОЗИЦИИ п-јиерных СИГНаЛОВ по oa3LlCV прямоугольных всплесков 115
![]()
![]() На рис. 5.3, 5.4 графически
отображењј результаты декомпозищи исходного цифрового сигнала [ [х] (а) по БПВ
(б), а также с помощью оконного преобразования Фурье (в). Из рисунков видно,
что рассмотренный способ (см. рис. 5.3, б и 5.4, б) позволяег выявить
распределение частот в области определекшя функции f[x] . По сравнению с
преобразованием Фурье локализащи частот выполнена более эффекгивно, особенно —
для меандроподобного сутгнала, это обусловлено тем, чго элементарные всплески
тиеют прюлоутольную форму, следовательно, являются наилучшей мерой для таких
сигналов. лм
На рис. 5.3, 5.4 графически
отображењј результаты декомпозищи исходного цифрового сигнала [ [х] (а) по БПВ
(б), а также с помощью оконного преобразования Фурье (в). Из рисунков видно,
что рассмотренный способ (см. рис. 5.3, б и 5.4, б) позволяег выявить
распределение частот в области определекшя функции f[x] . По сравнению с
преобразованием Фурье локализащи частот выполнена более эффекгивно, особенно —
для меандроподобного сутгнала, это обусловлено тем, чго элементарные всплески
тиеют прюлоутольную форму, следовательно, являются наилучшей мерой для таких
сигналов. лм
а
х
х
х Рис. 5.3. Графическое отображение декомпозиции сигнала f[x] :
красный цвет всплески с положительной амплитудой, синий — с отрицательной
![]() 10 а
10 а
-100 х
х
о
х Рис. 5.4. Графическое отображение декттозиции меандроподобного сигнала f[x] : красный цвет — всплески с положительной амплитудой, синий — с отрицательной 116
![]()
Декомпозицию многомерных сигналов можно рассмотреть на примере двумерных, поскольку двумерный случай отражает практически все особенности преобразования многомерных сигналов и достаточно удобен с точки зрения графической иллюстрации [40].
На рис. 5.5 приведен пример частичной декомпозиции: из двумерного сигнала fl[) выделены элементарные всплески протяжённостью четыре единицы. В соответствии с принципом суперпозиции волн (сложения амплитуд в точке пересечения) выполнена декомпозиция, результат которой зависит от последовательности обхода направлений (х1 ,х2) или (х, , л; ) . Рассмотрены случаи выделения компонентов S 4 и S4х2 очевидно, что конфигурация остаточных сигналов Лм и Лх различается.
|
|
|
|
||||||
|
|
|
|||||||
|
|
|
|
||||||
Рис. 5.5. Частичная декомпозиция двумерного сигнала в пространстве, заданном координатами (Xl , )
На рис. 5.6 представлена полная декомпозиция двумерного
сигнала ![]() Ло , определённого в пространстве с
координатами (-Xl , х2) . Все спектральные компоненты по направлениям
объединены в у, S„ Sl согласно кри-
Ло , определённого в пространстве с
координатами (-Xl , х2) . Все спектральные компоненты по направлениям
объединены в у, S„ Sl согласно кри-
![]() C110COÖ DeKOJM'203LlUUbl n-ult%_)HblX C「nog
110 OULICV」0-71bHblX gcn-WCKOG
C110COÖ DeKOJM'203LlUUbl n-ult%_)HblX C「nog
110 OULICV」0-71bHblX gcn-WCKOG![]()
TepVIK)
paBeHCTBa IIPOT%KéHHOCTVI 3JIeMeHTaPHbIX BCHJRCKOB (丆4 , , 0 ![]() 3
3
![]() e MeHTbI OCTaTOMHOI*O
CHI*Hana; S , So S - 3JRMeHTbI meKOME103MI-lMH).
e MeHTbI OCTaTOMHOI*O
CHI*Hana; S , So S - 3JRMeHTbI meKOME103MI-lMH).

Ha PHC. 5.7 IIpeACTaBJ1eH HCXOÅHbIÜ CHI*H&II (a) H cneKT'P ABYMQHOE0 curHa,J1a (), , 110J1yqeHHb1ü c 110M01UbK) (I)YHKUVIH , )刂= sm x十y Ha
HHTePBaJIe」, y e [一15兀, 15 · ClleKTpaJIbHM IlJIOTHOCTb p paCCHHTbIBaJIaCb KaK OTH()IIIeHIde CYMMbI BCex HeHYJIeBbIX 3JIeMeHTOB, 06pa3YOIIlIdX 3-11eMeHTapHble BCHJRCKM, KOKÅOM CIRKTpaJIbHOü COCTaBJI%K)I-Ileü S. (OTÅeJIbHO 110 HanpaBJIeHH%M ( , y)) K FIJIOI.UaAH BCeü 06JIaCTH, B KOTopoii 3anaHa (I)YHKI.IHH
![]()
f[x, у] . Очевидно, что максимальное
значение р соответствует протяжённости всплесков x=15 и у=15 и периоду
радиальных волн 21![]()
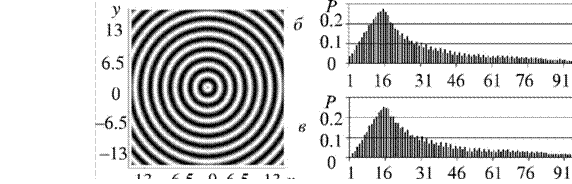 -13 -6.5 О 6.5 13 х
-13 -6.5 О 6.5 13 х
Рис. 5. 7. Исходный сигнал и спектр изображения радиальных волн, полученных способом декомпозиции по БПВ
На рис. 5.8 представлены некоторые варианты конфигурации элементов декомпозиции на примере одномерного сигнала f[x] с амплитудой
А . Приведены четыре варианта сигналов и некоторые возможные способы декомпозиции. Перечёркнутыми стрелками обозначены некорректные варианты декомпозиции (остальными стрелками — корректные).
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
лјпг |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
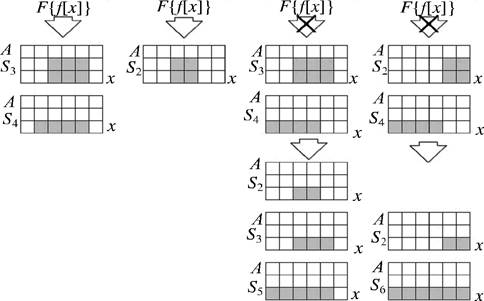
Рис. 5.8. Варианты конфигурации элементов декомпозиции по БПВ
119
![]()
Проанализировав корректные и некорректные варианты декомпозиции [45], можно сделать некоторые обобщения [35] :
![]() менее протяжённый элементарный всплеск
может быть расположен только полносП1ью «над» непрерывным, более протяжённым,
либо над «нулевым» (отсутствующим) всплеском;
менее протяжённый элементарный всплеск
может быть расположен только полносП1ью «над» непрерывным, более протяжённым,
либо над «нулевым» (отсутствующим) всплеском; ![]() между всплесками
должен быть разрыв, минимальное значение которого равно единице дискретизации
сигнала в данном направлении.
между всплесками
должен быть разрыв, минимальное значение которого равно единице дискретизации
сигнала в данном направлении.
Указанные обобщения декомпозиции можно отнести и на случай многомерного сигнала. Согласно второму обобщению, можно ввести понятие «период элементарного всплеска» Т = К + 1 минимально допустимый период повторения элементарных всплесков заданной протяжённости К .
Покажем, что декомпозиция по БПВ является линейным
преобразованием, т.е. обладает свойствами линейности: аддитивностью и
однородностью. Аддитивность обусловлена тем, что суммирование сигналов f[x]+
д[х] в пространственной области эквивалентно суммированию сигналов в
пространственно-частотной области F f[x] + Е д[х] причём при суммировании
сигналов в частотной области необходимо приводить результат суммирования к
конечному виду в соответствии с обобщениями. Аддитивность преобразования
является следствием равенства f[x]+ д[х] F f[x] + F д[х] для каждого
конкретного значения х и одновременно инвариантности декомпозиции по ![]()
Однородность декомпозиции по БПВ F mf[x] = mF f[x] являет-
к
ся следствием: тук [х] = mf[x] где т — рациональное число.
Для п-мерного пространства можно записать свойства линейности преобразования по БПВ: — аддитивность:
![]() f[R'1 ] +F д[Р]
f[R'1 ] +F д[Р]![]()
— однородность:
Стоит отметить, что декомпозиция по БПВ не является инвариантом относительно сдвига сигнала f[Rt ] , поскольку сдвиг исходного сигнала вызовет соответствующее смещение положения элементарных всплесков.
Если сигнал расположен в некотором закольцованном пространстве, т.е. за максимальным значением координаты направления следует минимальная, и таким же образом осуществляется сдвиг исходного сигнала
120
![]()
f[R Il ] , то инвариантом является спектральная плотность р , рассчитываемая как отношение суммы всех элементов каждой спектральной составляющей Sk [Р] к числу всех дискретных элементов, в которой задана функция f[P] .
Покажем, что при преобразовании по БПВ информация об энергии исходного сигнала сохраняется, что в определенном смысле эквивалентно равенству Парсеваля, энергия исходного сигнала может быть определена как:
Е Ef2[x] ,
х из выражения (5.2) следует, что:
2
f2[x] -
ESk[x] ![]()
Раскрывая выражение (5.6) как полиномиальный многочлен второй степени, получаем:
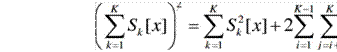
в итоге можно записать:
Ef 2 [x] 
Правую часть, стоящую под общей суммой выражения (5.8), можно представить в виде:
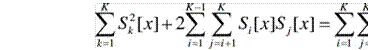
Далее, в соответствии с выражением (5.9) можно отобразить <<таблицу произведения»: на рис. 5.9 приведён пример для случая Sk Заметим, что произведения спектральных составляющих S. х S . = S . х 5. имеют протяжённость наименьшего всплеска min(i, ј) и размерность квадрата амплитуды ( А 2 ). После извлечения корня из суммы произведений S. х S . = S . х Si , выделенных по признаку равных протяжённостей, мы получим взаимно-ортогональные элементы спектральных составляющих:
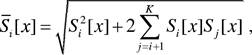
![]()
причём в силу ортогональности (выполняется равенство Парсеваля как обобщение теоремы Пифагора для п-мерного случая) обратное преобразование будет иметь вид:
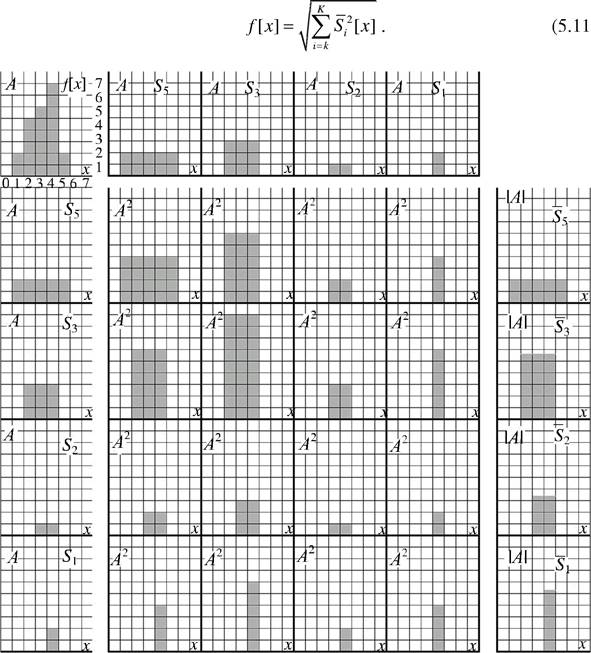
Рис. 5.9. Получение ортогональной формы декомпозиции по БПВ
Преобразуем выражение 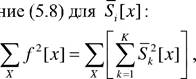 (5.8) для
[х] :
(5.8) для
[х] :
для пространства R '![]()
122
![]()
![]()
Рассмотрим в качестве примера переход к ортогональной форме
S.[x] для сигнала, представленного на рис. 5.9. Вначале рассчитывается
множество элементов спектральных составляющих S = 65 , у, у, S ![]() Далее
формируются элементы произведений S (упорядоченные пары), для которых
выполняется свойство коммугативности S. х S . = S . . Результат произведений
отображён в центральной части рис. 5.9. В качестве примера рассчитаем значения
амплитуд спектральных элементов декомпозиции для 4-го отсчёта (производится
слева, начржая с нуля по оси х , шкала отображена на графике f[x]) S5[4] — 457
=2 S3[4]
Далее
формируются элементы произведений S (упорядоченные пары), для которых
выполняется свойство коммугативности S. х S . = S . . Результат произведений
отображён в центральной части рис. 5.9. В качестве примера рассчитаем значения
амплитуд спектральных элементов декомпозиции для 4-го отсчёта (производится
слева, начржая с нуля по оси х , шкала отображена на графике f[x]) S5[4] — 457
=2 S3[4] ![]() 32
32
![]()
![]() Я [4] — 22 +2-2-2+2-2 -3 +2 -2 -1
Я [4] — 22 +2-2-2+2-2 -3 +2 -2 -1![]()
Результаты расчётов Si [х] приведены в правом столбце (рис. 5.9). Очевидно, что амплитуды исходного сигнала по значениям S. [х] могут быть восстановлены в соответствии с выражением (5.1 1). Далее рассчитаем полную энергию Е в соответствии с (5.12):
![]()
вычисление по выражению (5.5) даёт:
Ef2[x] = 02 +22 +52 +62 +82 +22 +02 +02 = 133 ![]()
х
Вычислительную сложность алгоритма прямого преобразования по БПВ для одномерного случая можно оценить как
где N — размер массива данных.
Для прямого преобразования по сигнала f[R" ] , ограниченного размерами Х1 , Х . Х1 пространства Xl, -и, . . ., хп, в котором задан сигнал, вычислительную сложность можно оценить как:
![]()
Отметим, что преобразования в соответствии с (5.1) и (5.2) могут быть выполнены на множестве целых чисел, что обеспечивает высокое быстродействие и простоту реализации преобразования по БПВ полностью аппаратными средствами.
Области применения способа декомпозиции по БПВ определяют ориентированность на цифровые сигналы, возможность декомпозиции мно-
гомерных сигналов, получение пространственно
определённого спектра сигнала f[R"] , т.е. отображение сигнала в фазовое
пространство. Рассмотренный способ преобразования по был успешно применён в
задачах распознавания образов и анализе частотного спектра графических
изображений.
В современном мире очень остро стоит проблема загруженности каналов связи при значительном времени простоя вычислительных мощностей. Ценность информации заключается, в частности, в ее доступности, что требует оперативной передачи, а по возможности и хранения на локальных ресурсах, потенциал которых в большинстве случаев сильно ограничен. Для поддержания актуальности данных необходимо синхронизироватъ источники информации. Такие факторы требуют разработки оптимальных способов форматирования, а следовательно, передачи информации — не только в пространстве, но и во времени (хранение). Потому возникает задача уменьшения объёма — сжатия (компрессии) [105, 107] — передаваемых данных с сохранением информации.
Эффективность применения методов и алгоритмов сжатия
характеризуется коэффициентом сжатия (измеряется в единицах bpb: bit per bit ![]() бит
на бит):
бит
на бит):
Dout
К![]()
где Dout и Din — объём сжатых (выходных) и исходных (входных) данных ( К <1 означает сжатие информации). Величина, обратная коэффициенту сжатия, фактор сжатия:
![]()
out
Современные методы сжатия информации требуют мощного математического аппарата для анализа специфических особенностей информации с целью повышения её энтропии (т.е. плотности). Методы компактного представления мещдаинформации (изображения, звуковые и видеоданные) базируются на устранении ее избыточности, в том числе исходя из психофизиологических особенностей восприятия.
Под избытком информации понимают ту часть объёма данных, которая может быть исключена специальными методами кодирования при восстановлении из сжатого вида (декодировании).
Стоит отметить, что при снижении избыточности возрастает вероятность повреждения информации, однако сжатая информация может содержать дополнительные данные для восстановления в случае повреждений. Таким образом, можно выделить два принципиально различных класса методов сжатия информации:
![]() без потерь — применяется в тех случаях,
когда любое искажение информации при декодировании недопустимо, пример —
управляющие кодовые последовательности (исполняемые коды), текстовые данные,
некоторые виды изображений, результаты некоторых исследований, наблюдений.
Сжатие без потерь обеспечивают алгоритмы Шеннона—Фано, Зива
без потерь — применяется в тех случаях,
когда любое искажение информации при декодировании недопустимо, пример —
управляющие кодовые последовательности (исполняемые коды), текстовые данные,
некоторые виды изображений, результаты некоторых исследований, наблюдений.
Сжатие без потерь обеспечивают алгоритмы Шеннона—Фано, Зива ![]() Лемпела
(LZ78), Хаффмана, арифметического кодирования, словарного кодирования и др. ;
Лемпела
(LZ78), Хаффмана, арифметического кодирования, словарного кодирования и др. ; ![]() с
ПОП1еРЯТШ — применяется в случаях, когда частичная потеря информации допустима
[17], например, фотографии, звуковые и видеоданные. Соответствующие алгоритмы
обычно строятся на анализе информации для выявления пространственных и (или)
частотных характеристик сигнала с последовательным исключением некоторой части
информации.
с
ПОП1еРЯТШ — применяется в случаях, когда частичная потеря информации допустима
[17], например, фотографии, звуковые и видеоданные. Соответствующие алгоритмы
обычно строятся на анализе информации для выявления пространственных и (или)
частотных характеристик сигнала с последовательным исключением некоторой части
информации.
Для оценки различий восстановленного после сжатия с потерями информации f[x] и исходного r[x] сигналов используют несколько критериев :
— среднеквадратическая ошибка (Меап Square Error, MSE):
— пиковое отношение сигнал/шум (Реак Signal to Noise Ratio, PSNR): тау. (1 .f[x] D
PSNR =![]()
MSE
— отношение сигнал/шум (Signal to Noise Ratio, SNR):
SNR =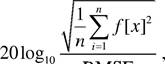
RMSE
где RMSE= MSE ![]()
Существуют и другие критерии ошибок. Отметим, что в каждом конкретном случае вопрос о допустимости частичной потери информации и её величине может решаться отдельно.
Различная природа цифровых сигналов определяет их особенности. Принято выделять сигналы, основной объем информации в которых сосредоточен либо в частотной, либо в пространственной области. Информация звукового сигнала преимущественно сконцентрирована в частотной области, графического изображения — в пространственной. При таком подходе необходимо учитывать специфику конкретного сигнала или некоторой группы сигналов. Существуют сигналы, основная информация которых сосредоточена в пространстве, например, дельта-функция при чёткой
126
![]()
пространственной локализации имеет неограниченный частотный спектр. В частотном диапазоне сконцентрирована превалирующая часть информации некоторых графических изображений, к примеру, графиков волновых поверхностей. Говоря о преимущественной области концентрации информации, часто подразумевают специфику восприятия информации человеком или техническим устройством. Например, на восприятие человеком звука больше влияет частота, чем фаза, для технических средств — наоборот, например, эхолот по разности фаз (запаздыванию) может определять расстояние, а по сдвигу частоты, на основании эффекта Допплера — скорость объекта отражения.
Частотные характеристики сигнала могут быть получены с помощью декомпозиции (Фурье, вейвлет и др.), пространственные — с помощью геометрической интерпретации сигнала, определения его производных, вейвлет-анализа, оконного преобразования Фурье.
Используя особенности концентрации информации, можно исключить некоторую («избыточную» часть из частотного или пространственного описания сигнала, что приведет к допустимым искажениям.
Методы получения частотных и пространственных характеристик и исключения некоторой <<избыточной>> части позволяют синтезировать компактную форму информационной составляющей сигнала. Многие способы перевода информации в компактную форму не обладают универсальностью: конкретный метод получения компактной формы, применимый к одному сигналу или группе сигналов, может быть малоэффективен для других сигналов. Неслучайно в современном мире цифровой обработки сигналов столь много разнообразных форматов компактного хранения данных, это обусловлено не только сражением за коммерческие интересы корпораций на рынке путём ограничения прав на использование с помощью механизмов патентного права, монополизации производства программного и аппаратного обеспечения, но и особенностями самих сигналов.
Значительный интерес для разработки способов компактного хранения представляют фотографии, видеофильмы, сигналы цифрового телевидения и прочие многомерные сигналы, сопряжённые с передачей графической информации. В большинстве случаев графические сигналы занимают существенные ресурсы памяти при значительном количестве избыточной информации. Применение только статистических способов сжатия (таких как алгоритм Хаффмана, арифметическое кодирование) или сжатия серий в большинстве случаев не даёт существенного эффекта. Поэтому применяют различные совокупности способов сжатия, часть которых основана на преобразовании передаваемой сигналом информации к компактной форме путем анализа сигнала как поля (спектральный анализ, анализ геометрической структуры, корреляционный анализ, дифференциальный анализ и др.).
Рассмотрение цифровых сигналов как полевых структур позволяет использовать численные методы расчёта полей в их анализе и преобразовании. Основы методов частотного анализа цифровых сигналов, в том числе с целью последующего сжатия, рассмотрены в классической литературе по ЦОС [85, 95, 1 12, 14], поэтому обратим внимание на пространственный анализ сигналов. Существует ряд способов формирования компактного вида цифровых сигналов с помощью анализа пространственной структуры. В частности, для получения компактной формы изображений применяют векторизацию, т.е. в ходе морфологического анализа изображения (в большинстве случаев это достаточно сложная вычислительная задача) выявляют графические примитивы (прямые, окружности, прямоугольники и т.д.). Наиболее эффективно таким способом можно сжимать техническую графику (чертежи, эскизы и др.) и некоторые виды изображений, объекты, которых имеют чёткие границы и относительно простые формы. Следующим способом является фрактальное сжатие, основанное на том, что изображение можно представить более компактно с помощью коэффициентов системы итерируемых функций (фракталов) [171]. Фрактальное сжатие очень затратно с точки зрения вычислений, но на некоторых образцах изображений показывает очень хорошие результаты. Известен способ формирования из изображения с помощью метода <<brush f1re» (лесной пожар) скелета многоугольника толщиной 1—2 пиксела — диаграммы Вороного [110]. Этот способ таюке достаточно затратен и не получил широкого распространения. Существуют и друтие способы пространственного анализа цифровых сигналов с целью получения компактной формы.
Рассмотрим способ, основанный на анализе дифференциальной структуры цифрового сигнала. Под дифференциальной структурой подразумеваются производные, обычно до третьего порядка, цифрового сигнала, для многомерных сигналов — частные производные. В самом простом случае дифференциальное кодирование строится следующим образом: для элементов цифрового сигнала f[x], х е Х , вычисляется ряд дельта-кода
![]() — + 1] — Г [х], х е (Х
—1) . В силу того что разность значений соседних элементов исходного сигнала
f[x] обычно существенно меньше диапазона его значений, полученный ряд может
быть эффективно сжат [105]. Для восстановления исходного сигнала необходимо
кроме ряда дельта-кода знать начальные условия. На рис. 6.1 получена диаграмма
дельта-кода, в табл. 6.1 — ряды численных значений. Очевидно, что значения
дельта-кода имеют меньшую амплитуду и для их кодирования потребуется меньшее
— + 1] — Г [х], х е (Х
—1) . В силу того что разность значений соседних элементов исходного сигнала
f[x] обычно существенно меньше диапазона его значений, полученный ряд может
быть эффективно сжат [105]. Для восстановления исходного сигнала необходимо
кроме ряда дельта-кода знать начальные условия. На рис. 6.1 получена диаграмма
дельта-кода, в табл. 6.1 — ряды численных значений. Очевидно, что значения
дельта-кода имеют меньшую амплитуду и для их кодирования потребуется меньшее
![]()
число разрядов, кроме того, они чаще повторяются, следовательно, к ним может быть применено статистическое кодирование.

Рис. 6.L а — исходный сигнал, б — дельта-код
Но далеко не все типы сигналов могуг быть успешно сжаты с помощью дельта-кода, дело в том, что эффективно могуг сжиматься достаточно гладкие функции, к примеру, полученные в результате оцифровки реальных физических сигналов: звук, фото- и видеоизображения и т.д.
Таблица 6.1. Значения функции f[x] и её дельта-кода d[x]
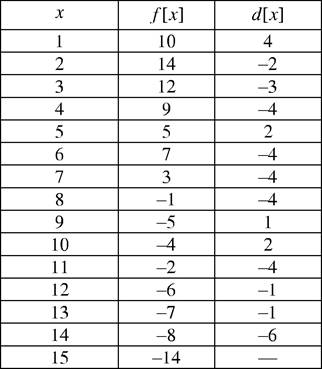
Большинство сигналов, полученных в результате регистрации реальных физических процессов, могут быть описаны, с той или иной степенью точности, уравнениями, в частности, дифференциальными.
Рассмотртл основњје тигм уравнений математической физики с частными производными второго порядка для дву- и трёхмерных пространств (х, у— координаты пространства, t — координата времени) [97, 103]. Волновые уравнения:
![]()
ГР Гх2 Гу2
К уравнениям этого типа приводит рассмотрение колебаний газа, электромагнитного поля в проводнике, поперечных колебаний струны, продольных — стержней, кругильных — валов и т.д. Один из вариантов эквивалентного решения (6.6) получен при помощи гармонического анализа в 1824 г. Ж. Фурье. Отметим, что не все процессы, квалифицируемые современной физикой как волновые, описываются приведёнными волновыми уравнениями, примерами может быть распространение волн в нелинейной среде, солитоны и др.
Уравнения теплопроводности,
иии уравнения Фурье: ГГ (Х, t) 2![]()
![]() Гх2 af(x, y,t)ГУ (х, y,t) ГУ
(х, y,t)
Гх2 af(x, y,t)ГУ (х, y,t) ГУ
(х, y,t)
6х2 Гу2 ![]()
К этим уравнениям приводит рассмотрение процессов теплопроводности, фильтрации жидкости и газов в пористой среде, некоторые задачи теории вероятностей и т.д.
Уравнения Лапласа и Пуассона:
![]()
Гх2 Гу2
Уравнения этого типа позволяют выполнять моделирование электромагнитных полей, стационарных и переходных тепловых состояний, задач гидродинамики, диффузии и т.д. Уравнения Пуассона (6.10) и (6.11) при равенстве правой части нулю (для всех значений х, у, z ) обращаются в уравнения Лапласа.
Таким образом, большинство процессов (стационарных и динамических), которые являются первичными источниками сигналов, могут быть аналитически описаны дифференциальными уравнениями. Важно заметить,
![]() 130
130
что дифференциал и производная функции, в соответствии с теоремой о почленном дифференцировании [67], связаны с рядом Фурье.
Теорема. Пусть функция f(x) и все её прошвоДные до некоторого порядка т (т — целое неотрицательное число) непрерывны на сегменте [—тс, л] и удовлетворяют условиям:
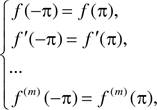
п1огДа тригонометрический
ряд Фурье функции f(x) можно т раз почленно Дифференцировать на сегменте [—я,
тс] ![]()
Можно записать выражение, связывающее производную порядка р Ф=1, 2,. т) и члены ряда Фурье функции f(x) [67]:
![]() (х) = Ак sin
Кх— + вк cos Кх—
(х) = Ак sin
Кх— + вк cos Кх— ![]() тср
тср ![]()
2 2 где Ак, Вк — коэффициенты ряда Фурье функции f(x) (4.25). Из уравнения (6.12) следует, что производные более высокого порядка больше зависят от высокочастотных составляющих ряда Фурье.
Особая значимость теоремы (6.12) состоит во взаимозависимости гармонического ряда отображения функции и её производной, это свойство обеспечивает предпосылки для композитного сжатия цифровых сигналов, когда один метод позволит производить сжатие в пространстве-времени и частоте одновременно. Вейвлет-анализ, как и оконное преобразование Фурье, интересен тем, что позволяет получить не только частотную характеристику, но пространственную локализацию спектра.
Обычно, говоря о сжатии битовых пос:ледовательностей, имеют в виду способы сжатия без потерь. В общем случае, поскольку цифровой сигнал можно рассматривать как битовую последовательность, любой способ сжатия, в том числе и с потерями, можно соотносить со способом сжатия битовых последовательностей.
Особенно эффективно происходит сжатие битовых полей, содержащих значительное число повторяющихся элементов (0 или 1) или серий (упорядоченных множеств элементов — кортежей). Сжатие битовых последовательностей может быть эффективно применено для битовых матриц изображений, звуковых данных, текстовых сообщений, управляющих кодов.
Можно выделить два класса способов сжатия битовых последовательностей: с учётом и без учёта статистических особенностей. Для способов первого класса, к которым относятся коды Шеннона—Фано, код Хафмена, арифметическое кодирование и др., требуется предварительный анализ частоты повторения некоторых серий с целью формирования кодовых таблиц. Недостаток этих способов заключается в необходимости статистического анализа данных и передачи кодовой таблицы вместе с данными. Ко второму классу способов сжатия битовых последовательностей относят способы, не учитывающие статистические закономерности распределения элементов данных в сигнале.
В качестве примера рассмотрим сжатие битовых серий на основе
системы счисления Фибоначчи ![]()
Напомним, что префиксным называется код, ни одно слово которого не может быть начальной строкой другого слова кода. Суффиксным кодом называют такой, ни одно слово которого не может быть конечной строкой другого слова кода [6].
Ряд Фибоначчи образован рекуррентной последовательностью вида:
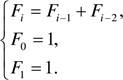
Система счисления на базе чисел Фибоначчи построена следующим образом: любое неотрицательное число представлено единственным образом при помощи упорядоченной последовательности единиц и нулей, каждый элемент такой бинарной последовательности соответствует числу из ряда Фибоначчи, причём число может быть преобразовано в десятичную систему счисления при помощи выражения:
![]() -EqFl (6.14)
-EqFl (6.14)
где а элемент последовательности в соответствующем разряде записи числа. Ещё одной важной особенностью, исключающей несколько вариантов записи одного численного значения, является недопустимость единиц в соседних разрядах, т.е. в соответствии с рекуррентным выражением (6.13) при наличии двух идущих подряд единиц происходит перенос единицы в старший разряд. Например, для числа, записанного при помощи
![]() Леонардо Пизанский (2 1170—1250, Пиза) — первый
крупный математик средневековой Европы, наиболее известен под именем Фибоначчи.
Леонардо Пизанский (2 1170—1250, Пиза) — первый
крупный математик средневековой Европы, наиболее известен под именем Фибоначчи.
132
![]()
системы счисления Фибоначчи вида 10011001 (младший разряд справа), правильной будет запись 10100001 .
Таблица 6.2. Соответствие записи чисел от 0 до 7 в различных системах счисления
|
Число в десятичной системе счисления |
Число в двоичной системе счисления |
Образующие числа Фибоначчи |
Число в системе счисления Фибоначчи |
|
0 |
0 |
|
0 |
|
1 |
1 |
|
|
|
2 |
10 |
|
10 |
|
|
|
|
100 |
|
4 |
100 |
|
lOl |
|
5 |
101 |
|
1 ООО |
|
6 |
110 |
F(l) |
|
|
7 |
111 |
|
|
|
8 |
1000 |
|
10000 |
|
9 |
|
|
lOOOl |
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
100000 |
|
14 |
|
|
100001 |
|
15 |
|
|
lOOOlO |
Следует отметить, что существует несколько разновидностей систем счисления, построенных на ряде Фибоначчи, в которых возможны идущие подряд единицы.
Отсутствие в записи числа идущих подряд единиц ( 11 ) позволяет создать систему кодирования — префиксную или суффиксную — в зависимости от положения млащиего разряда (справа или слева) и выбрать начало последовательности данных сообщения. Запись числа в системе счисления Фибоначчи в старшем разряде (при отсечении незначащих разрядов) всегда будет иметь единицу (кроме записи нулевого значения), младший разряд может содержать единицу или нуль. Таким образом, для образования (префиксной или суффиксной) последовательности конкатенацию единицы необходимо производить к старшему разряду. Такая система кодирования может быть применена для сжатия битовых серий [145]. Рассмотрим пример. Пусть имеется битовая последовательность
![]()
соответствующий ей префиксный код, согласно табл. 6.2, будет иметь вид:
![]()
Поскольку в исходном сообщении присутствуют последовательности единиц и нулей небольшой протяжённости, сжатие незначительно.
Длину кода на базе системы счисления Фибоначчи можно оценить в соответствии с выражением:
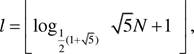
где N — число
повторяющихся битов. Сжатие будет тем более эффективным, чем больше
протяжённость повторяющихся серий битов последовательностей. Средняя длина кода
для последовательности серий протяжённостью ла , N2,![]()
![]() —Е $Nl+1
—Е $Nl+1 ![]()
![]() -(1+6)
-(1+6)
![]() 2
2
Условие эффективности сжатия можно записать следующим образом:
$Nl+1 - Nl < О![]()
![]() -(1+3)
-(1+3)
В соответствии с выражением (6.1) получим коэффициент сжатия
к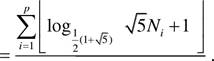 (6.18)
(6.18)
Р
В пространственной и частотной областях представления некоторого сигнала плотность информации может существенно различаться. Многие методы сжатия с потерями исключают часть информации из частотной, но не из пространственно-временной области. Из разнообразных цифровых сигналов, в частности изображений, можно выделить такие, для которых исключение информации из пространственной области обеспечивает результат не хуже, а в некоторых случаях лучше, чем исключение информации из частотной области. Специфика предлагаемого метода состоит в исключении некоторой информации из пространственной или пространственно-временной области. Многопоточность современных вычислительных средств позволяет реализовать рассматриваемый метод с приемлемым быстродействием.
Введем определения некоторых понятий. Совокупность условий, описывающих состояние системы в пространстве на границах и в некоторых внутренних областях, называют граничными условиями; совокупность, описывающая состояние системы в некоторые моменты времени (обычно начальные t = 0), называется начальными УСЛОВИЯМИ. Совокупность граничных и начальных условий называется краевыми условиями.
Пусть в области W задан сигнал f(R") , предположим, что в некоторой части заданной области U [ ( Р) удовлетворяет дифференциальному уравнению вида:
![]()
где А — дифференциальный оператор, жР) — функция правой части. Краевые условия p(W) заданы в области В таким образом, что
U U В = W . Функцию p(R") будем называть паттерном исходного сигнала f(R 11 ) . Используя уравнение (7.1) и паттерн сигнала p(R IL ) , можно с заданной точностью восстановить f(RJ ) в области U . Таким образом, анализ дифференциальной структуры сигнала f(R") сводится к выбору анализирующего уравнения (или системы уравнений) (7.1) и отыскании паттерна p(R 'l ) .
Отметим, что определение краевых условий путём анализа дифференциальной структуры является обратной задачей численных методов.
Cuamue u cunme3 JUHOZOJIUPHbZX cuznanog
PaccM0Tpurvr (bopvmp0BaHue naTTepHa
Ha npvmepe 0AH0MepHoro curHaJia f [X] . ![]() HTO f (X) eCTb HenpePb1BHb1vY1
np006pa3 AUCKPeTHOFO 06pa3a HeKOToporo CHEHaJ1a f[x] , 3TOM OH OITHCb1BaeTCA BO
Bcex qacTqx 06J1aCTV1 U ypaBHeHuervr:
HTO f (X) eCTb HenpePb1BHb1vY1
np006pa3 AUCKPeTHOFO 06pa3a HeKOToporo CHEHaJ1a f[x] , 3TOM OH OITHCb1BaeTCA BO
Bcex qacTqx 06J1aCTV1 U ypaBHeHuervr:
d2f(x)
d.x2
Elepexozll K
AHCKpeTHOMY 06pa3Y f[xz.] m nonaraq, HTO OH 3anaH Ha ceTKe xo, xv...,x eW c
paBHOMePHb1M marorvf h ![]() i e 0, ...,n —1 , Bcex e U MO)KHO 3anmcaTb ypaBHeHme (7.2) B
BHAe:
i e 0, ...,n —1 , Bcex e U MO)KHO 3anmcaTb ypaBHeHme (7.2) B
BHAe:
![]()
dx2 h
![]()
h2
0TKYÅa
![]()
2
BblHHCJUITb llaTTepH p[Xi] 6yneM 110 cneÅYH)1ueü cxeMe.
l. FIOJIOXHM, I-ITO BO Bceü 06J1aCT'V1
W BCe 3HayeHH% naTTepHa paBHb1 3HaqeHH%M cm-Hana: p[xz. ]![]()
2. Bb16epeM HeKOTopoe 1-1MCJ10Boe 3HaqeHme A -Rpumepun, corJ1acH0 KOToporvry 6Y)xeM HCKJ1roqaTb 3J1eMeHTb1 naTTepHa.
3. C yqéT0M (7.4) Bcex f[xz.] B 06naCTV1 W BblHHCJIMM 3HaqeHmn:
ecJ11å ycJ10Bue s HCTHHHO, TO 3HaqeHne p[Xi] (AWI COOTBeTCTBYK)1-qero
![]() ) HCKmoqaeTC% naTTepHa, B HPOTHBHOM cnyqae 3JTewreHT OCTaéTc% B
naTTepHe.
) HCKmoqaeTC% naTTepHa, B HPOTHBHOM cnyqae 3JTewreHT OCTaéTc% B
naTTepHe.
B pe3YJ1bTaTe Bb1110JIHeHuq YKagaHHoÜ 110CJRÅOBaTeJTbHOCTV1 neÜCTBVIÜ 110J1y-1eH naTTepH cHPHaJTa Jf [x.] . I-rpmMep (bopMHP0BaHH}1 naTTepHa mpHBeneH B JIVICTHHre 7.1, Ha pnc. 7.1 npeACTaBJ1eHb1 pe3YJ1bTaTb1 Bb1110JIHeHHA nporpaMMb1.
![]()
Иистинг 7.1. Формирование паттерна (MATLAB)
![]()
c1ear а 11; удаление переменных c10s a
а 11; 0 закрыти а вс.— х окон ![]() 0 очистка командного окна
0 очистка командного окна
![]() D задание исходного сигнала
D задание исходного сигнала
![]() -1 -2 -3
-1 -2 -3![]()
patt=data; 0 значения пашт а рна равны знач а ниям сигнала
de1=O . 1; д—кришерий для исключения значений из патш а рна
![]() D цикл исключения некоторых значений
из пашт а рна
D цикл исключения некоторых значений
из пашт а рна
for 1=2 : 1 : (l a ngth (data) —1 )
s=O.5* (data (1+1) +data Е—1) ) ;
if (abs (s—data < del)
![]() о если
условие истинно
о если
условие истинно
![]() о исключение из паттерна patt
о исключение из паттерна patt ![]() elseif (patt (i) =
elseif (patt (i) =![]()
![]() о исключение неоднозначности patt (1) =del; end end
о исключение неоднозначности patt (1) =del; end end ![]() графики результатов расчётов figure;
subp10t (2, 1 , 1 ) ; stairs (data) ;
графики результатов расчётов figure;
subp10t (2, 1 , 1 ) ; stairs (data) ; ![]() (data) ' ) subp10t (2, 1 , 2 ) ;
stairs (patt) ; tit1e ( ' I1aTTepH (patt) ' )
(data) ' ) subp10t (2, 1 , 2 ) ;
stairs (patt) ; tit1e ( ' I1aTTepH (patt) ' )
![]()
![]() а
а
6
Рис. 7.1. Результаты выполнения программы (листинг 7.1 ).
а — исходный сигнал, б — паттерн
Очевидно, что паттерн (рис. 7.1, б) содержит значительно больше равнозначных элементов, чем исходный сигнал, это позволяет его эффективнее сжать. Приравненное нулю значение элемента паттерна служит признаком его исключения (patt (i) -0 ; ), такой принцип может привести к неоднозначности, если, например, в исходном сигнале присугствуют нулевые
значения, — ведь для восстановления сигнала необходимо точно знать, принадлежит конкретный элемент паттерна краевым условиям или нет. Избежать неоднозначности трактовки паттерна поможет изменение значений отсчетов в исходном сигнале. Допустимый форматом данных выход значений сигнала из определенного диапазона — признак того, что элемент не является частью краевых условий. В программе (см. листинг 7.1) неоднозначность исключается путём изменения нулевых значений сигнала (нулей), вошедших в патгерн, на величину д -критерия (del).
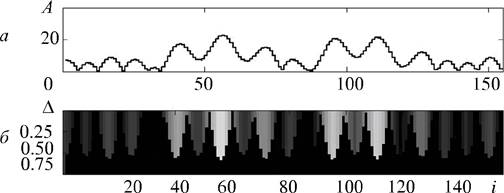
Рис. 7.2. Зависимость поля паттернов сигнала от Д-критерия. а — исходный сигнал, б — поле паттернов
Паттерн, содержащий относительно небольшое число элементов, являющихся краевыми условиями, позволяющими вполне точно восстановить исходный сигнал, может быть получен только для гладких функций. Следовательно, применение данного способа с целью сжатия шумоподобных сигналов неэффективно.
Изменяя порядок производных дифференциального оператора А
(7.1) и выбирая некоторые функции u(Rt ) , можно влиять на качество восстановления сигнала и число исключённых из него элементов, т.е. размер патгерна, что, в свою очередь, скажется на эффективности сжатия.
Восстановление исходного сигнала осуществляется мепюДOМ конечных разностей (МКР) при помощи соотношения, выбранного в качестве анализирующего дифференциального уравнения, и краевых условий, содержащихся в паттерне. Программа (листинг 7.2) и результаты её выполнения (рис. 7.3) иллюстрируют возможность анализа дифференциальной структуры с формированием паттерна и последующего восстановления сигнала.
Иистинг 7.2. Формирование паттерна и восстановление сигнала (MATLAB)
![]()
c1ear а 11; удаление переменных c10se
а 11;![]() 0 закрытие всех окон
0 закрытие всех окон
![]() 0 очистка командного
окна задание исходного сигнала х data abs (10*sin (х) +8*sin (2 * х) +7*cos (12
* х) ) ,
0 очистка командного
окна задание исходного сигнала х data abs (10*sin (х) +8*sin (2 * х) +7*cos (12
* х) ) ,
% формирование паттерна patt data;
значения паттерна равны значениям сигнала de1 д —критерий для исключения
значений из паттерна ![]() о цикл исключения некоторых значений из
патт а рна for i=2 : 1 : (1 a ngth (data) —1 )
о цикл исключения некоторых значений из
патт а рна for i=2 : 1 : (1 a ngth (data) —1 )
if (abs (s—data < de1) ![]() о
если условие истинно, исключение из патт а рна patt
о
если условие истинно, исключение из патт а рна patt ![]() e1seif (patt
(1) —
e1seif (patt
(1) — ![]() patt (i) =de1; end end б восстановление
сигнала по пашт а рну методом конечных разностей resu1t patt ;
patt (i) =de1; end end б восстановление
сигнала по пашт а рну методом конечных разностей resu1t patt ;
for 1=2 : 1 : (1 a ngth (data) —1 ) if (patt (1) 0) resuIt (i) =O . 5* (r a sult С +1) +r=sult Е—1) ) ; end end end
![]() D графики результатов расч а тов
figure; subpIot (2, 1, 1 ) ; stairs (data) ; title ( ' Исходный сигнал (data) '
) subp10t (2, 1 , 2 ) ; stairs (patt) • title ( ' Паттерн (patt) ' ) ; figure;
subp10t (2, 1 , 1 ) ; stairs (data) ;
D графики результатов расч а тов
figure; subpIot (2, 1, 1 ) ; stairs (data) ; title ( ' Исходный сигнал (data) '
) subp10t (2, 1 , 2 ) ; stairs (patt) • title ( ' Паттерн (patt) ' ) ; figure;
subp10t (2, 1 , 1 ) ; stairs (data) ;
title ( ' Исходный сигнал (data) ' ) subp10t ( 2 , 1 , 2 ) ; stairs (result) • title ( ' Восстановленный сигнал (result)
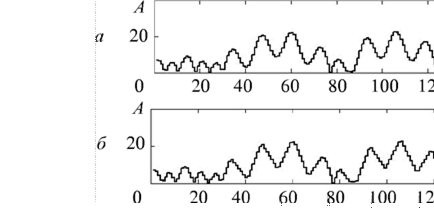
В 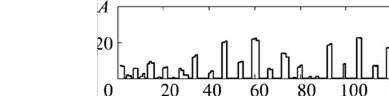
Наиболее часто необходимо применять операции сжатия к так называемому медиаконтенту: статическим и динамическим (видео) изображениям, аудиоданным и др. В последнее время активно развиваются различные форматы видеоданных, на базе которых синтезируются объёмные видеосцены [1 08, 123]. Цифровые изображения — это один из видов сигналов, к которым можно эффективно применять сжатие на основе анализа дифференциальной структуры. Многие изображения содержат значительные поля градиентных переходов (цвета, яркости), контрастные границы объектов (статические изображения — границы в пространстве, динамические — во времени и в пространстве). Соседние кадры видеопоследовательностей обычно различаются незначительно. Границы объектов, содержащихся в изображениях, можно рассматривать как краевые условия, а поля плавных переходов — как области, удовлетворяющие выбранному анализирующему дифференциальному уравнению.
В качестве примера рассмотрим все этапы сжатия и восстановления статического изображения при помощи анализа дифференциальной структуры [38, 39].
Сжатие изображения:
![]() выбор дифференциального анализирующего
уравнения (или системы) и цветового пространства для формирования паттерна;
выбор дифференциального анализирующего
уравнения (или системы) и цветового пространства для формирования паттерна; ![]() при
необходимости — преобразование цветового пространства;
при
необходимости — преобразование цветового пространства;
— формирование паттерна (граничных условий);
— сжатие паттерна без потери информации и формирование дополнительных данных для восстановления сигнала. Восстановление изображения:
![]() декомпрессия паттерна и дополнительных
данных;
декомпрессия паттерна и дополнительных
данных; ![]() восстановление изображения с помощью
выбранного при сжатии анализирующего щфференциального уравнения (системы) с
учётом граничных условий, содержащихся в паттерне;
восстановление изображения с помощью
выбранного при сжатии анализирующего щфференциального уравнения (системы) с
учётом граничных условий, содержащихся в паттерне;
— при необходимости — преобразование цветового пространства.
Подробно рассмотрим каждый этап. В качестве уравнения (системы) для формирования паттерна и последующего восстановления двумерного сигнала изображения f[x, у] , заданного на плоскости ХОУ , выберем уравнение Лапласа, хорошо описывающее плавные переходы в областях между граничными условиями:
Гх2 Гу2 ![]()
После выбора шаблона дифференцирования для функции f[x, у]
(рис. 7.4) и перехода к дискретной форме, с
учётом шага сетки![]()
и выражения (7.3), уравнение (7.5) можно записать в виде:
Гх2 Гу2
f[x + Ах, у] — 2f[x, у] + f[x — Ах, у] дх2
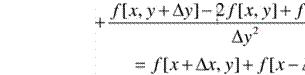
+f[x, у + Ау] + f[x, у — Ду] — 4f[x, у] = 0, откуда
![]()
1 ![]() f[x + Ах, у] + f[x — Ах, у] + f[x, у
+ Ау] + f[x, у Ау]
f[x + Ах, у] + f[x — Ах, у] + f[x, у
+ Ау] + f[x, у Ау]![]()
4
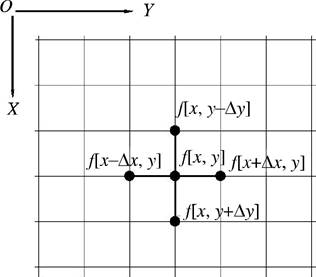
Рис. 7.4. Шаблон дифференцирования функции f[x, „у]
При использовании предлагаемого метода сжатия выбранный шаблон (см. рис. 7.4) показал достаточно высокую эффективность.
Далее необхощдмо выбрать цветовое пространство. Практические исследования показали, что наиболее компактный паттерн, и следовательно наиболее высокую степень сжатия, в зависимости от специфики изображения можно получить в цветовом пространстве RGB и YCbCr, см. выражения (1.11) и (1.12). Цветовое пространство RGB адаптировано к особенностям восприятия зрительной системы человека, оно наилучшим образом передаёт специфику цветового градиента, а YCbCr может более эффективно обеспечить сохранение границ объектов изображения при некоторой потере цветовой информации.
Формирование паттерна является ключевым этапом сжатия изображения, от этого зависит качество восстановленного сигнала и в конечном итоге — эффективность сжатия. Отметим некоторые особенности, выявленные при экспериментах с различными подходами к формированию паттерна. Наиболее высокое качество восстановленного сигнала удаётся получить при генерации паттерна, каждому значащему элементу которого ставятся в соответствие все компоненты цветового пространства (т.е. с точки зрения положения элементов граничных условий конфигурация паттернов всех цветовых слоёв одинакова), таким образом, цвет граничных элементов соответствует цвету исходного изображения. Поскольку паттерны всех цветовых компонентов (слоёв) совпадают, возможно сжать последовательность серий не значащих элементов одного слоя и затем использовать его как шаблон для восстановления других слоев, что позволяет существенно повысить фактор сжатия.
В паттерн обязательно включаются граничные пикселы, для статического изображения это две вертикальные строки — справа и слева, и две горизонтальные сверху и снизу. Для исключения элементов из паттерна сравнивают Д -критерий и абсолютную величину разности фактического значения сигнала в точке [х, у] и вычисленного по (7.7). Причём для каждого компонента цветового пространства можно выбрать значение Д-критерия и, следовательно, количество исключённой информации о дифференциальной структуре сигнала (число сохранённых значащих элементов в паттерне для каждого цветового компонента одинаковое).
В листинге 7.3 приведён пример кода формирования паттерна. Двумерный массив data [ ] [ ] содержит исходное изображение, каждый элемент массива имеет тип IImage, паттерн формируется в массиве pattern каждый элемент массива имеет тип C010rSpace. Изначально в pattern [ 1 [ 1 полностью копируется изображение data [ ] [1, далее в двух циклах (листинг 7.3) часть элементов исключается (исключением считается приравнивание к нулю). Переменные (delLo, de1Av, da 1Hi) содержат значения д-критериев сравнения для исключения элементов из каждого цветового канала и формирования паттерна. Необходимо маскирование (корректировка) изначально нулевых значений, содержащихся в изображении и скопированных в паттерн, для того чтобы отличать их от исключённых из паттерна. Разность фактического значения сигнала в точке [х, у] и вычисленного по (7.7) рассчитывается по формуле:
![]()
причём умножение на четыре в программе производится с помощью поразрядного сдвига (на два бита влево), замена операции деления (7.7) на поразрядный сдвиг (7.8) позволяет существенно сократить время вычислений. От величины д -критериев зависит число исключённых из паттерна элементов, а значит степень сжатия изображения. Чем больше Д-критерий для цветового канала, тем больше значений будет исключено.
Листинг 7.3. Фрагмент программы формирования паттерна полноцветного изображения (С++)
![]()
/ / цветовая палитра
/ / покомпонентное представление, в скобках указаны компоненты
/ / палитр (RGB) и (YCbCr) соответственно struct C010rSpace {
|
uchar byteLo; / / компонент младший байт |
(Lower) |
|
uchar byteAv; / / компонент средний байт |
(Averaqe) (G) (СЬ) |
|
uchar byteHi; / / компонент старший байт |
(Hight) |
|
/ / структура для сохранения цветов в ВИДО |
int |
/ / один условный ” байт ” соответствует переменной шипа int struct IImaqe {
|
int iLo; int iAv; int iHi ; for (iy=1; |
/ компонент младший ” байт ” (Lower) / компонент средний ” байт ” (Average) (G) (СЬ) /
компонент с арший ” байт ” iy<Ysize; iy++) |
/ / расчёт разностных элементов для сравнения с критерием int sLo=abs (data [iy—1] [ ix] . iLo+data [iy+1j [ixj . iLo+ data [iy] [ix—1] . iLo+data [iyj [ix+1j . iLo—
(data [ iy] [ ix] . iAv<<2) ) ; int sHi=abs (data [iy—1] [ ix] . iHi+data [iy+1j [ixj . iHi+ data [iy] [ix—1] . iHi+data [iyj [ix+1j . iHi— (data [iy] [ix] . iHi<<2 ) ) ;
/ / сравнение разностных элементов с критериями / /
исключение из паттерна if (sLo<=de1Lo sAv<=de1Av sHi<=de1Hi)
![]()
/ / установка признака исключения элемента из паттерна / / (не являются краевыми условиями) pattern [iy] [ix] .byteLo 0; pattern [iy] .byteAv—O; pattern [1 у] [1х1 .byteHi—O;
/ / корректировка нулевых элементов паттерна
-if ( ![]() [ix] .byteAv)
[ix] .byteAv) ![]() pattern
[1 у] [1 х] .byteAv=1;
pattern
[1 у] [1 х] .byteAv=1;
![]()
Если полученный в результате рассмотренного преобразования паттерн содержит значительное число повторяющихся элементов и граничных условий достаточно для восстановления исходного сигнала с заданной точностью, можно говорить об эффективном (с целью сжатия) исключении избыточной информации.
Для сжатия паттерна предлагаются следующие преобразования. Первое ориентировано на сжатие значительного числа повторяющихся элементов паттерна (кодирование длин серий), отмеченных в данной реализации нулевым значением. Как уже было сказано, структура (расположение исключённых элементов) совершенно одинакова для всех цветовых компонентов, следовательно, число последовательных серий исключённых элементов кратно числу цветовых каналов, это учитывается при сжатии серий. Полученные на выходе после кодирования длин серий (например, при помощи кода на базе чисел Фибоначчи) данные могуг быть сжаты статистическим методом на основе преобразования Хаффмана или арифметического кодирования.
Восстановление изображения производится в обратной последовательности, начиная с декомпрессии паттерна. После получения массива паттерна его используют в качестве граничных условий для решения методом конечных разностей (МКР) анализирующего дифференциального уравнения (7.5), или другого выбранного при сжатии, в соответствии с разностной схемой (7.7) и шаблоном (рис. 7.4). Итерационную схему решения можно представить уравнением:
1
![]()
+ ft 1[Х, y+Ay]+ft 1[Х, у — Ду] ![]() где t
— номер итерации. Если сопоставлять начало итерации с началом циклов обхода
массива восстанавливаемого изображения, а завершение
где t
— номер итерации. Если сопоставлять начало итерации с началом циклов обхода
массива восстанавливаемого изображения, а завершение ![]() с их завершением, то,
выбрав в циклах положительное приращение значений счётчиков и используя для
последующих расчётов ранее вычисленные значения ( — Ах, у], f[x, у — ду]),
уравнение (7.9) можно записать в виде:
с их завершением, то,
выбрав в циклах положительное приращение значений счётчиков и используя для
последующих расчётов ранее вычисленные значения ( — Ах, у], f[x, у — ду]),
уравнение (7.9) можно записать в виде:
1
![]()
4
![]()
Завершить итерационный процесс можно по критерию невязки, вычисляемой, например, как сумма разностей всех значений элементов (без граничных условий) для соседних итераций.
Цифровые сигналы очень многообразны, потому разнообразны и методы сжатия. Успешность сжатия цифровых сигналов зависит от того, какой способ использован. Сжатие с использованием анализа дифференциальной структуры может быть наиболее эффективно применено к сигналам, содержащим значительные поля градиентных переходов амплитуд и достаточно контрастные границы полей в области существенного изменения амплитуд. Примерами изображений подобного вида могут быть высококонтрастные фотографии объектов, содержащих чёткие контуры и однотонные или градиентные поля:
![]() рисованные изображения с контрастными
границами объектов;
рисованные изображения с контрастными
границами объектов;
— некоторые качественные пейзажные фотографии;
— высококонтрастные фотографии космических объектов; ![]() высококонтрастные
снимки дистанционного зондирования Земли; — текстурные изображения и др.
высококонтрастные
снимки дистанционного зондирования Земли; — текстурные изображения и др.
Проведенные исследования показали, что эффективность сжатия изображений с помощью анализа дифференциальной структуры можно повысить, используя дополнительные преобразования. Анализирующее уравнение Пуассона (6.10), (6.11) позволяет сформировать более компактный, по сравнению с уравнением Лапласа, паттерн, но при этом необходимо определить правую часть уравнения. В качестве правой части можно использовать матрицу определённых значений, сформированную по исходному изображению, разделённому на области, например, 8х8 пикселов. Значения матрицы могут быть получены выбором минимальной амплитуды области, этот подход в большинстве случаев позволяет корректировать плотность распределения значений амплитуд таким образом, что к паттерну можно более эффективно применять статистическое сжатие.
При сжатии фотоизображений можно применять специальную обработку для удаления шума, возникающего, например, из-за дефектов ПЗСматрицы.
Применение швкочастотных фильтров к изображению позволяет исключть из патерна случайный шум, свойственный цифровьпи фотографитл, однако при этом возможна потеря высокочастотной полезной информации, например, мелких деталей изображения; в некоторых случаях положительный эффект дает использование высокочастотных фильтров. Следует отметить, что в качестве граничных условий в паттерн сохраняются элементы исходного неотфильтрованного изображения. Фильтрация может быть выполнена с помощью свертки с ФРТ небольшого размера (3х3, 5х5, 7х7), при больших размерах ФРТ эффективен фильтр, использующий операцию «быстрая свертка, основанная на быстром фурье-преобразовании».
В некоторых случаях повысить эффективность сжатия позволяет использование при анализе дифференциальной структуры производных высших порядков и различных шаблонов дифференцирования. Выбор порядка и вида штфференциального уравнения в значительной мере зависит от особенностей изображения. Отображения многих реальных и синтезированных объектов хорошо анализируются с помощью производных второго порядка, т.е. уравнений Лапласа или Пуассона.
В области сигнала, где значение второй производной мало, возможна потеря полезной информации (рис. 7.5). Наиболее подвержены потере информации области, в которых плавно изменяется функция сигнала, особенно критичным это может быть для областей, где меняется знак первой производной. Избежать потери позволяет включение в паттерн локальных минимумов и максимумов сигнала.
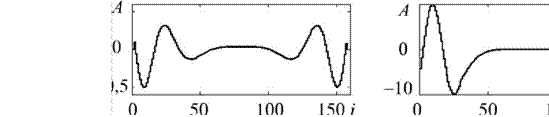
Рис. 7.5. Потеря информации о сигнале при малых значениях второй производной: а — исходный сигнал, б — паттерн, в — вторая производная, г — восстановленный сигнал
В листинге 7.4 приведен пример кода программы формирования паттерна с применением операции на базе свертки с ФРТ (3х3 ), в качестве примера задана ФРТ скользящего среднего, подавляющая высокие частоты сигнала (в том числе случайные шумы) и усиливающая сигнал до 9 раз. Применение низкочастотного фильтра дает хорошие результаты формирования паттерна для последующего сжатия цифровых фотографий, содержащих контрастные объекты и однотонные поля со случайными шумами. Обратим внимание, что в паттерн копируются не результаты свёртки изображения, а элементы исходного изображения, что позволяет оставить больше исходной информации и получить более приемлемые результаты при восстановлении. Свёртка с заданной ФРТ приводит к размытию полей и границ, что, в свою очередь, позволяет учесть в паттерне не только элементы самих границ, но и соседние, удалённые от границ, элементы. Элементы вне границы могуг отличаться от граничных, в качестве граничных необходимо выбирать соседние элементы, близкие по значениям к элементам области, и пиковые значения границы. В результате выполнения свёртки сигнал усиливается, поэтому необходимо нормировать значения элементов сигнала или изменить д -критерии. Нормирование динамического диапазона или использование нецелочисленных коэффициентов ФРТ вызовет увеличение времени вычислений, при ограниченных размере и амплитуде ФРТ более эффективно изменять значения Д -критериев (de1Lo, de1Av,
![]()
Лиспзинг 7.4. Фрагмент программы формирования паттерна с предварительной свёрткой полноцветного изображения (С++)
![]()
/ / цв а товая палитра
/ / покомпонентное представление, в
скобках указаны компоненты / / палитр (RGB) и (YCbCr) соответств а нно
struct C010rSpace { uchar byt a Lo; / / компонент младший байт
(Lower) ![]() uchar byt a Av; / / компонент
средний байт (Average)
uchar byt a Av; / / компонент
средний байт (Average) ![]() uchar byt a Hi; / / компонент
старший байт (Hight)
uchar byt a Hi; / / компонент
старший байт (Hight)![]()
|
int iLo ; / компонент |
младший |
” байт ” (Lower) |
|
int iAv; / / компонент |
среднии |
” байт ” (Average) (G) (СЬ) |
|
int 1 Н 1; / / компонент |
с ш арший |
” байт ” |
![]() / / структура для
сохран а ния цветов в виде -int
/ / структура для
сохран а ния цветов в виде -int
|
/ / один условный ” байт ” struct IImage { |
соответствует переменной шипа int |
uint jmax=Xsize—1; uint imax=Ysize—1;
uint 1 х, 1 у, tix, tiy, nzero;![]() счётчики const int psfxy=3; / размеры
функции рассеяния точки
счётчики const int psfxy=3; / размеры
функции рассеяния точки
/ / матрица ФРТ (PSF point spread function)
|
int pulse [psfxyj |
1 } , |
|
а, 1, а, 1, |
1 } ,
|
|
/ / выделение памяти для образца |
копии изображения |
Т Ттад а** itemp2d=new Т
Ттаде* [imax+psfxyj • for (unsign a d int i=O; i<imax+psfxy; i++)
![]() itemp2d
[ij =new Т Т таде [jmax+psfxy] ; memset (itemp2d [i] , о, sizeof (ТТ таде)
(jmax+psfxy) ) ;
itemp2d
[ij =new Т Т таде [jmax+psfxy] ; memset (itemp2d [i] , о, sizeof (ТТ таде)
(jmax+psfxy) ) ;
/ / выполнение 2 D быстрой свёртки в ц а лочисленной арифметике for (int iyd—O; iyd< (int) Ysize; iyd++) { for (int ixd—O; ixd< (int) Xsize; ixd++) {
ix=ixd+ixp;
|
itemp2d [iy] [i x] . iLo+=pulse [iypJ [ixp] itemp2d [iy] [i x] . i Av+=pulse [iypJ [ixp] itemp2d [iy] [i x] . iHi+=pulse [iypJ [ixp] |
(int) data I i yd J [ixd] . byteLo; (int) data I i yd J [ixd] . byteAv ; (int) data I i yd J [ixd] . byteHi; |
![]() n ammepHa
n ammepHa
//
KOFIMPOBaHMe ![]() TO T-1eK C zaMeHOÜ Hyrreü
Ha
TO T-1eK C zaMeHOÜ Hyrreü
Ha ![]() swap (pattern [C] [0] , data CO ] [C] ) ; swap
(pattern [O] [j max) , data [0] [j max] ) ; swap (pattern [i max] [ C) , data
[i max] [0] ) ; swap (pattern [i max] [j max] , data lima x] [j max] ) ;
swap (pattern [C] [0] , data CO ] [C] ) ; swap
(pattern [O] [j max) , data [0] [j max] ) ; swap (pattern [i max] [ C) , data
[i max] [0] ) ; swap (pattern [i max] [j max] , data lima x] [j max] ) ;
for (ix 1; ix<jmax; ix++) {
// KoopÅb1Hawa no x MaccMEa p o sy n b waw cEépTRb1 itemp2d tix=ix+ (psfxy>>l) •
![]()
// Ha
nepB0M npoxoue KonmpoBaHme ![]() cupoR
cupoR
// c saMeH01h H ynelh Ha emmH1.,114b1 swap (pattern [0) [i x) , data [0] [i x] ) ; swap (pattern [i max] [i x] , data Cimax] C i x] ) •
int tLo=abs ![]() It i x] .
iLo+itemp2d [tiy+1] It i x] . iLo+ it o mp2d [tiy] Itix—l] .
iLo+itemp2d [tiy] [tix+l]
It i x] .
iLo+itemp2d [tiy+1] It i x] . iLo+ it o mp2d [tiy] Itix—l] .
iLo+itemp2d [tiy] [tix+l] ![]() (itemp2d ltiyJ [t i x] . iLo<<2) ) ; int
t Av=abs
(itemp2d ltiyJ [t i x] . iLo<<2) ) ; int
t Av=abs ![]() It i x] . iAv+itemp2d [tiy+1] It i x] . iAv+
itemp2d [tiy] Itix—l] . iAv+itemp2d [tiy] [tix+l] . iAv— (itemp2d ltiyJ [t i x]
) ; int tHi=abs It i x] . iHi+itemp2d [tiy+1] It i x] . i Hi + itemp2d [tiy]
Itix—l] . iHi+itemp2d [tiy] [tix+l] . i Hi— (itemp2d ltiy] [t i x] .
iHi<<2) ) ;
It i x] . iAv+itemp2d [tiy+1] It i x] . iAv+
itemp2d [tiy] Itix—l] . iAv+itemp2d [tiy] [tix+l] . iAv— (itemp2d ltiyJ [t i x]
) ; int tHi=abs It i x] . iHi+itemp2d [tiy+1] It i x] . i Hi + itemp2d [tiy]
Itix—l] . iHi+itemp2d [tiy] [tix+l] . i Hi— (itemp2d ltiy] [t i x] .
iHi<<2) ) ;
![]() UBeTOBOMY
I-qaHaJIY if ( ) {
UBeTOBOMY
I-qaHaJIY if ( ) {
// ycmaH0BKa npM3HaKa MCKJ7FoqeHMA 3JTeMeHTa nam rrepHa / / (He ABJIAÆCTCA KPaeBb1MM YCJIOBMAMM) pattern [i y] [i x] . byteLo=O;
pattern Ду] [1 х] .byteAv=O; pattern Ду] [1 х] .byteHi=O; nzero+=3; / счётчик исключённых из паттерна элементов
элементы паттерна с нулевыми значениями, корректировка if ( !pattern [iy] [ix] .byteLo) { pattern [iy] [ix] .byteLo=1;
if ( !pattern [iy] [ix] .byteAv) { pattern [iy] [ix] .byteAv=1;
/ / очистка памяти if (itemp2d && ![]() for (ix 0;
ix<imax+psfxy; ix++) de1ete [ 1 itemp2d ;
for (ix 0;
ix<imax+psfxy; ix++) de1ete [ 1 itemp2d ; ![]() [ 1 itemp2d; itemp2d—0
;
[ 1 itemp2d; itemp2d—0
;
/ / Функция swap
/ / копирование точки (в трёхцветной палитре с заменой нул а й на единицы) in1ine void swap (C010rSpace& receiver, C010rSpace& source) { / / выполнение проверки, при необходимости замена нулей единицей rece1ver=sourc a • / / копирование if ( ! receiver.byt a Lo) { receiver .byteLo=1;
if ( ! receiver .byt a Av) { receiver . byteAv=1 ;
if ( !![]()
![]()
При восстановлежш сжатых данных немаловажным фактором является скорость. МКР — достаточно медленный итерационный способ решения дифференциальных уравнений, особенно значительное время может понадобиться для решения многомерных задач. Поэтому необходимо оптимизировать вычисления.
Известен способ сокращения времени вычислений МКР для мягких дифференциальных уравнений [11] в некоторой области U с краевыми (граничными для физических областей и начальными для времени) условиями в областях В , сущность которого состоит в укрупнении шага h сетки в области U . Вследствие этого происходит потеря точности решения вплоть до того, что оно становится непригодным. Например, в основной задаче электростатики могут быть построены модели, в которых заряды рассматриваются как точки, расположенные в узлах сетки. При укрупнении сетки такие граничные условия могут быть потеряны, что принципиально меняет сущность промежуточного решения. При формировании паттерна могут возникать краевые условия, например, в виде уединённой точки, таким образом, для наших задач потеря точности в результате укрупнения сетки таюке актуальна.
По этой причине распространен подход с последовательным использованием нескольких сеток. Сетка Ul с самым большим шагом позволяет получить приближенное решение, которое затем уточняют, последовательно применяя сетки с меньшими значениями h (общее число различных сеток обычно 2—3). Шаг сетки может варьировать в зависимости от требуемой точности р вычислений. Таким образом, согласно теореме о сходимости разностного решения [1 1 8], вычислительная оптимизация возможна за счет последовательного формирования некоторого промежуточного решения. При этом каждое уточнение решения является итерационным, имеющим вычислительную сложность
![]()
где п. — размерность рассматриваемой задачи; N.— число узлов сетки в каждом направлении; t — число итераций, обеспечивающих требуемую точность на данном этапе. В многомерных задачах вычислительная сложность может быть очень велика даже при разреженной сетке.
Задачу нахождения промежуточного (приближённого) решения в области U можно решить путем аппроксимации значений .f(W) уравнения (7.1) различными функциями, в зависимости от физической сущности задачи, например, многочленом вида:
где ao,q![]() коэффициенты
многочлена; z переменная, относительно которой происходит аппроксимация.
коэффициенты
многочлена; z переменная, относительно которой происходит аппроксимация.
В общем случае, если линии сетки не параллельны координатным осям, образующим пространство W , то z может не входить во множество переменных исходной задачи. В этом случае необходимо учитывать поворот системы координат, в которых рассмотрен аргумент z , относительно исходной. В случае п -мерной (п > 1 ) задачи аппроксимирование необходимо производить последовательно для всех линий, образующих сетку в каждом направлении, с последующей оценкой средних значений для каждого узла сетки, вычисляемых как средние аппроксимированные значения в точках линий сетки, принадлежащих данному узлу. В определенном смысле можно говорить, что для нахождения некоторого промежуточного решения задача МКР разбивается методом конечных элементов, число которых равно числу линий сетки МКР.
Возможно совместное применение способов укрупнения сетки и нахождения промежуточного решения за счет аппроксимации, ведь даже для укрупненной сетки задача ускорения сходимости остается актуальной. Предложенный способ следует применять с учетом физической сущности процессов и условий каждой конкретной задачи. При изменении шага сетки можно использовать некоторые усредненные граничные условия.
В некоторых случаях (в зависимости от особенностей граничных условий) промежуточное решение, полученное предлагаемым способом [50, 51], может быть не очень «гладким», избежать этого позволит, например, учет (с некоторыми весовыми коэффициентами) вычисленных значений в соседних узлах аппроксимации.
Предлагаемый способ нахождения предварительного решения базируется не на последовательных итерационных приближениях, а на аппроксимации промежуточного решения в области U по имеющимся данным о граничных условиях В с учетом правой части (7.1). Вычислительная сложность решения может быть оценена с помощью выражения (7.11), при этом значение будет существенно меньше, это позволяет говорить о снижении вычислительной сложности предлагаемого способа.
Способ тестировался на различных задачах электротехники, описываемых уравнением Лапласа и Пуассона в двух- и трехмерных пространствах:
![]() основная задача электростатики (в том
числе с зарядами, описываемыми единственным граничным элементом);
основная задача электростатики (в том
числе с зарядами, описываемыми единственным граничным элементом); ![]() расчет
поля конденсатора сложной формы;
расчет
поля конденсатора сложной формы; ![]() расчет магнитного поля в зазоре
электрической машины; — восстановление цифрового сигнала по паттерну.
расчет магнитного поля в зазоре
электрической машины; — восстановление цифрового сигнала по паттерну.
Во всех случаях полученное промежуточное решение с заданной точностью было получено меньшим числом итераций МКР. Особый выигрыш наблюдается при гладких краевых условиях, вплоть до того, что при некоторой степени гладкости может быть получено решение только с применением указанного способа без последующего итерационного решения МКР.
На рис. 7.6 проиллюстрировано существенное ускорение сходимости в результате оптимизации предложенным способом (кривая 2) на примере невязок в решении двумерной (плоскопараллельной) задачи электростатики. Для разбиения области W выбиралась прямоугольная сетка, образованная линиями, параллельными координатным осям, с равным во всех направлениях шагом h . В качестве многочлена (7.12) использовалось уравнение прямой а коэффициенты ао,а1 рассчитывались по двум элементам краевых условий из В .
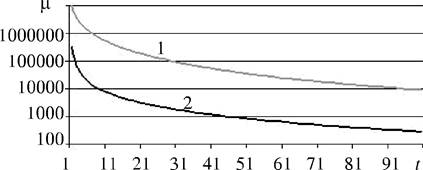
Рис. 7.6. Зависимость значения логарифма суммарных невязок џ по всем узлам сетки от номера итерации
Отметим, что применение рассмотренного способа в некоторых двумерных задачах с целью достижения решения заданной по невязке точности позволило уменьшить число итераций в 10—100 раз, это свидетельствует о существенном повышении эффективности МКР.
Рассмотрим некоторые результаты практического применения принципа сжатия с помощью анализа дифференциальной структуры на примере цифровых графических изображений. В качестве анализирующего было выбрано уравнение Лапласа (7.5). Изображения для тестирования выбирались из базы данных стандартных изображений [178] с учётом того, что сжатие на основании анализа дифференциальной структуры наиболее эффективно может быть применено к графическим объектам, содержащим контрастные границы и значительные поля градиента или одного тона.
Одно из выбранных для тестирования изображений (рис. 7.7) обладает следующими свойствами: является цифровой фотографией реального физического объекта; содержит контрастные границы объектов; содержит значительные поля одного тона. Размер исходного файла 196 662 байт, размер изображения 256 х 256 пикселов, глубина цвета 24 бита, размер цифрового сигнала изображения 256х 256х3 = 196 608 байт.
Рассмотрим зависимости от значения Д -критерия: числа исключённых из паттерна элементов; коэффициента сжатия К (6.1 среднеквадратичной ошибки MSE (6.3); пикового отношения сигнал/шум PSNR (6.4); отношения сигнал/шум SNR (6.5). В общем случае можно ожидать закономерности: чем больше д -критерий, тем больше элементов исключено из паттерна и тем менее точно можно восстановить исходный сигнал. Когда значение д -критерия превысит некоторое (критическое), паттерн полноцветного изображения, полученный с помощью программы, приведенной в листинге 7.3, будет содержать только элементы, принадлежащие границе изображения. Следовательно, при критической величине Д -критерия можно получить максимальное сжатие. При этом вопрос о качестве восстановленного изображения остаётся открытым.

Рис. 7. 7. Стандартное тестовое изображение «4.1.05.bmp»
В табл. 7.1 приведены численные результаты экспериментов,
для всех цветовых каналов было выбрано одинаковое значение д -критерия, паттерн
формировался в ![]() Для восстановления изображения применялся
МКР (1000 итераций) с предварительным отысканием промежуточного решения. Время
формирования паттерна (ОС Windows, С++) 31 250 мкс, время восстановления — 1
343 750 мкс. Коэффициент и фактор сжатия рассчитывались путём сопоставления
размера файла исходного изображения
Для восстановления изображения применялся
МКР (1000 итераций) с предварительным отысканием промежуточного решения. Время
формирования паттерна (ОС Windows, С++) 31 250 мкс, время восстановления — 1
343 750 мкс. Коэффициент и фактор сжатия рассчитывались путём сопоставления
размера файла исходного изображения ![]() и размера полученного в результате сжатия
с помощью анализа штфференциальной структуры файла. Помимо самих изображений
файлы обычно содержат некоторую служебную информацию (время создания, цветовая
схема, размеры и т.д.). Длина служебных данных в сжатых файлах 52 байта, в
исходном файле
и размера полученного в результате сжатия
с помощью анализа штфференциальной структуры файла. Помимо самих изображений
файлы обычно содержат некоторую служебную информацию (время создания, цветовая
схема, размеры и т.д.). Длина служебных данных в сжатых файлах 52 байта, в
исходном файле ![]() 54 байта.
54 байта.
Таблица 7.1. Некоторые оценки сжатия изображения «4.1.05.bmp»
|
д-критерий |
Исключённых элементов |
|
|
MSE |
PSNR |
SNR |
|
|
байтов |
|
||||||
|
|
60 |
0.0.30518 |
0.889 |
|
0.001302 |
76.98 |
72.37041 |
|
5 |
23535 |
11.97052 |
0.840 |
|
0.121638 |
57.28 |
52.66611 |
|
10 |
57828 |
29.41284 |
0.699 |
|
0.800832 |
|
44.48139 |
|
15 |
84129 |
42.79022 |
0.582 |
|
2.204839 |
44.70 |
40.08ЗОЗ |
|
20 |
107364 |
54.60815 |
0.481 |
2.080 |
5.200922 |
40.97 |
36.356 |
|
25 |
127779 |
64.99176 |
0.388 |
2.578 |
11.78631 |
37.42 |
32.80302 |
|
зо |
144492 |
73.49243 |
0.304 |
3.290 |
22.84199 |
34.54 |
29.92946 |
|
35 |
157290 |
80.00183 |
0.234 |
4.275 |
36.16757 |
32.55 |
27.93361 |
|
40 |
166086 |
84.47571 |
|
5.436 |
56.36549 |
30.62 |
26.00667 |
|
45 |
171954 |
87.46ОЗЗ |
|
6.759 |
85.77358 |
28.80 |
24.18327 |
|
50 |
176058 |
89.54773 |
0.123 |
|
127.981 |
27.06 |
22.44535 |
|
55 |
179193 |
91.14227 |
о. 1 04 |
|
192.4735 |
25.29 |
20.67309 |
|
60 |
181608 |
92.37061 |
0.089 |
1 1.239 |
268.6562 |
23.84 |
19.22483 |
|
65 |
|
93.32428 |
0.077 |
12.991 |
384.8277 |
22.28 |
17.66414 |
|
70 |
|
|
0.068 |
14.710 |
|
|
16.49875 |
На рис. 7.8 приведены полученные при сжатии паттерны и восстановленные изображения.
Обычно для изображений приемлемого качества PSNR =20-40
[105]. Сопоставляя табл. 7.1 и рис. 7.8, можно заметить, что при д ![]() наблюдается
существенное для визуального восприятия ухудшение качества изображения,
возникают области размытия вблизи границ объектов, при этом для д = 40 PSNR =
30.62 Д = 50 — 27.06. Коэффициент сжатия К = 0.184 (для д = 40) и К =0.123 (для
Д = 50). При дальнейшем росте значения д -критерия наблюдается снижение
качества, особенно проявляющееся на границах графических объектов. Изучение
структуры паттерна показывает, что снижается и качество отображения
текстуроподобной однотонной области кирпичных стен: сравнив рис. 7.8, и и .лј,
можно заметить, что пропадают граничные условия, соответствующие
мелкотекстурным элементам. При д =70—80 изображенные предметы, несмотря на
значительные искажения, оставались узнаваемыми.
наблюдается
существенное для визуального восприятия ухудшение качества изображения,
возникают области размытия вблизи границ объектов, при этом для д = 40 PSNR =
30.62 Д = 50 — 27.06. Коэффициент сжатия К = 0.184 (для д = 40) и К =0.123 (для
Д = 50). При дальнейшем росте значения д -критерия наблюдается снижение
качества, особенно проявляющееся на границах графических объектов. Изучение
структуры паттерна показывает, что снижается и качество отображения
текстуроподобной однотонной области кирпичных стен: сравнив рис. 7.8, и и .лј,
можно заметить, что пропадают граничные условия, соответствующие
мелкотекстурным элементам. При д =70—80 изображенные предметы, несмотря на
значительные искажения, оставались узнаваемыми.


Рис. 7.8. Исходное изображение (а); изображения, восстановленные МКР с использованием промежуточного решения (о, г, д, ж, з, к, л); паттерны (в, е, и, м).
Рассмотрим результаты сжатия, полученные с помощью наиболее распространённых методов (табл. 7.2—7.4). Сжатие в частотной области методом JPEG [84] основано на дискретно-косинусном преобразовании, визуальное качество полученного изображения оценивается по шкале от 0 до 12. Формат PNG (Portab1e Network Graphik) базируется на сокращении числа разрядов для задания цветового пространства, а следовательно и цветовой палитры, и последующем статистическом сжатии изображения [105]. В отличие от PNG формат GIF позволяет работать с динамическими изображениями.
Таблица 7.2.
Некоторые оценки ![]() изображения «4.1.05.bmp»
изображения «4.1.05.bmp»
|
Качество |
|
|
MSE |
PSNR |
SNR |
|
12 |
0.494 |
2.023 |
1.56 |
|
|
|
|
0.359 |
2.778 |
5.63 |
40.62 |
36.01 |
|
10 |
0.282 |
3.538 |
9.35 |
|
33.80 |
|
9 |
0.245 |
4,069 |
|
37.00 |
|
|
8 |
0.222 |
4.497 |
|
35.79 |
|
|
7 |
0.201 |
4.970 |
|
34.45 |
29.84 |
|
6 |
|
5.006 |
|
|
27.49 |
|
|
|
5.333 |
46.79 |
|
26.82 |
|
|
|
5.556 |
|
|
26.40 |
|
З |
|
5.746 |
58.72 |
30.44 |
25.83 |
|
|
|
6.064 |
75.88 |
29.33 |
24.72 |
|
|
|
6.243 |
96.81 |
28.27 |
23.66 |
|
|
|
|
|
27.89 |
23.28 |
Таблица 7.3.
Некоторые оценки ![]() изображения «4.1.05.bmp»
изображения «4.1.05.bmp»
|
Число разрядов |
Число цветов |
|
|
MSE |
PSNR |
SNR |
|
24 |
16777216 |
0.609136 |
1.641668 |
0 |
|
|
|
8 |
256 |
0.191079 |
5.233434 |
10.80395 |
37.79498 |
33.1 8098 |
|
7 |
128 |
0.15489 |
6.45619 |
16.1552 |
36.04768 |
З 1.43368 |
|
6 |
64 |
|
8.957504 |
24.60652 |
|
29.6063 |
|
5 |
32 |
0.091278 |
10.95549 |
34.69823 |
32.72773 |
28.11373 |
|
4 |
16 |
0.040465 |
24.71249 |
50.41061 |
31.10559 |
26.49158 |
|
|
8 |
0.026284 |
38.04643 |
140.4574 |
26.65536 |
22.04136 |
|
2 |
4 |
0.01436 |
69.63952 |
252.7536 |
24.10383 |
19.48983 |
|
|
|
|
139.973 |
569.2647 |
20.57766 |
15.96366 |
Таблииа 7.4.
Некоторые оценки ![]() изображения «4.1.05.bmp»
изображения «4.1.05.bmp»
|
Число цветов |
К |
|
MSE |
PSNR |
SNR |
|
128 |
0.171243 |
5.839653 |
|
35.84856 |
31.23455 |
|
|
о. 123583 |
8.091754 |
26.3118 |
33.9293 |
29.3153 |
|
32 |
о. 100335 |
9.966653 |
|
32.36599 |
27.75199 |
Выберем по одному полученному различными способами (табл. 7.5) сжатия (при минимальном значении коэффициента сжатия) изображению визуаиьно приемлемого качества (рис. 7.9). Несмотря на субъективность, такой подход к выбору позволяет учесть специфику восприятия изображения человеком.


Рис. 7.9. Сжатие: а — методом анализа дифференциальной структуры ( ![]() б — методом анализа дифференциальной
структуры с предварительной свёрткой; в - .JPEG (качество 0); г - PNG (32
цвета); д - GIF (32 цвета)
б — методом анализа дифференциальной
структуры с предварительной свёрткой; в - .JPEG (качество 0); г - PNG (32
цвета); д - GIF (32 цвета)
Таблица 7.5. Результаты сжатия изображения «4.1.05.bmp»
|
Метод |
К |
|
MSE |
PSNR |
SNR |
|
Анализ дифференциальной структуры |
|
|
52.1964 |
|
26.34 |
|
Анализ дифференциагњной структуры с предваритејњной свёрткой |
|
|
76.36 |
29.30 |
24.69 |
|
JPEG |
|
|
|
27.89 |
23.28 |
|
PNG |
0.091 |
10.955 |
|
32.72 |
|
|
GIF |
|
9.967 |
|
32.37 |
27.75 |

в г
Рис. 7.10. Паттерны (а — без
применения; б— с применением свёртки) и восстановленные изображения (в — по
паттерну а; г![]()
Табиица 7.6. Оценка влияния низкочастотного фильтра
|
Свёртка |
Число исключённых из паттерна элементов |
К |
|
MSE |
PSNR |
SNR |
|
нет |
166086 |
|
5.434 |
|
30.640 |
26.026 |
|
Есть |
166119 |
|
5.829 |
66.427 |
29.907 |
25.293 |
Полученные результаты показывают конкурентоспособность
предложенного метода сжатия с помощью анализа дифференциальной структуры.
Дополнительно повысить эффективность сжатия можно, применив арифметическое
кодирование вместо использованного нами кода Хаффмана, уравнение Пуассона —
вместо уравнения Лапласа. Отметим, что предложенный метод может быть реализован
по принципам параллельных вычислений, например, технологии GPGPU. С учётом
сказанного способ имеет определённый потенциал развития и перспективы практического
применения.
Постоянно растущий поток данных самой различной природы не может быть эффективно обработан без применения вычислительных средств. Машинная обработка сигналов требуется в различных циклах производства и проектирования, научных исследованиях, военно-стратегических приложениях. Одной из наиболее сложных и актуальных задач цифровой обработки является распознавание образов. Проблема распознавания образов охватывает более широкий круг задач, чем классификация объектов на графических изображениях.
Образ (некоторые авторы используют слово киасс) является привычной единицей мышления, и в общем случае он сложно формализуем, обладает некоторыми свойствами (признаками); методы, доступные какомулибо образу, возможно выделить в отдельную категорию. Характерным свойством образа является наследование, т.е. образ может относиться к некоторым другим образам как родитель или потомок, передавая или наследуя их свойства. Следовательно, в общем случае задача распознавания сводится к выделению свойств некоторого объекта и их анализу на предмет принадлежности объекта к некоторому образу (классу). Распознавание образов может быть применено к большому кругу задач. Например, в промышленности актуально распознавание образов некоторых изделий и (или) их элементов при автоматизации; в медицине анамнез пациента можно рассматривать как многомерный сигнал или вектор в многомерном пространстве, характерные особенности которого могут быть использованы для постановки диагноза; в акустике задача распознавания образов — выявление некоторых сигналов или их последовательностей.
Сложность машинной реализации задачи распознавания образов обусловлена отсутствием чёткого определения фундаментального понятия
1 5
множества. По определению Кантора , «множеспшом является соединение в некоторое целое М хорошо различимых предметов т нашего созерцания или нашего мышления» [72]. Невозможность в общем случае решения задачи распознавания образов с помощью формальной арифметики целесообразно рассматривать как ограничение в соответствии с парадоксами теории множеств и теоремой Гёделя о неполноте.
Итак, объекты, хорошо различимые нашим сознанием, в большинстве случаев достаточно сложно или невозможно классифицировать доступными современными вычислительными методами. Поэтому для исследова-
![]() Георг Фердинанд Людвиг Филипп Кантор
(З марта 1845, Санкт-Петербург — 6 января 1918, Галле, Германия) — математик,
наиболее известен как создатель теории множеств.
Георг Фердинанд Людвиг Филипп Кантор
(З марта 1845, Санкт-Петербург — 6 января 1918, Галле, Германия) — математик,
наиболее известен как создатель теории множеств.
ния и распознавания образов наряду с обычными методами ЦОС применяют методы нечёткой логики, выделяемые в отдельную категорию как содержащие некоторое подобие биологических систем, к ним относят нейронные сети, генетические алгоритмы. Но даже применение таких методов не позволят решить задачу распознавания образов в общем случае.
Природа исходного сигнала во многом определяет принципы обработки его цифровой формы с целью распознавания образов. Основываясь на модели, предложенной в монографии [33], приведем этапы работы систем распознавания образов с учетом представления и управления данными, структуры машинных алгоритмов и организации вычислительных процессов
1. Аналого-цифровое преобразование или синтез сигнала, смоделированного при помощи вычислительных средств.
2. Предварительная обработка сигнала (фильтрация шума или для графических данных изменение цветового пространства и т.д.).
З. Формирование графического препарата цифрового сигнала, т.е. некоторой совокупности сигналов, более пригодных для дальнейшего анализа. Например, может быть получен спектр сигнала, рассчитаны производные, произведена его сегментация, аффинные преобразования и т.д.
4. Анализ сигнала. На данном этапе путём оценки различных параметров формируются описание и характеристика сигнала. Например, могут быть выявлены некоторые особенности спектра, функциональные зависимости и геометрические структуры, присутствующие в сигнале.
5. Классификация (распознавание) образов, этот этап обычно является завершающим.
В существукощих системах распознавания образов несколько этапов могут быть связаны между собой в единый вычислительный комплекс. Например, этапы 3—5 могут быть связаны в вычислительной операции при использовании нейронных сетей, некоторые системы могут выполнять несколько последовательных вычислительных операций, каждая из которых содержит все этапы или их часть.
Статистические методы могут быть использованы на самых различных этапах решения задачи распознавания образов, область их применения зависит от конкретной задачи. Регрессионный анализ достаточно распространён как метод оценки степени влияния изменения некоторых векторных величин хл, х , хп, Е Х на характеристику (вектор) У наблюдаемого явления или объекта при выявлении схожести, прогнозировании, в различных аналитических исследованиях. Этот метод позволяет выделять из множества Х ведущие факторы влияния на характеристику У и строить регрессионные модели. Существуют различные линейные и нелинейные
А. Ю. Гришенцев, А. Г. Коробейников
![]()
регрессионные модели, определяемые выбранной функцией зависимости характеристики У от факторов х1 , х2 , хт [21], например, для „у е У и
![]()
![]() простая линейная регрессия:
простая линейная регрессия:
У
C11X1 + Е![]()
![]() множественная линейная регрессия:
множественная линейная регрессия:
у C11X1 + С12Х2 + + а Х + Е ![]()
— полиномиальная регрессия:
у = ао
-FalX-FC12X + + а хт Е ![]()
— линейная по параметрам регрессионная модель общего вида:
![]()
![]() + ат(Рт (Х1 , ху...
+ ат(Рт (Х1 , ху...![]()
— нелинейная по параметрам модель:
у
= ln(b1X1 ) + ![]() + ат tg(bmxm) + Е
+ ат tg(bmxm) + Е ![]()
где ao, q, ..., а и Ь параметры
регрессии; ошибка; ![]() (Рт — функции факторов.
(Рт — функции факторов.
На практике множество характеристик сложным образом нелинейно зависит от факторов (р; при определённых допущениях с точностью, приемлемой для решения конкретной задачи, в большинстве случаев удаётся получить линейные регрессионные зависимости. Количественной оценкой линейной зависимости между векторами Хи У служит коэффициент корреляции, вычисляемый по формуле:
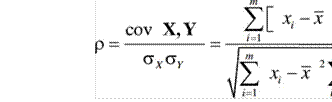
где cov Х, У — ковариация векторов Хи У ; ох среднеквадратическое отклонение Х; о среднеквадратическое отклонение У ; Х, у — математическое ожидание Хи У .
![]()
Корреляцию между двумерными матрицами Х и У можно вычислить по следующей формуле:
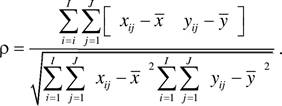
При распознавании образов в многомерных сигналах можно использовать корреляционные оценки между отдельными фрагментами этих сигналов. В общем случае корреляционными считают все методы, основанные на вычислении оценок подобия анализируемого и эталонного сигналов, например, свёртку. Достаточно хорошие помехоустойчивость и эффективность распознавания сложноструктурированных объектов возможно получить за счет разделения сигнала на фрагменты, оценки корреляции между ними и набором эталонов при последующей классификации [32, 124]. При корреляционном анализе многомерных сигналов необходимо решать многопараметрическуто задачу оптимизации с целью выбора размеров и положения фрагментов. С одной стороны, при малых размерах фрагмента корреляционные оценки более устойчивы к повороту относительно эталона и требуют меньших расчётов, с другой — высока вероятность ложного распознавания.
Задачу определения положения фрагментов, подобных эталонным, можно решить с помощью скользящего окна, когда выбранная область (фрагмент) плавно перемещается по всему сигналу, что требует значительного количества вычислений. Дополнительные сложности обусловлены необходимостью соответствия масштабов искомого объекта во фрагменте сигнала и объекта в эталонном сигнале. Наиболее подходящий способ выбирается с учётом специфики условий задачи и требований к ее решению. Например, существенную часть вычислений можно сократить и получить хороший результат при корректировке размеров и положения фрагментов оператором. В большинстве случаев мерой эффективности систем распознавания образов служит уровень их автоматизации, т.е. способности самостоятельно выполнять этапы распознавания — от получения входных данных до выдачи готовых результатов.
Пример программы вычисления с помощью двумерной свёртки вероятного положения искомого образа приведён в листинге 8.1, результаты выполнения программы представлены на рис. 8.1. Если размеры сигнала, содержащего искомый образ, невелики, то свёртка выполняется достаточно быстро, в противном случае можно применять быструю свёртку на основе БПФ.
![]()

![]() 0 3a1n
pY3Ka mccnenyemnoro M306paxeHMA
0 3a1n
pY3Ka mccnenyemnoro M306paxeHMA
![]() ( ' 4 . 1 .
05 . bmp' ) •
( ' 4 . 1 .
05 . bmp' ) •
![]() 0
np=06pa30BaHme mccneÅY O Moro 1-4306paxeH1,1A E rpauaumm
ceporo
0
np=06pa30BaHme mccneÅY O Moro 1-4306paxeH1,1A E rpauaumm
ceporo
![]() (rgb2gray
(imgRGB) ) ;
(rgb2gray
(imgRGB) ) ;
![]() 0 3a1n
pY3Ka
0 3a1n
pY3Ka ![]() c CM 17 HaJIOM, cozepxaL1-1MM
MCKOMb11h 06pa3 testRGB=imread ( ' test . 05 . bmp' ) •
c CM 17 HaJIOM, cozepxaL1-1MM
MCKOMb11h 06pa3 testRGB=imread ( ' test . 05 . bmp' ) •
![]() 0
npe05pa30BaHme M30ÖpaxeHMA B rpamaL.LMM ceparn a
testGray=im2doub1e (rgb2gray (testRGB) ) ;
0
npe05pa30BaHme M30ÖpaxeHMA B rpamaL.LMM ceparn a
testGray=im2doub1e (rgb2gray (testRGB) ) ;
![]() 0 nom 17
0TOBKa npenapa rra MCKOM017 0 06pa3a
0 nom 17
0TOBKa npenapa rra MCKOM017 0 06pa3a ![]() nonyqeHne
pa 3Mepa sz=size (testGray) , objGray=zeros (s z (1) , s z (2) ) ;
nonyqeHne
pa 3Mepa sz=size (testGray) , objGray=zeros (s z (1) , s z (2) ) ;
![]() 0
sepKaJTbHoe o rrpaxeHMe BBICIMCJTeHMA
0
sepKaJTbHoe o rrpaxeHMe BBICIMCJTeHMA ![]() obi Gray (l
: a nd, 1 • o nd) =testGray ( a nd: —1 : 1, end: —1 : 1)
•
obi Gray (l
: a nd, 1 • o nd) =testGray ( a nd: —1 : 1, end: —1 : 1)
•
![]() 0 HOPMMPOBaHMe
0 HOPMMPOBaHMe ![]() ript.4BeneH1.,1eM
cpeÄHeMY 3HageHMF0,
ript.4BeneH1.,1eM
cpeÄHeMY 3HageHMF0,![]()
H yJiff) ,
![]() 0
YMeHb111eHMfi OTKJIMKa Ha OZHOTOHHb1e OÖJ1aCTM tM—m a an2 (obi
Gray)
0
YMeHb111eHMfi OTKJIMKa Ha OZHOTOHHb1e OÖJ1aCTM tM—m a an2 (obi
Gray) ![]() obi Gray obi Gray—tM;
obi Gray obi Gray—tM;
![]() 0
Eb1FIOJIHeHMe CEéPTRM cResu1t=conv2 (imgGray, obi Gray, ' sam o )
0
Eb1FIOJIHeHMe CEéPTRM cResu1t=conv2 (imgGray, obi Gray, ' sam o )
![]() -6 Ha xoxmeHme Makcmnnynna B Mawpmue
cBépTKM,
-6 Ha xoxmeHme Makcmnnynna B Mawpmue
cBépTKM,
![]() 0 1-cak
Ham60J1ee eep0fiTH017 0 nonoxeHMA MCKOMOI'O 06pasa
0 1-cak
Ham60J1ee eep0fiTH017 0 nonoxeHMA MCKOMOI'O 06pasa
[T, y] =max (max (cR o su1t, [ l , 2) ) ;
[T, x] =max (max (cR o su1t, , 1) ) ;
BL,13yanmsaumn
pe3YJ1bTaTOB figure; colormap (Gray) ; subplot (2, 2, 1) ; L mag n sc
(imgGray) ; titl a ( 'MccneÅY O Moe 1-4306paN O
Hme ) ; subplot (2, 2, 2) ; -L mag n sc (testGray) , title ( '
3uaJIOHHOe 1-4306pa>K O Hme (mCKOMb11h 06pas) ![]() subplot
subplot ![]() L mag n
sc (0b j Gray) ; titl a ( ' Ilpenapau mcK0M011 0
06pasa ' )
L mag n
sc (0b j Gray) ; titl a ( ' Ilpenapau mcK0M011 0
06pasa ' ) ![]() subplot (2, 2, 4) ; i mag—sc (cR n su1t)
• title ( L ' BePOATHoe 110J10xeHne 06%eKTa , num2str (x) ,
subplot (2, 2, 4) ; i mag—sc (cR n su1t)
• title ( L ' BePOATHoe 110J10xeHne 06%eKTa , num2str (x) , ![]()
![]() , num2str
(y) ] ) ; text (x, y, ' \ left arrow point ' , ' Font Size ' , 14)
, num2str
(y) ] ) ; text (x, y, ' \ left arrow point ' , ' Font Size ' , 14)
![]()
![]()

50 100 150 200 х 20 40 60 80 100 х а
![]() 20
40 60 80 100 х
20
40 60 80 100 х 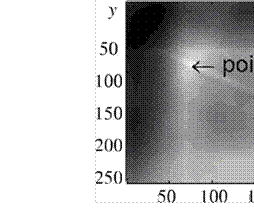
Рис. 8.1. Определение вероятного положения образа а — исследуемое изображение, б — эталонное изображение (искомый образ) в — препарат искомого образа, г — результат свёртки, вероятное положение объекта (Х=77, У=89)
Оценку подобия фрагмента сигнала и некоторого образа также можно получить, вычислив их среднеквадратическую ошибку.
Рассмотренный способ определения положения образа устойчив к шумам (см. листинг 8.1 сложности могут возникнуть при повороте образа или изменении его масштаба. В этом случае могут потребоваться дополнительные преобразования (поворот, масштабирование) образа и дополнительное вычисление свёртки, что может существенно увеличить время вычислений.
В ряде случаев отыскание образов необходимо выполнять в частотной, а не пространственной области, например, для распознавания звуковых сигналов частотное представление в виде спектра информативней временной диаграммы. Пример распознавания в частотной области — выявление на изображении объектов некоторых линейкњјх размеров по пространственному
А. Ю. Гришенцев, А. Г. Коробейников
![]()
спектру. Для получения пространственного и/или временного спектра могут быть использованы фурье-, вейвлет-преобразование или преобразование по БПВ.
При распознавании образов можно использовать как пространственный и/или временной (для динамического изображения) спектр, определяющий характеристики расположения объектов, так и энергетический спектр, соответствующий энергетическим характеристикам, т.е. собственному и отражённому излучению сигнала.
Для определения истинных энергетических характеристик необходимо учитывать искажения и преобразования, вносимые измерительным прибором. Исследовательский спутник SDO (Solar Dynamics 0bservatory) обеспечивает наблюдения динамики Солнца преимущественно в области спектра УФ-излучения, не видимого для глаза человека [130, 175]. Визуализация полученных изображений производится при помощи подмены истинного спектра (true color) ложными цветами (false color). Замена энергетического спектра сигнала производится достаточно часто, например, с целью акцентирования внимания на некоторых объектах.
В листинге 8.2 выполнено отображение цветового спектра изображения в пространства RGB и HSV.
Мистинг 8.2. Визуальный анализ цветового спектра изображения
![]()
c1ear а 11; удаление п а р а менных c10se а 11; о закрытие всех окон окна
![]() с, загрузка и трансформация данных
изображения imgRGB imr a ad ( ' 1atest 512 0094 .bmp ' ) ;
с, загрузка и трансформация данных
изображения imgRGB imr a ad ( ' 1atest 512 0094 .bmp ' ) ;
|
imgHSV странства |
rgb2hsv (imgRGB) ; |
D преобразование цветового про— |
|
RGB1ine сив |
reshap a (imgRGB, [ ) , З) ; |
преобразование в двум а рный ма с— |
|
HsM1ine |
reshap a (imgHSV, [ ) , З) ; |
преобразование в двум а рный ма с— |
сив
![]() D визуализация pview
repmat (5, size (RGB1ine, 1) , 1 ) ; pcolor double (RGB1ine ( : , :
D визуализация pview
repmat (5, size (RGB1ine, 1) , 1 ) ; pcolor double (RGB1ine ( : , :![]()
![]()
![]()
![]()
![]()
![]() scattar pview, pcoIor, ' filled ' ) ;
xlabel ( ' H—component ylabel ( ' S—component ' ) ;
scattar pview, pcoIor, ' filled ' ) ;
xlabel ( ' H—component ylabel ( ' S—component ' ) ;
![]()
На рис. 8.2 визуализирован цветовой спектр фотографии Солнца (http://sdo.gsfc.nasa.gov/), полученной SDO на длине волны 9.4 нм. Графические результаты выполнения программы приведены на рис. 8.3. Визуальный анализ цветовых гистограмм позволяет сделать выводы об интенсивности излучения, наличии вспышек. На диаграмме RGB заметен характерный «хвост», уходящий в область белого цвета (область максимальных значений интенсивности RGB). На диаграмме HSV область вспышек отображена в окрестности значения 0.21 Н-компонента. Таким образом, анализ цветового спектра изображения позволяет получить информацию об интенсивности вспышек.
Дополнительную информацию может дать анализ цветового спектра отдельных фрагментов изображения. В некоторых случаях цветовые диаграммы позволяют выявить почти незаметные на исходном изображении объекты.

Рис. 8.2. Изображение Солнца (ложные цвета) в УФ-диапазоне, SDO 18 декабря 2012 г., UT
в 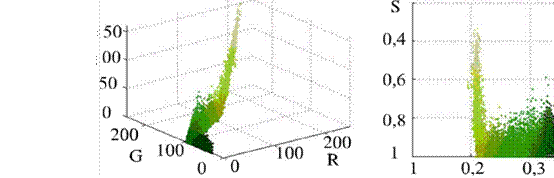
а б
Рис. 8.3. Диаграммы цветового спектра изображения Солнца: а — RGB; б— HSV
А. Ю. Гришенцев, А. Г. Коробейников
![]()
Анализ энергетического спектра изображения при распознавании образов, активно применяют для автоматизированного или автоматического исследования космических фотографий, данных дистанционного зондирования Земли, анализа медицинских изображений и др.
Всесторонний анализ спектра цифрового сигнала позволяет получить значительное количество информации, в том числе для решения задачи распознавания образов.
На основании вычисленных оценок подобия возможно классифицировать объекты, выделенные в сигнале. Для этого обычно используют кластерный анализ, позволяющий разделить исходную совокупность объектов на группы схожих, близких (по некоторому множеству критериев) объектов. Выделенные кластеры могут быть полезны для выявления некоторых признаков, например, определённого взаимного расположения и классификации образов в анализируемом сигнале. Разнообразие алгоритмов кластеризации объясняется широким кругом решаемых с их помощью задач и различием подходов к кластерному анализу. Один из подходов состоит в разбиении исходного множества объектов на основе значения целевой функции, параметрами которой являются, например, среднеквадратическая ошибка, коэффициент корреляции и др.
Вычислить сходность данных позволяют:
![]() евклидова
метрика:
евклидова
метрика:
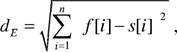
где f[i], s[i]
— векторы; ![]() взвешенная евклидова метрика:
взвешенная евклидова метрика:
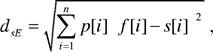
где p[i]— вес (значимость) признака; — lm -нормы:
1
![]()
при т = 1 ll служит манхеттоновской мерой (Manhatten distance metric);
— супремум-норма, или расстояние Чебышева16![]()
![]() Пафнутий Львович Чебышев (4 мая 1821,
Окатово, Калужская губерния — 26 ноября 1894, Санкт-Петербург) — выдающийся
математик и механик.
Пафнутий Львович Чебышев (4 мая 1821,
Окатово, Калужская губерния — 26 ноября 1894, Санкт-Петербург) — выдающийся
математик и механик.
![]()
![]()
![]() дистанция Хемминга используется
номинальная двухпозиционная шкала сравнения схожести символов, стоящих в
одинаковых позициях некоторых сигналов f[i] и s[i] :
дистанция Хемминга используется
номинальная двухпозиционная шкала сравнения схожести символов, стоящих в
одинаковых позициях некоторых сигналов f[i] и s[i] :
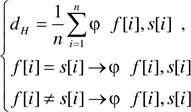 - 1.
- 1.
Существуют и другие метрики, позволяющие оценивать схожесть и производить классификацию различных данных. В листинге 8.3 рассмотрен пример классификации графических образов при помощи евклидовой метрики.
Лисупинг 8.3. Классификация графических образов (MATLAB)
![]()
|
c1ear а 11; |
удаление переменных |
|
c10se а 11; |
% закрытие всех окон |
очистка командного окна
nimg—25; % число изображений объектов с исходным размером 81х81
% выделяем память для массивов
imgObj=zeros (nimg, 81, 81) ; imgH=zeros (nimg, 81, 81) • metr=zeros (nimg) ![]() x=z a
ros (1,nimg) • y=z a ros (1,nimg) ;
x=z a
ros (1,nimg) • y=z a ros (1,nimg) ; ![]() д а скрипшоры
окон вывода графических данных hig=figure; hic=figure; hib=figure; nt=ceil
(sqrt (nimg) ) ; о число элементов графического поля п 1=1; счётчик
д а скрипшоры
окон вывода графических данных hig=figure; hic=figure; hib=figure; nt=ceil
(sqrt (nimg) ) ; о число элементов графического поля п 1=1; счётчик
![]() 0 загружаем массив
изображений for i=1 : 1 :nimq imgRGB=imread ( [num2str (1) ,
0 загружаем массив
изображений for i=1 : 1 :nimq imgRGB=imread ( [num2str (1) , ![]() imgGray=im2double
(rgb2gray (imgRGB) ) ; imgObj (1, : , : )=imgGray;
imgGray=im2double
(rgb2gray (imgRGB) ) ; imgObj (1, : , : )=imgGray;
![]() 0 двумерная функция
Гаусса для вычисления свёртки и
0 двумерная функция
Гаусса для вычисления свёртки и ![]() 0 определения графического ” центра
тяжести ” изображения winH=fspecia1 ( ' gaussian ' , 81, 10) •
0 определения графического ” центра
тяжести ” изображения winH=fspecia1 ( ' gaussian ' , 81, 10) •
![]() 0 свёртка cnv—conv2
(imgGray, winH, ' same ' ) •
0 свёртка cnv—conv2
(imgGray, winH, ' same ' ) •
![]() 0 ищем максимум в матрице результате
свёртки,
0 ищем максимум в матрице результате
свёртки,
![]() 0 как наиболее вероятное положение
искомого образа
0 как наиболее вероятное положение
искомого образа
[Т,рхј =тах (тах (cnv, [ ] , 2 ) ) ;
![]()
[T,py] =max (max (cnv, [ J , 1) ) ;
![]() 0 3an0MYIHaH1.,1 0 nonoxeH1.,1A
0 3an0MYIHaH1.,1 0 nonoxeH1.,1A ![]() 'ueHTpa
TAXecnm" x (i) =px;
'ueHTpa
TAXecnm" x (i) =px;
![]()
![]() 0
BM3yaJ11„13aLIMA MCXOZHb1X 1,1306paxeHMÉ1 figure (hi g) , subplot
0
BM3yaJ11„13aLIMA MCXOZHb1X 1,1306paxeHMÉ1 figure (hi g) , subplot ![]() • colormap
(Gray) imagesc (imgGray) , title ( [num2str (n1) J ) ;
• colormap
(Gray) imagesc (imgGray) , title ( [num2str (n1) J ) ;
![]() 0
BM3yaJIM3aUMA pe3yr1bTaT0B CBéPTKM figure (hic) , subplot (nt, nt, nl) ;
color-map (Gray) , imagesc (cnv) ;
0
BM3yaJIM3aUMA pe3yr1bTaT0B CBéPTKM figure (hic) , subplot (nt, nt, nl) ;
color-map (Gray) , imagesc (cnv) ; ![]() nopAAK0B0T7
0 H0Mepa M30ÖpaxeHMA M
nopAAK0B0T7
0 H0Mepa M30ÖpaxeHMA M
![]() K00PA1,-fHa rr
"ueHmpa mnxec rrv-f" title ( [num 2 str (n 1) , ( ' ,
num 2 str (PX) , , num 2 str (py) ,
K00PA1,-fHa rr
"ueHmpa mnxec rrv-f" title ( [num 2 str (n 1) , ( ' ,
num 2 str (PX) , , num 2 str (py) , ![]()
![]() rrpmpa11xeHMe
cuéT T-1MKa nl=nl+l; end
rrpmpa11xeHMe
cuéT T-1MKa nl=nl+l; end
![]()
n 1=1; n 2=1;
![]() 0 BblC11.,fCJ1eHMe
0 BblC11.,fCJ1eHMe
![]() cxoxecTM, Knac rnepM3a1_1MA for i l
: l :nimg
cxoxecTM, Knac rnepM3a1_1MA for i l
: l :nimg
![]()
![]() 0 rreKY1.uee
öasoeoe M30ÖpaxeHM 0 cpaBHeHMA, 0 BblmeneHHOe c
yuéT0M "ueH rrpa nnxec rm.,f" base ( : ,
0 rreKY1.uee
öasoeoe M30ÖpaxeHM 0 cpaBHeHMA, 0 BblmeneHHOe c
yuéT0M "ueH rrpa nnxec rm.,f" base ( : ,
![]() (i, x (i) —18 : x (i) +18, y (i) —18 : y (i)
+18) ;
(i, x (i) —18 : x (i) +18, y (i) —18 : y (i)
+18) ;
![]() c, on06paxeHme
c, on06paxeHme ![]() ms06paxeHmj1
figure (hi b) • subplot
ms06paxeHmj1
figure (hi b) • subplot ![]() colormap (Gray) i mag—sc (base)
colormap (Gray) i mag—sc (base) ![]() titl a
( [num2str (n 1) J ) ;
titl a
( [num2str (n 1) J ) ; ![]() npmpa1-ueHme cuéQHbåRa nl=nl+l;
npmpa1-ueHme cuéQHbåRa nl=nl+l;
![]() Menp1.,1K cxoxecTL-•1 for j=i+l :
l :nimg
Menp1.,1K cxoxecTL-•1 for j=i+l :
l :nimg
![]() 0 oq=p 0
ÄHoe 1,1306paxeHm n ATI A cpa BHeHMA
0 oq=p 0
ÄHoe 1,1306paxeHm n ATI A cpa BHeHMA
![]() 0
Eb1neneHHOe c yge rroM "uewrpa nnxecnm"
0
Eb1neneHHOe c yge rroM "uewrpa nnxecnm"
![]() 0
Bbl-1MCJ1eH1„1e eBKJIMAOB01h Me rpMKM ed=test—base; clast (n 2) =sqrt (sum (sum
(ed. *ed) ) ) ;
0
Bbl-1MCJ1eH1„1e eBKJIMAOB01h Me rpMKM ed=test—base; clast (n 2) =sqrt (sum (sum
(ed. *ed) ) ) ;
![]() 0
npmpa1.ueH1,1e cgéTHMKa n2=n2+1; end end
0
npmpa1.ueH1,1e cgéTHMKa n2=n2+1; end end ![]() nocnpoeHme
KJ-raCC1@MKaUMOHHOj'1 nemaporpaMMb1 Z=linkage (c last, ' average ' ) ; figure;
dendrogram (Z) ;
nocnpoeHme
KJ-raCC1@MKaUMOHHOj'1 nemaporpaMMb1 Z=linkage (c last, ' average ' ) ; figure;
dendrogram (Z) ;
![]()
![]()
Вначале выполняются инициализация переменных и
резервирование памяти для некоторых данных. Поскольку исходные положения
символов имеют достаточно существенный разброс на плоскости изображений (рис.
8.4, цифры сверху — условный номер графического символа), в цикле загрузки
происходит определение «центров тяжести» графических образов при помощи свёртки
с двумерной функцией распределения Гаусса. По максимальному значению матрицы,
являющейся результатом свёртки (рис. 8.5, цифры сверху — условный номер графического
символа и координаты максимального значения свёртки), определяется условная
точка — «центр тя![]() графического объекта. Выделенные
центрированные графические объекты представлены на рис. 8.6 (цифры сверху —
условный номер графического символа). По осям рис. 8.4—8.6 приведены координаты
пространства изображений.
графического объекта. Выделенные
центрированные графические объекты представлены на рис. 8.6 (цифры сверху —
условный номер графического символа). По осям рис. 8.4—8.6 приведены координаты
пространства изображений.

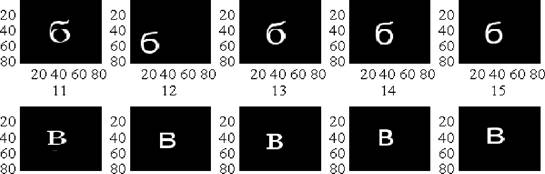
20 40 ба за 2а4а ба 80 20 40 60 за 2040 ба за да 60 за
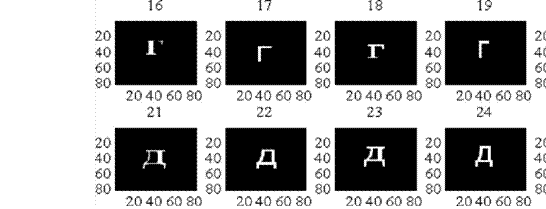
Рис. 8.4. Визуализация исходных изображений
![]()
![]() 20
20
40
60
80
20 40 60 80 2040 60 80 20 40 60 80 20 40 60 80 20 40 60 80 б, (40,40) 7, (55,20) е, (43,37) 9, (43,35) 10, (43,35)
![]() 20
20
40
60
80
20 40 60 80 2040 60 80 20 40 60 80 20 40 60 80 20 40 60 80
1 1, (40,37) 12, (43,38) 13, (45,36) 14, (40,37) 15, (38,37)
![]() 20
20
40 60 во
20 40 60 80 2040 60 80 20 40 60 80 20 40 60 80 20 40 60 80
16, (34,37) 17, (39,37) 18, (38,40) 19, (34,37) 20, (35,35)
![]() 20
20
40
60
80
20 40 60 80 2040 60 80 20 40 60 80 20 40 60 80 20 40 60 80
21, (40,43) 22, (41 ,43) 23, (36,42) 24, (38,40) 25, (40,43)
![]() 20
20
40
60
80
20 40 60 80 2040 60 80 20 40 60 80 20 40 60 80 20 40 60 80 Рис. 8.5. Визуализация результатов свёртки с целью определения «центров тяжести» графических объектов

10 20 зо 10 20 зо 10 20 зо 10 20 зо 10 20 зо

![]() 10
20 зо 10 20 зо 10 20 зо
10
20 зо 10 20 зо 10 20 зо
10 20 зо 10 20 зо 10 20 зо Рис. 8.6. Визуализация выделенных графических объектов для последующей кластеризации
173
![]()
В соответствии с вычисленной евклидовой метрикой (8.8) осуществляется классификация графических образов. Результаты классификации приведены на рис. 8.7: видно, что все символы корректно распределены по группам (см. рис. 8.4—8.6), исключение составляют 21 и 23 («кд»), это связано со значительной вариабельностью начертания символов данной группы. При сравнении расстояний внутри группы и между группами можно сделать вывод об устойчивости алгоритма. Наилучшим образом были классифицированы символы группы Введение дополнительных параметров кластеризации позволяет повысить устойчивость, зачастую применяются дополнительные способы обработки информации, для графических изображений это может быть векторизация, скелетонизация и др.
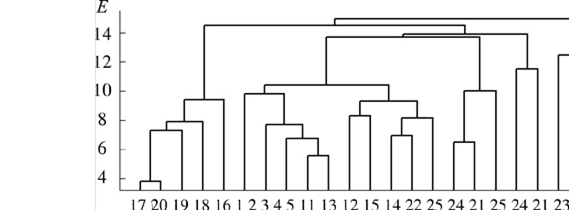 1 2 3 4 5 l l
В 12 15 1422 25 2421 25 2421 23 6 7 9 10 8 d
1 2 3 4 5 l l
В 12 15 1422 25 2421 25 2421 23 6 7 9 10 8 d
Рис. 8.7. Дендрограмма классификации графических символов d — условный номер графического символа, Е — евклидова метрика
В морфологическом анализе цифровых сигналов можно выделить
два этапа распознавания: морфем (элементарных образов) и некоторых
морфологических групп, которые могут формировать образы различной сложности. В
практической системе распознавания образов анализ может выполняться как от
частного к общему (от отдельных морфем к группам) ![]() индуктивный, так и
наоборот (от морфологической группы к морфемам)
индуктивный, так и
наоборот (от морфологической группы к морфемам) ![]() дедуктивный. Морфемы
могуг образовывать фрактальные конструкции, если неделимые морфологические
элементы на одном уровне содержат морфологические группы другого уровня.
Например, амплитуда речевого звукового сигнала представлена на рис. 8.8; видно,
что периоды произнесения слов и пауз между словами хорошо различимы. При
дедуктивном подходе на некотором этапе распознавания звуковых образов можно
выделить периоды произнесения слов и считать, что такие периоды неделимы, т.е.
являются морфемами, на следующем этапе детализации возможно анализировать
каждый выделенный фрагмент, находя в нём определённые
дедуктивный. Морфемы
могуг образовывать фрактальные конструкции, если неделимые морфологические
элементы на одном уровне содержат морфологические группы другого уровня.
Например, амплитуда речевого звукового сигнала представлена на рис. 8.8; видно,
что периоды произнесения слов и пауз между словами хорошо различимы. При
дедуктивном подходе на некотором этапе распознавания звуковых образов можно
выделить периоды произнесения слов и считать, что такие периоды неделимы, т.е.
являются морфемами, на следующем этапе детализации возможно анализировать
каждый выделенный фрагмент, находя в нём определённые
174
![]()
морфологические элементы их группы и последовательности. На практике для распознавания звуковых образов, например речи, более эффективно работать с сигналом в частотной или в частотной и временной областях. Это обусловлено тем, что при восприятии звука решающее значение имеет амплитуда присутствующей в сигнале частоты, а не фаза.
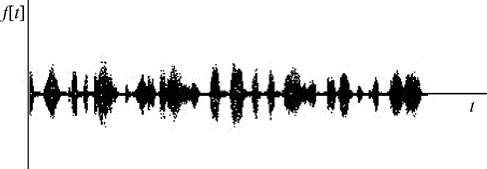
Рис. 8.8. Временная диаграмма звукового потока речи
Рассмотрим пример индуктивного подхода: в некотором цифровом сигнале идентифицировать достаточно сложный объект по присугствию в нём заранее известной морфемы.
Немаловажным этапом при распознавании образов, в частности при морфологическом анализе, является подготовка морфологических препаратов. Под подготовкой подразумевается приведение элементов цифрового сигнала к виду, более удобному для обработки, например, выделение границ объектов, скелетонизация. Границы объектов позволяет выделять операция дифференцирования, которую можно выполнить с использованием свёртки, например, для двумерного сигнала с помощью функций рассеяния точки вида (4.14)—(4.16).
Схожие (например, по цвету или яркости) и/или соприкасающиеся области могут быть объединены, для этого используется алгоритм заливки с последовательным перебором направлений, обычно реализуемый рекурсивно, но при ограниченных объёмах памяти и значительных областях, подлежащих заливке, — в виде цикла.
При выделении морфологических препаратов также используется скелапонизация, т.е. для графического, точечного изображения выделяется некоторый многосвязный (для двумерного изображения — плоский) граф, ему соответствующий [85].
Полученные морфологические препараты классифицирукот по некоторым признакам, находя сходства и различия с некоторыми базовыми элементами. В некоторых случаях морфологический анализ позволяет получить существенные результаты при решении задачи распознавания образов.
175
![]()
В системах распознавания образов широко применяются нейронные сети, моделью которых служат биологические системы [24], поскольку единицей восприятия, или мыслительной единицей, живых организмов является образ. Нейронные сети обычно решают комплекс задач, в том числе выделение полезного сигнала из шума, разделение сигнала на некоторые фрагменты (пототовка препарата), непосредственно распознавание и классификщия образа. Их основная особенность — способность к обучению, что позволяет формировать алгоритм принятия решения, сложно формализуемый привычными способами. Поэтому вычислительные системы, построенные на базе нейронных сетей, иногда называют интеллектуальными системами.
В силу того что большинство нейронных сетей ориентированы на решение определённого круга задач, существует значительное число их разновидностей. Основным элементом любой нейронной сети является ячейка, моделирующая работу биологического нейрона. Нейрон имеет несколько входов (рис. 8.9), по аналогии с синаптическими волокнами биологического нейрона, и единственный выход — аксон. Сигналы, поступающие на вход нейрона, подаются в качестве аргумента на функцию активации нейрона:
![]()
где N — число входов (синапсов) нейрона; х. — сигнал на i -м входе нейрона; а весовой коэффициент i -го входа нейрона; f — функция активации нейрона.
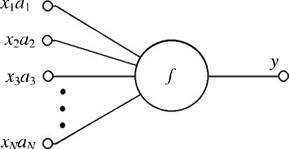
Рис. 8.9. Функциональная структура нейрона
На выходе нейрона получается значение его функции состояния; задача обучения нейрона состоит в выборе весовых коэффициентов, обеспечивающих наилучшее решение. Обучение обычно производится на некоторой, заранее сформированной, выборке, ещё одна выборка обычно используется для оценки качества обучения. Для активации нейрона обычно используется нелинейная функция, например, пороговая, сигмоид и др.
176
![]()
На сегодняшний день выбор оптимальной структуры сети для решения конкретной задачи недостаточно формализован [14, 85]. Помимо того, нейронные сети ориентированы на задачи, решение которых затруднительно другими методами, и именно такие задачи могуг иметь нестандартные исходные условия, значительно отличающиеся от обучающих выборок. Качество решения конкретной задачи зависит от обучения нейронной сети, при котором, однако, невозможно учесть существенные отклонения от ограниченной обучающей выборки. Преодолеть эту проблему позволяет увеличение обучающей выборки и размеров нейронной сети, но при этом возникает так называемая проблема «проклятия размерности».
Отличительной особенностью нейронных сетей является возможность интеграции последовательных этапов распознавания образа.
Практические исследования проблемы распознавания образов и изучение искусственных нейронных сетей способствуют пониманию механизмы работы мозга и высшей нервной деятельности.
ЗАКЛЮЧЕНИЕ
Исследования в области информационных технологий значительно
продвинулись с развитием вычислительной техники. Особое значение для
человечества имеют развитие сетевых технологий и возможность доступа к
огромному объёму информации. В современных условиях доступность информации
определяется не только пропускной способностью вычислительных сетей, но и
эффективностью методов обработки данных, т.е. анализа, синтеза и моделирования.
Таким образом, развитие научных основ построения методов и средств
автоматической и автоматизированной обработки изображений в вычислительных
системах с применением CALSтехнологий и распределённых вычислений при
внутренней и межсистемной интероперабельности является актуальным направлением
научных исследований в сфере создания систем автоматизированного проектирования
(САПР), позволяющих решать научную задачу повышения эфф ![]() тивности использования
вычислительных ресурсов. Возможности современных вычислительных систем
определяют их «интеллектуальность», заключающуюся в способности к самоорганизации
и упорядочиванию информации. Всё это благодаря обратным связям определило
развитие не только вычислительной техники и технологии, но и физиологии,
психологии личности и социума. Значительный вклад в понимание многих механизмов
высшей нервной деятельности человека и животных привнесло исследование
нейронных сетей.
тивности использования
вычислительных ресурсов. Возможности современных вычислительных систем
определяют их «интеллектуальность», заключающуюся в способности к самоорганизации
и упорядочиванию информации. Всё это благодаря обратным связям определило
развитие не только вычислительной техники и технологии, но и физиологии,
психологии личности и социума. Значительный вклад в понимание многих механизмов
высшей нервной деятельности человека и животных привнесло исследование
нейронных сетей.
Многие аспекты современных информационных технологий, подобно «мирному атому», содержат в себе реальные утрозы для отдельных людей и целых социальных групп. Поэтому хочется видеть цивилизацию, применяющую достижения науки лишь в созидательном направлении, позволяющем развиваться и реализовывать свой творческий потенциал каждому человеку в гармонии с природой и внутреннем миром высокоразвитой личности.
СПИСОК ЛИТЕРАТУРЫ
1. Аверин Д. В., Лихарев К. К. Когерентные колебания в туннельных переходах малых размеров // ЖЭТФ. 1986. Т. 90, вып. 2. С. 733—743.
2. Агафонцев Д. С. Устойчивость и коллапс солитонов вблизи перехода от мягкой к жесткой бифуркации в системах гидродинамического типа: Дис. канд. физ.-мат. наук. Черноголовка, 2008. 70 с.
З. Аксентов Ю. В., Джакония В. Е., Жебель Б. Г., Колин К. Т., кондратьев А. Г. Телевидение / Под ред. П.В. Шмакова. М.: Связь, 1970. 540 с.
4. Александров Е Н., Борисов В. В., Капин Г. С., Кукеков Г. А., Карпенко Л. Н., Кузнецов В. Е., лунин В. П., Моисеев М. Б., Пирятинский А. В.,
Соснин В. А., Тонконогов Е. Н., Филиппов Ю. А., Ярмаркин М. К. Проектирование электрических аппаратов. Л.: Энергоатомиздат, 1985. 448 с.
5. Анго А. Математика для электро- и радиоинженеров. М.: Наука, 1967. 780 с.
6. Андерсон Дж.-А. Дискретная математика и комбинаторика. М.: Вильямс, 2004. 960 с.
7. Андреева Г.М. Социальная психология: векторы новой парадигмы.
Психологические исследования. 2009. N2 1(3) [Электронный ресурс] : <http://www.psystudy.ru/index.php/num/2009n1-3/55-andreeva3>.
8. Анищенко В. С., Нейман А. Б., Мосс Ф., ШИЛТНСКИЙ-ГеЙер Л. стохастический резонанс как индуцированный шумом эффект увеличения степени порядка // УФН. 1999. Т. 1 69, 1. С. 7-38.
9. Антонов В. Ф. Липидные поры: стабильность и проницаемость мембран // Соросовский образовательный журнал. 1998. N2 10. С. 10—17.
10. Антонов В. Ф., Смирнова Е. Ю., Шевченко Е. В. Липидные мембраны при фазовых превращениях. М.: Наука, 1992. 125 с.
11. Бахвалов Н. С., Воеводин В. В. Современные проблемы вычислительной математики и математического моделирования. Т. 1. Вычислительная математика. М.: Наука, 2005. 343 с.
12. Бегунов Б. Н. Геометрическая оптика. М.: изд-во мгу, 1966. 209 с.
13. Большой энциклопедический словарь. М.: Астрель, 2008. 1248 с.
14. Бондаренко И. Б., Ганшин Ю. А., Гераничев В. Н. синтез оптимальных искусственных нейронных сетей с помощью модифицированного генетического алгоритма // Научно-технический вестник информационных технологий, механики и оптики. 2012. -N9 2 (78). С. 51—55.
15. Бугатенко Е. И., титов В. С., Труфанов М. И. способ определения коэффициентов сферической аберрации. Патент -N2 2295712 РФ, МКИ GOlMl 1/02. Опубл. 20.03.2007. Бюл. 8. 6 с.
16. Васиченко О. Н. Теоретико-числовые алгоритмы в криптографии. М.: мцнмо, 2003. 328 с.
17. Ватолин Д., Ратушняк А., Смирнов М., Юкин В. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. М.: ДИАЛОГ-МИФИ, 2003. 384 с.
18. Висвани В. Полный справочник по MySQL. М.: Вильямс, 2006. 528 с.
19. Владимирский Б. М. Активные процессы на Солнце и биосфера: Автореф. дис. д-ра физ.-мат. наук. Пущино, 1997. 28 с.
20. Щ, М., Т., НейДер Дж., ШрайнерД. OpenGL руководство по программированию. Библиотека программиста. СПб: Питер, 2006. 624 с.
21. Вуколов Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL. М.: Форум, 2004. 464 с.
22. Выгодский М. Я. Справочник по математике. М.: АСТ, 2011. 1055 с.
23. Вяткин А. П. Психология экономической социализации личности в условиях изменяющегося общества: Автореф. дис. д-ра педаг. наук. СПб: РГПУ им. А.И. Герцена, 2012. 45 с.
24. Гаазе-Рапопорп М. Г., кокишйский Н. В., Берг А. И., Брайнес• С. Н. и др. Проблемы бионики. М.: Наука, 1973. 528 с.
25. Гад С. Я., Крючков А. Н., Яшин А. А. Биофизика полей и излучений и биоинформатика / Под ред. Е. И. Нефедова, А. А. Хадарцева, А. А. Яшина. Тула: тул ГУ, 2000. 286 с.
26. Галушкин А. И. Нейрокомпьютеры и их применение. М.: ИПРЖР, 2000. 528 с.
27. Гельман Р. Н., Цунц А. Л. Лабораторная калибровка цифровых камер с большой дисторсией // Геодезия и картография. 2002. N2 7. С. 23—31.
28. Гербер Р., Бик А., Смит К., Тиан К. Оптимизация ПО. Сборник рецептов. СПб: Питер, 2010. 325 с.
29. Гинзбург В. Л., Рухадзе А. А. Волны в магнитоактивной плазме. М.: Наука, 1975. 256 с.
30. Голыгин В. А., Сажин В. И., Унучков В. Е. Коррекция модели ионосферы по данным о максимально-применимых частотах реперных радиолиний // Исследовано в России. 2006 [Электронный ресурс]: <http://zhurnal.ape.relarn.ru/articles/2006/255.pdf>.
31. ГольДен6ерг Л. Г., Матюшкин Б. Д., Поляк М. Н. Цифровая обработка сигналов: Справочник. М.: Радио и связь, 1985. 312 с.
32. Гороховатский В. А., Передрий Е. О. Корреляционные методы распознавания изображений путём голосования систем фрагментов //
![]() Тнформатика.
Тнформатика. ![]() 2009. N2 1. С. 74—81.
2009. N2 1. С. 74—81.
33. Гридин В. Н., Титов В. С., Труфанов М. И. Адаптивные системы технического зрения. М.: Наука, 2009. 441 с.
34. Гришенцев А. Ю. Аппаратно-программный комплекс ИПЧ блоксхема реализации и некоторые результаты применения // Естественные и технические науки. М.: Компания Спутник +, 2008. N2 4(36). С. 281—284.
35. Гришенцев А. Ю. Моделирование распределения плотности тока в сложном неоднородном проводнике. Ч. 1 // Науч.-техн. вестн. СПбГУИТМО. 2006. вып. 29. С. 87-94.
36. Гришенцев А. Ю. Моделирование распределения плотности тока в сложном неоднородном проводнике. Ч. 2 // Науч.-техн. вестн. СПбГУИТМО. 2006. вып. 29. С. 95-99.
37. Гришенцев А. Ю. Свойства преобразования п-мерных цифровых сигналов по базису прямоугольных всплесков // Науч.-техн. вестн. информационных технологий, механики и оптики. 2012. N2 5 (81). С. 75—79.
38. Гришенцев А. Ю. Способ сжатия изображения. Патент N9 2500067 РФ. Опубл. 27.11.2013.
39. Гришенцев А. Ю. Эффективное сжатие изображений на базе дифФеренциального анализа // Журн. радиоэлектроники. 2012. N2 11 [Электронный ресурс]: <http://jre.cplire.ru/jre/nov12/index.html>.
40. Гришенцев А. Ю., Бондаренко И. Б., Коробейников А. Г. Программа анализа алгоритмов декомпозиции многомерных цифровых сигналов «(Декомпозиция сигналов». Программа для ЭВМ N2 2013614439. Опубл. 07.05.2013.
41. Гришенцев А. Ю., Коробейников А. Р. Декомпозиция п-мерных цифровых сигналов по базису прямоугольных всплесков // Науч.-техн. вестн. информационных технологий, механики и оптики. 2012. N2 4 (80). с. 75-79.
42. Гришенцев А. Ю., Корооейников А. Г. Математическое моделирование процессов вертикального зондирования ионосферы // Тр. Междунар. конгр. по интеллектуальным системам и информационным технологиям AIS-IT' 11. М.: Физматлит, 2011. Т. 1. С. 418-424.
43. Гришенцев А. Ю., Коробейников А. Г. Обратная задача радиочастотного зондирования ионосферы Журн. радиоэлектроники. 2010. -NQ 10 [Электронный ресурс] : <http://jre.cplire.ru/jre/oct 10/6/text.htm1>.
44. Гришенцев А. Ю., Коробейников А. Г. Обратная задача радиочастотного зондирования ионосферы // Сб. тр. IV Всерос. конф. «Радиолокация и радиосвязь». М.: ИРЭ РАН, 2010. С. 201—207.
45. Гришенцев А. Ю., Коробейников А. Г. Программа обработки и анализа данных ионосферного спектрографа АИС-М <<SkySpectrum». Программа для ЭВМ 201161756928. Опубл. 28.09.2011.
46. Гришенцев А.Ю., Коробейников А.Г. Разработка модели распределения плотности токов при возбуждении ионосферы высокочастотным облучением // Изв. вузов. Приборостроение. 2010. .N912 (53). С. 41—47.
47. Гришенцев А. Ю., Коробейников А. Г. Разработка математической модели решения обратной задачи вертикального зондирования ионосферы на основе методов распознавания образов // Сб. матер. Всерос. науч.практ. конф. «Информационные технологии в профессиональной деятельности и научной работе». Йошкар-Ола: Марийский государственный технический университет, 2011. Ч. 1. С. 46—53.
48. Гришенцев А. Ю., Коробейников А. Г. Разработка модели решения обратной задачи вертикального зондирования ионосферы // Науч.-техн. вестн. информационных технологий, механики и оптики. 2011. N2 2 (72). с. 109-112.
49. Гришенцев А. Ю., Коробейников А. Г. Способ построения спектра п-мерных неразделимых цифровых сигналов. Патент N9 2484523 РФ. Заявл. от 29.06.2011.
50. Гришенцев А. Ю., Коробейников А. Г. Увеличение скорости сходимости метода конечных разностей на основе использования промежуточного решения // Сб. матер. Всерос. науч.-практ. конф. «(Информационные технологии в профессиональной деятельности и научной работе». Йошкар-Ола: Марийский государственный технический университет, 2012. ч. 2. с. 9-14.
51. Гришенцев А. Ю., Коробейников А. Г. Улучшение сходимости метода конечных разностей с помощью вычисления промежуточного решения // Науч.-техн. вестн. информационных технологий, механики и оптики. 2012. JV2 З (79). С. 124-127.
52. Гришенцев А. Ю., Муромцев Д. И. Система управления данными наблюдений солнечно-земной физики <<MI». Программа для ЭВМ N9 2011615714. 21.07.2011.
53. Гришенцев А. Ю., Ярош А. М. Анализ зависимости числа клинических случаев от некоторых факторов природного происхождения // Сб. тр. «(Информатика и вычислительная техника>> / Под ред. В. Н. Негоды. Ульяновск: УлГТУ, 201 О. С. 579-586.
54. Гришенцев А. Ю., Ярош А. М., Коробейников А. Г. Особенности влияния солнечного радиоизлучения на число клинических состояний человека // Журн. радиоэлектроники. 2010. -N2 11 [Электронный ресурс]: <http://jre.cp1ire.ru/jre/nov1 0/3/text.htm1>.
55. Гусятинский И. А., Нелшровский А. С., Соколов А. В., ТРОИЦКИЙ В. Н. Дальняя тропосферная радиосвязь. М.: Связь, 1968. 248 с.
56. Давыдов А. В. Цифровая обработка сигналов: Тематические лекции. Екатеринбург: УГГУ, 2007 [Электронный ресурс ] : <http://www.prodav.narod.ru/dsp/index.html>.
57. Девятков Н. Д., Голант М. Б., Бецкий О. В. Миллиметровые волны и их роль в процессах жизнедеятельности. М.: Радио и связь, 1991. 168 с.
58. Девятков Н. Д., Голант М. Б., БецкиЙ О. В. особенности медикобиологического применения миллиметровых волн. М.: ИРЭ РАН, 1994.
59. Цейт К. Дж. Введение в системы баз данных. М.: Вильямс, 2005. 1328 с.
60.
![]() К. С., Нейман Л. Р., Коровкин Н. В.,
Чечурин В. И. теоретические основы электротехники. СПб: Питер, 2006. Т. 2. 576
с.
К. С., Нейман Л. Р., Коровкин Н. В.,
Чечурин В. И. теоретические основы электротехники. СПб: Питер, 2006. Т. 2. 576
с.
61. Домбровский А. Н. Стохастический резонанс и фильтрация сигналов в нелинейных радиотехнических системах: Автореф. дис. канд. техн. наук. М., 2009.
62 Думин Ю. В. Концентрация носителей заряда в метастабильной плазме с сильной кулоновской неидеальностью // Прикладная физика. 1999. N2 5. С. 18-21.
63. Зверев В. А., Стромков А. А. Выделение сигналов из помех численными методами. Нижний Новгород: ИПФ РАН, 2001. 188 с.
64. Зевеке Г. В., Ионкин П. А., Нетушил А. В. Основы теории цепей. М.: Энергия, 1975. 752 с.
65. Зимичев А.М. Психология политической борьбы. СПб: Санта, 1993. 160 с.
66. Зуев В. В., Розова С. С. Проблема способа бытия таксона в биологической таксономии // Вопросы философии. 2003. N2 2. С. 90—103.
67. Ильин В. А., Поздняк Э. г. Линейная алгебра. М.: Наука, 1974. 296 с.
68. Ильичёв А. Т. Уединённые волны в моделях гидродинамики. М.: Физматлит, 2003. 256 с.
69. Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей. Справочная книга. Л.: Энергоатомиздат, 1986. 488 с.
70. Калинин А. И., Черенкова Е. Л. Распространение радиоволн и работа радиолиний. М.: Связь, 1971. 450 с.
71. Кант И. Критика чистого разума / Пер. с нем. Н. Лосского; под ред. Ц. Г. Арзакаяна и М. И. Иткина. М.: эксмо, 2006. 736 с.
72. Кантор Г. Труды по теории множеств. М.: Наука, 1985. 431 с.
73. Касперски К. Техника оптимизации программ (+CD). СПб: БХВПетербург, 2003. 464 с.
74. Кестр У. Проектирование систем цифровой и смешанной обработки сигналов. М.: Техносфера, 2010. 328 с.
75. Кии Ю. В. Модернизация ионосферной станции <<АИС». Отчёт по теме 690. Троицк: ИЗМИРАН, 2002. 24 с.
76.
Киреев О. С. Нейрокалибровка стереопары // ![]() машини i
системи. 2005. М 1. С. 13—25.
машини i
системи. 2005. М 1. С. 13—25.
77. Клюев Н. И. Информационные основы передачи сообщений. М.: Сов. радио, 1966. 360 с.
78. Корис Р., Шмидт-Вальтер Х Справочник инженерасхемотехника. М.: Техносфера, 2008. 608 с.
79. Коробейников А. Г., Гатчин Ю. А. Математические основы криптологии. СПб: СПбГУ ИТМО, 2004. 106 с.
80. Коробейников А. Г., Копытенко Ю. А., Исмагилов В. С, Гришенцев А. Ю. Интеллектуальные системы магнитных измерений на железнодорожных сортировочных станциях // Сб. докл. междунар. науч. -практ. конф. <<Автоматизация и механизация технологических процессов на сортировочных станциях». М., 2010. С. 73—75.
81. Коротков К. Г. Основы ГРВ биоэлектрографии. СПб: спбгитмо, 2001. 360 с.
82. Котельников В. А. О пропускной способности <<эфира» и проволоки в электросвязи // Сб. Всесоюз. энергетический комитет. Матер. к I съезду по вопросам и технической реконструкции дела связи и развития слаботочной промышленности. М.: Управление связи РККА, 1933.
83. Котельникова Н. В. К 100-летию со дня рождения академика Котельникова Владимира Александровича. 2008 [Электронный ресурс] : <http://www.ras.ru/news/shownews.aspx?id=59dc9c27-d249-486e-b5372edfb02a0ede>.
84. Кувшинов С. С. Методы сокрытия больших объёмов данных на основе стеганографии: Дис. канд. техн. наук. СПб: СПбГУ ИТМО, 2010.
85. Лайонс Р. Цифровая обработка сигналов. М.: Бином-Пресс, 2009. 656 с.
86. Мандельштам Л. И. Полное собрание трудов. М.: Изд-во Академии наук СССР, 1955. 512 с.
87. Мировые центры данных (МЦД) России и Украины [Электронный ресурс]: <http://www.wdcb.ru>.
88.
Михайлов А. П., Чибј,ничев А. Г., Курков В. М., Piatti Е. 1.
Применение цифровых неметрических камер и лазерных сканеров для решения задач
фотограмметрии. Ракурс. 2003 [Электронный ресурс] :
<http://www.racurs.ru/www_downlo![]()
89. Мукушев Б. А. Проблемы формирования нелинейного стиля мышления личности // А1та mater. М.: РУДН, 2009. С. 16—22.
90. НамгалаДзе А. А., Юрик Р. Ю. Математическое моделирование возмущений верхней атмосферы Земли. Российский фонд фундаментальных исследований [Электронный ресурс] : <http://www.rtbr.ru/pics/ 28326ref/file.pdf>.
91. Нефедов Е. И., Протопопов А. А., Хадарцев А. А., Яшин А. А., Биофизика полей и излучений и биоинформатика. Ч. 1. Физикобиологические основы информационных процессов в живом веществе. Тула: изд-во ТулГУ, 1998. 333 с.
92. Нечаев Д. А., Гришенцев А. Ю. Исследование работы прибора «ИПЧ» при различных значениях влажности // Изв. вузов. Приборостроение. 2006. N2 2(49). С. 26—30.
93. Новгородцев А. Б. Теория электромагнитного поля. СПб: Изд-во СПбГТУ, 1994.
94. Новиков С. П., Тайианов И. А. Современные геометрические структуры и поля. М.: МЦНМО, 2005. 584 с.
95. Оппенгейм А., Шафер Р. Цифровая обработка сигналов. М.: Техносфера, 2009. 856 с.
96. Панасенко С. П. Алгоритмы шифрования. СПб: БХВ-Петербург, 2009. 576 с.
97. Пискунов Н. С. Дифференциальное и интегральное исчисления. М.: Интеграл-Пресс, 2005. Т. 2. 544 с.
98. Покровский В. М., Коротько Г. Ф. Физиология человека. М.: Медицина, 1997. Т. 1. 448 с.
99. Пономаренко П Н. Физиотерапия в косметологии. СПб: ВМедА, 2002. 356 с.
100. Прата С. Язык программирования С++. М.: Вильямс, 2013. 1248 с.
101. Программа моделирования электромагнитных, тепловых и механических задач, ELCUT. ООО «Тор>>, 2012 [Электронный ресурс]: <http://elcut.ru/>, MicroCap. MicroCad, Spectrum software [Электронный ресурс]: <http://www.spectrum-soft.com/>.
102. Рубин А. Б. Биофизика. М.: Наука, 2004. Т. 2. 448 с.
103. Самарский А. А., Вабищевич П. Н. Численные методы решения обратных задач математической физики. М.: Изд-во ЛКИ, 2009. 480 с.
104. Самойлов В. О. Медицинская биофизика. СПб: СпецЛит, 2007. 560 с.
105. Селмон Д. Сжатие данных, изображений и звука. М.: Техносфера, 2006. 368 с.
106. Семёнов А. М., Сикарев А. А. Широкополосная радиосвязь. М.: Воениздат, 1970. 280 с.
107. Сергеенко В. С., Баринов В. В. Сжатие данных, речи, звука и изображений в телекоммуникационных системах. М.: РадиоСофт, 201 1 . 360 с. 108. Серов А. В. Эфирное цифровое телевидение DVB-T/H/. СПб: БХВ-Петер6ург, 2010. 464 с.
109. Седжевик Р. Алгоритмы на С++. М.: Вильямс, 201 1. 1056 с.
110. Скиена С. Алгоритмы. Руководство по разработке. СПб: БХВПетербург, 2011. 720 с.
111. Смирнов В. М., Смирнова Е. В. Реконструкция пространственновременной структуры ионосферы по данным спутниковых наблюдений // Современные проблемы дистанционного зондирования Земли из космоса». М.: Изд-во «Институт космических исследований РАН» , 2008. Т. 5. с. 561-566.
112.
Смит С. Цифровая обработка сигналов. М.: ![]() 2011. 720
с.
2011. 720
с.
113.
Создание комплекса научной аппаратуры с новыми информационными
каналами регистрации корпускулярного и электромагнитного излучений Солнца;
приоритетные результаты в наблюдениях солнечной активности и ее воздействий на
Землю со спутника КОРОНАС-Ф (2001 ![]() 2005 гг.). ИЗМИРАН, 2007 [Электронный
ресурс] : <http://www.izmiran.rssi.ru/achievments/press-release>.
2005 гг.). ИЗМИРАН, 2007 [Электронный
ресурс] : <http://www.izmiran.rssi.ru/achievments/press-release>.
114. СОЛОНИНа А. И., Улахович Д. А., Арбузов С. М., Соловьёва Е. Б. Основы цифровой обработки сигналов. СПб: БХВ-Петербург, 2005. 768 с.
115. Стивенс Р., Раго С. UNIX. Профессиональное программирование. СПб: Символ-Плюс, 2007. 1040 с.
116. Стрелкова А. Н., Титов В. С., Труфанов М. И. Патент N2 2292()23 РФ, МКИ G01M1 1/02. Способ определения комы оптической системы. Опубл. 20.01.2007. Бюл. 2. 5 с.
117. Фадеев М. А., Чупрунов Е. В. Лекции по атомной физике. М.: Физматлит, 2008. 612 с.
118. Формалёв В. Ф., Ревезников Д. .Ј. Численные методы. М.: Физматлит, 2004. 400 с.
119. Харкевич А. А. Передача сигналов модулированных шумом // Электросвязь. 1957. N2 11. С. 42-46.
120. Харт Дж. М. Системное программирование в среде Windows. М.: Вильямс, 2005. 592 с.
121. Хлыбов Е. С., Гаврилов Б. Г., Егоров Д. В. Исследование влияния сильных сейсмических событий на полное электронное содержание в ионосфере // Тр. Междунар. Байкальской молодежной науч. шк. по фундаментальной физике. 2006. С. 1 77—180.
122. Хортон А. Visual С++ 2010. М.: Диалектика, 2010. 1216 с.
123. Чобану М. Многомерные многоскоростные системы обработки сигналов. М.: Техносфера, 2009. 480 с.
uvumepamypt)l
![]()
124. Wanupo Jl., CmorcnaaH K0M11b}0TepHoe 3peHue. M.: BHHOM, 2006. 752 c.
125. IllogeæepDm P. A. AuctaHAHOHHoe 30HÅHPOBaHue. MoneJ1u MeTOAbl 06pa60TKH M306paxeHHü. M.: TexHoc(bepa, 2010. 560 c.
126.111mapR F. -T. IIpHMeHeHue BeÜBJ1eTOB ÅOC. M.: TexHocd)epa, 2007. 192 c.
127.3xmep Ill., P06epmc HR. MH0F0flÅepHoe mporpaMMup0BaHue. C116: ITHTep, 2010. 316 c.
128.flR06Jteg O. H. , llagejlbeg A. T. , Mamrocoog C. C. CHYTHHKOBb1Ü MOHHTOPHHF 3ervn-m: Pann03aTMeHHb1Ü MOHHTOPHHF aTMOCdEPb1 Id H0Hoc(EPb1. M.: JIH6p0K0M, 2010. 208 C.
129. AKOBJ1eB O. H. , AKY60B B. ff., Yp}1Å0B B. ff., IlaBeJ1beB A. r. Pacnpocu-paHeHme paAHOBOJIH. M.: JIeHaHA, 2009. 496 c.
130. A Big Surprise from the Edge of the Solar System. NASA. 2012 [Electronic resource]: <http://www.nasa.gov/mission_pages/voyager/ heliosphere-surprise.html>.
131. Background to Ionospheric Sounding [Electronic resource]: <http://ulcar.uml.edu/DPS.htm>.
132. Benzi R., Sutera A., Vulpiani A. Some Problems in Statistical Physics // J. Phys / Ed. by G. H. Weiss. SIAM, Philadelphia, 1992. P. 453-467.
133. Benzi R., Parisi G., Sutera A., Vulpiani A. Stochastic resonance in climatic change // Tellus. 1982. Vol. 34. P. 10-16.
134. Biggs D.S. C. Acceleration of Iterative Image Restoration Algorithms // Applied Optics. 1997. Vol. 36, N 8. P. 1766-1775.
135. Boschi D., Branca S., DeMartini F., Hardy L., Popescu S. Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels // Phys. Rev. Lett. 1998. Vol. 80.
![]() D.,
Pan J.-W., Mattie 1<., Eibl M., Weinfurter H., Zeilinger A. Experimental
Quantum Teleportation // Nature. 1997. Vol. 390. P. 575-579.
D.,
Pan J.-W., Mattie 1<., Eibl M., Weinfurter H., Zeilinger A. Experimental
Quantum Teleportation // Nature. 1997. Vol. 390. P. 575-579.
137. Bremermann H. J. Optimization through Evolution and Recombination // Self-Organizing Systems / Ed. by M. C. Yovits and S. Cameron. Washington: Spartan, 1962. P. 93—106.
138. Canadian Advanced Digital Ionosonde. System Manuals / Scientific Instrumentation Limited. Canada, 2009. 22 p.
139. coolev J. W, J. W. An Algorithm for the Machine Calculation of Complex Fourier Series // Mathematics Computation. 1965. Vol. 19. P. 297-301.
140. DeHaan G. Progress in Motion Estimation for Video Format Conversion// IEEE Trans. on Consumer Electron. 2000. Vol. 46, N 3. P. 449-450.
Jiumepamypbl
141. DeMarco G. Minority Rules: Scientists Discover Tipping Point for the Spread of Ideas. Rensselaer Polytechnic Institute (RPI). 2011 [Electronic resource]: <http://news.rpi.edu/update.do?artcenterkey=2902>.
142. Douglass J. K. et al. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance // Nature. 1993. Vol. 365. P. 337-340.
143. Einstein A. , Podolsky B., Rosen N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? // Phys. Rev. 1935. Vol. 47(10). P. 777-780.
144. Fauve S. , Heslot F. Stochastic resonance in a bistable system // Phys. Lett. A. 1983. vol. 97. P. 5-7.
145. Fraenkel A, Klein S. Robust Universal Complete Codes for Transmission and Compression // Discrete Applied Mathematics. 1996. Vol. 64.
![]()
146. Gammaitoni L et al. Observation of stochastic resonance in bistable electron-paramagnetic-resonance systems // Phys. Rev. Lett. 1991. Vol. 67. P. 1799-1802.
147. Gray J. The Transaction Concept: Virtues and Limitations. Tandem Computers Incorporated, 1981.
148. Grigorenko A. N., Nikitin P. 1., Konov V. 1. Magnetostochastic Resonance // sov. Phys. JETP Lett. 1990. Vol. 52. P. 993.
149. Guide to Reference and Standard Ionosphere Models. American Institute of Aeronautics and Astronautics, 1999. 55 p.
150. Hanisch R. J., While R. L., and Gilliland R. L. Deconvolution of Hubble Space Telescope Images and Spectra. Deconvolution of Images and Spectra / Ed. by P. A. Jansson. Boston, MA: Academic Press, 1997. P. 310-356.
151. Heikkila J., Silven O. A. Four-step Camera Calibration Procedure with Implicit Image Correction // CVPR97. 1997. P. 1106-1112.
152. Heisenberg W. Physikalische Prinzipien der Quantentheorie. Mannheim, 1958. 45 s.
153. ITU-R Recommendation BT.601-7. Studio encoding parameters of digital television for standard 4:3 and wide-screen 16:9 aspect ratios. ITU, Geneva, Switzerland, 201 1 .
154. ITU-R Recommendation BT.709, Basic Parameter Values for the HDTV Standard for the Studio and International Programme Exchange. ITU, Geneva, Switzerland, 2002.
155. Keitll J. Video Demystified: a Handbook for the Digital Engineer. LLH Technology Publishing, 2001.
156. Levin J. E., Miller J. P. Broadband Neural Encoding in the Cricket cereal Sensory System Enhanced by Stochastic Resonance // Nature. 1996. Vol. 380. P. 165-168.
uvumepamypt)l
![]()
157. Longuet-Higgins M. S. Capillary-gravity Waves of Solitary Type and Envelope Solitons on Deep Water // J. Fluid Mech. 1993. vol. 252. P. 703-711.
158. Malvar H. S., Sullivan G. J. Transform, Scaling & Color space Impact of Professional Extensions. ISO/IEC JTC/SC29/WG11 and ITU-T SG16 Q.6 Document JVT-H031. Geneva, 2003.
159. MATLAB GPU Computing Support for NVIDIA CUDA-Enabled GPUs. 2012 [Electronic resource]: <http://www.mathworks.com/discovery/ matlab-gpu.html>.
160. McNamara B., Wiesenfeld 1<., Roy R. Observation of Stochastic Resonance in a Ring Laser // Phys. Rev. Lett. 1988. vol. 60. P. 2626-2629.
161.MSDN. Microsoft, [Electronic resource] : <http://msdn.microsoft.com>.
162. National Oceanic and Atmospheric Administration (NOAA) [Electronic resource]: <http://www.noaa.gov/>.
163. NOAA's National Geophysical Data Center (NGDC) [Electronic resource]: <http://www.ngdc.noaa.gov/>.
164. Rasmussen C. E. , Schunk R. W. A Three-dimensional Time-dependent Model of the Plasmasphere // J. Geophys. Res. 1990. Vol. 95. P. 6133-6144.
165. Richmond A. D., Ridley E. C., Roble R. G. A Thermosphere/ionosphere General Circulation Model with Coupled Electrodynamics // Geophys. Res. Lett. 1992. Vol. 19, N 6. P. 601-604.
166. Rogers D. Procedural Elements for Computer Graphics. McGraw-Hill, 1985. P. 68-81.
167. Rvcrofl M. J. Solar-terrestrial energy program: handbook of ionospheric models // J. of Atmospheric and Solar-Terrestrial Physics. Elsevier Science Publishing Company, Inc., 1998. P. 403—404.
168. X., Wilkens L., Moss F. Noise-mediated spike Timing Precision from Aperiodic Stimuli in an Array of Hodgekin-Huxley—type Neurons // Phys. Rev. Lett. 1996. Vol. 77. P. 4679-4682.
169. Piggott W. IR., K. Rawer. URSI handbook of Ionogram Interpritation and Reduction. INAG (Ionospheric Network Advisory Group). World data center A. National Academy of Sciences. Washington, 1972. 145 p.
170. Price D. J. de Solla. An Ancient Greek Computer // Scientific American. 1959. June. P. 60-67.
171.
saupe D., Hamzaoui IR., Hartenstein H. Fractal Image Compression ![]() An
introductory overview // Fractal Models for Image Synthesis, Compression, and
Analysis. ACM SIGGRAPH96 [Electronic resource]: <Course Notes,
http://www.factbites.com/topics/Fractal-co mpression>.
An
introductory overview // Fractal Models for Image Synthesis, Compression, and
Analysis. ACM SIGGRAPH96 [Electronic resource]: <Course Notes,
http://www.factbites.com/topics/Fractal-co mpression>.
172. Shannon C. E. A mathematical theory of communication // The Bell System Techn. J. 1948.V01. 27. P. 379—423, 623-656.
Jiumepamypbl
173. Simonotto E., Rani M., Seife C. et al. Visual Perception of Stochastic Resonance // Phys. Rev. Lett. 1997. vol. 78. P. 1186-1189.
174. Space Weather Prediction Center [Electronic resource]: <http://www.swpc.noaa.gov/>.
175. The Solar Dynamics Observatory. NASA, 2012 [Electronic resource]: <http://sdo.gsfc.nasa.gov/>.
176. Tsai R. Y. A Versatile Camera Calibration Technique for Highaccuracy 3D Machine Vision Metrology Using off-theshelf TV Cameras and Lenses // IEEE Int. J. on Robotics and Automation. 1987. Vol. 3. P. 323-344.
177. United States Geological Survey's (USGS) [Electronic resource]: <http://earthquake.usgs.gov/>.
178. University of Southern California. The USC-SIPI Image Database. US, 2012 [Electronic resource]: <http://sipi.usc.edu/database/>.
Научное издание
Гришенцев Алексей Юрьевич Коробейников Анатолий Григорьевич
МЕТОДЫ И МОДЕЛИ
ЦИФРОВОЙ ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
Налоговая льгота — Общероссийский классификатор продукции
![]()
Подписано в печать 02.06.2015. Формат 60х 84/16. Печать цифровая. Усл. печ. л. 12,0. Тираж 32. Заказ 13160b.
![]()
Отпечатано с готового оригинал-макета, предоставленного Издательством Политехнического университета, в Типографии Политехнического университета.
195251, Санкт-Петербург, Политехническая ул., 29. тел.: (812) 552-77-17; 550-40- И.

9 785742 248927 >
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.