
МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ
Государственное автономное учреждение дополнительного профессионального образования
«Саратовский областной институт развития образования»
Кафедра математического образования
Методы решения рациональных уравнений n-ой степени в 10-11 классах
Выпускная творческая работа
слушателя курсов повышения квалификации
по дополнительной профессиональной программе
«Теоретические основы и методика обучения математике
в общеобразовательных организациях (с использованием ДОТ)»
учителя математики МОУ «Лицей №15» Заводского района г.Саратова
Коповой Ольги Васильевны
Руководитель
доцент кафедры
математического образования,
Коник О.Ю., к.ф.н.
Саратов 2016
СОДЕРЖАНИЕ
1. Введение………………………………………………………………….3
2. Основная часть…………………………………………………………..3
a) История развития науки о решении алгебраических уравнений.
b) Теоретические сведения…………………………………………….5
c) Основные методы решения уравнений высших степеней………11
1. Разложение на множители…………………………………..11
2. Введение новой переменной………………………………...23
3. Функционально-графический……………………………….28
4. Другие виды уравнений……………………………………...29
3. Заключение………………………………………………………………33
4. Список используемых источников…………………………………….35
Введение
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека.
Практически все, что окружает современного человека – это всё так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Знаменитый русский математик Н.И. Лобачевский говорил о том, что «решение уравнений составляло всегда главный предмет алгебры». Значение теории уравнений состоит в том, что она не только служит теоретической основой для познания естественных законов природы, но и применяется в конкретных практических целях. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. С другой стороны при изучении любой темы школьного курса математики уравнения могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности учащихся.
1. История развития науки о решении алгебраических уравнений.
Уже в древности люди осознали, как важно научиться решать алгебраические уравнения. Общее правило решения квадратных уравнений, приведённых к виду x2+bx=c, было сформулировано немецким математиком М. Штифелем (1487-1567г.). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Одно своё утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид. Необходимость решать уравнения не только первой, но и второй и высших степеней ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Однако уже при решении уравнений третей степени математики столкнулись с большими трудностями. История открытия способа решения кубических уравнений полна тайн, так как в древности учёные часто на открытых диспутах соревновались в решении трудных задач. От исхода этих состязаний зависела их научная репутация и материальное благополучие. Тот, кто первым овладел решением кубических уравнений, мог легко победить своих соперников давая им задачи, сводящиеся к кубическим уравнениям. Поэтому способы решения уравнения тщательно скрывались. Историки полагают, что первым нашёл способ решения кубических уравнений известный итальянский алгебраист Специна дель Ферро (1465-1576), но впервые опубликовал общую формулу решения кубических уравнений итальянский математик Джераламо Кордано (1501-1576г.). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.
В дальнейшем математики активно пытались найти формулы вычисления корней уравнений пятой и более степени. И только почти через три столетия впервые итальянский учёный Паоло Руффини (1765-1822), а затем норвежский математик Нильс Хенрих Абель (1802-1829г.) доказали, что не существует формулы, выражающей корни любого целого уравнения пятой степени через конечное число алгебраических операций над его коэффициентами. Да и найденные формулы вычисления корней для уравнений третьей и четвёртой степени столь сложны, что ими практически не пользуются. Поэтому в современной математике разработаны методы, позволяющие находить с любой степенью точности приближенные значения корней уравнений. Использование компьютеров значительно облегчают эту работу. И сегодня на уроках математики, начиная с первой ступени обучения, решению уравнений различных видов уделяется большое внимание.
2. Теоретические сведения
![]()
![]() Алгебраическим многочленом n-ой
степени называют выражение вида:
Алгебраическим многочленом n-ой
степени называют выражение вида:
a0 xn +а1х + a2 x + …+аn-1х + an , (1)
где n принадлежит Z , n≥0, a 0, a1 ,...an принадлежат R и a0≠0, и обозначают его через Pn (х).
Равенство Pn (х)=0 называют алгебраическим уравнением n-ой степени. (2)
Число α называют корнем многочлена (1) , а также корнем (решением) уравнения (2) , если α удовлетворяет уравнению (2) ,
т.е. если верно числовое равенство Pn(ɑ) =0 .
Решить уравнение (2) −значит найти множество всех его корней (решений).
Если n=1 , то уравнение (2) называют уравнением 1-ой степени, а при n=2 – квадратным уравнением. Формулы для решения таких уравнений хорошо известны и они достаточно просты. Однако для уравнений выше 2-ой степени таких простых формул нет. Для уравнений третьей степени существуют формулы Кардано и Феррари, выражающие корни этих уравнений через радикалы. Но эти формулы слишком громоздки и неудобны. Поэтому на практике ими редко пользуются. Таким образом, если n≥3, а коэффициенты многочлена (1) −произвольные действительные числа, отыскание корней уравнения (2) −задача непростая.
Тем не менее, во многих частных случаях эта задача решается до конца. Остановимся на некоторых из них.
Теорема Безу. Остаток от деления многочлена Pn (х) на двучлен x- α равен Pn (х).
Основой многих знаний о делении многочлена на двучлен является теорема, принадлежащая французскому математику Этвену Безу (1730-1783) и носит его имя.
Докажем эту теорему для случая, когда n=3. Для этого разделим многочлен P3 (х) на двучлен x- αn уголком.
|
a0 x³ + a1 x² + a3 |
x- α |
|
a0 x³ - αa 0 x² |
a0x²+(a1+ αa0)x + (a2+ α(a1+ αa0)) |
|
(a1+ αa0)x² + a2 x + a3 |
|
|
(a1+ αa0)x² - α(a1 + αa0)x |
|
|
(a2 + α(a1 + αa0))x+a3 |
|
|
(a2+ α(a1+ αa0))x- α(a2+ α(a1+ +αa0)) |
|
|
a3+ α(a2+ α(a1+ αa0))-остаток |
Обозначим остаток от деления P3(х) на x- α через r. Тогда:
r=a3+ α (a2 + α(a1 + αa0))=a3+ αa2+ α²a1 + α³+a0=a0a³+ a1 α² + a2 α +a3=P3(α) ,
т.е. остаток r=P3(∞)
Из теоремы Безу вытекают следующие практические следствия:
Следствие 1. Если многочлен Pn(x) делится без остатка на двучлен x- α,(т.е.r=0) то α является корнем многочлена Pn(x) ,т.е. Pn(α) =0. поэтому решения уравнения Pn (x)=0 сводится к решению уравнения Pn-1(x) =0 , на единицу меньшей степени.
Следствие 2. Если число α является корнем многочлена Pn (x) , то Pn (x) делится без остатка на двучлен x- α , т.е. в этом случае справедливо разложение: Pn (x)=(x- α)∙Pn-1 (x) .
Следствие 3. Если многочлен Pn-1 (x) делится без остатка на двучлен x- α , то Pn (x)=(x- α)² ∙Pn-2 (x)
Если при этом многочлен Pn-2 (x) не делится на x- α, то число α называют двукратным корнем многочлена (1) или уравнения (2).
Число α называется m-кратным корнем многочлена Pn (x) если Pn (x)=Pn-m (x) ∙(x- α) в m-ой степени и многочлена Pn-m (x) не делится на x- -α .
Однократные корни называются простыми, m-кратные корни, при m>1 называются кратными.
Особо отметим: Теорема о целых корнях. Если целое число α - корень многочлена с целыми коэффициентами, то α - делитель его свободного члена.
Доказательство. Пусть:
P (x)=a0xⁿ +a1xⁿ-¹ +…+an-1x +an−многочлен с целыми коэффициентами и целое число α −его корень.
Тогда по определению корня выполняется равенство P (α)=0;
a0 αⁿ+a1 αⁿ-¹+…+an-1 α +an=0
Вынося общий множитель α за скобки, получим равенство:
α(a0 αⁿ-¹ +a1 αⁿ-² +…+an-1)+ad=0, откуда
an= -α(a0 αⁿ-¹ + a1 αⁿ-² +…+ αn-1)
Так как числа a0, a1,…an-1, an и α −целые, то в скобке стоит целое число, и, следовательно, an делится, на α, что и требовалось доказать.
Доказанная теорема может быть сформулирована и следующим образом: всякий целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Дополнительная теорема о целых корнях
Если целое число α−корень многочлена P(x) с целыми коэффициентами, то α-1−делитель числа P(1), α+1−делитель числа P(-1)
Доказательство. В самом деле, при a=1, P (α)-P (1),а значит, и P(1) делится на α-1. Аналогично рассматривается второй случай.
На теореме (1) основан алгоритм поиска целых корней многочлена с целыми коэффициентами: выписать все делители свободного члена и поочерёдно выписать значения многочленов этих чисел.
В то же время проведение этого алгоритма с вычислительной точки зрения может показаться достаточно трудным, однако он может быть существенно упрощён, если применить дополнительное утверждение, основанное на одной из известных формул сокращённого умножения.
Именно: из тождества
xⁿ-yⁿ=(x-y)(xⁿ-¹+xⁿ-²y+…+ xyⁿ-²+yⁿ-¹)
вытекает, что для целых чисел b и c число bⁿ-cⁿ делится на b∙c. Но для любого многочлена P разность
P (b)-P(c)= (a0bⁿ+a1bⁿ-¹+…+an-1b+an)-(a0cⁿ+a1cⁿ-¹+…+an-1c+an)=a0(bⁿ- cⁿ)+a1(bⁿ-¹-cⁿ-¹)+…+an-1(b-c)
и, следовательно, для многочлена P с целыми коэффициентами и целых чисел b и c разность P(b)-P(c) делится на b-c.
Итак, задача нахождения целых корней многочлена с целыми коэффициентами полностью решена −с помощью теоремы делимости целых чисел. A(x)=B(x)*a(x)+R(x)
СхемаГорнера. Пусть дан произвольный многочлен Р(х)=а0хn+ а1хn-1+ …+ аn-1х+ аn. Деление этого многочлена на х-с – это представление его в виде Р(х)=(х-с)g(х) + r(х). Частное g(х)=в0хn-1+ вnхn-2 +…+вn-2х + вn-1, где в0=а0, вn=свn-1 +аn, n=1,2,3,…n-1. Остаток r(х)= свn-1 +аn . Этот метод вычисления и называется схемой Горнера. Слово « схема» в названии алгоритма связана с тем, что обычно его выполнение оформляют следующим образом. Сначала рисуют таблицу 2(n+2). В левой нижней клетке записывают число с, а в верхней строке коэффициенты многочлена Р(х). При этом левую верхнюю клетку оставляют пустой.
|
|
а0 |
а1 |
а2 |
… |
аn-1 |
аn |
|
с |
в0=а0 |
в1=св1 +а1 |
в2=св1+а2 |
… |
вn-1=свn-2+аn-1 |
r(х)=f(с)=свn-1 +аn |
Число, которое после выполнения алгоритма оказывается записанным в правой нижней клетке, и есть остаток от деления многочлена Р(х) на х-с. Другие числа в0, в1, в2,… нижней строки являются коэффициентами частного. Найдём остаток от деления многочлена A(x)=x4-6x3+8 на x+2. Решение: по теореме Безу остаток от деления на x+2 равен А(-2)= (-2)4-6(-2)3+8=72. Чтобы вычислить A(-2) в верхней строке таблицы перечисляем коэффициенты данного многочлена, записанного в стандартной форме x4-6x3+8=x4-(6)x3+0x2+0x+8. Коэффициенты при старшей степени дублируем в нижней строке, а перед ним записываем значение переменной x=-2, при котором вычисляем значение многочлена. Получается следующая таблица:
|
|
1 |
-6 |
0 |
0 |
8 |
|
-2 |
1 |
|
|
|
|
Пустые клетки таблицы заполняем по следующему правилу: крайнее справа число нижней строки умножается на -2 и складывается с числом, стоящим над пустой клеткой. По этому правилу в первой пустой клетке стоит число (-2)1+(-6)=-8, во второй клетке становится число (-2)8+0=16, в третьей клетке – число (-2)16+0=-2, в последней клетке – число (-2)*(-32)+8=72.
Полностью заполненная по схеме Горнера таблица выглядит так:
|
|
1 |
-6 |
0 |
0 |
8 |
|
-2 |
1 |
-8 |
16 |
-32 |
72 |
Число в последней клетке и есть остаток от деления на x+2, A(-2)=72.
Процесс отыскания решений уравнения заключается обычно в замене уравнения равносильным. Замена уравнения равносильным основана на применении четырёх аксиом:
1. Если равные величины увеличить на одно и то же число, то результаты будут равны.
2. Если из равных величин вычесть одно и то же число, то результаты будут равны.
3. Если равные величины умножить на одно и то же число, то результаты будут равны.
4. Если равные величины разделить на одно и то же число, то результаты будут равны.
Поскольку левая часть уравнения Р(х) = 0 представляет собой многочлен n-й степени, то полезно напомнить следующие утверждения:
Утверждения о корнях многочлена и его делителях:
1. Многочлен n-й степени имеет число корней не превышающее число n, причем корни кратности m встречаются ровно m раз.
2. Многочлен нечетной степени имеет хотя бы один действительный корень.
3. Если α – корень Р(х), то Рn (х) = (х - α)·Qn - 1(x), где Qn - 1(x) – многочлен степени (n – 1).
4. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
5. Приведенный многочлен с целыми коэффициентами не может иметь дробных рациональных корней.
6. Для многочлена третьей степени
Р3(х) = ах3 + bx2 + cx + d возможно одно из двух: либо он разлагается в произведение трех двучленов
Р3(x) = а (х - α)(х - β)(х - γ), либо разлагается в произведение двучлена и квадратного трехчлена Р3(x) = а(х - α)(х2 + βх + γ).
7. Любой многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов.
8. Многочлен f (x) делится на многочлен g(х) без остатка, если существует многочлен q(x), что f(x) = g(x)·q(x). Для деления многочленов применяется правило «деления уголком».
9. Для делимости многочлена P(x) на двучлен (x – c) необходимо и достаточно, чтобы с было корнем P(x) (Следствие теоремы Безу).
10. Теорема Виета: Если х1, х2, …, хn – действительные корни многочлена
Р(х) = а0хn + а1хn - 1 + … + аn, то имеют место следующие равенства:
х1 + х2 + … + хn = -а1/а0,
х1 · х2 + х1 · х3 + … + хn - 1 · хn = a2/а0,
х1 · х2 · х3 + … + хn - 2 · хn - 1 · хn = -a3/а0,
х1 · х2 · х3 · хn = (-1)n an/а0.
3. Основные методы решения уравнений высших степеней
1) Разложение на множители
2) Введение новой переменной
3) Функционально-графический
1) Разложение на множители
a) формулы сокращенного умножения
b) способ группировки
c) теорема Безу
d) схема Горнера
e) метод неопределенных коэффициентов
a-b). Разложение на множители методом группировки и формул сокращенного умножения
Основа данного метода заключается в группировке слагаемых таким образом, чтобы каждая группа содержала общий множитель. Для этого иногда приходится применять некоторые искусственные приемы.
Пример 1. х4 - 3x2 + 4х – 3 = 0.
Решение. Представим - 3x2 = -2x2 – x2 и сгруппируем:
(х4 - 2x2) – (x2 - 4х + 3) = 0.
(х4 - 2x2 +1 – 1) – (x2 - 4х + 3 + 1 – 1) = 0.
(х2 – 1)2 – 1 – (x – 2)2 + 1 = 0.
(х2 – 1)2 – (x – 2)2 = 0.
(х2 – 1 – х + 2)(х2 – 1 + х - 2) = 0.
(х2 – х + 1)(х2 + х - 3) = 0.
х2 – х + 1 = 0 или х2 + х - 3 = 0.
В первом уравнении нет корней, из второго: х1, 2 = (-1 ± √13)/2.
Пример 2. Дано: 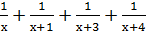
Решение. Сгруппируем слагаемые в левой части, но следует заметить, что х=0; х=-1; х=-3; х=-4 не могут быть решениями. Получим:
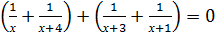 ,
,
Проводим преобразования и получаем:
![]() +
+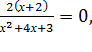 2(х+2)(
2(х+2)(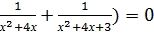 ,
,
2(х+2)=0, или 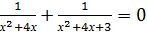
х1=-2. Введем
замену: х2+4х=t,
тогда 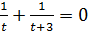
Решая уравнения, получаем:
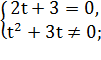
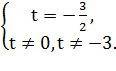
Подставляем значение t, получаем уравнение:
х2+4х=![]() , х2+4х+1,5=0, D=16-6=10,
, х2+4х+1,5=0, D=16-6=10,
х2,3= Ответ: х1=-2; х2=-2+
Ответ: х1=-2; х2=-2+![]() ; х3= -2-
; х3= -2-![]() .
.
Пример 3. Дано: х4+2х3+2х+1=0
Решение. Поделим на уравнение на х2, получим:
х2+2х+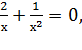 перегруппируем слагаемые таким образом:
перегруппируем слагаемые таким образом:
(х2+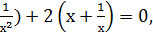 (х+
(х+![]() 2-2+2(
2-2+2(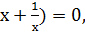
вводим новую переменную: t= х+![]() , t2+2t-2=0, D=4+8=12,
, t2+2t-2=0, D=4+8=12,
t1,2=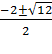 =
=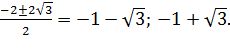
Подставляем обратно:
1)
х+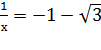
x2 + (1− ![]() )x +1 = 0, D=-1-2
)x +1 = 0, D=-1-2![]() <0 – решений нет.
<0 – решений нет.
2)
х+![]() =
=![]() , x2 + (1+
, x2 + (1+ ![]() )x +1 = 0, D=
)x +1 = 0, D=![]() ,
,
х1,2=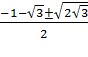 .
.
Ответ. х1,2=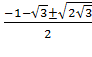
Пример4. Дано: х4+х3-72х2+9х+81=0
Решение. Поделим уравнение на х2 и сгруппируем:
х2+х-72+![]() =0,
=0,
(х2+![]() +(х+
+(х+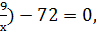 проведем некоторые преобразования до полного квадрата в
одной из скобок, получим:
проведем некоторые преобразования до полного квадрата в
одной из скобок, получим:
(х2+18+![]() +(х+
+(х+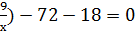 ,
,
(х+![]() )2+( х+
)2+( х+![]() )-90=0, вводим новую переменную: t= х+
)-90=0, вводим новую переменную: t= х+![]() , решаем уравнение:
, решаем уравнение:
t2+t-90=0, D=1+360=361,
t1,2=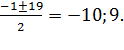 Решаем уравнения, подставляя значения t:
Решаем уравнения, подставляя значения t:
1)
х+![]() =-10, х
=-10, х![]() 0 х2+10х+9=0, D=100-36=64
0 х2+10х+9=0, D=100-36=64
х1,2=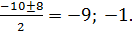
2)
х+![]() =9, х
=9, х![]() 0 х2-9х+9=0, D=81-36=45 х3,4=
0 х2-9х+9=0, D=81-36=45 х3,4=![]() .
.
Ответ: х1![]() х2=-1; х3,4=
х2=-1; х3,4=![]()
c). Теорема Безу
При делении многочлена n-й степени относительно x на двучлен x-a остаток равен значению делимого при x=a. (Буква a может обозначать любое действительное или мнимое число, т.е. любое комплексное число.)
При решении уравнений с помощью теоремы Безу необходимо:
· найти все целые делители свободного члена;
· из этих делителей найти хотя бы один корень уравнения (a);
· левую часть уравнения разделить на (x-a);
· записать в левой части уравнения произведение делителя и частного;
· решить полученное уравнение.
1. Решить уравнение x4+3x3-13x2-9x+30=0.
30![]()
![]() 1;
1;
![]() 2,
2,
![]() 3,
3,
![]() 5,
5,
![]() 6,
6,
![]() 10.
10.
(x-2)(x3+5x2-3x-15)=0
(x-2)(x+5)(x2-3)=0
_x4+3x3-13x2-9x+30 x-2
x4-2x3 x3+5x2-3x-15
_5x3-13x2
5x3-10x2
_-3x2-9x
-3x2+6x
_-15x+30
-15x+30
0
Ответ:
x1=2, x2=-5,
x3,4=![]() .
.
2. Решить уравнение x6+x5-7x4-5x3+16x2+6x-12=0.
-12![]()
![]() 1;
1;
![]() 2;
2;
![]() 3;
3;
![]() 4;
4;
![]() 6;
6;
![]() 12.
12.
_x6+x5-7x4-5x3+16x2+6x-12 x-1
x6-x5 x5+2x4-5x3-10x2+6x+12
_ 2x5-7x4
2x5-7x4
_-5x4-5x3
-5x4+5x3
_-10x3+16x2 _x5+2x4-5x3-10x2+6x+12 x+2
-10x3-10x2 x5+2x4 x4-5x2+6
_6x2+6x _ -5x3-10x2
6x2-6x -5x3-10x2
_ 12x-12 _ 6x+12
12x-12 6x+12
0 0
x6+x5-7x4-5x3+16x2+6x-12=(x-1)(x5+2x4-5x3-10x2+6x+12)=0
x6+x5-7x4-5x3+16x2+6x-12=(x-1)(x+2)(x4-5x2+6)=0
x4-5x2+6=0
– биквадратное уравнение, x1,2=![]()
![]() ,
x3,4=
,
x3,4=![]()
![]() .
.
Ответ:
x1,2=![]()
![]() ,
x3,4=
,
x3,4=![]()
![]() , x5=1,
x6=-2.
, x5=1,
x6=-2.
3. Решить уравнение x3-5x2+8x-6=0.
-6![]()
![]() 1;
1;
![]() 2;
2;
![]() 3;
3;
![]() 6.
6.
_x3-5x2+8x-6 x-3
x3-3x2 x2-2x+2
_-2x2+8x
-2x2+6x
_2x-6
2x-6
0
x3-5x2+8x-6=(x2-2x+2)(x-3)=0
x2-2x+2=0 – квадратное уравнение, корней не имеет, т.к. D<0.
Ответ: x=3.
4. Решить уравнение 6x3+11x2-3x-2=0.
-2![]()
![]() 1;
1;
![]() 2.
2.
_6x3+11x2-3x-2 x+2
6x3+12x2 6x2-x-1
_-x2-3x
-x2-2x
_-x-2
-x-2
0
6x3+11x2-3x-2=(6x2-x-1)(x+2)=0
6x2-x-1=0 – квадратное уравнение, x1=½, x2=-⅓.
Ответ: x1=½, x2=-⅓, x3=-2.
d). Схема Горнера
Схема Горнера, основанная на теореме Безу, позволяет за
считанные секунды решить сложное уравнение без мучительных подстановок и деления многочленов в столбик.
Пример 1. Решить уравнение 2х4 - 5х3 + 5х2 - 2 = 0 Решение: Так как сумма коэффициентов многочлена , записанного в левой части уравнения, равна нулю, то один из корней 1. Воспользуемся схемой Горнера:
|
|
2 |
-5 |
5 |
0 |
-2 |
|
|
1 |
2 |
-3 |
2 |
2 |
0 |
Х=1 - корень |
Получаем Р(х)=(х-1) (2х3 -3х2+2х +2). Будем искать корни среди делителей свободного члена 2.
|
|
2 |
-3 |
2 |
2 |
|
1 |
2 |
-1 |
1 |
3 |
|
-1 |
2 |
-5 |
7 |
-5 |
|
2 |
2 |
1 |
4 |
10 |
|
-2 |
2 |
-7 |
16 |
-30 |
Выяснили, что целых корней больше нет. Проверим 1/2; -1/2.
|
|
2 |
-3 |
2 |
2 |
|
|
1/2 |
2 |
-2 |
1 |
2,5 |
|
|
-1/2 |
2 |
-4 |
4 |
0 |
Х= -1/2 - корень |
Итак (х-1) (х+1/2) (2х2 – 4х +4)=0. Далее решаем квадратное уравнение 2х2-4х +4 = 0. Д/4=1-2= -1. Значит это уравнение корней не имеет. Ответ: 1; -1/2. Пример 2. Решить уравнение 5х4 – 3х3 – 4х2 -3х+ 5 = 0. Решение: Корни данного уравнения будем искать среди делителей свободного члена 5: 1;-1;5;-5. х=1 - корень уравнения, так как сумма коэффициентов равна нулю. Воспользуемся схемой Горнера:
|
|
5 |
-3 |
-4 |
-3 |
5 |
|
1 |
5 |
2 |
-2 |
-5 |
0 |
Можно записать (х-1) (5х3 +2х2 -2х-5)=0. Для 5х3 +2х2 -2х-5=0 х=1 также является корнем и
|
|
5 |
2 |
-2 |
-5 |
|
1 |
5 |
7 |
5 |
0 |
уравнение представим в
виде произведения трех множителей: (х-1) (х-1) (5х2 -7х + 5)=0.
Решая квадратное уравнение 5х2 -7х+5=0, получили Д=49-100=-51,
корней нет.
Ответ:1.
Пример 3. Дано: ![]() . Делители
свободного числа:
. Делители
свободного числа: ![]() , но это очень большое
количество делителей, поэтому можно воспользоваться тем, что если сумма
коэффициентов равна 0, то один из корней 1.
, но это очень большое
количество делителей, поэтому можно воспользоваться тем, что если сумма
коэффициентов равна 0, то один из корней 1.
1-5-9+41+32-60=0
![]() 1 – корень.
1 – корень.
|
|
1 |
-5 |
-9 |
41 |
32 |
-60 |
|
1 |
1 |
-4 |
-13 |
28 |
60 |
0 |
|
2 |
1 |
-2 |
-17 |
-6 |
20 |
- |
|
3 |
1 |
-1 |
-16 |
-20 |
0 |
|
|
4 |
1 |
3 |
-4 |
0 |
|
|
|
5 |
1 |
4 |
4 |
0 |
|
|
![]()
х-1=0, или х-3=0, или х-5=0, или (х+2)2=0,
х=1. х=3. х=5. х=-2.
Ответ: 1; 3; 5; -2.
Пример 4. ![]() . Делители
свободного числа:
. Делители
свободного числа: ![]()
|
|
1 |
-1 |
-8 |
14 |
1 |
-13 |
6 |
|
1 |
1 |
0 |
-8 |
6 |
7 |
-6 |
0 |
|
1 |
1 |
1 |
-7 |
-1 |
6 |
0 |
|
|
1 |
1 |
2 |
-5 |
-6 |
0 |
|
|
|
-1 |
1 |
1 |
-6 |
0 |
|
|
|
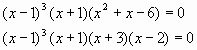
(х-1)3=0, или х+1=0, или х+3=0, х-2=0,
х=1. х=-1. х=-3. х=2.
Ответ: 1; -1; -3; 2.
Пример 5. Решить уравнение: х3 – 5х + 4 = 0
Определим корни многочлена третьей степени
![]() :± 1; ± 2; ± 4
:± 1; ± 2; ± 4
f(1) = 1 – 5 + 4 = 0
Одним из корней является х = 1
|
|
1 |
0 |
– 5 |
4 |
|
1 |
1 |
1 |
– 4 |
0 |
х3 – 5х + 4 = 0
(х – 1) (х2 + х – 4) = 0
х-1=0, или х2 + х – 4=0
х=1. D = 1 + 16 = 17
х1
= ![]() ; х2 =
; х2 = ![]()
Ответ: 1; ![]() ;
;
![]() .
.
Пример 6. Дано: 6х4-29х3-89х2-19х+35=0
Решение. Делители свободного числа: ![]() .
.
Находим по схеме Горнера целочисленные решения уравнения:
|
|
6 |
-29 |
-89 |
-19 |
35 |
|
1 |
6 |
-23 |
-112 |
-131 |
|
|
-1 |
6 |
-35 |
-54 |
35 |
0 |
|
5 |
6 |
1 |
-84 |
-439 |
|
|
7 |
6 |
13 |
2 |
-5 |
0 |
Итак, 6х4-29х3-89х2-19х+35=(х+1)(х-7)(6х2+7х-5)=0,
х+1=0 или х-7=0 или 6х2+7х-5=0
х1=-1, х2=7, х3,4=![]() .
.
Ответ: ![]()
Пример 7. Решить уравнение: х5+5х-42=0
Решение. Делители свободного числа: ![]()
Находим по схеме Горнера целочисленные решения уравнений:
|
|
1 |
0 |
0 |
0 |
5 |
-42 |
|
|||||||||||||||||||||||||||||||
|
-1 |
1 |
-1 |
1 |
-1 |
6 |
|
|
|||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
6 |
|
|
|||||||||||||||||||||||||||||||
|
-2 |
1 |
-2 |
4 |
-8 |
21 |
|
|
|||||||||||||||||||||||||||||||
|
2 |
1 |
2 |
4 |
8 |
21 |
0 |
Корень |
|||||||||||||||||||||||||||||||
|
х4+2х3+4х2+8х+21=0 Делители свободного числа:
|
|
|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
Ответ: х=2.
Пример 8. Дано: х4-8х+63=0
Решение.
Делители свободного числа: ![]() Решаем по схеме
Горнера:
Решаем по схеме
Горнера:
|
|
1 |
0 |
0 |
-8 |
63 |
|
-1 |
-1 |
1 |
-1 |
-7 |
70 |
|
1 |
1 |
1 |
1 |
-7 |
70 |
|
-63 |
1 |
63 |
-3969 |
Не корень |
|
|
63 |
1 |
63 |
3969 |
Не корень |
|
Ответ: решений нет.
Пример 9. Решить уравнение: х4-4х3-13х2+28х+12=0
Решение.
Делители свободного числа: ![]()
По схеме Горнера находим целочисленные решения уравнения:
|
|
1 |
-4 |
-13 |
28 |
12 |
|
|
1 |
1 |
-3 |
-16 |
12 |
24 |
|
|
2 |
1 |
-2 |
-17 |
-6 |
0 |
Корень |
|
3 |
1 |
-1 |
-16 |
-20 |
|
|
|
-3 |
1 |
-7 |
8 |
4 |
0 |
Корень |
Уравнение принимает вид: (х-2)(х+3)(х2 -5х-2)=0
х-2=0 или х+3=0 или х2 -5х-2=0
х1=2,
х2=-3, х3,4=![]()
Ответ:
х1=2, х2=-3, х3,4=![]()
e). Разложение на множители методом неопределенных коэффициентов
Суть метода состоит в том, что исходный многочлен раскладывается на множители с неизвестными коэффициентами. Используя свойство, что многочлены равны, если равны их коэффициенты при одинаковых степенях, находят неизвестные коэффициенты разложения.
Пример1: х3 + 4x2 + 5х + 2 = 0.
Решение. Многочлен 3-й степени можно разложить в произведение линейного и квадратного множителей.
х3 + 4x2 + 5х + 2 = (х - а)(x2 + bх + c),
х3 + 4x2 + 5х + 2 = х3 +bx2 + cх - ax2 - abх - ac,
х3 + 4x2 + 5х + 2 = х3 + (b – a)x2 + (c – ab)х – ac.
Решив систему: 
получим 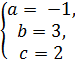
х3 + 4x2 + 5х + 2 = (х + 1)(x2 + 3х + 2).
Корни уравнения (х + 1)(x2 + 3х + 2) = 0 находятся легко.
Ответ: -1; -2.
2) Метод введения новой переменной
1) Биквадратные уравнения
2) Возвратные и симметрические уравнения
Метод введения новой переменной заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = xn или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни: (t1, t2, …, tn). После этого получают совокупность n уравнений q(x) = t1, q(x) = t2, … , q(x) = tn, из которых находят корни исходного уравнения.
Пример 1; (х2 + х + 1)2 – 3х2 - 3x – 1 = 0.
Решение: (х2 + х + 1)2 – 3х2 - 3x – 1 = 0.
(х2 + х + 1)2 – 3(х2 + x + 1) + 3 – 1 = 0.
Замена (х2 + х + 1) = t.
t2 – 3t + 2 = 0.
t1 = 2, t2 = 1. Обратная замена:
х2 + х + 1 = 2 или х2 + х + 1 = 1;
х2 + х - 1 = 0 или х2 + х = 0;
Из первого уравнения: х1, 2 = (-1 ± √5)/2, из второго: 0 и -1.
1) Биквадратные уравнения
Уравнение вида: ax 4 + bx 2 + c = 0 называется биквадратным.
Оно приводится к квадратному уравнению заменой: x2 = z .
Если уравнение имеет вид: ax2n + bxn + c = 0 ,
оно приводится к квадратному уравнению заменой: xn = z ;
действительно, после этой замены получаем: az 2+ bz + c = 0 .
Пример 1. Решим уравнение: x 4 – 13 x 2 + 36 = 0 .
После замены: x 2 = z получим уравнение: z 2 – 13 z + 36 = 0 .
Его корни: z1 = 4 и z2 = 9. Теперь решаем уравнения: x 2 = 4 и x 2 = 9 . Они имеют соответственно корни: x1 = 2 , x2 = – 2 , x3 = 3 ; x4 = – 3 . Эти числа являются корнями исходного уравнения
Пример 2. Решить биквадратное уравнение: 3x 4 – 123x 2 + 1200 = 0 .
Решение. Заменяя: x 2 = z , и решая уравнение: 3z 2 – 123z + 1200 = 0, получаем:
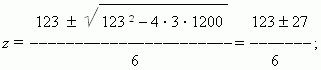
отсюда, z1 = 25 и z2 = 16. Используя нашу замену, получим:
x 2 = 25 и x 2 = 16, отсюда, x1 = 5, x2 = – 5, x3 = 4, x4 = – 4.
2) Возвратные и симметрические уравнения
Метод введения новой переменной находит применение при решении возвратных уравнений. Алгебраические уравнения вида a0xn+a1xn-1+…+an=0 называют возвратными уравнениями, если его коэффициенты, одинаково удалены от начала и от конца, равны между собой (ak=an-1, k=0, 1, … , n).
Примерами таких уравнений являются:
X3-2x2-2x+1=0, a0=a3=1, a1=a2=-2
2x4-3x3+5x2-3x+2=0; a0=a4=2; a1=a3=-3;
Уравнения вида ах3 + вх2 + вх + а = 0, а ≠ 0, (1) называются возвратными уравнениями третьей степени. Поскольку ах3 + вх2 + вх + а = а (х3 + 1) + вх (х+1) = а (х+ 1) (х2 - х+ 1) + вх (х+ 1) = (х+1) (ах2 + (в - а) х + а), то уравнение (1) равносильно совокупности уравнений х + 1 = 0 и ах2 + (в - а) х + а = 0, решить которую просто.
Пример 1. Решить уравнение. 3х3 + 4х2 + 4х + 3 = 0. – возвратное, уравнение третьей степени, т.к. a0= a3 =3; a1=a2=4. Разложим на множители левую часть уравнения 3х3 + 4х2 + 4х + 3 = 3 (х3 + 1) + 4х (х + 1) = ( х + 1) (3х2 – 3х + 3 + 4х) = ( х+ 1) (3х2 + х + 3). Уравнение равносильно совокупности уравнений х + 1 = 0 и 3х2 + х + 3 = 0, х= - 1 D< 0 , уравнение решений не имеет. Ответ: - 1. Пример 2. Решить уравнение. 2x3+7x2+7x+2=0 – возвратное, уравнение третьей степени, т.к. a0= a3 =2; a1=a2=7. Разложим левую часть на множители: 2(x3+1)+7x(x+1)=2(x+1)(x2-x+1)+7x(x+1)=(x+1)(2x2-2x+2+7x)=(x+1)(2x2+5x+x) Ответ: - 1.
Уравнения вида ах4 + вх3 + сх2 + вх + а = 0 , а≠ 0, называются возвратными уравнениями четвертой степени. Возвратные уравнения решаются методом введения новой переменной. Поскольку х = 0 не является корнем уравнения , то , разделив обе части уравнения на х2 , получим уравнение , равносильное исходному: ах2 + а/х2 + вх + в/х + с = 0. Перепишем уравнение в виде: а [(х + 1/х)2 - 2 ] + в ( х + 1/х) + с = 0. В этом уравнении сделаем замену х + 1/х = у, тогда получим квадратное уравнение ау2 + ву +с – 2а = 0. Если уравнение имеет два корня у1 и у2 , то исходное уравнение равносильно совокупности уравнений х2 - х у1 + 1 = 0 и х2 - х у2 + 1 = 0. Если же уравнение имеет один корень у0 , то исходное уравнение равносильно уравнению х2 - у0х+ 1 = 0. Если уравнение не имеет корней, то и исходное уравнение не имеет корней.
Пример 3. Решить уравнение х4 – 5х3 + 8х2 – 5х- 1 =0. Решение. Так как х= 0 не является его корнем, то , разделив уравнение на х2, получим равносильное ему уравнение х2 – 5х + 8 – 5/х + 1/ х2= 0. Сгруппировав слагаемые, перепишем уравнение в виде (х2 + 1/ х2)2 – 5 (х + 1/х) + 6 =0. Пусть х + 1/х = у, получим уравнение у2 - 5у +6 = 0, имеющее два корня у1= 2, у2 = 3. Следовательно, исходное уравнение равносильно совокупности уравнений х + 1/х =2 и х + 1/х =3. Решение первого уравнения этой совокупности есть х1 = 1, а решения второго есть х2 =(3+√5)/2, х3 =(3-√5)/2. Следовательно, исходное уравнение имеет три корня. Ответ: х1 = 1, х2 =(3+√5)/2, х3 =(3-√5)/2. Пример 4. Решить уравнение 6x4-35x3+62x2-35x+6=0 (6x4+6)-(35x3+35x)+62x2=0 6 (x4+1)-35 (x3+x)+62x2=0 Разделим обе части на x2 6 (x2+1/x2)-35(x+1/x)+62=0 пусть t=x+1/x, тогда t2=(x+1/x)2=x2+2+1/x2, то x2+1/x2=t2-2 6(t2+2)-35t+62=0; 6t2-12-35t+62=0; 6t2-35t+50=0; D=1225-1200=25 t1=(35+5)/12=40/12=10/3; t2=(35-5)/12=30/12=5/2; x+1/x=5/2; x+1/x=10/3 2x2-5x+2=0 3x2-10x+3=0 D=25-16=9 D=100-36=64 x1=(5+3)/4=2; x2=(5-3)/4=1/2; x3=(10+8)/4=3; x4=(10-8)/4=1/3. Ответ: 1/3; 1/2; 2; 3.
Частным
случаем возвратных уравнений являются симметрические уравнения ax4+bx3+cx2+bx+a=0
и кососимметрические уравнения ax4+bx3+cx2-bx+a=0.
Заменой ![]() для симметрического и
для симметрического и ![]() для кососимметрического уравнений
эти уравнения сводятся к квадратным уравнениям.
для кососимметрического уравнений
эти уравнения сводятся к квадратным уравнениям.
Пример 5: Решить уравнение x4-2x3-x2-2x+1=0
Разделим данное уравнение
на x2 ![]()
![]()
Пусть
![]() . Тогда
. Тогда ![]()
![]() ; t2-2-2t-1
=0; t2-2t-3=0;
t1=3;
t2=-1
При t=3
; t2-2-2t-1
=0; t2-2t-3=0;
t1=3;
t2=-1
При t=3 ![]() ; x2-3x+1=0;
D=9-4=5;
; x2-3x+1=0;
D=9-4=5; ![]() При
t=-1
При
t=-1 ![]() x2+x+1=0;
D=1-4=-3<0 — корней нет Ответ:
x2+x+1=0;
D=1-4=-3<0 — корней нет Ответ:
![]() .
.
Пример 6. Решить уравнение 6х4 – 5х3 – 38x2 – 5х + 6 = 0. Решение. 6х2 – 5х – 38 – 5/х + 6/х2 = 0. 6(х2 + 1/х2) – 5(х + 1/х) – 38 = 0. Вводим t: подстановка (x + 1/x) = t. Замена: (x2 + 1/x2) = t2 – 2, имеем: 6t2 – 5t – 50 = 0. t = -5/2 или t = 10/3. Вернемся к переменной х. После обратной замены решим два полученных уравнения: 1) x + 1/x = -5/2; х2 + 5/2 х +1 = 0; х = -2 или х = -1/2. 2) x + 1/x = 10/3; х2 – 10/3 х + 1 = 0; х = 3 или х = 1/3. Ответ: -2; -1/2; 1/3; 3.
Пример 7.
Решить уравнение х4 – 7х3+14х2 – 7х + 1 = 0 Решение.
Разделим
данное уравнение на х2 и получим: х2 – 7х + 14 - ![]() +
+ ![]() =
0 Группируем и выносим за скобки общий множитель, где это возможно.
=
0 Группируем и выносим за скобки общий множитель, где это возможно.
(![]() +
+![]() ) - 7(
) - 7(![]() )+14
= 0. Пусть
)+14
= 0. Пусть ![]() = у, тогда уравнение
примет вид у2 – 2 – 7у + 14 = 0; у2 – 7у +
12 = 0; D = 1; у1= 4;
у2 = 3 Возвращаясь к нашей замене, получим
= у, тогда уравнение
примет вид у2 – 2 – 7у + 14 = 0; у2 – 7у +
12 = 0; D = 1; у1= 4;
у2 = 3 Возвращаясь к нашей замене, получим
![]() - 4 = 0 или
- 4 = 0 или ![]() - 3 = 0
D = 12 D
= 5
х1,2 =2±
- 3 = 0
D = 12 D
= 5
х1,2 =2±![]() х3,4
=
х3,4
=![]() Ответ: х1,2 =2±
Ответ: х1,2 =2±![]() ; х3,4
=
; х3,4
=![]()
3. Графический метод.
Данный метод состоит в построении графиков и использовании свойств функций.
1. Решить уравнение: х5 + х – 2 = 0
Представим уравнение в виде х5 = - х + 2. Функция у = х5 является возрастающей, а функция у = - х + 2 - убывающей. Значит, уравнение х5 + х – 2 = 0 имеет единственный корень -1.
2. Решить уравнение: ![]() Решение.
Решение.
Перейдем к равносильному уравнению: ![]()
Можно заметить, что х=2
является решением данного уравнения. Давайте докажем, что это единственный
корень.
Функция y=![]() – возрастает на всей
области определения.
– возрастает на всей
области определения.
Функция y=134−3x –
убывает на всей области определения.
Тогда графики этих функций либо вообще не пересекаются, либо пересекаются в
одной точке, это точку мы уже нашли х=2.
Ответ: х=2.
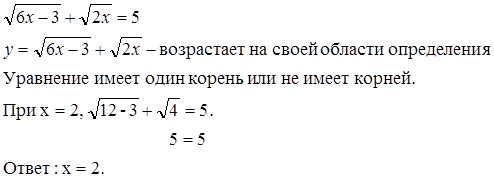 3.Решить уравнение:
3.Решить уравнение:
4.Другие виды уравнений.
Решение уравнений вида:
1.
![]() ;
;
2.
![]()
3. (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b.
Уравнение ![]() сводится к
биквадратному, если сделать подстановку
сводится к
биквадратному, если сделать подстановку ![]() Уравнение
Уравнение
![]() ac=bd
и т.д., тогда делим на x
ac=bd
и т.д., тогда делим на x![]()
Уравнения
вида (х + а)(х + b)(x + c)(x
+ d) = А, где а + d = c + b. Методика решения подобных уравнений заключается в частичном
раскрытии скобок, а затем введении новой переменной.
1. Решить уравнение: ![]()
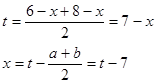
![]()
![]() Ответ: 6; 8
Ответ: 6; 8
2.
Решить уравнение: ![]()
![]() Делим
на
Делим
на ![]()
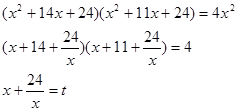
![]()
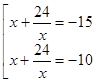 Ответ: -6;
-4;
Ответ: -6;
-4; ![]()
3. Решить уравнение: (х + 1)(х + 2)(x + 3)(x + 4) = 24. Решение. Вычисляем: 1 + 4 = 2 + 3. Группируем скобки по парам: ((х + 1)(x + 4))((х + 2)(x + 3)) = 24, (х2 + 5х + 4)(х2 + 5х + 6) = 24. Сделав замену х2 + 5х + 4 = t, имеем уравнение t(t + 2) = 24, оно является квадратным: t2 + 2t – 24 = 0, t = -6 или t = 4. После выполнения обратной замены, легко находим корни исходного уравнения. Ответ: -5; 0.
Примеры для самостоятельного решения.
Решите уравнения:
1. 9х³ - 18х = х – 2,
2. х³ - х² = х – 1,
3. х³ - 3х² -3х + 1 = 0,
4. Х ⁴ - 2х³ + 2х – 1 = 0,
5. Х⁴ - 3х² + 2 = 0,
6. х⁵ + 5х³ - 6х² = 0,
7. х³ + 4х² + 5х + 2 = 0,
8. Х⁴ + 4х³ - х² - 16х – 12 = 0
9. 4х³ + х² - х + 5 = 0
10. 3х⁴ + 5х³ - 9х² - 9х + 10 = 0.
Ответы: 1) ±1/3; 2 2) ±1, 3) -1; 2 ±√3 , 4) ±1, 5) ± 1; ±√2 , 6) 0; 1 7) -2; -1, 8) -3; -1; ±2, 9) – 5/4 10) -2; - 5/3; 1.
Уравнения вида (х + а)(х + в)(х + с)(х + d)… = А.
1. (х + 1)(х + 3)(х + 5)(х + 7) = -15,
2. х(х + 4)(х + 5)(х + 9) + 96 = 0,
3. х(х + 3)(х + 5)(х + 8) + 56 = 0,
4. (х – 4)(х – 3)(х – 2)(х – 1) = 24,
5. (х – 3)(х -4)(х – 5)(х – 6) = 1680,
6. (х² - 5х)(х + 3)(х – 8) + 108 = 0,
7. (х + 4)² (х + 10)(х – 2) + 243 = 0
8. (х² + 3х + 2)(х² + 9х + 20) = 4, Указание: х + 3х + 2 = (х + 1)(х + 2),
х² + 9х + 20 = (х + 4)(х + 5)
Ответы: 1) -4 ±√6; - 6; - 2. 6) - 1; 6; (5± √97)/2 7) -7; -1; -4 ±√3.
Возвратные уравнения.
1. 78х⁴ - 133х³ + 78х² - 133х + 78 = 0,
2. х⁴ - 5х³ + 10х² - 10х + 4 = 0,
3. х⁴ - х³ - 10х² + 2х + 4 = 0,
4. 6х⁴ + 5х³ - 38х² -10х + 24 = 0,
5. х⁴ + 2х³ - 11х² + 4х + 4 = 0,
6. х⁴ - 5х³ + 10х² -10х + 4 = 0.
Ответы: 1) 2/3; 3/2, 2) 1;2 3) -1 ±√3; (3±√17)/2, 4) -1±√3; (7±√337)/12 5) 1; 2; (-5± √17)/2, 6) 1; 2.
а) х⁴ -3х² + 2 = 0,
б) х⁵ +5х³ -6х² = 0.
Ответы: а) ± 1; ±√2 , б) 0; 1. Используя свойство монотонности функции, докажите, что уравнение имеет единственный корень, и найдите этот корень:
а) х³ = 10 – х, б) х⁵ + 3х³ - 11√2 – х.
Ответы: а) 2, б) √2.
Решите уравнение (х + 3)⁴ + (х + 5)⁴ = 16. Ответ: -5; -3.
Контрольная работа.
1 вариант.
1. Решите уравнение (х² + х) – 8(х² + х) + 12 = 0.
2. Решите уравнение (х + 1)(х + 3)(х + 5)(х + 7) = - 15.
3. Решите уравнение 12х²(х – 3) + 64(х – 3)² = х⁴.
4. Решите уравнение х ⁴ - 4х³ + 5х² - 4х + 1 = 0
5. Решите систему уравнений: х² + 2у² - х + 2у = 6,
1,5х² + 3у² - х + 5у = 12.
2 вариант
1. (х² - 4х)² + 7(х² - 4х) + 12 = 0.
2. х(х + 1)(х + 5)(х + 6) = 24.
3. х⁴ + 18(х + 4)² = 11х²(х + 4).
4. х⁴ - 5х³ + 6х² - 5х + 1 = 0.
5. Решите систему уравнений: х² - 2ху + у² + 2х²у – 9 = 0, х – у – х²у + 3 = 0.
3 вариант.
1. (х² + 3х)² - 14(х² + 3х) + 40 = 0
2. (х – 5)(х-3)(х + 3)(х + 1) = - 35.
3. х4 + 8х²(х + 2) = 9(х+ 2)².
4. х⁴ - 7х³ + 14х² - 7х + 1 = 0.
5. Решите систему уравнений: х + у + х² + у² = 18, ху + х² + у² = 19.
4 вариант.
1. (х² - 2х)² - 11(х² - 2х) + 24 = о.
2. (х -7)(х-4)(х-2)(х + 1) = -36.
3. х⁴ + 3(х -6)² = 4х²(6 – х).
4. х⁴ - 6х³ + 7х² - 6х + 1 = 0.
5. Решите систему уравнений: х² + 3ху + у² = - 1, 2х² - 3ху – 3у² = - 4.
Ответы и указания:
|
вариант |
№1 |
№2 |
№3 |
№4 |
№5 |
|
1 |
- 3; ±2; 1 |
1;2;3 |
-5; -4; 1; 2. Однородное уравнение: u = x -3, v =x² |
-2; -1; 3; 4. |
(2;1); (2/3;4/3). Указание: 1·(-3) + 2· 2 |
|
2 |
-6; -2; -4±√6. |
-3±2√3; - 4; - 2. |
1±√11; 4; - 2. Однородное уравнение: u = x + 4, v = x² |
1; 5;3±√13. |
(2;1); (0;3); ( - 3; 0). Указание: 2· 2 + 1. |
|
3 |
-6; 2; 4; 12 |
-3; -2; 4; 12 |
-6; -3; -1; 2. Однородное u = x+ 2, v = x² |
-6; ±3; 2 |
(2;3), (3;2), (-2 + √7; -2 - √7); (-2 - √7; -2 + √7). Указание: 2 -1. |
|
4 |
(3±√5)/2 |
2±√3 |
2±√3; (3±√5)/2 |
(5 ± √21)/2 |
(1;-2), (-1;2). Указание: 1·4 + 2. |
Заключение.
Практически всё, что окружает нас, связано в той или иной мере с математикой. А достижения в физике, технике, информационных технологиях только подтверждают это. И что очень важно – решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
В данной работе на конкретных примерах рассмотрели различные способы решения уравнений. Все указанные способы позволяют понизить степень уравнения и свести решение его к решению квадратного или линейного уравнения.
Заниматься решением уравнений высших степеней можно на факультативных занятиях, спецкурсах в старших классах. Хорошо подготовленные ученики с интересом изучают этот материал, а затем представляют одноклассникам решённые уравнения. Данный материал дает возможность подготовиться к ЕГЭ.
1. Адамская Н. Алгебра и математический анализ: Тематическое планирование. Контрольные работы. Математика, 2000. - №28.
2. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч.1 Учебник для учащихся общеобразовательных учреждений (профильный уровень). А.Г. Мордкович. Изд. «Мнемозина», 2010.
3. Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики.
4. Галицкий М.Л. и др. Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидакт. материалы: Пособие для учителя. – М.: Просвещение, 1990.
5. Звавич Л. И., Шляпочник Л. Я., Чинкина М. В., Алгебра и начала анализа 8–11. Дидактические материалы, М: Дрофа, 1999.
6. Зильберберг Н.И. Урок математики: Подготовка и проведение: Кн. для учителя. – М.: Просвещение: АО «Учеб. лит.», 1995.
7. Ивлев Б. М., Задачи повышенной трудности по алгебре и началам анализа: учебное пособие для 10–11 классов средней школы, М: Просвещение, 1990.
8. Математика. Интенсивный курс подготовки к экзамену. О. Ю. Черкасов, А. Г. Якушев. Москва, изд. “Айрис”, 1997.
9. Профильное обучение математике старшеклассников. Учебно-дидактический комплекс. – Новосибирск. Сиб. унив. изд-во, 2003.
10. Тумаркин Л.А. «История математики», Москва, 1975 г.
11. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. – М.: Просвещение, 1989.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.