
В. К. Никишев
Методы построения и исследования моделей динамических объектов и систем на основе компьютерного моделирования
2014
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Чувашский государственный университет имени
И.Н. Ульянова»
В. К. Никишев
Методы построения и исследования моделей динамических объектов и систем на основе компьютерного моделирования
2014
УДК 510.67(075.8)
ББК в181 я 73
Н62
Рецензенты:
И. Т. Артемьев – д-р. физ-мат. наук, профессор
(Чувашский государственного университета им. И.Н. Ульянова)
Т. А. Лавина - д-р. пед. наук, профессор
(Чувашский педагогический университет им. И. Я. Яковлева)
Никишев В. К.
Н62 Методы построения и исследования моделей динамических объектов и систем на основе компьютерного моделирования / В. К. Никишев. – Чебоксары: Изд-во Чуваш. ун-та, 2014. – 332 с.
ISBN978-5-7677-1876-4
В монографии представлен теоретический материал по основам построения моделей и моделирования для различных объектов, процессов и систем, примеры математических, информационных и функциональных моделей, алгоритмы и особенности реализации моделей на современных языках моделирования и специальные системы для моделирования. Приведены авторские методы моделирования сложных управляемых кибернетических систем и объектов. Монография будет полезна для работ как преподавателям, аспирантам и студентам высших учебных заведений, использующих в научно-исследовательской работе различные методы моделирования.
Ответственный редактор канд. техн. наук,
Профессор В. П. Желтов
Утверждено Учебно-методическим советом университета
ISBN 978-5-7677-1739-2 УДК 004/92(076/5)
ББК в181 я 73
© Издательство Чувашского
Университета, 2014
© Никишев В. К., 2014
ПРЕДИСЛОВИЕ
В настоящее время все значимыми являются вопросы моделирования на ЭВМ, проведения вычислительных экспериментов. Если ранее эти задачи были прерогативой ученых и инженеров, то в настоящее время увеличиваются объемы использования ЭВМ в учебном процессе высших учебных заведениях актуальными становятся именно процессы познания окружающего мира, проектирование, прогноза или выбора оптимальных параметров на основе моделей объектов, процессов и явлений, реализованных на ЭВМ. Использование ЭВМ в различных сферах человеческой деятельности ̶ в управлении, проектировании, диагностике, обучении, экономике и др. требует предварительной проверки исследуемых или изучаемых объектов, процессов, явлений, систем на функционирование или оптимальную целесообразность их применения в рассматриваемых сферах. По результатам моделирования на ЭВМ можно конструировать самолеты и ракеты, синтезировать химические вещества, строить промышленные и сельскохозяйственные объекты с учетом экологических требований к природным ресурсам, планировать выпуск наиболее рентабельной и прибыльной продукции, прогнозировать неисправности технических устройств и принимать меры по их устранению, сэкономив при этом огромные средства. Необходимость предварительного исследования объектов с использованием моделей на ЭВМ очевидна. В обучении вопросы моделирования становятся одними из основополагающих к системе образования. Включение компьютера в учебный процесс обеспечит активный вид познавательной деятельности. Именно использование компьютерного моделирования в учебном процессе предусматривает изучение и исследование объектов, явлений на основе готовых моделей, построение моделей, создаваемых самими студентами, что повышает интенсивность и эффективность обучения. По моему мнению, использование ЭВМ для моделирования различных систем и процессов, разработки оптимальных управлений будет способствовать тому, что один из разделов информатики и вычислительной техники, а именно моделирование, станет одним из необходимых и обычных занятий в высших учебных заведениях.
Глава 1. МОДЕЛИ. МОДЕЛИРОВАНИЕ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1 Сущность моделирования. Модели. Классификация.
Как правило изучение, анализ, исследование процессов или явлений, протекающих в сложных системах, объектах, сопряжено с различными трудностями. В то же время те или иные свойства, присущие какой-либо системе, процессу или явлению, сходны по определенным признакам с другими системами, процессами или явлениями. Данная закономерность дает возможность использовать в процессе познания аналогии, т.е. для изучения более сложных материальных объектов или систем исследовать более простые системы или объекты, представленные в более доступной форме, которая может служить средством познания нераскрытых признаков и свойств исследуемых объектов или систем. Например, наблюдая процессы жизнедеятельности человека и ряда животных и отмечая наличие многих совпадающих свойств, можно сделать вывод, что и другие свойства у них являются общими. Это позволяет проводить на животными или иных экспериментов с целью получения данных для лечения людей.
Большое сходство с методом аналогий при познании явлений или процессов имеет метод моделирования, основанный на исследовании систем, объектов, процессов и явлений с использованием существующих моделей. Впервые высказал мысль о возможности машинного моделирования человеческих функций и ввел термин “модель” В. Лейбниц (1646-1716 )
Модели - это материальные или мысленно представленные в виде математических формул, рисунков, макетов, знаков, текстовой информации и других форм объекты и системы, процессы и явления, которые в процессе познания (изучения, исследования) замещают объект-оригинал, сохраняя некоторые наиболее важные для данного познания характерные его черты, характеристики, параметры.
Иными словами, модель - это некоторое упрощение подобия реального объекта.
Под моделью понимается отражение наиболее существенных признаков, свойств и отношений объектов, систем, процессов или явлений окружающего мира. А исследование, познание или проверка модели это процесс моделирования. Если в качестве модели используется математическая модель, построенная с использованием математических зависимостей, символик или знаков, то ее исследование на ЭВМ тоже является моделированием или вычислительным экспериментом.
Такое определение основано из формулировке энциклопедических понятий «моделирования» и «эксперимента».
Моделирование - исследование каких-либо явлений, процессов или систем, объектов путем построения и изучения их моделей.
Приведем еще несколько определений понятия моделирование и эксперимента.
Моделирование - использование моделей для определения или уточнения характеристик и рационализация способов построения вновь конструируемых объектов.
Моделирование - одно из основных категорий теории познания, на котором базируется любое научное исследование, как теоретическое, так и экспериментальное.
Эксперимент ( от лат., experimentum, проба, опыт) - чувственно-предметная деятельность в науке. В более узком смысле - опыт, воспроизведение объектов познания, проверка гипотез. Поэтому под вычислительным экспериментом, или моделированием, следует понимать познание или изучение объектов, явлений, процессов или систем путем исследования моделей этих объектов, явлений, процессов или систем на ЭВМ.
Можно дать и такое толкование соотношения между понятием моделирования и вычислительным экспериментом. Под вычислительным экспериментом следует понимать исследование моделей объектов, систем, явлений и процессов путем моделирования их на ЭВМ с заранее продуманным планом исследования с целью изучения влияния конкретных параметров на эти системы. В этом случае под моделированием понимается реализация моделей объектов, систем, явлений и процессов на ЭВМ путем построения алгоритмов, и разработки программ на одном из алгоритмических языков и их решение с помощью ЭВМ.
Система - множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство. Или, иными словами, система есть множество, элементы которого закономерно связаны между собой.
Системы могут быть материальными и абстрактными. К материальным системам относятся, например, системы неорганической природы (физические, химические, технические), системы живой природы (биологические системы, организмы, популяции, виды и т. д.) и системы социальные (социальные объединения и структуры, экономические системы, производственные комплексы). Абстрактные системы включают понятия, гипотезы, теории и т. д.
Сложные динамические системы являются предметом исследования и изучения кибернетики - науки об общих закономерностях строения сложных систем управления; - науки об общих законах получения, хранения, передачи и преобразования информации в сложных управляющих системах. В общем случае кибернетику можно подразделить на техническую, биологическую и экономическую. Аналогично и модели могут быть техническими, биологическими и экономическими.
Объект, с точки зрения философской категории, выражает то, что противостоит субъекту в его практической и познавательной деятельности.
Явление - это внешняя форма существования предмета или то, что обнаруживает предмет. Явление, с точки зрения познания, является ступенью постижения предмета моделирования.
Процесс - последовательность смены явлений, состоящий в развитии чего-либо, совокупность последовательных действий для достижения результата.
Для подтверждения необходимости построения и познания моделей приведем ряд примеров.
Конструктор разработал летательный аппарат, например самолет или ракету. Перед тем как построить действующий образец в реальных размерах, необходимо проверить устойчивость полета самолета или ракеты при воздействии различных внешних факторов, измерить различные напряжения, которые возникают в корпусе, для исключения случаев разрушения отдельных частей самолета или ракеты во время полета. Для этих целей можно выполнить модель самолета в уменьшенных размерах и провести исследования в аэродинамической трубе, а для исследования устойчивости необходимо составить математическую модель самолета в виде системы дифференциальных уравнений и исследовать реакции объекта на различные воздействия.
Архитектор, прежде чем построить здание, изготовляет его модель в уменьшенных габаритах, например, из кубиков, для оценки его с эстетической точки зрения, и как оно вписывается в окружающий рельеф.
Картина, на которой изображены море или горы, является моделью конкретного природного ландшафта.
Учитель объясняет устройство ЭВМ по плакату, который тоже можно назвать графической моделью устройства ЭВМ.
Эффективность производства существенно зависит от эффективности управления. Поэтому прежде чем принимать какое-либо решение, необходимо проанализировать соотношение «затраты – результаты». А такой вывод можно сделать только после исследования так называемой экономико-математической модели конкретного производства на ЭВМ.
Одним из препятствий для построения скоростных самолетов в одно время стало явление “флаттер”. Во время экспериментальных полетов в некоторых критических режимах неожиданно возникали резкие вибрации конструкции и машина буквально разваливалась в воздухе по частям. Причина - резонансные явления, которые могли бы быть исследованы на моделях: в аэродинамической трубе или с использованием ЭВМ.
Вопросами устойчивости кораблей очень много занимался русский математик и кораблестроитель Крылов, который еще в 1905 г. во время русско-японской войны предсказал неустойчивость корабля “Петропавловск” при попадании снарядов. Поэтому одним из советов А. Н. Крылова было создание опытного водохранилища для исследования устойчивости строящихся кораблей, а также выбор оптимальной формы конструкции после проведенного математического моделирования.
Справка
КРЫЛОВ Алексей Николаевич (1863-1945)
Русский математик,
кораблестроитель, академик А.Н. Крылов родился 3 (15) августа 1863 г. в селе
Висяга Алатырского уезда Симбирской губернии (ныне село Крылово Порецкого
района Чувашии) в семье отставного офицера-артиллериста. В 1878 г. в возрасте
15 лет он поступает в одно из самых  привилегированных учебных заведений России - Петербургское
Морское училище (с 1939 г. - Высшее военно-морское училище им. Фрунзе),
выдержав вступительные экзамены "с небывало высокими баллами". А. Н.
Крылов — русский и советский кораблестроитель, инженер-изобретатель, специалист
в области механики и математики, всю свою жизнь связавший с теорией магнитных и
гирокомпасов, развил учение адмирала Макарова Макарова С.О. о живучести и
непотопляемости корабля — их совместные труды стали классикой и до сих пор
широко применяются в морском деле. Автор около 300 книг и статей, посвященных,
в частности, судостроению, магнетизму, артиллерийскому делу, математике,
астрономии и геодезии. Перевел на русский язык «Математические начала
натуральной философии» Ньютона (1915) и запись лекций 1822 г. по теоретической
астрономии знаменитого математика и астронома Гаусса (1916). Доктор прикладной
математики, ординарный академик (1916). После Октябрьской революции передал советскому
правительству все суда Русского общества пароходства и торговли, которое
возглавлял, и продолжил развивать отечественный флот, несмотря на дворянское
происхождение и предложение переехать в Америку. Шесть лет (1921—1927) провел
в заграничной командировке, куда его отправили как представителя советского
правительства для восстановления зарубежных научных связей страны. А. Н. Крылов
награжден орденом святого Станислава I степени и тремя орденами Ленина. Лауреат
Сталинской премии (1941), Герой Социалистического Труда (1943).
привилегированных учебных заведений России - Петербургское
Морское училище (с 1939 г. - Высшее военно-морское училище им. Фрунзе),
выдержав вступительные экзамены "с небывало высокими баллами". А. Н.
Крылов — русский и советский кораблестроитель, инженер-изобретатель, специалист
в области механики и математики, всю свою жизнь связавший с теорией магнитных и
гирокомпасов, развил учение адмирала Макарова Макарова С.О. о живучести и
непотопляемости корабля — их совместные труды стали классикой и до сих пор
широко применяются в морском деле. Автор около 300 книг и статей, посвященных,
в частности, судостроению, магнетизму, артиллерийскому делу, математике,
астрономии и геодезии. Перевел на русский язык «Математические начала
натуральной философии» Ньютона (1915) и запись лекций 1822 г. по теоретической
астрономии знаменитого математика и астронома Гаусса (1916). Доктор прикладной
математики, ординарный академик (1916). После Октябрьской революции передал советскому
правительству все суда Русского общества пароходства и торговли, которое
возглавлял, и продолжил развивать отечественный флот, несмотря на дворянское
происхождение и предложение переехать в Америку. Шесть лет (1921—1927) провел
в заграничной командировке, куда его отправили как представителя советского
правительства для восстановления зарубежных научных связей страны. А. Н. Крылов
награжден орденом святого Станислава I степени и тремя орденами Ленина. Лауреат
Сталинской премии (1941), Герой Социалистического Труда (1943).
Именем академика названы учреждения и корабли, институты и научные общества, улица (с 1952) в Петербурге и даже кратер на Луне, а на доме, где он жил и работал, установлена мемориальная доска. В 1963 г. в честь 100-летия со дня рождения ученого деревня Висяга переименована в Крылово. в октябре 1984 г. на его родине был открыт музей.
История науки и техники полна примеров того, какое значение имеет использование моделирования для решения тех или иных задач. Вот лишь некоторые из них. Перед спуском на воду английского корабля «Кэпетен» инженер Рид предупредил лордов адмиралтейства, что корабль на воде неизбежно перевернется. Он установил это с помощью моделирования: изготовил физическую модель корабля и провел соответствующие испытания. Однако лорды не прислушались к предупреждению, и это стало причиной трагедии: при спуске корабля на воду он перевернулся и затонул. С тех пор в соборе Святого Павла в Лондоне висит памятная доска об этом печальном событии, надпись на которой гласит: «Вечное порицание невежественному упрямству лордов адмиралтейства...» [Л8].
Многие объекты или процессы при описании их математическими зависимостями являются нелинейными, поэтому их изучение без использования моделей очень затруднено. Так, например, у сложных систем, состоящих из многих взаимодействующих подсистем, могут возникнуть качественные особенности, которыми ни одна из частей не обладает. Такая теория самоорганизации называется синергетикой. Нахождение общих принципов, управляющих самоорганизующимися системами, является невозможным без исследования их на ЭВМ по построенным моделям.
В настоящее время все большее значение приобретают вопросы размещения предприятий, ферм или других сельскохозяйственных объектов с учетом экологических требований. Какой вред нанесут здоровью людей, сохранению флоры и фауны выбросы всех предприятий. Все эти задачи должны быть прежде исследованы на моделях и после различных оптимальных вариантов размещения приняты соответствующие решения.
Таким образом, все модели могут использоваться для следующих целей:
1. Чтобы понять, как устроен конкретный объект, какова его структура, основные свойства и взаимодействие его с окружающим миром.
2. Чтобы научиться управлять объектом, системой или процессом с целью определения наилучших способов управления с учетом требуемых критериев качества.
3. Чтобы прогнозировать прямые и косвенные последствия реализации данных способов и форм воздействия на объект, процесс или явление.
4. Чтобы выбрать оптимальный план из множества вариантов предложений или действий.
Научная мудрость гласит: «Если построенная Вами модель никуда не годится - не огорчайтесь, это все равно самый дешевый способ строительств».
Модели можно подразделить на следующие виды: графические (геометрические), физические, математические и информационные.
К графическим моделям следует отнести такие модели, которые получаются путем отображения реальных объектов, процессов или явлений на бумаге, киноленте, слайде, дисплее и т. д.
К физическим моделям следует отнести такие модели, которые допускают исследования на реальных объектах, но при увеличенной или уменьшенной копии объекта, например планетарий, малые водохранилища, макеты зданий, модели летательных или плавающих аппаратов и т. д.
К математическим (знаковым) моделям следует отнести такие модели, которые используют знаковые преобразования формул, графиков, чертежей, наборов символов с включением совокупности законов отношений, по которым можно оперировать с выбранными знаковыми образованиями и их элементами.
Математические модели в свою очередь можно условно подразделить на динамические (дескриптивные), оптимизационные, игровые, имитационные и лингвистические.
Динамические модели (дескриптивные, от англ. description - описание) предназначены для описания различных процессов, явлений или исследования динамических объектов. В основе исследования этих моделей лежат математические методы решения дифференциальных и алгебраических уравнений. Оптимизационные (экстремальные) модели используются для выбора множества переменных управления с учетом различных соотношений, связывающих некоторые параметры, для обеспечения необходимого критерия качества. В основе оптимизационных моделей лежат различные оптимальные методы: метод линейного и динамического программирования, метод сетевого планирования, методы целочисленного и нелинейного программирования и т. д.
Игровые модели предназначены для исследования различных конкретных ситуаций, когда интересы участников игр не совпадают. В основе таких моделей лежит математический аппарат теории игр.
Логико-лингвистические модели предназначены для использования в системах автоматического перевода, ввода информации в технические устройства, представляющие языки знаний в различных областях науки и техники.
Наиболее общими являются информационные модели. Под информационной моделью понимается набор величин, содержащий всю необходимую информацию об исследуемых объектах и процессах [5]. Математический энциклопедический словарь определяет понятие информационной модели более широко: информационная модель - модель, в которой изучаемое явление или объект представлены в виде процессов передачи и обработки информации, а параметры как самой модели, так и ее составляющих представлены в числовой, текстовой или иной сигнальной форме. Информационная модель - это такой объект-заменитель, который в определенных условиях может заменить объект-оригинал, воспроизводя интересующие свойства и характеристики. Информационная модель имеет преимущество в удобстве использования (наглядность, обозримость, доступность, легкость оперирования моделью и т.д.). Допустим, что Вам описали внешность человека, которого вы не видели. В Вашем сознании сложился некоторый образ человека, информационная модель конкретного человека, по которой можно его узнать. Расписание занятий - это тоже информационная модель учебного процесса, представленная в табличной форме. В то же время А.П. Ершов, характеризуя информатику как отдельную науку, считает, что она имеет место в том случае, когда для изучения фрагментов мира строится информационная модель, которая представляет то сопряжение, через которое информатика вступает в отношения с частными науками, не сливаясь с ними и в то же время не вбирая их в себя.
Справка
 Андре́й Петро́вич Ершо́в (1931-1988) — советский учёный, один из пионеров
программирования, создатель Сибирской школы информатики. Его работы оказали
огромное влияние развитие вычислительной техники в СССР.
Андре́й Петро́вич Ершо́в (1931-1988) — советский учёный, один из пионеров
программирования, создатель Сибирской школы информатики. Его работы оказали
огромное влияние развитие вычислительной техники в СССР.
Окончил механико-атематический факультет МГУ в 1954 г.. Ученик А. А. Ляпунова. До 1950-х г. в СССР не существовало специальности «программист». Он оказался одним из первых программистов, имевших специальное образование. Ершов в 1957 г. возглавил отдел программирования Вычислительного центра АН СССР. Вскоре после окончания МГУ становится руководителем работ и автором одной из первых программ для ЭВМ — «БЭСМ» и «Стрела». В 1958 г. опубликовал монографию «Программирование для БЭСМ». В 1960 году работал в Новосибирском Академгородоке, с которым была связана вся научная и педагогическая деятельность Андрея Петровича. Под его руководством были созданы такие языки программирования, как Альфа, Альфа-6 с трансляторами.
В 1970-х г. разработал для многих языков оптимизированные трансляторы. В середине 1980-х гг. предложил создать открытый, т. е. развиваемый язык, на котором можно описать будущую программу, конструкции и объекты предметной области задачи. Этот язык получил наименование «Лексикон». С 1966 по 1972 г. руководил созданием программно-аппаратной системы разделения времени АИСТ («Автоматическая информационная станция»). В 1981 г. на 3-й Всемирной конференции Международной федерации по обработке информации в Лозанне (Швейцария) сделал доклад: «Программирование — вторая грамотность». Название доклада быстро становится лозунгом. В Новосибирске начинаются эксперименты по преподаванию программирования и информатики школьникам. Разрабатывается компьютер Агат, обучающая система «Школьница» и язык «Рапира». В 1985 г. Ершовым совместно с группой соавторов был выпущен школьный учебник «Основы информатики и вычислительной техники» (ОИВТ) началось преподавание информатики во многих школах Советского Союза. Для записи алгоритмов в этом учебнике применялся Алголо-подобный язык, так называемый Русский алгоритмический язык . Реализацией этого языка стал Е-практикум, разработанный на механико-математическом факультете МГУ. А. П. Ершов был организатором и участником многих международных конференций, учёных групп, главных редколлегий советских и иностранных научных журналов, активным деятелем Международной федерации по обработке информации (ИФИП). Труды Ершова по информатике, в том числе по теоретическому и системному программированию, получили международное признание: он был членом Ассоциации вычислительной техники (1965), почётным членом Британского общества по вычислительной технике (1974). С апреля 1987 г. был председателем Научного совета АН СССР по комплексной проблеме «Кибернетика». А. П. Ершов был удостоен премии имени академика А. Н. Крылова. Похоронен в Новосибирске. Имя А. П. Ершова носит Институт систем информатики, премия для молодых учёных СО РАН, аудитория и студенческая стипендия в НГУ, в институте хранится его мемориальная библиотека и научный архив [17].
Наиболее общее определение информационной модели дал В. М. Глушков [3]. Информационная модель представляет собой просто описание строения и закономерностей поведения моделируемого объекта. Средством фиксации любой конкретной информационной модели являются языки, причем не только те человеческие языки, которые изучаются традиционным языкознанием, но и любые искусственные языки, строящиеся в процессе накопления и передачи знаний. Объект, явление, процесс и прочее явление любой природы становится доступным компьютерной обработке только после представления его в виде текста над конечным алфавитом. Такое представление называется информационной моделью.
Информационная модель может быть использована при исследовании или познании наиболее сложных систем, например, предприятий, отраслей промышленности, различных билетных касс, процесса обучения в учебных заведениях и т. д.
Справка
 Ви́ктор Миха́йлович Глушко́в (1923 - 1982) — советский математик,
кибернетик. Решил обобщённую пятую проблему Гильберта. Под его руководством в
1966 г. была разработана первая персональная ЭВМ «МИР-1» (вычислительная машина
для инженерных расчётов).
Ви́ктор Миха́йлович Глушко́в (1923 - 1982) — советский математик,
кибернетик. Решил обобщённую пятую проблему Гильберта. Под его руководством в
1966 г. была разработана первая персональная ЭВМ «МИР-1» (вычислительная машина
для инженерных расчётов).
Заведовал кафедрой теоретической механики Уральского лесотехнического института. Докторскую диссертацию защитил на учёном совете МГУ 12 декабря 1955 г. Оставшаяся после переезда из Киева в Москву С. А. Лебедева его лаборатория, в которой была создана первая в СССР вычислительная машина МЭСМ, была переведена в Институт математики АН УССР, директором которого был Б. В. Гнеденко, в которой В. М. Глушков работал с 1956 г.. С 1962 г. он вице-президент Академии наук УССР. [5]
В 1964 г. под его руководством и непосредственном участии была разработана АСУП «Система Львов» на Львовском телевизорном заводе, принятой в эксплуатацию в 1967 г.. В 1966 г. на механико-математическом факультете Киевского государственного университета им. Т. Шевченко была создана кафедра теоретической кибернетики, которую возглавил В. М. Глушков, а в 1969 г., был создан факультет кибернетики. В 1967 г. в Киеве под руководством академика В. М. Глушкова была организована кафедра МФТИ при Институте кибернетики АН УССР, который в будущем был преобразован в Институт кибернетики им. В. М. Глушкова НАН Украины. В. М. Глушков был советником генерального секретаря ООН по кибернетике. В. М. Глушков был инициатором и главным идеологом разработки и создания Общегосударственной автоматизированной системы учёта и обработки информации (ОГАС), предназначенной для автоматизированного управления всей экономикой СССР в целом. Для этого им была разработана система алгоритмических алгебр и теория для управления распределёнными базами данных [18].
В настоящее время выделяют следующие виды моделирования: математическое, физическое , информационное, компьютерное, эволюционное, логическое, педагогическое, статистическое, графическое, натурное, имитационное и другие виды специальных видов моделирования.
1.2 Этапы моделирования.
Для моделирования необходимо иметь следующие элементы: исследователь, объект моделирования и модель, на которой будут проводить исследования и которая отражает наиболее существенные связи и отношения между объектом и моделью. На первом этапе проводится анализ объекта оригинала на наличие наиболее существенных и необходимых в достаточной мере связей.
На втором этапе модель является основным предметом исследования с уже выбранными формулами, уравнениями и т. д.
На третьем этапе после проведенных исследований проводится перенос полученных с модели параметров на объект.
Четвёртый этап — проверка получаемых с помощью моделей параметров для формирования окончательного варианта построения объекта, его преобразования или управления им.
Моделирование — это процесс, в котором после проведенных исследований происходит повторение исследования для уточнения и расширения знаний о моделируемом объекте. В настоящее время трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания продуктов сельского хозяйства, функционирования отдельных органов человека, последствий атомной , да и любой войны. В общем для каждой системы должны быть созданы свои модели, перед реализацией каждого технического проекта должно проводиться моделирование.
В процессе моделирования (проведения вычислительного эксперимента) можно выделить ряд этапов: постановка задачи, выбор и описание модели, выбор и обоснование метода моделирования, алгоритмизация модели и метода моделирования, разработка и отладка программы, моделирование анализ и тестирование полученных результатов.
Постановка задачи
На этом этапе формируется цель моделирования на основе технического задания, который составляется разработчиком системы, производится анализ исходных данных и результатов моделирования, определяются условия, при которых будет выполняться моделирование и ориентировочно прикидываются приближенные значения величин и их размерности.
Выбор и описание модели
Данный этап характеризуется тем, что определяются зависимости между исходными данными и результатами моделирования. Эти зависимости представляются в математической, текстовой или другой информационно-логической форме.
Выбор и обоснование метода моделирования
Для получения результата моделирования необходимо выбрать численный метод исследования модели, особенно, когда речь идет о математической модели или информационной модели. Выбор производится с учетом точности вычисления, времени моделирования и т. д. Могут быть использованы следующие методы: различные методы решения систем дифференциальных или алгебраических уравнений; методы, основанные на многочисленных, оптимальных или статистических, способах получения прогнозируемого или управляющего результата. Особенно часто используется метод имитационного моделирования
Алгоритмизация модели и метода моделирования
На данном этапе составляются алгоритмы модели и метода моделирования в соответствии с выбранными математическими или информационными моделями и численными методами решения уравнений или моделей функционирования систем, явлений или процессов. В соответствии с понятием алгоритма данный этап разбивается на ряд самостоятельных участков и устанавливается последовательность их реализации на ЭВМ.
Алгоритм может быть представлен в словесной (текстовой, текстово-знаковой) форме, в виде блок-схемы или псевдокода (алгоритмического языка). Если рассматривать процесс моделирования в целом, то целесообразно разработать на данном этапе алгоритмы моделей проведения эксперимента (моделирования), представления исходных данных и результатов моделирования. Алгоритм проведения эксперимента должен включать следующие данные: параметры модели и внешних условий, последовательность их изменения и фиксации. На данном этапе особенно важным является исследование сложных моделей. К сожалению, процесс алгоритмизации очень часто игнорируется или выполняется формально. Я убедился в течение многих лет, что вопросы алгоритмизации в учебных заведениях обучают без знания мировых стандартов для описания алгоритмом. В соответствии с понятием алгоритма данный этап разбивается на ряд самостоятельных участков и устанавливается последовательность их реализации на ЭВМ. Алгоритм может быть представлен в словесной форме, в виде блок-схемы или псевдокода (алгоритмического языка). Для практических задач особенно при оформлении документации используется блок-схемы. Именно с помощью блок-схем можно понять структуру программы для моделирования и ход исследования модели. Алгоритм проведения эксперимента должен включать данные: параметры модели и внешних условий, последовательность их изменения. Если в качестве исполнителя алгоритма используются языки визуального программирования, например Delphi, Bulder C++, Visual Studio 2010(2012, 2013) и особенно метод объектно-ориентированного программирования ООП, то необходимо учитывать то, что действия выполняются не над переменными, а над объектами. В качестве объектов могут быть и переменные и элементы управления. В этом случае разрабатываются проекты, которые состоят из форм, на которых формируются элементы управления, и программ, в которых преобразования переменных выполняются с учетом выбранных элементов управления. Вообще, сам процесс алгоритмизации можно разбить на два этапа: общий и частный. При общей алгоритмизации составляется последовательность действия над переменными, которая представляет общую структуру алгоритма исследования. А частный алгоритм должен составляться с учетом исполнителя алгоритма и использования элементов управления. Такой алгоритм позволяет любым пользователям разобраться с последовательностью преобразований в соответствии с моделью объекта и методом реализации исследования. Примеры составления алгоритмов исследований и основные графические символы приведены в разделе приложения, в котором приводятся примеры моделирования объектов, процессов и явлений.
Разработка и отладка программ
Программа составляется на одном из языков программирования, например, Delphi , языков на платформе .NET, ( C#, C++, VB.NET), или специальных программ для моделирования MatLab, SciLab и т. д. Выбор языка программирования производится с учетом конкретной ЭВМ и опыта работы. В результате отладки программы обнаруживаются и устраняются ошибки, допущенные в программе. Ошибки в программах бывают синтаксические и логические. С помощью синтаксического контроля программы транслятором выявляются и устраняются недопустимые конструкции с точки зрения правил их построения, принятых в выбранном алгоритмическом языке. Сообщения о таких ошибках выдаются на печать. После устранения синтаксических ошибок проверяется логика работы разработанной программы в процессе ее выполнения. На этом этапе могут быть предусмотрены округленные контрольные результаты, которые сопоставляются с результатами, полученными на ЭВМ.
В отладку программ исследования объектов должны входить элементы тестирования программ, с помощью которых
определяется правильность создания алгоритма и программы.
Моделирование и анализ полученных результатов
После отладки программы производится моделирование (эксперимент) в соответствии с выбранными вариантами исходных данных. Полученные результаты анализируются и оцениваются с учетом физической или символической структуры объекта, явления или процесса.
В настоящее время для разработки новых систем все чаще стали использовать метод, который основан на методологии SADT, а сам процесс моделирования является частью разработки сложного объекта или системы.
SADT (Structured Analysis and Design Technique) — методология структурного анализа и проектирования, интегрирующая процесс моделирования, управление конфигурацией проекта, использование дополнительных языковых средств и руководство проектом со своим графическим языком. Процесс моделирования может быть разделен на несколько этапов: опрос экспертов, создание диаграмм и моделей, распространение документации, оценка адекватности моделей и принятие их для дальнейшего использования. Этот процесс хорошо отлажен, потому что при разработке проекта специалисты выполняют конкретные обязанности, а библиотекарь обеспечивает своевременный обмен информацией.
SADT возникла в 60-х гг. ХХ в. в ходе революции, вызванной структурным программированием, когда большинство специалистов работали над созданием сложных программ для сложных систем. Таким образом, процесс создания системы, имеет следующие фазы:
1. анализ — определение того, что система будет делать, операция мысленного или реального расчленения целого (вещи, свойства, процесса или отношения между предметами) на составные части, выполняемая в процессе познания или предметно-практической деятельности человека;
2. проектирование — определение подсистем и их взаимодействие, деятельность человека или организации по созданию проекта в виде модели объекта, комплекта документации, предназначенной для создания определённого объекта, его эксплуатации, ремонта, а также для проверки промежуточных и конечных решений, на основе которых был разработан данный объект;
3. реализация — разработка подсистем по отдельности, объединение — соединение подсистем в единое целое;
4. тестирование — проверка работы системы, применяется для определения соответствия предмета испытания заданным требованиям. В задачи испытания не входит определение причин несоответствия заданным требованиям. Испытание — один из разделов диагностики.
5. Установка — введение системы в действие,
6. Эксплуатация — использование системы.
1.3. Формы представления моделей и алгоритмов.
Для моделирования объектов, систем, процессов и явлений очень важной с точки зрения понимания задач и целей моделирования является первоначальная форма представления моделей. При этом необходимо придерживаться применения системного и функционального подхода при описании и исследовании объектов.
Системный подход выражается в комплексном изучении объекта (системы, процесса или явления) с позиции системного анализа, т.е. анализа проблем и объектов как совокупности взаимосвязанных элементов. Цель функционального анализа,выявление и изучение функциональных последствий тех или иных явлений или событий для исследуемого объекта.
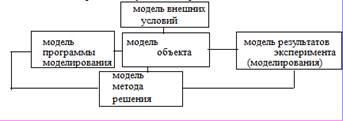
С этих позиций модель целесообразно представлять в виде последовательности моделей: объекта, внешних факторов, воздействующих на объект, метода моделирования, программы моделирования (проведения эксперимента), программ оформления исходных данных и результатов моделирования.
В целом процесс моделирования можно рассматривать как следующую замкнутую схему, имитирующую действия объекта в реальных условиях среды ( рис.1).
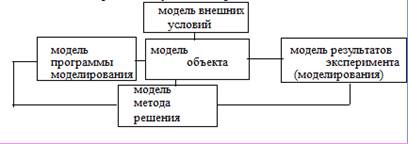
Рис.1. Общая модель процесса моделирования.
Модель программы моделирования задает порядок изменения параметров моделей объекта и внешних условий, время моделирования и т.д. Модель объекта может представляться совместно с моделью внешних условий, так как математически или информативно бывает довольно трудно разделить эти модели. В свою очередь, модель объекта может задаваться в словесной форме; в виде дифференциальных или алгебраических уравнений или в ином математическом виде; в форме графа или графическом изображении; комплексной форме.
Основные формы представления моделей: словесная, знаковая ( математическая), на основе теории графов.
Словесная форма информационной модели. Требуется составить модель продажи билетов в кинотеатре. Начальные условия: количество сеансов, количество мест, стоимость билета. Результаты моделирования: общий вид зрительного зала с отображением проданных билетов на конкретный сеанс, количество проданных билетов на конкретный сеанс и общая дневная выручка. Словесная форма представления моделей чаще всего задается в виде таблицы данных.
Знаковая (математическая) форма модели представляется следующими уравнениями:
алгебраическими (информационная модель производства)
a1 x1 + b2 x2 <= c1;
a1 x1 + b2 x2 <= c2; z<=k1 * x1 + k2* x2.
дифференциальными (динамическая модель систем)
a 2 ẍ+ a 1 ẋ + a0 = 0,
систем дифференциальных уравнений
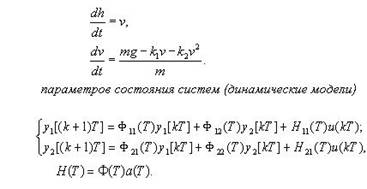
В практике моделирования могут использоваться и другие формы представления математических моделей как например, передаточные и импульсные характеристики и функции, разностные уравнения и z- преобразования, параметрические модели оценивания и т. д.
Модели на основе теории графов
Многие задачи при моделировании рассматриваются как совокупность объектов с описываемыми связями между ними. К ним можно отнести следующие объекты: карта автомобильных дорог с населенными пунктами, электрические цепи как соединение резисторов, конденсаторов, источников, структуры органических молекул, свойства которых определяются связями между атомами, отношение и связи между предприятиями и людьми. Такие объекты можно изображать точками, называемыми вершинами, а связи между ними - линиями, называемыми ребрами. Представление объектов, явлений и процессов множеством вершин V и ребер Е называют графом, который обозначается G=(V,E).
Примером графа является задача о кенигсбергских мостах (рис.1а), которая впервые была опубликована двадцатилетним Леонардом Эйлером в 1736 г., когда он работал в Российской Академии Наук.
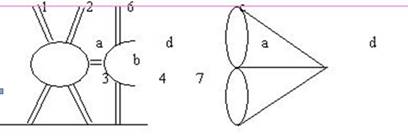
Рис 2а. Пример графа Рис. 2б. Граф вариантов
Суть задачи состоит в том, можно ли совершить прогулку таким образом, чтобы выйдя из любого места города, вернуться в него, пройдя только один раз по каждому мосту. По условию задачи имеется 4 части суши a,b,c,d, на которых расположен город. Их можно представить вершинами. Связи между частями города осуществляются через 7 мостов, которые представляются ребрами.
Граф вариантов «прогулка по городу» изображен на рис.2б.
Часто объекты характеризуются связями с определенной ориентацией (одностороннее движение, протекание тока от положительного полюса к отрицательному полюсу источника, различные отношения между числами (неравенства).
С этой целью ребра в графах отмечаются стрелками, а ориентированное ребро называется дугой. Граф с такими связями есть ориентированный граф (рис.3).
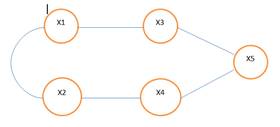
Рис. 3. Ориентированный граф.
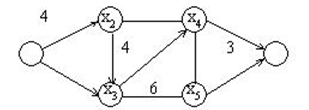
Рис. 4. Пример взвешенного графа.
Если начало и конец ребра совпадают, то такое ребро называют петлей. Последовательность вершин Xi, при которых каждая пара определяет ребро, называется маршрутом в графе. В том случае, если дугам, ребрам и вершинам приписываются количественные значения (приоритет, длина, напряжение и т. д.), то такой граф называется взвешенным (рис.4).
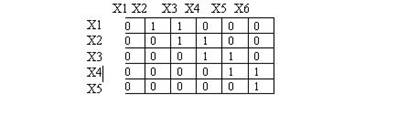
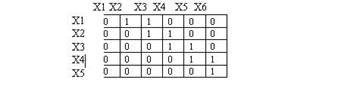
Рис 5. Матрица смежности
Две вершины графа называются смежными, если они являются граничными вершинами ребра. Граф можно представить также матрицей смежности. Строки и столбцы этой матрицы соответствуют вершинам графа.
Матрицей смежности называется квадратная матрица M=(mij) размерности n*n, элементы которой определяются так:
1, если в графе имеется ребро от Xi к Xj,
Mij =
O, в остальных случаях.
Граф, представленный на рис.5, имеет матрицу смежности.
Матрицей достижимости называется квадратная матрица C=(сij ), в которой элемент cij=1 только тогда, когда вершина Xj достижима из вершины Xi, иначе cij=0.
Алгоритм построения матрицы достижимости графа, исходя из матрицы смежности, представляет довольно сложную задачу.
Суть алгоритма сводится к следующему. Допустим имеется вершина Xk, в которую входят дуги, например, Xi-Xk. Далее рассматриваются пути, исходящие из Xk, например, Xk-Xj. Следовательно, в графе имеется путь Xi- Xj путь, проходящий через вершину Xk. В матрице достижимости графа элемент сij должен ранятся 1. Таким образом, просматриваются все вершины.
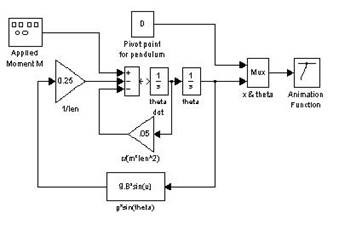 Блочная ( структурная ) форма представления моделей может
быть реализована тогда, когда каждый функциональный блок (элемента) описывается
математическими зависимостями и и имеются средства для моделирования таких систем,
например, с помощью пакета программ MatLab. Блочная (структурная) форма
моделей представлена на рис.6.
Блочная ( структурная ) форма представления моделей может
быть реализована тогда, когда каждый функциональный блок (элемента) описывается
математическими зависимостями и и имеются средства для моделирования таких систем,
например, с помощью пакета программ MatLab. Блочная (структурная) форма
моделей представлена на рис.6.
Рис. 6. Блочная( структурная) форма представления моделей
Функциональная форма модели
Данная форма представления моделей используется для представления сложных моделей, например, модели бизнес процессов, моделей предприятий, социальных объектов, сложных процессов и т. д. Этот метод представления моделей основан на использовании языка моделирования UML (Unified Modeling Language), который является на данный момент самым распространенным и общеизвестным способом моделирования программного обеспечения сложных объектов и систем. Формами представления на основе языка UML моделирования являются структурные диаграммы (классов, объектов, компонент и т. д.) Такие диаграммы используются для отображения систем на основе объектно - ориентированной структуры, которая является современным способом программирования и моделирования систем. В основе такого подхода система представляется в виде классов, объектов и другие форм и способов динамики работ таких систем (рис.7).
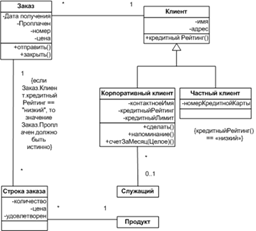
Рис. 7. Пример диаграммы классов
Основные типы функциональных моделей
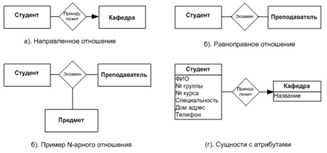
Визуальная модель «сущность-связь»
Для разработки баз данных обычно использовалось моделирование, а затем разрабатывалась база данных например, на основе БД ACCESS, Oracle, Microsoft SQL Server, MySQL. Для реализации процессов записи, хранения, удаления и поиска данных в БД используются запросы на языке программирования SQL. Для представления баз данных используется функциональная модель "сущность-связь", предложенная Петером Ченом в 1976 г..
Питер Чэнь Пиньшань— американский ученый в области информатики, предложивший в 1976 году ER-модель данных. Родился в Тайване, где получил степень бакалавра в области электротехники в 1968 году в Национальном университете Тайваня и степень доктора философии в области компьютерных наук в Гарвардском университете в 1973 году. В последующие годы работал профессором в различных американских университетах. Профессор Чэнь удостоен ряда наград за достижения в области информатики.
Для управления БД в настоящее время многими пользователями разрабатывается СУБД (система управления базами данных) - это программное обеспечение, предназначенное для процесс, ввода, вывода, поиска, хранения и программного доступа к большим массивам данных. Эти СУБД создавались с помощью современных языков программирования VC#, VC++, VB.NET, PHP. Одним из видов функциональной модели является визуальная модель «сущность-связь», которая представляется в виде сущностей, связей и атрибутов.
Сущность (entity) - это "предмет" разрабатываемой области, который можно отличить от других "предметов". Примеры сущностей: студент, университет, событие или процесс. Сущность изображается в виде прямоугольника, содержащем её имя, выражаемое существительным. Имя сущности должно быть уникальным в рамках одной модели.
Атрибут сущности - это любая деталь, которая служит для уточнения, идентификации, классификации, числовой характеристики или выражения состояния сущности. Имена атрибутов заносятся в прямоугольник, изображающий сущность, под именем сущности и изображаются малыми буквами.
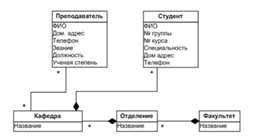
Связь (relationship) - это отношение между сущностями, которое отражает взаимодействие между ними.. Так, две сущности - "Студент" и "Кафедра", связаны отношением "Принадлежит", т. е. студент с приведенным атрибутом (ФИО, № группы и т. д.) принадлежит кафедре( рис.8)..
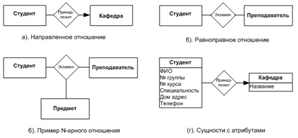
Рис. 8. Элементы ER-диаграммы
Графическое изображение функциональной модели «сущность-связь» обычно называют - диаграмма сущность-связь (ER-диаграмма) (англ. entity-relationship diagram, ERD).
Для задания схем реляционных баз данных промышленных СУБД используется язык SQL/DDL, который является промышленным стандартом для разработки сложных объектов.
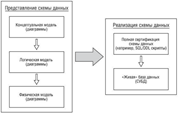
ER диаграмма «сущность-связь» представляется в виде следующих моделей: концептуальная, логическая и физическая ( рис. 9).
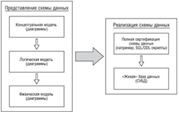
Рис. 9. Схема использования моделей БД
Концептуальная ( инфологическая) модель предназначена для извлечения знаний о предметной области. Эта модель помогает программистам разобраться с той сферой человеческой деятельности, для которой им предстоит создать программное приложение, выявив там основные сущности и связи между ними. Данная модель предназначена для обсуждения с непрограммистами и не должна содержать конструкций и понятий, которых последним не понять ( рис. 9).
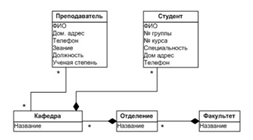
Рис. 9. Пример концептуальной модели
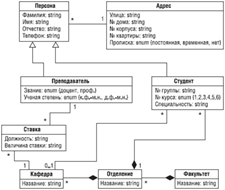
Логическая модель предназначена для задания структуры данных, однако без "привязки" к конкретной платформе реализации. С одной стороны, такое описание получается компактнее, чем физическая модель, позволяя взглянуть на схему данных в целом, без лишних деталей; с другой - такая спецификация может быть в дальнейшем реализована для разных СУБД. Логическая модель содержит абстракции, которые уже могут быть непонятны экспертам предметной области - эта модель служит для уточнения информации о предметной области в виде, удобной для последующей реализации ( рис. 10).
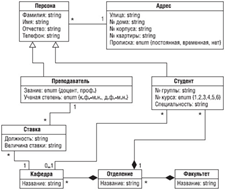
Рис. 10. Пример логической модели
Физическая модель ( рис.11) предназначена для описания структуры данных в терминах выбранной платформы реал- изации - конкретной БД. Данная модель уже содержит информацию о различных деталях реализации - индексах и ключах, типах данных и других, которые определены в терминах целевого языка программирования.
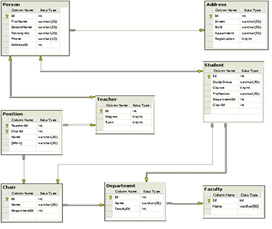
Рис. 11. Пример физической модели.
Функциональная модель IDEF
IDEF — методологии семейства ICAM (Integrated Computer-Aided Manufacturing) для решения задач моделирования сложных систем, позволяют отображать и анализировать модели деятельности широкого спектра сложных систем в различных разрезах. При этом широта и глубина обследования процессов в системе определяется самим разработчиком, что позволяет не перегружать создаваемую модель излишними данными.
IDEF- современная методология функционального моделирования. С помощью наглядного графического языка IDEF0 изучаемая система предстает перед разработчиками и аналитиками в виде набора взаимосвязанных функций (функциональных блоков — в терминах IDEF0) ( рис. 12). Как правило, моделирование средствами IDEF0 является первым этапом изучения любой системы. Методологию IDEF0 можно считать следующим этапом развития хорошо известного графического языка описания функциональных систем SADT (Structured Analysis and Design Technique);
В настоящее время IDEF включает ряд частных методологий для моделирования систем, в том числе: IDEF0 - функциональное моделирования, IDEF1 - информационное моделирование, IDEF1X – моделирование данных, IDEF3 - моделирование процессов, IDEF4 - объектно-ориентированное проектирование и других методологий.
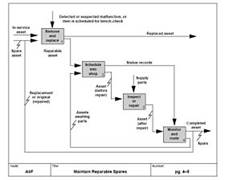
Рис. 12. Пример модели в форме IDEF0
На рис. 13. представлена модель IDEF4 объектно - ориентированной системы.
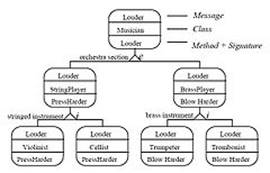
Рис. 13. Пример модели IDEF4
В свою очередь модели можно классифицировать, как:
статические или динамические;
линейные и нелинейные;
непрерывные и дискретные;
стационарные и нестационарные;
с сосредоточенными или распределенными параметрами.
1.4 Разработка моделей
Модели формируются или описываются с помощью известных уравнений, формул каждой структурной единицы системы или объекта в соответствии с методологией системного анализа. В том случае если для исследуемого объекта неизвестны уравнения, с помощью которых описывается объект, то в этом случае используется метод идентификации параметров объекта, аналитических математических зависимостей. Суть метода состоит в том, что на вход объекта подаются известные сигналы или входные воздействия и по фиксации выходных сигналов идентифицируется модель объекта. идентификацией динамических объектов следует понимать процедуру определения структуры и параметров их математических моделей, которые при одинаковых входном сигнале объекта и модели обеспечивают близость выхода модели к выходу объекта при наличии какого - то критерия качества. Модели разрабатываются в зависимости от выполнения задачи моделирования, которые подразделяются на исследовательские, управляющие и прогнозируемые. Если необходимо исследовать просто объект, то разрабатывается модель объекта и исследуется влияние отдельных параметров на динамику объекта. Если модель управляющая, то разрабатывается модель объекта и модель системы управления для исследования влияния на объект различных законов управления.
2.5 Особенности моделирования систем.
В основе исследования систем или объектов лежит системный анализ. Под системным анализом принято понимать совокупность приемов и методов для изучения сложных систем или объектов. Исследование таких объектов в системном анализе разбивается на несколько этапов. Первый этап - постановка задачи - состоит из определения объектов исследования, постановки целей, а также задание критериев для изучения этих объектов и управления ими. Неправильная или неполная постановка целей может свести на нет результаты анализа. Второй этап системного анализа состоит в очерчивании границ изучаемой системы и ее структуризации. Смысл этого этапа состоит в том, что вся совокупность объектов, имеющих отношение к поставленной цели, разбивается на два класса - собственно изучаемый объект и внешнюю среду.
На третьем этапе составляется математическая модель изучаемой системы. Вначале выполняется параметризация, т.е. выделение элементов системы и воздействий на нее, а также основные параметры системы. В качестве параметров могут как непрерывные, так и дискретные с заданием области их определения. Далее устанавливаются различные зависимости между введенными параметрами, которые представляются в виде систем уравнений как алгебраических, так и дифференциальных. Для качественных параметров
3.14 Информационные модели объектов и систем
3.14.1 Структура модели управления учебными
заведениями. Цели и задачи управления учебными
заведениями
Структуры управления учебными заведениями с использованием ЭВМ и компьютерных сетей должны разрабатываться с учетом эффективности организационного управления и информационно-методического обеспечения учебного заведения (системы учебных заведений, системы образования), которое обеспечит:
- общедоступность информационно-методических материалов и использования их всеми основными пользователями образовательного процесса;
- систематизацию, централизованное хранение и оперативное использование необходимой информации потенциальных пользователей и предполагаемых заказчиков в форме удобной для каждой категории пользователей;
- автоматизацию процессов ведения, хранения, накопления, анализа информации, а также фиксирование необходимой информации, представление возможности получения необходимых сведений;
- автоматизацию контроля за деятельностью учащихся и возможности индивидуальной работы со средствами автоматизированного обучения с выходом на глобальные (локальные) компьютерные центры для получения учебной информации.
Особенно важным является тенденция высших учебных заведений вводить методы дистанционного обучения студентов.
В настоящее время все чаще стали использоваться система моделирования и проектирования SADT ( Structured Analysis and Design Technique) — методология структурного анализа, проектирования и моделирования, сложных проектов, с использованием собственного языка программирования. На основе данной методологии процесс моделирования разделяется на несколько этапов: опрос экспертов, создание диаграмм и моделей, создание документации.
SADT была создана в 60-х годах в ходе преобразования методов структурного программирования. В это время многие специалисты занялись разработкой методов проектирования и моделирования сложных системы, которые могут включать в себя: вычислительную технику и обслуживающих людей, а также программное обеспечение в различных сферах использования вычислительной техникой, например, в промышленности, связи, для управлении и контроля за различными процессами.
Весь процесс создания сложных систем был разбит на следующие этапы:
• Анализ — что система будет делать,
• Проектирование — разработка подсистем и их взаимодействие между собой,
• Реализация — разработка подсистем по отдельности, объединение — соединение подсистем в единое целое,
• Тестирование — проверка работы сложной системы,
• Установка — введение системы в действие,
• Эксплуатация — использование системы.
Анализ - операция мысленного или реального разделения целого (предметы, свойства, или отношения между предметами) на составные части, выполняемая в процессе предметно-практической деятельности человека.
Проектирование - деятельность разработчика по созданию системы с использованием модели системы, комплекта документации по эксплуатации, ремонту, а также для проверки промежуточных и конечных решений, на основе которых была разработана система.
Тестирование применяется для соответствия системы ( модели) заданным требованиям.
2.3. Формы представления моделей и алгоритмов.
Для моделирования объектов, систем, процессов и явлений очень важным с точки зрения понимания задач и целей моделирования является первоначальная форма представления моделей. При этом необходимо придерживаться применения системного и функционального подхода при описании и исследовании систем или объектов.
Системный подход выражается в комплексном изучении системы с позиции системного анализа, т.е. анализа составляющих объектов системы как совокупности взаимосвязанных элементов. С этих позиций модель целесообразно представлять в виде последовательности моделей: системы (объекта), внешних факторов, воздействующих на объект, метода моделирования, программы моделирования (проведения эксперимента), программ предствления исходных данных и результатов моделирования.
В целом процесс моделирования можно рассматривать как следующую замкнутую схему, имитирующую действия системы в реальных условиях среды.
Модель программы моделирования задает порядок изменения параметров моделей объекта и внешних условий, время моделирования и т.д. Модель системы (объекта) может представляться совместно с моделью внешних условий, т.к. математически или информативно бывает довольно трудно разделить эти модели. В свою очередь модель системы или объекта может задаваться в словесной форме; в виде дифференциальных или алгебраических уравнений, или в ином математическом виде; в форме графа или графическом изображении; комплексной форме.
Основными формами представления моделей являются:.
Словесная форма информационной модели. Требуется составить модель продажи билетов в кинотеатре. Начальные условия: количество сеансов, количество мест, стоимость билета. Результаты моделирования: общий вид зрительного зала с отображением проданных билетов на конкретный сеанс, количество проданных билетов на конкретный сеанс и общая дневная выручка. Словесная форма представления моделей чаще всего задается в виде таблицы данных.
Знаковая (математическая) форма модели.
Данная форма выражения модели представляется следующими уравнениями:
алгебраическими (информационная модель производства)
a1x1 + b2x2 <= c1,
a2x1 + b2x2 <= c2; z<=k1x1 + k2x2.
дифференциальными ( динамическая модель систем)
a2d2X/dt2 + a1dX/dt + a0=0,
систем дифференциальных уравнений
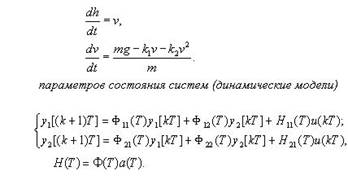
В практике моделирования могут использоваться и другие формы представления математических моделей, как например, передаточные функции, разностные уравнения и z- преобразования, параметрические модели оценивания и т. д.
Модели на основе теории графов.
Многие задачи при моделировании рассматриваются как совокупность объектов с описываемыми связями между ними. К ним можно отнести такие объекты: карта автомобильных дорог с населенными пунктами, электрические цепи как соединение резисторов, конденсаторов, источников и т.д., структуры органических молекул, свойства которых определяются связями между атомами, отношение и связи между предприятиями и людьми.
Такие объекты можно изображать точками, называемыми вершинами, а связи между ними - линиями, называемыми ребрами. Представление объектов, явлений и процессов множеством вершин V и ребер Е называют графом, который обозначается G=(V,E).
Примером графа является задача о кенигсбергских мостах (рис.1а), которая впервые была опубликована двадцатилетним Леонардом Эйлером в 1736 г., когда он работал в Российской Академии Наук.
Суть задачи состоит в том, можно ли совершить прогулку таким образом, чтобы выйдя из любого места города, вернуться в него, пройдя только один раз по каждому мосту. По условию задачи имеется 4 части суши a,b,c,d, на которых расположен город. Их можно представить вершинами. Связи между частями города осуществляются через 7 мостов, которые представляются ребрами.
Граф “прогулка по городу” изображен на рис.1б.
 Часто объекты характеризуются связями с определенной
ориентацией (одностороннее движение, протекание тока от (+) полюса к (-) полюсу
источника, различные отношения между числами (неравенства).
Часто объекты характеризуются связями с определенной
ориентацией (одностороннее движение, протекание тока от (+) полюса к (-) полюсу
источника, различные отношения между числами (неравенства).
С этой целью ребра в графах отмечаются стрелками, а ориентированное ребро называется дугой. Граф с такими связями есть ориентированный граф (рис.2).
Если начало и конец ребра совпадают, то такое ребро называют петлей. Последовательность вершин Xi, при которых каждая пара определяет ребро, называется маршрутом в графе. В том случае, если дугам, ребрам и вершинам приписываются количественные значения (приоритет, длина, напряжение, ток и т.д.), то такой граф называется взвешенным (рис.3).
Две вершины графа называются смежными, если они являются граничными вершинами ребра. Граф можно представить также матрицей смежности. Строки и столбцы этой матрицы соответствуют вершинам графа.
Матрицей смежности называется квадратная матрица M=(mij) размерности n*n, элементы которой определяются так:
1, если в графе имеется ребро от Xi к Xj,
mij=
O, в остальных случаях.
Граф, представленный на рис.3, имеет матрицу смежности:
Матрицей достижимости называется квадратная матрица C=(сij), в которой элемент cij=1 только тогда, когда вершина Xj достижима из вершины Xi, иначе cij=0.
Алгоритм построения матрицы достижимости графа, исходя из матрицы смежности, представляет довольно сложную задачу.
Суть алгоритма сводится к следующему. Допустим имеется вершина Xk, в которую входят дуги, например, Xi-Xk. Далее рассматриваются пути, исходящие из Xk, например, Xk-Xj. Следовательно, в графе имеется путь Xi- Xj путь, проходящий через вершину Xk. В матрице достижимости графа элемент сij должен ранятся 1. Таким образом, просматриваются все вершины.
Блочная ( структурная ) форма представления моделей может быть реализована тогда, когда каждый функциональный блок (элемента) описывается математическими зависимостями и и имеются средства для моделирования таких систем, например, с помощью пакета программ MatLab, SciLab.
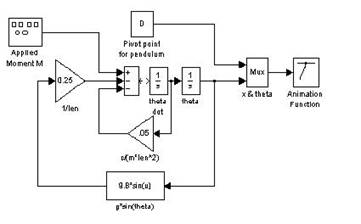
Рис. 6. Блочная форма моделей
Функциональная форма модели
Данная форма представления моделей используется для представления сложных моделей, например, бизнес процессов, предприятий, социальных объектов, сложных процессов и т. д. Этот метод представления моделей основан на использовании языка моделирования UML (Unified Modeling Language), который является на данный момент самым распространенным и общеизвестным способом моделирования программного обеспечения сложных объектов и систем. Формами представления на основе языка UML моделирования являются структурные диаграммы (классов, объектов, компонент и т. д.). Такие диаграммы используются для отображения систем на основе объектно - ориентированной структуры, которая является современным способом программирования и моделирования систем. В основе такого подхода система представляется в виде классов, объектов и других форм и способов таких динамических систем( рис.7).
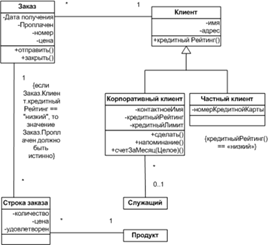
Рис. 7. Пример диаграммы классов
Разновидности функциональных моделей
Визуальная модель «сущность-связь»
Для разработки структур баз данных обычно использовалось моделирование, а затем составлялась программа например, в БД ACCESS, SQL. Чаще всего использовалась модель «сущность-связь», предложенная Петером Ченом в 1976 г. . Языки программирования баз данных ACCESS, Microsoft SQL Server, MySQL, Oracle являются стандартом для программ реляционных баз данных и использовались многими пользователями СУБД. СУБД (система управления базами данных) - это программное обеспечение, предназначенное для разработки, хранения и программного доступа к большим массивам данных.
Примером языка программирования для БД является язык SQL.
Сущность (entity) - это «предмет» разрабатываемой области, который может быть идентифицирован так, чтобы отличить его от других «предметов». Примеры сущностей: человек, компания или событие.
Связь (relationship) - это отношение между сущностями, отражающее их взаимодействие друг с другом.
На рис. показаны две сущности - "Студент" и "Кафедра", - которые связаны отношением "Принадлежит", т.е. студент принадлежит кафедре. Это пример направленного отношения между двумя сущностями.
 Концептуальная модель предназначена для извлечения знаний о предметной
области. Эта модель помогает программистам разобраться с той сферой
человеческой деятельности, для которой им предстоит создать программное
приложение, выявив там основные сущности и связи между ними. Данная модель
предназначена для обсуждения с непрограммистами и не должна содержать
конструкций и понятий, которых последним не понять.
Концептуальная модель предназначена для извлечения знаний о предметной
области. Эта модель помогает программистам разобраться с той сферой
человеческой деятельности, для которой им предстоит создать программное
приложение, выявив там основные сущности и связи между ними. Данная модель
предназначена для обсуждения с непрограммистами и не должна содержать
конструкций и понятий, которых последним не понять.
Логическая модель предназначена для задания структуры данных, однако без "привязки" к конкретной платформе реализации; с одной стороны, такое описание получается компактнее, чем физическая модель, позволяя взглянуть на схему данных в целом, без лишних деталей; с другой стороны, такая спецификация может быть в дальнейшем реализована для разных СУБД; логическая модель содержит абстракции, которые уже могут быть непонятны экспертам предметной области - эта модель служит для уточнения информации о
предметной области в виде, удобном для последующей реализации.
Физическая модель предназначена для описания структуры данных в терминах платформы реализации - конкретной СУБД. Данная а модель уже содержит информацию о различных деталях реализации - индексах и ключах, типах атрибутов и т.д., которые определены в терминах целевого языка программирования и т. д.;
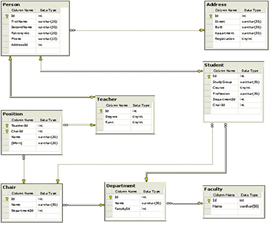
Пример физической модели. Эта диаграмма создана в Microsoft Visual Studio и ориентирована на реализацию схемы базы данных на СУБД Microsoft SQL Server.
Функциональная модель IDEF.
IDEF —методологии семейства ICAM (Integrated Computer-Aided Manufacturing) для решения задач моделирования сложных систем, позволяет отображать и анализировать модели деятельности широкого спектра сложных систем в различных разрезах. При этом широта и глубина обследования процессов в системе определяется самим разработчиком, что позволяет не перегружать создаваемую модель излишними данными.
IDEF- современная методология функционального моделирования. С помощью наглядного графического языка IDEF0 изучаемая система предстает перед разработчиками и аналитиками в виде набора взаимосвязанных функций (функциональных блоков — в терминах IDEF0). Как правило, моделирование средствами IDEF0 является первым этапом изучения любой системы. Методологию IDEF0 можно считать следующим этапом развития хорошо известного графического языка описания функциональных систем SADT (Structured Analysis and Design Technique);
В настоящее время общая методология
IDEF включает ряд частных методологий для моделирования систем, в том числе:
IDEF0 - функциональное моделирования
IDEF1 - информационное моделирование
IDEF1X - моделирование данных
IDEF3 - моделирование процессов
IDEF4 - объектно-ориентированное проектирование и анализ
IDEF5 - определение онтологий (словарей)
IDEF9 - моделирование требований
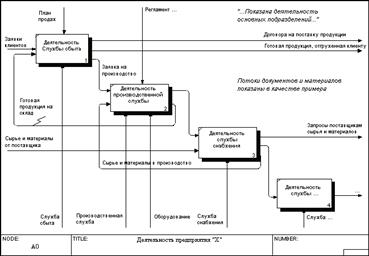
Пример функциональной схемы фирмы, в которой имеются служба сбыта, производственная служба и снабжения и т. д.
В свою очередь модели можно классифицировать, как:
статические или динамические;
линейные и нелинейные;
непрерывные и дискретные;
стационарные и нестационарные;
с сосредоточенными или распределенными параметрами
2.4 Разработка моделей
Модели формируются или описываются с помощью известных уравнений, формул каждой структурной единицы системы или объекта в соответствии с методологией системного анализа. В том случае если для исследуемого объекта неизвестны уравнения, с помощью которых описывается объект, то в этом случае используется метод идентификации параметров объекта, аналитических математических зависимостей. Суть метода состоит в том, что на вход объекта подаются известные сигналы или входные воздействия и по фиксации выходных сигналов идентифицируется модель объекта. идентификацией динамических объектов следует понимать процедуру определения структуры и параметров их математических моделей, которые при одинаковых входном сигнале объекта и модели обеспечивают близость выхода модели к выходу объекта при наличии какого - то критерия качества. Модели разрабатываются в зависимости от выполнения задачи моделирования, которые подразделяются на исследовательские, управляющие и прогнозируемые. Если необходимо исследовать просто объект, то разрабатывается модель объекта и исследуется влияние отдельных параметров на динамику объекта. Если модель управляющая, то разрабатывается модель объекта и модель системы управления для исследования влияния на объект различных законов управления.
2.5 Особенности моделирования систем.
В основе исследования систем или объектов лежит системный анализ. Под системным анализом принято понимать совокупность приемов и методов для изучения сложных систем или объектов. Исследование таких объектов в системном анализе разбивается на несколько этапов. Первый этап - постановка задачи - состоит из определения объектов исследования, постановки целей, а также задание критериев для изучения этих объектов и управления ими. Неправильная или неполная постановка целей может свести на нет результаты анализа. Второй этап системного анализа состоит в очерчивании границ изучаемой системы и ее структуризации. Смысл этого этапа состоит в том, что вся совокупность объектов, имеющих отношение к поставленной цели, разбивается на два класса - собственно изучаемый объект и внешнюю среду.
На третьем этапе составляется математическая модель изучаемой системы. Вначале выполняется параметризация, т.е. выделение элементов системы и воздействий на нее, а также основные параметры системы. В качестве параметров могут как непрерывные, так и дискретные с заданием области их определения. Далее устанавливаются различные зависимости между введенными параметрами, которые представляются в виде систем уравнений как алгебраических, так и дифференциальных. Для качественных параметров используются табличные формы задания зависимостей. Описывающие параметры могут изменяться во времени и представляться вероятностными соотношениями.
Современный системный анализ имеет дело с большим количеством параметров различной природы, зависимости между которыми являются сложными и разнообразными. Поэтому при построении математической модели используется способ разбиения системы на подсистемы, установление иерархии подсистем и установление связей между системами. На следующих этапах производится исследование построенной модели. Здесь необходимо выполнить прогноз развития изучаемой системы, который представляется зависимостями параметров системы от вероятностных воздействий.
В связи с тем, что сложные объекты или системы не имеют точных аналитических зависимостей, то прогноз выполняется путем моделирования объектов или систем. После исследования систем производится анализ его результатов на соответствие заданным целям и критериям и, в случае необходимости, производится выработка предложений по улучшению управления системой или объектом. Такая процедура повторяется с новыми параметрами управления, пока не получится требуемый результат. Такой подход называется методом проб и ошибок.
После разработки модели необходимо выбрать методы реализации моделей и методы решения уравнений модели. Для реализации моделей можно выбрать следующие информационные технологии: языки программирования ( Pascal, Delphi, Visual Basic, Visual C/C++; математические пакеты программ такие как: MathCad, Maple, Mathematica, MatLab.
Для решения уравнений моделей можно использовать следующие методы: решение алгебраических или дифференциальных уравнений, методы решения оптимальных задач (линейное, нелинейное или динамическое программирование, транспортные задачи, методы массового обслуживания и т. д. При моделировании систем, объектов или процессов прежде всего необходимо продумать удобный интерфейс диалоговой моделирующей системы. Удобный интерфейс предусматривает: выбор режимов моделирования систем (ввод исходных данных, выбор метода моделирования, установление форм вывода результатов моделирования, выбор исследуемых параметров на динамику движение объекта или процесса, а также просмотр подсказки для моделирования систем и т. д). Удобный интерфейс можно обеспечить с помощью современных языков программирования (Visul Basic, Delphi, языков программирования на платформе .NET ( C++.NET, C#.NET, VB.NET), а из математических пакетов программ наиболее удобным является MatLab, с помощью которого можно не только выбрать необходимый метод решения, но и разработать программу на внутреннем языке программирования. Такой интерфейс обычно устанавливается с помощью кнопок или разработанного специального меню. В качестве результирующих объектов обычно выбираются графики, таблицы, в которых отображаются различные траектории движения или зависимости непосредственно выбранного параметра на процесс или динамику объекта. Для исследования следует использовать изолинии, т. е. построения поверхностей, вдоль которых функции имеет одинаковое значение. В примерах моделирования будут использоваться различные методы, которые могут быть полезны для исследователя.
3. МОДЕЛИ ОБЪЕКТОВ, СИСТЕМ, ЯВЛЕНИЙ И ПРОЦЕССОВ.
3.1. Математические модели физических объектов, явлений и процессов.
3.1.1. Математическая модель объектов падения
Если в качестве модели используется материальная точка, которая не обладает внутренней структурой, то уравнения движения объектов падения будут представляться в следующем виде:
y(t) = F/m, где (3.1)
F - равнодействующая сила, m - инертная масса,
. y(t) - ускорение падения тела.
Если не учитывать гравитационное поле Земли, то F и m - постоянные величины, а движение называется свободным падением.
В случае, когда необходимо учитывать зависимость силы тяжести от расстояния до центра Земли, то сила, действующая на объект, представляется уравнением
g * m
F = —————— , где (3.2)
(1 + y/R)2
y - расстояние объекта от поверхности Земли,
R - радиус Земли (6.37*106 м),
g = G*M/R2,
G - постоянная всемирного тяготения,
M - масса Земли.
С учетом сопротивления воздуха
F = m*g - Fс, где Fс - сила сопротивления воздуха.
Fс = k1*V+ k2*V2. ;
Параметры k1 и k2 зависят от
свойств среды и геометрии тела. Например, для шарика k1 =61![]()
![]() r (формула Стокса), где -
r (формула Стокса), где - ![]() динамическая вязкость среды, r - радиус
шарика. Так, для воздуха
динамическая вязкость среды, r - радиус
шарика. Так, для воздуха ![]() = 0,0182 Н*с*м-2 при t=20o C и давлении 1
атм. Соответственно для воды
= 0,0182 Н*с*м-2 при t=20o C и давлении 1
атм. Соответственно для воды ![]() = 1,002 Н*с*м-2.. Для малых скоростей
составляющей k1 можно пренебречь и Fс = k2*V2, где k2 = 0,5сS
= 1,002 Н*с*м-2.. Для малых скоростей
составляющей k1 можно пренебречь и Fс = k2*V2, где k2 = 0,5сS ![]() ;
; ![]() -плотность среды ; с-
коэффициент лобового сопротивления, который зависит от формы тела. Так, для
диска в форме прямоугольника с=1.11, для сферы с=1.33 и с=0.55 в зависимости от
направления расположения сферы, для шара с=0.4, а для каплевидных тел с=0.045
с=0.1 в зависимости от направления тела.
-плотность среды ; с-
коэффициент лобового сопротивления, который зависит от формы тела. Так, для
диска в форме прямоугольника с=1.11, для сферы с=1.33 и с=0.55 в зависимости от
направления расположения сферы, для шара с=0.4, а для каплевидных тел с=0.045
с=0.1 в зависимости от направления тела.
Если представить исходное дифференциальное уравнение в виде системы уравнений первого порядка, то уравнение (3.1) будет представляться выражением
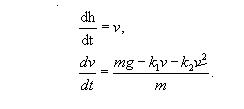
Представленные уравнения моделей могут быть реализованы с помощью различных методов решения дифференциальных уравнений (Эйлера, Рунге-Кутта, Рунге-Кутта-Мерсона и т. д.). В том случае, если необходимо исследовать простую линейную модель с постоянными параметрами, то уравнение (3.1) может быть представлено в виде:
V(t) = V0 + g*t
y(t) = y0 + V0*t + 0.5*g*t
где y0 и V0 - начальные условия (высота падения и скорость), g = 9.8 м/с2 (у поверхности Земли).
3.1.2. Математическая модель объектов, брошенных под начальным углом к горизонту с начальной скоростью V0
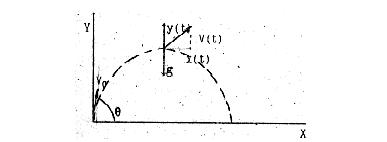
Уравнения движения могут быть представлены в виде системы двух уравнений по осям X и Y.
d2X/dt2 =0;
d2Y/dt2 =g, (3.3)
где d2X/dt2 = dvx/dt - горизонтальная составляющая ускорения;
d2Y/dt2 = dvy/dt - вертикальная составляющая ускорения;
vx=v0cosq - горизонтальная составляющая скорости V;
vy=v0sinq - вертикальная составляющая скорости V;
q - начальный угол бросания.
С учетом сопротивления воздуха (тормозящей силы) уравнение (3.3) представляется выражениями:
mdvx/dt = -Fccosq;=-Fcvx/v0(3.4)
mdvy/dt = -m*g - Fcsinq,=-m*g - Fcvy/v0
где Fc =k1V+ k2*V2 - линейная и квадратичная составляющая сопротивления воздуха.
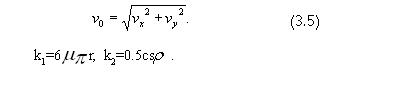
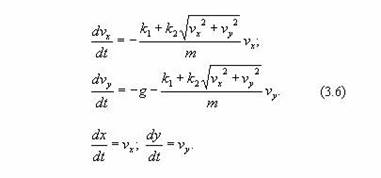
Уравнения (3.3), учитывающее сопротивление воздуха, реализуется с использованием методов решений дифференциальных уравнений. Для реализации модели по уравнениям (3.6) более простым способом надо последовательно преобразовать эти уравнения путем интегрирования, т.е.
vx=v0*cos(q); (3.7)
vy=v0*sin(q )- g*t;
x = x0 + v(x)*t; (3.8)
y = y0 + v(y)*t - g*t*2/2.
После исключения переменной t из уравнения (3..6) можно получить выражение для максимальных значений высоты и дальности полета, т.е.
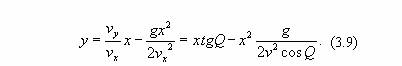
При Vy= 0 имеем:
ymax= v2 sin2q / 2g,
![]()
Представленные модели являются относительно простыми.
3.1.3. Модель гармонического осциллятора
Гармонический осциллятор представляет собой колебания тела массой m, прикрепленного к свободному концу пружины.
F = - k*x, (3.11)
где k - мера жесткости пружины (знак “-”- указывает на то, что сила стремится вернуть тело в положение равновесия).
Уравнение движения тела представляется в виде:
d2X/dt2 = - w02*X (3.12)
где - угловая частота вынужденной силы.
В общем случае колебания осциллятора можно получить путем решение дифференциального уравнения (3.15). В простейшем случае модель колебания получается при использовании выражения
X(t) = A*cos(w0*t + d), (3.13)
где A - амплитуда колебаний,
d - начальная фаза.
Модель гармонического осциллятора с затухающими колебаниями имеет вид:
X = - 2*X - g*X, (3.14)
где g - коэффициент затухания (тормозящая фаза).
Для моделирования возмущенных колебаний необходимо использовать уравнение:
Х = - w2*X -g*Х + F(t) /m, (3.15)
где F(t) - функция, зависящая от времени произвольным образом, например, вида:
F(t) = A0*cos (w*t.) (3.16)
Функция F(t) может иметь и более сложный вид.
![]()
3.1.4.
3.1.4 Математическая модель маятника
Для построения модели маятника в качестве объекта предполагается груз на жестком подвесе длиной l, который колеблется в зависимости от угла отклонения. Учитывая, что движение груза происходит по дуге окружности (R=l), линейная скорость (v) и ускорение груза (a) будут соответственно равны:
v = l*q, a = l*q , где (3.17)
q - начальное отклонение маятника.
В отсутствии трения на груз действуют две силы: сила тяжести m*g и сила со стороны стержня F. С учетом действующих сил имеем
..m*l2*q = - m*g*l*sinq. (3.18)
Если амплитуда колебаний маятника достаточна мала, то sinq = q и уравнение можно переписать в виде: m*l*q = - m*g*l*q , (3.19)
которое после двойного интегрирования имеет вид:
q = A * cos (w*t + j), (3.20)
где j - начальная фаза,
w - частота колебаний = 2*p /Т,
Т - период колебаний = 2p*/w = 2*p* Ö l /g.
Уравнение затухающих колебаний:
q = А0*е^(-б)* t*cos(w*t + j), * (3.21)
где А0 - начальная амплитуда колебаний,
е(-б*t) - текущая амплитуда колебаний.
В том случае, если надо учитывать сопротивление воздуха (среды), то к правой части уравнения (3.17) добавляется выражение
Мтр = -а*w- b*w3, (3.22)
где w - угловая скорость,
a,b - коэффициенты сопротивления среды.
Если в качестве груза, подвешенного на нити, используется шар, то момент инерции I=m*l2 будет определяться формулой
![]() (3.23)
(3.23)
Для железного прута, на котором подвешен груз, момент инерции равен
![]() (3.24)
(3.24)
![]() (3.25)
(3.25)
Уравнения свободных колебаний маятника при наличии трения имеет вид
![]() (3.26)
(3.26)
После преобразование, получим
![]() (3.27)
(3.27)
где ![]() (3.28)
(3.28)
При малых колебаниях и имеем затухающие колебания
![]() (3.29)
(3.29)
При ![]() решение уравнения имеет вид
решение уравнения имеет вид
![]()
![]() (3.30)
(3.30)
Если на маятник действует внешняя сила F(t), то уравнения движения маятника преобразуется к виду где (3.31)
![]()
![]()
Решение уравнения для малых колебаний маятника представляется выражением
(3.32)
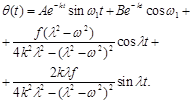
Затухающие колебания при ![]() с частотой
с частотой ![]() и вынужденных
колебаний с частотой
и вынужденных
колебаний с частотой![]() . При t>>1/k остаются только
вынужденные колебания, амплитуда которых зависит от соотношения
. При t>>1/k остаются только
вынужденные колебания, амплитуда которых зависит от соотношения ![]() ,
, ![]() . При
. При![]() =
= ![]() возникает
явление резонанса.
возникает
явление резонанса.
3.1.5 Движение тел с переменной массой
Полет и особенно взлет ракеты является очень сложным процессом. Поэтому описать движение ракеты в виде обычной модели просто невозможно. Дело в том, что масса ракеты является переменной величиной, которая может меняться в сотни - десятки раз. Например, стартовая масса ракеты « Энергия» составляет 20000 тонн, а к концу взлета масса равна порядка 200 тонн. Сила сопротивления воздуха резко меняется. При плотных слоях атмосферы плотность окружающей среды, например на высоте 5 км. вдвое меньше, чем у поверхности Земли. А на высоте 11 км. - уменьшается вчетверо. Так, зависимость плотности воздуха от атмосферы, определяется формулой
![]() (3.33)
(3.33)
Полет и особенно взлет ракеты является очень сложным процессом. Поэтому описать движение ракеты в виде обычной модели просто невозможно Дело в том, что масса ракеты является переменной величиной, которая может меняться в сотни - десятки раз. Например, стартовая масса ракеты « Энергия» составляет 20000 тонн, а к концу взлета масса равна порядка 200 тонн. сила сопротивления воздуха резко меняется. При плотных слоях атмосферы плотность окружающей среды, например на высоте 5 км. вдвое меньше, чем у поверхности Земли. А на высоте 11 км. - уменьшается вчетверо. Так, зависимость плотности воздуха от атмосферы определяется формулой
![]() (
3.33)
(
3.33)
где β =1,29810-4 ( h измеряется в метрах, плотность вблизи поверхности Земли). С учетом этой зависимости динамика полета тела с переменной массой может быть представлена следующей системой дифференциальных уравнений
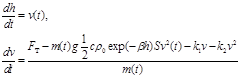 (3.34)
(3.34)
m0-at, если m(t)>mкон,
где m(t) =
mкон, если m(t)=mкон,
где m0 - начальная масса ракеты, mкон - конечная масса ракеты, а - расход топлива.
3.1.6 Модель движения небесных тел
По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними
. ![]()
В этой формуле G=6,67*10-11 m3/(kг*с2) -гравитационная постоянная.
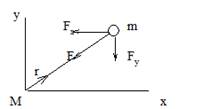
В данной системе координат начало координат расположено на одном теле M. Уравнения, описывающие движение тела m в указанной системе координат, имеет вид
![]()
В проекциях на оси координат уравнение можно привести с следующей системе из 4-х дифференциальных уравнений
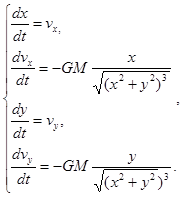
3.2 Математические модели динамических
объектов и систем.
3.2.1. Математическая модель движения ракеты
с постоянными параметрами
Исходные данные. Движение ракеты характеризуется 6-ю степенями
свободы, т. е. ее динамика должна описываться 3-мя уравнениями движения центра
масс относительно координат X, Y, Z, а также 3-мя уравнениями движения
относительно центра масс ракеты, т.е. угловыми координатами![]() ,
которые соответственно обозначают повороты в вертикальной, горизонтальной
плоскостях и относительно собственной оси вращения.
,
которые соответственно обозначают повороты в вертикальной, горизонтальной
плоскостях и относительно собственной оси вращения.
В простейшем случае можно представить движение ракеты в виде следующих дифференциальных уравнений:
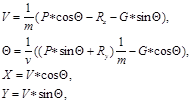 ( 3.35)
( 3.35)
где m - масса ракеты;
![]() - угол между осью ракеты и горизонтом в вертикальной
плоскости (угол наклона);
- угол между осью ракеты и горизонтом в вертикальной
плоскости (угол наклона);
X, Y - текущие координаты ракеты;
P - вектор силы тяги;
![]() - составляющие вектора аэродинамической силы.
- составляющие вектора аэродинамической силы.
Динамика ракеты рассматривается только в вертикальной плоскости XOY, без учета переменности коэффициентов от времени и действующих внешних возмущающих факторов.
Конечная цель.
Построить графики зависимостей X
![]() ,где
,где
![]() - максимальные значения дальности и высоты;
- максимальные значения дальности и высоты;
t выкл.дв. - время выключения двигателя в конце активного участка полета.
После выключения двигателя ракета продолжает полет по баллистической траектории под действием вектора скорости V.
3.2.2 Математическая модель движения ракеты с изменяющимися параметрами
Исходные данные. Представленная выше модель движения ракеты отличается от модели с переменными параметрами тем, что переменные m, R, P изменяются от времени в связи с тем, что топливо в ракете сгорает и масса ракеты изменяется. Кроме того, ракета летит в среде, в которой меняются температура, давление, ветер в зависимости от высоты полета, а они влияют на аэродинамические коэффициенты внешних возмущающих факторов. Таким образом, модель динамики полета представляется следующими уравнениями:
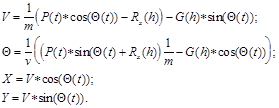 (3.36)
(3.36)
Конечная цель. В дополнение к рассмотренной цели необходимо исследовать влияние переменности параметров на дальность полета, а также зависимость динамики полета от внешних факторов, например, ветра Fx(H), Fy(H) и ускорения силы тяжести G(H).
![]()
3.2.4 Математическая модель движения ракеты с управлением в вертикальной плоскости
Исходные данные. Уравнения движения ракеты в вертикальной плоскости с учетом управления представляются следующей системой дифференциальных уравнений:
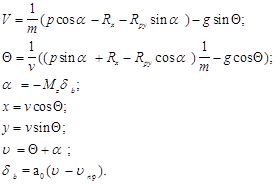
(3.38)
где - ![]() угол
атаки, угол между вектором скорости и осью ракеты;
угол
атаки, угол между вектором скорости и осью ракеты;
![]() - угол между
вектором скорости и горизонтом;
- угол между
вектором скорости и горизонтом;
![]() - угол поворота
рулей ракеты;
- угол поворота
рулей ракеты;
![]() - коэффициент
эффективности рулей;
- коэффициент
эффективности рулей;
![]() - программный
угол поворота ракеты на активном участке траектории полета;
- программный
угол поворота ракеты на активном участке траектории полета;
![]() -
аэродинамический коэффициент рулей;
-
аэродинамический коэффициент рулей;
![]() - коэффициент
закона управления в вертикальной плоскости.
- коэффициент
закона управления в вертикальной плоскости.
Законы управления могут быть
выбраны различные в зависимости от целей управления: ![]()
.![]()
Конечная цель. Определить значение коэффициентов закона управления для выведения ракеты по заданной траектории в расчетную точку пространства (x,y) для выключения двигательной установки.
3.2.5 Полная математическая модель движения ракеты в 3-х плоскостях
Исходные данные. Система дифференциальных уравнений, описывающих движение ракеты в трехмерном пространстве, имеет вид:
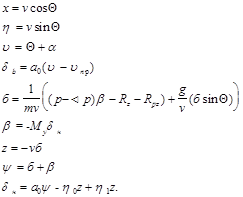
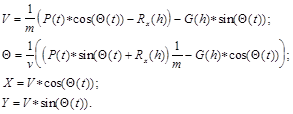 (3.40)
(3.40)
где - угол отклонения ракеты в боковой плоскости;
p - сила тяги;
![]() - подъемная сила рулей;
- подъемная сила рулей;
![]() - угол отклонения между вектором скорости и продольной
осью ракеты в вертикальной плоскости земной системы координат;
- угол отклонения между вектором скорости и продольной
осью ракеты в вертикальной плоскости земной системы координат;
![]() - коэффициенты закона управления в боковой плоскости.
- коэффициенты закона управления в боковой плоскости.
Конечная цель. Определить значения коэффициентов закона управления для выведения ракеты по заданной траектории в расчетную точку пространства (x,y,z) для выключения двигательной установки.
3.2.6 Основные модели управления ракетами
« Земля - Земля»
В уравнениях ракеты входят составляющие законов управления полетом ракеты на активном участке траектории полета, которые представляют зависимости угла поворота руля от приращения углов тангажа ( в вертикальной плоскости), рыскания( в боковой плоскости) и вращения( плоскость вращения ракеты). В общем для управления полетом ракеты используются три метода:
- управление на активном участке полета ракеты;
- управление в конце пассивного участка полета с учетом различных карт местности;
- управление на всей траектории полета с использованием спутников Земли.
Для управления на активном участке полета необходимо иметь систему управления по дальности и автомат стабилизации для управления ракетой относительно программной траектории полета.
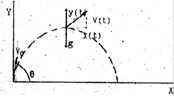
При управлении на активном участке траектории полета( траектории оа) необходимо прежде всего обеспечить попадание ракеты в точку (к), в которой скорость ракеты должна быть такой, чтобы ракета, точнее боевая часть, которая отделяется в точке (к), при свободном полете без двигателя могла обеспечить попадание в точку (в). А для попадания в точку (к) необходимо обеспечит полет ракеты по программной траектории полета, чтобы иметь необходимое значение угла тангажа. Для выполнения второй задачи в ракете имеется устройство для разворота ракеты по программной траектории полета и автомат стабилизации, который обеспечивает поворот ракеты при условии воздействия различных помех.
Для выполнения первой задачи имеется автомат дальности, который измеряет скорость ракеты и в момент достижения заданной скорости полета выключает двигательную установку. Момент выключения двигателя, т. е. требуемая скорость полета определяется перед запуском ракеты с помощью специализированной вычислительной машины. Система управления ракетой в общем имеет следующую структуру
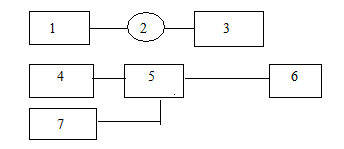
1- измеритель скорости ракеты;2-сравнение с заданной v 3 - устройство для выключения двигательной установки и отсоединения боевой части от корпуса ракеты; 4 измерители
( гироскопы) углов тангажа, рыскания и вращения; 5 - автомат стабилизации, вырабатывающий законы управления;6 - рули 9два вертикальных и два горизонтальных);7-измерительбДля повышения точности наведения в настоящее время используется метод наведения по картам местности. Суть метода состоит в том, что карты местности могут быть представлены в виде высотного рельефа местности, так и в виде радиометрической карты местности ( активная и пассивная). Ракета подлетает в район наведения, а затем местность скани руется и сравнивается с эталонной картой местности. В качестве методов распознавания могут быть: минимальное расстояние между эталоном и реальными расстояниями: боковой
![]()
![]()
координаты ракеты z.
![]()
![]()
3.3 Модели управления дискретными системами.
3.3.1 Общая модель систем автоматического управления(САУ)
В настоящее время существуют в основном три различных метода по синтезу систем управления объектами. Первый основан на операторном подходе, т.е. на использовании Р или Z преобразованиях систем, описывающих динамику движения объектов. В этом случае необходимо, чтобы системы автоматического управления ( САУ) удовлетворяли ряду требований к частотным и временным характеристикам систем, например, запасам устойчивости, показателям колебательности, времени регулирования, перерегулирования и т. д. С этой целью производятся регулировки усиления и коррекция частотных и временных характеристик систем.
Второй метод, называемый аналитическим, основан на использовании в качестве критерия качества системы интегральной квадратичной и среднеквадратичной ошибки. Проектирование сводится к расчету фильтра при использовании различных методов оптимизации.
Третий метод основан на задании функционала от переменных управления, т.е. критерия качества и состояния процесса, затем накладываются ограничения на переменные и с помощью оптимальных законов управления определяется закон управления. Обычно такой подход называется современным методом управления. Эти методы значительно упрощают процесс проектирования нестационарных и многомерных систем и позволяют установить структуру оптимальной системы с использованием ЦВМ.
Современная теория управления основывается на описании систем методами пространства состояния и применении методов, оптимизирующих движении в пространстве возможных состояний. В общем случае уравнение разомкнутой САУ представляется в следующей матричной форме
![]() (3.42).
(3.42).
где - векторы координат управляемого объекта;
U - вектор управления;
F - вектор возмущений ( воздействий);
В - матрица параметров объекта управления;
T - такт дискретности работы системы управления.
Приведенная форма уравнения может быть преобразована в уравнения параметров состояния( Подробно методы преобразования рассмотрены в разделе моделирование систем методом параметров состоянияМодель управления САУ в течение одного такта с учетом всех координатЕсли объект описывается N уравнениями первого порядка, то управление должно описываться вектором управления N -го порядка. Так, если матричное уравнение параметров состояния предс3.3.2
3.3.2 Модель управления САУ в течение одного такта с учетом всех координат
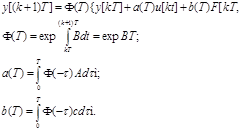
Если объект описывается N уравнениями первого порядка, то управление должно описываться вектором управления N -го порядка. Так, если матричное уравнение параметров состояния представляется в форме
![]()
то вектор управления будет иметь следующий вид
![]()
Если Yтр=0, то
![]()
3.3.3 Модель управления САУ по одной координате с запоминанием информации на N тактов
Для перевода системы из начального состояния в требуемое необходимо иметь Nтактов. Цель управления
Y[(k+n)T]=YTP (3.47)
Для управления выбирается номер старшей производной, т.е. при n=2 имеем u2<>0, u1=0 и AU=u2. Управляющие воздействие представляется выражением
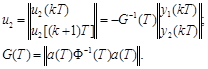
Для вычисления управляющих воздействий необходимо сохранять информацию о начальном состоянии в течении n тактов, которая стареет.
3.3.4 Модель управление САУ по одной координате с замером состояния системы в каждом такте
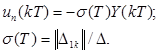
![]() матрица
- строка, равной первой строке обращенной фундаментальной матрицы;
матрица
- строка, равной первой строке обращенной фундаментальной матрицы;
Y(kT) - вектор состояния в каждом такте;
u(kT) - управление в каждом такте.
3.3.4 Модель управления на основе тактовой линии
Метод управления объектами с использованием тактовой линии, который позволяет получить минимальное время переходного процесса и в выборе оптимальных коэффициентов интегральных квадратичных критериев качества. Сущность метода состоит в следующем.
Пусть имеется объект, динамика которого описывается дифференциальным уравнением вида:
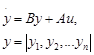 (3.50)
(3.50)
y - вектор выходных координат объекта размерности n;
u=| u1;u2;u3 …ul| - вектор управляющих воздействий размерности l;
B – матрица коэффициентов объекта управления типа
( n*n);
A- матрица коэффициентов управляющих воздействий типа ( n*l).
Управляющие воздействия представляются сигналами управления, которые постоянны в течение такта работы. Решение уравнения имеет вид алгебраического уравнения параметров состояния
 (3.51)
(3.51)
В основе метода управления с использованием тактовой линии лежит принцип приведения объекта в начало координат через такт работы системы, т.е. если y1[(k+1)]=y2[(k+1)]=0, то после разрешения полученный системы уравнений относительно u[kT], получим уравнения тактовой линии
![]()
(3.52)
где к – угол наклона тактовой линии
![]()
Уравнение тактовой линии представляет собой уравнение прямой линии в фазовом пространстве y2[kT] , y1[kT], с которой объект может быть переведен в начало координат через такт работы без учета ограничений на величину управляющего воздействия, которое определяется из выражения
![]()
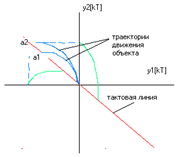
3.3.5 Оптимальная модель управления на основе метода максимума
При использовании метода максимума, разработанного под руководством академика Л.С.Понтрягина, движение объекта представляется системой дифференциальных уравнений
![]()
где
xi - фазовые координаты;
ui - управляющие воздействия.
Для перевода системы из начальных координат в конечное положение вычисляются управляющие воздействия, обеспечивающие экстремум функционалу качества
![]() Причем на управляющие
воздействия могут быть наложены ограничения
Причем на управляющие
воздействия могут быть наложены ограничения
![]()
Принцип максимума основан на теорема, в основе которой лежит следующие утверждение. Если u - оптимально, то существует такая ненулевая вектор-функция ,при которой функция Н((x,u, ) в любой момент вр емени на интервале t0 <=t <=tk т достигает максимального значения.
Помимо основной системы уравнений вводится система сопряженных уравнений для вспомогательных переменных
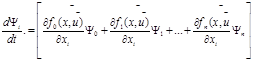
После составляется функция Гамильтона в виде
![]()
Полученная функция позволяет объединить основную и вспомогательную системы уравнений
![]()
Таким образом, для определения оптимальных значений управляющих воздействий необходимо: найти максимум функции Гамильтона по отношению к управляющему воздействию u(t). В дальнейшем вычисляется оптимальноеуправление как функция вспомогательной вектор-функции. Затем вектор u( )подставляется в каноническое уравнение, которое разрешается относительно векторов x, В конце получаем оптимальное управление как функцию от времени u(t).
3.3.6 Модель оптимального фильтра Калмана -Бьюси
Для определения структуры и параметров фильтра необходимо составить модель системы с обратной связью,
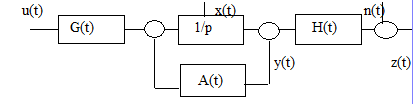
в которой выходной сигнал вычисляется в соответствии с дифференциальным уравнением
![]() где
где
![]() -
процесс на выходе оптимального фильтра;
-
процесс на выходе оптимального фильтра;
Q(t,t) - матрица переменных коэффициентов.
Синтез сводится к определению фильтра, который на основе измерения вектора z(t) на выбранном отрезке времени дает несмещенную оценку х(t) вектора координат системы x(t) в момент времени t, при котором минимизируется дисперсия ошибок
x(t) - процесс на выходе оптимального фильтра;
Q(t,t) - матрица переменных коэффициентов.
![]() (3.61)
(3.61)
Для определения параметров фильтра необходимо вычислить
![]()
Матрица ошибок определяется из нелинейного дифференциального уравнения типа Риккати
![]()
3.4 Модель идентификации параметров объекта на основе обобщенно - инвариантных уравнений
Для управления объектами, параметры которых изменяются во времени, необходимо знать состояние объекта, т. е параметры объекта и действующие внешние возмущающие воздействия. В таких системах управления рассматривается задача совместной идентификации параметров систем управления с переменными во времени коэффициентами и действующими внешними возмущениями. Предлагаемый метод управления позволяет оценивать состояния объектов в течение такта работы на основе метода использования обобщенно – инвариантных уравнений объекта и определять как состояния объекта, так и внешние возмущения. К настоящему времени разработано достаточно много способов совместной идентификации состояний и возмущений объектов.
В основе идентификации объектов лежат как детерминированные, основанные на использовании моделей объектов, так и статистические, в которых используются различные варианты фильтров Р.Калмана. Во всех случаях сходимость методов определяется внешними возмущениями и моделями внешних возмущений, помехами и скоростью изменения параметров объекта.
В данном методе лежит способ представления уравнений объектов с переменными параметрами в виде обобщенно – инвариантных уравнений. Допустим, что имеется объект с постоянными параметрами, который является моделью для различных уравнений объекта. В данном случае под моделью здесь понимается объект, относительно которого определяются коэффициенты для различных объектов, параметры которых изменяются во времени.
Пусть динамика объекта описывается следующей системой дифференциальных уравнений
![]()
Или в матричной форме
![]() (3.65)
(3.65)
Решения уравнений представляются системой алгебраических уравнений для определенного такта работы Ти, в течение которого коэффициенты
![]()
Решения уравнений представляются системой алгебраических уравнений для определенного такта работы Ти, в течение которого коэффициенты коэффициенты исходных дифференциальных уравнений являются постоянными величинами
![]()
Обобщенно- инвариантные уравнения составляются с учетом равенства конечных координат уравнения с неизвестными параметрами и уравнения с известными параметрами, которое является моделью. Так, для объекта - модели, динамика которого описывается уравнением второго порядка с известными параметрами,
![]() (3.68)
(3.68)
уравнения состояния представляются следующей системой алгебраических уравнений
![]() (3.69)
(3.69)
Уравнения параметров состояния для объекта с неизвестными параметрами имеет вид
![]() (3.70)
(3.70)
Обобщенные уравнения получаются из условия равенства конечных координат объекта и модели
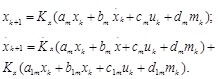 (3.71)
(3.71)
В представленном уравнении
коэффициенты Kx, ![]()
являются обобщенными параметрами объекта, а координаты xk, xk+1,dxk/dt, dxk+1/dt. являются известными измеренными координатами объекта. Если разрешить систему уравнений относительно внешнего возмущающего воздействия “m” получим обобщенное инвариантное уравнение
![]()
( 3.72)
Полученное уравнение относится к разряду уравнений Бернулли
![]() (3.73)
(3.73)
Решение данного уравнения представляется выражением
![]()
(3.74)
Начальное значение K0 может быть получено из начальных условий xk=dx/dt=0, т.е.уравнение в этом случае принимает вид
![]()
(3.75)
Вычисления внешнего воздействия выполняется по зависимости
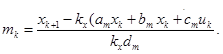 ( 3.76)
( 3.76)
Для формирования управляющего воздействия необходимо: определить для модели конечные координаты xk+1 dxk+1/dt. в которые объект приводится через такт работы на тактовую линию ;вычислить управляющее воздействие, приводящее модель через такт работы в координаты xk+1, dxk+1/dt; определить обобщенные коэффициенты ; вычислить внешнее воздействие ;определить управляющее воздействие для приведения объекта с неизвестными параметрами в вычисленные координаты.
3.5 Математические модели биологических объектов, явлений и процессов
3.5.1. Модель однородной популяции
Численность (плотность) популяции в момент t равна x(t). Относительный прирост популяции через промежуток времени
d(x) = (x(t + Dt) - x(t)) / (3.77)
Закон изменения численности популяции представляется следующим дифференциальным уравнением:
x(t) = kx(t) , (3.78)
где k - коэффициент пропорциональности. Решение дифференциального уравнения имеет вид:
x(t) = x(0)exp(kt), где (3.79)
x(0) - начальное значение численности.
Это - простая (мальтусовская) модель изменения численности популяций. Для учета ограниченности среды обитания (пища,свет,вода и т.д) составляется более сложная модель Ферхюльта-Пирла.
. x(t) = [a - bx(t)]x(t) (3.80)
Решение уравнения:
x(t) = [x(0)exp(at)/[1 + bx(0)*(exp(at) - 1)/a]. (3.81)
Дискретная модель:
xi+1 = xi+axi-bxi2; x0 = c, i = 0.1...n, (3.82)
где n предельное время моделирования.
Усложнение модели может быть выполнено за счет учета переменности коэффициентов - a (скорости роста) и b (скорости гибели) - в зависимости от времени, а также с учетом половых, возрастных различий индивидумов. Необходимо определить значение коэффициентов 0<a, b<1, при которых достигнуто стационарное состояние, периодические колебания численности популяций.
Рассчитайте, как меняется численность популяции со временем, если а=1, b=0,0001 при начальной численности, равной 10. Какова численность популяции через очень большой промежуток времени (стабильная популяция).
3.5.2 Модель “хищник - жертва”
Имеются популяции двух видов, которые представляются отношениями
xi+1 = xi + a1xi - b1xi2 - g1xiyi , x0 = c1, (3.83)
yi+1 = yi - a2yi + b2yi2 - g2xiyi , y0 = c2,
где xi - численность (плотность) жертв,
yi - численность хищников,
g1 - коэффициент защиты жертв,
g2 - коэффициент прожорливости хищников.
Определить характер зависимости периодических коле-баний численности жертв (хищников) от ai, bi, ci, gi и динамику зависимости y=f(x).
3.5.3 Модель эпидемии болезни
В изолированном поселке с населением m человек возникла эпидемия болезни, распространение которой описывается соотношениями:
xi+1 = xi - bxiyi; (3.84)
yi+1 = yi - cyi + bxiyi;
zi+1 = zi + cyi;
x0=a0, y0=b0, z0=c0,
где xi, yi, zi - число здоровых, больных (инфицированных) и невосприимчивых (переболевших) в момент времени i=0.1...n;
b - частота контактов больных и здоровых;
c - величина, обратная среднему времени выздоровления и зависящая от эффективности лекарств 0<L<1.
Более строго соотношение может быть получено из системы дифференциальных уравнений:
dx
—— = - bxy;
dt (3.85)
Построить графики изменений
x, y, z = f(b,c,a0,b0,c0).
dx
—— = - bxy;
dt (3.85)
Построить графики изменений
x, y, z = f(b,c,a0,b0,c0).
![]()
3.5.4 Модель прогноза урожая
Для определения прогноза урожая можно воспользоваться экспериментальной зависимостью
, i = 1.2....5, (3.86)
где y - урожайность сельхозкультуры (ц/га),
x1 - глубина обработки почвы (см),
x2 - густота высева (ц/га),
x3 - содержание влаги в почве (кг/га),
x4 - температура почвы ( С),
x5 - содержание минерального питания (ц/га).
Вычислить прогноз урожайности сельхозкультуры по различным значениям факторов xi.
3.5.5 Рост опухоли
Раковая опухоль обычно увеличивается экспоненциально в соответствии с дифференциальным уравнением:
, ![]() (3.87)
(3.87)
где v - размер опухоли,
с,a,b - константы.
Определить, при каких значениях параметров С существует предельный размер опухоли. Выяснить, при каких значениях С рост опухоли не превосходит некоторой конечной величины.
3.5.6 Модель растворения лекарственного
препарата
В процессе растворения лекарственного препарата в определенном объеме жидкости различают твердые F и жидкие (уже растворенные) вещества. Причем скорость растворения веществ может быть пропорциональна количеству вещества или величиa не F (если препарат вводится в виде таблетки сферической формы, а=2/3), а также пропорциональна разности (Lmax-L), где Lmax - растворимость препарата в данной жидкости. Модель кинетики растворения представляется следующими дифференциальными уравнениями:
dL
—— = - k1 * Fa (Lmax-L) - kaLn . (3.88)
dt
Рассчитать кинетику расходования лекарственного препарата при следующих параметрах: а = 2/3, k1= 0-1, Lmax = 0.1-0.8, n = 1, ka = 0.1.
Как будет изменяться кинетический процесс при изменении параметров путем увеличения и уменьшения на шаг h. Как зависит процесс расходования лекарственных препаратов от температуры.
3.5.7 Модель процесса переноса тепла
Природа переноса тепла от нагретого тела к окружающему пространству сложен и в общем случае включает в себя механизмы конвекции, излучения, испарения и теплопроводности. Если разность температур между объектом и окружающей средой не очень велика, то скорость изменения температуры можно считать пропорциональной этой разности температур. Для данного случая модель переноса тепла можно описать следующим дифференциальным уравнением:
T + R(T – Т0), (3.89)
где Т - температура тела;
Т0 - температура окружающей среды;
R - коэффициент “остывания”, зависящий от механизма теплопередачи, площади тела, тепловых свойств этого тела. Соотношения обычно называются законом теплопроводности Ньютона.
Требуется определить время остывания кофе от tнач до температуры окружающей среды. Как зависит скорость остывания от коэффициента остывания.
3.6 Оптимизационные математические
модели объектов и систем
3.6.1 Модель выпускаемой продукции
Имеются определенные виды сырья b1, b2, ... bm, из которых могут быть изготовлены различные виды продукции x1, x2, ... xn. Цена единицы j-го вида продукта равна cj. Для изготовления j-го продукта необходимо затратить i-й вид сырья в количестве аij единиц. Приведенные условия изготовления i-ой продукции можно представить в виде таблицы и уравнений:
xi і 0, i=1,2,...n (условие неотрицательности производимых продуктов).
![]() i=1,2…..m
(3.90)
i=1,2…..m
(3.90)
Суммарные затраты сырья каждого вида не должны превышать имеющиеся ресурсы.
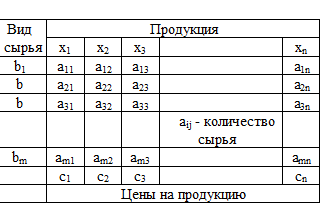
Требуется вычислить, какие виды продукции выгодно выпускать предприятию, т.е. найти максимум целевой функции
![]()
3.6.2 Модель рационального раскроя
На предприятии (мастерской)
из листов металла (материала) размером n*m требуется выкроить заготовки
определенных размеров ![]() . Кроме того, необходимо иметь S таких
заготовок.
. Кроме того, необходимо иметь S таких
заготовок.
Обозначим xi (i=1,2,3,...,k) количество листов материала, которые раскраиваются i-тым способом.
Условия выполнения плана для заготовок A и B:
![]()
(3.91)
Требуется выкроить заготовки с минимальными затратами металла (материала), т.е. вычислить минимум целевой функции
![]()
(3.92)
![]()
3.6.3 Модель размещения предприятий
Пусть в нескольких пунктах ![]() расположены
предприятия, производящие некоторый продукт. В пунктах размещаются
потребители готовой продукции с соответствующими потребностями
расположены
предприятия, производящие некоторый продукт. В пунктах размещаются
потребители готовой продукции с соответствующими потребностями ![]() .
Затраты на производство единицы продукта в пункте равны , обьем производства в
этом пункте равен , а затраты по транспортировке единицы продукта из i в j
равны . Количество перевезенных продуктов из i в j составляет единиц.
.
Затраты на производство единицы продукта в пункте равны , обьем производства в
этом пункте равен , а затраты по транспортировке единицы продукта из i в j
равны . Количество перевезенных продуктов из i в j составляет единиц.
Уравнения модели:
1.(перевозится неотрицательное количество продукта);
![]()
2. (выпускаемое количество продукта не
больше возможного обьема производства и равно вывозимому количеству продукта);
![]()
![]()
3. , j=1,...,n (потребности потребителей),
![]()
(3.93)
(каждый пункт потребления получает столько, сколько ему требуется).
Необходимо получить минимальные затраты на производство и на транспортировку продукции, т.е. обеспечить минимум функции
![]() ,
(3.94)
,
(3.94)
где - затраты на производство,
![]()
- затраты на транспортировку.
Целевая функция состоит из аналогичной целевой задачи. Однако, различие состоит в том, что здесь добавляются затраты на производство. Для однотипности подхода к решению этих двух моделей добавляется фиктивный пункт с характеристикой: потребность равна разности между возможным обьемом производства продукта и суммарной потребностью, а затраты на перевозку из всех пунктов равны 0.
3.6.4 Модель выбора предприятия
Затраты на выпуск продукции различными предприятиями можно разделить на постоянные, не зависящие от обьема производства, и переменные, зависящие от обьема производства, т.е.
,
(3.95)
![]()
где x - объем выпускаемой продукции;
U - постоянные затраты;
![]() -
переменные затраты.
-
переменные затраты.
![]()
![]()
![]() В отрасли, выпускающей
определенный вид продукции, имеется m - предприятий . Каждое предприятие
характеризуется функцией , которая выражает затраты в зависимости от объема
выпуска . Суммарная потребность равна X.
В отрасли, выпускающей
определенный вид продукции, имеется m - предприятий . Каждое предприятие
характеризуется функцией , которая выражает затраты в зависимости от объема
выпуска . Суммарная потребность равна X.
Уравнение модели:
i=1,2,...m (объем выпуска продукции
предприятием не может быть отрицательным).
![]()
(потребность в продукции должна быть удовлетворена).
Целевая функция модели представляется зависимостью:
![]()
где y - количество выпускаемой продукции.
3.6.5 Модель транспортной задачи
Имеются m складов товаров и n пунктов потребления
![]() .- количество товаров,
перевозимых с i-го склада на j-ый пункт потребления.
.- количество товаров,
перевозимых с i-го склада на j-ый пункт потребления.
- стоимость перевозки с i-го склада на j-ый пункт потребления. Ограничения:
![]()
(3.97)
![]() где
где
- количество единиц груза соответственно на пунктах потребления и складах.
Общая сумма заявок на доставку товаров равна имеющимся запасам товаров, т.е.
![]()
(3.98)
Требуется найти такие неотрицательные значения переменных Xij, чтобы выполнялись ограничения, а линейная функция суммарной стоимости перевозок L обращалась в минимум.
![]() (3.99)
(3.99)
3.6.6 Модели транспортных задач с дополнительными условиями
1. Модель транспортной задачи с неправильным балансом.
Во многих практических задачах условие баланса не выполняется, т.е.
![]() или
(3.100)
или
(3.100)
![]()
![]() Для составления модели
транспортной задачи вводится дополнительный фиктивный пункт назначения ВФ
или фиктивный пункт отправления АФ.
Для составления модели
транспортной задачи вводится дополнительный фиктивный пункт назначения ВФ
или фиктивный пункт отправления АФ.
( 3.101)
Таким образом, путем введения фиктивного пункта отправления или назначения транспортную задачу с неправильным балансом сводят к задаче с правильным балансом.
2. Модель транспортной задачи с максимизацией целевой функции.
![]() Для определения максимума
целевой функции необходимо
Для определения максимума
целевой функции необходимо
преобразовать исходную матрицу
![]() по следующему правилу.
Каждый элемент матрицы равен разности между максимальным элементом
соответствующего столбца и элементом исходной матрицы. В результате такого
преобразования получается новая матрица , которая используется для составления
модели транспортной задачи.
по следующему правилу.
Каждый элемент матрицы равен разности между максимальным элементом
соответствующего столбца и элементом исходной матрицы. В результате такого
преобразования получается новая матрица , которая используется для составления
модели транспортной задачи.
3. Модель транспортной задачи с ограниченной
пропускной способностью.
В рассмотренных моделях предполагалось, что и . Однако, в реальных условиях может оказаться, что пропускная способность по отдельным маршрутам ограничена и составляет (здесь имеется в виду количество перевозимого груза). В этом случае вводятся дополнительные пункты отправления или назначения. Например, имеется оптимальный план перевозок:
![]()
![]()
![]()
![]()
![]()
![]() В1 В2 В3 ai
В1 В2 В3 ai
![]()
А1 1 4 7 60
![]() 50 10
50 10
А2 3 2 4
![]() 20 20 40
20 20 40
bj 50 30 20 100
![]()
![]() - количество перевозимого
груза из пункта в
- количество перевозимого
груза из пункта в
пункт (150,10.....20);
![]()
- стоимость перевозок (1,4,7.......4);
![]()
![]()
![]() - расстояние между
пунктами. Допустим, что пропускная способность . Строка, соответствующая
маршруту с ограниченной способностью
- расстояние между
пунктами. Допустим, что пропускная способность . Строка, соответствующая
маршруту с ограниченной способностью
разбивается на две строки:
- в первой строке запасы ;
![]()
- во второй .
![]()
![]() Стоимость одинакова в обеих
строках, но в первой строке, в клетке, соответствующей участку с ограниченной
пропускной способностью, вместо ставится большое число
Стоимость одинакова в обеих
строках, но в первой строке, в клетке, соответствующей участку с ограниченной
пропускной способностью, вместо ставится большое число
![]()
, где
![]()
![]()
![]()
![]()
![]()
В1 В2 В3 ai
![]()
А1* M 4 7
![]() 30 10 40
30 10 40
А1** 1 4 7
![]() 20 20 20 20
20 20 20 20
А2 3 2 4
![]() 30 10 40
30 10 40
bj 50 30 20
Результаты расчета показывают, что ограничение пропускной способности увеличивает стоимость перевозки.
4. Модель транспортной задачи по критерию времени.
В некоторых моделях эффективность перевозок определяется временем Т перевозок. Допустим, что - время перевозок груза из пункта в пункт назначения . В таком случае план перевозок будет представляться целевой функцией
![]()
при обычных ограничениях.
![]()
![]() Такие модели могут быть
составлены и реализованы последовательным решением задачи по критерию стоимости
перевозок, запрещая после каждого решения элементы матрицы ,
Такие модели могут быть
составлены и реализованы последовательным решением задачи по критерию стоимости
перевозок, запрещая после каждого решения элементы матрицы ,
![]()
для которых . Запрещение производится заменой данного элемента матрицы на достаточно большое число М. Если на следующей итерации стоимость перевозок будет превышать М, то план предыдущей операции является оптимальным.
![]()
![]()
![]()
![]() Например,
задана матрица:
Например,
задана матрица:
ai
10 4 6 20
![]()
7 8 3 20
![]()
bj 10 15 15
После решения по критерию стоимости, получим план
![]()
Максимальное значение maxtij =10 обозначим через М и подставим в исходную матрицу
![]()
![]()
(1)
Далее подставим и повторим процедуру вычислений
![]()
(2)
Т.к. все элементы первого столбца равны М, то целевая функция L>М. Следовательно, оптимальный план решения по критерию времени соответствует матрице и Т = 7.
3.6.7 Модель планирования производства
![]()
![]()
![]() Исходные условия. Предприятие производит изделия m видов: . По каждому
виду изделия имеется план выпуска единиц изделий . Для изготовления данных
изделий на складе имеется n видов сырья С, запасы которых ограничены. Для
составления модели представим исходные данные в виде таблицы:
Исходные условия. Предприятие производит изделия m видов: . По каждому
виду изделия имеется план выпуска единиц изделий . Для изготовления данных
изделий на складе имеется n видов сырья С, запасы которых ограничены. Для
составления модели представим исходные данные в виде таблицы:
![]()
Изделия
Вид сырья b1 b2 b3 ... bm
С1 С11 С12 С13 С1m
С2 С21 С22 С23 С2m
Сij
Cn Cn1 Cn2 Cn3 Cnm
![]()
где - количество сырья на изготовление конкретного изделия.
Готовые изделия приносят предприятию прибыль: изделие приносит прибыль соответственно и т.д.
![]() Необходимо так спланировать
производство, чтобы определить, сколько и каких изделий производить, чтобы
получить максимальную суммарную прибыль, т.е.
Необходимо так спланировать
производство, чтобы определить, сколько и каких изделий производить, чтобы
получить максимальную суммарную прибыль, т.е.
![]() (3.102)
(3.102)
при соответствующих ограничительных уравнениях m
![]()
(3.103)
В том случае, когда необходимо составить модель производства с учетом трудовых материальных и финансовых затрат (ресурсов) целесообразно составить таблицу.
По таблице составляется система уравнений
![]()
(3.104)
![]() или в общем виде
или в общем виде
(3.105)
Ограничения:
![]()
Конечной целью исследования модели является достижение максимальной прибыли
![]()
(3.106)
при заданных исходных ресурсах. Кроме этого в рассматриваемой модели можно минимизировать количество ресурсов при заданной прибыли.
![]()
3.7 ГРАФОВЫЕ МОДЕЛИ ОБЪЕКТОВ И СИСТЕМ
3.7.1 Математическая модель размещения аварийных служб и пунктов обслуживания
Для обслуживания нескольких жилых районов или населенных пунктов, связанных между собой дорожной сетью, необходимо иметь пункты обслуживания (больницы, милицейские участки или магазины). Причем, пункт обслуживания должен располагаться в каком-либо определенном районе, а не в произвольной точке, например, дороге. Условия задачи задаются в виде графа G, вершины которого соответствуют районам, а дуги - дорогам. Коэффициенты матрицы графа обозначают время проезда между районами. Вершины графа могут иметь весовые коэффициенты, определяющие, например, количество проживающих в этом районе жителей.
Пусть исходный граф представлен в следующем виде:
![]() x1
x1
![]()
![]()
![]()
![]()
![]() x6 x2
x6 x2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x5 x3
x5 x3
x4
Матрица расстояний графа записана таблицей:
![]() x1 x2 x3 x4 x5 x6 S0(xj)
x1 x2 x3 x4 x5 x6 S0(xj)
x1 0 1 2 3 2 3 3
x2 3 0 1 2 1 2 3
x3 4 3 0 1 2 3 4
x4 3 2 2 0 1 2 3
x5 2 1 1 2 0 1 2
x6 1 2 3 4 3 0 4
St(xi) 4 3 3 4 3* 3**
![]() где - число
внешнего разделения вершин (наибольшее число в строке);
где - число
внешнего разделения вершин (наибольшее число в строке);
![]() - число
внутреннего разделения вершин (наибольшее число в строке);
- число
внутреннего разделения вершин (наибольшее число в строке);
![]() - веса вершин;
- веса вершин;
![]() - длины
вершин.
- длины
вершин.
Конечная цель. Требуется разместить милицейский участок (больницу и т.д.) с учетом минимального времени проезда в наиболее отдаленные районы.
Данный участок должен располагаться в районе, который удовлетворяет следующим требования
![]() (3.107)
(3.107)
3.7.2 Модель определения кратчайшего пути.
Объекты моделирования (сеть железнодорожных или автомобильных дорог, информационные компьютерные сети, различные лабиринты магистралей городов и т.д.) задаются графом вида G(x,y) , дугам которого приписаны веса (стоимости, расстояния, время передачи), задаваемые матрицей C=[CI].
Необходимо найти кратчайший путь от заданной начальной вершины Xi заданной конечной вершины Xj при условии, что такой путь существует. Кроме того, могут быть заданы условия нахождения кратчайших путей между и всеми другими вершинами (между парами вершин).
Модель задана в виде исходного графа.
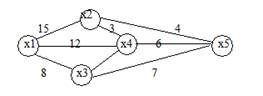
и матрицей расстояний.
x1 x2 x3 x4 x5
x1 0 15 8 12 0
x2 15 0 0 3 4
x3 8 0 0 2 7
x4 12 3 2 0 0
x5 0 4 7 6 0
3.7.3 Модель задачи “коммивояжера”.
Имеется N пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт за конкретное время. Обычно условия для разработки модели представляются в виде таблицы.
В пункт
Из пункта 1 2 3 4 n
1 t11 t12 t13 t14 t(1n)
2 t21 t22 t13 t24 t(2n)
n t(n1) t(n2) t(n3)t(n4) t(nn)
Требуется найти такой маршрут, начинающийся и заканчивающийся в данном пункте и проходящий через все N пунктов, чтобы продолжительность прохождения маршрута была минимальной.
Математическая модель представляется следующим выражением:
![]() ,
(3.108)
,
(3.108)
Σdij=1; j=1,n;dij=(0,1) , (3.109)
![]()
; (3.110)
где δij =1, если из пункта i есть путь в пункт j;
δij =0 , если из пункта i нет пути в пункт j.
3.7.4 Модель сетевого графа
Необходимо выполнить комплекс работ. Причем некоторые виды работ зависят от исхода предшествующих работ. Информация о начальных условиях задана в виде таблицы и сетевого графа.
![]() Требуется минимизировать
критический путь при ограниченных ресурсах, т.е. обеспечить решение минимаксной
задачи.
Требуется минимизировать
критический путь при ограниченных ресурсах, т.е. обеспечить решение минимаксной
задачи.
где tij - длительность выполнения отдельной работы. Критический путь выбирается по максимуму среди всех путей в графе по времени выполнения работ, а минимум берется по ресурсам для работ, лежащих на критическом пути.
Параметры сетевой модели.
Параметрами сетевой модели являются:
- критическое время Tkp - минимальное время, за которое можно выполнить весь комплекс работ;
- критический путь Lkp - полный путь, продолжительность прохождения которого составляет время Tkp;
- критические работы ai- работы, лежащие на критическом пути;
- ранний срок наступления событий Tk(P);
![]()
- поздний срок наступления событий Tk(n);
- фиктивные работы (на графе обозначаются пунктирной линией), обозначающие зависимость работ от предшествующих.
Значение Tk(P) определяется как продолжительность максимальных путей, ведущих от основного события к “к”- тому событию.
![]() ;
;
или в общем виде:
![]() ,
,
где - ![]() множество дуг
(i ,j), входящих в j-ую вершину. Рассчитаем ранние сроки
наступления событий для приведенного графа.
множество дуг
(i ,j), входящих в j-ую вершину. Рассчитаем ранние сроки
наступления событий для приведенного графа.
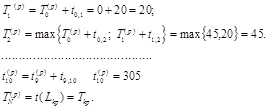
Вычисление поздних сроков наступления событий может производится по зависимостям:
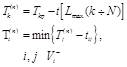
где - Vi- множество дуг (i, j), выходящих из i-ой вершины.
Вычисление ![]() ведется
от завершающего события, т.е.
ведется
от завершающего события, т.е.
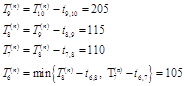
В качестве параметров могут быть :
- ранний срок начала работ ![]() ;
;
- ранний срок окончания работ
![]() ;
;
- поздний срок начала работ ![]() ;
;
- поздний срок окончания
работ ![]() ;
;
- резерв времени ![]() ;
;
- полный резерв ![]() ;
;
- свободный резерв ![]() .
.
Резерв в ремени - это промежуток времени, в пр еделах

которого может меняться момент наступления события без увеличения критического времени.
Полный резерв - максимальное время, на которое можно отсрочить начало и увеличить продолжительность работ.
Примеры сетевых моделей:
- составление плана изучения дисциплины в учебных заведениях;
- составление плана работ по изготовлению каких-либо объектов;
- подготовка и проведение различных мероприятий;
- разработка моделей строительства сложных объектов;
- планирование производства предметов потребления;
- разработка вычислительных алгоритмов наиболее сложных задач.
3.8 Экономические (вероятностные) модели объектов и систем.
3.8.1 Математическая модель управления запасами
Для составления модели управления запасами необходимо иметь следующие данные:
- интенсивность спроса d (количество товаров в год);
- организационные издержки S (стоимость партии товара);
- стоимость товара С (стоимость единицы товара);
- издержки содержания запасов h (стоимость за единицу товара в год);
- размер партии q (единиц товара в одной партии).
Определить значение q (размер партии), при котором минимизируются годовые затраты.
Для определения конечной цели модель управления запасами включает следующие разделы.
1. График изменения запасов Q
2. Уравнение издержек.
![]() ,
(3.111)
,
(3.111)
![]()
где - общие организационные издержки,
Cd - стоимость товара,
![]() - общие издержки
содержания запасов.
- общие издержки
содержания запасов.
Для случая, когда поставки доставляются не мгновенно, а в течении какого-то промежутка времени, уравнение издержек представляется следующим выражением:
![]() ,
(3.112)
,
(3.112)
где p - скорость поставок, равная количеству товаров, выпускаемых производством за год.
График изменения запасов имеет вид:
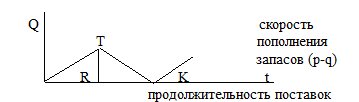 Q
Q
0T - скорость пополнения поставок (p-q);
0t - продолжительность поставки;
TK - постоянный спрос с интенсивностью d.
В том случае, когда учитываются штрафы за несвоевременную поставку, уравнение издержек будет описываться выражением:
![]() ,
где (3.113)
,
где (3.113)
h - издержки хранения единицы товара за единицу времени;
P - затраты на штраф в расчете на единицу товара за один день отсрочки;
y - запас единиц товара за период L, в течении которого будет наблюдаться дефицит товара, т.е. величина (q - y) - невыполнение заявок.
График изменения запасов в этом случае представляется в виде:
BCD - периоды дефицита.
Таким образом, конечной целью исследования моделей управления запасами является выбор такого значения y, которое ведет к минимизации всех затрат (т.е. затрат на хранение запасов и затрат на штрафы). В результате произведенного исследования модели фирма (завод, фабрика) может принять решение: какое количество товара должно находиться в запасе, в какое время производить пополнение запаса.
3.8.2. Статистическая модель распределения ресурсов
В детерминированных моделях распределения ресурсов начальные данные определены: а - ресурсы (заявки) i-го поставщика; b - заявки j-го потребителя; с - стоимость перевозки i-го поставщика к j-му потребителю. B реальных условиях величины a, b, c являются случайными, которые определяются реализацией, количественными характеристиками и законом распределения. В этом случае целевая функция может быть записана в виде:
![]() ,
(3.114)
,
(3.114)
где M - математическое ожидание целевой функции, или в виде:
F = е CJ XJ - max (min), j=1,n, (3.115)
где CJ - математическое ожидание случайной величины .
Необходимо найти такие значения xj , при которых математическое ожидание целевой функции будет иметь оптимальное, т.е. максимальное (или минимальное) значение.
Ограничения представляются выражениями:
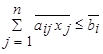 (3.116)
(3.116)
Или
![]()
![]()
![]()
![]()
![]()
![]() , (3.117)
, (3.117)
![]()
![]() где , - математические
ожидания и дисперсия случайных величин
где , - математические
ожидания и дисперсия случайных величин ![]() и
и ![]() ;
;
![]() - значение нормированной
случайной величины в нормальном законе распределения соответствующее
заданному уровню вероятности ограничения ;
- значение нормированной
случайной величины в нормальном законе распределения соответствующее
заданному уровню вероятности ограничения ;
![]() - дисперсия
ресурсов;
- дисперсия
ресурсов;
![]() - дисперсия
значений норм расхода .
- дисперсия
значений норм расхода .
![]() В отличие от
детерминированных величин
В отличие от
детерминированных величин ![]() ,
, ![]() ,
, ![]() в условие
входят математические ожидания случайных величин
в условие
входят математические ожидания случайных величин ![]() ,
, ![]() ,
, ![]() , уменьшающихся на
величину
, уменьшающихся на
величину ![]() , т.е. это приводит к уменьшению ресурса.
Величина является тем дополнительным ресурсом, который является гарантией
выполнения заказа на ресурсы (продукцию).
, т.е. это приводит к уменьшению ресурса.
Величина является тем дополнительным ресурсом, который является гарантией
выполнения заказа на ресурсы (продукцию).
3.9 Математические модели распознавания образов.
3.9.1 Общие сведения о теории распознавания образов
Предметы или явления, которые необходимо распознать, обладают общими свойствами и имеют ряд отличительных признаков. Те предметы, которые имеют общие свойства, называются классами. A {A1, A2,...Am}, где m - общее количество классов (набор классов).
Каждый класс может быть представлен некоторым количеством реализаций, образующих множество реализаций. Кроме того, каждый класс имеет ряд признаков.
Распознавание объектов (предметов) имеет два этапа: обучение и собственно распознавание. Существуют различные способы распознавания, критериями которых могут быть: расстояние от центральной точки (центра тяжести) множества данного образа, сумма расстояний до всех эталонов данного образа и т.д.
3.9.2 Модель распознавания объектов и процессов на основе формулы Байеса
Имеются независимые признаки,
которыми могут обладать предметы, явления или процессы. Например, имеются
четыре признака х1, х2, х3, х4 (температура, кашель, покраснение горла,
вялость), ![]() которые характеризуют три болезни
(простудное заболевание, грипп, ангина).
которые характеризуют три болезни
(простудное заболевание, грипп, ангина).
В результате обучения модели
распознавания определяются условные вероятности ![]() как отношение
признаков, характеризующих данную болезнь
как отношение
признаков, характеризующих данную болезнь ![]() ко всем признакам.
ко всем признакам.
Требуется распознать прототипы событий (болезней) по введенным признакам с учетом формулы Байеса.
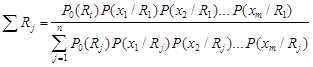 ,
,
где - априорные вероятности существования образов , которые определяются в результате опыта работы врача по распознаванию болезней. Если опыта нет, то выбираются одинаковые вероятности для всех болезней. В общем случае модель распознавания на основе формулы Байеса включает две модели: модель признаков болезней и модель метода распознавания, в которую входит формула Байеса и определение максимума по полученным результатам распознавания болезней .
Исходные данные и результаты распознавания можно свести в таблицу.
Исходные данные
![]()
x(i)/Nk 1 2 N P[x(i)/R1] P[x(i)/R2] P[x(i)/Rj]
1x1 +1 +1 +1 P(x1/R1) P(x1/R2) P(x1/Rj)
2x2 -1 +1 -1 P(x2/R1) P(x2/R2) P(x2/Rj)
3x3 +1 +1 +1 P(x3/R1) P(x3/R2) P(x3/Rj)
4x4 -1 -1 -1 P(x4/R1) P(x4/R2) P(x4/Rj)
Rj1 Rj2 Rj
3.9.3 Модель распознавания образа с учетом матрицы потерь
Данные задаются экспериментальной матрицей вероятностей E, таблицей априорных вероятностей Р и матрицей потерь L.
Матрица потерь представляет собой таблицу цифр, показывающих все последствия данного решения распознающей системы:
![]()
![]()
d
![]()
![]()
![]() R
R
d1 d2 d3
![]()
R1 0 1 1
![]()
R2 0 0 1
![]()
R3 1 0 0
где d - решаемая функция,
![]() - решение
- решение ![]() ,
,
![]() - решение
- решение ![]() ,
,
![]() - решение
- решение ![]() . Экспериментальная матрица вероятностей
. Экспериментальная матрица вероятностей
составляется из наблюдений за
распознаванием данных образов человеком и выражается через условные априорные
вероятности для каждого признака ![]() .
.
![]()
![]() x1
x1
![]()
![]() R
R
x = +1 x = -1
![]()
R1 P(x/R1)=0,8 P(x/R1)=0,2
R2 P(x/R2)=0,4 P(x/R2)=0,6
R3 P(x/R3)=0,2 P(x/R3)=0,8
Требуется при наличии входных сигналов выбрать тот образ (вид неисправности в аппаратуре, выбор действий и т.д.), при котором величина потерь будет наименьшей,
![]()
где R - число образов,
q - количество значений выходного сигнала,
![]() - априорные
вероятности,
- априорные
вероятности,
![]() - решающая
функция,
- решающая
функция,
![]() - условные
вероятности событий.
- условные
вероятности событий.
3.9.4 Модель перцептрона
Перцептрон представляет собой модель зрительного и слухового восприятия человеческого мозга, предложенную Ф.Розенблаттом.
Эта модель образует определенный класс систем по распознаванию различных образов.
Особенностями перцептрона являются:
1. Структура перцептрона многорядна, причем каждый из А-элементов может решать задачи по распознаванию самостоятельно.
2. После каждого ряда А-элементов находится порог, позволяющий отсеять малоэффективные комбинации входных признаков.
3. Сложность комбинаций от ряда к ряду перцептрона возрастает.
Модель перцептрона можно представить в виде следующей структурной схемы:
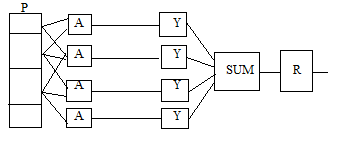
где P - зрительные рецепторы (поле рецепторов, оптических датчиков);
A - пороговые логические блоки со случайными связями с рецепторами;
У - усилительные элементы;
R - пороговый элемент с настраиваемыми коэффициентами .
Математическую модель перцептрона можно описать уравнениями:
1. Уравнение первого слоя (выход элементов А):
1 при ![]() ;
;
y = (3.118)
0 при , ![]()
где - некоторый порог;
- входы элементов А от рецепторов;
- весовые коэффициенты пороговых блоков А.
2. Уравнение 2-го слоя:
1, если ![]() ;
;
R = (3.119)
0, если ![]() ,
,
где ![]() - весовые
коэффициенты;
- весовые
коэффициенты;
![]() -
сигналы с выхода 1-го слоя перцептрона.
-
сигналы с выхода 1-го слоя перцептрона.
Необходимо в процессе обучения
подобрать коэффициенты ![]() , чтобы выходной сигнал перцептрона R
соответствовал требуемому зрительному объекту, например, букве, рисунку.
, чтобы выходной сигнал перцептрона R
соответствовал требуемому зрительному объекту, например, букве, рисунку.
3.10 Математические модели объектов и систем массового обслуживания
Моделирование задач по обслуживанию покупателей, пассажиров, больных и т.д., а также по организации информационно-справочной службы, телефонной и телеграфной связи, ремонтных работ основаны на теории массового обслуживания. Для моделирования таких систем разрабатываются модели систем обслуживания, в которых потоки требований (запросов) подчиняются статистическим закономерностям.
Модель системы массового обслуживания, в которую в отдельные случайные моменты времени поступают заявки, состоит из n каналов (пунктов обслуживания). Поток заявок представляет собой простейший (пуассоновский) поток. Интервал времени между двумя последовательными событиями есть случайная величина, которая может быть распределена, например, по закону Пуассона, показательному (экспоненциальному) закону и т.д.
Так, если интервал времени есть случайная величина, распределенная по экспоненциальному закону, то
![]() ,
(3.120)
,
(3.120)
- интенсивность потока заявок (среднее число заявок в единицу времени);
R - случайная величина, равномерно распределенная в интервале (0,1).
В соответствии с законом Пуассона функция распределения и - интенсивность потока заявок (среднее число заявок в единицу времени);
R - случайная величина, равномерно распределенная в интервале (0,1).
В соответствии с законом Пуассона функция распределения
![]()
![]()
имеет вид меет вид
Каждая заявка поступает в канал, который освободился раньше всех. Если есть несколько свободных каналов, то заявка поступит в канал с меньшим номером. Время обслуживания k-той заявки обслуживания является случайной величиной, равномерно распределенной в интервале (a,b) и определяется по формуле
![]() (3.122)
(3.122)
Требуется определить показатели эффективности системы за время функционирования , т.е. время обслуживания каждой заявки, количество обслуживаемых заявок, число отказов, длину очереди. Для оценки качества работы системы массового обслуживания могут быть использованы:
а) средняя стоимость обслуживания за единицу времени
![]() , где
, где
K - среднее число заявок в очереди;
![]() - среднее
число свободных обслуживающих приборов;
- среднее
число свободных обслуживающих приборов;
![]() - стоимость
отпуска одной заявки;
- стоимость
отпуска одной заявки;
![]() - стоимость
простоя одного обслуживающего прибора;
- стоимость
простоя одного обслуживающего прибора;
б) вероятность надежной работы системы (надежность системы).
Основными показателями эффективности работы системы являются:
![]() - вероятность
отказа ;
- вероятность
отказа ;
![]() - абсолютная
пропускная способность ,
- абсолютная
пропускная способность ,
где ![]() -
интенсивность потока обслуживания, n - число каналов;
-
интенсивность потока обслуживания, n - число каналов; ![]() - относительная
пропускная способность ,
- относительная
пропускная способность ,
где - ![]() интенсивность
заявок;
интенсивность
заявок;
![]() - среднее
число занятых обслуживающих приборов ,
- среднее
число занятых обслуживающих приборов , ![]() где - параметр
обслуживания (среднее необходимое число обслуживающих приборов),
где - параметр
обслуживания (среднее необходимое число обслуживающих приборов), ![]() -
случайная величина, распределенная по показательному закону;
-
случайная величина, распределенная по показательному закону;
- ![]() средняя длина
очереди L - математическое ожидание от числа заявок;
средняя длина
очереди L - математическое ожидание от числа заявок; ![]()
- среднее время пребывания заявки в системе , где - среднее время от момента начала обслуживания до момента окончания обслуживания, - время ожидания заявки в очереди;
- экономическая эффективность системы массового обслуживания (прибыль в единицу времени)
,
![]() (3.124)
(3.124)
где С 0 - прибыль при обслуживании заявки;
С - функция стоимости потерь;
- стоимость эксплуатации прибора в единицу времени;
![]() - стоимость
единицы времени простоя;
- стоимость
единицы времени простоя;
Сn- стоимость потерь, связанных с простаиванием заявки в очереди, в единицу времени;
![]() Cy- стоимость убытков, связанных с уходом заявки из
системы;
Cy- стоимость убытков, связанных с уходом заявки из
системы;
Cз- коэффициент занятости приборов, ;
3.11 Математические игровые модели объектов и систем
Имеются два или множество объектов, систем (игроков). Каждому объекту (игроку) задается стратегия действий, которая оформляется в виде платежной матрицы (или матрицы игры). Допустим, что рассматривается игра m x n, где m - количество стратегий игрока А, а n - количество стратегий игрока В. Тогда платежная матрица будет иметь вид:
![]()
B1 B2 B3 . . . Bn
A1 a11 a12 a13 a1n
A2 a21 a22 a23 a2n
Am Am1 Am2 Am3 Amn
Если первый игрок применяет стратегию , то второй игрок будет стремиться к тому, чтобы, выбрав стратегию , свести выигрыш первого игрока к минимуму . С точки зрения первого игрока надо выбрать стратегию, чтобы обращалась в максимум (нижняя цена игры)
Аналогично определяется минимальный проигрыш для второго игрока
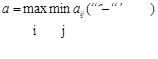
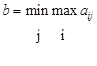
3.12 Нейрокомпьютерные модели
Нейрокомпьютерные системы - это системы, состоящие из нейронных сетей, способные к обучению для решения конкретных задач ( прогнозированию, анализу, тестированию, оптимизации, принятия решения и во всех областях, в которых требуется интелектуальная человеческая интуиция.
В основе построения нейрокомпьютерных систем является нейрон, который связан «синаптической» связью с другими нейронами, образуя нейронную сеть.
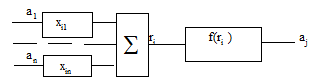
![]()
![]() Каждый нейрон имеет:
синаптические контакты, которые умножает входной сигнал от i-того нейрона ai на
коэффициент S, сумматор
Каждый нейрон имеет:
синаптические контакты, которые умножает входной сигнал от i-того нейрона ai на
коэффициент S, сумматор ![]() с выходнм сигналом и преобразователь
сигналов
с выходнм сигналом и преобразователь
сигналов
В качестве функции преобразования могут использоваться
![]() следующие
следующие
Нейронные сети собираются из нейронов. Существуют три различные группы нейронных сетей:
- формируемые сети;
- сети с формируемой матрицей связи;
- обучаемые сети.
Наиболее перспективной сетью является обучаемая сеть, которая сама вычисляет свои параметры в зависимости от задач
![]() Для обучения используется
метод, основанный на принципе двойственности. Суть метода состоит в следующем.
Пусть на каждый нейрон поступает внешний сигнал и снимается
Для обучения используется
метод, основанный на принципе двойственности. Суть метода состоит в следующем.
Пусть на каждый нейрон поступает внешний сигнал и снимается ![]() сигнал . Синаптический коэффициент связи , с
помощью которого сигнал с i-го нейрона передается на j -й нейрон. Тогда
уравнение функционирования нейронной сети будет представляться выражением
сигнал . Синаптический коэффициент связи , с
помощью которого сигнал с i-го нейрона передается на j -й нейрон. Тогда
уравнение функционирования нейронной сети будет представляться выражением
![]()
Для каждой задачи принцип
обучения сводится к следующим операциям:
1. Вычисляются выходные сигналы со всех нейронов;
2. Определяются функции оценки H(x);
3. Вычисляется градиент функции grad H(x);
4. Корректируется карта синапсов xk=x+h*gradH(x). обучени Наиболее простой функцией оценок является функция, полученная по принципу: если объект относится к 1-му классу, то на выходе 1-го нейрона сигнал равен 1, а на других нейронах сигналы равны -1. Такая функция представляется следующим
выражением
![]()
Наиболее простым методом является метод случайного направления. Суть метода состоит из выполнения следующих опрераций: вычисляется оценка H(x), генерируется случайное напрвление v, изменяется синаптическая карта по формуле x1=x0+h*v, если H(x1)>H(x0), то x0=x1, иначе вычисляется карта x2 по формуле x1=x0 - h*v, если H(x2)>H(x0), то x0=x2.
3.13 Язык моделирования UML
3.13.1 История методов моделировния сложных систем
Методы
объектно-ориентированного анализа и проектирования , основанные на
использовании графических языков моделирования, появились сравнительно недавно.
Основу построения графических языков моделирования сложных систем предложил Гради
Буч — американский инженер, руководитель исследований в IBM.
Совместно с Иваром Якобсоном и Джеймсом
Рамбо Гради Буч являются создателями унифицированного языка
моделирования UML![]() .
.
Гради Буч родился в 1955 в городе Амарилло, штат Техас. В 1977 Гради Буч закончил обучение в Академии ВВС США. Затем он проходил службу на базе ВВС в Ванденберге, где руководил разработкой целого ряда проектов, управляющих полетом ракет. В 1979 Гради Буч получил степень магистра Университета Калифорнии в Санта-Барбаре. Известность Буч получил в 1980-х годах благодаря созданию метода разработки программного обеспечения, впоследствии названного методом Буча. Данный метод был изложен в книге «Объектно-ориентированный анализ и проектирование». Также Буч был автором одной из самых популярных в то время книг о программировании на языке Ada.
В 1994 году Гради Буч и Джеймс Рамбо, работавшие в компании Rational Software, объединили свои усилия для создания нового языка объектно-ориентированного моделирования. За основу языка ими были взяты методы моделирования, разработанные Бучем (метод Буча) и Рамбо (Object-Modeling Technique — OMT). OMT был ориентирован на анализ, а метод Буча — на проектирование программных систем. Осенью 1995 года к ним присоединился Ивар Якобсон, автор метода Object-Oriented Software Engineering — OOSE, обеспечивавшего превосходные возможности для спецификации бизнес-процессов и анализа требований при помощи сценариев использования. Первые версии унифицированного языка UML версии 0.9 появились в октябре 1996 года.
С середины 1990-х Гради Буч занимал должность руководителя исследований компании Rational Software, где работал до 18 марта 2008 года . В настоящий момент Буч руководит исследованиями и проектами IBM Research.
Графический язык послужил основой для создания целого семейства методов моделирования сложных систем, обозначаемых аббревиатурой IDEF. Все методы IDEF основаны на использовании визуальных языков. Наиболее известными из многочисленного семейства методов IDEF являются методы IDEF0, IDEF1X и IDEF3. Метод IDEF0 предназначен для моделирования функций сложных информационных систем и их процессов. Он поддерживается инструментальными программами BPwin (бизнес процессы и окна). Метод IDEF1X используется для моделирования реляционных баз данных. Он поддерживается программами ERwin (сущности-взаимосвязи и окна). Метод IDEF3 предназначен для детального моделирования бизнес процессов.
Во многих странах методы IDEF0 и IDEF1X оформлены и утверждены как стандарты обработки информации (FIPS), которые обязаны использовать все федеральные организации и предприятия при разработке новых информационных систем. В результате в значительной мере, обеспечивается, стандартизация программных средств. Методы IDEF0, IDEF1X используются и в России как государственными, так и частными организациями.
![]()
Пример простейшей диаграммы IDEF0 для образовательного процесса в высшем учебном заведении
Основными элементами любой IDEF0 диаграммы являются прямоугольники ( процессы)и стрелки( вход и выход).
Однако диаграммы IDEF0 обладают рядом недостатков. В частности, они не имеют математической основы. Другой недостаток заключается в отсутствии визуальных средств для объектно-ориентированного представления сложных систем. Метод IDEF0 в сочетании с другими методами моделирования сложных систем послужил основой для создания методов объектно-ориентированного моделирования систем и унифицированного языка моделирования UML.
По определению Гради Буча унифицированный язык моделирования (Unified Modelling Language, UML) является графическим языком для визуального представления, составления спецификаций, проектирования и документирования систем, в которых большая роль принадлежит программному обеспечению, которые обычно называются системами автоматизированных информационных систем (АИС) . В этих системах участвуют разработчики систем. С помощью языка UML можно разработать общесистемную документацию, обеспечить взаимосвязь между базовыми понятиями моделей концептуального, программного и физического уровней, которые понятны как системным аналитикам, так и и программистам. Данный язык моделирования поддерживается специальными инструментальными программными средствами, реализованными на различных компьютерных платформах.
В настоящее время разработаны инструментальные программы поддержки языка UML. Наиболее известной из них является программы Rational Rose 2000 фирмы Rational Software. Кроме того создан ряд средств визуального программирования, обеспечивающую прямую генерацию кода программ из UML моделей. Эти средства интегрированы с наиболее распространенными языками программирования Java, C++ и многими другими. В настоящее время наиболее удобными программи являются Visio 2010, StarUML, Visual Studio 2010.
Необходимость появления языка моделирования была связана с тем, чтобы связать наглядными диаграммами объект моделирования и исходный код программы.
.
![]()
![]()
На рисунке изображены две схемы. Первая из них (а ) изображает процесс создания объекта автоматизации и код программы, существовавшую в области технологий программирования до создания языка UML, вторая (б) - показывает изменение процесса после появления UML. На обеих схемах слева показаны программисты и воображаемые ими модели компьютерных программ, а справа изображены коды программ и предметные области, в которых эти программы используются. На второй схеме между предметными областями и программными кодами появились диаграммы языка UML и их математическая основа – теории множеств и графов.
В чем заключаются негативные моменты ситуации, существовавшей до появления языка UML? Как видно из рис. объединение текста программы (ее исходного кода) с характеристиками объекта автоматизации осуществляется только в сознании программиста, а документальная связь между ними отсутствует.
Диаграммы и спецификации языка UML связали исходный текст программы с характеристиками объекта автоматизации. При этом UML диаграммы опираются на теоретический фундамент в виде теории множеств и теории графов. Наличие теоретической основы позволяет упростить операции преобразования UML диаграмм, нарисованных на экранах дисплеев, в память компьютеров и уменьшить объем памяти, необходимой для хранения диаграмм.
Рисунок также показывает, что UML диаграммы могут преобразовываться в исходный код (прямое преобразование) и наоборот исходный код может преобразовываться в диаграммы (обратное преобразование). В некоторых случаях прямое преобразование может осуществляться автоматически с помощью программ конверторов. Язык UML способствует очень наглядно в минимальное время разобраться с принципом построения кода программы. Диаграммы позволяют документировать исходные коды программ UML диаграммами и спецификациями создает единый язык общения между программистами, а также между программистами, системными аналитиками и заказчиками автоматизированной системы. Но самое главное, что дал UML - это возможность широкой стандартизации языков программирования. Известно, что в разных языках программирования используются одинаковые операции и методы, но они имеют разные названия и символьные обозначения. Язык UML позволяет стандартизовать как сами операции и методы языков программирования так и их терминологию.
Структура языка UML
![]() Язык UML имеет сложную
иерархическую структуру, показанную на рисунке
Язык UML имеет сложную
иерархическую структуру, показанную на рисунке
Как видно из рисунка, первый иерархический уровень языка UML составляют сущности, отношения между сущностями и наглядные диаграммы. Язык UML имеет четыре вида сущностей: структурные, поведенческие, группирующие и аннотационные сущности. Далее на третьем уровне дерева показано, что понятие "структурные сущности" является именем семи видов пиктограмм (выразительных рисунков), которые называются классами, интерфейсами, кооперациями, прецедентами, активными классами, компонентами и узлами.
Поведенческие сущности делятся на два вида диаграмм. Диаграммы первого вида называются взаимодействиями, второго вида - автоматами. Группирующие сущности имеют только один вид пиктограмм, называемых пакетами. Аннотационные сущности также имеют один вид пиктограмм, называемых примечаниями.
На рисунке в качестве примеров показаны пять видов пиктограмм – классы, прецеденты, актеры, пакеты и примечания.
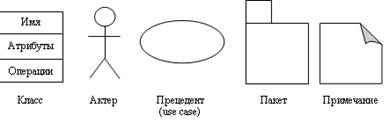
Класс изображается прямоугольником, разделенным на три поля. В первом поле помещается имя класса, однозначно определяющее данный класс среди множества других классов. Во втором поле помещаются атрибуты (общие свойства) класса. В третьем поле располагаются типовые операции, выполняемые объектами, принадлежащими данному классу. Таким образом класс - это совокупность (множество) объектов с общими атрибутами и операциями, а также с общими отношениями и семантикой. Объектами, объединенными в класс, могут быть, например, люди, окна системы Windows, экранные кадры и другие реальные или абстрактные объекты.
Левая пиктограмма показывает класс с именем "окно" и основные свойства (характеристики) присущие объектам этого класса. Правая пиктограмма показывает класс "кадр (frame)"с его основными характеристиками и подробными характеристиками, детализирующими основные характеристики. Детальная нотация класса дает возможность программистам и аналитикам визуализировать, специфицировать, конструировать и документировать класс на любом желаемом уровне детализации свойств класса, достаточном для поддержки прямого и обратного проектирования моделей и кода.
Пиктограммы типа "прецеденты" и "актеры". Прецедент это описание множества последовательных событий, выполняемых компьютерной системой, которые приводят к наблюдаемому актером результату. Графически прецедент изображается в виде ограниченного непрерывной линией эллипса, обычно содержащего только имя прецедента.
Актер – это кто-то (или что-то) внешний по отношению к компьютерной системе, кто взаимодействует с ней. Графически актер изображается в виде пиктограммы, представляющей человека, поскольку актер это человек или группа людей, использующих данные, предоставляемые компьютерной системой. Например, в системе модель знаний студентов, актером являются студенты, которые получают оценки за знания по соответствующим темам.Пиктограмма "пакет" изображает единственную в языке UML первичная группирующая сущность. В пакет можно поместить структурные и поведенческие сущности и даже другие пакеты. Изображается пакет в виде папки с закладкой. Существуют также вариации пакетов, например, каркасы, модели и подсистемы.
Примечание изображается в виде прямоугольника с загнутым краем. На UML диаграмме примечание присоединяется к одному или нескольким элементам диаграммы. Внутри прямоугольника-примечания помещаются комментарии или ограничения, относящиеся к элементу (или нескольким элементам) диаграммы. Комментарий может быть текстовым или графическим.
Пиктограммы (рисунки) отношений, используемых в UML диаграммах составляют вторую ветвь структурного дерева языка UML Однонаправленные отношения представляются на UML диаграммах стрелками различных видов, а двунаправленное отношение представляется линией.
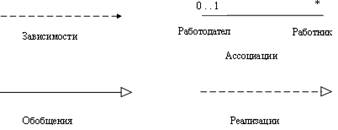
Показанное на рисунке однонаправленное отношение "зависимость" - это семантическое отношение между двумя сущностями, такое при котором изменение одной (первичной) сущности вызывает изменение семантики другой, зависимой сущности.
Ассоциация – это структурное двунаправленное отношение, описывающее совокупность взаимоотношений между объектами. По сути дела ассоциация является сверткой бинарных отношений между объектами. Эту свертку может мысленно выполнить в своем сознании специалист (например, программист), который видит пиктограмму ассоциации на UML диаграмме.
Пометка единица (1) на левом конце линии ассоциации означает, что в двунаправленном отношении, наряду с многими работниками участвует один работодатель. Единица и звездочка на правом конце линии означает "единица или больше" (1..*). Если один конец линии ассоциации помечен единицей (1), то пометка на другом конце линий называется кратностью ассоциации. Кратность правого конца ассоциации, показанной на рисунке, равна единице или больше.
На линии ассоциации можно также задать кратность равную единице (1), можно указать диапазон кратности: ноль или единица (0..1), много (0..*). Разрешается также указывать кратность определенным числом (например 5). С помощью списков можно задавать и более сложные кратности. Например, список 0..1, 3..4, 6..* означает "любое число объектов кроме 2 и 5".
Частным случаем ассоциации является отношение типа "часть/целое". Отношение такого типа называется агрегированием. В языке UML оно причислено к отношениям вида "имеет". Агрегирование изображается в виде ассоциации с незакрашенным ромбом со стороны целого, как показано на рисунке
Обобщение - это однонаправленное отношение, называемое "потомок/прародитель", в котором объект "потомок" может быть подставлен вместо объекта прародителя (родителя или предка). Потомок наследует структуру и поведение своего родителя. Стрелка всегда указывает на родителя.
Наконец, реализация – это семантическое однонаправленное отношение, которое может устанавливаться, во-первых, между интерфейсами и реализующими их классами или компонентами, во-вторых, между прецедентами и реализующими их кооперациями. Интерфейсы, компоненты и кооперации это еще три вида пиктограмм, относящихся к структурным сущностям. Пиктограммы интерфейса, кооперации и компонента показаны на рисунке.
![]()
Интерфейс – это совокупность операций, предоставляемых классом или компонентом. Следовательно интерфейс описывает поведение класса или компонента, видимое извне. Интерфейс определяет только описание (спецификации) операций класса или компонента, но он никогда не определяет физические реализации операций. Графически интерфейс изображается небольшим кружочком под которым пишется его имя. Кооперация определяет взаимодействие, например классов. Участвуя в кооперации классы совместно производят некоторый кооперативный результат. Один и тот же класс может принимать участие в нескольких кооперациях. Графически кооперация изображается в виде эллипса, ограниченного пунктирной линией.
Компонент – это физическая часть компьютерной или иной системы. Компонент соответствует некоторому набору интерфейсов и обеспечивает физическую реализацию этого набора. Компоненты могут быть разных видов. Например, одним из видов компонент, используемых для моделирования программного обеспечения компьютерной системы, могут быть файлы исходного кода. Компонент, как правило, представляет собой физическую упаковку логических элементов, таких как классы, интерфейсы и кооперации. Графически компонент изображается в виде прямоугольника с вкладками. Внутри прямоугольника обычно пишется только имя компонента.
Рисунки других видов пиктограмм языка UML, с пояснением их смысла, вы найдете в книге Г. Буча. Пиктограммы - это логические кирпичики из которых составляются UML диаграммы.
UML диаграммы
С помощью комбинации пиктограмм строятся UML диаграммы. Девять основных видов диаграмм перечисленных в третьей ветви структурного дерева языка UML. Мы не будем изучать все девять видов UML диаграмм, а рассмотрим только три из них - диаграммы прецедентов, диаграммы классов и диаграммы действий.
Диаграмма прецедентов (use case diagram) – это графическое представление всех или части актеров, прецедентов и
![]()
взаимодействий между ними. В каждой системе обычно есть главная диаграмма прецедентов, которая описывает внешнюю границу системы и основные внешние функции (внешнее поведение) системы. Пример диаграммы прецедентов , изображающую все прецеденты для одного актера, которым является секретарь кафедры учебных курсов.
Диаграммы классов применяются для моделирования объектно-ориентированных систем. На простых диаграммах показываются классы и отношения между классами. На сложных диаграммах показываются классы, интерфейсы, кооперации и отношения между ними. Диаграммы классов дают статический вид системы. Можно также сказать, что диаграммы классов представляют собой взгляды разработчиков на статические состояния проектируемых систем. С помощью диаграмм классов составляется словарь системы. Диаграммы классов являются основой для создания диаграмм компонентов и развертывания. Следует особо подчеркнуть, что диаграммы классов важны не только для визуализации, специфицирования и документирования структурных моделей, но также для прямого и обратного проектирования исполняемых кодов систем. На рисунке приведен пример простой диаграммы классов, моделирующей объекты системы регистрации курсов и отношения между ними.
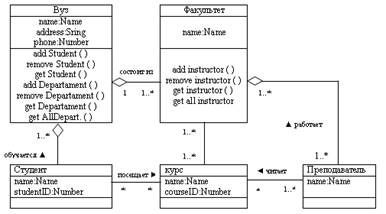
UML диаграммы классов включают в себя как частный случай диаграммы "сущность-связь" (Entity-relationship diagrams), которые используются для логического проектирования реляционных, объектно-ориентированных и гибридных объектно-реляционных баз данных.
![]()
Диаграммы действий..
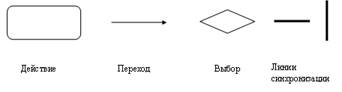
В языке UML действие изображается в виде прямоугольника с закругленными углами, переходы - в виде направленных стрелок, элементы выбора - в виде ромбов, линии синхронизации - в виде горизонтальных и вертикальных линий На рис. приведен пример диаграммы действий моделирующей действия, выполняемые в процессе создания системы регистрации учебных курсов.
Программы поддержки языка UML
Рассмотрены лишь отдельные фрагменты языка UML. Они дают общее представление о языке и могут быть использованы как вспомогательный материал при его изучении по специальной литературе по языку UML. Однако, если пользоваться только литературными источниками, то очень трудно усвоить синтаксис и семантику языка UML. Наилучший способ изучения языка UML заключается в создании UML диаграмм для конкретных систем с помощью инструментальных программ поддержки. Наиболее известной программой поддержки языка UML является пакет Rational Rose 2000. В настоящее время наиболее удобными программи являются Visio 2010, StarUML, Visual Studio 2010.
3.14 Информационные модели объектов и систем
3.14.1 Структура модели управления учебными
заведениями. Цели и задачи управления учебными
заведениями
Структуры управления учебными заведениями с использованием ЭВМ и компьютерных сетей должны разрабатываться с учетом эффективности организационного управления и информационно-методического обеспечения учебного заведения (системы учебных заведений, системы образования), которое обеспечит:
- общедоступность информационно-методических материалов и использования их всеми основными пользователями образовательного процесса;
- систематизацию, централизованное хранение и оперативное использование необходимой информации потенциальных пользователей и предполагаемых заказчиков в форме удобной для каждой категории пользователей;
- автоматизацию процессов ведения, хранения, накопления, анализа информации, а также фиксирование необходимой информации, представление возможности получения необходимых сведений;
- автоматизацию контроля за деятельностью учащихся и возможности индивидуальной работы со средствами автоматизированного обучения с выходом на глобальные (локальные) компьютерные центры для получения учебной информации.
3.13.2 Структура информационной модели учебного заведения
Структура информационной модели системы
«Кафедра компьютерных технологий»
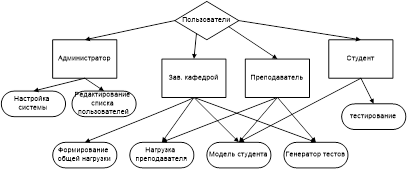
ИС «Кафедра» предназначена для решения следующих задач: планирование учебного процесса заведующим кафедрой, автоматизация процесса анализа учебной деятельности с использованием модели знаний студента и т.д.
Данная информационная система включает в себя следующие подсистемы:
· «Администратор»;
· «Заведующий кафедрой»;
· «Преподаватель»;
· «Студент»;
· «Библиотека»;
· «Дистанционное обучение студентов».
Для разработки модели « Кафедра» необходимо иметь, т.е. разработать следующию документацию в соответствии со стандартом докумнтации информационных систем: техническое задание, алгоритм и текст программы
УТВЕРЖДАЮ
Заведующий кафедрой КТ
__________ .Желтов В.П.
«___»___________ 2012 г.
ИНФОРМАЦИОННАЯ СИСТЕМА
«КАФЕДРА КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ.»:
Техническое задание
Руководитель проекта
Профессор, к.т.н.
_________ Никишев В.К.
«___»__________ 2012 г.
Исполнитель
Студентка ФМФ
ЧГУ им. И.Н Ульянова
________ Иванова В.М..
«___»__________ 2012 г.
1. ВВЕДЕНИЕ
1.1. Наименование программы
Наименование - «Информационная система «Кафедра компьютерных технологий»
1.2. Краткая характеристика области применения программы
Информационная система предназначена для управления кафедрой ВУЗа.
2. ОСНОВАНИЕ ДЛЯ РАЗРАБОТКИ
2.1. Основание для проведения разработки
Основанием для проведения разработки является необходимость повысить эффективность управления кафедрой компьютерных технологий ЧГУ им. И.Н.Ульянова.
2.2. Наименование и условное обозначение темы разработки
Наименование темы разработки - «Разработка ИС: Администратор. Заведующий кафедрой. Преподавателью Студенты. Библиотека.Дистанционное обучение студентов».
3. НАЗНАЧЕНИЕ РАЗРАБОТКИ
3.1. Функциональное назначение программы
Функциональным назначением программы является: администрирование всей информационной системы кафедры , состоящей из модели студента, преподавательского состава, электронных учебников и дистанционного обучения студентов, управления кафедрой заведующим – планирование учебной нагрузки; мониторинг успеваемости со стороны преподавателя; самообучение и самоконтроль с со стороны студента.
3.2. Эксплуатационное назначение программы
Программа должна эксплуатироваться в ЧГУ им. И.Н.Ульянова на кафедре компьютерных технологий для повышения эффективности работы кафедры, а также для других кафедр высших учебных заведений.
4. ТРЕБОВАНИЯ К ПРОГРАММЕ
4.1. Требования к функциональным характеристикам
4.1.1. Требования к составу выполняемых функций
Программа должна обеспечивать возможность выполнения перечисленных ниже функций:
1) Администратора:
а) настройка системы для работы с базой данных;
б) добавление, изменение, удаление данных, необходимых для работы системы (данные о курсах, группах, специальностях, дисциплинах и т.д.);
в) управление списком пользователей и назначение ролей.
2) Заведующего кафедрой:
а) возможность изменения настроек по формированию нагрузки;
б) возможность составления общей учебной нагрузки кафедры;
в) возможность составления индивидуальной нагрузки для каждого преподавателя.
4.Контроль учебного процесса (функции преподавателей):
· Преподаватель несколько раз в семестр записывает в модель знаний текущую успеваемость студентов по всем предметам по каждой изучаемой теме кафедры или автоматически заносит их в базу данных.
· Вводит в систему справочный и учебный материал в опции «Литература» с помощью администратора системы.
· Вводит в систему новые информационные технологии и языки программирования с помощью администратора системы.
5. Автоматизированное рабочее место студента дает возможность обучающемуся:
· Каждый семестр просматривать свою успеваемость по всем предметам кафедры в модели знаний, чтобы быть в курсе своей успеваемости и соответственно направлять свою учебную деятельность в нужном направлении.
· Работать со всеми программами, которые есть в опциях оболочки АРМ «Студент», так как все они предназначены для обучения студента в курсе информатики. Здесь можно выделить два основных раздела: информационные технологии и языки программирования.
· Использовать опцию «Литература» для нахождения необходимого материала по работе в различных средах и программах.
6. Дистанционное обучение студентов
· Просмативать расписание занятий, мероприятия кафедры, просматиривать и при неоходимости копировать как учебный материал, так и литературу по изучаемым дисциплинам кафедры.
· Вводить выполеные работы по дисциплинам, курсовые и дипломные работы.
· Просматиривать успеваемость по всем дисциплинам .
4.2. Условия эксплуатации
4.2.1. Требования к численности и квалификации персонала
Минимальное количество персонала, требуемое для разработки информационной системы: администирование, преподаватель, студент, библиотека, дистанционное обучение. Количество входящих пользователей программы: администратор, преподавательский состав кафедры, и студенты кафедры.
В перечень задач, выполняемых администратором, должны входить:
а) задача поддержания работоспособности сервера базы данных и рабочих станций;
б) задача установки (инсталляции) программы.
Конечный пользователь программы должен обладать практическими навыками работы с графическим пользовательским интерфейсом операционной системы.
4.3. Требования к составу и параметрам технических средств
В состав технических средств должен входить IBM-совместимый персональный компьютер (ПЭВМ), включающий в себя:
а) процессор с тактовой частотой, 1.2 ГГц, не менее;
б) оперативную память объемом, 512 Мб, не менее;
в) жесткий диск объемом 40 Гб, и выше;
г) оптический манипулятор типа «мышь»;
4.4. Требования к информационной и программной совместимости
4.4.1. Требования к исходным кодам и языкам программирования
База данных Microsoft SQL. Исходные коды программы должны быть реализованы на языке Visual С#. В качестве интегрированной среды разработки программы должна быть использована среда Microsoft Visual Studio 2010.
4.4.2. Требования к программным средствам, используемым программой
Системные программные средства, используемые программой, должны быть представлены локализованной версией операционной системы Windows 7 или WindowsХР.
4.4.3. Требования к защите информации и программ
Требования к защите информации и программ не предъявляются.
5. ТРЕБОВАНИЯ К ПРОГРАММНОЙ ДОКУМЕНТАЦИИ
5.1. Предварительный состав программной документации
Состав программной документации должен включать:
1) техническое задание;
3) текст программы;
4) описание программы;
5) программу;
6) пояснительную записку;
9) описание применения;
10) руководство пользователя;
6. СТАДИИ И ЭТАПЫ РАЗРАБОТКИ
6.1. Стадии разработки
Разработка должна быть проведена в три стадии:
1) разработка технического задания (до 1 июля 2011 г.);
2) рабочее проектирование (до 1 января 2012 г.);
3) внедрение (до 1 июня 2012 г.).
6.2. Этапы разработки
На стадии разработки технического задания должен быть выполнен этап разработки, согласования и утверждения настоящего технического задания.
На стадии рабочего проектирования должны быть выполнены перечисленные ниже этапы работ:
1) разработка программы;
2) разработка программной документации;
3) испытания программы.
На стадии внедрения должен быть выполнен этап разработки - подготовка и передача программы.
6.3. Содержание работ по этапам
На этапе разработки технического задания должны быть выполнены перечисленные ниже работы:
1) постановка задачи;
2) определение и уточнение требований к техническим средствам;
3) определение требований к программе;
4) определение стадий, этапов и сроков разработки программы и документации на неё;
5) выбор языков программирования;
6) согласование и утверждение технического задания.
На этапе разработки программы должна быть выполнена работа по программированию и отладке программы.
На этапе разработки программной документации должна быть выполнена разработка программных документов в соответствии с требованиями ГОСТ 19.101-77 и требованиям п. «Предварительный состав программной документации» настоящего технического задания.
На этапе испытаний программы должны быть выполнены перечисленные ниже виды работ:
1) разработка, согласование и утверждение программы и методики испытаний;
2) проведение приемо-сдаточных испытаний;
3) корректировка программы и программной документации по результатам испытаний.
На этапе подготовки и передачи программы должна быть выполнена работа по подготовке и передаче программы и программной документации в эксплуатацию.
6.4. Исполнители
Руководитель разработки:
Ппрофессор, к.т.н. Никишев В.К.
Исполнитель: студентка кафедры компьютерных технологий ЧГУ им. И.Н.Ульянова Иванова.
В целом, задачами информационной модели управления учебным заведением являются:
- оперативная связь с выше и ниже стоящими структурами (передача данных по компьютерной сети с использованием электронной почты);
- получение в короткие сроки необходимой информации о результатах учебной деятельности учебного заведения;
- хранение и использование учебно-методической и научной информации, организационно-учебных документов (учебных планов, рабочих программ);
- систематический ввод и получение информации о текущей успеваемости студентов(учащихся);
- ведение безбумажной канцелярии о кадрах учебного заведения;
- автоматическое обновление информации об успеваемости учащихся, об учебно-методических документах;
- планирование учебного процесса с использованием моделирующих программ (расписание, сетевой график, прохождение учебных дисциплин).
Задачами информационной модели обучения учащихся являются:
- ввод, хранение, обновление и использование в учебном процессе вопросов, задач, упражнений и т.д. для проведения контрольных мероприятий (зачетов, экзаменов, коллоквиумов, контрльных работ, самостоятельных занятий и т.д.);
- формирование модели ученика класса, школы с целью проведения педагогических игр, обучения и т.д.
- получение модели ученика класса учебного заведения на основе статистических данных по результатам тестирования и проведения контрольных мероприятий;
- анализ отрицательных факторов учебной деятельности и пути их устранения;
- прогнозирование результатов учебной деятельности класса, группы, учебного заведения в целом;
- ориентированное планирование дальнейшей деятельности учащихся.
Системы управления базами данных производят выбор следующих видов информации.
СУБД заведующего кафедрой учебного заведения:
- справочник, включающий данные о мероприятиях и планах учебного заведения, классов, учебных групп ;
- ежедневник, предназначенный для мероприятий и личных планов ;
- кадры - для хранения и использования данных о преподавателях (учителях) и других работниках кафедры;
- студенты - для хранения и использования данных об учащихся (включая успеваемость и характеристику каждого учащегося с его обобщенным показателем интеллекта как общего, так и предметного;
- расписание занятий предназначено для получения информации об учебном процессе (где, когда и какие проводятся занятия, кто проводит занятия).
- сбор, анализ, хранение, выборку и вывод информации;
- статистическую обработку;
- создание графиков, диаграмм на основе произведенной обработки полученной информации (от сети);
- прогнозирование и формирование рекомендаций на основе полученных результатов контроля;
- использование локальных и глобальных компьютерных сетей для получения учебно-методической информации.
Некоторые образцы различных моделей кафедры
1. Концептуальная модель студентов кафедры
Кконцептуальная модель данных студентов – пользователей информационной системы представлена , в виде следующих связанных таблиц: «Специальности», «Курсы», «Группы», «Подгруппы», «Студенты», «Пользователи», «Информация о студентах», идентифицирующими столбцами которых являются соответственно: «ID_специальности», «ID_курса», «ID_группы», «ID_подгруппы», «ID_студента», «ID_пользователя». Связь между таблицами «Студенты» и «Пользователи» - один к одному, между остальными таблицами, представленными на диаграмме – один ко многим.
![]()
Физическая модель модели данных (пользователи), соответствующая модели
![]()
2. Концептуальная модель данных нагрузки преподавателей – пользователей информационной системой
![]() Концептуальная модель
данных нагрузки преподавателей – пользователей информационной системы, в виде
следующих связанных таблиц: «Пользователи», «Преподаватели», «Должности»,
«Подгруппы», «Нагрузка преподавателя», идентифицирующими столбцами которых
являются соответственно: «ID_пользователя», «ID_преподавателя»,
«ID_должности». Связь между таблицами «Преподаватели» и
«Пользователи» - один к одному, между остальными таблицами, представленными на
диаграмме: «Должности» и «Преподаватели», «Преподаватели» и «Нагрузка
преподавателя» – один ко многим.
Концептуальная модель
данных нагрузки преподавателей – пользователей информационной системы, в виде
следующих связанных таблиц: «Пользователи», «Преподаватели», «Должности»,
«Подгруппы», «Нагрузка преподавателя», идентифицирующими столбцами которых
являются соответственно: «ID_пользователя», «ID_преподавателя»,
«ID_должности». Связь между таблицами «Преподаватели» и
«Пользователи» - один к одному, между остальными таблицами, представленными на
диаграмме: «Должности» и «Преподаватели», «Преподаватели» и «Нагрузка
преподавателя» – один ко многим.
4. физическая модель модели данных (нагрузка преподавателя),
![]()
3.13.3 Структура управления высшим учебным заведением
В основе построения структуры управления высшим учебным заведением должны быть заложены принципы информатизации образования, которые обеспечивали бы гибкость и автоматизацию управления, систематический контроль за результатом учебного процесса, прогнозирование и коррекцию методов и форм управления учебным процессом, получение информации в различных областях знаний по компьютерным сетям, возможность дистанционного обучения студентов и т.д.
Структура может включать следующие разделы меню БД.
1. Ректор.
1.1. Справочник -консультант.
1.2. Электронный журнал мероприятий.
1.3. Графики расписаний.
1.4. Планирующие документы.
1.5. БД “Кадры”.
2. Учебный отдел (проректор по учебной части).
2.1. Справочник-консультант.
2.2. Электронный журнал мероприятий.
2.3. График расписаний всех факультетов.
2.4. Планирующие документы (учебные планы и программы).
2.5. БД “Кадры” (преподаватели и студенты).
2.6. БД “Успеваемость студентов института”.
2.7. БД “Тесты”.
2.8. БД “Модель института”.
3. Научно-исследовательский отдел (проректор по научной работе).
3.1. Справочник-консультант.
3.2. Электронный журнал мероприятий.
3.3. Планирующие документы.
3.4. БД “Научные кадры”.
4. Хозяйственный отдел.
4.1. Справочник -консультант.
4.2. Электронный журнал мероприятий.
4.3. БД “Бухгалтерия”.
4.4. БД “Материальное имущество”.
5. Библиотека (заведующий библиотекой).
5.1. Справочник-консультант.
5.2. Электронный журнал “Учет выдачи литературы”.
5.3. Электронный каталог “Новые поступления”.
6. Факультеты (декан).
6.1. Справочник-консультант.
6.2. Электронный журнал мероприятий.
6.3. БД “Кадры факультета”.
6.4. БД “Успеваемость студентов факультета”.
6.5. График успеваемости.
6.6. Планируемые документы.
6.7. БД “Модель факультета”.
7. Кафедры (заведующий кафедрой).
7.1. Справочник-консультант.
7.2. Электронный журнал мероприятий.
7.3. БД “Кафедра”.
7.4. БД “Успеваемость студентов по дисциплинам каф”.
7.5. БД “Учебно-методическое обеспечение.
7.6. График расписаний.
7.7. Планируемые документы.
8. Лаборатории (заведующий лабораторией).
8.1. Справочник-консультант.
8.2. Электронный журнал мероприятий.
8.3. БД “Кафедра”.
8.4. БД “Материальное обеспечение”
.8.5. График расписаний.
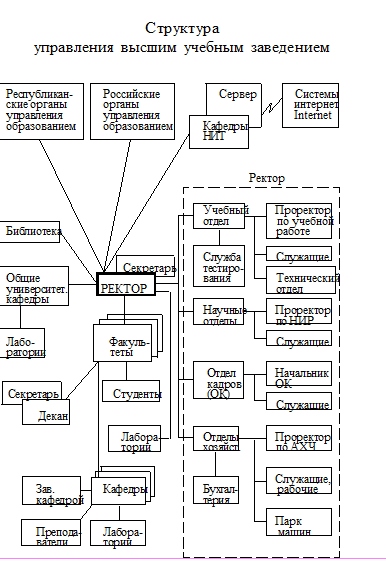
3.14 Модели знаний студентов по дисциплинам кафедры
компьютерных технологий
Процесс обучения в высшем учебном заведении является сложным динамическим процессом и зависит от многих факторов, среди которых можно выделить следующие: профессионализм преподавательского состава, информационный фонд учебников и различных пособий, представленных как в обычной, т. е. печатной форме, так и в электронной, организация процесса обучения со стороны ректората и деканата, потенциальные возможности студентов, полученные в школе, и многие другие. Объективность обучения анализируется по данным контроля знаний в виде оценок, выставленных на экзаменах и других контрольных мероприятиях. С целью получения объективных данных по успеваемости студентов предлагается информационная система модели знаний студента ( студентов), которая представлена следующими моделями: модель знаний предмета или группы предметов, модель знаний студента по предмету или группе предметов по кафедре и в конечном счете модель знаний студента по специальности. За основу построения модели знаний берется учебная программа. Модель знаний состоит из подмодулей, в которые включаются базовые, как теоретические, так и практические навыки работ по всем разделам дисциплины. Информационная система, в которой реализуется модель знаний, в общем случае должна включать: компьютеры, соединенные в локальную или корпоративную сеть, программное обеспечение, с помощью которого формируются модели знаний (тестирующие, контролирующие, автоматизированные системы контроля и обучения). В соответствии с государственным стандартом высшего образования по дисциплинам кафедры компьютерных технологий ( специальность программная инженерия) можно предложить следующие разделы, с помощью которых формируются модели знаний.
![]() Для формирования модели
знаний студентов необходимо иметь темы всех предметов учебного плана. В
качестве примера приводится подмодель знаний студентов по программированию. (
на каждой кафедре имеются свои рабочие программы по программированию, в которую
входят следующие дисциплины: информатика и программирование, основы информатики
и объектно-ориентированное программирование. В качестве языков программирования
используются TP, TC,DELPHI, VB, VC++ и другие варианты)
Для формирования модели
знаний студентов необходимо иметь темы всех предметов учебного плана. В
качестве примера приводится подмодель знаний студентов по программированию. (
на каждой кафедре имеются свои рабочие программы по программированию, в которую
входят следующие дисциплины: информатика и программирование, основы информатики
и объектно-ориентированное программирование. В качестве языков программирования
используются TP, TC,DELPHI, VB, VC++ и другие варианты)
В данной подмодели приводится авторский вариант изучения основ программирования, в который входят: базовые основы программирования, которые могут давать или в дисциплине информатика и программирования или на факультативных занятиях, цель которых состоит в том, чтобы уровнять знания по программированию, полученные в школе. А метод обучения предлагается тоже авторский на основе параллельного изучения языков программирования. Дело в том, что студенты 1-го курса обучались в школе по программированию с использованием языков программирования TP – 80%, QBASIC-5%, а остальные ничего не изучали. Анализ знаний всех студентоы показывает, что их уровень, очень разный, а практически поверхностный. В настоящее время в практике обучения студентов разработано много современных языков програаммирования. Если готовить студентов на современном уровне, то надо, чтобы студенты знали действительно те языки программирования, на котрых работают современные программисты. Это языки программирования на платфоме . NET ( VC++,VC#, VB.NET, F.NET). Речь идет о классических языках программировния, которые применяются для изучения основ программирования. Что касается языков программирования ( тоже современных, как PHP, PHIZON, и другие ), то они изучаются в других дисциплинах. Такой подход необходим для специальностей, связанных с компьютерными технологиями. Обычно некоторые преподаватели и особенно руководители говорят, что хватит и одного, а в будущем сами студенты могут доучить то, что необходимо. Можно давать параллельно 2 или 3 языка, но на основе одного в прошлом уже изученного и давать в сравнении с другими, но близкими языками. Да и оценивать студентов можно в обязательном порядке по одному языку, любому из даваемых на занятиях, а для отлично успеваемых почему и не 2 или 3 языка программирования. Сложность материала определяется не по уровню знаний плохих студентов, по уровню знаний «хорошистов». Только в таком варианте можно ожидать таких результатов, которые включают знания , полученные студентами по основам программирования. А уж где они будут использовать, то все завасит от от той фирмы или предприятия, куда они хотят устроиться.
Темы базового курса по программироанию
Введение. . Основы алгоритмизации – 2 час.
Программирование: сущность и назначение. Предмет дисциплины и ее задачи.
Структура, содержание дисциплины, ее связь с другими дисциплинами учебного плана специальности. Этапы решения задач на ЭВМ. Понятие алгоритма, свойства алгоритма. Данные и величины. Запись алгоритма в виде блок-схемы. Операторный и условный блоки.
2. Введение в языки программирования.
История и классификация языков программирования. Поколения ЭВМ. Компилятор и интерпретатор. Структура и способы описания языков программирования высокого уровня. Общая структура языков программирования высокого уровня. Основные составляющие языка программирования.
3. Структура программ, типы данных на языках С++, Паскаль
Структура программы на Паскале. Элементы языка: алфавит, идентификаторы, комментарии. Этапы обработки программы на Турбо Паскале. Компоненты системы программирования Турбо Паскаль. Типы данных. Основные стандартные типы данных: целый, вещественный, логический, символьный. Порядковые типы. Идентификаторы типов. Описания переменных. Константы. Типы пользователя. Перечисляемый и интервальный типы.
4. Арифметические операции, функции, выражения. на языках С++, Паскаль
Арифметические операции, функции, выражения. Арифметические типы данных. Арифметические операции, выражения. Арифметический оператор присваивания.
Ввод с клавиатуры и вывод на экран. Ввод и вывод данных. Устройства ввода-вывода. Форматы вывода.
5. Циклы и условные операторы на языках С++, Паскаль
Ветвления и циклы в алгоритмах. Условный оператор. Оператор выбора Программирование циклов. Цикл с предусловием. Цикл с постусловием. Цикл с параметром. Оператор continue. Метки и оператор goto.
6. Массивы. на языках С++, Паскаль
Табличные данные и массивы. Одномерные и многомерные массивы. Ввод и вывод массивов. Основные операции с массивами. Поиск и сортировки
7. Специальные типы данных, функции на языках С++, Паскаль
Для с++.Указатели . Описание указателей. Операции над указателями. Использование указателей для передачи параметров функции. Указатели и массивы.
Для языка Паскаль Процедуры
8. Графика. Основные понятия на языках С++, Паскаль
Общие понятия о графике. Установка графических режимов. Графический режим экрана
9. Основные графические операторы и функции на языках С++, Паскаль
Основные графические функции, процедуры и операторы. Цвет фона и цвет рисунка. Графические координаты. Графический курсор. Графические примитивы.
10. Простейшие графические программы.
Построение простейших графических фигур. Вычисление площадей методом Монте-Карло, вычисление интегралов
11. Построения графиков функций
Системы координат. Масштабы. Построение графиков функций.
11. Файлы.
Запись в файл и чтение из файла. Внешние файлы. Текстовые файлы.
12. Комбинированный тип данных .
Записи, структуры и объединения Организация данных. Работа с файлами
Темы по дисциплине « Основы программирования»
1. Введение. Основы алгоритмизации. – 2 час.
Программирование: сущность и назначение.. Предмет дисциплины и ее задачи.
Структура, содержание дисциплины, ее связь с другими дисциплинами учебного плана специальности. Этапы решения задач на ЭВМ. Понятие алгоритма, свойства алгоритма. Данные и величины. Запись алгоритма в виде блок-схемы.
2. Введение в современные платформы и языки программирования
История создания вычислительных платформ NET для современных языков программирования. Цели и задачи. Структура платформ. Работа.
3. Характеристика современных языков программирования
консольный вариант
Характеристика современных языков программирования на платформе NET
VC++.net, VC#.NET, VB.NET
4. Арифметические операции, функции, выражения
Структура программ в консольном варианте для языков программирования
VC++. NET ( VC#.NET, VB.NET). Основные арифметические операции операции
5. Циклы и условные операторы
Операторы условия и и циклов. Программирование условий и циклов. Цикл с предусловием. Цикл с постусловием. Цикл с параметром.
6. Массивы
Массивы. на языках VC++. NET ( VC#.NET, VB.NET). Табличные данные и массивы. Одномерные и многомерные массивы. Ввод и вывод массивов. Основные операции с массивами. Поиск и сортировки
7. Графика
Основные понятия на языках VC++. NET ( VC#.NET, VB.NET). Общие понятия о графике. Установка графических режимов. Графический режим экрана
Основные графические операторы и функции на языках VC++. NET ( VC#.NET, VB.NET).
8. Характеристика современных визуальных языков программирования
( Window вариант )
Характеристика и основные компоненты языков программирования VC++. NET ( VC#.NET, VB.NET). Основные объекты приложений. Структура проектов.
9. Элементы визуального управления (компоненты )
Основные компоненты языков визуального программирования (форма, метки, кнопки, текстовые окна, списки, переключатели, флажки, диалоговые окна.
10. Функции, операции и выражения
Сравнительная характеристика арифметических операций и выражений для языков программирования VC++. NET ( VC#.NET, VB.NET).
11. Линейные программы
Первые программы. Структура. Вычисление арифметических выражений
12. Программирование ветвлений и циклов
13. Функции
15.Символы
1 В скобках указаны: общее количество часов – количество лекций
Концептуальная UML модель знаний студентов по кафедре компьютерные технологии иммет вид, которая выполнена с помощью программы Microsoft Visio
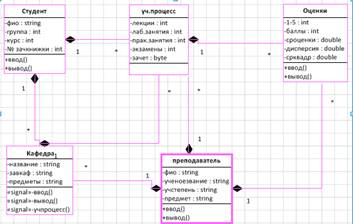
Модель может бвть реализована в средах: VisualStudio 2010( vc#,vc++,vb.net), баз данных ( SQL, Access), Excel и т. д.
Общий вид в среде VisualStudio2010 vc#,
![]()
![]() Модель знаний студентов
в среде Excel
Модель знаний студентов
в среде Excel
Общая индивидуальная модель знаний студентов
по дисциплинам кафедры
–
![]() .
.
Групповая модель знаний для конкретной дисциплины
Динамическая групповая модель знаний студентов по дисциплинам кафедры
Такие модели знаний хранятся
в банке данных кафедры, факультета, университета или могут выдаваться студентам
после окончания университета. В течение обучения динамические модели знаний
могут быть доступны студентам для оценки успеваемости по конкретной дисциплине
или теме. Модели знаний являются составной частью информационной системы
«Кафедра» или «Факультет». Доступность для каждого студента реализуется с
помощью автоматизированных рабочих мест (АРМ) студентов.Для получения
обобщенных моделей знаний необходимо использовать статистические зависимости
регрессионного и корреляционного анализа, общие характеристики статистических
данных (дисперсия, среднее квадратичное отклонение и т. д.) результатов учебы
студентов для конкретного преподавателя кафедры. С целью исследования
эффективности учебного процесса, проведения вычислительных экспериментов с
помощью моделирования на ЭВМ необходимо иметь обобщенные информационные модели
знаний 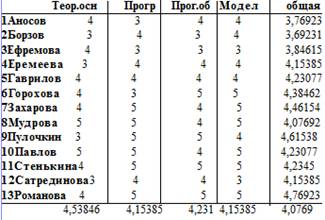
учащихся группы, университета. Статистическая модель фиксирует отдельные параметры (характеристики) учебного процесса. Для объективного анализа состояния учебного процесса в учебных заведениях необходимо знать и учитывать различные факторы, влияющие на процесс обучения в целом. Такими факторами могут быть: реальная успеваемость студентов (курса, факультета, университета), представленная в виде математических статистических показателей состояния учебы за определенный период времени; отсутствие студентов на занятиях в силу определенных причин, которое оказывает влияние на успеваемость студентов, так как неаттестованные по каким - либо темам студенты имеют неудовлетворительные оценки; информационное обеспечение учебного процесса (плакаты, слайды, видеофильмы, программы для ЭВМ и т. д.); качество преподавания, объективность заданий и выставления оценок в соответствии с принятыми критериями; взаимоотношения вне университета, участие в олимпиадах, конкурсах и т.д. Для реализации приведенных факторов предлагается вариант обобщенной информационной модели знаний, которая включает различные оценки как отдельных студентов, так и факультета и университета в целом. Модель, включающая фактические оценки за определенный отрезок времени, характеризует общий уровень образования студентов в университете и может быть представлена как частичная модель знаний, которая является составной частью информационной модели знаний учебного заведения.
Одной из важных составляющих обобщенной модели учебного процесса является модель знаний студентов, группы, курса, факультета и университета в целом.
Информационная модель знаний студентов характеризуется следующими параметрами:
Средняя общая индивидуальная оценка
![]() где mi- оценки за
период , N- количество оценок за период T.
где mi- оценки за
период , N- количество оценок за период T.
Средняя предметная индивидуальная оценка
![]() где mpi- оценки по i-му
предмету за период T, NP- количество оценок по предмету за период T.
где mpi- оценки по i-му
предмету за период T, NP- количество оценок по предмету за период T.
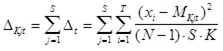 где N -
количество оценок на курсе за период T;
где N -
количество оценок на курсе за период T;
NP - количество оценок на курсе по предмету за период Т ;
S- количество студентов;
xi- оценка (1, 2, 3, 4, 5);
K- количество курсов;
P- количество предметов.
Прогнозируемая вероятность оценки курса
![]()
Обобщенная интегральная оценка курса
![]()
Обобщенная интегральная оценка факультет
![]()
Среднее отклонение оценок как общих, так и предметных
![]()
![]()
Cреднее отклонение от максимальной (отличной) оценки
![]()
![]()
Прогнозируемая вероятность оценки учащихся
![]()
где Nm- количество положительных оценок,
Ni- количество всех оценок за период Т.
Обобщенная интегральная оценка учащихся
Информационная интегральная оценка учащихся
![]()
Информационная модель знаний курса (факультета или университета).
Средняя оценка курса
![]()
Средняя оценка факультета (университета
![]()
![]()
Средняя предметная оценка факультета
![]()
Средняя оценка университета может быть составлена из суммы предметных оценок факультетов.
Среднее отклонение от максимальной оценки
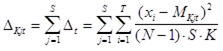 где
где
N - количество оценок на курсе за период T;
NP - количество оценок на курсе по предмету за период Т ;
S- количество студентов;
xi- оценка (1, 2, 3, 4, 5);
K- количество курсов;
P- количество предметов.
Прогнозируемая вероятность оценки курса
![]()
Обобщенная интегральная оценка курса(факультета)
![]()
Таким образом, предметная динамическая модель знаний студентов курса или факультета позволит получить следующие характеристики учебного процесса:
- качество обучения в целом по университету, факультету, курсу и успеваемость отдельных студентов;
-стабильность обучения по отдельным предметам, темам и дисциплинам;
- прогнозирование результатов обучения в предстоящем семестре;
-систематическое уточнение модели знаний студентов с использованием тестовых программ;
- разработка индивидуальных вопросов и задач на основе моделей знаний студентов;
- сравнительные оценки состояния учебного процесса как на факультете, так и по университету в целом.
![]() Коэффициент выполнения
теста (задания) каждым студентом ( учащимся) будет определяться
формулой где
Коэффициент выполнения
теста (задания) каждым студентом ( учащимся) будет определяться
формулой где
pi – значение успешности выполнения теста i - м студентом;
qj - количество баллов за j -е задание;
n - количнство заданий в тесте;
max - максимальная оценка за выполение задания.
Степень решаемости каждого задания может определяться выражением
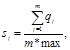
Где m - количество студентов.
Коэффициент трудности для каждого задания вычисляется по следующей формуле
![]()
Коэффициент трудности будет отражать реальные показатели при большом количестве студентов, которые участвуют в решении теста (задания).
Знания студентов можно определить по общему показателю с учетом степени решаемости и трудности задания.
3.15 Имитационное моделирование
При решении разнообразных вопросов в различных сферах деятельности, в частности задач управления экономикой, находят все большее распространение так называемые имитационные модели. Имитационные модели связаны обычно с многократным воспроизведением особенностей системы и окружающей ее среды, с выбором случайного, но реально возможного соотношения анализируемых параметров без фактического воспроизведения реальной системы
Имитационное моделирование может осуществляться в различных формах физической (например, испытание модели геометрического подобия — макета самолета в аэродинамической трубе, военные учения, проведение экономического эксперимента на предприятии), различных игр ненатурные военные, деловые и др , но чаще оно принимает форму машинной имитации, то есть воспроизведения различных проблем на ЭВМ (ЭВМ могут применяться и при реализации других видов имитаций)
К числу методов машинной имитации относится и рассмотренный выше метод статистических испытаний, если он основан на применении ЭВМ. Машинная имитационная модель — это отображение на ЭВМ численных характеристик исследуемого процесса во взаимосвязанной форме Подобно математическим моделям они основаны на символическом описании конкретного процесса, и в этом их существенное сходство. Однако если в математической модели можно получить решение, выраженное аналитически (то есть безотносительно к конкретным значениям численных характеристик), то имитационная модель дает возможность лишь «проигрывать» выбираемые случайно или целенаправленно различные решения, определяемые набором численных характеристик Это позволяет предсказывать и анализировать динамику возможных ситуаций в будущем и тем самым оценивать последствия проверяемых стратегий с целью нахождения наилучшей стратегии.
Другим важным свойством имитационных моделей является «анализ чувствительности» решений на их основе, то есть проверки устойчивости выходных характеристик решения по отношению к варьированию исходных предпосылок
Имитационная модель помогает выявить, если и не наилучшее решение, то «хорошее» для широкого набора условий, которые могут изменяться под влиянием не контролируемых внешних факторов
Машинная имитация основана на многократной машинной или человеко-машинной имитации моделируемой системы в чрезвычайно ускоренном масштабе времени с использованием случайных элементов и с последующей обработкой полученных статистических результатов Последнее дает возможность оценить показатели системы как средние значения по данным большого количества реализации (имитаций) работы системы Это позволяет целенаправленно воздействовать на систему, управлять происходящими в ней процессами
Машинная имитация, как правило, используется в тех случаях, когда аналитическое решение проблемы невозможно (при широком истолковании термина «имитация» в состав имитационных моделей входят и любые аналитические зависимости), а непосредственное экспериментирование на реальной системе или на физической ее модели по тем или иным причинам нецелесообразно моделирования при системном анализе социально-экономических систем
1. Путем сравнения экономических показателей определение из нескольких возможных форм организации системы наилучшей в смысле достижения целей, поставленных перед нею. Для этого воспроизводится поведение различных вариантов организационной структуры и сравниваются такие экономические показатели, как прибыль, рентабельность, фондоотдача и ряд других.
2 На основе фактических данных максимально близкое воспроизведение поведения систем и их звеньев, что служит базой для теоретического осмысливания поведения систем, анализа законов их функционирования, а также для прогнозирования. Имитация дает возможность в чрезвычайно уплотненном масштабе времени «проиграть» последствия каждого решения для определенных моментов времени в будущем, получить материал о наиболее вероятном состоянии поведения системы в дальнейшем. о состояниях, которые необходимо избежать.
3. Оценка на основе воспроизведения наиболее существенных черт системы и целей ее развития, стратегий ее деятельности в различных областях (производство, финансы, сбыт, ценообразование, освоение новых продуктов и т. п.), а также способов и методов управления системами
4 Обучение специалистов по управлению, развитие у них навыков принятия решений.
При всех достоинствах метода имитации нужно отметить его большую сложность и трудоемкость, а также тот факт, что исходные данные могут быть результатом эмпирических субъективных оценок, а не математических расчетов. Метод имитации следует применять только когда накоплено и отлажено значительное количество моделей экономических объектов и явлений, которые могут изменяться в широких пределах во времени по мере накопления знаний о реальной системе; проанализированы связи между ними; собран значительный статистический материал. Кроме того, использование данного метода предполагает высокий уровень искусства программирования.
Распространенным видом имитации являются игры, включающие исполнение определенных ролей их участниками. Это представляет большую ценность в том случае, когда для рассмотрения различных аспектов проблем необходимо привлекать экспертов различных специальностей. Здесь, исходя из структуры игры, то есть по существу из модели, ее участникам выдаются искусственные, имитированные данные об обстановке, в которой они совместно и одновременно выполняют различные эксперименты, получая по обратной связи сведения, необходимые для предсказания развития событий в рамках содержания игры, а следовательно, косвенно и в действительной обстановке
С большими трудностями системные аналитики сталкиваются при моделировании социально-экономических процессов.
Пример модели имитационного моделирования управления проедприятием. Деловая игра « Дельта»
Глобальной целью предприятия является получение максимальной прибыли. Она может быть достигнута за счет: маркетинговой, производственной и финансовой деятельности.Целью маркетинга - определить, в чем нуждается рынок, а затем как можно выгодно сбыть максимум этой произведенной продукции. Конечной целью производственной деятельности является снижение себестоимости продукции. Цели финансовой политики - поддерживать финансы предприятия на оптимальной уровне. В рыночной экономике цена определяется на основе спроса и предложения. Прибыль предприятия определяется зависимостью
П = Об(х) - И(х), где
П - прибыль; Об(х) - оборот как функция объема сбыта;
И(х) - издержки как функция объема производства.
О(х)=Ц*х, Ц - цена, х - объем сбыта.Максимум прибыли можно получить путем дифференцирования выражения
П = Об(х) - И(х), т.е. Об(x)/dx=И(х)/dx.
Оптимальный объем выпуска продукции находится в точке пересеченя графиков функции предельного оборота и предельных издержек.
![]()
![]()
![]()
![]()
3.16 Структурно – последовательное моделирование
В настоящее время в учебном процессе кафедр всё большее внимание уделяется вопросам моделирования. Моделирование позволяет реализовать активную форму познания, изучение объектов, явлений или процессов. С помощью моделирования можно вводить на занятиях исследовательские формы обучения, то есть получение результатов на основе проведенных вычислительных экспериментах на ЭВМ. Само понятие моделирование обозначает исследование процессов, явлений и объектов с помощью моделей. Формами проведения моделирования могут быть также: простое моделирование, интегрированное моделирование, программное моделирование и структурное моделирование. Под простым моделированием следует понимать такую форму, в которой последовательно выполняются все этапы моделирования: постановка задачи моделирования, разработка или выбор математической или информационной модели, выбор метода моделирования, разработка алгоритма и программы, набор и отладка программы, дальнейший анализ результатов эксперимента моделирования. При интегрированной форме моделирования используют интегрированные оболочки наподобие оболочек языков программирования (Delhi, Vasial Basic). Каждая интегрированная оболочка является специализированной для каждого научного направления, но в общем интегрированная оболочка должна включать: уравнения, исходные данные, метод решения, результаты моделирования. Интегрированная оболочка позволяет выбирать из предлагаемых блоков такие уравнения, методы, которые необходимы для моделирования конкретной задачи. Под программным моделированием следует понимать такое моделирование, которое использует современные программы как MathCad, MathLab, Maple и другие программы. Такое моделирование основано на умение вводить различные виды уравнений в специальные программы и их решать с использованием удобного графического интерфейса. Под структурной формой следует понимать выбор структур, систем, объектов, явлений или процессов, а также систем, которые управляют, прогнозируют, исследуют или анализируют объекты или явления. В качестве структур моделирования могут быть: объекты (явления, системы или процессы), системы управления объектами, прогнозированием, анализ), структуры внешних условий , структуры проведения эксперимента, структуры получения результатов эксперимента и структуры процесса моделирования. Такая форма проведения моделирования позволяет:
1. Облегчить сам процесс моделирования, то есть упрощает все этапы моделирования;
2. Выбрать такие условия эксперимента и такие формы предоставления результатов моделирования, которые бы облегчили сам процесс анализа результатов моделирования.
3. Систематизировать процесс моделирования объектов(система, явление, процесс) и повысить эффективность проведения эксперимента при различном подборе структур, которые оказывают влияние на процесс моделирования.
4. Упростить исследование систем при различных внешних и внутренних условиях системы, то есть возможно выбрать структуры без знаний математических особенностей описания различных процессов или явлений. В качестве примеров можно привести моделирование объектов, основанных на динамики тел, брошенных под углом к горизонту, задача, которая известна многим и к которым можно отнести моделирование движения различных летательных и плавательным аппаратов.
1. Объект может быть описан следующими
структурами:
1.1 Дифференциальными уравнениями движения, которые в общем виде представляются следующими системами уравнений:
при движении в 2-х мерном пространстве
![]()
![]() при движении в 3 -х мерном
пространстве
при движении в 3 -х мерном
пространстве
![]()
1.2 алгебраическими уравнениями движения
![]()
2 .
Внешние условия могут быть представлены следующими структурами:
![]()
![]()
![]()
Системы управления могут быть представлены такими закономи управления :
![]()
![]()
![]() 4 . Структуры проведения
моделирования ( решение систем дифференциальных уравнений ) могут быть
использованы
4 . Структуры проведения
моделирования ( решение систем дифференциальных уравнений ) могут быть
использованы
1. Метод Эйлера,
2. Метод Рунге-Кутта,
3. Метод Рунге-Кутта-Мерсона,
4. Метод Рунге-Кутта с переменными коэффициентами.
5 . Структуры результатов моделирования:
1 . Таблицы, графики, спрайты, графы;
2 . Зависимости:
![]()
![]() .
.
Структуры проведения эксперимента:
![]()
.
Структура моделирующей системы:
![]()
4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ОБЪЕКТОВ, СИСТЕМ, ЯВЛЕНИЙ И ПРОЦЕССОВ
4.1. Методы решения дифференциальных уравнений
4.1.1. Метод Эйлера
![]() Дифференциальное уравнение
представляется в канонической форме Коши:
Дифференциальное уравнение
представляется в канонической форме Коши:
y = f(x,y), при начальных условиях
Решение основано на разложении функции y(x) в ряд Тейлора
![]()
![]()
В точке при малых значениях h можно
ограничиться двумя членами ряда, тогда
![]()
,
![]()
![]()
где )- бесконечно малая величина порядка .
![]() Заменим
производную значением f (x,y), в результате получим:
Заменим
производную значением f (x,y), в результате получим:
![]()
![]() или
или
,
где , k=1,2,...n, h - шаг вычислений.
![]()
![]() Метод обладает погрешностью
за счет отбрасывания членов ряда Тейлора, пропорциональных h во второй степени.
Для оценки погрешности можно воспользоваться первой формулой Рунге:
Метод обладает погрешностью
за счет отбрасывания членов ряда Тейлора, пропорциональных h во второй степени.
Для оценки погрешности можно воспользоваться первой формулой Рунге:
Где yn(x) - приближенное решение дифференциального уравнения в точках с шагом h;
Ykn(x) - приближенное решение уравнения с шагом kh;
p - порядок метода.
С учетом погрешности метод Эйлера можно представить зависимостью:
yk+1=yk + ∆yk + R. .
Для систем дифференциальных уравнений формула Эйлера имеет вид:
y1,k+1 = y1,k + hf(x1,k;y1,k).
Исходные дифференциальные уравнения приводятся к системе уравнений 1-х порядков.
Например:
d2y/dt2 + 2dy/dt + 3y = 6x
Обозначим: Система уравнений первого порядка:
![]()
С учетом записи начальных и конечных значений y в массивы системы уравнений будут иметь вид:
y(1) = y(2),
y(2) = 6x - 2y(2) - 3y(1).
Алгоритм
1. Ввод: n - порядок системы,
![]()
![]() -начальные условия,
-начальные условия,
- шаг и конечное значение интегрирования.
2. Запись правых частей уравнений в программу.
3.Вычисление значений y1,k+1.
4. Расчет ошибки R и уточненное значение y1,k+1 .
5. Проверка на конечное значение xk. Если x1 < xk,
![]() то печать значений
то печать значений
и переход к п.3, иначе - к п.6.
![]() 6. Конец.
6. Конец.
4.1.2. Метод Рунге-Кутта четвертого порядка
Данный метод использует зависимость ряда Тейлора, в котором учитываются члены разложения до четвертой степени включительно. Вычислительная процедура основана на следующих уравнениях:
![]()
где
![]()
Погрешность решений дифференциальных уравнений можно оценить по зависимости
R0 = [yn(x) - y2n(x)]/15
В качестве примера рассмотрим приведение уравнений типа .. . y + p(y 2-1)y+y = 0 к форме Коши. Данное уравнение является математической моделью автоколебательных механических и электрических систем. Для малых (р<<1) и больших (p>>1) значений параметров в теории колебаний развиты приближенные методы аналитического решения уравнений Ван дер Поля. Для промежуточных значений Р уравнение приходится решать численным методом.
Для приведения уравнения к форме Коши введем обозначение:
y1 = y,
y2 = dy/dx.
Уравнения для записи в программу с учетом введенных изменений будут иметь следующий вид:
dy1/dx = y2;
dy2/dx = p(1-y12)y2-y1 (4.1.2.)
Для разработки алгоритма используется таблица (4_1_2.), в которой приводятся этапы вычисления правых частей дифференциальных уравнений.
АЛГОРИТМ
1. Ввод исходных данных: n, x0, xk, yi0(n).
2. Запись правых частей уравнений fi(x,yi).
3. Организация цикла от x0 до xk.
4. Организация цикла от j=1 до 4.
5. Расчет коэффициентов веса
6. Организация цикла от i до n, вычисление правых частей f(i)(x,y(i)) и коэффициентов kij.
7. Вычисление y(ij).
8. Вычисление y(i,x+1).
9. Вывод на экран значений y(i,x+h), x.
10. Формирование аргументов для последующих вычислений y(i,x) = y(i,x+h).
11. Если x = x(k),то выход на конец, иначе - повторение пункта 4.
4.1.3 Метод Рунге-Кутта-Мерсона
Данный метод позволяет оценивать погрешность вычисления на каждом шаге и при определенных условиях изменять значение шага. В основе метода положены следующие преобразования: y(x0+h)=y0 + (k4+k5)/2 + O(h^5), где k1 = hзf(x0,y0), hз=h/3, k2 = hзf(x0+hз, y0+k1), k3 = hзf(x0+hз, y0+(k1+k2)/2), k4 = k1 + 4*hзf(x0+h/2, y0+0.375(k1+k3)), k5 = hзf(x0+h, y0+1.5(k4-k3)), hз - заданное значение шага (начальное). Погрешность определяется в соответствии с формулой:
10R = 2k4-3k3-k5
Если ¦R¦> E, шаг h уменьшается в 2 раза и вычисления повторяются с точки (x0,y0).
Если выполняется условие 32¦R¦< E, то шаг h удваивается (¦R¦абсолютное значение величины R).
АЛГОРИТМ
1. Ввод исходных данных
n, x0, xk, y0(n), hз, E
2. Запись правых частей уравнений f(i)(x,y(i)).
3. Организация цикла от x0 до x(k).
4. Организация цикла по j от
1 до 5. ![]()
5. Организация цикла по i от 1 до n.
6. Вычисление правых частей f(i)(x,y).
7. Расчет коэффициентов k(ij).
8. Вычисление R.
9. Если 32¦R¦< E, то h=2h и переход к п.4,
иначе- переход к п.15.
10. Вычисление y(x0+h)
11. Формирование аргументов для последующего выражения y(i,x) = y(i,x+h).
12. Вывод на печать y(i),x.
13. Если x=x(k), то выход на конец программы.
14. Переход к п. 4. h Если ¦R¦> E, то h = - и переход к п.4, иначе - к п.10. 2 Блок-схема алгоритма представлена на рис.Bs4_1_3.
![]()
4.1.4. Метод решения дифференциальных уравнений с переменными коэффициентами
Дифференциальные уравнения с переменными коэффициентами обычно описывают динамику полета летательных аппаратов и других движущихся объектов с переменными параметрами. Для решения таких уравнений могут быть использованы рассмотренные методы решения обыкновенных дифференциальных уравнений. Общий вид уравнений представляется выражением
.. . a2(t) x(t) + a1(t) x(t) + a0(t) x(t) = M(t) ,
где коэффициенты a2(t), a1(t), a0(t) и M(t) обычно задаются в табличной форме для дискретных интервалов времени. В связи с этим возникает необходимость интерполирования исходных коэффициентов. Суть интерполирования состоит в следующем: если известна функция f(x) в (n+1) точках (x0, x1, x2 ... x(n)), то можно построить многочлен
Z(n)(x) = a0 + a1*x + ... + a(n)x(n)
таким образом, что
f(x(j)) = g(n)(x(j)), j = 0,1,... n .
Представим Z(n)(x) в виде линейной комбинации многочленов n-ой степени
![]()
Tаким образом, имеем
![]()
Интерполяционный многочлен Лагранжа для функции, заданной таблично, например,
x = 1 , 2 , 3
f(x) = 12 , 4 , 6
будет иметь вид:
![]()
Блок-схема алгоритма решения дифференциальных уравнений с переменными коэффициентами представлена на рисунке
![]()
M - количество переменных коэффициентов
Т- количество точек(аргументов и значений коэфф.)
4.2 Представления систем на основе метода пространства состояния
В основе метода пространства состояния систем все пере- менные, характеризующие систему, можно разделить на три группы: входные переменные или входные воздействия (gj), выходные переменные, характеризующие реакцию сис- темы на входные воздействия (yi), и переменные состояния (координаты), характеризующие динамическое поведение исследуемой системы (xn). Обычно переменные состояния объекта относятся к так называемому «черному ящику», так как описать точно состояние систем очень трудно и поэтому при исследовании систем используют модель объ- екта, т.е. упрощенное описание состояния объекта.
Обычно совокупность переменных представляется многомерными векторами. Вектор входа g=[g1, g2, g3,…gj ], вектор выхода y=[ y1, y2, y3,...yi ] и вектор состояния x=[x1, x2, x3,…xn ]. Совокупность состояния систем образует пространство входа, выхода и состояния. В любой момент времени состояние системы является функцией начального состояния x(t)=F[x(t0),g(t0,t)], а вектор выхода представляет ся следующей функцией: y(t)=x[x(t0),g(t0,t)]. Приведенные уравнения являются уравнениями состояния систем. Для систем, которые описываются дифференциальными уравне- ниями, уравнения состояния систем могут быть записаны в следующей форме:
x(t) = A(t) x(t)+B(t) g(t);
y(t) = C(t) x(t)+D(t) g(t), где
A(t) – матрица коэффициентов, определяющая характер переходной матрицы состояния;
В(t) – матрица управления;
С(t) – матрица выхода;
D(t) – матрица обхода системы.
Если дифференциальное уравнение задано в виде
![]()
![]() то исходное уравнение можно
представить системой уравнений с учетом обозначений x1 =y; x2 =dy/dt
то исходное уравнение можно
представить системой уравнений с учетом обозначений x1 =y; x2 =dy/dt
Данное уравнение можно записать в виде
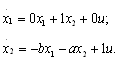
Матрицы коэффициентов будут равны
![]()
Таким образом, исходное уравнение представляется следующим уравнением параметров состояния
![]()
![]() Однородное дифференциальное
уранение представляется в векторной форме в виде
Однородное дифференциальное
уранение представляется в векторной форме в виде
где А – матрица с постоянными коэффициентами размерности (n*n),
вектор x – матрица–столбец, состоящая из n переменных состояния
В соответствии с решением обыкновенных дифференциальных уравнений решение данного уравнения представляется следующим выражени
![]()
где матрица состояния eAt может быть представлена в виде бесконечного ряда:
![]() Матрица состояния обычно
обозначается как Ф(t). Иногда эта матрица называется фундаментальной матрицей
или переходной матрицей состояния. Переходная матрица состояния «описывает»
движение конца вектора в пространстве состояния из некоторых начальных
координат. Вычисление переходной матрицы состояния может выполняться различными
методами.Например: метод разложение в бесконечный ряд, частотный метод с
использованием преобразований Лапласа и машинные методы.
Матрица состояния обычно
обозначается как Ф(t). Иногда эта матрица называется фундаментальной матрицей
или переходной матрицей состояния. Переходная матрица состояния «описывает»
движение конца вектора в пространстве состояния из некоторых начальных
координат. Вычисление переходной матрицы состояния может выполняться различными
методами.Например: метод разложение в бесконечный ряд, частотный метод с
использованием преобразований Лапласа и машинные методы.
С учетом перемноженных значений матриц переходная матрица состояния будет иметь вид
![]()
После вычислений бесконечного ряда переходная матрица состояния представляется выражением
![]()
Метод частотной области основан на преобразовании Лапласа от исходного уравнения
![]()
которое имеет следующий вид:
где I – единичная матрица, в которой диагональные элементы равны единице, а выражение pl представляется матрицей
После обратного преобразования получим:
![]()
![]()
Для матрицы коэффициентов
фундаментальная матрица принимает следующие выражения:
![]()
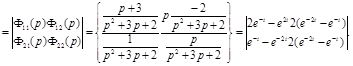
Примечание. Для перехода выражений из «р» преобразований используются следующие зависимости:
![]()
Общее уравнение параметров состояния объекта, т.е. уравнение, которое связывает состояние объекта в t и в t+T моменты времени, представляется векторно-матричным уравнением вида
![]()
Матрицы B (коэффициентов объекта), А (коэффициентов управляю-щих воздействий) и С (коэффициентов внешних возмущений) имеют вид
![]()
Решение уравнения представляется в виде
![]()
Уравнения можно переписать в другом виде, которое чаще используется в практике анализа систем.
![]()
Пример.Исходное дифференциальное уравнение имеет вид
![]()
Представим исходное уравнение в нормальной форме Коши, вводя обозначения
![]()
В результате имеем систему уравнений второго порядка, которая преобразуется в удобную форму
![]()
![]()
![]()
Уравнение параметров состояния можно представить в виде
![]()
4.Машинные методы определения матриц в уравнениях параметров состояния основаны на представлении формул матриц в виде разложения в степенной ряд:
![]()
В представленных выражениях для вычисления элементов матриц необходимо знать период дискретности Т. Определение периода дискретности является очень сложной задачей и зависит от целей исследования систем. Наиболее часто используется метод, основанный на критерии минимума числа шагов при синтезе автоматических систем. Идея метода состоит в том, что параметр Т выбирается таким образом, чтобы последовательности значений U,Y не выходили за пределы максимальных значений U max, Ymax.
4.3 Способы решения задач линейного программирования на основе симплекс-метода
Общая задача линейного программирования, на основе которой предлагается моделировать различные оптимальные модели, сводится к определению максимума (минимума) линейной функции.
![]()
при ограничениях:
x(j) > 0, j=1.2.3...,n
Для L max и L min
![]()
где
C(j), j=1,n - стоимость единицы изделия j-го типа,
a(ij) - расход i-го ресурса на единицу изделия j-го типа,
x(j) - количество изделий j-го типа,
Пример 1. Максимизировать функцию
L =7/4X1 +3/2X2 -> max при ограничениях:
x1 > 15, x2 > 10,
8x1 + 5x2 < 320,
4x1 + 5x2 < 200,
x(i) > 0, i=1,2 .
Пример 2. Минимизировать функцию
L =x1 + x2 + x3 + x4 -> min
при ограничениях:
4x1 + 3x2 + x3 > 180,
4x2 + 9x3 + 12x4 > 900,
x(i) > 0, i=1,4 .
Алгоритм решения
1. Представить систему неравенств в систему равенства путем ввода базисных переменных.
1а.
x3 = b1 - (a11x1 + a12x2), x3 = 320 - (8x1 + 5x2),
x4 = b2 - (a21x1 + a22x2), x4 = 200 - (4x1 + 5x2),
L - (c1x1 + c2x2) -> max. L - 7/4x1 - 3/2x2) -> max.
1б.
L1 + (x1 + x2 + x3 + x4) -> min,
4x1 + 3x2 - x3 - x5 = 180,
4x2 + 9x3 + 12x4 - x6 = 900.
x5 = b1+(a11x1 + a12x2 + a13x3), x5 = 180+(4x1+3x2+ax3),
x6 = b2+(a22x2 + a23x3 + a24x4), x6 = 900+(4x2-9x3-12x4),
L1+(c1x1+c2x2+c3x3+c4x4)>min L1-(x1+x2+x3+x4)>min.
2. Записать коэффициенты в стандартную Симплекс-таблицу. 2а.
Б Bi x1 x2 x3 x4
x3 320 8 5 1 0
x4 200 4 5 0 1
L L0 -7/4 -3/2 0 0
2б.
Б Bi x1 x2 x3 x4 x5 x6
x5 180 -4 -3 -1 0 1 0
x6 900 0 -4 -9 -12 0 1
L -L0 1 1 1 1 0 0
3. Перевести переменные x в базисные:
- столбец отмечается по наибольшему коэффициенту целевой функции, для C1= -7/4 выбирается переменная x1;
- строка отмечается по наименьшему значению b(i)/x(i),
min (320/8, 200/4) , min = 40 (строка x3).
Разрешающим элементом на пересечении отмеченных столбца и строки является 8 (a11).
После деления элементов строки x3 на разрешающий элемент, имеем таблицу:
x1 x2 x3 x4 b(i)
x3 1 5/8 1/8 0 40
x4 4 5 0 1 200
L -7/4 -7/2 0 0 0
Подстановка x1 вместо x3 осуществляется таким образом, чтобы все элементы столбца х1, за исключением разрешающих, стали равными 0. Для этого из строки х3 вычитается строка х4, деленная на 4; к строке х3 прибавляется строка L, умноженная на 7/4.
После выполнения операций имеем следующую таблицу:
x1 x2 x3 x4 b
x1 1 5/8 1/8 0 40
x4 0 5/2 -1/2 1 40
L 0 -13/32 7/32 0 70 < - прибыль
4. Если в целевой функции имеются отрицательные коэффициенты, то перейти к п.3, иначе - к п.5. После перевода переменной x2 в базисную, имеем:
x1 x2 x3 x4 b
x1 1 0 1/4 -1/4 30
x2 0 1 -1/5 2/5 16
L 0 0 11/80 13/80 76 1/2 <- прибыль
![]()
Получение оптимального решения: так как коэффициенты в строке L неотрицательны, то оптимальным решением будет
x1 = 30, x2 = 16, Lmax = 76 1/2.
Для задачи минимизации функций процесс выбора оптимальных решений будет продолжаться до получения отрицательных коэффициентов в целевой функции. В результате будем иметь:
x2 = 60, x4 = 55, x1 = x3 = 0, L1 = 115.
4.4. Способы определения опорного плана транспортной задачи
4.4.1 Способ “северо-западного угла”
Опорный план - это такое допустимое решение, которое удовлетворяет условиям ограничения .
Допустим, что требуется определить опорный план для следующих исходных данных.
В1 В2 В3 а(i)
А1 10 1 3 40
А2 6 2 5 80
А3 2 5 14 60
b(j) 30 100 50 180
![]()
.
4.4.2 Способ “наименьшего элемента в матрице”
Суть метода состоит в том, что в таблице с исходными данными (см. раздел 4.2.3.1.) выбирается клетка с минимальным элементом. В данном случае такой клеткой является А1-В2. Потребности пункта назначения В2=100 единиц, а запасы пункта отправления А1=40 единиц. Назначается перевозка А1-В2=40 единиц. Следующая клетка А2-В2 с минимальным элементом для пункта назначения В2=60единиц. В результате такой операции будет получена таблица.
В1 В2 В3 а(i)
10 1 3
А1 40 40
6 2 5
А2 60 20 80
12 5 14
А3 30 30 60
b(j) 30 100 50 180
Алгоритм способа наименьшего элемента:
1. Ввод данных i=M, j=N, Si,j, Ai, Bj.
2. Сортировка массива Si,j с записью индексов i и j возрастающих чисел в одномерном массиве SIk, SJk; k=1..i*J.
3. Организация цикла от k=1 до T=I*J.
4. I1=SI(k), J1=SJ(ki), если A(I1)<B(J1), то G(I1,J1)=A(I1), A(I1)=0, B(J1)=B(J1)-A(I1) переход на 6.
5. Если A(I1)=>B(J1), то G(I1,J1)=B(J1), A(I1)=A(I1)-B(J1), B(J1)= G(I1,J1).
6. Если k>J*J, то переход на 7,
иначе k=k+1 и иереход на 4.
7. Вывод G(I1,J1).
8. Конец.
4.2.3.3. Способ Фогеля
Процесс составления опорного плана начинается с определения разностей между двумя наименьшими элементами каждой строки и каждого столбца. Затем из всех разностей строк и столбцов выбирается наибольшая. Для конкретного случая эта разность равна 7. Определяем клетку с минимальным элементом в этой строке A3-B2 и в эту клетку записываем поставки 60 единиц. В последующем определяются другие максимальные разности (4) которой соответствует минимальный элемент в клетке А2-В1 (6).
Результаты составления опорного плана по Фогелю сведены в таблицу.
В1 В2 В3 а(i) i
10 1 3
А1 40 40 2
6 2 5
А2 30 40 10 80 3
12 5 14
А3 60 60 7
b(j) 30 100 50 180
j 4 1 2
Алгоритм способа Фогеля:
1. Ввод данных M, N, S(M,N), A(M), B(N).
2. Сортировка по строкам S1(i,j).
3. Сортировка по столбцам S2(j,i).
4. Вычисление (i)=S1(i,1)-S1(i,2).
5. Вычисление (j)=S2(1,j)-S2(2,j).
6. Определение (i)max, i(m).
7. Организация цикла по M, M=1,N .
8. Определение S(i(m),j)min, j(m).
9. Если A(i(m)) > B(j(m)), K(i,j) = B(j(m)),
B(j(m)) = 0, A(i(m)) = A(i(m))-B(j(m)), переход на п.11.
10. Если A(i(m)) > B(j(m)), K(i,j) = A(i(m)),
A(i(m)) = 0, B(j(m)) = B(j(m))-K(i,j).
11. Если M > N, то переход на п.12,
иначе M = M+1 и переход на п.8.
12. Вывод K(i,j).
13. Конец.
Эффективность планов можно получить, используя зависимость:
![]()
где C - стоимость перевозок.
Для способа “северо-западного угла“ стоимость перевоза С1 = 1220. Для способа “ наименьшего элемента в матрице“ - С2 = 1040. Для способа Фогеля - С3 = 730.
Для уточнения планов используются методы потенциалов и “венгерский”.
4.4.4 Решения транспортных задач
методом потенциалов
Определение допустимого плана на оптимальность методом потенциалов осуществляется с помощью чисел ui и vj, которые называются потенциалами.
Рассмотрим транспортную задачу в общем виде:
![]()
при ограничениях
![]()
![]()
Определим функцию Лагранжа для приведенных уравнений:
![]()
![]() ,
,
![]()
![]() где ,
где ,
,
ui , vj - множители Лагранжа.
Условия экстремума имеют вид
![]()
![]()
![]()
![]() ,
,
,
,
,
После дифференцирования получим:
;
![]() ;
;
;
.
![]()
![]()
![]()
При ограничениях xij>0
cij = ui + vj
при xij = 0
cij > ui + vj.
Полученные уравнения потенциалов могут быть использованы для определения индексов свободных клеток
kij = cij - (ui + vj) > 0,
где kij - индексы свободных клеток. Если условие kij не выполняется, то из всех свободных клеток, для которых kij< 0 выбирается одна с максимальным по абсолютной величине индексом. Вычислительный процесс заканчивается при выполнении условий kij для всех свободных клеток.
Рассмотрим метод потенциалов на примере. Исходные данные и допустимый план представлены в таблице.
B1 B2 B3 U(i)
A1 10 1 340 0
A2 6 270 510 2
A3 12/30 5/30 14 5
V(j) 7 0 3
Определим потенциалы Ui и Vj. Потенциал первой строки выбирается произвольно, например, u1 = 0. Для этой строки
находится базисная клетка A1B3, следовательно,
V3 = c1,3 - u1 = 3 - 0 = 3.
Зная V3, можно найти
U2 = c2,3 - V3 = 5 - 3 = 2.
Используя следующую базисную клетку A2B2, определяем
V2 = c2,2 - u2 = 2 - 2 = 0.
По базисным клеткам третьей строки последовательно рассчитаем:
U3 = c3,2 - V2 = 5 - 0 = 5;
V1 = c3,1 - u3 =12 - 5 = 7.
После определения потенциалов строк и столбцов можно рассчитать индексы свободных клеток:
k1,1 = 10 - (0+7) = 3 > 0;
k2,1 = 6 - (2+7) = -3 < 0;
k1,2 = 1 - (0+0) = 1 > 0;
k3,3 = 14 - (5+3) = 6 > 0.
Так как k2,1 < 0, то данный план не является оптимальным. Отрицательный индекс имеет клетка A2B1 (k2,1<0). Составляем для этой клетки цикл A2B2 A3B2 A3B1, затем производим перераспределение перевозок и рассчитываем потенциалы для нового опорного плана.
B1 B2 B3 U(i)
A1 10 1 3/40 0
A2 6 2/40 5/10 2
A3 12/30 5/60 14 5
V(j) 7 0 3
По потенциалам определяем индексы свободных клеток
k1,1 = 10 - (0+4) = 6;
k1,2 = 1 - (0+0) = 1;
k3,1 = 12 - (5+4) = 3;
k3,3 = 14 - (5+3) = 6.
Все индексы положительны. Значит данный план является оптимальным. Таким образом, алгоритм метода потенциалов будет сводится к следующим операциям:
1) определяем опорный план (например, методом “северо-западного угла”);
2) рассчитываем для базисного опорного плана потенциалы;
3) определяем индексы свободных клеток;
4) проверяем план на оптимальность, т.е. наличие отрицательных индексов свободных клеток;
5) если имеются отрицательные индексы, то производится перераспределение плана для соответствующей свободной клетки, т.е. переход к п.2;
6) если индексы свободных клеток положительны, то план является оптимальным.
Блок-схема алгоритма метода потенциалов
![]()
4.4.5 Метод решения транспортных оптимизационных
задач на основе “венгерского метода”
4.4.5.1 Общие сведения
В основу метода положены теоремы, доказанные венгерскими математиками Д.К.Кенигом и Е.Эгервари. На основании этих теорем американские математики Т.Кун и Д.Манкрее разработали метод, названный венгерским. Идея метода состоит в том, что прибавление и вычитание некоторого числа из всех элементов строки или столбца матрицы ¦ Сij ¦ не изменяет оптимального плана. В связи с этим исходную матрицу можно преобразовать к такому виду, чтобы все ее элементы были неотрицательны и все перевозки можно назначить по нулевым элементам.
4.4.5.2 Алгоритм “венгерского метода”
Математически она формулируется так: требуется минимизировать
![]()
при ограничениях:
![]()
Алгоритм будем рассматривать на примере, который представлен в виде схемы: ai
![]()
![]() 10 1 3 40
10 1 3 40
CIJ = 6 2 5 80
12 5 14 60i
![]()
bj 30 100 50
1. Преобразуем матрицу ¦ Сij ¦ так, чтобы в каждом столбце и в каждой строке был хотя бы один нулевой элемент. Для этого вычитаются минимальные элементы столбцов (строк) из всех элементов соответствующих столбцов (строк).
,
![]()
![]()
![]()
![]() 4 0 0 4 0 0 40
4 0 0 4 0 0 40
Сij = 0 1 2 ; Cij = 0 1 2 80
6 4 11 2 0 7 60
bj 30 100 50
2. Определяем начальный план ¦ хij ¦, назначая перевозки способом “северо-западного угла” в нулевые элементы ¦ Сij ¦. В 1-й строке нулевые элементы во 2 и 3 столбцах. Потребности В2=100, В3=50. Таким образом, для удовлетворения потребностей (bj) можно заполнить матрицу так:
![]()
![]() - 40 - 0
- 40 - 0
Xij = 30 - - 50
- 60 - 0
0 0 50
3. Находим невязки по строкам
![]()
![]() и столбцам
и столбцам
.
Cуммарная невязка:
![]()
![]()
![]() Если , то полученный
план является оптимальным. Если ,то план недопустимый и необходимо
ликвидировать невязки.
Если , то полученный
план является оптимальным. Если ,то план недопустимый и необходимо
ликвидировать невязки.
+ +
![]()
![]() 4 0 0
4 0 0
С”(ij) = 0 1 2
2 0 7
h = min (0,2,7) = 0
Если h=0, то переходим к п.6. 5. Вычитаем h из всех элементов невыделенных строк матрицы ¦ С(ij) ¦ и прибавляем h ко всем элементам выделенных столбцов.
Возвращаемся к п.4 до получения hmin= 0.
6. Отмечаем нулевой элемент h матрицы ¦ С(ij) ¦ знаком “штрих” (0') - (E2(1.3)). Проверяем невязку строки
+ + (i)
![]()
![]() 4 0 0 0
4 0 0 0
С(ij) = 0 1 2 50
3 0 7 0
————
(j) 0 0 50
где находится элемент (0'). Если (j)>0, то переходим к п.12, иначе к п.7.
7. Выделяем в матрице ¦ С(ij) ¦ знаком “+” строку, где находится 0' - (E3(1)). + + (i)
4 0 0' 0 +
С(ij) = 0 1 2 50
3 0 7 0
—————
(j) 0 0 50
8. В выделенной строке проверяем значения ¦ хij ¦. При хij=0 переходим к п.10, иначе - к п.9.
9. Отмечаем нулевой элемент в матрице ¦ Сij ¦ знаком (*), т.е. E4(1,2).
+ +
![]()
![]() 4 0* 0' +
4 0* 0' +
С(ij) = 0 1 2
3 0 7
после чего переходим к п.14.
10. Отмечаем нулевой элемент в помеченном столбце (+) знаком “штрих” - E5(3,2)
+ +
![]()
![]() 4 0* 0' +
4 0* 0' +
С(ij) = 0 1 2
3 0' 7 +
11. Переходим к п.8, а если проверяем все столбцы, то переходим к п.4. После возвращения к п.4 находим h = min(1,2,0,7) = 0. Т.к. h=0, то повторно выполнив п.п.6,7,8,9,10,11, получим
+ (+)
![]()
![]() 4 0* 0' +
4 0* 0' +
С(ij) = 0 1 2
2 0' 7 +
Находим h = min(1,2,7) = 1. Т.к. h=1>0, то переходим к п.5. После выполнения п.5 имеем
+ (+)
![]()
![]() 5 0* 0' +
5 0* 0' +
С(ij) = 0 0 1
3 0” 7 +
Далее имеем h = min(0,1) = 0.
+ (+)
![]()
![]() 4 0* 0' +
4 0* 0' +
С(ij) = 0 0' 1
3 0' 7 +
![]() В связи с
невязкой переходим к п.12.
В связи с
невязкой переходим к п.12.
![]()
![]() 12. Строим цепочку по
столбцу от 0' к 0*, по строке от 0* к 0', т.е. цепочка начинается от 0' в
строке с и заканчивавася в 0' в столбце с . (Возможен случай,
когда 0' находится в одном столбце или строке).
12. Строим цепочку по
столбцу от 0' к 0*, по строке от 0* к 0', т.е. цепочка начинается от 0' в
строке с и заканчивавася в 0' в столбце с . (Возможен случай,
когда 0' находится в одном столбце или строке).
![]() 13. Определяем величину
сокращения невязки:
13. Определяем величину
сокращения невязки:
где ![]() (i) - невязка
строки,
(i) - невязка
строки,
![]() (j)- невязка
столбца,
(j)- невязка
столбца,
xij* - минимальное значение перевозок, соответствующее 0*, входящему в цепочку. Если в цепочку входит только один 0', то .
В соответствии с пп.12,13 находим =min(50,40,50)=40.
14. Находим новый план, прибавляя Ɵ к элементам ¦xij¦, соответствующим 0' цепочки, и, вычитая из элементов ¦xij¦, соответствующих 0* цепочки. Остальные элементы плана ¦xij¦ остаются без изменения.
Новый план:
![]() (i)
(i)
![]()
![]() 0
0 40 0
0
0 40 0
х’(ij) = 30 40 0 10
0 60 0 0
—————
![]() (j) 0 0 10
(j) 0 0 10
![]()
Суммарная невязка: если =20, то продолжается процесс, возвращаемся к п.4 и т.д.
Новая матрица
+ +
![]()
![]() 6 1 0'
6 1 0'
С(ij)(1) = 0 0 0'
3 0 6
включает только один 0'. Окончательный план
![]() (i)
(i)
![]()
![]() 0 0 40 0
0 0 40 0
х(ij)2 = 30 40 10 0
0 60 0 0
![]() (j) 0 0
0
(j) 0 0
0
![]() Однако рассмотренный
алгоритм достаточно сложен. Эффективность метода может быть повышена за счет
методики преобразования матрицы до тех пор, пока не будет выполнено условие:
Однако рассмотренный
алгоритм достаточно сложен. Эффективность метода может быть повышена за счет
методики преобразования матрицы до тех пор, пока не будет выполнено условие:
где yij = 1, если cij = 0 , yij = 0, если сij > 0.
Эти условия означают, что число элементов каждой строки и столбца матрицы Сij должно обеспечивать возможность распределения всех запасов (а) по нулевым элементам i-той строки и всех потребностей (b) по нулевым элементам j-того столбца. Выполнение условий обеспечивает получение начального плана х более близкого к оптимальному, что уменьшает невязки и число итераций при поиске допустимого плана. Исходная матрица
![]()
![]() 10 1 3
10 1 3
Сij = 6 2 5
12 5 11
После первого пункта имеем
аi
4 0 0 40
Сij = 0 1 2 80
2 0 7 60
bj 30 100 50
Рассмотренные условия не выполняются для второй строки
и третьего столбца. Вычитая из элементов второй строки 1 и прибавляя ее к элементам первого столбца ( чтобы не получилось с =-1),
получим 5 0 0
Сij = 0 0 1
3 0 7
Вычитая из элементов третьего столбца 1 и прибавляя ее к элементам первой строки, получим
6 1 0
Сij = 0 0 0
3 0 6
Окончательно получим
аi
6 1 1 40
Сij = 0 0 0 80
3 0 6 60
bj 30 100 50
После проделанных операций данные условия выполняются.Определив исходный план способом Фогеля
0 0 40 0
Xij = 30 40 10 0
0 60 0 0
0 0 0
и рассчитав невязки, можно убедится, что полученный план
является оптимальным.
Предлагаемый вариант вычисления оптимального решения позволяет повысить эффективность венгерского метода в 1.5 – 2 раза.
Блок-схема алгоритма решения транспортных
задач венгерским методом.
![]()
4.6 Метод динамического
программирования
Сущность метода. Идея метода заключается в замене большого количества
параметров избирательным их выбором. Многомерная задача оптимизации сводится к
многошаговой задаче меньшей размерности. В основу метода положен принцип
оптимальности, сформулированный американским математиком Р.Беллманом. В таком
представлении “оптимальное поведение областей обладает тем свойством, что,
каковы бы ни были первоначальные состояния и решения в начальный момент,
последующие решения должны составлять оптимальное поведение относительно
состояния, получающегося в результате первого решения”. Суть метода можно
рассмотреть на следующем примере. Допустим, что задан граф.
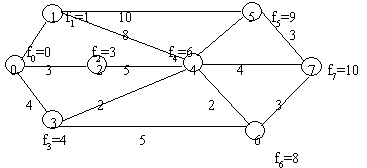
![]() Необходимо определить
кратчайший путь из начальной вершины в конечную. Время перехода из одной
вершины в другую указано около каждой дуги графа. Построим матрицу расстояний.
Обозначим через f(i()1,7) кратчайший путь из начальной вершины в j-тую вершину
графа. Вычислим кратчайшие пути из начальной в j-тые вершины.
Необходимо определить
кратчайший путь из начальной вершины в конечную. Время перехода из одной
вершины в другую указано около каждой дуги графа. Построим матрицу расстояний.
Обозначим через f(i()1,7) кратчайший путь из начальной вершины в j-тую вершину
графа. Вычислим кратчайшие пути из начальной в j-тые вершины.
В соответствии с приведенным выражением можно написать общую зависимость для определения:
![]()
Алгоритм метода
динамического программирования
1. Ввод n - количество вершин,
tij - расстояние между двумя вершинами.
2. Организация общего цикла по i от 1 до n.
3. Организация внутреннего цикла по j от 1 до n (соединения).
4. Расчет min пути от i до j.
5. Формирование кратчайших путей и определение min расстояния.
6. Формирование кратчайшего пути на графе.
Блок-схема алгоритма метода динамического программирования представлена на
рис.Bs4_2_6.
В большинстве практических задач имеются ограничения на выбор: параметров,
критического пути, последовательности действий (работ) и т.д.
Рассмотрим получение уравнений на следующем примере. Система состоит из четырех устройств, каждое из которых имеет несколько вариантов технической реализации, отличающихся друг от друга весовыми параметрами и вероятностью отказа устройств. Необходимо определить оптимальную структуру системы при допустимом увеличении веса прибора
(Рдоп=<.4) и минимальной вероятностью отказа системы, т.е.
![]()
при ограничении
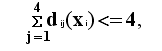
где qj - вероятность
отказа j-го прибора;
dij - увеличение веса j-го прибора по сравнению с первым.
Целевая функция справедлива при Q[xj]1, что соответствует для
современных высоконадежных систем. Если в общем виде использовать параметры
управления (qj) и ресурсы работ (dj), то можно записать условие
получения min(max) в следующем виде
![]()
при ограничении
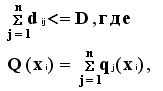
де D - максимальный ресурс.
Вычислительный алгоритм должен последовательно состоять из операций по расчету функции. Для i=1.
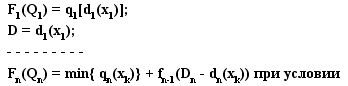
![]() Пример. Требуется минимизировать
вероятность отказа системы
Пример. Требуется минимизировать
вероятность отказа системы
![]()
![]() Так как
Так как
то в соответствии с общей формулой
![]()
где i = 1,2...k. (В общем случае величины x(1,i) и x(2,i) могут иметь различные значения).
Таким образом
![]()
Для первого члена последовательности выбираются максимальные вероятности отказа и минимальный вес, т.е.
x1 = 1, х2 = 1.
![]()
Второй член последовательности должен удовлетворять условиям:
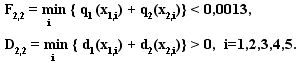
Эти условия выполняются при
![]()
![]()
![]()
Для определения последовательностей
используются следующие зависимости
![]()
Для определения последовательностей
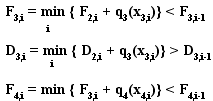
После всех вычислений можно получить такие данные: для
Зная функцию F4(D4), определяем минимальное значение вероятности отказа системы. Остальные параметры управления и варианты технической реализации вычисляются в обратной последовательности. Параметры управления x4 = 4, d4 = 3 определяют 4-й вариант технической реализации и его вес d4= 3. По зависимости Dj-1 = Dj - dj(xi) вычисляются соответствующие параметры x3 и d3 и т.д.
Необходимо заметить, что параметры управления можно запоминать при выборе минимальных значений Fj(Dj), которые соответствуют
Для рассмотренного примера имеем:
![]()
Таким образом, оптимальный приборный состав для D = 10 должен быть реализован из устройств x1= 5, x2= 2,x3= 3, x4 = 4, которые обеспечивают вероятность отказа Q = 0,006. Изменяя исходные данные, например, ограничение на вес, можно получить требуемый состав устройств (приборов) для технической системы.
При решении задач с несколькими ограничениями процедура усложняется. Рассмотрим решение предыдущей задачи с двумя ограничениями. Требуется определить
![]()
Функциональное уравнение, к которому сводится решение, имеет вид

Минимальному значению F4 =
0,015 при D1,4 = 5 D2,4 = 5 соответствует
оптимальный план x1 = 2, x2 = 2, x3 =
1, x4 = 4.
Основные трудности при решении задач динамического программирования связаны с
необходимостью запоминать большое количество промежуточной информации.
Максимальный объем членов оптимальной последовательности в общем случае определяется
выражением
![]()
Например, при Dj = 99, V = 106.
Для повышения эффективности использования метода динамического программирования при больших размерностях можно рекомендовать метод двойственной задачи динамического программирования и комбинированный способ, включающий метод ветвей и границ.
4.2.7. Матричный метод сетевого планирования
Для определения критического пути составляется матрица продолжительности работ tij, по которой вычисляются параметры сетевого графа: Ti(p); Tj(n) - соответственно ранние и поздние сроки наступления событий.
С учетом Ti(p) и Tj(n) определяются резервы времени Rk для каждого номера событий. Критический путь находят по тем событиям, в которых резервы времени Rk равны нулю.
Параметр Ti(p) вычисляется по формуле
Ti(p) = max { Tj(p) + tij } , где i=0,N-1; j=1,N (T0(P)=0.
Параметр tjn вычисляется по формуле
Tj(n) = min { Ti(n)-tij} , где TN(n) = TN(p);
Rk = Tk(n) - Tk(p).
Матричный метод рассмотрен на примере сетевой модели, расcмотренной в разделе (3.4.2).
В соответствии с моделью и формулами Ti(p) и Tj(n) составляется матрица графа с tij, по которой определяются ранние и поздние сроки событий по следующему алгоритму.
0 1 2 3 4 5 6 7 8 9 10 Tip
0 20/0 45/20 0
1 0/20 25/0 20/95 20
2 40/20 45
3 60/0 45
4 80/0 30
5 0/5 10/0 85
6 0/5 10/0 105
7 5/0 105
8 90/0 145
9 100/0 205
10 305
Tjn 0 20 65 45 125 105 105 110 115 205 305
Критический путь: 0-1-3-6-8-9-10.
Ранний срок события с номером i (i=1,n) равен сумме элемента матрицы tij с ранним сроком предшествующего события, причем, если предшествующих событий несколько, то берется максимальное из сумм.
Например, событие 1 связано с нулевым событием (t0,1=20), т.к. T0(p)=0, то имеем T1(p)=20. Событие 2 связано с двумя предшествующими событиями 0 и 1 столбца j=2 с длительностями t0,2 = 45; t1,2 = 0. После составления сумм t0,2 + T0(p) = 45 + 0 = 45;
t1,2 + T1(p) = 0 + 20 = 20
в строку 2 записываем большую сумму, т.е. T2(p) = 45.
Возьмем восьмой столбец (j=8), что соответствует восьмому событию, которое связано с предшествующи ми событиями 5, 6 и 7. Составляем суммы:
10 + 85 = 95; 10 + 105 = 115; 5 + 105 = 110.
Большую сумму записываем в восьмую строку, т.е. T8(p)=115. Поздний срок событий определяется путем вычитания элемента матрицы tij из позднего срока последующего события. Если последующих событий несколько, то берется минимальная из разностей, результат записывается в столбец с номером j.
Вычисления начинают с завершающего события, для которого TN(n)=TN(p) , т.е. T10(n)=305.
Событие 9 связано с событием 10 (t9,10 = 100). В соответствии с формулой имеем
T9(n) = T10(n) - t9,10 = 305 - 100 = 205.
Для T8(n) = T9(n) - t8,9 = 205 - 90 = 115.
Событие 5 связано с двумя событиями 7 и 8, для которых t5,7=0 и t5,8=10. Составляем две разности 110-0=110; 115-10=105. выбирается меньшая, т.е. T5(n)=105.
цей свободного времени Rk (в таблице значения Rk показаны в дроби, например, для i=0 j=1-20/0, что означает: 20 - время работы, а Rk=0). Таким образом, начиная с 0 работы имеем Rk=0 для 1-й работы, далее 1-я работа имеет Rk=0 для 3-й работы, 3-я работа имеет Rk=0 для 6-ой работы и т.д.
Критический путь равен 0-1-3-6-8-9-10.
После подсчета времени работ
L = 20+25+60+10+90+100 = 305.
Блок-схема алгоритма вычисления критического пути в сетевом графе Рис. Bs4_2_7. Программа на алгоритмическом языке Turbo-Pascal представлена в Приложении (Pr5_6_4).
4.2.8. Метод “ветвей и границ”
Метод “ветвей и границ” использует последователь но-параллельную схему построения дерева возможных вариантов. Первоначально ищут приближенное решение и для каждого возможного варианта определяют верхнюю границу целевой функции. Ветви дерева возможных вариантов, для которых верхняя граница ниже приближенного решения, из дальнейшего рассмотрения исключают.
Эффективность вычислительных алгоритмов зависит от точности и простоты способа определения верхней границы возможных решений и точности определения приближенного решения. Чем точнее способ определения верхней границы целевой функции, тем больше беспер- спективных ветвей отсекается в процессе оптимизации. Однако увеличение точности расчета верхних границ связано с возрастанием объема вычислений. Например, если для оценки верхней границы использовать симплексный метод, то оценка будет достаточно точная, но связана с большим объемом вычислительной работы. Рассмотрим алгоритм решения задачи: требуется максимизировать выражение
Критический путь определяется в соответствии с матрицей
![]()
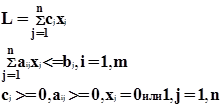
методом “ветвей и границ” с простым и эффективным
способом оценки верхней границы целевой функции.
Обозначим: U - множество переменных xj; S - множество фиксированных переменных, вошедших в допустимое решение; Es - множество зависимых переменных, которые не могут быть включены в множество S, так как для них выполняется неравенство
![]()
Gs - множество свободных переменных, из которых производится выбор для включения в S очередной переменной.
![]() Рассмотрим первоначально
одномерную задачу, т.е. m=1 и задача имеет только одно ограничение.
Рассмотрим первоначально
одномерную задачу, т.е. m=1 и задача имеет только одно ограничение.
Обозначим и
![]() допустим, что
допустим, что
и выполняются условия
h1,k+1> h1,k+2> ...> h1,i , l<= n;
![]()
Для определения верхней границы решения может быть использовано выражение
![]()
где
Из условия следует, что
![]()
при ограничении
![]()
xj=0;1
рассмотрим алгоритм решения задачи на примере.Пусть необходимо определить максимум выражения
![]()
при ограничениях
![]()
Исходные данные для расчета приведены в таблице. При этом все элементы пронумерованы в порядке убывания градиента h.
j 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
cj 6 10 4 16 6 6 12 10 16 3 6 2 4 1 1 2
a1 j 1 2 1 4 2 3 6 5 8 3 6 4 8 3 4 10
h1j 6 5 4 4 3 2 2 2 2 1 1 0,5 0,5 0,33 0,25 0,2
На первом шаге вычислительного процесса S =0 ,
Es =0 , xj Gs
Условия для hi выполняются для l=6. действительно,
![]()
Определив
![]()
с помощью выражений для Hs находим
![]()
Из условия
![]()
выбираем xr=xi и расcчитываем HS(x1)=46;
![]()
На втором шаге xi S, Es = , xj Gs(j=2, 3, ..., 16), Hs = Hs(xi) = 46. Выбираем xr = x2 и рассчитываем
H(x2) = 46; Hs(x2) = 40.
Аналогичным способом
производятся вычисления на всех последующих шагах. Результаты расчета приведены
в таблице. На шестом шаге xj S(J=1,5) , xj Es (j=6, 7, ..., 16), Gs = .
![]() Следовательно, значение
Следовательно, значение
может быть принято в качестве первого приближенного решения L0. Условия HS(xr)>42 выполняются только для двух неисследованных ветвей Hs(x5)=44 и Hs(x3)=44. Исследование первой из этих ветвей не приводит к увеличению приближенного решения (шаг 7, 8 в таблице). Вторая ветвь приводит к новому результату (шаг 9-12 в таблице).Дерево возможных вариантов изображено на рисунке. Так как для всех оставших ся ветвей выполняются неравенства
![]()
, то полученное решение является оптимальным.
![]()
Блок-схема алгоритма
метода ветвей и границ
![]()
.
4.8 Методы обработки экспериментальных данных
4.8.1. Числовые характеристики выборки
Для обработки экспериментальных данных из n чисел (x1, x2, x3... xn) используются следующие зависимости:
![]() - средние арифметические
значения
- средние арифметические
значения
![]()
- дисперсия
![]() - среднеквадратическое
отклонение
- среднеквадратическое
отклонение
![]() - медиана (значение, для
которого одна половина значений данных меньше ее, а вторая - больше)
- медиана (значение, для
которого одна половина значений данных меньше ее, а вторая - больше)
- мода (значение признака, встречающегося в выборке наиболее часто)
![]()
где xmо - нижняя граница модального интервала;
h - ширина интервала группировки;
nmо - частота модального интервала;
nmо-1 - частота модального интервала, предшествующего модальному;
nmо+1 - частота интервала, следующего за модальным; R - размах вариаций.
где xmax xmin - максимальные и минимальные значения выборки.
4.3.2. Регрессионный анализ экспериментальных
данных
После получения результатов измерений (например, в виде таблицы зависимости) в процессе проведения эксперимента встает
x x1 x2 x3 . . . x(n)
f(x) y1 y2 y3 . . . y(n)
вопрос: как найти формулу, выражающую эту зависимость аналитически. С этой целью используется метод наименьших квадратов. Суть метода состоит в определении наиболее близких значений известных функций Fi(x) к измеренным значениям результатов эксперимента. Степень близости вычисляется по минимуму величины
![]()
где y1, y2, ... yn - значения приближающихся функций в точках x1, x2, ... xn.
В качестве приближающихся функций выбираются следующие зависимости:
![]()
Определение параметров приближающейся функции выполняется в соответствии с условиями нахождения экстремума функций.
![]()
![]()
т.е.
![]() или
или
![]()
Основные зависимости:
![]() 1. Для линейной функции F
(x1,a,b)=ax+b уравнения регрессии представляются в виде системы:
1. Для линейной функции F
(x1,a,b)=ax+b уравнения регрессии представляются в виде системы:
![]()
2. Для квадратичной функции F(x,a,b,c) = ax2 + bx + c уравнения регрессии имеют вид:
![]()
3. Для степенной функции F(x,a,m) =axm уравнение регрессии:
![]()
Параметры вычисляются путем замены значений линейной функции на обратные.
4. Для показательной функции F(x,a,m)=a*exp (mx), a=0 уравнение представляется в виде:
LnF= Ax + B
Параметры вычисляются путем замены значений линейной функции на обратные.
5. Для дробно-линейной функции
![]()
![]() Уравнения регрессии имеют
вид
Уравнения регрессии имеют
вид
Параметры вычисляются путем
замены значений линейной функции F(x,a,b) = a lnx + b на обратные.
6. Для логарифмической функции F(x,a,b) = a lnx + b параметры вычисляются после
логарифмирования значений x c использованием выражения для линейной функции.
6. Для логарифмической функции F(x,a,b) = a lnx + b параметры вычисляются после логарифмирования значений x c использованием выражения для линейной функции.
![]() 7. Для гиперболической
функции уравнение регрессии преображается в
7. Для гиперболической
функции уравнение регрессии преображается в
![]() форму:
форму:
Для использования выражения линейной функции надо вначале заменить u на 1/x.
![]() 8. Для дробно-рациональной
функции
8. Для дробно-рациональной
функции
уравнение регрессии
представляется следующим выражением: ![]()
Решение выполняется аналогично с гиперболической функцией.
Блок-схема алгоритма регрессионного анализа результатов
эксперимента
![]()
4.8.3. Корреляционный анализ
Часто при проведении эксперимента результаты опыта описываются не одной случайной величиной, а двумя или более. Если при определении вида функции выбрана функция вида
f(x) = ax + b ,
то значения параметров a, b называются коэффициентом регрессии, а прямая с уравнением f(x) есть линия регрессии Y на x.
![]()
Чем меньше величина , тем зависимость между Y и X
![]()
становится более близкой к линейной.
Для вычисления тесноты линейной связи между X и Y используется коэффициент корреляции:
![]()
![]()
![]()
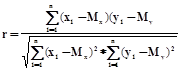
Для вычисления внешнего воздействия используется зависимость
![]()
4.4 Моделирование объектов методом статистических испытаний
Метод статистических испытаний позволяет заменить эксперимент с реальной системой экспериментом с моделью этой системы на ЭВМ. Сущность метода состоит в имитации на ЭВМ случайных процессов, протекающих в реальной системе с учетом структуры системы, связей и взаимовлияния между ее элементами. Для использования метода статистических испытаний необходимо:
- построить математическую модель реальной системы;
- сформировать случайные величины с заданным законом распределения вероятностей;
- произвести статистическую оценку результатов моделирования.
Ошибка метода может быть оценена с определенной степенью достоверности:
![]()
![]() где вероятность
характеризует степень достоверности оценки, а все выражение будет означать
вероятность того, что будет выполняться неравенство , где
где вероятность
характеризует степень достоверности оценки, а все выражение будет означать
вероятность того, что будет выполняться неравенство , где
my - математическое ожидание, - среднее арифметическое значение, определяемое по результатам N независимых испытаний.
Вероятность отклонения может быть вычислена по формуле
![]()
Где y - среднее квадратическое отклонение,
- функционал Лапласа.
![]()
![]()
![]()
![]() Если , то ошибка метода не
превышает величину E с вероятностью . С учетом приведенных зависимостей можно
определить число испытаний:
Если , то ошибка метода не
превышает величину E с вероятностью . С учетом приведенных зависимостей можно
определить число испытаний:
![]()
где вычисляется с помощью таблиц функций Лапласа по
заданной доверительной вероятности. Ошибка метода статистических испытаний
пропорциональна величине т.е., чтобы уменьшить ![]()
![]()
![]() ошибку в 10 раз, нужно увеличить
число испытаний N в 100 раз. Формирование случайных чисел производится по
плотности распределения f(x)
ошибку в 10 раз, нужно увеличить
число испытаний N в 100 раз. Формирование случайных чисел производится по
плотности распределения f(x)
![]()
![]() где F(x) - функция распределения
случайных величин. Отсюда случайная величина х определяется из выражения
где F(x) - функция распределения
случайных величин. Отсюда случайная величина х определяется из выражения
![]() х = F -1 (R),
х = F -1 (R),
![]()
![]() где F -1 (R) - обратное
отображение величины R в области изменения х; х - случайная величина c
плотностью распределения f(x).
где F -1 (R) - обратное
отображение величины R в области изменения х; х - случайная величина c
плотностью распределения f(x).
![]()
![]() Пример формирования случайных
величин по экспоненциальному закону:
Пример формирования случайных
величин по экспоненциальному закону:
![]()
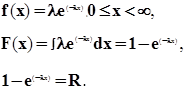
После логарифмирования
получим ![]()
Формируя случайные числа R, можно получить реализацию случайных чисел х по экспоненциальному закону. Для получения случайных чисел необходимо:
1. Разбить область определения функции f(x) на n интервалов, длины которых соответственно равны (они являются одновременно координатами точек деления
2. Произвести случайный выбор интервала (1 - интервал).
3. Выполнить случайный выбор числа R на i-том интервале:
![]()
которое будет![]() соответствовать
данному закону распределения.
соответствовать
данному закону распределения.
4. Если случайное число R будет находиться в интервале y1-1<R<y1, то случайная величина X будет принадлежать интервалу (х1-1, х1).
5. Получить случайное число в соответствии с зависимостью
(Случайная величина в интервале х1-1, х1 имеет равномерное
распределение, т.е. аппроксимирована отрезком ступенчатой линии).
Границы интервала можно получить по формулам:
4.10 Динамический метод исследования моделей управления запасами
Определение количества
поставок запасов q по уравнению издержек в форме ![]()
где d - годовой спрос запаса;
S - организационные издержки;
C - стоимость товара;
h - издержки содержания запасов, производится с учетом выражения:
![]()
Решая уравнение относительно q, получим
, которое является оптимальным размером партии (заказа).
В результате моделирования системы строится график C=f(q).
![]()
c2
c1
q* q
Из графика видно, что увеличение q ведет к резкому снижению C, и увеличению C3 (C1 - организационные издержки, С2 - стоимость товаров, С3 - общие издержки содержания запасов).
Блок-схема алгоритма
модели управления запасами
Алгоритм
1.Ввод данных d, S, C, h.
2.Организация
3. Определение q, числа поставок h, продолжительности цикла.
4. Определение издержек при уменьшении и увеличении поставок запасов.
Основная модель
управаления запасами - определение оптимального размера партии.
Организационные издержки (s) - расходы связанные с оформлением и доставкой
товаров, необходимых для каждого цикла складирования.
Размер партии (q) -
количество товара поставляемого на склад.
Издержки содержания запасов (h) - затраты на хранение и амортизацию.
Интенсивность спроса ( d) –
Стоимость товара (с) –
ЗАДАЧА:определить значение q, при котором минимизируются годовые затраты.
Уравнение издержек:
C1=s*(d/q)
общие организационные издержки
C2=c*d стоимость товаров
C3=h*(q/2)
общие издержки на содержание запасов
C = C1 + C2 + C3
C = s*(d/q) + c*d + h*(q/2)
q - неизвестная величина
С-должна обращаться в минимум
Положим
(dC/dQ)=0 Получим (dC/dQ)=-(s*d)/(q*q)+0+(h/2)=0
Откуда q^2=(2*s*d)/h - оптимальный размер партии.
Блок-схема алгоритма управления запасами
![]()
4.11 Методы моделирования графовых моделей
4.11.1. Метод определения кратчайших расстояний. Метод Дейкстра.
Для нахождения кратчайших расстояний задается объект в виде графа G = (x,y) и матрицей расстояний S = [Si,j]. Задача определений кратчайших расстояний состоит в нахождении минимального расстояния от заданной начальной вершины Si до заданной конечной вершины Sj. Условие решения предполагает, что неориентированные дуги графа не могут иметь отрицательных значений. Метод основан на приписывании вершинам графа временных пометок, которые являются максимальной границей длины пути от хi к вершине S. Отмеченные пометки с помощью итерационной процедуры постепенно становятся постоянными в соответствии с выражением:
![]()
где l(xj) - пометка вершины j,
l(p) - постоянная пометка вершины,
S(p,xj) - путь от вершины хp к хj.
Алгоритм определения кратчайшего расстояния сводится к следующим операциям:
1. Ввести данные n, S(i,j) (количество вершин графа и матрицу расстояний);
2. Присвоить начальной вершине l(S)=0, а всем остальным
вершинам l(xi)= и считать их временными;
3. Изменить все пометки l(xi) в соответствии с выражением l(xi);
4. Определить среди всех i-х временных пометок те, которые удовлетворяют выражению:l(xi* ) = min(l[xi]) = l[pi]
и считать их постоянными;
5. Если i=p=t, то l[pi] является длиной кратчайшего пути и перейти к п.6, иначе - к п.4;
6. Вывод кратчайшего пути.
Матрица расстояний представлена в виде таблицы.
![]()
Шаг 1: Первую вершину получаем как постоянную.
l(x1) = 0' , l(x1) = , p = x1.
Шаг 2: 1-я вершина x1 имеет связи с x2, x7, x8, x9. l(x2) = min[, 0'+10] = 10; l(x7) = min[, 0'+3] = 3; l(x8) = 6; l(x9) = 12.
Шаг 3: Определяем минимальное расстояние min(10, 3, 6, 12,) = 3 (x7).
Таким образом, p = x7. Вершина x7 будет иметь постоянную пометку.
Шаг 4: Повторение итераций для других вершин, т.е. переход на шаг 2.
Шаг 2: x7 = (x2, x4, x6, x9); l(x2) = min[10, 3'+2] = 5; l(x4) = 7; l(x6) = 17; l(x9) = 12.
Шаг 3: min(5, 7, 17, 6, 12, ) = 5 (x2); p = x2; x2' - будет иметь
постоянную пометку.
Шаг 4: Переход на шаг 2.
Аналогичные процедуры надо проделать для всех временных вершин, т.е.
x2 = (x1, x3, x7, x9); min(23, 7, 17, 6, 12, ) = 6 (x8); p = x8;
x8' - постоянная пометка.
Окончательная картина расстановки пометок представлена на графе:
![]()
Для нахождения кратчайшего пути, например, между вершиной x2 и начальной вершиной x1 используем соотношение
l(xi’) = S(xi’xi) = l(xi),
т.е. xi = x2 , что соответствует l(x2') + S(x2’x2) = l(x2) = 5 Далее xi = x7, что соответствует l(x7') + S(x7’x7) = l(x7) = 3. Таким образом, кратчайшим путем является путь x1 x7 x2.
Аналогично выполняется операция и для других вершин.
4.11.2. Метод вычисления абсолютных центров.
Метод Хакими.
Данный метод может быть использован для неориентированного графа. Допустим, что одно ребро заданного графа представлено в виде рисунка
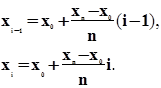
Блок-схема алгоритма определения кратчайших
расстояний метода Дейкстра
![]()
Для каждого ребра aк надо найти точки yк * , которые имеют наименьшее число разделения. Из всех точек yк * абсолютным центром будет точка, у которой имеется наименьшее число разделения (числа внешнего и внутреннего разделения - это числа, имеющие наибольшее значение в строке и соответственно в столбце).
Для ребра графа aк с учетом выражения для модели (раздел 3.4.1) можно записать следующее соотношение:
S(yк) = max {vid[yк,xi]} = max [vi min {l[yk,x2] +
d[x2,x1]l[yk,x1] + d[x1,x1]}]
Обозначим длины соответствующих частей ребра ak как l(yk,x1) и l(yk,x2). Пусть l(yk,x2) = z, а
C1,2 = l(yk,x1) + l(yk,x2), тогда l(yk,x1) = C1,2 - l(yk),x2) = C1,2- z.
С учетом введенных параметров соотношение для S(yk) будет представлено в виде:
S(yk) = max min[ vi {z + d[x2,x1]},vi{C1,2 +
d[x1,x1]- z}].
Для каждой фиксированной вершины xi и значения z
(0<z<C1,2) можно найти наименьшие значения из выражений
Ti = vi{z + d[x2,xi]}, Ti’ = vi{C1,2 + d[x1,xi]- z} .
По полученным выражениям можно построить графики зависимостей для различных значений z и xi. Из графиков находится минимальное значение для Ti, которое будет соответствовать абсолютному центру графа, т.е. наименьшему значению для всех ребер ak (К = 1,2...m).
Пример: В пяти районах необходимо построить больницу, которую надо разместить на дорогах, ведущим к абсолютным центрам какого-либо района.
Расположение районов задано графом:
Таблица матрицы расстояний будет иметь вид:
x1 x2 x3 x4 x5
x1 0 8 8 6 2
x2 8 0 2 10 6
x3 8 2 0 12 8
x4 6 10 12 0 4
x5 2 6 8 4 0
Длины ребер хi, хj равны времени (минуты, часы) для проезда из района хi в район хj. Для каждого ребра а с учетом выражений Ti и Ti’ можно получить определенное соотношение. Так, для ребра а1 = х1х3 имеем:
T1 = z + d(x3,x1) = z + 8
T1' = C(3,1) + d(x1,x1) - z = 8 - z
T2 = z + d(x3,x2) = z + 2
T2' = C(3,1) + d(x1,x2) - z = 8 + 8 - z
T3 = z; T3' = 16 - z
T4 = z + 12; T4' = 14 - z
T5 = z + 8; T5' = 10 - z
![]() Аналогично можно получить
выражения для ребер а2, а3...а6. По полученным выражениям можно найти
минимальные значения локальных центров (для ребра а1 этот центр определяется
шагом 8 от вершины х3). Абсолютный центр для графа находится на ребре а3 в 2-х
минутах от вершины х5.
Аналогично можно получить
выражения для ребер а2, а3...а6. По полученным выражениям можно найти
минимальные значения локальных центров (для ребра а1 этот центр определяется
шагом 8 от вершины х3). Абсолютный центр для графа находится на ребре а3 в 2-х
минутах от вершины х5.
Примеры моделей
Пример 1. Интегрированный пакет для моделирования объектов, динамика которых описывается дифференциальными уравнениями 1 и 2 -го порядков.
Задачи исследования:
1. Исследовать динамику объектов, представленных в списках данных, т.е. получить таблицы и графики зависимости изменения координат y,dy/dx =f(x) в пределах выбранных интервалов времени.
2. Исследовать влияние параметра Р на характер динамики движения объектов.
Исходные данные:
1.Модели объектов представляются дифференциальными уравнениями, которые задаются в списках данных.
2. Для исследования вводятся следующие исходные данные: x-начальное значение, xk-конечное значение, h-шаг изменения x, y(0),dy/dx(0), параметр p.
Результат.
Построить таблицы и графики изменения y=f(x),
dy/dx=f(x) при Р -const, y=f(p),dy/dx=f(p) при x -const.
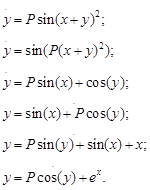
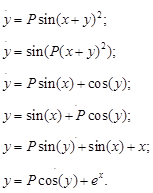
Блок схема алгоритма интегрированного пакета для моделирования объектов, динамика которых описывается дифференциальными уравнениями 1 и 2 порядков.
![]()
Титульный лист интегрального пакета для
моделирования
![]()
![]() Форма для выбора дифференциальных
уравнений
Форма для выбора дифференциальных
уравнений
![]() Форма для ввода исходных
данных и вывода графика y(x),dy(x) при a const
Форма для ввода исходных
данных и вывода графика y(x),dy(x) при a const
Форма для ввода исходных данных и вывода графика y(a),dy(a) при x - const
![]()
Пример 2. Моделирование объекта, динамика которого описывается дифференциальным уравнением 2 - го порядка y’’+a*x*y’-y=0,4.
Задачи исследования:
Исследовать заданное уравнение методом Рунге – Кутта и построить семейства кривых у(х) и у’(х) при изменении параметра a, графики решений при фиксированном a и графики функции y(a), y’(a) при фиксированном x.
1. Получить зависимости y=f(x), dy/dx=f(x) при начальных значениях y0,a,x0,xn,dx
2. Получить семейство графиков y=f(x,a),dy/dx=f(x,a).
![]() 3. Получить зависимость
y=f(a), dy/dx=f(a) при x - const
3. Получить зависимость
y=f(a), dy/dx=f(a) при x - const
Исходные данные:
1. Модель объекта представляется дифференциальным уравнением вида y’’+axy’-y=0,4, где а - параметр, влияние которого необходимо исследовать.
2. Метод исследования
Использовать метод Рунге – Кутта с построением графиков решения.
Функциональная модель
Информационная система для исследования динамических объектов
![]()
Блок схема алгоритма моделирования объекта, динамика которого описывается дифференциальным уравнением 2 порядка y’’+axy’-y=0,4.
![]()
Форма для ввода исходных данных и построения
графика функций y(a),dy(a)
![]()
Форма для ввода исходных данных и построения c семейства графиков функций y(x),dy(x) при значениях параметра an,ak,
![]()
![]()
Табличный вывод данных
![]()
Пример 3. Моделирование падения шарика
радиуса R с высоты h.
Задачи исследования:
1. Получить зависимости h=f(t), v=f(t) при начальных значениях r,v0,h0,k1,k2.
2. Получить семейство графиков h=f(t,r), v=f(t,r).
3. Получить зависимость h=f(r), v=f(r) при t – const
Исходные данные:
1. Модель объекта падения, R - радиус шарика, h - высота падения, v0 - начальная скорость падения, k1 k2 - коэффициенты внешней среды.
Модель объекта и внешних условий
![]()
![]() - площадь сечения тела,
поперечного по отношению к потоку
- площадь сечения тела,
поперечного по отношению к потоку
![]() - динамическая вязкость
воздуха;
- динамическая вязкость
воздуха;
![]() плотность шарика;
плотность шарика;
![]() – плотность воздуха.
– плотность воздуха.
c = 0.4 – коэффициент лобового сопротивления шарика;
Блок - схема алгоритма
исследования модели![]()
.
Титульный лист проекта « Свободное падение тела»
![]()
Форма для ввода исходных данных
![]()
Форма для вывода табличных
![]()
Форма для построения графика h=f(t), v=f(t) при r=
![]()
Форма для построения семейства графиков функций
![]()
Форма для построения графика функции v=f(r)
![]()
Пример Моделирование системы с использованием программы MatLab.
![]()
Графики зависимостей v(t), h(t) для r=5mm c
помощью решателей ode15,ode45
![]()
m-файл для решения ДУ с помощью решетелейM-
file f1.m:
function F1=pli(t,y)
mu=0.018; //динамическая вязкость воздуха
p1=800; //плотность шарика
p2=1.29; //плотность воздуха
c=0.4; //лобовое сопротивление шарика
g=9.8;
k=1000; //число разбиений
r=0.005; //радиус шарика
F1=[-y(2);9.8-9*mu/(r*r*p1*2)*y(2)-
3*c*y(2)*y(2)*p2/(8*r*p1)];
m-файл для решения ДУ с помощью программы на языке программы MatLab // вычисление коэффициентов для метода Рунге - Кутта
k11=-dx*y(2);k21=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*y(2)*y(2)*p2/(8*r*p1));
k12=-dx*(y(2)+k21/2);
k22=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k21/2)*(y(2)+k21/2)*p2/(8*r*p1)); k13=-dx*(y(2)+k22/2); k23=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k22/2)*(y(2)+k22/2)*p2/(8*r*p1));
k14=-dx*(y(2)+k23);k24=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k23)
*(y(2)+k23)*p2/(8*r*p1)); //расчёт разности
d1=(k11+2*k12+2*k13+k14)/6; d2=(k21+2*k22+2*k23+k24)/6;
//вычисление новых значений у1 и у2
y(11)=y(1)+d1; y(21)=y(2)+d2;
plot([x x+dx],[y(1) y(11)],’r’);plot([x x+dx],[y(2) y(21)],’b’),
x=x+dx; //новое значение х
y(1)=y(11); y(2)=y(21);
end;
grid on; //добавляет сетку к текущему графику
title(“Kpuvue v(t) u h(t) npu r = 5mm”); //установка на
графике титульной надписи
legend(“vucota”,’ckopoct’); //добавление к текущему графикуy(2)=0;y(1)=10;x0=0;xk=10;dx=(xk-x0)/k;
r0=0.002;rk=0.005;dr=(rk-r0)/3;
n=2;x=x0;r=r0;
subplot(2,1,2);hold on;
while r<=rk
for i=0:k-1
if y(1)<0 break,end;
k11=-dx*y(2);
k21=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*y(2)*y(2)*p2/(8*r*p1));
k12=-dx*(y(2)+k21/2);
k22=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k21/2)*(y(2)+k21/2)*p2/(8*r*p1)); k13=-dx*(y(2)+k22/2);
k23=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k22/2)*(y(2)+k22/2)*p2/(8*r*p1)); k14=-dx*(y(2)+k23);
k24=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k23)*(y(2)+k23)*p2/(8*r*p1));
d1=(k11+2*k12+2*k13+k14)/6; d2=(k21+2*k22+2*k23+k24)/6;
y(11)=y(1)+d1; y(21)=y(2)+d2;
plot([x x+dx],[y(1) y(11)],'r'); plot([x x+dx],[y(2) y(21)],'b');
x=x+dx; y(1)=y(11); y(2)=y(21); end;
x=x0; y(2)=0; y(1)=10;
r=r+dr; end;grid on;
title('Cemeuctvo v(t) u h(t): 2mm < r < 5mm');
legend('vucota','ckopoct');xlabel('t');ylabel('v,h');
plot([0 5],[0 0],'k');axis tight;hold off;
Графики зависимостей v(t),h(t) при r=5 mm и
семейство графиков для 2mm<R<5mm
![]()
Блок-схема моделирования с помощью системы
Simulink
![]()
Графики решений с использованием Simulink
![]()
Пример 4. Моделирование колебаний математического маятника1. Получить зависимости угла отклонения маятника от времени Ɵ =f(t) при гармонических колебаниях, с учетом трения и вынужденных колебаниях.
Исходные данные
1. Модели объекта для различных режимов исследований;
2. Начальный угол отклонения Ɵ(0), , время исследований t, начальная фаза колебаний φ, коэффициенты трения внешней среды А, В.
Задачи исследования
1. Исследовать зависимости Ɵ =f (t) от параметров: амплитуды А, массы m, длины нити l, коэффициента трения k и начальной фазы φ, а также от параметров вынужденных колебаний: частоты и коэффициентов А, В Исходные данные1. Модели объекта для различных режимов исследований;
2. Начальный угол отклонения Ɵ(0) , время исследований t, начальная фаза колебаний φ , коэффициенты трения внешней среды А, В.
Результат. ![]()
Модель маятника
1. Для незатухающих колебаний
![]()
2. Для затухающих колебаний
![]()
3. Для вынужденных колебаний
Блок - схема алгоритма моделирования маятника
![]()
Form 1. Титульный![]() лист
лист
Form2. Форма для ввода начальных условий, задания условия и выбора режима исследования.
![]()
График незатухающих колебаний маятника
![]()
Form3. Форма для ввода начальных условий, задания условия и выбора режима исследования для
![]() затухающих колебаний.
затухающих колебаний.
График затухающих колебаний маятника![]()
![]() Form4. Форма для ввода начальных условий, задания
условия и выбора режима исследования для
Form4. Форма для ввода начальных условий, задания
условия и выбора режима исследования для
вынужденных колебаний.
. График вынужденных колебаний маятника
![]()
Пример 5. Исследовать динамику объекта, брошенного под углом к горизонту
Задачи исследования
1.Исследовать зависимость дальности бросания объекта от угла бросания;
2. Исследовать зависимость дальности бросания от направления и скорости ветра;
3. Найти оптимальные углы бросания и начальные значения скорости для попадания в цель.
Исходные данные
Начальное значение угла бросания и скорости объекта, направление и скорость ветра; координаты цели
( дальность до цели). Результат.
Дальность бросания в зависимости от угла и от скорости ветра, оптимальные начальные данные для попадания в цель.
Модель объекта1. Динамика объекта описывается системой дифференциальных уравнений
![]()
mdvx/dt = -Fccosq =-Fcvx/v0
mdvy/dt = -m*g - Fcsinq,=-m*g - Fcvy/v0,
где Fc =k1V+ k2*V2 - линейная и квадратичная составляющая сопротивления воздуха
2. Динамика объекта может представляется и алгебраическими уравнениями вида
![]()
![]()
![]()
Титульный лист проекта исследования динамики
тела, брошенного под углом к горизонту
Блок - схема алгоритма исследование траектории
тела, брошенного под углом к горизонту .
![]()
![]() Исследования тела для различных скоростей ветра W
Исследования тела для различных скоростей ветра W
Исследования динамики тела для диапазона
![]() изменений скорости
ветра от Wn до Wk
изменений скорости
ветра от Wn до Wk
Исследование зависимости дальности бросания
![]() объекта от
угла бросания
объекта от
угла бросания
Определения оптимальных траекторий объекта
от начального угла бросания и скорости объекта
![]()
Пример 6. Исследование динамики полета ракеты. Задачи исследования:
1.Исследовать траекторию полета ракеты на активном и пассивном участках траектории полета в зависимости от исходных данных;
2.Представить полет ракеты в виде динамической графики.
Исходные данные:
масса корпуса и головки ракеты m, M, время выключения двигательной установки t, начальные координаты ракеты x,y,
начальный угол тангажа между осью ракеты и горизонтом
вектор силы тяги двигателя ракеты Р, аэродинамические коэффициенты среды и рулей
Результаты:
дальность полета ракеты Х, высота полета ракеты Y, время полета ракеты Т.
![]() Модель ракеты
Модель ракеты
. ы
![]()
Титульный лист проекта исследования
динамики полета ракеты
Блок-схема алгоритма
![]()
Форма для ввода исходных данных для исследования
![]()
Форма для вывода табличных данных
результатов исследования
![]()
Форма для вывода траектории полета головки
и корпуса ракеты
![]()
Форма для динамической имитации полета ракеты
![]()
Исследование динамики полета ракеты
с помощью программы MatLab
Математическая модель ракеты
![]()
Меню исследования с помощью решателей ДУ
и программы Simulink
![]()
![]() Траектории полета головки и корпуса ракеты,
Траектории полета головки и корпуса ракеты,
полученные с помощью решателей ДУ
![]()
![]()
![]() Сравнение результатов моделирования без изменения ссы
и с изменением массы ракеты
Сравнение результатов моделирования без изменения ссы
и с изменением массы ракеты
Изменение угла наклона тангажа в полете
![]() Схема моделирования в
системе Simulink
Схема моделирования в
системе Simulink
Траектории полета корпуса ракеты и головки
![]()
function F0=mmm(t,y)
v=10;
g=9.8;
if t>=tv
p=0;
m=95000; F0=[(p*cos(y(2))-cos(y(2))-g*sin(y(2)))/m;10*((p*sin(y(2))+sin(y(2)))/m
-g*cos(y(2)))/y(1);-y(1)*cos(y(2))/10;y(1)*sin(y(2))/10];
else
p=1000000;
m=10000; F0=[(p*cos(y(2))-cos(y(2))-g*sin(y(2)))/m;((p*sin(y(2))+sin(y(2)))/m
-g*cos(y(2)))/y(1);-y(1)*cos(y(2))/10;y(1)*sin(y(2))/10];
end;
M - файл программы траектории полета головки ракеты
Y0=[1000 pi/2 0 0]; [T,Y]=ode15s(@F0,[0 1000],Y0); plot(Y(:,3),Y(:,4),’r’);
hold on;
[T,Y]=ode15s(@F1,[0 1000],Y0); plot(Y(:,3),Y(:,4),’b’); title(“Traektoria”);
xlabel(“x km”);
ylabel(“y km”);
axis([0, 5000, 0, 5000]);
![]()
Пример 7. Моделирование полета кометы
Условия задачи
![]()
Исходные данные
Расстояние от Солнца до кометы = 100 астрономических единиц ( 1 а.е.=1.5 *10 11 м) Начальная скорость кометы ( в пределах 10км/с) Угол к оси « Комета - Солнце» Траектория движение кометы ( S расстояние до Солнца, x,y - координаты движение
Результат
Траектория движение кометы ( S расстояние до Солнца, x,y - координаты движение
![]()
Математическая модель
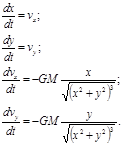
M -масса «большого» тела;
G - гравитационная постоянная = 6,67*10-11 m3/кг с2x,y,vx,vy - координаты и скорость «малого» тела
( планеты)
![]()
![]()
c = 0.4 – коэффициент лобового сопротивления шарика;
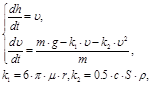
![]()
Блок - схема алгоритма моделирования
движения кометы в солнечной системе
![]()
Пример 8. Моделирование динамической системы
« хищники - жертвы»
Задачи исследования:
Исследовать динамику численности популяций хищника и жертвы в зависимости от условий их существования.
Исходные данные :
Начальная численность популяций хищников C и жертв N, скорость роста численности жертв r, коэффициент поиска a, скорость убывания хищников q при отсутствии жертв, скорость поедания f, время испытаний t.
Результат
Количество хищников и жертв в течении конкретного времени.
Модель объекта.
1. Модель объекта представляется системой дифференциальных уравнений вида
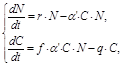
Пример.
С=100
N=300
r=3
a`=0.03
q=3
f=0.3
Результат: t=10, С=176; N=131.
Блок-схема алгоритма
моделирование численности хищников и жертв
![]()
Титульный лист проекта исследования динамики
![]() численности хищников и жертв
численности хищников и жертв
Условия моделирования
![]()
Форма для ввода исходных данных и графика
![]() Исследования
Исследования
Исследования системы с помощью решения
дифференциальных уравнений в среде MatLab
m-файл для решения ДУ с помощью решателей
M-file ekologya.m:
Y0=[3 4]; //вектор начальных условий
[T,Y]=ode15s(@F,[0 10],Y0); //решение системы с помощью ode15s
subplot(2,1,1); //деление формы на 2 граф. окна, исп-ние первого из них
plot(Y(:,1),Y(:,2)); //построение графика функции y2(y1)
grid on; //добавляет сетку к текущему графику
title(“Xusniki u gertvu”); //установка на графике титульной надписи
xlabel(“xusniki”); //установление надписи на оси ОХ
ylabel(“gertvu”); // установление надписи на оси ОУ
legend(“xusniki u gertvu”); //добавление к текущему графику легенды
subplot(2,1,2); // переход ко второму граф. окну
plot(T,Y); //построение графиков функций y1(t) и y2(t)
grid on; //добавляет сетку к текущему графику
title(“Xusniki u gertvu”); //заголовок графика
xlabel(“t”); // установление надписи на оси ОХ
ylabel(“koluchestvo”); // установление надписи на оси ОУ
legend(“gertvu”,’xusniki’); // добавление к текущему графику легенды
Во второй строке этот m-file обращается к m-file’у F.m, в котором записана сама система ДУ:
function F=eko(t,y)
F=[3*y(1)-y(1)*y(2);-2*y(2)+y(1)*y(2)];
Графики зависимости количество популяций
хищников от жертв и от времени исследования
![]() Исследования системы с
помощью программы решения дифференциальных уравнений в среде MatLab
Исследования системы с
помощью программы решения дифференциальных уравнений в среде MatLab
M-file Ekosr.m:
subplot(2,1,1); //деление формы на 2 граф. окна
k=1000; //количество разбиений
y(1)=3; y(2)=4;//начальные условия
x0=0;xk=5;x=x0;//границы изменения времени
dx=(xk-x0)/k; //шаг интегрирования
hold on; //обеспечивает продолжение вывода графиков в текущее окно for i=0:k-1
if y(1)<0 break,end; //если высота < 0, то выход из цикла
// вычисление коэффициентов для метода Рунге - Кутта
k11=dx*(3*y(1)-y(1)*y(2));
k21=dx*(-2*y(2)+y(1)*y(2));
k12=dx*(3*(y(1)+k11/2)-(y(1)+k11/2)*(y(2)+k21/2));
k22=dx*(-2*(y(2)+k21/2)+(y(1)+k11/2)*(y(2)+k21/2));
k13=dx*(3*(y(1)+k12/2)-(y(1)+k12/2)*(y(2)+k22/2));
k23=dx*(-2*(y(2)+k22/2)+(y(1)+k12/2)*(y(2)+k22/2));
k14=dx*(3*(y(1)+k13/2)-(y(1)+k13/2)*(y(2)+k23/2));
k24=dx*(-2*(y(2)+k23/2)+(y(1)+k13/2)*(y(2)+k23/2));
//расчёт разности
d1=(k11+2*k12+2*k13+k14)/6;
d2=(k21+2*k22+2*k23+k24)/6;
//вычисление новых значений у1 и у2
y(11)=y(1)+d1; y(21)=y(2)+d2;
plot([x x+dx],[y(1) y(11)],’r’);
plot([x x+dx],[y(2) y(21)],’b’),
x=x+dx; //новое значение х
y(1)=y(11);
y(2)=y(21);
xlabel(“t”); // установление надписи на оси ОХ
ylabel(“koluchestvo”); // установление надписи на оси ОУ
legend(“gertvu”,’xusniki’); //добавление к графику легенды
plot([0 x],[0 0],’k’);
![]() hold off; //отменяет режим
продолжения графических
hold off; //отменяет режим
продолжения графических
й
Исследование системы с использованием
![]() программы Simulink
программы Simulink
Исследование системы численности популяций
хищников и жертв
![]()
Пример 9. Моделирование развития эпидемии в
деревне с течением времени.
Задачи исследования:
Для исходных данных: количество здоровых, больных и переболевших людей с учетом коэффициентов, влияющих на время выздоровления, определить количество здоровых, больных и переболевших людей в течение заданного промежутка времени. Начальные условия. Начальные численности людей ( здоровых, больных и переболевших) соответственно x0, y0, z0; частота контактов здоровых и больных людей b (0 -20), величина обратная времени выздоровления, зависящая от эффективности лекарств с (0- 20), время исследования T
Результат.
Получить графики зависимости числа здоровых, больных и переболевших людей от времени x=f(t), y=f(t), z=f(t). Математическая модель
1. Дифференциальная форма уравнений
dx/dt=-bxy;
dy/dt=-cy+bxy;
dz/dt=cy, где
x,y,z -количество здоровых, больных и переболевших в момент времени t;
b - частота контактов;
c- время выздоровления.
2. Алгебраическая форма уравнений
x(i+1)=x(i)-bx(i)y(i);
y(i+1)=y(i)=y(i)-cy(i)+bx(i)y(i);
z(i+1)=z(i)+cy(i).
Блок - схема алгоритма исследования развития эпидемии
![]()
![]()
![]()
Пример 10. Моделирование прироста коз на изолированном острове от наличия травы.
Задачи исследования: Исследовать зависимость прироста коз на острове от роста травы. Рост травы определяется разностью между максимальным и текущим количеством травы и численностью коз. Исходные данные.
Текущая численность коз n1, текущие запасы травы n2, максимальное количество травы, которая может вырасти на острове N max, коэффициент смертности коз А, коэффициент размножения коз В, коэффициент роста травы К1, количество травы, съедаемой одной козой К2.
Результат. Построить график зависимости прироста количества коз от запасов травы.
Математическая модель.
![]()
Пример.
Текущая численность коз 2000
Запасы травы 60000 кг
Максимальное количество травы 100000 кг
Коэффициент смертности 0.002
Коэффициент роста травы 0.95
Коэффициент размножения коз 0.009
Количество травы, съедаемой одной козой 10кг
Блок - схема алгоритма исследования прироста коз
от роста травы.
![]()
![]()
Форма для ввода данных и вывода результата моделирования
![]()
Пример 11. Моделирование производства
и транспортировки товаров.
Задачи исследования.
Минимизировать производство и транспортировку товаров. Исходные данные. Количество пунктов размещения предприятий - m, количество пуктов потребности в товарах - n, количество продукции на пунктах потребности b(n), затраты на производство единицы продукции - с(m), затраты на транспортировку единицы продукции с(i,j), максимальный объем производства a(m), количество перевезенных продутов из i - пункта предприятия в j -ый пункт потребности - x(i,j). Результат.
Вычислить минимальные затраты на производство и транспортировку продукции.
Математическая модель. Критерий обеспечения минимума
![]()
Пример.
m=2, n=5,b=(4,4,5,3,5), c(2,3), a(10,15),
cij=( 1 2 3 2 3)
( 1 2 1 2 3).
Результат:
xij= 4 4 0 2 0 0
0 0 5 1 5 4
Количество производимых продуктов 10 11.
Затраты на производство
min(4+3+4+4+2+4+5+4+1+5+5+6)= 91
Блок - схема алгоритма производства
и транспортировки товаров.
![]()
Пример 13. Моделирование системы
![]() массового обслуживания. Форма
для вывода результата исследования
массового обслуживания. Форма
для вывода результата исследования ![]() Основная
форма для ввода исходных данных
Графическая форма результатов исследования
Основная
форма для ввода исходных данных
Графическая форма результатов исследования
![]()
Пример 13. Моделирование системы
массового обслуживания.
Задачи исследования.
В систему, состоящую из n пунктов обслуживания, поступают в отдельные случайные моменты времени заявки. Поток заявок представляют собой простейший поток со случайным интервалом времени по экспоненциальному закону.
Исходные данные:
n - число каналов системы массового обслуживания;
Т - время работы системы;
λ - интенсивность потока заявок;
а - начало рабочего дня ( работы);
tc - среднее время пребывания заявки в системе;
Е - экономическая эффективность системы массового обслуживания. Основные показатели эффективности работы:
Ротк - вероятность отказа;
QH - абсолютная пропускная способность;
q - относительная пропускная способность;
NЗ - среднее число занятых обслуживающих приборов:
L -средняя длина очереди;
Математическая модель.
E = C0Q - C; C = n(KЗCЗ + KпCп) + CожL + Cy(1 - q) ,
где
C0 - прибыль при обслуживании заявки;
С - функция стоимости потерь;
CЗ - стоимость эксплуатации прибора в единицу времени;
Cп - стоимость единицы времени простоя;
Cож - стоимость потерь, связанных с простаиванием заявки в очереди, в единицу времени;
Cy- стоимость убытков, связанных с уходом заявки из
системы;
KЗ - коэффициент занятости приборов, KЗ = Nз/n;
Kп- коэффициент простоя, Kп = 1 - KЗ.
Пример - T = 7 часов;
- =10 ;
- а = 8 часов;
- N - 10.
Результатами моделирования являются:
m(i) - число поступивших заявок за время работы системы =67,
О(i) - число обслуженных системой заявок в каждом из испытаний =17,
ОТ(i) - число отказов системы в каждом из испытаний.
Основными показателями эффективности работы системы являются:
- вероятность отказа Ротк=75%;
- абсолютная пропускная способность Qн = 19 ,
где - интенсивность потока обслуживания,
n - число каналов=2;
q - относительная пропускная способность q = Q/ =191
где - интенсивность заявок;
Nз =478- среднее число занятых обслуживающих приборов = aq, где a = tобсл /tс - параметр обслуживания (среднее необходимое число обслуживающих приборов), tобсл - случайная величина, распределенная по показательному закону;
L=4- средняя длина очереди - математическое ожидание от числа заявок;
tc =5- среднее время пребывания заявки в системе
= tож + tобсл , где tобсл - среднее время от момента начала обслуживания до момента окончания обслуживания,
tож =1- время ожидания заявки в очереди;
E =10784 - экономическая эффективность системы массового обслуживания (прибыль в единицу времени).
Блок - схема алгоритма моделирования системы
массового обслуживания
![]()
Пояснение к блок-схеме
1. Ввод данных:
,a,b - параметры закона распределения потока заявок и времени обслуживания;
T - время работы системы;
N - заданное число испытаний.
2. Установка начальных условий перед очередным испытанием.
3. Поступление k-той заявки на обслуживание.
4. Определение принадлежности k-той заявки заданному интервалу времени T.
5. Сравнение моментов освобождения каналов системы и выбор освободившихся ранее других каналов.
6. Сравнение моментов освобождения выбранных каналов tm с моментом поступления k-той заявки Tk. Если условие не выполняется, то все каналы к моменту Tk заняты и система выдает отказ.
7. Подсчет числа отказов. 8. Формирование потока заявок по формуле Tk= -1/ lnR, определение интервала времени между двумя заявками и выработка случайных чисел R.
9. Формирование моментов поступления следующей заявки по формуле Tk+1 = Tk + k
10. Формирование номера очередной заявки.
11. Определение времени обслуживания k-той заявки по формуле tkобсл = a + (b - a)R.
12. Вычисление времени освобождения t(m) канала с номером m по формуле tm = Tk + tkобсл
13. Счетчик числа обслуженных заявок.
14. Счетчик числа испытаний.
15. Условие на проверку окончания испытаний N.
16. Осуществление статистической обработки полученных результатов и вычисление требуемых показателей эффективности функционирования системы за время T.
Основная форма для ввода и вывода данных
![]()
График зависимости выполненных заявок
в каждом испытании n - число каналов системы;
![]()
Пример 13. Моделирование систем
массового обслуживания
« Очередь к одному продавцу», «Работа телефониста по обслуживанию разговоров»,
« Работа студентов в компьютерном классе» и т.д..
Задачи исследования.
1.Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, то он начинает обслуживать покупателя, если покупателей много , то выстраивается очередь. 2. К телефонисту поступают звонки через случайные интервалы времени. Время разговоров также случайное. Если линия занята, то формируется очередь. 3. В компьютерный класс входят студенты для работы на компьютерах. Время работы ограничено. Если все компьютеры заняты, то формируется очередь. Исходные данные: t1 - начало рабочего дня ( работы);
t2 - конец рабочего дня ( работы);
ti - интентивность потока заявок;
Результат
tpok - среднее время ожидания в очереди покупателем (соединения разговора, студентов для работы на компьютерах);
tprod - среднее время простоя продавца (непоступление звонков, отсутствие студентов в классе);
n =- количество обслуженных покупателей;
Математическая модель
![]() Случайный процесс
прихода покупателей описывается функцией Пуассона
Случайный процесс
прихода покупателей описывается функцией Пуассона
Случайный процесс обслуживания продавцами покупателей по равновероятному закону
x=a+(b-a)*r
Для разработки алгоритма используются следующие переменные и формулы:
а - промежутки времени между приходами покупателей (звонками, студентов) в диапазоне аmin, amax;
в - длительность обслуживания покупателей ( абонентов, студентов) в диапазоне bmin, bmax;;
с - время прихода покупателей ( звонка, студентов);
d - момент ( время) начало обслуживания;
e - момент ( время) конца обслуживания;
f - длительность времени нахождения покупателя в магазине, разговора и работы студентов на компьютерах;
g - длительность времени нахождения в очереди;
h - время ожидания продавцом покупателя.
![]()
![]()
Блок -схема алгоритма систем массового
обслуживания с очередями
![]()
Пример.18. Моделирование процесса раскроя
материала
Задачи исследования.
Необходимо раскроить детали А и В из листа материала размером m*n. Детали имеют следующий вид и размеры:
Деталь А Деталь В
Программа эксперимента может включать вопросы:
1. Сколько надо спланировать листов материала размером m*n для получения К деталей А и K1 деталей В;
2. Какой из вариантов раскроя наиболее рациональный (экономный с точки зрения излишек материала от раскроя);
3. Какие размеры m*n необходимо иметь для раскроя нескольких деталей с различными размерами.
Исходные данные
Для выполнения поставленной задачи целесообразно иметь следующие модели: модель объекта моделирования (раскроя материала), модель метода моделирования, модель графического представления раскроя на экране дисплея, модель задания условий эксперимента. В качестве модели объекта моделирования составляются уравнения цели и ограничений, рассмотренных раннее. Для их реализаций надо иметь следующие исходные данные:
X - число листов для раскроя материала;
VR - варианты раскроя;
N - количество деталей раскроя;
CNK - число комплектов для получения заданного числа деталей;
l,h - длина и ширина материала раскроя. Для модели реше ния используется модель метода решения линейного программирования - модель симплекс-метода (М2).
Результат
Расчет минимального количества листов материала для раскроя требуемого количества деталей.
Для построения модели графического представления (М3) необходимо предусмотреть следующие возможности такой модели:
- задание исходного листа материала для раскроя деталей;
- рисование заданных деталей раскроя;
- ввод размеров деталей;
- просмотр и выбор вариантов раскроя.
Математическая модель
Функция цели
![]()
Условия
![]()
Необходимо найти максимум линейной функции
( функции цели).
![]()
Блок - схема алгоритма моделирования
раскроя материала
![]()
Формы для ввода и вывода данных и результата
![]()
![]()
Пример15 . Моделирование системы планирования
на основе метода сетевого графа
Задачи исследования
Необходимо спланировать временный график обучения школьных предметов (математика, физика, химия) с учетом прохождения тем по каждой дисциплине. Допустим, что в математике имеется 6 тем, в физике - 5 тем, а в химии - 4 темы. Причем в физике 4-я тема должна проходить после 5-й темы по математике, а 3-я тема по химии - после 6-й темы. по математике.
Требуется определить критический путь (время) прохождения исходных предметов.
Исходные данные
N (количество предметов) = 3,
продолжительность прохождения каждой темы tij.
MAT (t10,1 = 8час, t11,2= 6час, t12,3 = 12час, t13,4 = 14час,
t14,5 = 10час, t15,6 = 6час).
FIZ (t20,1 = 10час, t21,2 = 8час, t22,3 = 4час, t23,4 = 12час,
t24,5= 14час).
HIM (t30,1 = 8час, t31,2 = 10час, t32,3 = 12час, t33,4 = 6час).
Связь с дисциплинами t1(5) - t2(4) = 0 , t1(6) - t3(3) = 0 .
Результат
Необходимо получить сетевой граф прохождения школьных дисциплин, который для данных исходных данных имет вид:
![]() Критический путь
0 - 1 - 2 - 3 - 4 - 5 - 6 - 14 - 15 L = 62
Критический путь
0 - 1 - 2 - 3 - 4 - 5 - 6 - 14 - 15 L = 62
Математическая модель
Ранний срок наступления событи1С учетом Ti(p) и Tj(n) определяются резервы времени Rk для каждого номера событий. Критический путь находят по тем событиям, в которых резервы времени Rk равны нулю.
Параметр Ti(p) вычисляется по формуле
Ti(p) = max { Tj(p) + tij } , где i=0,N-1; j=1,N (T0(P)=0.
Параметр tjn вычисляется по формуле
Tj(n) = min { Ti(n)-tij} , где TN(n) = TN(p);
Резерв времени определяется по формуле
Rk = Tk(n) - Tk(p).
Блок-схема алгоритма моделирования включает:
- модель 1 - модель сетевого графа, которая состоит из графа и таблицы матрицы tij; - модель 2 - модель матричного метода сетевого планирования, определяющая ранние и поздние сроки наступления событий;
- модель 3 - модель графического отображения результатов моделирования.
![]()
Блок-схема алгоритма моделирования
задачи планирования на основе сетевого графа
![]()
![]()
Пример 16 Моделирование экспертной системы
распознавания болезней
Задачи моделирования
Сформировать модель экспертной системы распознавания болезней с использованием статистического метода на основе формулы Байеса, обучить модель распознаванию простудные болезней и провести вычислительный эксперимент по определению болезней по характерным признакам простудных заболеваний ( ОРЗ, грипп, ангина)..
Исходные данные: Простудные заболевания: R1,R2,R3 (ОРЗ, грипп, ангина );Характерные признаки простудных болезней; x1,x2,x3,x4 (температура, кашель, покраснение горла и вялость).
Результат: Конкретная болезнь с учетом введенных характерных признаков на основании условных вероятностей P(xi/Rj), вычисленных по формуле Байеса.
Математическая модель
1. Вычисляются условные вероятности для каждой болезни и признака p(xi/Rj) в режиме обучения экспертной системы
p(x1/R1)=0,8 p( 1/R1)=0,2 p(x2/R1)=0,8 p( 2/R1)=0,2
p(x3/R1)=0,4 p( 3/R1)=0,6 p(x4/R1)=0,2 p( 4/R1)=0,8
![]()
p(x1/R2)=0,4 p( 1/R2)=0,6 p(x2/R2)=0,6 p( 2/R2)=0,4
p(x3/R2)=1,0 p( 1/R2)=0,0 p(x4/R2)=0,2 p( 4/R2)=08
p(x1/R3)=0,2 p( 1/R3)=0,8 p(x2/R3)=0,4 p( 2/R3)=0,6
p(x3/R3)=0,4 p( 3/R3)=0,6 p(x4/R3)=1,0 p( 4/R3)=0,0
Априорные вероятности болезней обычно задаются с учетом опыта «врача», если таких данных нет, то устанавливаются равновероятные значения
p0(R1)=0,33 p0(R2)=0,33 p0(R3)=0,33
2. В процессе работы устанавливаются признаки больного человека. Например, такими признаками являются
x1= (+), x2=( - ), x3=(-), x4=(+).
3. C учетом условных вероятностей и формулы Байеса имеем
R1=1/3*0,8*0,2*0,6*0,2=0,0066;
R2=1/3*0,4*0,4*0*0,2=0;
R3=1/3*0,2*0,6*0,4*1=0,018/
Таким образом, R3>R2>R1, то болезнь -R3 -Ангина.
Для распознавания болезней по характерным признакам, условным и априорным вероятностям необходимо иметь: модель признаков болезней, модель метода распознавания, модель проведения эксперимента. Модель признаков болезней состоит из условных вероятностей болезней P(xi/Rj) и характерных признаков Xi. Модель формируется в результате обучения модели по введенным характерным признакам. Модель метода распознавания включает в себя формулу Байеса и метод определения max Rj. В модель проведения эксперимента можно включить: режим ввода характерных признаков и вывода результатов моделирования в виде таблицы или блока признака болезней. Алгоритм моделирования представляется блок-схемой .
![]()
Диаграмма классов экспертной системы по диагностики
заболеваний
Блок-схема алгоритма моделирования
задачи распознавания болезней
![]()
Титульный лист экспертной системы
![]() распознавания
болезней
распознавания
болезней
Основная форма для ввода исходных данных
![]()
Задача 17 . Моделирование системы управления
хранения запасов на складах. Задачи исследования.
Необходимо определить размер партии товаров на складе при котором минимизируются годовые затраты.
Исходные данные.
Организационные издержки (s) - расходы связанные с оформлением и доставкой товаров, необходимых для каждого цикла складирования.
Размер партии (q) - количество товара поставляемого на склад.
Издержки содержания запасов (h) - затраты на хранение и амортизацию.
Интенсивность спроса ( d) -
Стоимость товара (с) -
Результат
Путем моделирования определить оптимальный размер партии q
Математическая модель
Уравнение издержек:
C1=s*(d/q) общие организационные издержки
C2=c*d стоимость товаров
C3=h*(q/2) общие издержки на содержание запасов
C = C1 + C2 + C3
C = s*(d/q) + c*d + h*(q/2)
q - неизвестная величина
С-должна обращаться в минимум
Если dC/dQ)=0 , то (dC/dQ)=-(s*d)/(q*q)+0+(h/2)=0. Из выражения q^2=(2*s*d)/h можно определить оптимальный размер партии.
Алгоритм задачи должен включать следующие модели:
модель управления запасами, модель производственных поставок и модель включающая штрафы.
МОДЕЛЬ ПРОИЗВОДСТВЕННЫХ ПОСТАВОК.
Модель описывает случай когда товары поступают на склад с производственной линии,скорость производства которой p товаров в год. Поступление заказов считаем непрерывным. Интенсивность спроса d. За каждый цикл изменения запасов на склад поступает q единиц товара с производственной линии. Как только уровень запасов упадет до нуля, с производственной линии начнет поступать следующее количество товаров. q - количество товара в одной поставке(партии). C3=(средний уровень запасов)*h
откуда нетрудно найти и оптимальный размер партии аналогично
Тогда C = C1 + C2 + C3 = (s*d)/q + c*d + ((p-q)*q*h)/2*p
МОДЕЛЬ ВКЛЮЧАЮЩАЯ ШТРАФЫ
Допустим существуют периоды дефицита товаров. Пусть по контракту некоторая фирма должна поставить q ед. товара в течение каждого промежутка времени про-
должительностью L, за единицу времени поставляется d ед. товара (q=L*d). Значения q и d постоянны и зафиксированы контрактом.
Предположим, что в начале каждого периода L фирма делает запас единиц товара (y<q), равный y. Это означает, что в течение периода будет наблюдаться дефицит товара и поставки в это время не будут осуществляться. Невыполненные заявки будут накапливаться до величины q-y, они будут удовлетворены, как только поступит следующая партия товаров в количестве q.
За то, что товары поставляются не вовремя, на нее возлагается штраф. Иногда выгоднее платить штрафы, чем расходовать средства на хранение запасов (y>q).
Задача управления: найти y, которое минимизирует затраты. Издержки одного цикла=Издержки на содержание + штраф С = С1 + С2 = h*(y/2)*(y/d) + p*((q-y)/d)*((q-y)/2)
Откуда оптимальное значение y*=(p*q)/(h+p)
![]()
![]()
![]()
Пример 18. Моделирование систем, определяющих минимальное расстояние между двумя объектами.
Задачи исследования.
Заданы N городов с координатами (xi,yi). Представить графически в системе координат XOY расположение городов с использованием графа и матрицы расстояний. Моделирование реализовать с помощью метода Дейкстра и определить кратчайшее расстояние из пункта x1 в пункт x2.Форма таблиц с координатами городов и наличие дорог
Исходные данные.
n - количество городов;
XnYn - координаты городов;
xi,yi,xj,yj - начальные и конечные координаты городов, между которыми необходимо определить кратчайшее расстояние;
Матрица смежности - таблица соединения городов дорогами
Результат.
![]() Граф сети городов с
представленным кратчайшим расстоянием между двумя городами;
Граф сети городов с
представленным кратчайшим расстоянием между двумя городами;
Расстояние и путь прохождения между двумя городами;
Математическая модель.
![]()
Форма для вывода матрицы расстояний и графа пути
с указанием пути и кратчайшего расстояния
![]()
Блок-схема метода Дейкстра определения
кратчайших расстояний между городами
![]()
Пример 19. Моделирование объекта методом
пространства состояния, динамика которого
описывается дифференциальным уравнением
Задачи исследования:
Исследовать динамику объекта методом пространства состояния с использованием информационных технологий Mathcad и MatLab методом уравнений пространства состояний.
![]()
Исходные данные:
Начальные и конечные координаты объекта x(0), x`(0), xk, такт исследования T, управляющее воздействие u(0).
Результат
Получить зависимости x(T), x`(T) с использованием
программ Mathcad, MatLab
Математическая модель объекта.
Исходное дифференциальное уравнение имеет вид
![]()
Представим исходное уравнение в нормальной форме Коши, вводя обозначения
![]()
В результате получим систему уравнений первого порядка
![]()
С целью определения матриц уравнения параметров состояния преобразуем систему:
![]()
матрицы коэффициентов соответственно равны
![]()
![]()
![]()
![]()
![]()
Уравнение параметров состояния будет иметь вид
![]()
![]()
![]()
Решение данных примеров в системе Matlab
Для этого создадим 3 m-файла (для каждого примера отдельно). Далее эти m-файлы запустим в командном окне(command Window).
Описание m-файлов
Пример 1
figure(1); //вызов графического окна;
clf; //очиска фигуры;
title(“solve equation d(dx)+k1*dx=k2*u”); //установка титульной надписи
syms k1 k2 p t T i Y01 Y02; //задание переменных;
//ввод данных;
k2=0.01;
k1=0.5;
//ввод исходных матриц;
B=[0 1;0 -k1];
U=[0.1];
E=eye(size(B)); //создание единичной матрицы
A=[0;k2];
D=E*p;
W=D-B;
W1=inv(W); //нахождение обратной марицы
W2=ilaplace(W1,p,t); //обратное преобразование Лапласа
H=(int(W2,t,0,T))*A; //марица управления
Y0=[Y01;Y02]; //матрица начальных условий
Y01=0;Y02=1;
W21=ilaplace(W1,p,T); //матрица состояния
T=0.1; // такт работы
for i=0:10,
Y=W21*Y0+H*U; //расчетная формула
Y1=Y01+(-2*exp(-1/2*T)+2)*Y02+1/500*T+1/250*exp(-1/2*T)-1/250;
Y2=exp(-1/2*T)*Y02-1/500*exp(-1/2*T)+1/500;
Y01=Y1; Y02=Y2;
hold on;.//обеспечение продолжение вывода графиков в текущее окно
plot(i,Y01,’o’,i,Y02,’or’);//построение графиков
legend(“x”,’dx’); //добавление к текущему графику легенды
xlabel(“i”); //установка надписи на оси OX
ylabel(“x,dx”); //становка надписи на оси OY
grid on; //сетка
end
![]()
Исходное дифференциальное уравнение имеет вид
![]()
Представим исходное уравнение в нормальной форме Коши, вводя обозначения
![]()
В результате имеем систему уравнений первого порядка
![]()
С целью определения матриц уравнения параметров состояния преобразуем систему:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 2
figure(2); //вызов графического окна;
clf; //очиска фигуры;
title(“solve equation d(dx)+2*dx-3*x=u”); //установка титульной
надписи
syms p t T i Y10 Y20; //задание переменных;
//ввод данных;
B=[0 1;3 -2];
E=eye(size(B)); //создание единичной матрицы
U=[0.1];
A=[0;1];
D=E*p;
W=D-B;
W1=inv(W); //нахождение обратной марицы
W2=ilaplace(W1,p,t); //обратное преобразование Лапласа
H=(int(W2,t,0,T))*A; //марица управления
Y10=0;
Y20=1;
Y0=[Y10;Y20]; //матрица начальных условий
W21=ilaplace(W1,p,T); //матрица состояния
T=0.1; // такт работы
for i=0:10,
Y=W21*Y0+H*U;
Y1=(1/4*exp(-3*T)+3/4*exp(T))*Y10+1/16*16^(1/2)*(exp(T*(-
1+1/2*16^(1/2)))-exp(T*(-1-1/2*16^(1/2))))*Y20+1/40*(exp(-
T)*exp(1/2*16^(1/2)*T)*16^(1/2)+8*exp(-T)*exp(1/2*16^(1/2)*T)-exp(-
T)*exp(-1/2*16^(1/2)*T)*16^(1/2)+8*exp(-T)*exp(-1/2*16^(1/2)*T)-
16)/(-2+16^(1/2))/(2+16^(1/2));
Y2=3/16*16^(1/2)*(exp(T*(-1+1/2*16^(1/2)))-exp(T*(-1-
1/2*16^(1/2))))*Y10+(3/4*exp(-3*T)+1/4*exp(T))*Y20-1/40*exp(-
3*T)+1/40*exp(T);
Y10=Y1;
Y20=Y2;
hold on; //обеспечение продолжение вывода графиков в текущее окно
plot(i,Y1,’o’,i,Y2,’or’); //построение графиков
legend(“x”,’dx’); //добавление к текущему графику легенды
xlabel(“i”); //установка надписи на оси OX
ylabel(“x,dx”); //становка надписи на оси OY
grid on; end //сетка
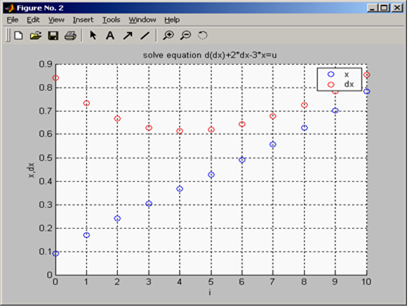
Краткая информация о вычислении отдельных выражений в программе MatLab
Создание единичной матрицы
Матрицы как двумерные массивы с числовыми элементами представляют собой самые распространенные объекты системы MATLAB.
Для создания единичной матрицы (она обычно обозначается как E) , которая имеет единичные диагональные элементы и нулевые все остальные, служит функция eye:
eye(n)-возвращает единичную матрицу размера
eye(m,n) или eye([m n])-возвращает матрицу размера m*nс единицами по диагонали и нулями в остальных ячейках;
eye(size(A))-возвращает единичную матрицу того же размера, что и A.
Пример использования функции eye:
>> t=eye(2)
t =
1 0
0 1
Обратное преобразование Лапласа.
Обратное преобразование Лапласа выполняется по следующей главной форме:
![]() где с- действительное число, такое, что все особенности функции L(s)
расположены слева от вертикали s=c, i-мнимая единица. Данное пробразование
осуществляется функцией ilaplace:
где с- действительное число, такое, что все особенности функции L(s)
расположены слева от вертикали s=c, i-мнимая единица. Данное пробразование
осуществляется функцией ilaplace:
F= ilaplace(L)-возвращает результат обратного преобразования Лапласа
Для скалярной символьной функции L с независимой переменной по умолчанию s.
Если L=L(t), то возвращается функция F=F(x).
Есть еще две формы преобразования:
F= ilaplace(L,y)-возвращает результат обратного преобразования Лапласа по
формуле
![]() F= ilaplace(L,y,x)-выполняет результат обратного преобразования Лапласа
F= ilaplace(L,y,x)-выполняет результат обратного преобразования Лапласа
по формуле
![]() Примеры обратного преобразования Лапласа:
Примеры обратного преобразования Лапласа:
syms s t w x
ilaplace(1/(s-1)) возвращает exp(t)
ilaplace(1/(t^2+1)) возвращает sin (x) ilaplace(t^(-sym(5/2)),x) возвращает 4/3/pi/^(1/2)*x^(3/2)
ilaplace(y/(y^2+w^2),y,x) возвращает cos(w*x)
Обращение матриц - функция inv
Обращение матриц - одна из наиболее распространенных операций матричного анализа. Обратной называют матрицу, получаемую в результате деления единичной матрицы E на исходную матрицу X.Таким образом, X-1=E/X.Для обращения (инвертирования) матрицы в символьном виде используется функция inv:
>> syms a b c d;
>> inv([a b;c d])
ans =
[ d/(a*d-b*c), -b/(a*d-b*c)]
[ -c/(a*d-b*c), a/(a*d-b*c)]
Вычисление интегралов
В практической работе часто возникает необходимость вычисления неопределенных и определенных интегралов вида
int(S)-возвращает символьное значение неопределенного интеграла от символьного
выражения или массива символьных выражений S по переменной, которая
автоматически определяется функцией findsym.Если S-скаляр или матрица, то
вычисляется интеграл по переменной ‘x’.
int(S,v)-возвращает неопределенный интеграл от S по переменной v.
int(S,a,b)- возвращает определенный интеграл от S с пределами интегрирования от a до b,причем пределы интегрирования могут быть как символьными, так и числовыми
int(S,v,a,b)-возвращает определенный интеграл от S по переменной v с пределами интегрирования от a до b.
Примеры применения этой функции приводятся ниже:
>> x=sym(“x”);
>> int(x^2,x)
ans =
1/3*x^3
>> int(sin(x)^3,x)
ans =
-1/3*sin(x)^2*cos(x)-2/3*cos(x)
Пример 20. Моделирование объекта, динамика которого описывается дифференциальным уравнением
в среде MAPLE с использованием решателей ДУ.
Задачи исследования:
Исследовать динамику объекта с использованием информационных технологий Maple методом составления и решения дифференциальных уравнений .
Исходные данные
Получить зависимости x(T), x`(T) с использованием
программ Mathcad, MatLab
> restart;
dsolve_symbolic
> p:=5;q:=-2;
> dsolve({diff(y(x),x,x)+p*diff(y(x),x)+q*y(x)=exp(-x)*sin(x),y(0)=2,D(y)(0)=0},y(x));
y(x) = -1/58*(3*cos(x)+7*sin(x)-58*(119/116+
201/1276*33^(1/2))*exp(1/2*(-5+33^(1/2))*x)*exp(x)
-1/66*(-603+119*33^(1/2))*33^(1/2)*
exp(-1/2*(5+33^(1/2))*x)*exp(x))/exp(x)
graph_numric
> p:=5;q:=-2;
> dsol:=dsolve({diff(y(x),x,x)+p*diff(y(x),x)+q*y(x)=exp(-x)*sin(x),y(0)=2,D(y)(0)=0},y(x),numeric,output=listprocedure);
> fy:=subs(dsol,y(x));
> a:=0;b:=1;n:=20;
>plot([seq([a+i*(b-a)/n,fy(a+i*(b-a)/n)], i=0..n)], color=black, labels=[x,y]);
 graph_model
graph_model
> q:=1;np:=10;hp:=0.5;
> for j from 1 to np do
> p:=j*hp;
> dsol:=dsolve({diff(y(x),x,x)+p*diff(y(x),x)+q*y(x)=exp(-x)*sin(x),y(0)=2,D(y)(0)=0},y(x),numeric,output=listprocedure);
> fy[j]:=subs(dsol,y(x))
> od:
> a:=0;b:=1;n:=20;
>plot({seq([seq([a+i*(b-a)/n,fy[j](a+i*(b-a)/n)],i=0..n)],
j=1..np)},color=black,labels=[x,y]); 
ЛИТЕРАТУРА
1. Алексеев О.Г. и др. Управление в системах РАВ. М.: МО, 1980г. - чI.
2. Белошапка В. Информатика как наука о буквах /Информатика и образование, 1992г.,N1, с 6-12.
3. Вершинин О.Е. Компьютер для менеджера. М.: Высшая школа, 1990г.
4. Глушков В.М. Кибернетика. Вопросы теории и практики. М.: Наука, 1986г.
5. Глушков В.М. Введение в АСУ. К.: Техника, 1974г.
6. Глушков В.М. Основы безбумажной информатики. М.: Наука,1978г.
7. Горстко А.Б. Познакомтесь с математическим моделированием. М.: Знание, 1991г.
8. Гулд Х. и др. Компьютерное моделирование в физике. М.: Мир, 1990г, - части I и II.
9. Ершов А.П. Об информационной модели машин./Микропроцессоре средства и системы, N4, 1985г., с2.
10. Заварыкин В.М. и др. Техника вычислений и алгоритмизация. М.: Просвещение, 1987г.
11. Заварыкин В.М. и др. Численные методы. М.: Просвещение,1991г.
12. Ивахненко А.Т. и др. Перцептрон - система распознавания образов, К.: Наукова думка, 1975г.
13. Кристофидес Н. Теория графов. Алгоритмическая наука. М.:Мир, 1978г.
14. Кузин Л.Т. Основы кибернетики. М.: Энергия, 1973г. -I и II тома.
15. Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение,1989г.
16 Кушниренко А.Г. и др. Основы информатики и вычислительной техники. М.: Просвещение, 1991г.
17. Лященко И.Н. Линейное и нелинейное программирование. К.:Виша школа, 1975г.
18. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик,Фортран и Паскаль. Т.: МП “Раско”, 1992г.
19. Никишев В.К. Математический справочник-словарь по информатике и вычислительной технике. Ч.: ЧГПИ, 1994г.
20. Никишев В.К. Использование IBM в учебном процессе. Ч.:ЧГПИ, 1994г.
21. Никишев В.К. Основы программирования на ЦВМ и СЦВМ. К.: Министерство обороны, 1985г.
22. Самарский Н.Н. и др. Компьютеры, модели, вычислительный эксперимент. Введение в информатику с помощью математического моделирования. М.: Наука, 1988г.
23. Фомин С.В. и др. Математические проблемы в биологии. М.: Наука, 1973г.
24. Фридман М.М. Наглядность и моделирование в обучении. М.: Знание, 1984г.
25. Эберт К. и др. Компьютеры. Применение в химии. М.: Мир, 1988г.
26. Словарь школьной информатики. /Математический энциклопедический словарь. М.: Советская энциклопедия, 1988г, - с847.
1. Голубев, И. С. Основы устройства, проектирования, конструирования и производства летательных аппаратов (дистанционно-пилотируемые летательные аппараты) Текст. / И. С. Голубев, Ю .И. Янкевич М.: МАИ, 2006. - 524 с.
3. Фильчаков, П. Ф. Справочник по высшей математике Текст. : справочник / П. Ф. Фильчаков. Киев: Наукова Думка, 1972. - 744 с.
5. Ланкастер, П. Теория матриц Текст. : Пер. с англ./ П. Ланкастер. М.: Наука, 1978.-280 с.
6. Буков, В.Н. Адаптивные прогнозирующие системы управления полетом. Текст. / В.Н. Буков. М.: Наука, 1987. -232 с.
7. Гуськов, Ю. П. Управление полётом самолёта Текст. / Ю. П. Гуськов, Г. И. Загайнов. М.: Машиностроение, 1980. - 456 с.
9. Попов, Е. П. Теория линейных систем автоматического регулирования и управления Текст. / Е. П. Попов. М.: Наука, гл. ред. физ.-мат. лит., 1989. -304 с.
12. Агеев, В. М. Приборные комплексы ЛА и их проектирование Текст. /
14. Дмитриевский, А. А. Прикладные задачи теории оптимального управления движением беспилотных JIA Текст. / А. А. Дмитриевский, Л. Н. Лысенко. М.: Машиностроение, 1978. -328 с.
15. Козлов, В. И. Системы автоматического управления ЛА Текст. / В. И. Козлов. М.: Машиностроение, 1979. - 216 с.
16. Байбородин, Ю. В. Бортовые систему управления полетом Текст. / Ю. В. Байбородин М.: Транспорт, 1975. - 336 с.
17. Дэбни, Дж. Б. Simulink 4. Секреты мастерства Текст. / Дж. Б. Дэбни. Т. Л Харман Т. Л.: пер. с англ. М. Л. Симонова. М.: БИНОМ, 2003. - 403 с.
19. Новоселов, А. С. Системы адаптивного управления летательного аппарата Текст. / А. С. Новоселов, В. Е. Болнокин, П. И. Чинаев, А. Н. Юрьев -М.: Машиностроение, 1987. 280 с.
20. Березин, Д. Р. Бортовой вычислитель навигационных параметров малоразмерного беспилотного летательного аппарата Текст. / Д. Р. Березин // Диссертация на соискание ученой степени канд. техн. наук. Рыбинск, 2002. -184 с.
21. Сейдж, Э. П. Теория оценивания и ее применение в связи и управлении Текст. / Э. П. Сейдж, Дж. П. Мелса: пер.с англ. под ред. Б. Р. Левина. М.: Радио и связь, 1976. - 356 с.
22. Сейдж, Э. П. Оптимальное управление системами Текст. / Э. П. Сейдж, Ч. С. Уайт: пер.с англ. под ред. Б. Р.Левина. М.: Радио и связь, 1982.392 с.
25. Бесекерский, В. А. Теория систем автоматического регулирования Текст. / В. А. Бесекерский, Е. П. Попов М.: Наука. - 1975.
26. Крамер, Г. Математические методы статистики Текст. / Г. Крамер: пер. с англ. -М.: Мир, 1975. 568 с.
27. Бендат, Дж. Измерение и анализ случайных процессов Текст. / Дж. Бендат, А. Пирсон: пер. с англ. М.: Мир, 1974. - 464 с.
30. Вентцель, Е. С. Теория вероятностей. Текст. : учебное пособие для вузов / Е. С. Вентцель М.: Высш. шк., 1999. - 576 е.: ил.
31. Боднер, В. А. Приборы первичной информации Текст. / В. А. Боднер -М.: Машиностроение, 1981. 344 с.
33. Ильинский, А. Ю. Ориентация, гироскопы и инерциальная навигация Текст. / А. Ю. Ильинский М.: Наука, 1976. - 670 с.
34. Тихонов, В. И. Оптимальная фильтрация дискретно-непрерывных процессов Текст. / В. И.Тихонов, В. А. Смирнов Радиотехника и электроника, 1978.- №7.- с.1441-1452.
35. Березин, Д. Р. Идентификация параметров БПЛА в условиях летных испытаний Текст. / Березин Д. Р // Сборник трудов молодых ученых. -Рыбинск: РГАТА, 2001. 232 с.
37. Бранец, В. В. Применение кватернионов в задачах ориентации твёрдого тела Текст. / В. В. Бранец, И. П. Шмыглевский М.: Наука, 1973. - 320 с.
38. Зайцев, В. И. Автоматическое управление угловыми движениями самолёта Текст. : учебное пособие / В. И. Зайцев М.: МАИ, 1985. - 54 с.
39. Михалёв, И. А. Системы автоматического управления самолётом Текст. / И. А. Михалёв М.: Машиностроение, 1971. - 464 с.
40. Боднер, В.А. Стабилизация летательных аппаратов и автопилоты В. А. Боднер, М. С. Козлов -М.: Оборонгиз, 1961. 508 с.
42. Помыкаев, И. И. Навигационные приборы и системы Текст. : учеб. пособие для вузов / И. И. Помыкаев, В. П. Селезнев, Л. А. Дмитроченко. М.: Машиностроение, 1983. -456 с.
43. Помыкаев, И. И. Навигационные приборы и системы: учебное пособие для вузов. Под ред. И. И.Помыкаева. Селезнев В. П., Дмитриченко Л .А. М.: Машиностроение, 1983.- 456 с.
44. Бабич, О. А. Обработка информации в навигационных комплексах Текст. / О. А. Бабич М.: Машиностроение, 1991. - 512 с.
46. Кузовков, Н. Г. Инерционная навигация и оптимальная фильтрация
49. Гуськов, Ю.П. Проектирование самолёта с учётом возможностей автоматической системы управления Текст. : учебное пособие / Ю. П. Гуськов -М.: МАИ, 1984.-37 с.
50. Малышев, В. В. Оптимизация наблюдения и управления летательных аппаратов Текст. / В. В. Малышев М.: Машиностроение, 1989. - 311 с.
51. Бородин, В. Т. Пилотажные комплексы и системы управления самолётов и вертолётов Текст. / В. Т. Бородин, Г. И. Рыльский М.: Машиностроение, 1978. — 216 с.
52. Вопросы прикладной теории систем ориентации и навигации Текст. : межвузовский сборник JL: ЛИАП, 1983. - 136 с.
53. Соколов, Н. И. Адаптивные системы автоматического управления летательными аппаратами: учебное пособие для вузов / Н. И. Соколов М.: Машиностроение, 1988. - 207 с.
54. Остославский, И. В. Динамика полёта. Устойчивость и управляемость летательных аппаратов Текст. / И. В. Остославский, И. В.Стражева М.: Машиностроение, 1969. -499 с.
55. Комплексы с беспилотными летательными аппаратами Текст. : Краткий аналитический обзор состояния и перспектив развития за рубежом и в Российской Федерации. Рыбинск, 2001. - 45 с.
.
58. Кизимов, А. Т. Стабилизация малоразмерного БПЛА в турбулентной атмосфере Текст. / А. Т. Кизимов, Л. Е. Фролова // Информационноизмерительные и управляющие системы. 2007. - №12, т. 5. - С. 8 - 12.
59. Кизимов, А. Т. Декомпозиция многомерного объекта управления Текст./ А. Т. Кизимов // Аэрокосмические технологии и образование на рубеже веков: тез. докл. науч-техн. конф. Рыбинск: РГАТА, 2002. - 4.2 - С. 74 - 75.
60. Фролова, JI. Е. Синтез параметров автопилота беспилотного летательного аппарата Текст. / JI. Е. Фролова, А. Т. Кизимов // Моделирование и обработка информации в технических системах: тез. докл. науч-техн. конф. -Рыбинск: РГАТА, 2004 . С. 215 - 216.
62. ГОСТ 20058-80 Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения Текст. Введ. 1981 - 01 - 07. - М.: Государственный комитет СССР по стандартам: Издательство стандартов, 1981.-51 с.
64. Рис. А. 1. Ориентация связанной системы координат относительно земнойнормальнойа угол атаки, Р - угол скольжения, oxayaza - Скоростная система координат.
65. Рис. А.2. Ориентация скоростной системы координат относительно связанной0 угол наклона траектории, V}/ - угол пути, OX Y Z ' траекторная система координат.
67. Относительное угловое положение траекторией и связанной системкоординатак траекторный угол атаки,рк — траекторный угол скольжения,
69. Рис. А.4. Ориентация траекторией системы координат относительносвязанной системы координат
70. Полная нелинейная модель JIA с системами измерения, оценивания и управления.
71. Рис Б.1. Обобщенная структура системы управления БПЛА
73. Рис. Б.2. Модель ДУС и акселерометров с погрешностями и шумами
74. Параметры нелинейной математической модели летательного аппарата
1. Анфилатов В.С.,. Емельянов
А.А,. Кукушкин А.А. Системный анализ в управлении: учебное пособие. - М.:
Финансы и статистика, 2002.
2. Советов Б.Я., Яковлев С.А..
Моделирование систем. М.: Высшая школа. 2001
3. Краснощеков П.С., Петров А.А. Принципы
построения моделей. - М.: Изд-во МГУ,1993.
4. Бобков С.П., Бытев Д.О. Моделирование
систем: учеб. пособие /Иван. гос. хим.-технол. ун-т. - Иваново, 2008.
5. Бобков С.П. Функциональные
математические модели. [Электронные ресурс]:[слайд-конспект лекций] - Электрон.
дан. в формате MS PowerPoint 2003. Иваново: Иван. гос. хим.-технол. ун-т.,
2008.
6. Прикладная информатика / Под ред. В.М. Савникова.- М.: Фин. и статистика,
2001.
7. Трудоношин В.А., Пивоварова Н.В.
Математические модели технических объектов. М.: Высш.шк.,1986.
8. Таганов И.Н. Моделирование процессов
массо- и энергопереноса. - Л.: Химия, 1979.
9. Коршунов Ю.М. Математические основы
кибернетики. - М.: Энергия, 1
Сайты по функциональному моделированию
1. Статьи,
посвещенные UML. Содержит более 2х десятков полезный статей о
UML.
2. Файлы по UML,
доступные для скачивания. Содержит книги и стандарты языка UML, как на
русском, так и на английском языке.
3. "UML
- объектно-ориентированный метод анализа бизнес-процессов и проектирования
приложений" Александр Мищук.
4. "Использование
UML и Rational Rose для моделирования данных" Вальтер Говард
5. "Использование
UML при моделировании сложных систем реального времени" Браин Селик
6. "Тенденции
в развитии языка UML и разработки ПО" Джеймс Рамбо В этой
статье рассказывается о новой эпохе разработки ПО, о ее влиянии на новые
требования, выдвигаемые к языку UML, и об оптимальных методах их
выполнения.
7. "Моделирование
данных в Rational Rose" Сергей Трофимов Описывается
моделирование физического представления данных с использованием Rational
Rose
8. Язык
UML. Общее представление о языке UML: структуры, графические элементы и
диаграммы языка.
9. Практический
UML. Этот документ является переводом документа "Practical UML. A Hands-On Introduction for Developers".
Практическое введение для разработчиков
10. "Стандартный
язык объектно-ориентированного моделирования UML" Вендров Александр
Михайлович. История создания UML
11. UML –
унифицированный язык моделирования. Данный материал содержит начальные
сведения о методах описания программных систем и нотациях, используемых в
UML
12. Язык UML.
Руководство пользователя. Авторы: Грейди Буч, Джеймс Рамбо, Айвар
Джекобсон
13. "UML
диаграммы в Rational Rose" Сергей Трофимов
14. "Анализ и
проектирование. Визуальное моделирование (UML) Rational Rose" Константин
Домолего
15. Библиотека
Геннадия Верникова. Полные описания стандартов проектирования и
моделирования.
16. "Пример
описания предметной области с использованием UML при разработке программных
систем" Е.Б. Золотухина, Р.В. Алфимов. В статье на конкретном
примере демонстрируется возможный подход к моделированию предметной области,
основанный на применении Унифицированного Языка Моделирования (Unified Modeling
Language) (UML)
17. http://ru.wikipedia.org/wiki/Ершов, Андрей Петрович
18. http://ru.wikipedia.org/wiki/Глушков, Виктор Михайлович
Оглавление
Предисловие 8
1. Модели. Моделирование. Основные понятия
и определения. 9
1.1. Сущность моделирования. Модели.
Классификация 9
1.2. Этапы моделирования. 21
1.3. Формы представления моделей и алгоритмов. 26
1.4. Разработка моделей 36
1.5. Особенности моделирования систем 37
2. Модели объектов, систем и процессов 40
2.1.Математические модели физических объектов,
явлений и процессов. . 40
2.1.1. Математическая модель объектов падения. 41
2.1.2. Математическая модель траектории
движения объектов, брошенных под начальным
углом к горизонту с начальной скоростью V0 42
2.1.3. Модель гармонического осциллятора 44
2.1.4. Математическая модель маятника 45
2.1.5. Модель движения тел с переменной массой 48
2.1.6. Модель движения небесных тел 49
2.2. Математические модели динамических
объектов и систем. 51
2.2.1. Математическая модель движения ракеты с
постоянными параметрами . . . . . . . . 51
2.2.2. Математическая модель движения
ракеты с изменяющимися параметрами 52
2.2.3. Математическая модель движения ракеты с
управлением в вертикальной плоскости. 52
2.2.4. Полная математическая модель движения
ракеты в 3-х плоскостях. . . . . . . . . . . 54
2.2.5 Основные модели управления ракетами
«Земля-Земля». 55
2.3 Модели управления дискретными системами 57
2.3.1 Общая модель систем автоматического
управления (САУ) 57
2.3.2 Модель управления САУ в течение одного
такта с учетом всех координат 59
2.3.3. Модель управления САУ по одной координате с
запоминанием информации на N тактов 59
2.3.4.Модель управления САУ по одной координате
с замером состояния системы в каждом такте. 60
2.3.5.Модель управления САУ на основе тактовой
линии в течение одного такта 60
2.3.6.Оптимальная модель управления САУ
на основе метода максимума 62
2.3.7.Оптимальная модель фильтра Калмана - Бьюси 63
2.4 Модель идентификации параметров объекта
на основе обобщенно-инвариантных уравнений 64
2.5 Математические модели биологических
объектов, явлений и процессов 69
2.5.1Модель однородной популяции 69
2.5.2.Модель «хищник-жертва» 69
2.5.3 Модель эпидемии болезни 70
2.5.4 Модель прогноза урожая. 71
2.5.5 Модель роста опухоли. 71
2.5.6.Модель растворения лекарственного аппарата 72
2.5.7. Модель процесс переноса тепла 72
2.6 Оптимизационные математические модели
объектов и систем 73
2.6.1. Модель выпускаемой продукции. 73
2.6.2. Модель рационального раскроя. 74
2.6.3. Модель размещения предприятий. 74
2.6.4Модель выбора предприятия 75
2.6.5. Модель транспортной задачи 76
2.6.6.Модели транспортных задач с
дополнительными условиями 76
2.6.7. Модель планирования производства 81
2.7.Графовые модели объектов и систем 83
2.7.1. Математическая модель размещения
аварийных служб и пунктов обслуживания 83
2.7.2. Модель определения кратчайшего пути 84
2.7.3. Модель задачи “коммивояжера” 85
2.7.4. Модель сетевого графа 86
2.8. Экономические (вероятностные) модели
объектов и систем 89
2.8.1.Математическая модель управления запасами 89
2.8.2.Статистическая модель распределения ресурсов 92
2.9. Математические модели распознавания образов.
2.9.1.Общие сведения о теории распознавания образов 94
2.9.2.Модели распознавания объектов, предметов
или процессов на основе формулы Байеса 95
2.9.3. Модель распознавания образа с
учетом матрицы потерь. 95
2.9.4. Модель перцептрона. 96
2.10.Математические модели объектов и систем
массового обслуживания 98
2.11. Математические игровые модели объектов 101
2.12. Нейрокомпьютерные модели 102
2.13. Язык моделирования UML 103
2.13.1. История методов моделирования
сложных систем 104
2.13.2.История языка моделирования UML 105
2.13.3. Структура языка моделирования UML
2.13.4. UML диаграммы
2.14 Информационные модели объектов и систем 117
2.14.1 Информационная модель управления
учебными заведениями. Цели и задачи
управления учебными заведениями 118
2.14.2 Информационная модель учебного заведения. 118
2.14.3 Информационная модель управления
высшим учебным заведением 130
2.15 Модели знаний студентов по дисциплинам кафедры информатики и вычислительной техники 132
2.16 Имитационное моделирование 146
2.17.Структорно- последовательное моделирование 151
3.Математические методы исследования моделей
объектов, систем, явлений и процессов. 155
3.1.Методы решения дифференциальных уравнений 155
3.1.1. Метод Эйлера 155
3.1.2. Метод Рунге - Кутта четвертого порядка 158
3.1.3. Метод Рунге - Кутта-Мерсона 159
3.2. Представление систем на основе метода
пространства состояния 164
3.3 .Способы решения задач линейного
программирования на основе симплекс-метода 171
3.4.Способы определения опорного
плана транспортной задачи 175
3.4.1.Способ “северо-западного угла” 177
3.4.2.Способ “наименьшего элемента в матрице” 177
3.4.3.Способ Фогеля 177
3.4.4. Способы решения транспортных задач
методом потенциалов 179
3.4.5.Метод решения транспортных оптимизационных
задач на основе “венгерского метода” 184
3.5. Метод динамического программирования 192
3.6. Матричный метод сетевого планирования 199
3.7Метод ветвей и границ 204
3.8.Методы обработки экспериментальных данных. 208
3.8.1.Числовые характеристики выборки 209
3.8.2.Регрессионный анализ экспериментальных
данных 209
3.8.3 Корреляционный анализ 213
3.9. Моделирование объектов методом
статистических испытаний 215
3.10. Математические методы исследования
моделей управления запасами 217
3.11. Методы построения и использования
графовых моделей 220
3.11.1. Метод определения кратчайших расстояний.
Метод Дейкстра 222
3.11.2. Метод вычисления абсолютных центров.
Метод Хакими 223
Заключение
Литература
Приложение
Примеры моделирования объектов, систем,
явлений и процессов
Пример 1.Интегрированный пакет для моделирования объектов, динамика которого описывается дифференциальными уравнениями 1 и 2 -го порядков 227
Пример 2. Моделирование объекта, динамика которого описывается дифференциальным уравнением вида
d2y/dt2 + a*x*dy/dt - y+0.4 231
Пример 3. Моделирование падения шарика
радиуса R с высоты h 235
Пример 4. Моделирование колебаний
математического маятника 243
Пример5. Моделирование динамики объекта,
брошенного под углом к горизонту 248
Пример 6. Моделирование динамики
полета ракеты 253
Пример 7. Моделирование полета кометы 264
Пример 8. Моделирование динамической системы
« хищники - жертвы» 267
Пример 9. Моделирование развития эпидемии
в деревне с течением времени 274
Пример 10. Моделирование прироста коз на
изолированном острове от травы 277
Пример 11. Моделирование производства
И транспортировки товаров 281
Пример 12. Моделирование системы
массового обслуживания 282
Пример 13. Моделирование случайных процессов в системах массового обслуживания 283
Пример 14. Моделирование процесса раскроя материала291
Пример 15. Моделирование систем планирования на основе метода сетевого графа. 295
Пример 16. Моделирование экспертной системы распознавания болезней 298
Пример 17. Моделирование систем управления хранения запасов на складах. 302
Пример 18. Моделирование систем, определяющих минимальное расстояние между двумя объектами. 305
Научное издание
Никишев Вячеслав Константинович
Современное компьютерное моделирование
Монография
Подписано в печать 24.12.04 Формат 60 Х80/15
Бумага писчая. Печать оперативная. Усл. печ.л. 19,8
Тираж экз Заказ N Цена свободная
ГОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова»
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.