Microsoft Excel

Microsoft Excel

Задание: дано нелинейного уравнения f(x) = 0 на заданном отрезке [a,b]. Требуется средствами табличного процессора Excel найти корни данного уравнения методом касательных с использованием циклических ссылок.

 x-x³+1=0     a=1  b=2

Решение:

Найдем корень нелинейного уравнения в табличном процессоре Excel  методом касательных с использованием циклических ссылок. Для нахождения корня будем использовать формулу:

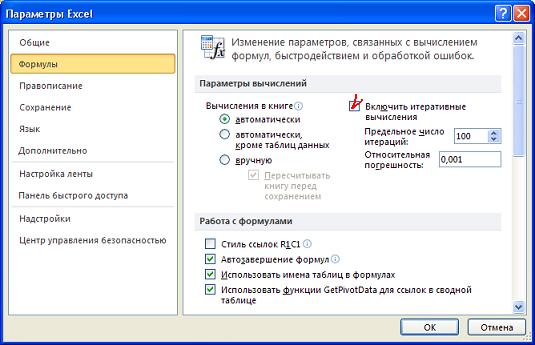
 Для включения режима циклических вычислений в Excel2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле "Включить итеративные вычисления":

Найдем производную функции f(x)=x-x³+1

f’(x)=1-3x²
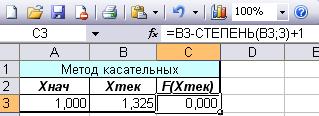
В ячейку А3 введем значение а =1, ячейку В3 введем формулу расчета текущего значения х: =ЕСЛИ(B3=0;A3;B3-(B3-СТЕПЕНЬ(B3;3)+1)/(1-3*СТЕПЕНЬ(B3;2)))
В ячейку С3 введем формулу для контроля значения f(x): =B3-СТЕПЕНЬ(B3;3)+1.
Получим корень уравнения в ячейке В3    х=1,325.

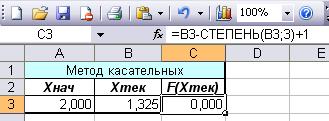
Введем начальное приближение в ячейку А3 =2. Но для того чтобы вычисления были правильные, недостаточно изменить число в ячейке А3 и запустить процесс вычислений. Потому что в этом случае вычисления продолжаться с последнего вычисленного ранее значения. Это значение,  в ячейке В3, необходимо обнулить, для этого можно заново записать туда формулу или просто выбрать ячейку  с формулой и дважды щелкнуть мышью на ней . После этого поставить курсор на ячейку с формулой и нажать клавишу Enter для запуска процесса итерационных вычислений.

Получим тот же результат, значит корень на данном промежутке один.