
Методические указания к практическому занятию
по теме «Миноры. Алгебраические дополнения»
(Раздел. Элементы линейной алгебры)
Учебная дисциплина: Математика СПО
Разработано преподавателем Загурской А.А.
1 Цели
1.1 В ходе выполнения работы студенты осваивают:
1.1.1 Общие компетенции:
- Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество
- Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность
- Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознано планировать повышение квалификации
1.2 В результате выполнения работы студенты:
1.2.1 Осваивают умения:
- производить операции над матрицами и определителями
1.2.2 Усваивают знания:
- основных понятий и методов линейной алгебры
2 Дидактическое обеспечение
2.1 Карточка с заданиями (6 вариантов)
2.2 Методические рекомендации по выполнению работы: необходимые формулы для выполнения заданий (Приложение А) и образцы выполнения заданий (Приложение Б)
3 Форма организации – индивидуальная
4 Инструктаж
4.1 Получить задание и послушать порядок выполнения работы, а также критерии оценки
4.2 В тетради для практических работ указать номер, тему и вариант практической работы
4.3 Изучить методические рекомендации и пособие.
4.4 Приступить к выполнению задания
5 Порядок выполнения
5.1 Практическая работа составлена в виде карточек с заданиями (6 вариантов). В каждой карточке два задания: выполнить действия над матрицами, вычислить определитель матрицы.
5.2 Для выполнения первого задания необходимо вспомнить порядок выполнения арифметических действий, а также правила сложения (вычитания) матриц, умножение матрицы на число и правило умножения двух матриц.
5.3 Во втором задании требуется вычислить определитель используя общее правило его вычисления, а именно разложением по строке или столбцу.
6 Методические рекомендации - см. приложения
7 Форма отчета - работа выполняется в течение 90мин в тетради для практических работ и сдается преподавателю на проверку
8 Контрольные вопросы
Не предусмотрены
Критерии оценок
5 (отлично) – Работа выполнена в полном объеме, аккуратно, без арифметических ошибок.
4 (хорошо) – Работа выполнена в полном объеме, аккуратно, допущены арифметические
ошибки, не нарушающие основной алгоритм решения.
3 (удовлетворительно) – Работа выполнена не в полном объеме или допущены ошибки, приводящие к нарушению алгоритма в одном, двух заданиях.
2 (неудовлетворительно) – Выполнено одно задание или неверно применен алгоритм во всех заданиях.
Тема: Миноры и алгебраические дополнения элементов определителя
Минором Мij
определителя ![]() ,
где I и j меняются от 1 до n, называется
такой новый определитель, который получается из
,
где I и j меняются от 1 до n, называется
такой новый определитель, который получается из ![]() вычеркиванием строки и столбца, содержащих данный
элемент.
вычеркиванием строки и столбца, содержащих данный
элемент.
Пример: Из ![]() =
=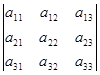 можно получить М12=
можно получить М12=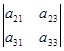
Задание: Записать и вычислить М32 и М24
определителя ![]() =
=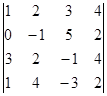
Решение:
М32=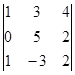 =
М24=
=
М24=
Алгебраическим дополнением элемента Аij называется минор этого элемента, взятый со знаком (-1)i+j. Аij=(-1)i+j Мij.
Примеры: 1. Найти алгебраические дополнения элементов а13
, а21 , а31 определителя ![]() =
=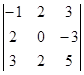 .
.
Решение:
А13=(-1)1+3∙![]() =
А21=(-1)1+2∙
=
А21=(-1)1+2∙![]() =
=
А31=
2. Найти алгебраические дополнения
элементов а12 , а22 , а32 определителя ![]() =
=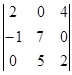 . Решение: А12=
. Решение: А12=
А22= А32=
Теорема о разложении определителя по элементам строки или столбца:
Сумма произведений элементов любой строки (или
столбца) определителя ![]() на
их алгебраические дополнения равна этому определителю.
на
их алгебраические дополнения равна этому определителю.
![]() =ai1Ai1+ai2Ai2+…+ainAin
или
=ai1Ai1+ai2Ai2+…+ainAin
или ![]() = a1jA1j+a2jA2j+…+anjAnj
= a1jA1j+a2jA2j+…+anjAnj
Эти соотношения называются разложением определителя по элементам i –той строки или j-го столбца.
Пример: Определитель ![]() =
=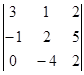 а) разложить
по элементам 1 строки
а) разложить
по элементам 1 строки
б) по элементам 2-го столбца
Решение:
а) ![]() =3
=3![]() -1
-1![]() +2
+2![]() =
=
б) ![]() =
=
Вычислить определители любым способом:
1.
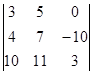 =
=
2. 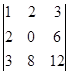 =
=
3. 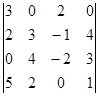 =
=
4.
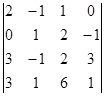 =
=
7.
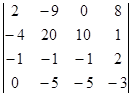 =
=
9.
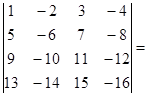
10. 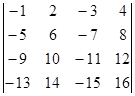 =
=
11. 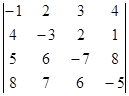 =
=
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.