МНОГОУРОВНЕВАЯ СИСТЕМА УЧЕБНО-ТРЕНИРОВОЧНЫХ ЗАДАЧ ПО ТЕМЕ: «ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ»

 

МНОГОУРОВНЕВАЯ СИСТЕМА УЧЕБНО-ТРЕНИРОВОЧНЫХ  ЗАДАЧ ПО ТЕМЕ:

«ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ». 8 класс.

Вводимые обозначения:

БЗ – базовая задача,

ЗЗ – знакомая задача,

МЗ- модифицированная задача,

НЗ- незнакомая задача.

Шаблон матрицы разноуровневых учебных заданий

Уровень	Подуровень	БЗ1  Уравнения с одинаковыми знаменателями	БЗ2 Уравнения с разными знаменателями, не имеющие одинаковых множителей	БЗ3 Уравнения с разными знаменателями, имеющие одинаковые множители	БЗ4 Уравнения вида , где - многочлены,	БЗ5 Применение дробно-рациональных уравнений к решению текстовых задач
Базовый уровень	ЗЗ	БУ-БЗ1-ЗЗ	БУ-БЗ2-ЗЗ	БУ-БЗ3-ЗЗ	БУ-БЗ4-ЗЗ	БУ-БЗ5-ЗЗ1, БУ-БЗ5-ЗЗ2, БУ-БЗ5-ЗЗ3
	МЗ	БУ-БЗ1-МЗ	БУ-БЗ2-МЗ	БУ-БЗ3-МЗ1, БУ-БЗ3-МЗ2, БУ-БЗ3-МЗ3	БУ-БЗ4-МЗ	БУ-БЗ5-МЗ1, БУ-БЗ5-МЗ2, БУ-БЗ5-МЗ3
	НЗ	БУ-БЗ1-НЗ1,   БУ-БЗ1-НЗ2	БУ-БЗ2-НЗ	БУ-БЗ3-НЗ	БУ-БЗ4-НЗ	БУ-БЗ5-НЗ
Продвинутый уровень	ЗЗ	ПУ-БЗ1-ЗЗ	ПУ-БЗ2-ЗЗ	ПУ-БЗ3- ЗЗ1,  ПУ-БЗ3- ЗЗ2,  ПУ-БЗ3- ЗЗ3,  ПУ-БЗ3- ЗЗ4, ПУ-БЗ3- ЗЗ5, ПУ-БЗ3- ЗЗ6	ПУ-БЗ4-ЗЗ	ПУ-БЗ5-ЗЗ1, ПУ-БЗ5-ЗЗ2,
	МЗ	ПУ-БЗ1-МЗ	ПУ-БЗ2-МЗ	ПУ-БЗ3-МЗ1, ПУ-БЗ3-МЗ2, ПУ-БЗ3-МЗ3, ПУ-БЗ3-МЗ4	ПУ-БЗ4-МЗ	ПУ-БЗ5-МЗ1, ПУ-БЗ5-МЗ2
	НЗ	ПУ-БЗ1-НЗ	ПУ-БЗ2-НЗ	ПУ-БЗ3-НЗ1, ПУ-БЗ3-НЗ2, ПУ-БЗ3-НЗ3, ПУ-БЗ3- НЗ4	ПУ-БЗ4-НЗ	ПУ-БЗ5-НЗ1, ПУ-БЗ5-НЗ2, ПУ-БЗ5-НЗ3, ПУ-БЗ5-НЗ4

 

Перечень заданий базового уровня

 

БЗ1 Уравнения с одинаковыми знаменателями

БУ-БЗ1-ЗЗ   Решите уравнение:

Ответ: -1; 1,5.

БУ-БЗ1-МЗ   Решите уравнение:

       Ответ: -3.

БУ-БЗ1-НЗ1    Укажите промежуток, которому принадлежит сумма корней уравнения: 

                          1) [0;4];                                         3) (- ∞; - 4];

                          2)                                   4)

Ответ:3)

БУ-БЗ1-НЗ2   При  каких значениях ч значение дробей  и являются противоположными числами?

     Ответ: при х = -8 выполняется требуемое условие.

 

БЗ2 Уравнения с разными знаменателями, не имеющие одинаковых множителей

БУ-БЗ2-ЗЗ    Решите уравнение:

     Ответ: - 5; - 1,5.

 

БУ-БЗ2-МЗ    Решите уравнение:

        

      Ответ: 1;

 

БУ-БЗ2-НЗ    Найдите среднее арифметическое корней уравнения:  

 

 1) – 24;                                 2) 248;

         

 3) 26;                                   4) 24.

 

    Ответ: 4)

 

 

БЗ3 Уравнения с разными знаменателями, имеющие одинаковые множители

БУ-БЗ3-ЗЗ  Решите уравнение:

   Ответ: 3

 

БУ-БЗ3-МЗ1  Решите уравнение:

   Ответ: 7.

 

БУ-БЗ3-МЗ2   Решите уравнение:

  Ответ: -3.

 

БУ-БЗ3-МЗ3  Решите уравнение:

 

  Ответ: 3.

 

БУ-БЗ3-НЗ  При каких значениях a разность дробей    и   равна их произведению?

 Ответ: при а = 4 и а = - 4

 

БЗ4  Уравнения вида , где - многочлены,

БУ-БЗ4-ЗЗ  При каких значениях аргумента x равны соответствующие значения функций  и .

Ответ: при х = -1 и х = 5

 

БУ-БЗ4-МЗ  Найдите координаты точек пересечения графиков функций    и .

Ответ: координаты точек пересечения (1,5; 0) и (1; 1).

 

БУ-БЗ4-НЗ    Решите уравнение:   

        Ответ:

 

БЗ5  Применение дробно-рациональных уравнений к решению текстовых задач

БУ-БЗ5-ЗЗ1  Автобус проехал половину 240 км трассы по расписанию. На середине пути он сделал остановку на 20

 минут, и чтобы приехать в конечный пункт вовремя, увеличил скорость на 4 км/ч. Найдите первоначальную  

скорость       автобуса.

Ответ:36 км/ч.

 

БУ-БЗ5-ЗЗ2  Моторная лодка прошла по течению 70 км. За тоже время она может пройти против течения 30 км. Найдите

      скорость течения, если скорость лодки в стоячей воде 10 км/.

Ответ:4 км/ч.

БУ-БЗ5-ЗЗ3  Пароход, отчалив от пристани А, спустился вниз по течению реки на 60 км, до устья впадающего в реку

      протока, и поднялся вверх про протоку (против течения) на 20 км до пристани В. Весь путь от А до В пароход

      прошел за 7 часов. Скорость течения реки и скорость течения протока равны 1 км/ч. Найти собственную

      скорость течения парохода.

Ответ:11 км/ч.

БУ-БЗ5-МЗ1  Мотоциклист проехал от села до озера 60 км. На обратном пути он уменьшил скорость на 10 км/ч поэтому

израсходовал времени на 0,3 ч больше. Сколько времени затратил мотоциклист на обратный путь?

Ответ: время движения от озера до села 1,5 ч.

 

БУ-БЗ5-МЗ2    Автобус – экспресс отправился от автовокзала в аэропорт, находящийся на расстоянии 40 км. Через 10

                   минут вслед за автобусом выехал опоздавший пассажир на такси. Скорость такси на 20 км/ч больше скорости

автобуса. Найти скорость автобуса и скорость такси, если в аэропорт они прибыли одновременно.

Ответ: скорость движения автобуса 60 км/ч, а скорость движения такси 80 км/ч.

 

БУ-БЗ5-МЗ3  Со станции А вышел в 5 ч утра почтовый поезд по направлению к станции В, отстоящей от А на 1080 км. В

                8ч   утра вышел со станции В по направлению к А скорый поезд, который проходил в час на 15 км больше, чем

       почтовый поезд. Когда встретились поезда, если их встреча произошла на середине пути между А и В?

Ответ: поезда встретились через 9  часов после выхода скорого поезда, т. е. в 17:00 ч.

 

БУ-БЗ5-НЗ     Расстояние между станциями А и В равно 120 км. В полночь из А в В отправляется поезд. В 3 ч той же

ночью из А в В отправляется другой поезд, проходящий в час на 10 км больше первого. Второй поезд прибывает в В на 2 ч позже первого. В котором часу второй поезд прибыл в В?

Ответ: поезд прибыл в В в 6 часов.

 

Перечень заданий продвинутого  уровня

 

БЗ1 Уравнения с одинаковыми знаменателями

ПУ-БЗ1-ЗЗ При каких значениях а уравнение:  имеет один корень?

Ответ: при a= 3; a=5.

 

ПУ-БЗ1-МЗ Решите уравнение:

       Ответ: а, при а ≠ - 3, а ≠ 4.

 

ПУ-БЗ1-НЗ Решите уравнение: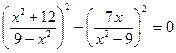

Ответ: - 4; 4.

 

БЗ2 Уравнения с разными знаменателями, не имеющие одинаковых множителей

ПУ-БЗ2-ЗЗ Решите уравнение:

Ответ: - 3;1.

 

ПУ-БЗ2-МЗ Решите уравнение:

Ответ:0; - 3.

ПУ-БЗ2-НЗ Решите уравнение:

Ответ:   2; 1.

БЗ3 Уравнения с разными знаменателями, имеющие одинаковые множители

ПУ-БЗ3- ЗЗ1  Решите уравнение:

         Ответ:; .

ПУ-БЗ3- ЗЗ2  Решите уравнение:

Ответ: - 2,2; 6.

 

ПУ-БЗ3- ЗЗ3  Решите уравнение:

  Ответ: - 3; 3.

 

ПУ-БЗ3- ЗЗ4  Решите уравнение:

Ответ: - 1; 1.

 

ПУ-БЗ3- ЗЗ5   Решите уравнение: 

 

Ответ: действительных корней нет.

 

ПУ-БЗ3- ЗЗ6    Решите уравнение:

 

Ответ:;

ПУ-БЗ3-МЗ1 Решить уравнение:

Ответ:        

ПУ-БЗ3-МЗ2 Решить уравнение:

Ответ: 2; 9.

 

ПУ-БЗ3-МЗ3 Решить уравнение:

 

Ответ: - 3; 4.

 

ПУ-БЗ3-МЗ4 Решить уравнение:  

Ответ: 3.

 

 

ПУ-БЗ3-НЗ1 Найдите среднее геометрическое корней уравнения    

 

Ответ: 0.

 

ПУ-БЗ3-НЗ2  Найдите среднее геометрическое корней уравнения    

 

Ответ:

 

ПУ-БЗ3-НЗ3  При каких значениях переменной разность дробей  и   равна дроби ?                                                                     

 

Ответ: при х = - 4 и х = - 5 выполняется исходное условие.

 

ПУ-БЗ3- НЗ4  Найдите все целые значения параметра a , при которых выполняется равенство:

Ответ: a=1

 

БЗ4  Уравнения вида ,где - многочлены,

ПУ-БЗ4-ЗЗ   Решите уравнение:  

 

Ответ: - 4; - 2; - 1; 1.

 

ПУ-БЗ4-МЗ Решите уравнение:

Ответ: - 2; 1.

ПУ-БЗ4-НЗ Решите уравнение: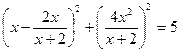

Ответ: - 1,2.

 

БЗ5  Применение дробно-рациональных уравнений к решению текстовых задач

ПУ-БЗ5-ЗЗ1  Расстояние по реке между пристанями равно 21 км. Отправляясь от одной пристани к другой, катер

      возвращается обратно через 4 ч, затрачивая из этого времени 30 минут на стоянку. Найдите собственную

      скорость катера, если скорость течения реки равна 2,5 км/ч.

Ответ: собственная скорость катера 12,5 км/ч.

 

ПУ-БЗ5-ЗЗ2 Плот проплывает по течению 60 км на 5 ч быстрее, чем такое же расстояние проходит моторная лодка

 против   течения. Найдите скорость лодки по течению, если ее  скорость в стоячей воде 10 км/ч.

Ответ:  скорость движения лодки по течению реки 16 км/ч.

 

ПУ-БЗ5-МЗ1  С двух станций А и В, отстоящих друг от друга на 400 км, навстречу друг другу идут два поезда. Если бы

      поезд со станции А вышел на 1 ч раньше другого, то встреча их произошла бы на середине пути. Если же они

      выйдут одновременно, то через 4 ч расстояние между ними будет равно 40 км. Определить скорость поездов.

Ответ: скорость поезда, движущегося из А в В , составляет 40 км/ч, а скорость поезда , движущегося из В в А,

составляет 50 км/ч.

 

ПУ-БЗ5-МЗ2  Два автомобиля выезжают навстречу друг другу, один из А в В, другой из В в А. После встречи один из

них находится в пути еще 2 часа, а другой 9/8 часа. Определите скорости автомобилей, если расстояние между А и      В равно 210 км.

Ответ:60 км/ч, 80 км/ч.

 

ПУ-БЗ5-НЗ1  Из города А в город В выехал автомобиль. Одновременно с ним из пункта С, расположенного между А и В,

в      город А выехал второй автомобиль. Первый прибыл в В одновременно с прибытием второго в А. Затем

       автомобили выехали одновременно навстречу друг другу, встретились в пункте Д и одновременно прибыли

       первый в А, а второй в В. Каждый автомобиль ехал со своей постоянной скоростью, но второй сделал

       остановку на пути от С к А, а первый – остановку той же продолжительности на пути от В к Д. Найти

       расстояние между С и Д, если известно, что расстояние от А до С равно  270 км, а расстояние от С до В равно

       180 км.

Ответ: расстояние между С и Д составляет20 км.

 

 

ПУ-БЗ5-НЗ2  Два туриста вышли из  А в В одновременно, причем первый каждый километр пути проходил на 5 минут

         быстрее второго. Первый , пройдя, пятую часть пути, вернулся в А, пробыл 10 минут, снова пошел в пункт В.

       При этом в В оба туриста пришли одновременно. Каково расстояние от А до В, если второй турист прошел его

       за 2,5 часа?

Ответ: расстояние от А до В  составляет10 км.

 

ПУ-БЗ5-НЗ3  Парусник и пароход одновременно вышли из порта А и должны прибыть в порт Д. Парусник, двигаясь с

постоянной скоростью, прибыл в порт Д, пройдя путь равный 1200 км. Пароход заходил в порты В и С, причем до порта В, расположенного от А на расстоянии 480 км, он плыл со скоростью, вдвое большей скорости парусника. Затем он увеличил свою скорость на 4 км/ч и прошел путь между портами В и С, равный 1420 км, и далее путь между портами С и Д, равный 1460 км. На стоянки в портах С и В он затратил одни сутки. В порт Д пароход прибыл на двое суток позднее парусника. Если бы пароход плыл из порта А до порта В с той же скоростью, что и из порта В до порта Д, то он прибыл бы в порт Д на 1 сутки 20 часов позднее парусника. Найти скорость парусника.

Ответ: скорость парусника 10 км/ч..

 

ПУ-БЗ5-НЗ4  От пристани А к пристани В, расположенной ниже по течению реки, отправился катер. Одновременно с ним из В в А (против течения) вышла моторная лодка. Дойдя до В , катер, не задерживаясь в В, повернул обратно и прибыл в А одновременно с моторной лодкой. Скорость течения реки равна 3 км/ч. Найти собственные скорости катера и моторной лодки, если известно, что у катера она была на 2 км/ч больше, чем у моторной лодки.

Ответ: скорость лодки 7 км/ч, а скорость катера 9 км/ч..