Множество и его элементы. Подмножества

Множество и его элементы. Подмножества

1. Понятие множества
2. Конечное, бесконечное и пустое множества
3. Способы задания множеств
4. Подмножества
5. Примеры

Понятие множества

Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».

Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».

Приведём примеры множеств:

Множество людей в салоне самолёта              Множество деревьев в парке

Множество планет Солнечной системы                  Множество электронов в атоме

Множество натуральных чисел

Множество «синих-синих презелёных красных шаров»

1,2,3,….

Конечное, бесконечное и пустое множества

Людей в салоне самолёта легко посчитать, это множество конечно.

С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.

Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.

Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.

Конечные множества

Бесконечные множества

Пустые множества

Игроки на поле

Помидоры на грядке

Пчёлы в улье

Числа (натуральные, рациональные, действительные и т.д.)

Количество рациональных чисел на отрезке [0;1]

Полосатые летающие слоны

Все точки пересечения двух параллельных прямых на плоскости

Способы задания множеств

1) Перечисление – в списке задаются все элементы множества.

Например:

Множество всех континентов Земли:

{Евразия,Северная Америка,Южная Америка,Африка,Австралия,Антарктида}

Множество букв слова «математика»: {м,а,т,е,и,к}

Множество натуральных чисел меньших 5: {1,2,3,4}

2) Характеристическое свойство – указывается особенность элементов множества.

3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)

Подмножества

Примеры подмножеств:

Множество людей является подмножеством приматов, живущих на Земле.

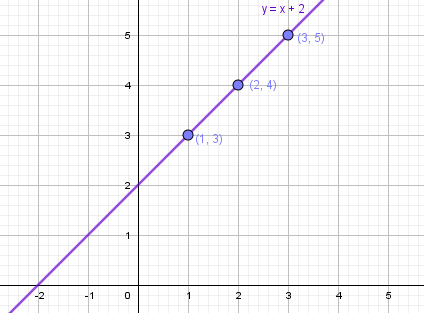
A = {(1;3);(2;4);(3;5) }

На графике:

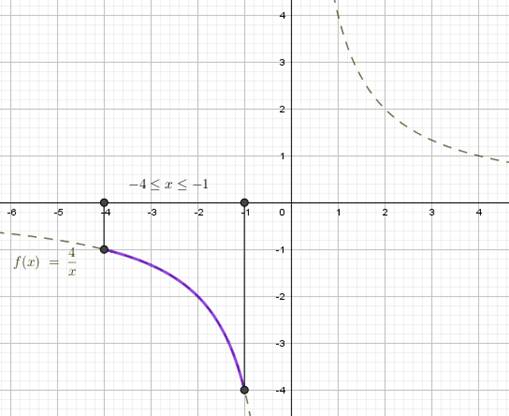
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:

Исходное множество состоит из n = 2 элементов, булеан состоит из 2²=4  элементов.

Скачано с www.znanio.ru