Модель идеального газа. Основное уравнение МКТ. Абсолютная температура. Газовые законы

Модель идеального газа. Основное уравнение МКТ.

Абсолютная температура. Газовые законы

Идеальный газ – это простейшая физическая модель настоящего газа. Идеальный газ состоит из огромного числа частиц, которые уподобляют шарикам (материальным точкам), имеющим конечную массу, и у которых отсутствует объем.

Моделью в физике называют упрощенную копию изучаемой настоящей системы. Она отражает самые значимые основные характеристики и свойства системы.

В модели идеального газа учитываются только основные свойства молекул, которые требуются для того, чтобы объяснить основы поведения газа. Идеальный газ напоминает реальный газ в довольно узком интервале давлений (p) и температур (T).

Главным упрощением идеального газа является предположение о том, что молекулы идеального газа не взаимодействуют на расстоянии. Кинетическая энергия движения молекул такого газа много больше, потенциальной энергии их взаимодействия. Данное упрощение ведет к уравнению состояния идеального газа:

где m – масса газа;  M – молярная масса; R – универсальная газовая постоянная.

Реальные газы можно уподобить идеальному газу с достаточно высокой точностью при низких делениях, когда расстояния (в среднем) между молекулами существенно больше, чем их размеры и (или) низких температурах. В таком случае силы притяжения между молекулами можно считать ничтожно малыми, а силы отталкивания возникают на очень маленькие промежутки времени при столкновениях молекул.

Столкновения частиц идеального газа описывают при помощи законов абсолютно упругого соударения шаров. Следует отметить, что имеются в виду законы столкновения именно шаров, так как точечные частицы испытывают только лобовые столкновения, которые не могут изменять направления скоростей на разные углы. В промежутках между столкновениями молекулы идеального газа движется по прямым линиям. Законы столкновений и соударений о стенки сосудов, в которых находится газ, известны. В МКТ движение каждой молекулы идеального газа описывают при помощи законов динамики. Однако из-за того, что число молекул в газе огромно, то практически не представляется возможным написать такое число уравнений.

С помощью модели идеального газа получают, например, основное уравнение молекулярно-кинетической теории (МКТ) (2). Которое показывает, что давление газа является результатом многочисленных ударов его молекул о стенки сосуда, в котором газ находится.

  где Е – средняя кинетическая энергия поступательного движения молекул газа;  – концентрация молекул газа (N – число молекул газа в сосуде; V – объем сосуда); m – масса молекулы газа; ʋ – среднеквадратичная скорость молекулы.

Модель идеального газа можно использовать для объяснения свойств газов. Так, горят, что газ занимает весь объем, который ему предоставляется, потому что силы взаимодействия его молекул малы, и они не способны удержать молекулы друг около друга.

Абсолютная температура - это температура по шкале Кельвина. За 0 градусов в этой шкале принимается температура, при которой все молекулы прекращают свое тепловое движение, "замирают" (абсолютный ноль, -273 С). При этом изменение температуры на 1 градус Кельвина соответствует изменению температуры на 1 градус Цельсия. Чтобы перевести температуру из градусов Цельсия (С) в Кельвины (К), нужно воспользоваться формулой T (K) = t (C) + 273.

Изотермические процессы

На прошлом уроке мы уже сформулировали так называемое уравнение состояния идеального газа – закон, связывающий между собой три макроскопических параметра газа: температуру, давление и объём.    или же 

То есть, каким бы ни был переход от одного состояния к другому (что, собственно, и подразумевается под газовым процессом), соотношение между тремя параметрами не меняется (естественно, при неизменном количестве вещества рассматриваемой порции газа).

Теперь же рассмотрим не произвольные процессы, а более частные случаи, когда неизменной величиной является один из макроскопических параметров. Начнём с изотермического процесса.

Изотермический процесс – процесс перехода идеального газа из одного состояния в другое без изменения температуры.

Закон, описывающий связь меду параметрами газа при таком процессе, называется закон Бойля-Мариотта в честь двух учёных, практически одновременно выведших его: англичанина Роберта Бойля и француза Эдма Мариотта (рис. 2).

Для начала запишем уравнения состояния идеального газа при постоянном количестве вещества:

 , а теперь учитывая:  и 

Получаем:   для любых различных состояний газа, или же просто:

 - закон Бойля-Мариотта

Из этого закона очевидно следует обратно пропорциональная связь давления и объёма: при увеличении объёма наблюдается уменьшение давления, и наоборот. График зависимости меняющихся величин в уравнении, то есть P и V, имеет следующий вид и называется изотермой (рис. 1):

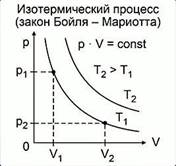
Рис. 1. Графики изотермических процессов в координатах P-V

Такая кривая в математике называется гиперболой. Также следствием закона Бойля-Мариотта является то, что площади показанных на графике прямоугольников равны между собой.

Рассмотрим следующий изопроцесс – изобарный процесс.

Изобарные процессы

Изобарный (или изобарический) процесс – процесс перехода идеального газа из одного состояния в другое при постоянном значении давления.

Впервые такой процесс рассмотрел французский учёный Жозеф-Луи Гей-Люссак (рис. 4), поэтому закон носит его имя.

Снова запишем обычное уравнение состояния: 

А теперь учитывая:  и 

Получаем:   для любых различных состояний газа, или же просто:  - закон Гей-Люссака

Из этого закона очевидно следует прямо пропорциональная связь между температурой и объёмом: при увеличении температуры наблюдается увеличение объёма, и наоборот. График зависимости меняющихся величин в уравнении, то есть T и V, имеет следующий вид и называется изобарой (рис. 3):

Рис. 3. Графики изобарных процессов в координатах V-T

Следует обратить внимание на то, что, поскольку мы работаем в системе СИ, то есть с абсолютной шкалой температур, на графике присутствует область, близкая к абсолютному нулю температур, в которой данный закон не выполняется. Поэтому прямую в области, близкой к нулю, следует изображать пунктирной линией.

Рис. 4. Жозеф Луи Гей-Люссак

Изохорные процессы

Изохорный (или изохорический) процесс – процесс перехода идеального газа из одного состояния в другое при постоянном значении объёма.

Процесс рассмотрен впервые французом Жаком Шарлем (рис. 6), поэтому закон носит его имя. Запишем закон Шарля:

Снова запишем обычное уравнение состояния: 

А теперь учитывая:  и 

Получаем:   для любых различных состояний газа, или же просто:

 - закон Шарля

Из этого закона очевидно следует прямо пропорциональная связь между температурой и давлением: при увеличении температуры наблюдается увеличение давления, и наоборот. График зависимости меняющихся величин в уравнении, то есть T и P, имеет следующий вид и называется изохорой (рис. 5):

Рис. 5. Графики изохорных процессов в координатах V-T

В районе абсолютного нуля для графиков изохорного процесса также существует лишь условная зависимость, поэтому прямую также следует доводить до начала координат пунктиром.

Рис. 6. Жак Шарль

Стоит обратить внимание, что именно такая зависимость температуры от давления и объёма при изохорных и изобарных процессах соответственно определяет эффективность и точность измерения температуры с помощью газовых термометров.

Интересен также тот факт, что исторически первыми были открыты именно рассматриваемые нами изопроцессы, которые, как мы показали, являются частными случаями уравнения состояния, а уже потом уравнения Клапейрона и Менделеева-Клапейрона. Хронологически сначала были исследованы процессы, протекающие при постоянной температуре, затем при постоянном объёме а последними – изобарические процессы.

Обобщение газовых законов

Скачано с www.znanio.ru