Моделі поведінки виробника

Моделі поведінки виробника

Розглянемо математичну постановку задачі виробника.        

          Фірма випускає продукцію одного виду. Обсяг продукції, який випускається за конкретний період часу (наприклад, за рік, місяць тощо) позначимо Y. Обсяг продукції фірми визначається виробничою функцією. Передбачається, що  ця функція безперервна та  диференційована

де  - обсяг витрат ресурсів або виробничих факторів.

 До виробничих факторів можуть бути віднесені: основні виробничі фонди, трудові ресурси (середня чисельність зайнятих людей або відпрацьованих людино-днів за конкретний період часу), витрачені за цей проміжок часу матеріали, сировина, енергія тощо.

Нехай  – вектор – рядок цін ресурсів, а p – ціна продукції.  Тоді прибуток фірми дорівнює

Тут - доход фірми при випуску розглянутої продукції, -  вартість витрат ресурсів за конкретний період часу.

Задача максимізації прибутку має вигляд

Для пошуку оптимальних значень вектору  необхідно розглянути перші похідні

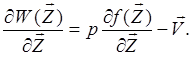
Цей вираз можна переписати таким чином

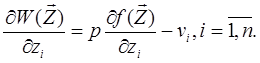
Прирівнюємо перші похідні нулеві

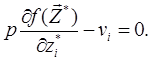
Перепишемо цей вираз у вигляді

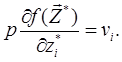
Звідси

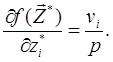
                     Тепер розглянемо модель, якщо фірма хоче максимізувати обсяг випуску продукції. До розглянутих умов додається така умова: відома вартість С витрат ресурсів за конкретний період часу, але невідома ціна одиниці продукції, що випускається. Цільову функцію  та обмеження представимо у вигляді

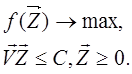
Побудуємо функцію Лагранжа

тут  – множник Лагранжа. Щоб максимізувати цю функцію необхідно розглянути перші похідні

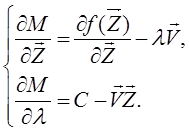
Перепишемо останні рівняння у вигляді

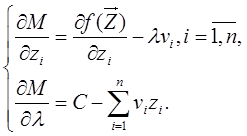
Прирівнюємо ці похідні нулеві

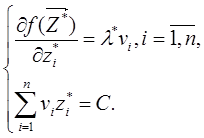
Вирішуючи цю систему, можна знайти оптимальні значення вектору