Моделирование линий

МОДЕЛИРОВАНИЕ ЛИНИЙ

Кривая Безье – полиномиальная кривая, задаваемая набором определяющих точек. Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий.

Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью ее опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путем применения соответствующих трансформаций к опорным точкам.

В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «Путь» (path).

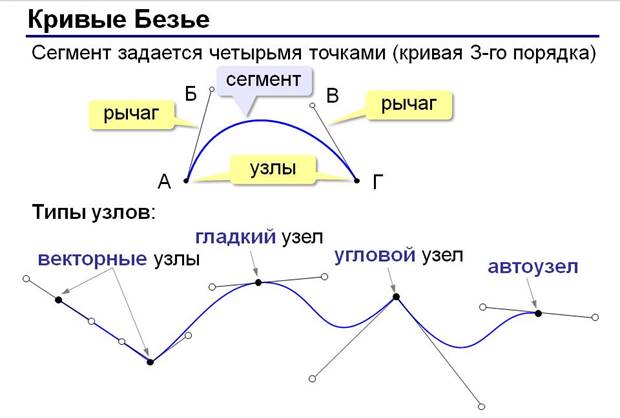
Свойства кривой Безье:

·                     непрерывность заполнения сегмента между начальной
и конечной точками;

·                     кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;

·                     при наличии только двух контрольных точек сегмент представляет собой прямую линию;

·                     прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;

·                     кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;

·                     масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;

·                     изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;

·                     степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой – парабола;

·                     окружность не может быть описана параметрическим уравнением кривой Безье;

·                     невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

Подавляющее большинство контуров реальных объектов (мы говорим прежде всего об обтравке фотографий, а не о рисовании дизайнером собственных композиций) имеют форму «волны». Эта «волна» может быть разной: пологой и почти неотличимой от прямой, или крутой
и напоминающей гребенку; регулярной и повторяющейся как синусоида или случайной и непериодической как складки на одежде, но принципиально она все равно остается волной. Основная задача при построении пути – разбить волну на элементарные участки, каждый из которых хорошо аппроксимируется единичным (т.е. расположенным между соседними опорными точками) криволинейным отрезком кривой Безье.

Чтобы было проще разобраться посмотрите на рисунок:

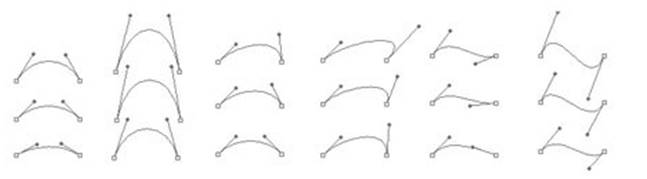
На нем показаны некоторые характерные формы (примитивы) единичного отрезка. Естественно, что это лишь капля в море – форм этих может быть практически бесконечное множество, но общую тенденцию можно заметить. Большинство таких примитивов представляют несколько искаженную четверть окружности.

Исключение составляют две правые колонки, где приведены волнообразные формы, но надо быть осторожнее: чем больше амплитуда такой волны, тем более вырожденной (прямолинейной) получается ее средняя часть.

После мысленного разбиения контура на подобные примитивы построение пути сводится к постановке опорных точек в местах разбиения и вытягиванию направляющих для придания примитивам необходимой формы. При этом в точке перегиба направляющие соседних примитивов должны быть связаны (т.е. направлены под одним и тем же углом).

Скачано с www.znanio.ru