Моделювання хіміко-технологічних процесів [4]

1.4.          Моделювання хіміко-технологічних процесів [4]

     Найбільш перспективним методом розв’язання задач дослідження й розрахунку хіміко-технологічних процесів є теоретичний метод, заснований на складанні й розв’язанні диференціальних рівнянь, що повністю описують процес (наприклад, рівняння переносу маси, енергії й імпульсу). У окремих, спрощених випадках рішення цих рівнянь знайдені, деякі з них наведені нижче (наприклад, рішення рівнянь Ейлера для умов рівноваги й усталеного руху ідеальної рідини приводять до основного рівняння гідростатики й рівняння Бернуллі, що широко використовуються в інженерній практиці).

     Диференціальні рівняння описують цілий клас однорідних явищ (наприклад, однією системою рівнянь Нав’є-Стокса описуються такі різні, на перший погляд, явища, як рух рідини по трубопроводах і каналах і переміщення великих об'ємів океанічної води й атмосферного повітря). Для практичного використання цих рівнянь треба при їхньому розв’язанні враховувати обмеження, що випливають із властивостей конкретного явища (процесу). Для хіміко-технологічних процесів такими обмеженнями можуть бути границі змін геометричних характеристик апаратів, фізичних властивостей речовин і т.п. Тому для виділення конкретного явища із класу явищ, що описуються єдиною системою диференціальних рівнянь, необхідно ці рівняння обмежити додатковими умовами, які називають умовами однозначності, тобто умовами, які повністю, однозначно характеризують дане явище (наприклад, температура насиченої пари, що однозначно визначається його тиском).

     Умови однозначності включають: 1) геометричну форму й розміри системи (апаратури); 2) фізичні властивості речовин, що беруть участь у процесі; 3) початкові умови (початкову швидкість, початкову температуру й т.п.); 4) граничні умови (наприклад, рівність нулю швидкості рідини на поверхні стінок каналу).

     Однак більшість хіміко-технологічних процесів настільки складні, що вдається лише скласти систему диференціальних рівнянь для їхнього опису й установити умови однозначності. Вирішити ж ці рівняння відомими в математиці методами звичайно не представляється можливим. У подібних випадках використовують метод моделювання. При цьому під моделюванням розуміють дослідження процесів, що протікають в об’єктах пізнання, на їхніх моделях.

      Моделювання знаходить широке застосування як при проведенні наукових досліджень, так і при розв’язанні великої кількості практичних задач у різних областях техніки: у гідравліці й гідротехніці (визначення конструктивних і експлуатаційних характеристик гідротехнічних споруджень, моделювання течії рік, хвиль, припливів і відливів і ін.); в авіації, ракетній і космічній техніці (визначення характеристик літальних апаратів і їхніх двигунів і ін.); у суднобудуванні (визначення характеристик корпуса судна й ін.); у теплотехніці (при конструюванні й експлуатації різних теплових апаратів) і т.п.

     Величезне значення має моделювання при дослідженні хіміко-технологічних процесів і проектуванні хімічних виробництв. При цьому під моделюванням розуміють метод дослідження хіміко-технологічних процесів на моделях, що відрізняються від об'єктів моделювання (натури) в основному масштабом. Моделювання можна здійснювати двома основними методами – за методом узагальнених змінних, або методом теорії подібності (фізичне моделювання), і за методом чисельного експерименту (математичне моделювання). Принципового розходження між цими методами немає, оскільки обидва вони в більшій або меншій мірі засновані на експериментальних даних і розрізняються лише підходом до їхньої обробки й аналізу.

     1.4.1. Метод узагальнених змінних (теорія подібності).

     Метод узагальнених змінних становить основу теорії подібності. Одним з основних принципів теорії подібності є виділення із класу явищ (процесів), що описуються загальним законом (процеси руху рідин, дифузії, теплопровідності й т.п.), групи подібних явищ.

     Подібними називають такі явища, для яких відношення подібних величин і величин, що характеризують ці явища, постійні. Розрізняють наступні види подібності: а) геометрична; б) часова; в) фізичних величин; г) початкових і граничних умов.

     Геометрична подібність припускає, що подібні розміри натури й моделі паралельні, а їхнє відношення виражається постійною величиною. Припустимо, що вивчається складне явище - рух газу в обертовому циліндрі (рис. 1.3). Щоб досліджувати процес у даному апарату, будуємо модель, дотримуючись геометричної подібності (рис. 1.3,б), тобто рівності відношення подібних лінійних розмірів натури й моделі.

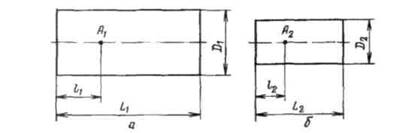
                  Рис. 1.3. До визначення умов подібності натури (а) і моделі (б)

     Якщо розглянута система (натура, модель) перебуває в русі, то при наявності геометричної подібності всі її точки повинні переміщатися за подібними траєкторіями, тобто проходити геометрично подібні шляхи (точки А₁ і А₂). Геометрична подібність дотримується за умов рівності відношень всіх подібних розмірів натури й моделі:

     Безрозмірну величину  називають константою геометричної подібності, або масштабним (перехідним) множником. Константа подібності характеризує відношення однорідних подібних величин у подібних системах (у розглянутому випадку - лінійних розмірів натури й моделі) і дозволяє перейти від розмірів однієї системи (моделі) до іншої (натури).

     Часова подібність припускає, що подібні точки або частини геометрично подібних систем (натури й моделі), рухаючись по геометрично подібним траєкторіям, проходять геометрично подібні шляхи в проміжки часу, відношення яких є постійною величиною:

,

де θ₁ і θ₂ - час проходження подібними частками всього апарата, відповідно натури й моделі; τ₁ і τ₂ час проходження подібними частками подібних шляхів 1₁ і 1₂; а_τ - константа часової подібності.

     Подібність фізичних величин припускає, що в розглянутих подібних системах (натури й моделі) відношення значень фізичних величин двох будь-яких подібних точок або часток, подібно розміщених у просторі й часі, є величина постійна. Наприклад, якщо в натурі частка за час τ₁ пройшла шлях l₁ (рис. 1.3, а), а в моделі - за час τ₂ шлях l₂, то для подібних точок А₁ і А₂ маємо:

де u₁ і u₂ - сукупність фізичних величин (але в загальному випадку  й т.д.).

     Подібність фізичних величин включає подібність не тільки фізичних констант, але й сукупності значень фізичних величин, або полів фізичних величин. Таким чином, при дотриманні геометричної й часової подібності буде дотримуватися також подібність полів швидкостей, температур, концентрацій і інших фізичних величин, тобто - константи.

     Подібність початкових і граничних умов припускає, що початковий стан і стан на границях систем (натури й моделі) подібні, тобто відношення основних параметрів на початку й на границях систем постійні. Це справедливо лише в тих випадках, коли для початкових і граничних умов систем витримується геометрична, часова й фізична подібність, тобто  Цим підкреслюється важливість подібності початкових і граничних умов, оскільки іноді в основному об'ємі системи подібність може дотримуватися не повністю. Разом з тим, навіть незначне відхилення початкових і граничних умов може привести до істотного порушення подібності системи в цілому (наприклад, неврахування сильних збурень всієї системи внаслідок так званих «вхідних ефектів»).

     Всі константи подібності постійні для різних подібних точок подібних систем, але змінюються залежно від співвідношення розмірів натури й моделі. Іншими словами, відношення однорідних подібних величин для натури й іншої моделі, також подібної до натури, буде іншим. Ця обставина представляє великі незручності для масштабування й долається введенням так званих інваріантів подібності.

     Інваріанти подібності й критерії подібності. Якщо всі подібні величини, що визначають стан даної системи (натури) і подібної їй системи (моделі), вимірювати у відносних одиницях, тобто брати подібне відношення величин для кожної системи, то воно також буде величиною постійною й безрозмірною, наприклад:

, 

     Величини i_l, i_τ і т.д. не залежать від співвідношення розмірів натури й моделі, тобто для іншої моделі, також подібної до натури, значення i_l, i_τ будуть такими ж. Таким чином, відношення геометричних розмірів, часу й фізичних констант у даній системі (натурі) дорівнюють відношенням тих же величин у подібній системі (моделі). При переході від однієї системи до іншої, їй подібної, чисельне значення величин, , ..., зберігається. Тому безрозмірні числа і, що виражають відношення двох однорідних величин у подібних системах, звуться інваріантами подібності.

     Інваріанти подібності, що представляють собою відношення однорідних величин, називають симплексами, або параметричними критеріями (наприклад, відношення  - геометричний симплекс). Інваріанти подібності, які виражені відношенням різнорідних величин, називають критеріями подібності. Звичайно їх позначають початковими літерами імен учених, що зробили істотний внесок у дану область знань (наприклад,  - число або критерій Рейнольдса).

     Можна отримати критерії подібності для будь-якого фізичного явища. Для цього необхідно мати аналітичну залежність між змінними величинами цього явища. Критерії подібності безрозмірні (як і інваріанти подібності), їхні значення для різних точок даної системи можуть мінятися, але для подібних точок подібних систем не залежать від відносних розмірів натури й моделі.

     Таким чином, явища, подібні між собою, характеризуються чисельно рівними критеріями подібності. Рівність критеріїв подібності - єдина кількісна умова подібності процесів. Звідси очевидно, що відношення критеріїв однієї системи до критеріїв подібної їй системи завжди дорівнює 1. Наприклад, для натури й моделі Rе₁ = Rе₂ . Тоді

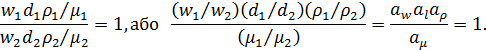
     Якщо відношення констант подібності дорівнює 1, воно носить назву індикатора подібності й указує на рівність критеріїв подібності. Отже, у подібних явищ індикатори подібності дорівнюють одиниці.

     Якщо константи подібності знайдені з умов однозначності, то утворені з них критерії називають визначальними. Критерій, у який входить шукана величина, називають визначуваним. Будь-яка комбінація критеріїв подібності також являє собою критерій подібності розглянутого явища.

     Для деякої групи подібних процесів критерії подібності мають певні чисельні значення. При переході до іншої групи подібних процесів, описуваних тими ж диференціальними рівняннями, при тому ж наборі критеріїв подібності їхні чисельні значення будуть іншими (внаслідок, наприклад, розходжень геометричних характеристик, швидкостей потоків і т. ін.).

     Із вищезазначеного випливає, що будь-яка залежність між змінними, що характеризують яке-небудь явище (наприклад, система диференціальних рівнянь), може бути представлена у вигляді залежності між критеріями подібності:

                            (1.8)

     Цю залежність називають узагальненим (критеріальним) рівнянням, а критерії подібності К_і  - узагальненими змінними величинами.

     Таким чином, теорія подібності дає можливість представити рішення диференціальних рівнянь і обробляти експериментальні дані у вигляді узагальнених критеріальних рівнянь. Це дозволяє скоротити число експериментів при одержанні конкретних рівнянь типу (1.8) за рахунок варіювання критеріїв подібності, минаючи визначення всіх величин, що входять у критерії подібності рівняння (1.8).

     Звичайно рівняння (1.8) записують у вигляді залежності визначуваного критерію подібності (у який входить шукана величина) від визначальних критеріїв:

                                                        ).                                      (1.9)

Наприклад,

де  - визначуваний критерій подібності; значення А, п, т знаходять дослідним шляхом.

     Якщо який-небудь ефект у досліджуваному процесі стає дуже слабким у порівнянні з іншими (чисельні значення критеріїв можуть бути при цьому досить малі або великі), то його впливом можна знехтувати. У цьому випадку критерії, що характеризують інтенсивність цього ефекту, можуть бути опущені з розгляду, і процес здобуває властивість автомодельності, тобто незалежності від цих критеріїв. Таке моделювання називають наближеним.

     Таким чином, теорія подібності вказує, як треба ставити досліди й обробляти дослідні дані, щоб, обмежившись мінімальним числом дослідів, мати підставу узагальнювати їхні результати й одержувати закономірності для цілої групи подібних явищ. Теорія подібності дозволяє з достатньою для практики точністю вивчати складні процеси на моделях (значно менших за розмірами і часто більш простих, ніж апарати натуральної величини), використовуючи при цьому не робочі речовини (іноді токсичні, пожежно- і вибухонебезпечні, дорогі й т.п.), а модельні (наприклад, воду, повітря й т.д.). Все це дозволяє істотно спрощувати й здешевлювати експерименти, швидше реалізовувати результати досліджень.

     Необхідно мати на увазі, що при використанні теорії подібності існують певні обмеження. Наприклад, використовуючи методи теорії подібності, не можна отримати інформації більше, ніж її закладено у вихідних рівняннях. Можна без звичайних математичних методів інтегрування цих рівнянь одержати їхні інтегральні рішення, але якщо вихідні рівняння невірно описують фізичну сутність процесу, то й отримані з використанням методів теорії подібності залежності будуть невірні. Крім того, моделювання на основі методу узагальнених змінних завжди пов'язане із проведенням експерименту, іноді досить складного й великого за об'ємом, що вимагає значних витрат часу. Отримані узагальнені рівняння працюють надійно тільки в тих інтервалах зміни змінних, які були використані при проведенні експерименту.

     Теореми подібності. Основні положення теорії подібності узагальнюються теоремами подібності. Перша теорема подібності сформульована Ньютоном:

      Подібні явища характеризуються чисельно рівними критеріями подібності.    1-а теорема подібності визначає, які величини треба вимірювати при проведенні дослідів, результати яких треба узагальнити: необхідно вимірювати ті величини, які входять в критерії подібності.

     Друга теорема подібності була доведена Бекінгемом, Федерманом та Афанасьєвою-Еренфест. Відповідно до цієї теореми, рішення любого диференціального рівняння, що зв’язує між собою змінні величини, які впливають на процес, може бути представлене у вигляді залежності між безрозмірними комплексами цих величин, тобто між критеріями подібності.

2-а теорема подібності відповідає на питання, яким чином обробляти результати дослідів, проведених на моделях: їх треба представляти у вигляді функціональної залежності між критеріями подібності, тобто у вигляді критеріальних рівнянь типу (1.8) - (1.9).

     Третя терема подібності (теорема Кирпичова та Гухмана) формулює необхідні і достатні умови подібності явищ. Подібні такі явища, які описуються однією і тією ж системою диференціальних рівнянь, і в яких дотримується подібність умов однозначності, тобто явища подібні, якщо їх визначальні критерії чисельно рівні. Наслідком рівності визначальних критеріїв є і рівність визначуваних критеріїв для моделі та натурного об’єкта. Тому критеріальна залежність (1.8) - (1.9), яка отримана узагальненням результатів дослідів, проведених на моделі, буде справедливою для всіх подібних процесів, у тому числі, і для натури.

     Перетворення диференціальних рівнянь методами теорії подібності. Отже, теорія подібності дає можливість виражати диференціальні рівняння у вигляді функціональної залежності між критеріями подібності. При цьому для визначення критеріїв подібності виконують наступні дії:

1)  формулюють подібність умов однозначності, тобто задають константи подібності або масштабні множники; звичайно передбачають, що вони задані (а_l, а_µ і т.д.);

2)  кожний з елементів диференціального рівняння процесу множать на відповідні константи подібності, причому останні виносять за знак диференціала (як постійні величини); при цьому похідна будь-якого порядку перетвориться в такий спосіб:

                                      (1.10)

3)    прирівнюють коефіцієнти, що стоять при однакових членах вихідних і перетворених рівнянь; тим самим виконується тотожність рівнянь для подібних процесів і інваріантості вихідних диференціальних рівнянь; отримані рівняння або інваріанти подібності зв'язують між собою константи подібності;

4)    в отриманих індикаторах подібності константи подібності заміняють відповідними відношеннями величин, виводять критерії подібності й установлюють залежність між ними (критеріальне рівняння).

     Можливий також спрощений формальний спосіб подібного перетворення диференціальних рівнянь. Критерії подібності отримують при цьому шляхом ділення одного з членів рівняння на другий, співвідношення між якими бажано ввести в критерій, відкидання знаків математичних операторів та необхідного скорочення однойменних параметрів.

     Таким чином, дослідження процесів методом теорії подібності повинно складатися з наступних етапів:

1)    отримавши повний математичний опис процесів, тобто склавши систему диференціальних рівнянь і встановивши умови однозначності, проводять подібні перетворення цих рівнянь і визначають критерії подібності, що характеризують процес;

2)    дослідним шляхом на моделях встановлюють конкретний вид залежності між критеріями подібності, при цьому отримане узагальнене рівняння буде справедливим для всіх подібних явищ у досліджуваних межах зміни визначальних критеріїв подібності.

     1.4.2. Метод аналізу розмірностей.

     Окремим спрощеним варіантом теорії подібності є теорія розмірностей, згідно з якою залежність між параметрами процесу може бути замінена залежністю між їхніми розмірностями.

     Речовини, що використовуються в хіміко-технологічних процесах, мають різні фізичні властивості (в'язкість, густина й т.п.), а їхній стан і умови проведення процесу характеризуються різними параметрами (температурою, тиском, швидкістю й т.п.), які можуть вимірюватися в різних одиницях.

     Вираження даної фізичної величини через величини, покладені в основу певної системи одиниць, називають розмірністю цієї величини. Та сама фізична величина може мати різну розмірність у різних системах одиниць.

     Якщо невідоме вихідне рівняння, що описує дане явище (процес), то для формування критеріїв подібності можна використати аналіз розмірностей - вчення про методи раціональної побудови систем одиниць виміру. При цьому величини розділяють на первинні, чисельні значення яких установлюють прямим виміром, і вторинні, обумовлені як функції первинних. Вторинна величина, виражена через первинні, завжди являє собою степеневий комплекс, що записується у вигляді формули розмірності, тому що тільки в цьому випадку відношення однойменних величин не залежить від вибору одиниць. Ця умова збігається з вимогою рівності розмірностей величин у лівій і правій частинах одержуваного рівняння. Формула розмірності якої-небудь фізичної величини А має вигляд

=                                              (1.11)

де [А] - символ розмірності визначуваної (вторинної) фізичної величини; L, М, Т... - символи вимірюваних (первинних, основних) фізичних величин (відповідно довжини, маси, часу й т.д.); l, m, τ ... - цілі або дробові, позитивні або негативні числа, що називають показниками розмірності, або розмірністю визначуваної величини А. Так, формула розмірності для прискорення а (м/с²) записується у вигляді  , для сили f (Н=кг∙м/с²) - у вигляді  і т.д.

     Вибір числа первинних (основних) фізичних величин у принципі довільний, але практичні міркування приводять до деякого обмеження свободи у виборі цих величин і їхніх одиниць.

     Якщо для досліджуваного процесу встановлено, які величини впливають на шукану (вторинну) величину, але вид зв'язку між ними невідомий, то можна скласти рівняння розмірностей, у якому в лівій частині буде стояти символ шуканої величини зі своїм показником розмірності, а в правій - добуток символів величин, від яких шукана величина залежить, але з невідомими показниками розмірності. Задача знаходження зв'язку між фізичними величинами зводиться в цьому випадку до відшукання значень відповідних показників розмірності.

     В основі методу аналізу розмірності лежить π-теорема Бекінгема: число безрозмірних комплексів дорівнює числу всіх фізично різнорідних величин п, які впливають на процес, за винятком числа первинних величин (розмірностей) т. Ця теорема зв'язує аналіз розмірностей з теорією подібності, оскільки за умови дотримання подібності безрозмірні комплекси, знайдені за допомогою π-теореми, є критеріями подібності, тобто число критеріїв подібності дорівнює

     Таким чином, з π-теореми витікає, що всяке співвідношення між деяким числом п розмірних величин, що характеризують дане фізичне явище, можна представити у вигляді співвідношення між меншим числом безрозмірних комбінацій, складених із цих величин.

     Метод аналізу розмірностей не універсальний; він вимагає попереднього знання числа змінних, від яких залежить дане явище, проведення великого об'єму експериментів, як для визначення числа змінних величин п, що впливають на дане явище, так і для встановлення конкретної степеневої залежності типу рівняння (1.11). Якщо не врахувати хоча б одну з п величин, які істотно впливають на досліджуваний процес, то при одержанні кінцевого розрахункового рівняння це може привести до серйозної помилки. Тому метод аналізу розмірностей, на відміну від теорії подібності, має обмежене застосування.

     1.4.3. Математичне моделювання.

     Однією з особливостей сучасних досліджень стала математизація фізичного пізнання, тобто інтенсивне застосування методів математичного моделювання. Математичне моделювання - це по суті визначення властивостей і характеристик розглянутого явища (процесу) шляхом рішення (як правило, за допомогою ЕОМ) системи рівнянь, що описують цей процес, - математичної моделі. При цьому дуже важливо скласти модель так, щоб вона досить точно характеризувала основні властивості розглянутого процесу й у той же час була доступною для дослідження. Однак варто обмовитися: досліди, будучи основою всякого дослідження, в той же час поставляють вихідні дані й для математичного моделювання, тобто математичне моделювання по суті є одним з методів фізичного моделювання й становить із ним єдину систему дослідження об'єктів пізнання.

     Математичне моделювання особливо важливо там, де не зовсім ясна фізична картина досліджуваного явища, не пізнаний внутрішній механізм взаємодії й, отже, немає можливості описати дане явище узагальненим рівнянням. У процесі чисельного експерименту відбувається по суті уточнення вихідної фізичної передумови (моделі). Шляхом розрахунків на ЕОМ різних варіантів ведеться нагромадження фактів, що дає можливість в остаточному підсумку зробити відбір найбільш реальних і ймовірних ситуацій. Математичне моделювання дозволяє різко скоротити строки наукових і проектних розробок. У порівнянні з натурним експериментом це звичайно й дешевше, і швидше Загальна схема процесу математичного моделювання (чисельного експерименту) включає 8 послідовних етапів.

     Постановка задачі. Постановка задачі визначає не тільки мету, але й шляхи рішення даної задачі. Це один з найважливіших етапів моделювання, оскільки не існує загальних правил, які можна було б використати у всіх випадках. Перед розробкою шляху рішення задачі необхідно досить повно усвідомити природу даної конкретної задачі. Чим глибше буде ясна фізична сутність явища, тим вірніше буде складена фізична модель досліджуваного процесу.

     Аналіз теоретичних основ процесу (складання фізичної моделі процесу). На цій стадії необхідно виявити, які фундаментальні закони лежать в основі даного процесу. Звичайно теоретичні основи процесів вивчають по різних джерелах - як опублікованих, так і неопублікованих. Якщо не вдається підібрати задовільну теорію, можна вдатися до розробки гіпотез (постулатів). Справедливість їх повинна бути перевірена шляхом порівняння результатів рішення математичної моделі, побудованої на основі прийнятих постулатів, з експериментальними даними.

     У ряді випадків для складання фізичної моделі процесу доцільно використати метод аналогії процесів з наступною експериментальною перевіркою.

     Складання математичної моделі процесу. На основі обраної фізичної моделі стосовно до розв'язуваної задачі складають систему відповідних математичних рівнянь - математичну модель процесу. Побудова математичної моделі полягає в створенні формалізованого опису об'єкта дослідження мовою математики у вигляді деякої системи рівнянь і функціональних співвідношень між окремими параметрами моделі. Математична модель може вміщувати як диференціальні, так і кінцеві рівняння, що не містять операторів диференціювання.

     Розрізняють два основних види математичних моделей: детерміновані (аналітичні), побудовані на основі фізико-хімічної сутності, тобто механізму досліджуваних процесів, і статистичні (емпіричні), отримані у вигляді рівнянь регресії на основі обробки експериментальних даних. Очевидно, що фізико-хімічні детерміновані моделі більш універсальні й звичайно мають більш широкий інтервал адекватності.

     Фізико-хімічна детермінована модель складається із трьох груп рівнянь:

     1) рівнянь балансів маси й енергії; ця група рівнянь дозволяє визначити потоки маси й теплоти, зміну фізико-хімічних властивостей системи (в'язкості, теплоємності й т.п.) у зв'язку зі зміною температури й складу;

     2) рівнянь стану (фазові рівноваги й т.п.);

     3) кінетичних рівнянь; до цієї групи відносяться описи кінетики тепло- і масопереносу, хімічної кінетики й т.д.

     На даному етапі варто розглянути можливість спрощення рівнянь шляхом знехтування деякими членами рівнянь, що мало змінюються в ході рішення задачі. Іноді можна з цієї причини виключати з розгляду цілі рівняння. Наприклад, при складанні теплового балансу з'ясувалося, що в заданому інтервалі температур і зміни концентрацій питома теплоємність багатокомпонентної суміші змінюється лише на 1-2% від номінального значення, чим в багатьох випадках можна знехтувати. Таким чином, перш ніж включити рівняння в математичну модель процесу, варто оцінити вплив вхідних у нього змінних на кінцеві результати рішення задачі й по можливості замінити слабко впливаючі змінні сталими середніми величинами.

     Алгоритмізація математичної моделі. Наступним етапом моделювання є алгоритмізація розробленої математичної моделі й вибір методу її рішення. У випадку досить простих процесів система рівнянь, що їх описує, може бути розв’язана аналітично. Коли ж математична модель являє собою складну систему диференціальних рівнянь, вибір ефективного алгоритму рішення набуває великого значення. При виборі методу рішення необхідно враховувати багато факторів: тип рівнянь, що входять у систему математичного опису моделі (звичайні диференціальні рівняння, диференціальні рівняння в частинних похідних і т.п.), розмірність задачі й т.п. Таким чином, на даному етапі варто вибрати загальний підхід до рішення задачі й визначити сукупність критеріїв, яким повинна задовольняти отримана система рівнянь моделі. Крім того, тут же необхідно провести аналіз задачі (математичний і фізичний), що повинен підтвердити існування й однозначність рішення.

     Після того, як складений повний математичний опис моделі, вибирають метод рішення, що представляється найбільш прийнятним, розробляють його у всіх деталях і записують у вигляді алгоритму. Потім алгоритм потрібно викласти на одній з мов програмування (фортран, бейсик, паскаль і ін.), тобто скласти програму для ЕОМ.

     Параметрична ідентифікація моделі. Під параметрами математичної моделі розуміють коефіцієнти, які враховують ті або інші особливості об'єкта - натури й характеризують властивості даної натури, що відрізняють її від інших натур подібного класу. Тому, чим більше параметрів входить у модель, тим докладніше й точніше вдається описати й охарактеризувати дану натуру. Однак багатопараметричні математичні моделі мають і істотні недоліки: це насамперед труднощі обробки таких моделей і висока чутливість до експериментальних помилок. Може виникнути така ситуація, коли внаслідок недостатньо високої точності експерименту фізичний зміст моделі може бути загублений, хоча модель у цілому буде давати досить точний збіг з експериментальними даними. Це відбувається тому, що помилки у величинах різних параметрів взаємно компенсуються. При цьому, кількісний опис натури в певних інтервалах змінних залишається придатним, але фізичний зміст моделі спотворюється й параметри моделі отримують роль підгінних параметрів, призначення яких зводиться до приведення у відповідність експериментальних даних і моделі. Часто деякі параметри моделі невідомі, і оцінити їхнє значення можна тільки за допомогою додаткових експериментів, тобто в цьому випадку необхідно провести параметричну ідентифікацію моделі.

     Процедура параметричної ідентифікації моделі достатньо формалізована. Основні методи параметричної ідентифікації математичних моделей розглянуті в спеціальній літературі.

     Перевірка адекватності математичної моделі. Об'єктивним критерієм якості моделей є їхня адекватність або ступінь наближення даних, прогнозованих по моделі, до експериментальних даних. Для перевірки адекватності математичної моделі реальному процесу необхідно порівняти спостережувані в ході експерименту величини із прогнозами по моделі при певних параметрах процесу. Звичайно це порівняння здійснюється шляхом перевірки деякої статистичної гіпотези.

     Моделювання процесу. Цей етап полягає в рішенні на ЕОМ математичної моделі процесу при варіюванні параметрів процесу в діапазоні, який є цікавим для даного дослідження.

     Аналіз отриманої інформації. Це заключний етап рішення задачі. Він зводиться до вивчення й перевірки результатів, отриманих при рішенні математичної моделі. При цьому будь-якому не передбачуваному заздалегідь рішенню необхідно дати раціональне пояснення, щоб гарантувати себе від помилок, які можуть виникнути в результаті обчислень.

     У кожному реальному процесі параметри в силу різних причин не залишаються постійними, причому вони можуть мінятися в досить широкому діапазоні. Тому необхідно проводити аналіз функціонування змодельованого процесу при зміні різних параметрів. Такий аналіз, як правило, переслідує три основні цілі:

1) досліджувати поводження моделі при варіюванні параметрів, що змінюються;

2) визначити, чи є дана модель працездатною при варіюванні змінних параметрів, і, відповідно, визначити межі працездатності моделі;

3) скорегувати модель із метою розширення діапазону її працездатності й поліпшення її експлуатаційних характеристик.

     На підставі проведеного аналізу приймають рішення - видати рекомендації для практичної реалізації або продовжити дослідження.