
Министерство образования Республики Казахстан
Управление образования Павлодарской области
Региональный научно-практический центр «Ертіс дарыны»
 |
Литвиненко Александра,
(Фамилия, имя)
titchenko_a@mail.ru
8 «Б» сыныбы
(класс)
Тема:
Недосказанные факты геометрии.
Направление: естественные и точные науки
Ғылыми жетекшісі: Титченко Анжелика Петровна (руководитель)
математика мұғалімі
titchenko_a@mail.ru
Павлодар
2020-2021 оқу жылы
Аннотация
Жұмыс бұрыштары геометриялық прогрессияны құрайтын үшбұрыштың қасиеттерін зерттеуге және дәлелдеуге арналған. Бұл тақырып бұрын математикада неге қозғалмады деп айту қиын, бірақ жұмыстың мазмұны мүлдем белгісізге арналған, сондықтан геометриялық тізбектегі бұрыштары бар үшбұрыштың қасиеттері туралы теоремалар зерттелмегендігі факт болып қалады.
Жоба жабылған материалдың кеңдігімен таң қалдырады. Бұрыштары геометриялық тізбекті құрайтын үшбұрышпен бірге жұмыс үшбұрыштардың бүкіл классын қарастырады: ортоцентрлік, медианалық. Сонымен қатар, бұл үшбұрыштар органикалық қажеттілікпен енгізіліп, зерттеледі. Геометриялық прогрессияны құрайтын бұрыштары бар таңдалған үшбұрыштың табиғаты осындай, оның ерекшелігі мен қасиеттері үшбұрыштардың басқа түрлерімен және геометриялық объектілердің басқа түрлерімен салыстырғанда дәл көрсетілген. Сондықтан жұмыстың өзектілігі даусыз.
Зерттеу жұмысы логикалық тұрғыдан дұрыс құрылымға ие. Ол кіріспеден, теориялық бөлімнен, практикалық бөлімнен, қорытындыдан, сондай-ақ зерттеу жұмысын жазуда қолданылатын әдебиеттер тізімінен және қосымшалардан тұрады. Жұмыс жақсы жақтаулы. Зерттеу жоспары мақсатқа жету үшін барлық қажетті қадамдарды қамтиды.
Онда оның негізгі нәтижелерін нақтырақ ашуға мүмкіндік беретін иллюстрациялық материалдың үлкен мөлшері бар.
Жоба ғылыми-зерттеу болып табылады, сондықтан ол танымдық қызығушылықты, талдау дағдыларын, ақпаратты қабылдау мен өңдеудің түрлі тәсілдерін дамытуға ықпал етеді. Жұмыста мақсат, міндеттер, зерттеу пәні мен объектісі, өзектілігі, жаңалығы белгіленеді, бұл жұмыстың зерттеушілік сипатын көрсетеді. Бірінші тарауда автор үшбұрыштың қасиеттерін дәлелдеп, жүйелеп, геометриялық дәйектілікті құрайды, бұл кезде оқулық материалын ғана емес, сонымен бірге тереңдетіп зерттеуге арналған қосымша материалдарды қолданады. Оның жұмысының соңғы өнімі - бұл Үшбұрыш жад.
Жұмыс жоғары деңгейде орындалды және практикалық қызығушылық тудыратын бірқатар тұжырымдардан тұрады. Автор тек теориялық материалдарды көрсетіп қана қоймайды, сонымен бірге зерттелген тақырыпты пайдалану шешімдерімен проблемалар ұсынады. Жұмыс нақты құрылымдалған: кіріспе, проблемалық шешім, негізгі мазмұны, тұжырымдары, зерттелген әдебиеттер тізімі бар. Жоба бойынша жұмыс нәтижесінде «Үшбұрыштар туралы жаңа фактілер» тақырыбында презентация жасалды. Өнім сапа талаптарына толығымен сәйкес келеді, қолдануға ыңғайлы және жобаның мақсаттарына сәйкес келеді.
Сонымен, мақсаттар мен міндеттер сәтті ашылды деген қорытынды жасауға болады. Ғылыми жоба мақтауға тұрарлық.
Аннотация
Работа посвящена исследованию и доказательству свойств треугольника, чьи углы составляют геометрическую прогрессию. Сложно сказать, почему данная тема ранее не была затронута в математике, но остается фактом, что содержание работы посвящено совершенно неизвестным, а поэтому и не изученным теоремам о свойствах треугольника с углами находящимися в геометрической последовательности.
Проект поражает широтой охватываемого материала. Вместе с треугольником, чьи углы составляют геометрическую последовательность в работе рассматривается еще целым класс треугольников: ортоцентрические, медианные. Причем, эти треугольники вводятся и исследуются по органичной необходимости. Такова уже природа избранного треугольника с углами, составляющими геометрическую прогрессию, что его своеобразие и свойства хорошо высвечиваются именно в сопоставлении с другими типами треугольников и другими типами геометрических объектов. Поэтому актуальность работы неоспорима.
Исследовательская работа имеет логически правильную структуру. Она состоит из введения, теоретической части, практической части, заключения, а также списка использованной при написании исследовательской работы литературы и приложений. Работа грамотно оформлена. План исследования включает в себя все необходимые этапы для достижения цели.
Она содержит большое количество иллюстративного материала, что позволяет более наглядно раскрыть ее основные результаты.
Проект является исследовательским, поэтому способствует развитию познавательного интереса, аналитических способностей, различных способов восприятия и обработки информации. В работе поставлены цель, задачи, предмет и объект исследования, актуальность, новизна, что указывает на исследовательский характер работы. В первой главе, автор доказывает и систематизирует свойства треугольника, с углами составляющими геометрическую последовательность при этом использует не только материал учебного пособия, но и дополнительный материал, предназначенный для углубленного изучения. Конечным продуктом его работы является памятка «Треугольник».
Работа выполнена высоком уровне, содержит ряд выводов, представляющих практический интерес. Автор не только показывает теоретический материал, но и предлагает задачи с решениями на использование изученной темы. Работа чётко структурирована: имеются введение, постановка задач, основное содержание, выводы, список изученной литературы. В результате работы над проектом была разработана презентация на тему « Новые факты о треугольниках». Продукт полностью соответствует требованиям качества, удобен в использовании, соответствует целям проекта.
Annotation
The work is devoted to the study and proof of the properties of a triangle, whose angles make up a geometric progression. It is difficult to say why this topic has not been previously touched upon in mathematics, but the fact remains that the content of the work is devoted to completely unknown, and therefore not studied theorems on the properties of a triangle with angles in a geometric sequence.
The project is striking in the breadth of the covered material. Together with the triangle, whose angles make up a geometric sequence, the work considers a whole class of triangles: orthocentric, median. Moreover, these triangles are introduced and investigated by organic necessity. Such is the nature of the chosen triangle with angles that make up a geometric progression that its originality and properties are well highlighted precisely in comparison with other types of triangles and other types of geometric objects. Therefore, the relevance of the work is undeniable.
The research work has a logically correct structure. It consists of an introduction, a theoretical part, a practical part, a conclusion, as well as a list of literature and applications used in writing the research work. The work is well-framed. The research plan includes all the necessary steps to achieve the goal.
It contains a large amount of illustrative material, which makes it possible to more clearly reveal its main results.
The project is research, therefore it contributes to the development of cognitive interest, analytical skills, various ways of perceiving and processing information. The work sets the goal, objectives, subject and object of research, relevance, novelty, which indicates the research nature of the work. In the first chapter, the author proves and systematizes the properties of a triangle, with angles making up a geometric sequence, while using not only the material of the textbook, but also additional material intended for in-depth study. The end product of his work is the Triangle memo.
The work was performed at a high level and contains a number of conclusions of practical interest. The author not only shows theoretical material, but also proposes problems with solutions for using the studied topic. The work is clearly structured: there is an introduction, problem statement, main content, conclusions, a list of studied literature. As a result of the work on the project, a presentation on the topic "New facts about triangles" was developed. The product fully complies with quality requirements, is easy to use, and meets the goals of the project.
Thus, we can conclude that the goals and objectives have been successfully disclosed. The research project is commendable.
ВВЕДЕНИЕ
Работа касается не то, чтобы малоисследованной, а совершенно неисследованной области: треугольников, чьи углы составляют геометрическую прогрессию. Почему такие треугольники с такими неожиданными, интересными и захватывающими свойствами, оказались в тени, пусть выясняют историки математики, а мы вернемся к работе, которая поражает широтой охватываемого материала.
В курсе геометрии мы изучаем понятие треугольник. Простейший из многоугольников – треугольник – играет в геометрии особую роль. За несколько тысячелетий, геометры подробно изучили треугольник, но он по-прежнему притягивает пытливые умы юных математиков.
Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. В Древней Греции изучение свойств треугольника достигает высокого уровня - это теорема Пифагора и формула Герона, которым более 2000 лет. В XV – XVI веках появилось огромное количество исследований свойств треугольника. Например, это большой раздел планиметрии, получивший название “Новая геометрия треугольника”. Большой вклад в изучение свойств треугольника внес русский ученый Н.И. Лобачевский. Его труд «Новое начало геометрии» получил применение в физике, кибернетике и математике. Вместе с собственно нашим треугольником в работе рассматривается еще целым класс треугольников: ортоцентрические, медианные, Такова уже природа избранного треугольника с углами, составляющими геометрическую прогрессию, что его своеобразие и с свойства хорошо высвечиваются именно н сопоставлении с другими типами треугольников и другими типами геометрических объектов. Исследуемый треугольник так богат свойствами, что их невозможно не только не исследовать, но и доказать в силу их полезности для расширения и углубления раздела геометрии «Треугольники»
Тема проекта – Недосказанные факты о треугольниках
Предмет исследования - свойства треугольников с углами ![]()
![]() и
и![]() .
.
Цель работы
Найти, исследовать и доказать свойства треугольника, углы которых составляют геометрическую прогрессию.
В этом и состоит новизна проекта. Если о треугольниках, стороны которых составляют арифметическую прогрессию еще можно отыскать информацию, то о треугольниках, углы которых составляли бы геометрическую прогрессию, систематических исследований не проводилось. Между тем, свойства такого рода треугольников богаты, глубоки и интересны.
Задачи
1. Изучить и доказать новые свойства треугольников, углы которых составляют геометрическую прогрессию.
2. Исследовать и доказать отличительные свойства прямой Эйлера, окружности девяти точек и линии центров.
Гипотеза: существует треугольник, углы которого составляют геометрическую прогрессию обладающй отличительными, неизученными свойствами.
Структура проекта: проект состоит из введения, в котором анонсируется название работы, выдвигаются ее цель, а также ее задачи, обосновываются новизна и практическая значимость; основной части, в которой достигаются выдвинутые цели и решаются сформулированные задачи, и заключения где подводятся итоги проделанной работы.
Методы исследования: анализ, синтез, индукция, дедукция, метод математического моделирования, метод сопоставительного анализа, метод полного и частичного перебора, а также прочие графические и численные методы.
Значимость работы может быть рассмотрена в двух аспектах:
а) научном,
б) практическом.
Так как в работе доказаны свойства нового объекта, а именно треугольника, углы которого составляют геометрическую прогрессию, то работа имеет научное значение.
Работа относится к внутренним областям математики и прямого выхода в практику не имеет, а выходит в нее опосредствованно, через другие разделы математики. Проект будет интересен и доступен учащимся, заинтересованным в расширении и углублении знаний в области геометрии. Материалы проекта могут быть использованы в математических классах, кружках и факультативах в качестве пособия для ознакомления с особыми типами треугольников и их свойствами. Окажется он полезным и для самих учителей.
Треугольники, углы которых составляют геометрическую
прогрессию это треугольники с углами ![]()
![]() и
и![]() .[ 1, с. 46]
.[ 1, с. 46]
Эти треугольники отличаются большим набором интересных свойств, нахождением и доказательством которых мы будем заниматься в нашем проекте.
Новые свойства треугольников, углы которых составляют геометрическую прогрессию
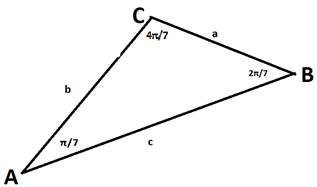 Теорема 1.
Теорема 1.
Сумма
квадратов сторон треугольника углы которого равны ![]()
![]() и
и ![]() равна 7
равна 7![]() , где R
есть радиус описанной окружности данного треугольника.
, где R
есть радиус описанной окружности данного треугольника.
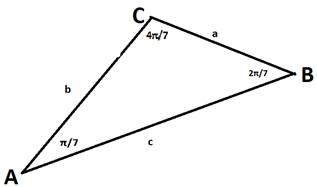
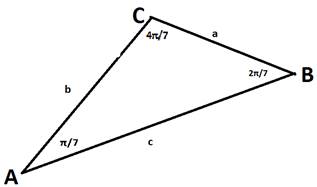
(рис. 1)
Доказательство.
Пусть
имеется треугольник АВС с указанными свойствами: ∠A
= ![]() ,
,
∠B
= ![]() , ∠C
=
, ∠C
= ![]() и сторонами, равными а. b.
с. (рис. 1)
и сторонами, равными а. b.
с. (рис. 1)
Тогда по теореме синусов (Теорема, устанавливающая зависимость между длинами сторон треугольника и величиной противолежащих им углов. Существуют два варианта теоремы; обычная теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
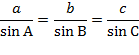
и расширенная теорема синусов: Для произвольного треугольника
![]()
Где a ,b ,c — стороны треугольника, ∠A,B,C — соответственно противолежащие им углы, а R — радиус окружности, описанной около треугольника.
![]() и
и ![]()
Отсюда получим:
![]()
Или используя формулу двойного угла синуса sin(2α) = 2sin(α)cos(α) получаем
![]() =
= 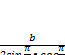 .
.
Тогда длина стороны а может быть выражена следующим равенством
a=![]() из которого выразим в :
в = 2а * cos
из которого выразим в :
в = 2а * cos ![]() .
.
Аналогично
выразим длину стороны с через в: ![]() ;
; ![]() =
= ![]() ;
;
b=![]() из которого
окончательно выразим длину с через b
:c = 2b
* cos
из которого
окончательно выразим длину с через b
:c = 2b
* cos ![]() .
.
Для рассмотрения выражения длины стороны а через с нам
понадобитья формула приведения тригонометрии: Sin
![]() = sin(
π-
= sin(
π-![]() )= sin
(
)= sin
(![]() )
)
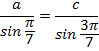
Sin
![]() Sin ( π-
Sin ( π-![]() )= Sin
)= Sin ![]() =2 sin
=2 sin ![]() cos
cos ![]()
![]() =
= ![]()
Тогда длина стороны а может быть выражена следующим равенством
a=![]() из которого выразим в :
в = 2а * cos
из которого выразим в :
в = 2а * cos ![]() .
.
Сложим теперь все три равенства, предварительно возведя каждое в квадрат,
получим
a2+ b2+c2=4a2![]() +4b2
+4b2![]() +4c2
+4c2![]()
С другой стороны,
a2=4R2![]()
b2=4R2![]()
c2=4R2![]()
Откуда окончательно
a2+
b2+c2=4a2![]() +4b2
+4b2![]() +4c2
+4c2![]() =4R2
=4R2![]()
=4R2(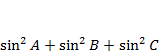 )=4R2(2+2cosA•cosB•cosC)=4R2•
)=4R2(2+2cosA•cosB•cosC)=4R2•
![]() =7R2 .
=7R2 .
Что и требовалось доказать
 Теорема
2
Теорема
2Если
a, b,
c стороны
треугольника АВС с углами ![]()
![]() и
и![]() ,
то сторона а равна половине среднего гармонического двух других его сторон.
,
то сторона а равна половине среднего гармонического двух других его сторон.
Доказательство.
Известно,
что в нашем треугольнике ![]() тогда
тогда
![]() =
= ![]() =
=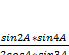 =
=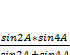 .
.
Учитывая, что
![]() =
=![]() =2R
=2R
получим:
a=![]() . Что и требовалось
доказать.
. Что и требовалось
доказать.
Используя
это утверждение можно показать, что b=![]() , c=
, c=![]()
Теорема 3.
Если
ha, hb,
hc - высоты, опущенные
соответственно на стороны а,b,c
треугольника АВС с углами ∠A=
![]() ∠B=
∠B=![]() , ∠C=
, ∠C=![]() , то ha1
= hb
+ hc
, то ha1
= hb
+ hc
Доказательство:
Используя предыдущие результаты, можем написать
![]() =
= ![]()
Кроме того, пользуясь обычной формулой площади, запишем
ha=![]() ha=
ha=![]() ha=
ha=![]() ,
,
где
S - площадь исходного треугольника АВС, откуда сразу же получим
результат ha = hb + hc
Теперь выпишем основные числовые соотношения, имеющие место между
элементами треугольника АВС,углы которого равны:
∠A= ![]() ∠B=
∠B=![]() , ∠C=
, ∠C=![]()
cos
A • cos В • cos C =-![]()
sin2
A + sin2 В +
sin2 C=![]()
sin
2 A + sin 2 В +
sin 2 C=![]()
cos2
A + cos2 В +
cos2 C =![]()
cos2
A + cos2B + cos2 C = - ![]()
sin2
A • sin2 В•
sin2 C = ![]()
sin
A • sin
В• sin C =![]()
sin2A
• sin2 В+
sin2 A•
sin2 C+
sin2 В•
sin C=![]()
sin4
A + sin4 В +
sin4 C=![]()
cos4
A + cos4 В +
cos4 C =![]()
cos2
A • cos2 В +cos2 A • cos2 C+ cos2 В• cos2 C=![]()
sec2A + sec2B+ sec2C=24
tg2A+ tg2B+ tg2C=21
cos ec2 A + cos ec 2 В + cos ec 2 C =8
ctg2A+ ctg2B+ ctg2C=5
tgA• tgB• tgC=-![]()
cos ec4 A + cos ec 4 В + cos ec 4 C =32
sec4A + sec4B+ sec4C=416
sec2A + sec2B+ sec2C=-4
ctgA+ ctgB+ ctgC=![]()
sin
A + sin В +
sin C=![]()
Способы получении этих равенств различны. Например, мы можем взять
sin7x расписать это по формуле и заменив sinx через X, получить уравнение
64х7 -112х5 + 56х7 - 7х =0
Корни которого:0;± ![]() ±
± ![]() ±
± ![]()
Тогда
дроби :![]()
Представляют суммы : sin2A , sin2 Вb sin2 C и так далее. Что и требовалось доказать
 Теорема
4
Теорема
4Суммы квадратов высот треугольника АВС с углами
![]()
![]() и
и![]() равны половине суммы
квадратов его
равны половине суммы
квадратов его
сторон
Надо
доказать, что ha2+
hb2+
hc2=
![]()
Доказательство ;Для этого запишем высоты и стороны исходного треугольника с помощью тригонометрических функций
ha= 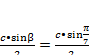
hb= 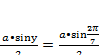
hc= 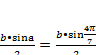
и сложив квадраты равенств, получаем откуда
ha2+
hb2+ hc2= 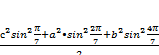
и далее применяя известные соотношения, получим искомое
ha2+
hb2+
hc2=
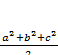 . Что и требовалось
доказать.
. Что и требовалось
доказать.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.