Некоторые вопросы механики в свете изменений ЕГЭ по физике для ЦТО

 

 

 

 

 

Некоторые вопросы механики в свете изменений ЕГЭ

по физике

для ЦТО

Преподаватель физики ЦТО

Советского района г. Брянска

Степаниденко Александр Иванович

 

 

 

 

 

 

 

§ 1.Ускорение и его виды.

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Говоря на уроках об ускорении следует отметить, что ускорение бывает средним и мгновенным. Понятно, что в школьном курсе очень трудно говорить о мгновенных значениях физических величин, но всё-таки обозначим данные понятия.
Среднее ускорение – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Именно с этим ускорением мы и работаем в школьном курсе физики, подразумевая что физические величины изменяются линейно. Определить среднее ускорение можно формулой:

где   – вектор ускорения.

Направление вектора ускорения совпадает с направлением изменения скорости   (здесь ₀ – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t₁ тело имеет скорость ₀. В момент времени t₂ тело имеет скорость . Согласно правилу вычитания векторов, найдём вектор изменения скорости

Тогда определить ускорение можно так:

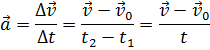
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

Направление ускорения совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями  ).

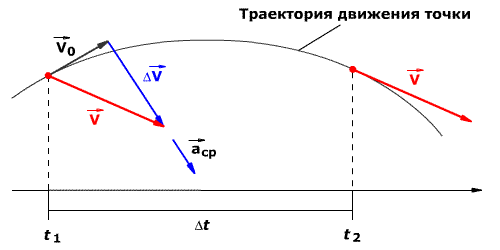
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

 а направление вектора ускорения совпадает с вектором скорости ₂.

Если скорость тела по модулю уменьшается, то есть , то направление вектора ускорения противоположно направлению вектора скорости . Иначе говоря, в данном случае происходит замедление движения, при этом проекция ускорения будет отрицательной  .

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Вектор тангенциального ускорения сонаправлен вектору скорости, если скорость тела увеличивается, и наоборот.

.

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой . Вектор нормального ускорения направлен по радиусу кривизны траектории к её центру. В школьном курсе об этой составляющей мы говорим, как о центростремительном ускорении.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Или

(согласно теореме Пифагора, для прямоугольного прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов

Задание 24 (ЕГЭ). Маленькая шайба движется из состояния покоя по неподвижной гладкой сферической поверхности радиусом R. Начальное положение шайбы находится на высоте R/2 относительно нижней точки поверхности. Сделайте рисунок с указанием сил, действующих на шайбу в момент, когда она движется вправо вверх, находясь на высоте R/6 над нижней точкой поверхности (см. рисунок). Покажите на этом рисунке, куда направлено в этот момент ускорение шайбы (по радиусу поверхности, по касательной к поверхности, внутрь поверхности, наружу от поверхности). Ответ обоснуйте. Сопротивление воздуха не учитывать.

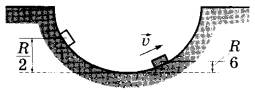
Решение.

1. К шайбе приложены сила тяжести  , направленная вертикально вниз, и сила реакции поверхности , направленная по радиусу вверх. Ускорение шайбы  направлено внутрь траектории левее направления силы N (см. рисунок).

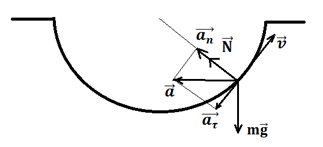
2. В исследуемой точке скорость шайбы , поэтому у шайбы есть Нормальная составляющая (центростремительное) ускорения  , направленное к центру окружности, по которой движется шайба.

3. Скорость шайбы в данной точке направлена по касательной, при этом её модуль уменьшается. Значит у шайбы есть тангенциальная составляющая ускорения , направленная противоположно вектору скорости, т. к. модуль скорости уменьшается.

4. Полное ускорение шайбы находим по формуле . Значит направление ускорения находим по правилу параллелограмма, т. е. оно направлено внутрь сферической поверхности левее направления силы .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МЕХАНИКА

§ 2. Относительность движения.

Напомним немного теории по данной теме. Наибольший интерес представляют задачи по данной теме, решение которых дается очень трудно детям.

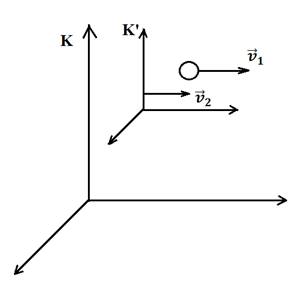Пусть К – неподвижная система отсчёта (НСО), К’ – подвижная система отсчета (ПСО)

 – скорость тела относительно ПСО,

 – скорость ПСО относительно НСО.

Обозначим за  – скорость тела относительно НСО. Тогда классический закон сложения скоростей имеет вид

 

Наибольший интерес представляют задачи по данной теме, решение которых дается очень трудно детям. Дело в том, что иногда нужно переходить в другие системы отсчета.

Задача №1. Корабль движется на запад со скоростью υ. Ветер дует с северо-запада под углом α к меридиану. Скорость ветра, измеренная на корабле, равна u. Найти скорость ветра   относительно земли.

Решение:

Разберёмся с условием:

 – скорость корабля (скорость ПСО),

 – скорость ветра относительно корабля (скорость относительно ПСО),

 – скорость ветра относительно земли (скорость относительно НСО).

Тогда по классическому закону сложения скоростей:

 

 

 

 

 

 

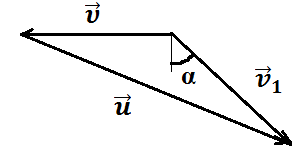
Изобразим на рисунке треугольник скоростей, в котором известны две стороны и угол, следовательно, можно применить теорему косинусов:

Или

Тогда

Значит, убирая отрицательный корень, получим

Ответ:

Задача №2. Корабль идет на запад со скоростью . Известно, что ветер дует с юго-запада (α=45°). Скорость ветра, измеренная на палубе корабля, равна . Найти скорость ветра  относительно Земли.

Решение: Изобразим всё на рисунке. По условию:

 – скорость ветра относительно Земли (относительно НСО),

 – скорость корабля относительно Земли (скорость ПСО относительно НСО),

  – скорость ветра, относительно палубы корабля (относительно ПСО).

Согласно классическому закону сложения скоростей:

 

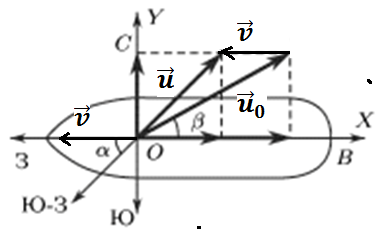
Из рисунка видно:

Ну коль задача в общем виде будем решать систему двух последних уравнений тоже в общем виде. Возведём оба уравнения в квадрат:

Сложив оба уравнения, получим:

Учитывая, что α=45°, приходим к квадратному уравнению:

Решая его, получим

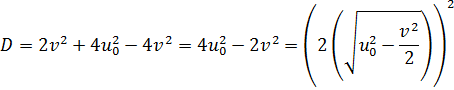
Тогда, исключая отрицательный корень, окончательно получаем:

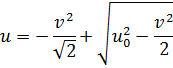
Ответ: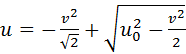

 

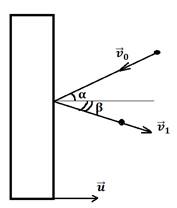Задача №3 Массивную плиту двигают горизонтально с постоянной скоростью, перпендикулярной вертикальной поверхности плиты. О плиту упруго ударяется шарик (см. рисунок). Скорость шарика непосредственно перед ударом ровна 8м/с и направлена под углом к нормали (для плиты) таким, что синус угла равен . Сразу после удара скорость направлена под углом к нормали таким, что синус угла равен  . Найти скорость плиты.

Решение: Данная задача относится к тому типу, когда понимание условия и происходящих процессов практически и приводят к полному решению. Кроме того, правильно выполненный рисунок, с соблюдением всех пропорций здесь тоже имеет большое значение.

За неподвижную систему отсчёта примем систему, связанную с Землёй, за подвижную – с плитой.

 – скорость плиты (скорость ПСО),

 – скорость шарика непосредственно перед ударом, относительно Земли (относительно НСО),

  – скорость шарика непосредственно после удара, относительно Земли (относительно НСО),

 – скорость шарика относительно плиты (относительно ПСО).

Тогда по закону сложения скоростей получаем:

Или

Изобразим всё на рисунке, где покажем составляющие относительной скорости (рис. 1)

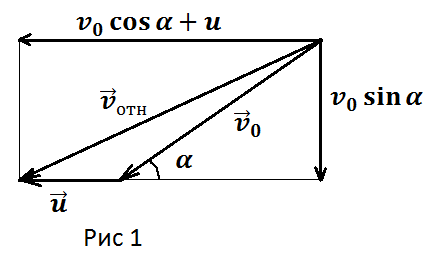
Теперь после удара. Дело в том, что закон упругого отражения (угол падения равен углу отражения) выполняется только в системе отсчёта, связанной с плитой и естественно только для относительной скорости, при этом её модуль не изменится. По законы сложения скоростей получим

И снова изобразим всё на рисунке

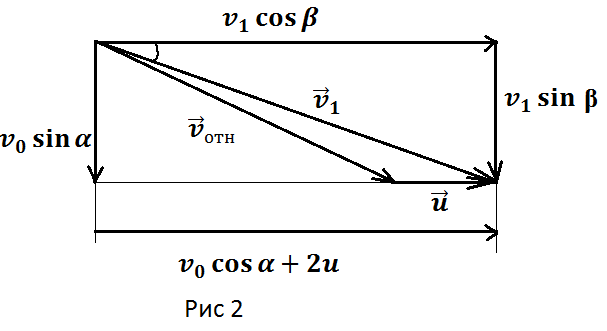
Анализируя рисунки получим:

Осталось решить полученную систему уравнений. Найдем предварительно косинусы углов

Тогда из уравнения (1) следует:

Из уравнения (2) следует:

 

Ответ: 1,1 м/с.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§ 3. Законы механики. Границы применимости и обоснования их применения.

Прежде чем говорить о законах механики, границах применимости и, как итог, обоснованиях применения, давайте разберемся с двумя понятиями, с которыми возникает большая путаница.

Материальная точка – тело, размерами которого в данных условиях можно пренебречь.

Поступательное движение - движение, при котором все точки тела движутся одинаково, при этом отрезок соединяющий две точки тела остается параллельным самому себе (нет ни поворотов, ни вращений).

Следует учитывать, что это два разных понятия и отождествлять их ни в коем случае нельзя. При обосновании в задании №30 ЕГЭ запись «….тела движутся поступательно, значит они являются материальными точками….» является неверной. Более правильным будет следующее: «так как тела движутся поступательно к ним можно применить модель материальной точки».

Таким образом обоснование в задании №30 для любого типа задач будут начинаться одинаково (возможны два варианта)

1.Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Тела, исходя из условия, считаем материальными точками.

Или

1. Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки.

Далее рассмотрим основные законы и их границы применимости.

Закон всемирного тяготения.

Силы гравитационного притяжения между двумя телами во Вселенной прямо пропорциональны произведению масс этих тел и обратно пропорциональны квадрату расстояния между ними.

Границы применимости:

1) Для двух материальных точек

2) Для двух шаров (расстояние между телами равно расстоянию между центрами тел)

3) Для шара и материальной точки (расстояние отсчитываем от центра шара)

Законы Ньютона

Первый закон: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка, сохраняет свою скорость постоянной, если на неё не действуют другие тела или действие других тел скомпенсировано.

Второй закон: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

Закон в такой формулировке применяется при решении задач по динамике, но очень часто встречаются задачи, в которых лучше использовать второй закон в иной формулировке:

Импульс равнодействующей силы равен изменению импульса тела

Данная формула (а в проекциях на ось ОХ имеет вид     еще пригодится при дальнейших обоснованиях применения законов.

Здесь я привел упрощенную формулировку, так как физика в школе очень страдает от отсутствия понятия производной хотя бы в упрощенной форме, но в начале 10 класса. Более правильно следует говорить

В инерциальной системе отсчёта скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил.

Третий закон: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Границы применимости:

1) Только в инерциальных системах отсчёта

2) Для материальных точек

3) Для тел, движущихся со скоростями значительно меньше скорости света

 Таким образом при обосновании применения законов Ньютона будем прописывать (дополняем вышеуказанные обоснования):

    Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки. Скорости тел значительно меньше скорости света, значит можем применять законы Ньютона.

Закон сохранения импульса

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях и движениях тел этой системы.

Что касается данного закона я бы предостерег от использования его в векторной форме. Лучше применять сразу в проекциях на произвольно выбранную ось. Поясню на примере:

Задача №1. На вагонетку массой 100кг, движущуюся со скоростью 5м/с с высоты 2 метра подает груз массой 25 кг. Найти скорость вагонетки с грузом. Сопротивлением воздуха и трением пренебречь.

Дано:                                                  Решение:

m1=100 кг     

v1=5м/с

H=2м

m2=25 кг

u-?

При записи закона сохранения в векторной форме

нарушаются законы векторной алгебры. При такой записи либо рисунок неверный (вектор скорости u должен быть направлен вниз под углом к горизонту), либо неверно векторное равенство. Поэтому закон сохранения импульса лучше записывать в проекциях на ось ОХ (это поможет и при обоснованиях).

Границы применимости:

 Система замкнутая – закон применим всегда. Однако, задач с замкнутыми системами взаимодействующих тел мы ни на уроках, ни в ЕГЭ не решаем.

 Система незамкнутая:

1) Внешние силы стремятся к нулю. Как правило в задачах оговаривается, что сопротивлением воздуха и трением, например, пренебречь. Поэтому при обосновании будем это учитывать.

2) Внешние силы компенсируют друг друга. Я бы не стал использовать это при обосновании.

3) Проекция внешней силы на выбранную ось равна нулю. Вот это утверждение будем использовать при неупругом столкновении тел (использовать для неупругого удара).

Так для предыдущей задачи обоснование было бы, например, следующее (применение каждого закона будем описывать с новой строки).

      Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки.

Сопротивлением воздуха и трением пренебречь. Во время столкновения на тела действуют внешние силы, проекции которых на выбранную ось ОХ равны 0. Значит, исходя из формулы , изменение проекции импульса на данную ось равно 0, следовательно, можно применять закон сохранения импульса в проекциях на ось ОХ.

4) Внешние силы достаточно велики, но время взаимодействия очень маленькое, поэтому изменением импульса под действием этих сил можно пренебречь (для упругого удара).

В случае абсолютно упругого взаимодействия обоснование звучать будет иначе    

Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки.

Сопротивлением воздуха и трением пренебречь. Время взаимодействия тел очень маленькое, следовательно, исходя из формулы   изменением импульса под действием внешних сил можно пренебречь, следовательно, можно применять закон сохранения импульса.

Закон сохранения энергии

Консервативные силы (потенциальные силы) — это силы, работа которых определяется начальным и конечным положением тел (сила тяготения, сила упругости). Работа таких сил не зависит от формы траектории, а по замкнутому контуру ровна нулю.

Энергия не исчезает и не создаётся. Она превращается из одного вида в другой или переходит от одного тела к другому, причём полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть в никуда.

E_k1 + E_p1 = E_k2 + E_p2

Следует отметить, что в задачах на упругое столкновение тел, мы на уроках забываем, как правило, пояснять учащимся о потенциальной энергии деформированного тела. Поэтому следует отмечать: «так как время взаимодействия очень маленькое, изменением потенциальной энергии  (  можно пренебречь».

Задача №2. Два тела массами 10кг и 15 кг движутся со скоростями 4м/с и 2м/с соответственно. Найти скорости тел после абсолютно упругого центрального удара.

Дано:                                                       Решение

m₁=10кг                m₂=15кг

v₁=4м/с

v₂=2м/с

 

u₁-?

u₂-?

По закону сохранения импульса в проекции на ось ОХ получим:

m₁v₁- m₂v₂= m₂u₂-m₁u₁   (1)

По закону сохранения энергии

    (2)

Решим систему уравнений (1) и (2). Из уравнения (1) получим 10=15u₂-10u₁ (*) или

u₁=1,5u₂-1, следовательно      (3)

Подставляя (3) в (2) и приведя подобные получим квадратное уравнение:

D=0,64+22,4=23,04=4,8². Следовательно

u₂₁=-2м/с – не имеет физического смысла, так как получается, что второе тело продолжает двигаться в прежнем направлении с той же скоростью.

u₂₂=u₂=2,8м/с. Из (*) следует u₁=3,2м/с.

Ответ: u₁=3,2м/с; u₂=2,8м/с

Обоснование: Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки.

Сопротивлением воздуха и трением пренебречь. Время взаимодействия тел очень маленькое, следовательно, исходя из формулы   изменением импульса под действием внешних сил можно пренебречь, следовательно, можно применять закон сохранения импульса.

Сопротивлением воздуха и трением пренебречь. Так как время взаимодействия очень маленькое, изменением потенциальной энергии  (  можно пренебречь. При взаимодействии на тела действуют только консервативные силы, следовательно, можно применить закон сохранения полной механической энергии.

Применение формул кинематики равноускоренного движения.

Часто в задачах необходимо применять формулу для проекции перемещения из кинематики. В этом случае можно писать: «При движении тела равнодействующая сил, действующих на тело, остаётся постоянной, следовательно, а=const, значит можно применять формулы кинематики равноускоренного движения.»

 

Баллистика.

При баллистическом движении сопротивлением воздуха можно пренебречь, на тело действует только сила тяжести, значит полное ускорение тела, а =g = const, следовательно, можно применять формулы кинематики равноускоренного движения.

Применение формулы   .

Данная формула вводится при изучении равномерного движения по окружности, поэтому обосновываем следующим образом: «В малых окрестностях исследуемой точки скорость тела можно считать постоянной, следовательно, можно применять формулу центростремительного ускорения.»

Статика.

Плечо силы - это кратчайшее расстояние от оси вращения до линии действия силы (т. е. длина общего перпендикуляра к двум этим прямым).

Момент силы относительно оси вращения - это произведение силы на плечо:

.

Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Условия равновесия.

 Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов. Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.

В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.

1. Векторная сумма всех сил, приложенных к телу, равна нулю. (для поступательного движения твердого тела)
2. Алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной, равна нулю. В этом случае момент силы, вращающей тело против часовой стрелки берется со знаком «+»

При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.

1'. Сумма проекций всех сил, приложенных к телу, на произвольную ось ровна нулю .
2'. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.

Обоснования: Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным). Движение твёрдого тела является суперпозицией поступательного и вращательного движений, поэтому условий равновесия твердого тела в ИСО два: одно для поступательного движения (геометрическая сумма внешних сил, действующих на тело равна нулю); другое – для вращательного движения (алгебраическая сумма моментов внешних сил, действующих на тело, относительно оси вращения равна нулю). Принимаем за ось вращения точку, через которую проходят линии действия сил, значения которых не даны и их значение определять не требуется.  В последнем предложении указывать точку конкретно для задачи.

Теперь рассмотрим несколько задач.

№1 Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно и равны v_пл=15м/с и v_бр=5м/с    Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ=0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?

Какие законы Вы используете для описания взаимодействия пластилина и бруска и их дальнейшего движения? Обоснуйте их применимость к данному случаю.

Дано:                            Решение:

m₁=m    

m₂=4m                                   

v₁=15м/с

v₂=5м/с

µ=0,17

u₁=0,7u                             

 

s - ?

По закону сохранения импульса в проекциях на ось ОХ получим:

Или

Следовательно, u₁=0,7м/с. Расстояние найдем по формуле

Для нахождения ускорения воспользуемся вторым законом Ньютона. В проекциях на оси получим:

     ОХ: -F_тр=-ma

     OY: N-mg=0

 Т. к. F_тр=µN=µmg, получим

a=µg=0,17*10=1,7м/с². Тогда

 

 

Ответ: 0,15м.

ОБОСНОВАНИЕ: Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки. Скорости тел значительно меньше скорости света, значит, можно применять законы Ньютона.

Сопротивлением воздуха и трением пренебречь. Во время столкновения на тела действуют внешние силы, проекции которых на выбранную ось ОХ равны 0. Значит, исходя из формулы , изменение проекции импульса на данную ось равно 0, следовательно, можно применять закон сохранения импульса в проекциях на ось ОХ.

При дальнейшем совместном движении тел равнодействующая сил, действующих на тела, остаётся неизменной, следовательно, a=const, значит можно применять формулы кинематики равноускоренного движения.

№2 Дан невесомый стержень, к концам которого подвешены шары массами m₁ и m₂ (см. рис.). Стержень опирается на две опоры в точках C и D. Длина стержня L равна 1 м, m₂ = 0,3 кг. Сила реакции опоры в точке D в два раза больше, чем в точке С. Также известно, что расстояния CD = 0,6 м, AC = 0,2 м. Найдите массу левого шарика m₁.

Какие законы Вы используете для описания равновесия тела? Обоснуйте их применение к данному случаю.

Дано:                                     Решение:

m₂ = 0,3 кг.                                                                                             

L=1м

CD =a= 0,6 м

AC=b = 0,2 м

 

m₁-?

 

Направим ось OY вертикально вверх. Пусть N₁=N, тогда N₂=2N. По второму закону Ньютона в проекциях на OY:

N₁+N₂=m₁g+m₂g.  Или    3N=g(m₁+m₂).    Отсюда

 

 

Согласно правила моментов, относительно оси, перпендикулярной плоскости рисунка и проходящей через точку А:

N_1*AC+N_2*AD=m₂g_*AB

N_*b+2N_*(a+b) =m₂gL

N(2a+3b) = m₂gL

Тогда 

Подставляя в (1) получим

Или

Ответ: 0,2 кг

Обоснование: Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной.

Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным). Движение твёрдого тела является суперпозицией поступательного и вращательного движений, поэтому условий равновесия твердого тела в ИСО два: одно для поступательного движения второй закон Ньютона); другое – для вращательного движения (Правило моментов). Принимаем за ось вращения ось, проходящую через точку А, перпендикулярно плоскости рисунка.

 

 

 

 

 

 

 

 

 

 

 

§ 4. ТЕОРИЯ погрешностей

Теории измерений и погрешностей в школьном курсе физики на мой взгляд уделяется очень мало времени. Это приводит к тому, что в ВУЗе ребенок сталкивается с проблемами при выполнении лабораторных работ. Разберем немного и эту тему. Сразу оговорюсь – опять возникают сложности из-за недостатков математики, а именно теории производной. Поэтому разбираем с детьми задачи при помощи таблицы, а уже в 11 классе можно объяснить при помощи производной. В прошедшем учебном году задачи на погрешность встречались, например, в олимпиаде «Робофест». Вспомним некоторые понятия из 7 класса

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений. Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.

Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямыми. Например, измерение длины бруска, ширины или высоты бруска.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B— физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

Тогда точное значение физической величины запишем в виде: А= A_пр± ΔA 

ε — относительная погрешность измерения физической величины, равная:

Если в условии задачи специально не оговаривается, то абсолютная погрешность прямого измерения ровна половине цены деления измерительного прибора.

Цена делений шкалы измерительного прибора – важная физическая величина.  Поэтому сформулируем правило для ее вычисления.

Чтобы подсчитать цену делений шкалы, нужно:

а) выбрать на шкале два ближайших штриха обозначенных цифрами;

б) сосчитать количество делений между ними (количество белых полей, а не штрихов!);

в) из большего значения вычесть меньшее и разделить на количество делений.

Приведу ниже таблицу для расчёта погрешностей косвенных измерений функции двух переменных:

Таблица 1
Вид функции y	Абсолютная погрешность Δy	Относительная погрешность
x1 + x2	Δx1 + Δx2
x1 − x2	Δx1 + Δx2
Cx	CΔx
x1x2	|x1| Δx2 + |x2| Δx1
xn	|n||x|n−1Δx
lnx
sinx	|cosx| Δx
cosx	|sinx| Δx	|tgx| Δx
tgx

Задача 1. Чтобы оценить, каков будет период малых колебаний математического маятника, используем для вычислений на калькуляторе формулу  . По оценке «на глазок» длина нити равна (1,5±0,1) м. Калькулятор показывает на экране число 2,4322335. Чему равен, с учётом погрешности оценки длины нити, период колебаний. маятника? (Ответ дайте в секундах, значение и погрешность запишите слитно без пробела.)

Решение: Для начала перепишем формулу в виде  , где С= величина постоянная. Тогда пользуясь формулами абсолютных погрешностей для функций Сх и хⁿ получим (имея в виду, что ∆l=0,1м):

Значит

Тогда ответ будет иметь вид: Т=(2,430,08) с.

В данной задаче произведено округление до первой значащей цифры в погрешности. Напомню, что это значит.

Значащей цифрой приближенного числа А называется всякая цифра в его десятичном представлении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда.

Пример. А = 0,002080. Здесь только первые три ноля не являются значащими. Следовательно, округление:

- до первой значащей цифры А=0,002

- до второй значащей цифры А=0,0021

- до третьей значащей цифры А=0,00208.

Разберём экспериментальное задание из ОГЭ

Задача 2. (Тип 17 № 893 ОГЭ)

Используя штатив с муфтой и лапкой, пружину, динамометр, линейку и 2 груза, соберите экспериментальную установку для определения жесткости пружины. Определите жесткость пружины, подвесив к ней два груза. Для определения веса грузов воспользуйтесь динамометром. Абсолютная погрешность измерения длины составляет ±1 мм. Абсолютная погрешность измерения силы составляет ±0,1 Н.

 В ответе:

1) сделайте рисунок экспериментальной установки;

2) запишите формулу для расчета жесткости пружины;

3) укажите результаты измерения веса грузов и удлинения пружины с учётом абсолютных погрешностей измерений;

4) запишите численное значение жесткости пружины.

Решение

1. Схема экспериментальной установки:

2. F_упр=mg=P ;    F_упр=kx. Значит

3. Р = (2,0 ± 0,1) H; x = (50 ± 1) мм = (0,050 ± 0,001) м

4.

Такое решение есть практически во всех источниках. Оно верное, если не учитывать погрешность вычисления жесткости, а вдруг попросят и её вычислить. Тогда получим:

 

 

Таким образом ответ имеет вид:

k=(40,0±2,8)Н/м

 

 

 

 

 

 

 

 

 

 

 

 

 

§ 5. КИНЕМАТИЧЕСКИЕ связи.

Кинематические связи – уравнения, связывающие между собой кинематические характеристики (координата, скорость, ускорение) тел системы.

Коснёмся наиболее распространенных физических моделей и кинематических связей, появляющиеся при их использовании.

1. Модель абсолютно твердого тела (АТТ).

Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого постоянно. Надо понимать, что указанное свойство присуще абсолютно твердому телу всегда, независимо от взаимодействия его с другими телами и от способа движения этого тела. Поэтому если мы рассмотрим две произвольные точки АТТ A и B, то в любой момент времени проекции скоростей этих точек  и  на ось ОХ, соединяющую A и B (см. рисунок), должны быть равны друг другу, иначе расстояние между точками будет меняться, что невозможно по определению АТТ. Таким образом, в данном случае уравнение кинематической связи связывает проекции скоростей:

        (1)

В некоторых источниках можно встретить так называемый «закон палочки», который и выражается формулой (1)

Задача 1. Палочка движется по плоскости. В некоторый момент скорость одного конца палочки направлена вдоль палочки и равна 25 см/с, а скорость второго конца направлена под углом 60° к линии палочки. Чему равна в этот момент скорость (в см/с) второго конца?

Решение.

Палочка движется по плоскости. Скорость одного конца палочки имеет известное значение и направление. Хотя с направлением возможны варианты (их два). Изобразим палочку (вид сверху) и выберем направление вектора скорости одного конца палочки (вдоль палочки), пусть это будет точка A (рис. 1).

Теперь перейдем ко второму концу палочки. Известно, что вектор скорости второго конца палочки направлен под углом 60° к линии палочки. Будем рассуждать логически. Палочка твердое тело и при движении все точки палочки в направлении палочки должны иметь одинаковые скорости. В противном случае палочка будет деформироваться. Тогда направление вектора скорости второго конца предопределено (рис. 2).

Тогда решение задачи очевидно  V_Bcosβ=V_A,

откуда

 

Ответ 50 см/с.

2. Связи между ускорениями и скоростями тел, соединенных натянутыми нитями. Например, в задачах с системами блоков. Если нить натянута и нерастяжима, то сохраняется ее длина. Поэтому скорости и ускорения связанных этой нитью тел должны за любой промежуток времени своими модулями и направлениями обеспечивать постоянство длины нити. Самый надежный способ – записать длину нити через координаты ее концов и блоков, через которые она перекинута. Затем перейти от координат к изменениям и потом — к проекциям скоростей или ускорений. В простых случаях достаточно установить связь между «укорачиванием» и «удлинением» нити при небольшом смещении ее концов и блоков.

Задача 2. В системе, изображённой на рисунке, нить невесома и нерастяжима, блоки невесомы, трение отсутствует. Массы грузов равны m₁=1кг и m₂=2кг. Найдите ускорение оси блока A, к которой приложена в вертикальном направлении сила F=12Н. Ускорение свободного падения равно g=10м/с².

Какие законы Вы используете для описания движения брусков? Обоснуйте их применение.

Дано:                                       Решение

m₁=1кг             Обоснования:                                                   

m₂=2кг

F=12Н

а_А-?

 

 

 

 

 

 

 

 

Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной. Из условия следует, что тела движутся поступательно, значит, к ним можно применить модель материальной точки. Скорости тел значительно меньше скорости света, значит, можно применять законы Ньютона. Предположим, что тела движутся вниз.Т₁=Т₂=Т₃=Т₄=Т₅=Т так как нить невесома. F_упр=2Т по третьему закону Ньютона. Составим выражение для длины нити:

L=x₁+πR₁+(x₁−x_A)+πR₂+(x₂−x_A) или

L-𝛑R₁-𝛑R₂=2x₁+x₂-2x_A

Так как нить нерастяжима L=const, а радиусы блоков не меняются, то дифференцируя последнее выражение и учитывая, что проекции всех ускорений положительны, получим связь между ускорениями: 2a₁+a₂=2a_A

Решение: По второму закону Ньютона в проекциях на ось ОХ получаем:

m₁a₁=m₁g−2T

m₂a₂=m₂g−T

F=2T следовательно,

Знак «-» говорит о том, что ускорение а₁ направлено противоположно.

Тогда

Ответ:

3. Связи при скольжении одного тела по другому без отрыва.

При таком движении должны быть равны проекции скоростей и ускорений тел на ось, перпендикулярную плоскости скольжения:

V_1z=V_2z

a_1z=a_2z

Задача 3. На неподвижном клине, образующем угол α с горизонтом, лежит груз, прикреплённый к стене, перекинутой через закреплённый на клине блок нерастяжимой нитью. В некоторый момент времени клин начинает двигаться вправо с постоянной скоростью х. С какой скоростью движется груз, пока он находится на клине?

Предположим, что клин движется вправо со скоростью v. При этом надо понимать, что расстояние между точками А и В все время меняется, несмотря на то, что веревка нерастяжима. Меняется потому, что есть перегиб на блоке. Перейдем в систему отсчета, которая движется вправо со скоростью v. В этой системе клин неподвижен, а стенка уходит вправо со скоростью v. Тогда очевидно, что по неподвижному клину груз может двигаться только вдоль наклонной плоскости, то есть вдоль веревки со скоростью v₁=v. Скорость груза относительно земли, согласно классическому закону сложения скоростей равна:

Определим результирующую скорость по теореме косинусов

 

4. Связи при движении без проскальзывания.

В этой ситуации должно выполняться векторное равенство скоростей для точек контакта тел:

Задача 4. Колесо катится без проскальзывания по ленте транспортера, движущейся горизонтально со скоростью v₀ = 1 м/с, в направлении движения ленты. Известно, что относительно неподвижного наблюдателя скорость v_B точки В, находящейся на ободе колеса на его горизонтальном диаметре, составляет с горизонтом угол α = 30^◦ Найти скорость v центра колеса относительно неподвижного наблюдателя. (ВМК МГУ)

Решение: По закону сложения скоростей скорость центра колеса относительно неподвижного наблюдателя (абсолютная скорость) равна

где   — скорость центра колеса относительно ленты транспортера (см. рисунок).

Из условия отсутствия проскальзывания следует, что

Где  - скорость точки В относительно центра колеса. Таким образом,

Как видно из рисунка,

Ответ: 2,36 м/с  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§ 6. Теорема о трёх силах.

Теорема о трёх силах — теорема статики, формулирующая необходимое условие равновесия абсолютно твёрдого тела под действием трёх непараллельных сил. Формулировка теоремы, следующая:

Если абсолютно твердое тело находится в равновесии под действием плоской системы трех непараллельных сил, то линии их действия пересекаются в одной точке.

Под тремя непараллельными силами в данном случае понимаются три силы, как минимум две из которых непараллельные.

Теорема даёт только необходимое условие равновесия тела. Чтобы условие стало достаточным, к нему необходимо прибавить требование равенства нулю геометрической суммы всех трёх сил.

Доказательство: Пусть тело находится в равновесии под действием сил F₁, F₂ и F₃, точки приложения которых соответственно A, B и C (рис. 1). Предположим для определённости, что силы F₁ и F₂ непараллельные. Следовательно, линии их действия пересекаются в некоторой точке O. Перенесём обе силы вдоль линий их действия в точку O и найдём равнодействующую этих сил F₄. Указанные операции не изменят состояния равновесия тела, следовательно, тело теперь будет находиться в равновесии под действием двух сил: F₃ и F₄. Но тело находится в равновесии под действием двух сил только в том случае, если эти силы направлены по одной линии. Следовательно, линия действия силы F₃ также проходит через точку O. Теорема доказана

Применение теоремы о трёх силах делает решение задач статики проще и нагляднее.

Задача 5. Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рис.). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы  действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.

Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.

Дано:                                  Решение(классический вариант)

α = 45°

m = 1 кг                  

                     

 

F-?

 

 

Стержень находится в равновесии под действием сил, изображенных на рисунке, где  — сила тяжести,  — сила натяжения нити,   и  — составляющие силы реакции шарнира вдоль горизонтальной и вертикальной осей, соответственно. Условия равновесия стержня имеют вид:

для сил:

F_x=T

F_y=mg

для моментов сил относительно точки :

где  — длина стержня. Учитывая, что

получаем

Ответ 11 Н.  

 

Обоснование: Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать её инерциальной.

Описываем стержень моделью твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным). Движение твёрдого тела является суперпозицией поступательного и вращательного движений, поэтому условий равновесия твердого тела в ИСО два: одно для поступательного движения (второй закон Ньютона); другое – для вращательного движения (правило моментов). Принимаем за ось вращения ось, проходящую через точку А, перпендикулярно плоскости рисунка.

Теперь приведем решение, используя теорему о трёх силах:

Решение. На стержень действуют три силы: сила натяжения нити , приложенная к точке крепления нити, сила тяжести , приложенная к центру масс стержня, и сила реакции шарнира , приложенная к шарниру. По теореме о трёх силах линии действия этих сил пересекаются в одной точке. Условие равенства нулю суммы действующих на стержень сил изобразим графически в виде треугольника сил. Поскольку линия действия силы тяжести проходит через центр масс стержня вертикально, то

tg β = 2_* tgα = 2,

следовательно, β ≈ 63,4◦.

Зная величину угла, который сила реакции составляет с горизонталью, можно рассчитать модуль силы реакции:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru