Нестаціонарний теплообмін

3.8. Нестаціонарний теплообмін

     У безперервно діючих теплообмінних апаратах нестаціонарний процес перенесення тепла виникає лише короткочасно в періоди пуску, зупинки або зміни режиму їх роботи. У таких умовах апарати розраховують тільки для основного, стаціонарного режиму теплообміну описаними вище методами.

      Разом з тим, у ряді випадків (при розрахунках нагрівальних печей, регенеративних теплообмінників, апаратів з оболонкою, апаратури для вулканізаціі, виробництва скла та ін.) важливе значення має розрахунок процесу нагрівання або охолодження тіл за умов режиму нестаціонарного теплообміну.

     Всі нестаціонарні теплові процеси обумовлені зміною ентальпії тіла до моменту практично повного вирівнювання його температури з температурою навколишнього середовища, тобто до досягнення теплової рівноваги. При розрахунку визначають або час, необхідний для нагрівання (охолодження) до заданої температури, або кінцеву температуру, що досягається за певний час, а також кількість тепла, переданого тілу або віднятого від нього.

     Для рідких і газоподібних речовин можна визначити лише залежність їх середньої температури від часу, оскільки температура рідини (газу) завжди вирівнюється за рахунок конвекції, супутньої передачі тепла теплопровідністю.

     3.8.1. Теплопровідність при нестаціонарному режимі

     У найбільш загальному вигляді залежність зміни температури твердого тіла і кількості переданого тепла від часу може бути встановлена шляхом вирішення диференціального рівняння теплопровідності (3.10). Для розв’язання  рівняння в конкретних випадках воно має бути доповнене умовами однозначності, що включають: а) початковий розподіл температури тіла , при рівномірному розподілу температури тіла в початковий момент часу ; б) вплив навколишнього середовища (потоку)  на поверхню тіла (граничні умови). Останні можуть бути задані  різними способами:

-      розподілом температури на поверхні тіла  в любий момент часу τ (граничні умови 1-го роду) -  = 

-      розподілом густини теплового потоку по поверхні тіла   в часі (граничні умови 2-го роду) -  = 

-      розподілом температури навколишнього середовища   (потоку, що омиває тіло) і коефіцієнтом тепловіддачі α від поверхні тіла до цього середовища (граничні умови 3-го роду):

     Однак аналітичні рішення, навіть при введенні припущень, які значно спрощують рівняння, виявляються громіздкими і складними для практичних цілей; такі рішення наводяться в спеціальній літературі.

     В інженерній практиці найбільш часто користуються графоаналітичним методом розрахунку, заснованим на перетворюванні рівнянь за допомогою теорії подібності і придатним для деяких тіл простої форми (куля, циліндр, пластина). Розрахунок  грунтується на тому, що кількість змінних, від яких залежить температура тіла, яка змінюється в просторі і в часі , може бути скорочена шляхом об'єднання їх в безрозмірні комплекси і симплекси подібності. При цьому один з визначальних критеріїв такого теплообміну - критерій Біо (Bi) визначається з граничних умов:

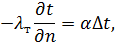
де лівий член, наприклад у випадку охолодження тіла, представляє собою інтенсивність підведення тепла з внутрішніх шарів твердого тіла до поверхні розділу, а правий – інтенсивність відведення тепла з поверхні тіла за рахунок тепловіддачі. Звідки, після ділення правого члена на лівий і відповідних подібних перетворень, отримуємо критерій Біо:

 .

     Критерій Біо, що характеризує подібність процесів нестаціонарної теплопровідності, зовні схожий з критерієм Нусельта (3.25), але відрізняється від останнього тим, що коефіцієнт тепловіддачі α, який входить в критерій Bi, не є шуканою величиною, а задається умовами однозначності. Величина λ_т в критерії Bi представляє собою коефіцієнт теплопровідності не рідини, а твердого тіла. Критерій - характеризує сталість відношення внутрішнього термічного опору теплопровідності до зовнішнього термічного опору тепловіддачі. Крім критерію Біо, з диференціального рівняння теплопровідності (3.10) визначається критерій теплової нестаціонарності Фур'є aτ/l² = Fo (безрозмірний час), а також додається  симплекс геометричної подібності  x/l, де l - характерний геометричний розмір (наприклад, для циліндра, кулі - їх радіус, для пластини – половина її товщини і т. д.);  х - відстань від поверхні тіла до даної його точки.

     Таким чином, рішення диференціального рівняння теплопровідності з відповідними умовами однозначності можуть бути виражене узагальненою залежністю безрозмірної температури в будь-якій частині тіла  ( деяка температура, що прийнята за масштаб температур) від вищеозначених визначальних критеріїв:

 .                                            (3.65)

     Ця функція справедлива для всіх подібних процесів нестаціонарної теплопровідності. Для кулі, циліндра і пластини вираження, отримані в результаті інтегрування рівнянь теплопровідності, представляють графічно (наприклад, рис. 3.15) у вигляді залежностей безрозмірних температур  на поверхні тіла і  в центрі тіла від критеріїв Bi і Fo. У даному випадку безрозмірні температури:

, ,

де - температура середовища, яка приймається постійною; — початкова температура тіла;  і — температура, що досягається за час τ відповідно на поверхні і в центрі тіла.

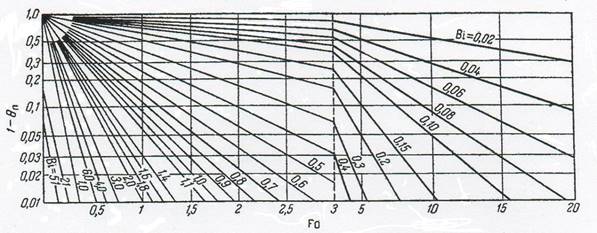
Рис. 3.15. Залежність  від Fo і Bi для поверхні кулі

 Рис. 3.15,а. Залежність  від Fo і Bi для кулі.

     Результати інтегрування рівняння (3.10) можна представити також у вигляді залежності Q/Q_∞ від тих же критеріїв подібності (рис. 3.15,а). Тут величина Q - кількість тепла, що передана за час τ, Q_∞  - кількість тепла, що передана за період повного нагрівання (або охолодження) твердого тіла, тобто до настання теплової рівноваги, яка досягається теоретично за час, що дорівнює нескінченності.

     Розрахунок за такими графіками проводиться наступним чином. Наприклад, для визначення часу охолодження виробу до заданої температури поверхні тіла  або температури в його центрі , визначають відповідні безрозмірні температури  або . Відповідно до умов тепловіддачі знаходять коефіцієнт α і розраховують критерій Bi. Із точки перетину горизонтальної лінії, що відповідає значенню 1- (або 1-), та лінії, що відповідає визначеному значенню Bi (рис.3.15), опускають перпендикуляр на вісь абсцис, де знаходять значення критерію Fo, з якого і отримують час охолодження τ. При зворотній задачі – необхідності визначення відповідних температур тіла  або  через заданий період часу τ, за точкою перетину перпендикуляра, проведеного з точки на осі абсцис, що відповідає значенню Fo, і лінії, що відповідає значенню Bi, визначають величину , а отже, і температури  або , по яких знаходять t_п або .

         Якщо графічно задана функція Q/Q_∞ = f(Bi, Fo) (рис. 3.15,а), то за відомим для матеріалу тіла (наприклад, кулі) значенням λ, c і ρ знаходять величину коефіцієнта температуропровідності і розраховують значення критерію Bi, приймаючи за визначальний розмір радіус r кулі. При цьому величина α має бути відома або попередньо розрахована (при розрахунку α задаються температурою поверхні тіла, яку потім перевіряють, і, таким чином, знаходять α методом послідовних наближень).

     Визначають відношення

,

 де   — об'єм кулі; t — середня по об’єму кулі температура за час

нагрівання τ (ця температура приймається або задається).

     Із точки на осі абсцис, яка відповідає даним , встановлюють перпендикуляр до перетину з ординатою, що відповідає значенням відношення . В точці перетину визначають величину , з якої знаходять шуканий час нагрівання кулі до температури t.

     При вирішенні низки практичних завдань по нагріванню і охолодженню тіл аналітичний розрахунок спрощують, виходячи з припущення, що перенесення тепла здійснюється в часі і в просторі не безперервно, а стрибкоподібно.

     Складність розрахунку нестаціонарних процесів теплопровідності пов'язана з відмінністю режимів, при яких вони протікають, у часі. Тому запропоновані наближені методи розрахунку, в яких нехтують наявністю початкового неупорядкованого режиму, що характеризується складною, нерівномірною зміною температури тіла.

     Крім того, успішно застосовуються експериментальні методи вирішення завдань нестаціонарної теплопровідності, засновані на аналогії між поширенням тепла теплопровідністю і ламінарним рухом рідини (гідротеплова аналогія), а також - на аналогії між тепловими і електричними явищами (електротеплова аналогія). Ці спрощені розрахункові та експериментальні методи описуються в спеціальній літературі (наприклад у.

     3.8.2. Регулярний тепловий режим

     Нестаціонарний процес нагрівання або охолодження твердого тіла з будь-яким початковим розподілом температур t за відсутності внутрішніх джерел тепла, сталості температури навколишнього середовища t_с і коефіцієнта тепловіддачі α може бути розділений в часі на два періоди (рис.3.16). У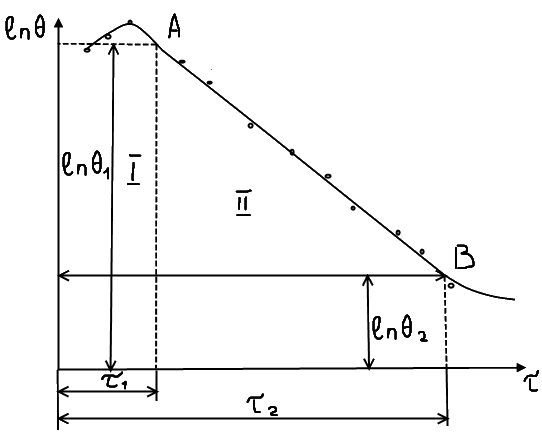

Рис.3.16. До визначення регулярного теплового режиму.

першому періоді, що носить назву неупорядкованого, швидкість зміни температури всередині тіла залежить від виду її початкового розподілу. У другому періоді, який отримав назву регулярного режиму, вплив початкового розподілу температури стає несуттєвим і процес визначається умовами теплообміну на границі тіло - середовище, фізичними властивостями, геометричною формою та розмірами тіла. Для цього періоду характерна залежність:

 або                            (3.66)

     Величина m називається темпом охолодження. Зауважимо, що темп охолодження є сталою величиною для всіх точок тіла, тобто не залежить від їх координат і часу, а залежить лише від інтенсивності теплообміну тіла з навколишнім середовищем, його фізичних властивостей, геометричної форми і розмірів. Для знаходження m досить виміряти температури тіла  и  у довільній точці тіла у два фіксованих моменти часу  и :

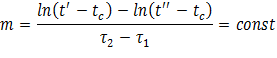
     Г. М. Кондратьєвим, який відкрив основні закономірності регулярного режиму, було знайдено:

                                  (3.67)

     Тут  и  — середні перепади температур по поверхні і об'єму тіла; F і V - поверхня і об'єм тіла; c_р - питома об'ємна теплоємність тіла. Величина ψ називається коефіцієнтом нерівномірності розподілу температури в тілі; вона залежить для даного тіла від умов теплообміну між його поверхнею і навколишнім середовищем, тобто від критерію Bi.

     Легко побачити, що при  або  (практично Bi < 0,1) розподіл температури в тілі буде залежати лише від його розмірів і фізичних властивостей, тому  і .

       При   або   (практично Bi > 100) завдяки великій інтенсивності зовнішнього теплообміну температура на поверхні прагне до температури навколишнього середовища,   и . Г. М. Кондратьєвим було показано, що в цьому випадку між темпом охолодження  і температуропровідністю тіла a існує наступне співвідношення:

.                                                        (3.68)

     Коефіцієнт С залежить тільки від геометричної форми і розмірів тіла. Аналітичним шляхом були знайдені вирази для С, наведені в наступній таблиці:

     За допомогою рівняння (3.68) і наведеної таблиці можна за експериментально знайденими температурами  та  у довільній точці тіла визначити коефіцієнт його температуропровідності а. Визначивши величину т  (3.67), можна знайти коефіцієнт тепловіддачі та швидкість нагрівання або охолодження тіла в середовищі певної температури.

     3.8.3. Теплопередача при нестаціонарному режимі

     До поширених процесів несталої теплопередачі відносяться періодичне нагрівання або охолодження рідини через стінку апарату або за допомогою встановленого всередині нього змійовика, нагрівання шару зернистого матеріалу та ін.

     При нагріванні або охолодженні рідин температура нагріваючого або охолоджуючого теплоносія може бути постійною або змінною. В останньому, найбільш загальному випадку температура нагріваючого або охолоджуючого теплоносія, а також температура середовища, що нагрівається (охолоджується), змінюються в часі.

     Для прикладу розглянемо процес охолодження рідини в апараті через стінку водою. Нехай на початку процесу (при τ = 0) температура рідини, яка  охолоджується, - , і до кінця процесу, тобто за час τ, її температура знижується до . Початкова температура охолоджувальної води постійна (=const), а її температура на виході  змінюється в часі. У деякий довільний момент часу, коли температура охолоджувальної рідини дорівнює t, різниця температур на вході води становить  а на виході води .

     У будь-який наступний момент часу температури   і  будуть вже іншими, тому середня різниця температур  також змінна у часі:

.

Відповідно, кількість тепла, яке відбирає вода за час dτ, складе:

.                                    (3.69)

     При масовій витраті охолоджувальної води G₂ та ж кількість тепла dQ за рівнянням теплового балансу дорівнює:

,           (3.70)

де    -  т.з. водяний еквівалент.

     Прирівнюючи праві частини виразів (3.69) і (3.70), отримаємо

,

звідки

,

причому , якщо наближено вважати середнє значення коефіцієнта теплопередачі K величиною сталою.

     З останньої залежності знаходять загальний вираз змінної кінцевої температури охолоджувального агента:

.                                 (3.71)

     Підставляючи отриманий вираз  в рівняння (3.70), отримаємо

.                               (3.72)

     Разом з тим, якщо знехтувати тепловою ємністю (водяним еквівалентом) самого апарату, як величиною дуже малою у порівнянні з тепловою ємністю рідини, яка знаходиться в ньому, то величину  можна виразити через падіння температури охолоджувальної рідини  за час dτ наступним чином:

.                        (3.73)

 де  - питома теплоємність охолоджувальної рідини.

     Прирівнюючи праві частини рівнянь (3.72) і (3.73), будемо мати

.

     Розділення змінних та інтегрування отриманого рівняння в межах зміни параметрів від 0 до τ і від  до  дає

або

.                                     (3.74)

     Користуючись рівнянням (3.74), визначають тривалість охолодження τ.

     Аналогічно можна отримати ідентичне рівняння для періодичного процесу нагрівання рідини в апараті від температури  до температури

     Початкову і кінцеву температури охолоджувальної рідини (води) знаходять на основі рівняння (3.71):

при  і початкова температура води

.                              (3.75)

при   - кінцева температура води

.                              (3.76)

     Середня температура відведеної води визначається з рівняння теплового балансу:

,

звідки

.                            (3.77)

     При нагріванні початкова, кінцева і середня температури гріючого теплоносія обчислюються за допомогою виразів (3.75) - (3.77) відповідно, в яких знак віднімання або додавання змінюється на зворотний.

     Якщо у вихідних даних заданої величиною є витрата охолоджувальної води G₂, а не поверхня тепловіддачі F, шукану величину F визначають за рівнянням
                                                         .                                            (3.78)

       Якщо в якості вихідної величини задано час τ охолодження рідини, то спочатку по рівнянню (3.74) визначають необхідну витрату води G₂, а потім шукану поверхню теплопередачі F з рівняння (3.78).