Nuqta va to‘g‘ri chiziq orasidagi masofani aniqlash

Nuqta va to‘g‘ri chiziq orasidagi masofani aniqlash.

 To‘g‘ri chiziq va unga tegishli bo‘lmagan nuqta orasidagi masofa shu nuqtadan mazkur to‘g‘ri chiziqqa tushirilgan perpendikulyarning uzunligi bilan o‘lchanadi.

a)                                                                                  b)­

125-rasm

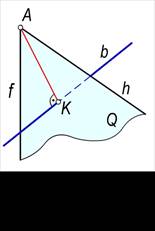
Nuqtadan to‘g‘ri chiziqqacha bo‘lgan masofani quyidagi tartibda aniqlanadi (125,a-rasm).

§  A nuqtadan b to‘g‘ri chiziqqa perpendikulyar qilib Q tekislik o‘tkaziladi: Q∋A, Q^b.

§  Berilgan b to‘g‘ri chiziqning Q tekislik bilan kesishish K nuqtasini aniqlanadi: A₁= bÇQ.

§  A va K nuqtalarni o‘zaro tutashtirilsa hosil bo‘lgan AK kesma A nuqtadan b to‘g‘ri chiziqqacha bo‘lgan masofa bo‘ladi.

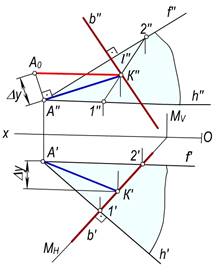
           Chizmada A(A′,A″) nuqtadan b(b′,b″) to‘g‘ri chiziqqacha bo‘lgan masofani (125,b-rasm) aniqlash uchun:

§  A nuqtadan b to‘g‘ri chiziqqa perpendikulyar Q tekislik o‘tkazish uchun bu tekislikning h(h′,h″) gorizontali va  f(f′, f ″) frontalini A(A′, A″) nuqtadan b(b′,b″) to‘g‘ri chiziqqa perpendikulyar qilib o‘tkaziladi: ya’ni h′∋A′, h′^b′ va h″∋A″, h″||Ox hamda f′∋A′, f″||Ox va f′∋A′, f″⊥b″.

§  Berilgan b to‘g‘ri chiziqning Q tekislik bilan kesishish nuqtasi K ning K′ va K″ proyeksiyalari aniqlash uchun b(b′, b″) to‘g‘ri chiziqdan yordamchi gorizontal proyeksiyalovchi M(M_H, M_V) tekislik o‘tkaziladi. Q va M tekisliklarning kesishish chizig‘i 12 =QÇM ning 1′2′, 1″2″ proyeksiyalari yasaladi.

§  Chizmada b to‘g‘ri chiziqning 12 chiziq bilan kesishgan K nuqtasining frontal proyeksiyasi K″=b″Ç1″2″ bilan aniqlanadi. Uning K′ gorizontal proyeksiyasi esa b′ chiziqqa tegishli bo‘ladi.

§  A nuqtaning A′ va A″ proyeksiyalarini K nuqtaning K′ va K″ proyeksiyalari bilan tutashtiriladi. Hosil bo‘lgan A′K′ va A″K″ kesmalar A nuqtadan b to‘g‘ri chiziqqacha masofaning proyeksiyalari bo‘ladi.

         Chizmadagi A₀K″ kesma A nuqtadan b to‘g‘ri chiziqqacha bo‘lgan masofaning haqiqiy o‘lchami bo‘lib, u to‘g‘ri burchakli DA₀A″K″ yasash yo‘li bilan aniqlangan.

         Shunindek, bu turdagi misolni A(A′, A″) nuqtadan o‘tuvchi b(b′, b″) to‘g‘ri chiziqqa perpendikulyar bo‘lgan Q tekislikni izlari orqali o‘tkazish yo‘li bilan ham yechish mumkin. [1]

Скачано с www.znanio.ru