
ПРОГРАММНЫЕ ТРЕБОВАНИЯ
|
Четверть |
4 |
|
Предмет |
Алгебра |
|
Класс |
7 |
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
|
Линейная функция и ее график. |
Функция вида у=кх+b,где х независимая переменная, у – зависимая переменная, к- угловой коэффициент не равный нулю, b – свободное число называется линейной функцией. Графиком является прямая. |
|
Линейное уравнение с двумя переменными |
Линейным уравнением с двумя переменными называют уравнение вида ах+bу=с, где х и у – переменные, а,b, с – некоторые числа. |
|
Решение системы двух линейных уравнений с двумя переменными |
Решением системы двух линейных уравнений с двумя переменными называется пара значений переменных, обращающую каждое уравнение в верное равенство. Решить систему уравнений – это значит найти все ее решения или доказать, что решений нет. |
|
Методы решения системы уравнений с двумя переменными: |
1. Графический 2. Подстановки 3. Сложения |
|
Алгоритм решения системы уравнений графическим методом: |
1) построить на одной координатной плоскости графики уравнений, входящих в систему; 2) найти координаты всех точек пересечения построенных графиков; 3) полученные пары чисел и будут искомыми решениями. |
|
Алгоритм решения системы уравнений методом подстановки: |
1)выразить из любого уравнения системы одну переменную через другую; 2)подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге; 3)решить уравнение с одной переменной, полученное на втором шаге; 4)подставить найденное значение переменной в выражение, полученное на первом шаге; 5)вычислить значение другой переменной; 6)записать ответ. |
|
Алгоритм решения системы двух линейных уравнений методом сложения: |
1)подобрать множители так, чтобы коэффициенты при одной из переменных в обоих уравнениях стали противоположными числами; 2)сложить почленно левые и правые части уравнений; 3)решить уравнение с одной переменной; 4)подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы; 5)вычислить значение другой переменной. |
ПРАКТИЧЕСКАЯ ЧАСТЬ
1. Решите систему уравнений методом подстановки:

2. Решите систему уравнений методом сложения:
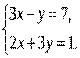
|
ОЦЕНОЧНЫЙ ЛИСТ
|
Четверть |
4 |
|
Предмет |
Алгебра |
|
Класс |
7 |
|
Обучающийся (фамилия, имя) |
|
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1. Сформулируйте определение линейного уравнения с двумя переменными __________________
____________________________________________________________________________________________________________________________________________________________________
2. Что является решением системы уравнений с двумя переменными?_________________________
__________________________________________________________________________________
__________________________________________________________________________________
3. Напишите методы решения системы уравнений с двумя переменными:_____________________
__________________________________________________________________________________
__________________________________________________________________________________
4. Напишите алгоритм решения системы способом подстановки_____________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
ПРАКТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1.
 Решите систему
уравнений методом подстановки:
Решите систему
уравнений методом подстановки:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: ______________
ЗАДАНИЯ ДОСТАТОЧНОГО И ВЫСОКОГО УРОВНЯ (2 б.)
1. Из двух сёл, расстояние между которыми равно 20 км, одновременно вышли навстречу друг другу два пешехода и встретились через 2 ч после начала движения. Найдите скорость каждого пешехода, если известно, что первый пешеход проходит за 4 ч на 12 км больше, чем второй за 3 ч.
2. Решите
систему уравнений: ![]()
|
ОЦЕНОЧНЫЙ ЛИСТ
|
Четверть |
4 |
|
Предмет |
Алгебра |
|
Класс |
7 |
|
Обучающийся (фамилия, имя) |
|
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1. Сформулируйте определение линейного уравнения с двумя переменными __________________
____________________________________________________________________________________________________________________________________________________________________
2. Что является решением системы уравнений с двумя переменными?_________________________
__________________________________________________________________________________
__________________________________________________________________________________
3. Напишите методы решения системы уравнений с двумя переменными:_____________________
__________________________________________________________________________________
__________________________________________________________________________________
4. Напишите алгоритм решения системы способом сложения_______________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
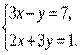 ПРАКТИЧЕСКАЯ ЧАСТЬ
(1,5 б.)
ПРАКТИЧЕСКАЯ ЧАСТЬ
(1,5 б.)
1. Решите систему уравнений методом сложения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: ______________
ЗАДАНИЯ ДОСТАТОЧНОГО И ВЫСОКОГО УРОВНЯ (2 б.)
1. Из двух городов, расстояние между которыми равно 52 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Найдите скорость каждого велосипедиста, если известно, что первый велосипедист проезжает за 3 ч на 18 км больше, чем второй за 2 ч.
2. Решите
систему уравнений: ![]()
ОТВЕТЫ:
ВАРИАНТ 1
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1. Линейным уравнением с двумя переменными называют уравнение вида ах+bу=с, где х и у – переменные, а,b, с – некоторые числа.
2. Решением системы двух линейных уравнений с двумя переменными называется пара значений переменных, обращающую каждое уравнение в верное равенство.
3. Методы решения системы уравнений с двумя переменными: графический, метод подстановки, метод сложения.
4. Алгоритм решения системы уравнений методом подстановки:
1) выразить из любого уравнения системы одну переменную через другую;
2) подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге;
3) решить уравнение с одной переменной, полученное на втором шаге;
4) подставить найденное значение переменной в выражение, полученное на первом шаге;
5) вычислить значение другой переменной;
6) записать ответ.
ПРАКТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1. (5;-2)
ЗАДАНИЯ ДОСТАТОЧНОГО И ВЫСОКОГО УРОВНЯ (2 б.)
1) 6 км/ч, 4 км/ч.
2) (2; 1)
ВАРИАНТ 2
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1. Линейным уравнением с двумя переменными называют уравнение вида ах+bу=с, где х и у – переменные, а,b, с – некоторые числа.
2. Решением системы двух линейных уравнений с двумя переменными называется пара значений переменных, обращающую каждое уравнение в верное равенство.
3. Методы решения системы уравнений с двумя переменными: графический, метод подстановки, метод сложения.
4. Алгоритм решения системы уравнений методом сложения:
1) подобрать множители так, чтобы коэффициенты при одной из переменных в обоих уравнениях стали противоположными числами;
2) сложить почленно левые и правые части уравнений;
3) решить уравнение с одной переменной;
4) подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
5) вычислить значение другой переменной.
ПРАКТИЧЕСКАЯ ЧАСТЬ (1,5 б.)
1. (2;-1)
ЗАДАНИЯ ДОСТАТОЧНОГО И ВЫСОКОГО УРОВНЯ (2 б.)
1) 14 км/ч, 12 км/ч.
2) (3; 2)
3) Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.