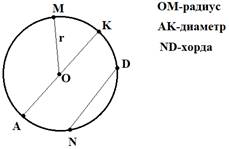
Окружность( основные свойства и теоремы)

Окружность –это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр окружности с какой-либо точкой окружности,- радиусом окружности. Из определения окружности следует, что все радиусы имеют одну и ту же длину.

Отрезок, соединяющий две точки на окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.

С окружностью связан ряд полезных теорем и следствий, перечислим их:

1.     Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

2.     Отрезки касательных, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

3.     Вписанный угол измеряется половиной дуги, на которую он опирается( угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным).

4.     Центральный угол измеряется дугой, на которую он опирается(угол с вершиной в центре окружности называется центральным).

5.     Вписанные углы, опирающиеся на одну дугу равны.

6.     Вписанный угол, опирающийся на полуокружность – прямой.

7.     Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

8.     Квадрат касательной, проведённой к окружности, равен произведению секущей этой окружности на её внешнюю часть.

Окружность в задачах всегда существует во взаимосвязи с какой-либо другой фигурой. Отсюда появляются такие понятия, как вписанная и описанная окружности.

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник - описанным около этой окружности. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Теперь перечислим ряд теорем, связанных с вписанной и описанной окружностями:

1.     В любой треугольник можно вписать окружность.

2.     В любом описанном четырехугольнике суммы противоположных сторон равны(Верно и обратное: если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность)

3.     Около любого треугольника можно описать окружность.

В любом вписанном четырёхугольнике сумма противоположных углов равно 180⁰. (Верно и обратное: если сумма противоположных углов равна 180⁰, то около него можно описать окружность