Опорный конспект по геометрии по теме «Признаки параллелограмма» (8 класс)

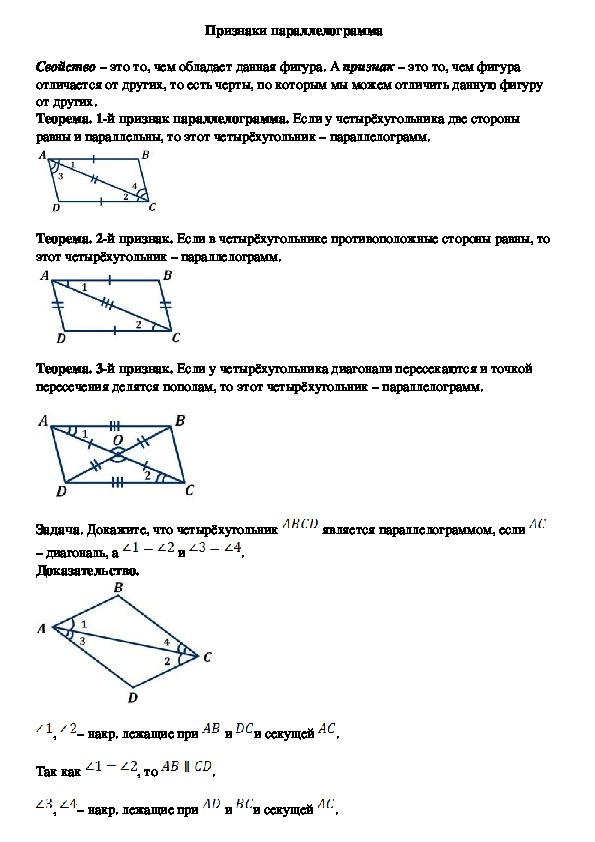
Признаки параллелограмма Свойство – это то, чем обладает данная фигура. А признак – это то, чем фигура  отличается от других, то есть черты, по которым мы можем отличить данную фигуру  от других. Теорема. 1­й признак параллелограмма. Если у четырёхугольника две стороны  равны и параллельны, то этот четырёхугольник – параллелограмм. Теорема. 2­й признак. Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм. Теорема. 3­й признак. Если у четырёхугольника диагонали пересекаются и точкой  пересечения делятся пополам, то этот четырёхугольник – параллелограмм. Задача. Докажите, что четырёхугольник  – диагональ, а  Доказательство.   и  .  является параллелограммом, если    ,  – накр. лежащие при   и  и секущей  Так как  , то  . ,  – накр. лежащие при   и  и секущей  . . Так как  параллелограмм. 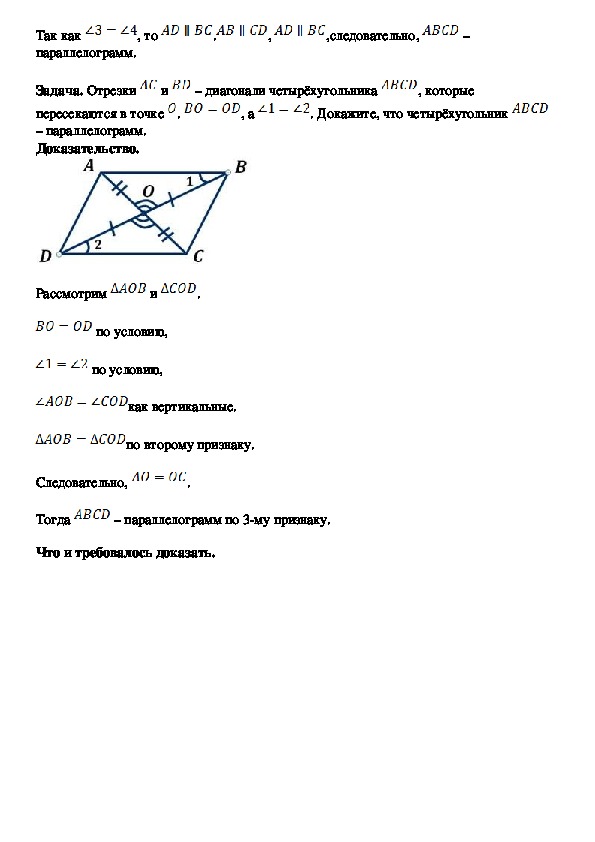, то  Задача. Отрезки   и  пересекаются в точке  – параллелограмм. Доказательство.  .  . ,  ,следовательно,   –   – диагонали четырёхугольника  , которые  , а  . Докажите, что четырёхугольник    Рассмотрим   и  .  по условию,  по условию, как вертикальные. по второму признаку. Следовательно,  . Тогда   – параллелограмм по 3­му признаку. Что и требовалось доказать.