Опорный конспект по геометрии по теме «Усеченная пирамида» (10 класс)

Усеченная пирамида

Пусть нам дана пирамида PA₁A₂…A_n. Проведем секущую плоскость β, параллельную плоскости основания пирамиды и пусть эта плоскость пересекает боковые ребра в точках B_1,B₂,…, B_n.

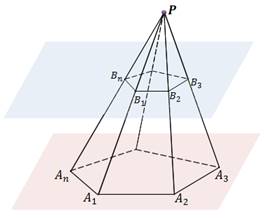
Плоскость β разбивает пирамиду на две фигуры: пирамиду PB₁B₂…B_n  и многогранник. Многогранник, гранями которого являются n-угольники A₁A₂…A_n и B₁B₂…B_n, расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂,…, A_nA₁B₁B_n называется усеченной пирамидой.

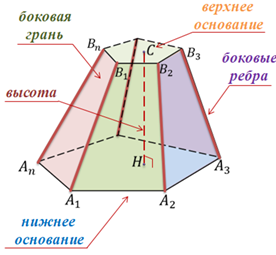
Боковые грани усеченной пирамиды – это трапеции.

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Основаниями усеченной пирамиды являются правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами.

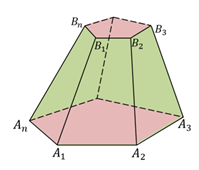
Объединение боковых граней называется боковой поверхностью усеченной пирамиды, а объединение всех граней называется полной поверхностью усеченной пирамиды.

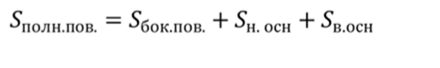
 Теорема о площади боковой поверхности правильной усеченной пирамиды.

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.

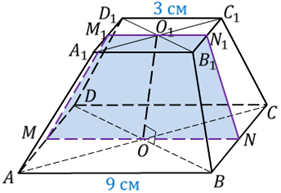
Задача. Стороны оснований правильной усеченной четырехугольной пирамиды  равны  и . Высота пирамиды равна . Найти площадь боковой поверхности.

Решение.

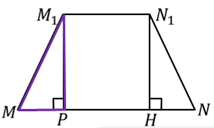
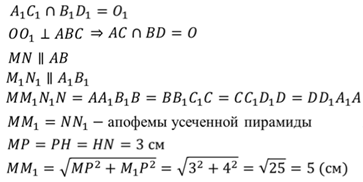
Ответ. 120 см²

Задача. Правильная треугольная пирамида  с высотой  и стороной основания равной  рассечена плоскостью , проходящей через середину  высоты  параллельно основанию . Найти площадь боковой поверхности полученной усеченной пирамиды.

Решение.

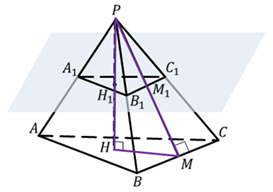
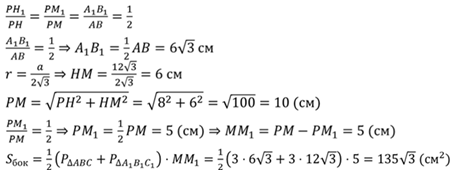
Ответ. 135 см².