
Основні визначення теорії біматрічних ігор
1) Попередні розгляди стосувалися ігор двох осіб, в яких інтереси ігроків були прямо протилежні (антагоністичні, або матричні ігри), а також позиційних ігор, що зводяться до матричних. Проте ситуації, в яких інтереси гравців хоч і не співпадають, але вже не обов'язково є протилежними, зустрічаються значно частіше.
2) Розглянемо, наприклад, конфліктну ситуацію, в якій кожний з двох учасників має наступні можливості для вибору своєї лінії поведінки:
3) гравець А – може вибрати будь-яку із стратегій А1, ... , Ат ,
4) гравець В – будь-яку із стратегій В1, …, Вn
5) При цьому всякий раз їх сумісний вибір оцінюється цілком визначено:
6)
якщо гравець А вибрав i-ю
стратегію ![]() ,
а гравець В – k-ю стратегію
,
а гравець В – k-ю стратегію ![]() ,
то у результаті виграш гравця А буде рівний деякому числу
,
то у результаті виграш гравця А буде рівний деякому числу ![]() ,
а виграш гравця В деякому, взагалі кажучи, іншому числу
,
а виграш гравця В деякому, взагалі кажучи, іншому числу![]() .
.
7) Іншими словами, всякий раз кожен з гравців отримує свій приз.
8) Послідовно перебираючи всі стратегії гравця А і всі стратегії гравця В, ми зможемо заповнити їх виграшами дві таблиці (перша з них описує виграші гравця А, а друга – виграші гравця В).
9)
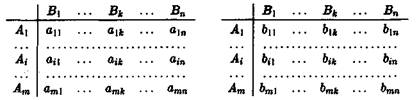
10) Зазвичай ці таблиці записують у вигляді матриць
11)
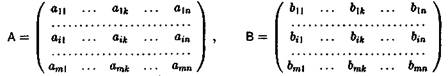
12) Тут А – платіжна матриця гравця А, а В – платіжна матриця гравця В.
13)
При виборі гравцем А i-й
стратегії, а гравцем В – k-й
стратегії їх виграші знаходяться в матрицях виплат
на перетині i-х
рядків і k-x стовпців: у матриці А це елемент ![]() , а в матриці В – елемент
, а в матриці В – елемент ![]() .
.
Таким чином, у разі, коли інтереси гравців різні (але не обов’язково протилежні), виходять дві платіжні матриці: одна – матриця виплат гравцеві А, інша – матриця виплат гравцеві В. Цьому звучить назва, яка зазвичай привласнюється подібній грі, – біматрічна.
Зауваження. Що розглядаються раніше матричні ігри, можна розглядати і як біматричні, де матриця виплат гравцеві В протилежна матриці виплат А:
![]()
![]()
У загальному випадку біматрічна гра – це гра з ненульовою сумою.
Клас біматрічних ігор значно ширше класу матричних (різноманітність нових модельованих конфліктних ситуацій вельми помітно), а, значить, неминуче збільшуються і труднощі, що встають на шляху їх успішного дозволу.
«Студент — Викладач».
Розглянемо наступну ситуацію. Студент (гравець А ) готується до заліку, який приймає Викладач (гравець В). Можно вважати, що у Студента дві стратегії – підготуватися до здачі заліку (+) і не підготуватися (-). У Викладача дві стратегії – поставити залік [+] і не поставити заліку [-].
В основу значень функцій виграшу гравців покладемо наступні мислення:


Кількісно це можливо виразити, наприклад, так
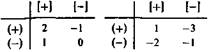
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.