Основні закони гідростатики

2.2. Основні закони гідростатики.

2.2.1.   Диференціальні рівняння рівноваги Ейлера.

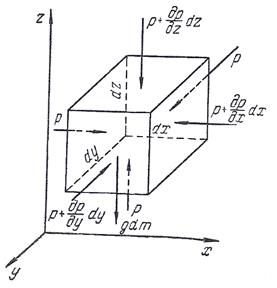      Рівняння рівноваги Ейлера визначають співвідношення між силами тиску і тяжіння, які діють на рідину в стані спокою. Гідростатичний тиск р в кожній точці об’єму рідини не залежить від розташування в просторі площі, на яку він діє, і є функцією тільки координат цієї точки p=f(x,y,z). Для визначення цієї функціональної залежності всередині рідини, що знаходиться в стані спокою, виділимо елементарний прямокутний паралелепіпед з об’ємом dV=dxdydz (де dx, dy, dz – ребра паралелепіпеда, розташовані паралельно осям координат x, y і z (рис. 2.3)

Рис.2.3. До виведення диференціальних рівнянь                                           

                         рівноваги Ейлера.

 Сила тяжіння, яка діє на паралелепіпед, виражається добутком його маси dm на прискорення вільного падіння g:

dG=g× dm=gr dxdydz.

Сила гідростатичного тиску на кожну із граней паралелепіпеда дорівнює добутку гідростатичного

 тиску р на площу відповідної грані dS:            

dP = p×dS.

      Складемо рівняння рівноваги цього паралелепіпеда у вигляді рівнянь проекцій діючих на нього об'ємних і поверхневих сил. Відповідно до основного принципу статики, сума проекцій сил, які діють на елементарний об’єм, що перебуває в рівновазі, дорівнює нулю.

      Розглянемо суму проекцій сил на вісь z. На цю вісь проектуються сили ваги, а також гідростатичного тиску на нижню й верхню грані. Сила ваги виразиться добутком його маси dm на прискорення вільного падіння g, тобто дорівнює gdm. При обраному позитивному напрямку осі z сила ваги буде проектуватися на цю вісь зі знаком мінус: . Сила гідростатичного тиску діє по нормалі на нижню грань, а її проекція на вісь z дорівнює . Якщо зміна гідростатичного тиску в даній точці в напрямку осі z дорівнює , то по всій довжині ребра dz вона складе. Тоді гідростатичний тиск на верхню грань паралелепіпеда буде дорівнювати , а проекція сили гідростатичного тиску на вісь z  відповідно               

.

Сума проекцій всіх сил на вісь z у цьому випадку буде дорівнювати:

.

     За аналогією (при відсутності проекцій сили ваги), проекції сил на осі x та y будуть дорівнювати:

,

.

     Зважаючи, що , то, після скорочення на dV, умови рівноваги елементарного паралелепіпеда приймуть вид системи рівнянь:

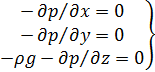                                                (2.15)

 що носять назву диференціальних рівнянь рівноваги Ейлера.

     2.2.2. Основне рівняння гідростатики.

     З диференціальних рівнянь рівноваги випливає, що тиск у рідині, що перебуває в стані спокою, змінюється тільки по вертикалі. Оскільки в системі (2.15) частинні похідні   й   дорівнюють нулю, то частинна похідна   може бути замінена на повну , тоді система перетвориться на рівняння:

.

     Розділивши обидві частини останнього рівняння на , після перетворень одержимо . Для нестисливої рідини  є сталим, тому   й, після інтегрування, одержимо:                     

                                         (2.16)

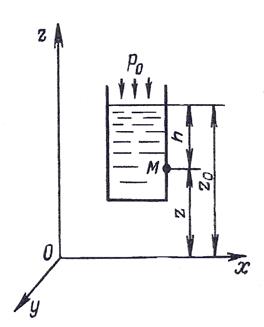      Розглянемо дві частки рідини, що перебувають у посудині на відстані z й z₀ від довільно обраної площини x-0-y (рис. 2.4). На них діє тиск відповідно p й p₀.

      На підставі рівняння (2.16) можна записати

          (2.17)

Рис. 2.4. До виводу основного рівняння

гідростатики.

Рівняння (2.16) або (2.17) є основним рівнянням гідростатики. Величину z називають нівелірною висотою, а - статичним або п’єзометричним напором. Отже, основне рівняння гідростатики можна сформулювати в такий спосіб: для кожної точки рідини, що знаходиться в стані спокою, сума нівелірної висоти й статичного напору постійна.

     Члени основного рівняння гідростатики мають певний енергетичний зміст. Так, z характеризує питому потенціальну енергію положення даної точки над площиною порівняння й тому називається також геометричним напором, а   - питому потенціальну енергію тиску в цій точці. Сума зазначених енергій являє собою загальну потенційну енергію, що приходиться на одиницю маси рідини. Отже, основне рівняння гідростатики є окремим випадком закону збереження енергії: питома потенціальна енергія у всіх точках спочиваючої рідини є величиною сталою.

     Рівняння (2.17) можна записати у вигляді

  або         (2.18)

      Рівняння (2.18) представляє собою закон Паскаля, відповідно до якого тиск, створюваний у будь-якій точці нестисливої рідини, передається однаково всім точкам її об’єму.

     На використанні основного рівняння гідростатики заснована робота гідравлічних пресів, які широко використовуються у промисловості будівельних матеріалів, наприклад при виробництві деревинно-волокнистих і склопластиковых плит, цегли напівсухого пресування й інших матеріалів.

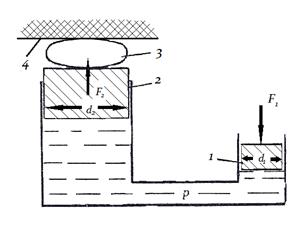
Гідравлічні преси широко використовуються й при випробуванні різного роду будівельних матеріалів. Принципова схема преса показана на рис. 2.5.

Рис.2.5. Схема роботи гідравлічного преса.

1, 2 – поршні, 3 – матеріал, 4 – плита.

     Якщо до поршня невеликого діаметра d₁ прикласти силу F₁, то, відповідно до закону Паскаля, тиск в обох циліндрах буде однаковим, а сила, що діє на поршень діаметром d₂, буде в стільки ж раз більше, у скільки площа поршня d₂ більше площі поршня d₁, а оскільки  й , то співвідношення сил в циліндрах буде пропорційно .

     Таким способом, за допомогою порівняно невеликих зусиль  в першому циліндрі, між поршнем d₂ другого циліндра і плитою створюються значні стискаючі навантаження.

      Основне рівняння гідростатики є основою і для пневматичного виміру рівня рідини в резервуарах (рис. 2.6.).

Для контролю за рівнем рідини в якомусь резервуарі 1 (наприклад, підземному), в ньому розміщують трубу 2, нижній кінець якої доходить майже до днища резервуара. Тиск над рідиною в резервуарі дорівнює р₀. По трубі подають стиснене повітря або інший газ, поступово підвищуючи його тиск, який заміряють манометром 3. Коли повітря подолає опір стовпа рідини в резервуарі і почне барботувати через рідину, тиск р, що фіксується манометром,

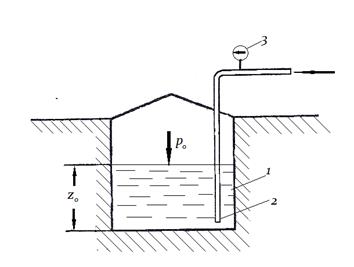
Рис.2.6. Пневматичний вимір рівня рідини в резервуарі. 1- резервуар, 2 – труба, 3 – манометр.

перестає зростати і буде дорівнювати, згідно рівнянню (2.18):

р = р₀ + rgz₀,

звідки рівень рідини в резервуарі

 .

       За величиною z₀ та відомою площею поперечного перерізу резервуара визначають об’єм рідини в ньому.