Основное свойство дробей. Сокращение дробей.

Կոտորակների հիմնական հատկությունը, կրճատում

Դիտարկենք այս երեք նկարները, որոնցում կանաչով ներկված է շրջանի կեսը:

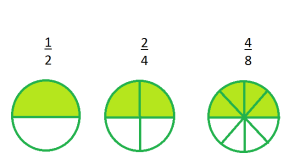
Առաջին նկարում ներկված է շրջանի 12-ը, երկրորդում՝ 24-ը և երրորդում՝ 48-ը:

Բոլոր երեք կոտորակները իրար հավասար են՝ 12=24=48, բայց դրանց համարիչներն ու հայտարարները տարբեր են: 

Նկատենք, որ առաջին կոտորակի համարիչն ու հայտարարը 2 անգամ փոքր են երկրորդի համարիչից և հայտարարից, իսկ երրորդ կոտորակի համարիչն ու հայտարարը 4 անգամ մեծ են առաջինի համարիչից և հայտարարից:

Այսինքն՝ 12=2:24:2=4:48:4 կամ 48=2⋅24⋅2=1⋅42⋅4

Սովորական կոտորակների հիմնական հատկությունը

Եթե կոտորակի համարիչն ու հայտարարը բազմապատկել կամ բաժանել միևնույն բնական թվով, ապա կստացվի տրված կոտորակին հավասար կոտորակ:

ab=a:nb:n,ab=a⋅nb⋅na,b,n∈N

Կոտորակի համարիչի ու հայտարարի բաժանումը միևնույն զրոյից տարբեր թվի, կոչվում է կոտորակի կրճատում:

Օրինակ

1216=12:416:4=34

Երկու սովորական կոտորակներ իրար հավասար են, եթե առաջին կոտորակի համարիչի և երկրորդ կոտորակի հայտարարի արտադրյալը հավասար է  առաջին կոտորակի հայտարարի և երկրորդ կոտորակի համարիչի արտադրյալին:

Օրինակ

2⋅35=70=7⋅10⇒27=1035